3-3 岩石强度理论

浅谈岩石的强度理论巖石强度反映材料的性质，岩石强度理论是研究岩石在各种应力状态下的强度准则的理论，它是岩土工程领域最重要、最基本的问题，用于岩石强度的预测和校核，确定岩石处于某种应力状态下是否破坏。

1900年莫尔教授建立了著名的莫尔-库仑理论。

100多年来，岩石强度理论的推广受到了各国工程地质学家物理学家的关注，对莫尔-库仑理论，中间主应力效应，双剪强度理论，统一强度理论进行了浅显研究。

标签：莫尔-库仑理论；中间主应力效应；双剪理论；统一强度理论1 引言岩体是由岩块和岩体结构组成的，在工程力学层次看，岩块强度反映的材料的性质，也可称之为岩石强度，岩体强度反映的是结构强度。

在工程的相关研究中，经常会遇到不同岩石强度理论选择的问题。

岩石强度理论是研究岩石在各种应力状态下的强度准则的理论。

岩石强度理论在矿山、地质、石油、水坝、桥梁、隧道的建设中应用十分广泛，用于岩石强度的预测和校核，确定岩石处于某种应力状态下是否破坏[1]。

到目前为止，在岩石的强度理论已经提出了上百个模型和准则，有关强度准则的应用研究论文则数以万计，但应用最广的强度理论是莫尔-库仑强度准则，莫尔理论中只认为最大主应力和最小主应力对材料破坏有影响，忽略了中间主应力的影响。

因此莫尔理论提出后的二十多年，它的理论一直受到检验和评论，直到20世纪30年代才开始被逐步认可才开始被逐步认可并应用到工程中来。

莫尔的单剪理论又受到各种真三轴试验的检验，并提出了各种修正的准则[2]；中间主应力效应即德鲁克-普拉格理论又受到重视被广泛用于工程及计算程序中，后续出现了双剪强度理论。

现在出现了一种全新的将单剪理论和双剪理论有机地结合起来的统一强度理论。

2 几种常见的岩石强度理论2.1莫尔-库仑理论莫尔-库仑强度准则是岩石力学中重要的强度理论之一，是以强度理论的基本思想为指导，在公式的基础上导出的。

不仅能反映岩体的碎性破坏，而且能反映其塑性破坏特征。

自1900年建立以来为人类工程结构的强度计算，设计和应用力学学科的发展做出了巨大的贡献。

岩石强度理论一、岩石的破坏类型岩石在不向的应力状态条件下，将发生不同形式的变形进而发展到破坏。

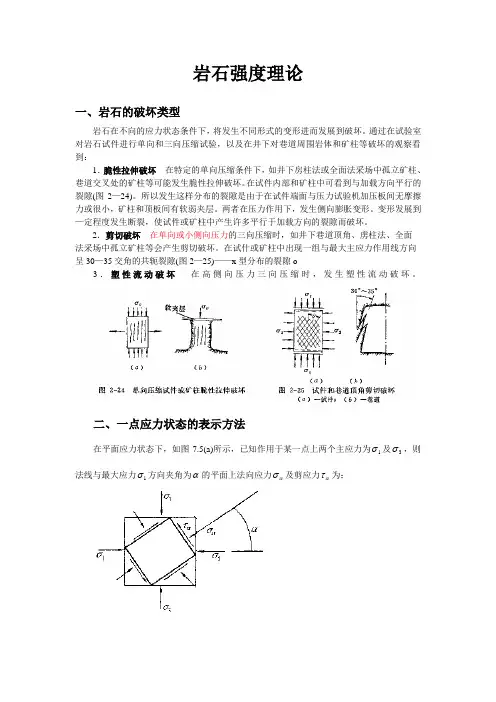
通过在试验室对岩石试件进行单向和三向压缩试验，以及在井下对巷道周围岩体和矿柱等破坏的观察看到： 1．脆性拉伸破坏 在特定的单向压缩条件下，如井下房柱法或全面法采场中孤立矿柱、巷道交叉处的矿柱等可能发生脆性拉伸破坏。

在试件内部和矿柱中可看到与加载方向平行的裂隙(图2—24)。

所以发生这样分布的裂隙是由于在试件端面与压力试验机加压板间无摩擦力或很小，矿柱和顶板间有软弱夹层。

两者在压力作用下，发生侧向膨胀变形。

变形发展到—定程度发生断裂，使试件或矿柱中产生许多平行于加载方向的裂隙而破坏。

2．剪切破坏 在单向或小侧向压力的三向压缩时，如井下巷道顶角、虏柱法、全面 法采场中孤立矿柱等会产生剪切破坏。

在试什或矿柱中出现一组与最大主应力作用线方向 呈30—35交角的共轭裂隙(图2—25)——x 型分布的裂隙o3．塑性流动破坏 在高侧向压力三向压缩时，发生塑性流动破坏。

二、一点应力状态的表示方法在平面应力状态下，如图7.5(a)所示，已知作用于某一点上两个主应力为1σ及3σ，则法线与最大应力1σ方向夹角为α的平面上法向应力ασ及剪应力ατ为：消夫角α，上式进一步变为莫尔应力圆上任一点P 的坐标(,)P ααστ代表法线与最大主应力1σ方向夹角为α的平面上法向应力ασ及剪应力ατ的大小，而莫尔应力圆上各个点的坐标代表材料中某一点不同方问平面上法向应力及剪应力的大小。

因此，材料中一点应力状态可以用一个莫尔应力圆来表。

三、强度曲线的获得当前广泛采用的是倾斜压模剪切法，是将圆柱形或立方体(5x5x5cm)试件放在两个钢制的倾斜压模之间，如图2—13所示。

而后把夹有试件的压模放在压力试验机上加压。

当施加强荷达到某一值时，试件沿预定剪切面AB 剪断。

为使加裁时在剪切破坏过程中，压模发生侧向移动不受加压板与压模端面之间摩擦力的阻碍，在压模端面与加压板之间放滚柱板。

（一）掌握岩石的物理力学指标及其试验方法；了解岩石的强度特性、变形特性、强度理论；掌握工程岩体分级标准。

1.物理力学指标（物理性质指标）
岩石的容重：单位体积内岩石(包括孔隙体积)的重量称为岩石的容重，单位（N/m³）。

干容重：就是指不含水分状态下的容重。

一般用于表示土的压实效果，干容重越大表示压实效果越好。

最大干容重：是在实验室中得到的最密实状态下的干容重。

密度：单位体积所具有的质量称为密度，公式ρ=m/V(kg/m3);单位体积所具有的重量称为容重，公式γ=G/V（N/m3)，容重等于密度和重力加速度的乘积，即γ=ρg，单位是牛/立方米（N/m³）。

岩石的比重：岩石的比重就是绝对干燥时岩石固体部分实体积(即不包含孔隙的体积)的重量与同体积水(4℃)的重量之比。

单轴压缩试验试件要求：
端部效应是指试样受压时，两端部受其与试验机承压极间摩擦力的束缚、不能自由侧向膨胀而产生的对强度试验值的影响。

渗透系数
2.物理力学指标（变形性质指标）
弹性模量
变形模量
泊松
弹性模量：单位应变的应力。

3.物理力学指标（强度性质指标）
强度指标：抗压强度、抗剪强度、抗剪断强度、抗切强度、抗拉强度
三轴压缩试验：
岩石的强度特性、变形特性、强度
岩石三轴试验要求尽可能地使岩石处于三轴受力情况下
、。

3 岩石的强度理论3.1概述岩石的应力、应变增长到一定程度，岩石就要发生破坏。

用来表示岩石破坏条件的函数（极限状态下的应力与应力函数关系（应力准则）或应变与应变函数关系（应变准则），以前者多见，即σ1=f(σ2，σ3)或τ=f(σ)）称为破坏判据或强度准则。

它是判断岩土工程是否安全的依据或条件。

强度准则的建立，应反映岩石的破坏机理。

所有研究岩石破坏的原因、过程及条件的理论，称为强度理论。

强度准则与坐标系的选取无关，因此通常用坐标不变量表示。

常见的坐标不变量包括主应力σ1、σ2、σ3，应力不变量I1、I2、I3，应力偏量不变量J1、J2、J3。

岩石强度准则反映岩石固有的属性，因此一定要来源于试验，通过对试验资料的归纳分析，而得到强度准则。

岩石由于本身性质的差异和受力条件的不同，其破坏形式复杂多变，破坏机理多种多样，因此，人们提出许多岩石的强度准则。

目前应用较广的强度理论有库仑准则、莫尔强度准则、格里菲斯准则、DRUCKER-PRAGER准则等。

3.2库仑准则最早提出的强度准则或塑性条件（1773年）。

最简单、最重要，工程中很常用。

通过摩擦试验、压剪试验或三轴试验等确定岩石的库仑准则。

库仑认为，岩石的破坏主要是剪切破坏，岩石的强度是由岩石本身的抗剪切摩擦的黏结力和剪切面上法向应力产生的摩擦力构成的。

剪切破坏面上的强度准则为：τtanσφ=c⋅+库仑准则的破坏机理是：材料为有正应力情况下的剪切破坏形式，即压剪破坏。

剪切破坏的一部分用来克服与正应力无关的黏结力c，使材料颗粒间脱离关系，另一部分用力克服与正应力成正比的摩擦力σtanϕ，使面间产生错动而破坏。

库仑准则（即上述的方程）在σ—τ坐标系中为一条倾斜的直线（图5-1），直线斜率为tgφ，直线与σ轴的夹角为φ，在τ轴上的截距为c。

图5-1 库仑准则如果岩石试件上作用着σ1和σ3，使岩石处于极限平衡状态，则由σ1、σ3确定的莫尔圆与库仑强度曲线相切，切点的位置为破坏面的位置（见上图）。

第四节岩石的强度理论•研究岩石破坏原因、过程及条件的理论—岩石的强度理论。

•将表征岩石强度条件的函数称为岩石的强度准则，•而将表征岩石破坏条件的函数称为岩石的破坏判据。

一、一点的应力状态•1、正负号的规定①压为正，拉为负；②剪应力是使物体产生逆时针转为正，反之为负；③角度以X轴正向沿逆时针方向转动所形成的夹角为正，反之为负。

•2、一点的应力的表示方法三个正应力：σx 、σy、σz，正应力的角标为正应力作用面的外法线方向；剪应力的角标为：第一个角标表示剪应力作用面的外法线方向； 第二个角标表示剪应力作用的方向。

三对剪应力： 在平面问题中，独立的应力分量只有三个，即： σx 、σy 、 τxyτxy = τyxτyz = τzyτzx = τxz3、平面问题的简化•①平面应力问题（垂直于平面方向应力为零），•如薄板问题；•②平面应变问题（垂直于平面方向应变为零）, •如大坝、路堤、隧道横断面等问题。

•不论那一种平面问题，用弹性力学的方法进行分析所得的结果，可以互相转换：平面应力计算公式中的E用 E /（1- μ2）、μ用μ/ （1- μ）代入，即可将平面应力问题的计算公式转换成平面应变问题的计算公式。

4、基本应力公式如图所示：以二维平面问题为例任意角度倾斜截面上的应力计算公式下：τxyτyxτyxτxyσxσyσyσxσnτnαατ-ασ-σ+σ+σ=σ2sin 2cos 22xy yx yx n ατ+ασ-σ=τ2cos 2sin 2xy yx n 若上述公式对求导，即可求得最大、最小主应力的表达式如下：223122xy y x yx τ+⎪⎪⎭⎫ ⎝⎛σ+σ±σ+σ=σσ应力圆点面对应——应力圆上某一点的坐标值对应着微元某一方向面上的正应力和切应力；转向对应——半径旋转方向与方向面法线旋转方向一致；二倍角对应——半径转过的角度是方向面法线旋转角度的两倍。

最大主应力与σx 的夹角可按下式求得：yx xytg σστθ-+=22此外，在分析任意角的应力状态时， 也常用最大、最小主应力表示：ασ-σ+σ+σ=σ2cos 223131n ασ-σ=τ2sin 231n莫尔应力圆的表示方法如下： 231223122⎪⎭⎫ ⎝⎛σ-σ=τ+⎪⎭⎫ ⎝⎛σ+σ-σn n )0,2(31σσ+圆心为 231σ-σ半径等于o ′σ3σ12αo στ2α-2ασ1σ1σ3σ3α-αDD ′τσσ1 σ3O DD ′强度理论：关于材料破坏原因和条件的假说。