陕西省西安市第一中学2011-2012学年高二下学期期中考

西安市第一中学2012-2013学年度第二学期期末高二年级生物（选修）试题审题人：屈胜利2分，共60分）目的基因与运载体结合目的基因的检测表达C．可定向地改造生物的遗传性状D．可能通过对天然基因库的影响对生物圈的稳态带来不利3、限制性内切酶的作用实际上就是把DNA上某些化学键打断，一种能对GAATTC专一识别的限制酶，打断的化学键是A、G与A之间的键B、G与C之间的键C、A与T之间的键D、磷酸与脱氧核糖之间的键4、下列育种所采用的生物技术或原理依次是美国科学家将生长激素基因注入小白鼠受精卵中，得到了体型巨大的“超级小鼠”；对胰岛素的改造；荷兰科学家将人乳高铁蛋白基因移植到牛体内，牛产出含高铁蛋白的牛奶；遨游过太空的青椒种子培育的“太空椒”比正常青椒大一倍①基因工程②蛋白质工程③诱变育种④杂交育种A.②③②④B.①①②③C.①②①③D.①②①④5、1976年，美国的H·Boyer教授首次将人的生长抑制素释放因子的基因转移到大肠杆菌，并获得表达。

此文中的“表达”是指该基因在大肠杆菌A．能进行DNA复制 B．能传递给细菌后代C．能合成生长抑制素释放因子 D．能合成人的生长素6、作为基因的运输工具——运载体，必须具备的条件之一及理由是A.能够在宿主细胞中稳定地保存下来并大量复制，以便提供大量的目的基因B.具有多个限制酶切点，以便于目的基因的表达C.具有某些标记基因，以使目的基因能够与其结合D.对宿主细胞无伤害，以便于重组DNA的鉴定和选择7、下列有关蛋白质工程的叙述，错误的是A．收集大量的蛋白质分子结构的信息，以便分析结构与功能之间的关系B．可以预测具有一定氨基酸序列的蛋白质的空间结构和生物功能C．根据特定的生物功能，设计蛋白质的氨基酸序列和空间结构D．根据人们的需要，直接对氨基酸的分子结构进行重新设计8、马铃薯利用它的块茎进行无性繁殖，种植的世代多了以后往往会感染病毒而减产，为此农户都希望得到无病毒的幼苗进行种植。

西安市第一中学2013-2014学年度第二学期期中高二年级数学（文科）试题参考公式： 用最小二乘法求线性回归方程系数公式1221ˆˆˆni ii ni i x y nx ybay bx x nx==-==--∑∑， 一、选择题：(本大题共10小题，每小题4分，共40分,在每小题给出的四个选项中，只有一项是符合题目要求的)1．下列有关样本相关系数的说法不正确的是（ ） Ａ．相关系数用来衡量x 与y 的之间的线性相关程度 Ｂ．1r ≤，且r 越接近0，相关程度越小 Ｃ．1r ≤，且r 越接近1，相关程度越大 Ｄ．1r ≥，且r 越接近1，相关程度越大 【答案】D【解析】由相关系数的概念可知：相关系数用来衡量x 与y 的之间的线性相关程度，1r ≤，且r 越接近0，相关程度越小，r 越接近1，相关程度越大。

2.当m<0时，复数2m i +⋅在复平面内对应的点位于( )（A ）第一象限 (B)第二象限 (C)第三象限 (D)第四象限 【答案】D【解析】因为m<0，所以复数2m i +⋅在复平面内对应的点()2,m 位于第四象限。

则y 与x 的线性回归方程为y=bx+a 必过（ ）点A ．（2，2）B ．（1.5，0）C ．（1，2）D ．（1.5，4） 【答案】D【解析】y 与x 的线性回归方程为y=bx+a 必过样本点的中心(),x y ，即点（1.5，4）。

4．“4=x ”是“042=-x x ”的（ ）.A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】A【解析】由042=-x x 得40x x ==或，所以“4=x ”是“042=-x x ”的充分不必要条件。

5．在极坐标系中，过点A （1，0）且垂直于极轴的直线的极坐标方程为（ ）A.sin ρθ=B.1ρ=C.1cos =θρD. 1sin =θρ 【答案】C【解析】如图所示，设点P （x ，y ）是所求的直线上的任意一点，∠AOP=θ． 则cos OAOPθ=，所以ρcosθ=1．6.已知：⌝p 且q 为真，则下列命题中的假命题是：（ ） ①p ；②p 或q ； ③p 且q ； ④⌝qA ．①④B ．①②③C ．①③④D ．②③④【答案】C【解析】因为⌝p 且q 为真，所以⌝p 为真命题，q 也为真命题，所以p 为假命题，p 且q 为假命题，⌝q 为假命题。

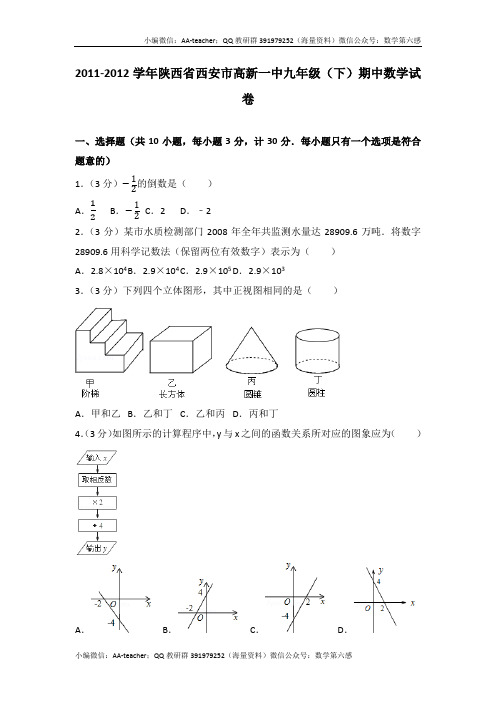
2011-2012学年陕西省西安市高新一中九年级（下）期中数学试卷一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）1．（3分）的倒数是（）A．B．C．2 D．﹣22．（3分）某市水质检测部门2008年全年共监测水量达28909.6万吨．将数字28909.6用科学记数法（保留两位有效数字）表示为（）A．2.8×104B．2.9×104C．2.9×105D．2.9×1033．（3分）下列四个立体图形，其中正视图相同的是（）A．甲和乙B．乙和丁C．乙和丙D．丙和丁4．（3分）如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（）A．B．C．D．5．（3分）“只要人人都献出一点爱，世界将变成美好的人间”．在今年的慈善一日捐活动中，市某中学八年级三班50名学生自发组织献爱心捐款活动．班长将捐款情况进行了统计，并绘制成了统计图．根据如图提供的信息，捐款金额的众数和中位数分别是（）A．20，20 B．30，20 C．30，30 D．20，306．（3分）用配方法解方程3x2﹣6x+1=0，则方程可变形为（）A．（x﹣3）2=B．3（x﹣1）2=C．（3x﹣1）2=1 D．（x﹣1）2=7．（3分）已知两圆半径分别为2和3，圆心距为d，若两圆没有公共点，则下列结论正确的是（）A．0＜d＜1 B．d＞5 C．0＜d＜1或d＞5 D．0≤d＜1或d＞58．（3分）菱形OABC在平面直角坐标系中的位置如图所示．∠AOC=45°，OC=，则点B的坐标为（）A．（，1）B．（1，）C．（+1，1） D．（1，+1）9．（3分）如图，过原点的直线l与反比例函数y=﹣的图象交于M，N两点，根据图象猜想线段MN的长的最小值是（）A．B．2 C．2 D．110．（3分）已知二次函数y=3x2﹣6x+5，若它的顶点不动，把开口反向，再沿对称轴平移，得到一条新抛物线，它恰好与直线y=mx﹣2交于点（2，4），则新抛物线的解析式为（）A．y=3x2+6x﹣4 B．y=3x2+6x+4 C．y=3x2﹣6x+4 D．y=6x2﹣3x+4二、填空题（本大题共6小题，每小题3分，共18分）11．（3分）计算：﹣（﹣3a2b3）4的结果是．12．（3分）分解因式：﹣x3﹣2x2﹣x=．13．（3分）如图，l∥m，矩形ABCD的顶点B在直线m上，则∠α=度．14．（3分）如图是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且CD=24m，OE⊥CD于点E．已测得sin∠DOE=．根据需要，水面要以每小时0.5m的速度下降，则经过小时能将水排干．15．（3分）如图，直线y=kx+b经过A（2，1），B（﹣1，﹣2）两点，则不等式1＞kx+b＞﹣2的解集为．16．（3分）如图，两同心圆的半径分别为6、10，矩形ABCD的边AB、CD分别为两圆的弦．当矩形面积取最大值时，其周长为．三、解答题（本大题共9小题，共72分．解答应写出文字说明、证明过程或演算步骤）17．（5分）解分式方程：+=1．18．（6分）如图，已知正方形ABCD，点E是AB上的一点，连接CE，以CE为一边，在CE的上方作正方形CEFG，连接DG．求证：BE=DG．19．（7分）某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况，随机抽样调查了某校初一学生一个学期参加综实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图（如图）请你根据图中提供的信息，回答下列问题：（1）求出扇形统计图中a的值，并求出该校初一学生总数；（2）分别求出活动时间为5天、7天的学生人数，并补全频数分布直方图；（3）如果该市共初一学生60000人，请你估计“活动时间不少于4天”的大约有多少人？20．（8分）如图，张明站在河岸上的G点，看见河里有一只小船沿垂直于岸边的方向划过来，此时，他测得小船C的俯角是∠FDC=30°，若张明的眼睛与地面的距离是1.5米，BG=1米，BG平行于AC所在的直线，tan∠BAE=4：3，坡长AB=10米，求小船C到岸边的距离CA的长？（参考数据：根号≈1.73，结果保留两位有效数字）21．（8分）某公司装修需用A型板材240块、B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm．现只能购得规格是150cm×30cm 的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（如图是裁法一的裁剪示意图）设所购的标准板材全部裁完，其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张，且所裁出的A、B两种型号的板材刚好够用．（1）上表中，m=，n=；（2）分别求出y与x和z与x的函数关系式；（3）若用Q表示所购标准板材的张数，求Q与x的函数关系式，并指出当x取何值时Q最小，此时按三种裁法各裁标准板材多少张？22．（8分）某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费，某顾客刚好消费200元．（1）该顾客至少可得到元购物券，至多可得到元购物券；（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．23．（8分）如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD、AC分别交于点E、F，且∠ACB=∠DCE．（1）判断直线CE与⊙O的位置关系，并证明你的结论；（2）若tan∠ACB=，BC=2，求⊙O的半径．24．（10分）已知，如图1，过点E（0，﹣1）作平行于x轴的直线l，抛物线y=x2上的两点A、B的横坐标分别为﹣1和4，直线AB交y轴于点F，过点A、B分别作直线l的垂线，垂足分别为点C、D，连接CF、DF．（1）求点A、B、F的坐标；（2）求证：CF⊥DF；（3）点P是抛物线y=x2对称轴右侧图象上的一动点，过点P作PQ⊥PO交x 轴于点Q，是否存在点P使得△OPQ与△CDF相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．25．（12分）如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．（1）求证：△MDC是等边三角形；（2）将△MDC绕点M旋转，当MD（即MD′）与线段AB交于一点E，MC（即MC′）同时与线段AD交于一点F时，点E、F和点A构成△AEF，点E、F和点M 构成△MEF，试判断△MEF的形状．△MEF的形状是三角形．（直接写出结论）（3）在（2）的条件下，探究将△MDC绕点M旋转的过程中是否存在点E、F，使△AEF的周长最小，周时△AEF的面积也最大？若存在，请说明理由并求出此时△AEF的周长最小值和△AEF的面积最大值；若不存在，请说明理由．2011-2012学年陕西省西安市高新一中九年级（下）期中数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）1．（3分）的倒数是（）A．B．C．2 D．﹣2【解答】解：﹣的倒数为﹣2．故选：D．2．（3分）某市水质检测部门2008年全年共监测水量达28909.6万吨．将数字28909.6用科学记数法（保留两位有效数字）表示为（）A．2.8×104B．2.9×104C．2.9×105D．2.9×103【解答】解：28 909.6≈2.9×104．故选：B．3．（3分）下列四个立体图形，其中正视图相同的是（）A．甲和乙B．乙和丁C．乙和丙D．丙和丁【解答】解：从物体正面看，乙和丁都是矩形．故选：B．4．（3分）如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（）A．B．C．D．【解答】解：由题意知，函数关系为一次函数y=﹣2x+4，由k=﹣2＜0可知，y 随x的增大而减小，且当x=0时，y=4，当y=0时，x=2．故选：D．5．（3分）“只要人人都献出一点爱，世界将变成美好的人间”．在今年的慈善一日捐活动中，市某中学八年级三班50名学生自发组织献爱心捐款活动．班长将捐款情况进行了统计，并绘制成了统计图．根据如图提供的信息，捐款金额的众数和中位数分别是（）A．20，20 B．30，20 C．30，30 D．20，30【解答】解：根据右图提供的信息，捐款金额的众数和中位数分别是30，30．故选：C．6．（3分）用配方法解方程3x2﹣6x+1=0，则方程可变形为（）A．（x﹣3）2=B．3（x﹣1）2=C．（3x﹣1）2=1 D．（x﹣1）2=【解答】解：原方程为3x2﹣6x+1=0，二次项系数化为1，得x2﹣2x=﹣，即x2﹣2x+1=﹣+1，所以（x﹣1）2=．故选D．7．（3分）已知两圆半径分别为2和3，圆心距为d，若两圆没有公共点，则下列结论正确的是（）A．0＜d＜1 B．d＞5 C．0＜d＜1或d＞5 D．0≤d＜1或d＞5【解答】解：若两圆没有公共点，则可能外离或内含，外离时的数量关系应满足d＞5；内含时的数量关系应满足0≤d＜1．故选：D．8．（3分）菱形OABC在平面直角坐标系中的位置如图所示．∠AOC=45°，OC=，则点B的坐标为（）A．（，1）B．（1，）C．（+1，1） D．（1，+1）【解答】解：作CD⊥x轴于点D，∵四边形OABC是菱形，OC=，∴OA=OC=，又∵∠AOC=45°∴△OCD为等腰直角三角形，∵OC=，∴OD=CD=OC×sin∠COD=OC×sin45°=1，则点C的坐标为（1，1），又∵BC=OA=，∴B的横坐标为OD+BC=1+，B的纵坐标为CD=1，则点B的坐标为（+1，1）．故选：C．9．（3分）如图，过原点的直线l与反比例函数y=﹣的图象交于M，N两点，根据图象猜想线段MN的长的最小值是（）A．B．2 C．2 D．1【解答】解：设N的横坐标是a，则纵坐标是﹣．则OM=ON=≥．则MN的最小值是2．故选：B．10．（3分）已知二次函数y=3x2﹣6x+5，若它的顶点不动，把开口反向，再沿对称轴平移，得到一条新抛物线，它恰好与直线y=mx﹣2交于点（2，4），则新抛物线的解析式为（）A．y=3x2+6x﹣4 B．y=3x2+6x+4 C．y=3x2﹣6x+4 D．y=6x2﹣3x+4【解答】解：y=3x2﹣6x+5=3（x﹣1）2+2，则抛物线的对称轴为直线x=1，顶点坐标为（1，2），设新抛物线解析式为y=﹣3（x﹣1）2+2+t，把（2，4）代入得﹣3•（2﹣1）2+2+t=4，解得t=5，所以新抛物线解析式为y=﹣3（x﹣1）2+2+5=﹣3x2+6x+4．故选：B．二、填空题（本大题共6小题，每小题3分，共18分）11．（3分）计算：﹣（﹣3a2b3）4的结果是﹣81a8b12．【解答】解：﹣（﹣3a2b3）4=﹣（﹣3）4a8b12=﹣81a8b12．12．（3分）分解因式：﹣x3﹣2x2﹣x=﹣x（x+1）2．【解答】解：﹣x3﹣2x2﹣x，=﹣x（x2+2x+1），=﹣x（x+1）2．13．（3分）如图，l∥m，矩形ABCD的顶点B在直线m上，则∠α=25度．【解答】解：延长DC交直线m于E．∵l∥m，∴∠CEB=65°．在Rt△BCE中，∠BCE=90°，∠CEB=65°，∴∠α=90°﹣∠CEB=90°﹣65°=25°．14．（3分）如图是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且CD=24m，OE⊥CD于点E．已测得sin∠DOE=．根据需要，水面要以每小时0.5m的速度下降，则经过10小时能将水排干．【解答】解：Rt△OED中，DE=CD=12，sin∠DOE=，∴OD=DE÷sin∠DOE=12÷=13．由勾股定理得：OE===5．∴将水排干需要的时间为：5÷0.5=10（小时）．15．（3分）如图，直线y=kx+b经过A（2，1），B（﹣1，﹣2）两点，则不等式1＞kx+b＞﹣2的解集为2＞x＞﹣1．【解答】解：∵直线y=kx+b经过A（2，1），B（﹣1，﹣2）两点，∴，解得，则该直线方程为y=x﹣1，∴不等式1＞kx+b＞﹣2变为1＞x﹣1＞﹣2，解得2＞x＞﹣1，故答案为：2＞x＞﹣1．16．（3分）如图，两同心圆的半径分别为6、10，矩形ABCD的边AB、CD分别为两圆的弦．当矩形面积取最大值时，其周长为．【解答】解：连接OA，OD，作OP⊥AB于P，OM⊥AD于M，ON⊥CD于N，过D作DE⊥OA于E，∵矩形APND的面积是AD×OM，△AOD的面积=AD×OM，矩形BCNP的面积是OM×BC，∴矩形的面积是三角形AOD的面积的4倍，在Rt△DEO中，DE=OD×sin∠DOE=OD×sin∠AOD，=×OA×OD×sin∠AOD，∵OA，OD的长是定值，S△AOD∴要使矩形ABCD的面积最大，必须△AOD的面积最大，即当∠AOD的正弦值最大时，三角形AOD的面积最大，∵当∠AOD≤90°时，正弦值随角度的增大而增大，最大，即当∠AOD=90°，S△AOD则勾股定理得：AD==2，根据三角形的面积公式求得OM=，即AB=．则矩形ABCD的周长是2（2+）=，故答案为：．三、解答题（本大题共9小题，共72分．解答应写出文字说明、证明过程或演算步骤）17．（5分）解分式方程：+=1．【解答】解：去分母得：x（x+1）﹣3x=x2﹣1，去括号得：x2+x﹣3x=x2﹣1，移项合并得：2x=1，解得：x=，经检验x=是分式方程的解．18．（6分）如图，已知正方形ABCD，点E是AB上的一点，连接CE，以CE为一边，在CE的上方作正方形CEFG，连接DG．求证：BE=DG．【解答】证明：∵在正方形CEFG中CG=CE，又∵在正方形ABCD中BC=CD，∠B=∠CDG=90°在直角△CBE与直角△CDG中，，∴△CBE≌△CDG（HL），∴BE=DG．19．（7分）某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况，随机抽样调查了某校初一学生一个学期参加综实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图（如图）请你根据图中提供的信息，回答下列问题：（1）求出扇形统计图中a的值，并求出该校初一学生总数；（2）分别求出活动时间为5天、7天的学生人数，并补全频数分布直方图；（3）如果该市共初一学生60000人，请你估计“活动时间不少于4天”的大约有多少人？【解答】解：（1）总人数是：20÷10%=200（人），则参加综实践活动的天数是6天的所占的百分比是：×100%=15%，则a=100%﹣30%﹣15%﹣10%﹣5%﹣15%=25%；（2）25%×200=50（人），5%×200=10（人）．；（3）10%+15%=25%，60000﹣60000×25%=45000（人）．故估计“活动时间不少于4天”的大约有45000人．20．（8分）如图，张明站在河岸上的G点，看见河里有一只小船沿垂直于岸边的方向划过来，此时，他测得小船C的俯角是∠FDC=30°，若张明的眼睛与地面的距离是1.5米，BG=1米，BG平行于AC所在的直线，tan∠BAE=4：3，坡长AB=10米，求小船C到岸边的距离CA的长？（参考数据：根号≈1.73，结果保留两位有效数字）【解答】解：过点B作BE⊥AC于点E，延长DG交CA于点H，得Rt△ABE和矩形BEHG．tan∠BAE==，∵AB=10m，∴BE=8，AE=6，DG=1.5，BG=1，∴DH=DG+GH=1.5+8=9.5，AH=AE+EH=6+1=7．在Rt△CDH中，∵∠C=∠FDC=30°，DH=9.5，tan30°==，∴CH=9.5．又∵CH=CA+7，即9.5=CA+7，∴CA≈9.45≈9.5（米）．答：CA的长约是9.5米．21．（8分）某公司装修需用A型板材240块、B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm．现只能购得规格是150cm×30cm 的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（如图是裁法一的裁剪示意图）设所购的标准板材全部裁完，其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张，且所裁出的A、B两种型号的板材刚好够用．（1）上表中，m=0，n=3；（2）分别求出y与x和z与x的函数关系式；（3）若用Q表示所购标准板材的张数，求Q与x的函数关系式，并指出当x取何值时Q最小，此时按三种裁法各裁标准板材多少张？【解答】解：（1）按裁法二裁剪时，2块A型板材块的长为120cm，150﹣120=30，所以无法裁出B型板，按裁法三裁剪时，3块B型板材块的长为120cm，120＜150，而4块块B型板材块的长为160cm＞150cm，所以无法裁出4块B型板；∴m=0，n=3；（2）由题意得：共需用A型板材240块、B型板材180块，又∵满足x+2y=240，2x+3z=180，∴整理即可求出解析式为：y=120﹣x，z=60﹣x；（3）由题意，得Q=x+y+z=x+120﹣x+60﹣x．整理，得Q=180﹣x．由题意，得解得x≤90．[注：事实上，0≤x≤90且x是6的整数倍]由一次函数的性质可知，当x=90时，Q最小．由（2）知，y=120﹣x=120﹣×90=75，z=60﹣x=60﹣×90=0；故此时按三种裁法分别裁90张、75张、0张．22．（8分）某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费，某顾客刚好消费200元．（1）该顾客至少可得到10元购物券，至多可得到50元购物券；（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．【解答】解：（1）10，50；（2）解法一（树状图）：从上图可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，因此P（不低于30元）=；解法二（列表法）：（以下过程同“解法一”）23．（8分）如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD、AC分别交于点E、F，且∠ACB=∠DCE．（1）判断直线CE与⊙O的位置关系，并证明你的结论；（2）若tan∠ACB=，BC=2，求⊙O的半径．【解答】解：（1）直线CE与⊙O相切．…（1分）理由如下：∵四边形ABCD是矩形，∴BC∥AD，∠ACB=∠DAC；又∵∠ACB=∠DCE，∴∠DAC=∠DCE；连接OE，则∠DAC=∠AEO=∠DCE；∵∠DCE+∠DEC=90°∴∠AE0+∠DEC=90°∴∠OEC=90°，即OE⊥CE．又OE是⊙O的半径，∴直线CE与⊙O相切．…（5分）（2）∵tan∠ACB==，BC=2，∴AB=BC•tan∠ACB=，∴AC=；又∵∠ACB=∠DCE，∴tan∠DCE=tan∠ACB=，∴DE=DC•tan∠DCE=1；方法一：在Rt△CDE中，CE==，连接OE，设⊙O的半径为r，则在Rt△COE中，CO2=OE2+CE2，即=r2+3 解得：r=方法二：AE=AD﹣DE=1，过点O作OM⊥AE于点M，则AM=AE=在Rt△AMO中，OA==÷=…（9分）24．（10分）已知，如图1，过点E（0，﹣1）作平行于x轴的直线l，抛物线y=x2上的两点A、B的横坐标分别为﹣1和4，直线AB交y轴于点F，过点A、B分别作直线l的垂线，垂足分别为点C、D，连接CF、DF．（1）求点A、B、F的坐标；（2）求证：CF⊥DF；（3）点P是抛物线y=x2对称轴右侧图象上的一动点，过点P作PQ⊥PO交x 轴于点Q，是否存在点P使得△OPQ与△CDF相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．【解答】解：（1）方法一：如图1，当x=﹣1时，y=；当x=4时，y=4∴A（﹣1，）（1分）B（4，4）（2分）设直线AB的解析式为y=kx+b（3分）则解得∴直线AB的解析式为y=x+1（4分）当x=0时，y=1∴F（0，1）（5分）方法二：求A、B两点坐标同方法一，如图2，作FG⊥BD，AH⊥BD，垂足分别为G、H，交y轴于点N，则四边FOMG和四边形NOMH均为矩形，设FO=x（3分）∵△BGF∽△BHA∴∴（4分）解得x=1∴F（0，1）（5分）（2）证明：方法一：在Rt△CEF中，CE=1，EF=2，根据勾股定理得：CF2=CE2+EF2=12+22=5，∴CF=（6分）在Rt△DEF中，DE=4，EF=2∴DF2=DE2+EF2=42+22=20∴DF=2由（1）得C（﹣1，﹣1），D（4，﹣1）∴CD=5∴CD2=52=25∴CF2+DF2=CD2（7分）∴∠CFD=90°∴CF⊥DF（8分）方法二：由（1）知AF=，AC=∴AF=AC（6分）同理：BF=BD∴∠ACF=∠AFC∵AC∥EF∴∠ACF=∠CFO∴∠AFC=∠CFO（7分）同理：∠BFD=∠OFD∴∠CFD=∠OFC+∠OFD=90°即CF⊥DF（8分）（3）存在．解：如图3，作PM⊥x轴，垂足为点M（9分）又∵PQ⊥OP∴Rt△OPM∽Rt△OQP∴∴（10分）设P（x，x2）（x＞0），则PM=x2，OM=x①当Rt△QPO∽Rt△CFD时，（11分）∴解得x=2∴P1（2，1）（12分）②当Rt△OPQ∽Rt△CFD时，=2（13分）∴=2解得x=8∴P2（8，16）综上，存在点P1（2，1）、P2（8，16）使得△OPQ与△CDF相似．（14分）25．（12分）如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．（1）求证：△MDC是等边三角形；（2）将△MDC绕点M旋转，当MD（即MD′）与线段AB交于一点E，MC（即MC′）同时与线段AD交于一点F时，点E、F和点A构成△AEF，点E、F和点M 构成△MEF，试判断△MEF的形状．△MEF的形状是等边三角形．（直接写出结论）（3）在（2）的条件下，探究将△MDC绕点M旋转的过程中是否存在点E、F，使△AEF的周长最小，周时△AEF的面积也最大？若存在，请说明理由并求出此时△AEF的周长最小值和△AEF的面积最大值；若不存在，请说明理由．【解答】解：（1）连接BD，∵AD=AB，∴∠ADB=∠ABD，又∵AD∥BC，∴∠ADB=∠DBC，∴∠ADB=∠DBC，∵在等腰梯形ABCD中，∠B=∠C=60°，∴∠ABD=∠DBC=30°，∴∠BDC=90°，∴DC=MC，∴△MDC是等边三角形；（2）解：连接AM，如图2，由（1）平行四边形ABMD是菱形，△MAB，△MAD和△MC′D′是等边三角形，∠BMA=∠BME+∠AME=60°，∠EMF=∠AMF+∠AME=60°，∴∠BME=∠AMF，在△BME与△AMF中，，∴△BME≌△AMF（ASA），∴BE=AF，ME=MF，AE+AF=AE+BE=AB，∵∠EMF=∠DMC=60°，故△EMF是等边三角形；（3）过D作DN⊥BC于N，如图2∵∠C=60°，∴∠CDN=30°，∵CD=2，∴CN=1，∴由勾股定理得：DN=，∵△EMF是等边三角形，∴EF=MF，∵MF的最小值为点M到AD的距离等于DN的长，即是，即EF的最小值是，△AEF的周长=AE+AF+EF=AB+EF，△AEF的周长的最小值为2+，此时△AEF面积=S平行四边形AMBN﹣S△EMF，即×2×﹣×××=．答：存在，△AEF的周长的最小值为2+，△AEF的面积最大值为．。

西安市第一中学2011-2012学年第二学期期中考试高一生物试题一、单项选择题（40*1.5=60分）1、下列关于孟德尔研究遗传规律获得成功原因的叙述，错误．．的是（ ） A ．科学地设计实验程序，提出假说并进行验证B ．正确地选用豌豆作为实验材料C ．先分析多对相对性状，后分析一对相对性状D ．运用统计学方法分析实验结果2、下列各组性状中，属于相对性状的是（ ）A ．豌豆的高茎与绿色豆荚B ．羊的黑毛与兔的白毛C ．棉花的细绒与长绒D ．人的双眼皮与单眼皮3、纯种甜玉米和纯种非甜玉米间行种植，收获时发现甜玉米果穗上有非甜玉米籽粒，而非甜玉米果穗上却无甜玉米籽粒。

原因是（ ）A ．甜是显性性状B ．非甜是显性性状C ．显性的相对性D ．环境引起的变异4、用纯种的黄色圆粒豌豆与绿色皱粒豌豆杂交，F 1全部是黄色圆粒，F 1自交的F 2，在F 2中杂合的绿色圆粒有4000个，推测纯合的黄色皱粒有（ ）A 、2000 个B 、4000个C 、6000个D 、8000个5、两株高茎豌豆杂交，后代高茎和矮茎的比例如图所示，则亲本的基因型为（ ）A ．GG×ggB ．GG×GgC ．Gg×GgD ．gg×gg6、牡丹的花色种类多种多样，其中白色的是不含花青素，深红色的含花青素最多，花青素含量的多少决定着花瓣颜色的深浅，由两对独立遗传的基因（A 和a ，B 和b ）所控制；显性基因A 和B 可以使花青素含量增加，两者增加的量相等，并且可以累加。

若一深红色牡丹同一白色牡丹杂交，就能得到中等红色的个体，若这些个体自交其子代将出现花色的种类和比例分别是（ ）A.3种；9：6：1B.4种；9：3：3：1C.5种；1：4：6：4：1D.6种；1：4：3：3：4：17、基因型为AAbbCC 与aaBBcc 的小麦进行杂交，这三对等位基因分别位于非同源染色体上，F 1杂种形成的配子种类数和F 2的基因型种类数分别是（ ）高矮A.4和9 B．4和27 C．8和27 D．32和818、据下图，下列选项中不遵循基因自由组合规律的是（）9、下图是某生物的精细胞，据图判断来自同一个次级精母细胞的是（）A．①②B．②④C．③⑤D．①④10、基因型为AA和aa的水稻进行杂交得F1代，让F1连续自交，F5代中杂合子的比例为（）A.1/32B. 1/16C.3/4 D．3/811、香豌豆中，当C、R两个显性基因都存在时，花呈红色。

西安市第一中学2011～2012学年度第二学期期中考试高一化学（必修2 ）试题相关原子量：N-14 O—16 S---32第I卷选择题（共50分）一、选择题（本题包括20小题，1---10题每小题2分，11---20题每小题3分，共50分，每小题只有一个．．．．选项符合题意）1、下列叙述错误的．．．是A．13C和14C属于同一种元素，它们互为同位素B．1H和2H是不同的核素，它们的质子数相等C．14C和14N的质量数相等，它们的中子数不等D．6Li和7Li的电子数相等，中子数也相等2、一种“即食即热型快餐”适合外出旅行时使用。

其内层是用铝箔包裹的、并已加工好的真空包装食品，外层则是分别包装的两包化学物质，使用时拉动预留在外的拉线，使这两种化学物质反应，此时便可对食物进行加热，这两包化学物质最合适的选择是A．浓硫酸与水 B．生石灰与水C．熟石灰与水 D．氯化钠与水3、下列含有非极性键的离子化合物是A．CH3COOH B．NaOH C．Na2O2 D．MgCl24、下列过程中，共价键被破坏的是A．碘升华 B．溴蒸汽被木炭吸附C．NaCl溶于水 D．HCl气体溶于水5、下列各对原子序数的原子不能以共价键结合成化合物的是A．9和1 B．14和17 C．11和1 D．6和176、下列各图中，表示正反应是放热反应的图是7、下列各组中的性质比较，正确的是①酸性：HClO4>HBrO4>HIO4②碱性：Ba(OH)2>Ca(OH)2>Mg(OH)2③稳定性：HCl>H2S>PH3④还原性：F－>Cl－>Br－A．①②④B．②③④C．①②③D．都正确8、某元素原子核内质子数为m,中子数为n,则下列论断正确的是A．不能由此确定该元素的原子量 B．这种元素的原子量为m+nC．若碳原子质量为Wg,此原子的质量为（m+n）WgD．核内中子的总质量小于质子的总质量9、甲、乙是周期表中同一主族的两种元素，若甲的原子序数为x，则乙的原子序数不可能是A．x+26 B．x+6 C．x+16 D．x+1010、下列反应中生成物总能量高于反应物总能量的是A．碳酸钙受热分解 B．乙醇燃烧C．铝粉与氧化铁粉末反应 D．氧化钙溶于水11、X、Y、Z三种短周期元素，X元素的原子最外层只有一个电子，Y元素的原子M电子层的电子数为K、L上电子总数的一半，Z元素的原子L层电子数比Y原子L层电子数少2个，由这三种元素组成的常见化合物的化学式不可能是A．X3YZ4 B．XYZ3 C．X3YZ3 D．X2YZ412、周期元素X、Y、Z的原子序数依次递增，其原子最外层电子数之和为13。

2015-2016学年陕西省西安市第一中学高二下学期期中考试数学理试题一、 选择题（本大题共12小题，每小题3分，共36分）1. 若复数2()12bib R i-∈+的实部与虚部互为相反数，则b =（ ） A.2 B. 23 C. 23- D. 22．用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，假设正确的是（ ）A ． 假设三内角都不大于60度B ． 假设三内角都大于60度C ． 假设三内角至多有一个大于60度D ． 假设三内角至多有两个大于60度 3． 若000(2)()lim1x f x x f x x∆→+∆-=∆，则0()f x '等于（ ）A ．2B ．－2C ．12 D ．12- 4．已知2()2(1)6f x x xf '=+-，则(1)f '等于（ ）A ．4B ．-2C ．0D ． 25．利用数学归纳法证明1n ＋1n ＋1＋1n ＋2＋ (12)<1(n ∈N *，且n ≥2)时，第二步由k 到k ＋1时不等式左端的变化是( )A ．增加了12k ＋1这一项B ．增加了12k ＋1和12k ＋2两项C ．增加了12k ＋1和12k ＋2两项，同时减少了1k 这一项D ．以上都不对6. 若在区间(,)a b 内，()0f x '>，且()0f a ≥，则在(,)a b 内有( )A ．()0f x >B ．()0f x <C ．()0f x =D ．不能确定7. 设P 为曲线2:23C y x x =-+上的点，且曲线C 在点P 处切线倾斜角的取值范围为[0,]4π，则点P 横坐标的取值范围为 （ ） A ．1[1,]2-- B ．[1,0]-C ．[0,1]D ．3[1,]28.观察下列的图形中小正方形的个数，则第6个图中有________个小正方形，第n 个图中有________个小正方形( )A ．28，1)(2)2n n ++（B.14，1)(2)2n n ++（C ．28， 2nD.12，2)2n n +（9.()22sin cos d x x x ππ-+⎰的值为( )A ．0B ．4πC ．2D ．410. 函数()f x 的定义域为(),a b ，导函数()f x '在(),a b 内的图像如图所示， 则函数()f x 在(),a b 内有极小值点( ) A ．1个 B ．2个 C ．3个 D ．4个 11. 12ex y =在点2(4e )，处的切线与坐标轴所围三角形的面积为（ ）A ．29e 2B ．24eC ．22eD ．2e12．已知二次函数2()f x ax bx c =++的导数为'()f x ，'(0)0f >，对于任意实数x 都有()0f x ≥，则(1)'(0)f f 的最小值为( ) A ．3 B ．52 C ．2 D ．32二、填空题（本大题共5小题，每小题4分，共20分）13. 物体的运动方程是s=－31t 3＋2t 2－5,则物体在t=3时的瞬时速度____________________. 14．用火柴棒按下图的方法搭三角形：按图示的规律搭下去，则所用火柴棒数n a 与所搭三角形的个数n 之间的关系式可以是 . 15．若函数()()2f x x x c =-在2x =处有极大值，则常数c 的值为_________；16．半径为r 的圆的面积2()s r r π=，周长()2C r r π=，若将r 看作(0，＋∞)上的变量，则2()'2r r ππ=①，①式用语言可以叙述为：圆的面积函数的导数等于圆的周长函数．对于半径为R 的球，若将R 看作(0,)+?上的变量，请写出类比①的等式：____________________．上式用语言可以叙述为_________________________．17．函数g (x )＝ax 3＋2(1－a )x 2－3ax 在区间⎝ ⎛⎭⎪⎫－∞，a 3内单调递减，则a 的取值范围是________．三、解答题（本大题共4小题，共44分）18. （本小题10分）已知数列{}n a 的前n 项和*1()n n S na n =-∈N ．（1） 计算1a ，2a ，3a ，4a ；（2） 猜想n a 的表达式，并用数学归纳法证明你的结论．19．（本小题10分）统计表明，某种型号的汽车在匀速行驶中每小时的耗油量y （升）关于行驶速度x （千米/小时）的函数解析式可以表示为：3138(0120)12800080y x x x =-+<≤．已知甲、乙两地相距100千米（Ⅰ）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？ （II ）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？20. （本小题12分）已知函数44()ln f x ax x bx c =+-⋅在1x =处取得极值c --3，(1)试求实数,a b 的值； (2)试求函数()f x 的单调区间；(3)若对任意0x >,不等式22)(c x f -≥恒成立,求实数c 的取值范围. 21．（本小题12分） 已知函数f (x )＝ln x －ax 2＋(2－a )x . (1)讨论f (x )的单调性；(2)设a ＞0，证明：当0＜x ＜1a 时，f (1a ＋x )＞f (1a－x )；(3)若函数y ＝f (x )的图象与x 轴交于A ，B 两点，线段AB 中点的横坐标为x 0， 证明：f ′(x 0)＜0. 附加题:22．（不计入总分）设函数f （x ）=x axxln 1+-在[1，+∞)上为增函数。

陕西省西安市第一中学2013-2014学年高二下学期期中考试语文试题一、积累运用（共20分，1-7题，每小题2分，14分；8题6分）1、下列加点字注音无误的一项是（A、箨．龙（ｚã）踌躇．（c h ú）满志歌数阕．（q uâ）B、砍斫．（ｚｈｕó）庖．（p áｏ）丁解牛麾．（h uī）下C、沦丧．（ｓàｎｇ）兔起鹘．（ｇǔ）落刈．（yì）旗D、缣．（ｊｉāｎ）素亲密无间．（ｊｉàｎ）曝．（b àｏ）晒2、对下列句中的词语的解释，不正确的一项是（）A、袜材当萃于子矣萃：聚集。

B、田父绐曰“左”绐：欺骗C、月落庭空影许长许：多，表概数D、被十余创被：遭受。

3、下列句中没有通假字的一项是（）A、将成家而致汝B、与可没于陈州C、技盖至此乎？D、少纵即逝矣4、下列各组句子中，加点词的意义和用法不相同的一组是（）A、①轮扁，斫轮者也，而读书者与．之②夫子喟然叹曰：“吾与．点也。

”B、①今画者乃．节节而为之②项王乃．复引兵而东C、①与可无以．．至千里．．答，则曰②故不积跬步，无以D、①发．函得诗，失笑喷饭满案②窥父不在，窃发．盆5、下列词语解释有误的一项是（）A、是．（这）疾易传染为上昌言．．（直说）B、俾．（使）困苦不可忍而轻者、无罪者罹．（遭受）其毒C、行刑者先俟．（等候）于门外有郭四者，凡．（总共）四杀人D、贫亦罄．（尽）衣装傥．（风流倜傥）仁人君子为上昌言6、下列加点词语与现代汉语意义相同的一项是（）A、仇温柔．．与死者并踵顶而卧．．也B、生人C、吾辈无生理．．以警其余．．矣D、唯极贫无依，则械系不稍宽，为标准7、下列加点词语词类活用情况判断正确的一项是（）①惟大辟无可要，然犹质．其首②贫者席．地而卧③予我千金，吾生．若④舞．幽壑之潜蛟，泣．孤舟之嫠妇A、①和②相同③和④也相同B、①和②不同③和④相同C、①和②相同③和④不同D、①和②不同③和④也不同8、诗文原句和文学常识填空（6分）（1）六国破灭，非兵不利，战不善，。

2015-2016学年陕西省西安市第一中学高二下学期期中考试数学文试题一、选择题（每题3分，共36分，在每小题给出的四个选项中，只有一项是符合要求的） 1．在复平面内，复数2z i =+对应的点在（ ）A ． 第一象限B ．第二象限C ．第三象限D ．第四象限 2.已知复数 z = 2 -i ，则z ⋅z 的值为（ ） A.5 B.5 C.3 D.33.从甲乙丙三人中任选两名代表，甲被选中的概率为（ ） A ． B ． C ． D ．14.如图是根据x ，y 的观测数据()i i y x ,（i=1，2，，10）得到的散点图，由这些散点图可以判断变量x ，y 具有线性相关关系的图是 （ ）A ．①②B ．①④C ．②③D ．③④ 5.212(1)ii +=-（ ） A.112i --B.112i -+C.112i +D.112i - 6．用反证法证明命题“设a ，b 为实数，则方程x 2+ax+b=0至少有一个实根”时，要做的假设是（ ） A ． 方程x 2+ax+b=0恰好有两个实根 B ．方程x 2+ax+b=0至多有一个实根 C ．方程x 2+ax+b=0至多有两个实根 D ．方程x 2+ax+b=0没有实根7．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．根据收集到的数据(如下表)，由最小二乘法求得回归直线方程 y ^＝0.67x ＋54.9.表中一个数据模糊不清，请你推断出该数据的值为( )A ．75B ．62C ．68D ．818．如图是今年元宵花灯展中一款五角星灯连续 旋转闪烁所成的三个图形，照此规律闪烁，下一个 呈现出来的图形是( )9．盒中装有10个乒乓球，其中6个新球，4个旧球，不放回地依次取出2个球使用，在第一次取出新球的条件下，第二次也取到新球的概率为（ ） A ．B ．C ．D ．10. 右边程序框图的算法思路来源于我国古代数学名著 《九章算术》中的“更相减损术”,执行该程序框图, 若输入的,a b 分别为14,18,则输出的a 为（ ）A.0B.2C.4D.1411. 设复数(1)z x yi =-+(,)x y R ∈，若||1z ≤，则y x ≥的概率（ ） A ．3142π+ B ． 112π+ C ．1142π- D ． 112π- 12.执行如右图的程序框图，如果输入的,x y R ∈，那么输出的S 的最大值为（ ） A.0 B.1 C.2 D.3二、填空题：（本大题共5小题，每小题4分，共20分，把最简答案填在答题卡横线上） 13. 观察下列等式: 23(11)21(21)(22)213(31)(32)(33)2135+=⨯++=⨯⨯+++=⨯⨯⨯……照此规律, 第n 个等式可为 14.复数()1i i +的虚部为 ．15. 在极坐标系中，ρ＝4sin θ是圆的极坐标方程，则点A (4，π6)到圆心C 的距离是________．16．直线⎩⎨⎧x ＝－2－2t ，y ＝3＋2t(t 参数)上与点A (－2,3)的距离等于2的点的坐标是________．17.甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服种选择1种，则他们选择相同颜色运动服的概率为_______.三．解答题（本大题共4小题，44分.请写出必要的文字说明、证明过程或演算步骤）． 18.(10分) 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x （吨）与相应的生产能耗y （吨标准煤）的几组对照数据： x 3 4 5 6 y2.5344.5（1）请根据上表提供的数据，用最小二乘法求出y 关于x 的线性回归方程∧∧∧+=a x b y ；（2）已知该厂技改前50吨甲产品的生产能耗为45吨标准煤．试根据（1）求出的线性回归方程，预测生产50吨甲产品的生产能耗比技改前降低了多少吨标准煤？（参考公式：∑∑==∧--=ni in i i i x n xy x n y x b 12_21__)(，参考数值：3×2.5＋4×3＋5×4＋6×4.5＝66.5）19.（10分）用适合的方法证明下列命题： （1）112(2)b b b b b +-<---≥ （2）若a ，b 为两个不相等的正数，且a+b=2，则＞2．20.（12分）为贯彻“咬文嚼字抓理解，突出重点抓记忆”的学习思想．某校从高一年级和高二年级各选取100名同学进行现学段基本概念知识竞赛．图(1)和图(2)分别是对高一年级和高二年级参加竞赛的学生成绩按[40,50)，[50,60)，[60,70)，[70,80]分组，得到的频率分布直方图．(1)分别计算参加这次知识竞赛的两个年级学生的平均 成绩；(注：统计方法中， 同一组数据常用该组区间的 中点值作为代表)(2)完成下面2×2列联表，并回答是否有99%的把握认为“两个年级学生现学段对基本知识的了解有差异”？成绩小于60分人数 成绩不小于60分人数合计 高一年级高二年级合计附： K 2＝n ad －bc 2a ＋bc ＋d a ＋cb ＋d.临界值表： P (K 2≥k )0.10 0.05 0.010 k2.7063.8416.63521．(12分) 已知直线l 的极坐标方程为，圆C 的参数方程为：．（1）判断直线l 与圆C 的位置关系； （2）若椭圆的参数方程为（φ为参数），过圆C 的圆心且与直线l 垂直的直线l′与椭圆相交于两点A ，B ，求|CA|•|CB|的值．西安市第一中学2015-2016学年度第 二学期期中 高二数学（文科）参考答案一、选择题（每小题3分，共36分） 题号12 3456789 101112 答案AA CDBDCABB CC 二、填空题（每小题4分，共20分） 13. )12(5312)()3)(2)(1(-⋅⋅⋅⋅=++++n n n n n n n ΛΛ14. 1 15. 2 3 16. (－3,4)或(－1,2) 17. 31三、解答题（共44分） 18．解析：由题意，得∑=41i ji yx ＝3×2.5＋4×3＋5×4＋6×4.5＝66.5，5.446543=++==x 5.345.4435.2=+++=y ．8665432222412=+++=∑=i ix则7.08186635.665.44865.35.445.66ˆ2=--=⨯-⨯⨯-=b． 35.05.47.05.3ˆˆ=⨯-=-=x b y a． 故线性回归方程为35.07.0ˆ+=x y． （2）根据线性回归方程的预测，现在生产50吨产品消耗的标准煤的数量为0.7×50＋0.35＝35.35，故消耗能源减少了45－35.35＝9.65（吨）． 19.（略）20.解：(1)高一年级学生竞赛平均成绩为(45×30＋55×40＋65×20＋75×10)÷100＝56(分)， 高二年级学生竞赛平均成绩为(45×15＋55×35＋65×35＋75×15)÷100＝60(分)． (2)2×2列联表如下：成绩小于60分人数成绩不小于60分人数合计 高一 70 30 100 高二5050100合计12080 200∴K 2＝200×50×30－50×702100×100×120×80≈8.333>6.635，∴有99%的把握认为“两个年级学生现学段对基本知识的了解有差异” 21．解:（1）∵直线l 的极坐标方程为，即，即ρsinθ+ρcosθ=4，故直线l 的直角坐标方程为：x+y ﹣4=0，∵圆C 的参数方程为：．∴圆C的普通方程为：x 2+（y+2）2=4， 圆心（0，﹣2）到直线l 的距离d==3＞2，故直线l 与圆C 相离； （2）∵椭圆参数方程（φ为参数），∴标准方程，过C （0，﹣2）点直线l 垂直的直线l′的方程为：x ﹣y ﹣2=0，联立方程得：或，故|CA|•|CB|=.=87。