各向同性材料的应力应变关系(广义胡克定律)

广义胡克定律
杨氏模量
单向应力状态时的胡克定律是
x E x
式中 E 称为弹性模量。对于一种材 料在一定温度下，E 是常数。
Chapter 5.1
广义胡克定律
泊松比
在单向拉伸时，在垂直于力作用线的方向发生收缩。
在弹性极限内，横向相对缩短 x 和纵向相对伸长 y
成正比，因缩短与伸长的符号相反，有：
ν
x y
Chapter 5.1
广义胡克定律
根据实验可知，xy只引起 xy 坐标面内的剪应变xy，
而不引起 xz、yz，于是可得
xy
xy
G
同理
yz
yz
G
zx
zx
G
Chapter 5.1
广义胡克定律
于是，得到各向同性材料的应变-应y
1 E
y
ν x
z
z
ij
1 2
ui, j u j.i
协调条件：
ij,kl kl,ij ik , jl jl,ik 0
对于一个假定位移场ui ，其相应的协调应变分量ij 可直接由应
变－位移关系得到。显然，这组协调的应变和位移，仅仅是许 多其他可能的应变和位移场中的一组。
几何可能的位移未必是真实的，真实位移在弹性体内部须满足 以位移表示的平衡微分方程。
应力和应变的关系
1. 本构关系的概念 2. 广义胡克定律 各向同性体 3. 各向异性弹性体 4. 热力学定律与应变能函数 5. 应变能和应变余能(自学) 6. 热弹耦合本构关系(自学) 7. 例题
应力和应变的关系
1. 本构关系的概念 2. 广义胡克定律 各向同性体 3. 各向异性弹性体 4. 热力学定律与应变能函数 5. 应变能和应变余能(自学) 6. 热弹耦合本构关系(自学) 7. 例题

l
b=50mm h=100mm
解: 梁为拉伸与弯曲的组合变形. A点有拉伸引起的正应力和弯曲 引起的切应力.
（拉伸） （负）
（1）A点处的主应变1， 2 ， 3
A
x = 20
x = 30
（2）A点处的线应变 x , y , z
例题14 简支梁由18号工字钢制成. 其上作用有力F= 15kN, 已知
2.三向等值应力单元体的体积应变（The volumetric strain of triaxial-equal stress element body）
三个主应力为
m
单元体的体积应变
m
m
这两个单元体的体积应变相同 单元体的三个主应变为
2
1
dy
3
dz dx
m
m
m
如果变形前单元体的三个棱边成某种比例,由于三个棱边应 变相同,则变形后的三个棱边的长度仍保持这种比例. 所以在三向
因此,该圆筒变形后的厚度并无变化,仍然为 d =10mm .
例题13 已知矩形外伸梁受力F1,F2作用. 弹性模量E=200GPa,泊
松比m= 0.3, F1=100KN,F2=100KN. 求:（1）A点处的主应变 1,2 , 3 （2）A点处的线应变 x , y , z
F1
b
F2 A
F2 z
a
例题10 边长 a = 0.1m 的铜立方块,无间隙地放入体积较大,变形
可略去不计的钢凹槽中,如图所示. 已知铜的弹性模量E=100GPa,
泊松比μ=0.34,当受到F=300kN的均布压力作用时,求该铜块的主
应力,体积应变以及最大切应力.
解:铜块横截面上的压应力
Fa

s2 0
即为平面应力状态，有
1
1 E
s 1 s 3
3
1 E
s 3 s 1
联立两式可解得：
s1
E 1
2
1 3
210 10 1 0 .3
2
9
240
0 . 3 160 10
6
s3
44 . 3 M Pa 9 E 210 10 3 1 160 0 . 3 240 10 2 2 1 1 0 .3
利用空间应力状态下最大切应力的计算式可得：
t max s1 s3
2 7.25MPa
§7-5 平面应力状态下的电测法
对各向同性材料图示平面应力状态，在线弹性、 小变形条件下，sx、sy与切应变无关，即有：
sy sx
x y
1 E 1 E
s s
E
x
s s s
y

y F a
sy sx sz
x
a
(a)
z
(b)
解：铜块应力状态如图b所示，横截面上的压应力为：
s
y

F A
30 MPa
受钢槽的限制，铜块在另两个方向的应变为零， 并产生压应力，即有：
x z
1 E 1 E
s s

x
s s
y
s s
z
0 0
所以，应变能密度为： v
d V dxdydz

1tx 2 G
而对纯剪应力状态，其主应力为：
s 1 tx
s2tx
s1 t
x
s
2

22
例题7-7 边长 a = 0.1m 的铜立方块, 无间隙地放入体积较
大, 变形可略去不计的钢凹槽中, 如图 所示。 已知铜的弹 性模量 E=100GPa, 泊松比 =0.34, 当受到P=300kN 的均布 压力作用时, 求该铜块的主应力. 体积应变以及最大剪应力。
P a
y
z
x
23
y
解：铜块上截面上的压应力为
9
3、 特例
（1）平面应力状态下(假设 Z = 0 )
x
1 E
(
x
y)
y
1 E
(
y
x)
z E ( x y)
xy
xy
G
10
（2） 广义胡克定律用主应力和主应变表示时 三向应力状态下：
1
1
E [ 1
(
2
3)]
2
1 E
[
2
(
3
1)]
3
1 E
[
3
( 1
2)]
(7-7-6)
11
平面应力状态下 设 3 = 0, 则
x y z x y y z z x
y
σy
上面
x y z x y y z z x
1、各向同性材料的广义胡克定律 （1）符号规定
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量：拉应力为正
σz
x
o
压应力为负。 z
前面
3
(b)三个剪应力分量: 若正面(外法线与坐标轴
dxdydz
dxdydz(1 1 2 3) dxdydz
dxdydz

• 广义胡克定律的比例式：
x y y z z x xy yz zx 1 x y y z z x xy yz zx 2G
弹性应力应变关系的特点
• 应力与应变完全呈线性关系，应力主轴与应变主 轴重合。 • 弹性变形是可逆的，应力与应变单值对应。 • 弹性变形时，应力球张量使物体产生体积变化， 泊松比υ＜0.5

' y

z

' z

xy
xy

yz
yz

zx
zx
d
d 3 2

x y
z x d x y y z z x 1 2 2 3 3 1 d 1 2 2 3 3 1
• 流动理论是描述材料处于塑性状态时，应 力与应变增量或应变速率之间关系的理论。 该理论针对是加载过程的任一瞬间，认为 应力状态确定的不是全量应变，而是该瞬 时的应变增量，从而撇开了加载路线和加 载历史的影响。
Levy—Mises方程
' ' ij ij d
x

' x

y
第五节 塑性应力应变关系（本构关系）
• 一、弹性应力应变关系———Hooke’s Law 对于各向同性材料，有广义虎克定律：
1 1 x y z ; xy xy E 2G 1 1 y y x z ; yz yz E 2G 1 1 z z x y ; zx zx E 2G
• 弹塑性
塑性应变

因主应力和主应变相对应，则由题意可得： 解：因主应力和主应变相对应，则由题意可得：
σ2 = 0
即为平面应力状态， 即为平面应力状态，有
1 ε 1 = (σ 1 −νσ 3 ) E
1 ε 3 = (σ 3 −νσ 1 ) E
8
E 210 ×10 (ε1 +νε 3 ) = (240 − 0.3 ×160)×10 −6 σ1 = 1 −ν 2 1 − 0.32 = 44.3MPa E 210 ×109 (ε 3 +νε 1 ) = (− 160 + 0.3 × 240)×10−6 σ3 = 1 −ν 2 1 − 0. 3 2 = −20.3MPa 主应变ε2为： ν 0.3 (44.3 − 20.3)×106 ε 2 = − (σ 1 + σ 3 ) = − E 210 ×109 = −34.3 ×10 −6
§10-5 应力与应变之间的关系 101、各向同性材料的广义胡克定律 单向应力状态： 1）单向应力状态：
s
σ ≤ σ P 时， ε x =
横向线应变： 横向线应变：
σ
E
ε y = −ν
纯剪应力状态： 2）纯剪应力状态：
tx
σ
E
ε z = −ν
σ
E
τ ≤ τ P 时，
γ xy =
τx
G
1
gxy
空间应力状态： 3）空间应力状态：
1 ε x = (σ x −νσ y ) E 1 ε y = (σ y −νσ x ) E
εz = − γ xy
ν
E 1 = τ xy G
(σ
x
+σ y )
5
若用主应力和主应变来表示广义胡克定律， 若用主应力和主应变来表示广义胡克定律，有：

121112111211xyxyyzyzzxzx第三节各向同性体中的弹性常数c沿二轴转动任何角度后的方向弹性关系相121112121112121112xyxyyzyzzxzx第三节各向同性体中的弹性常数当绕z轴转一角度第三节各向同性体中的弹性常数利用ijsinxy1211121144变换后有因此有由原式第常数中只有2个独立
σ = c ε + c (ε + ε ) y 11 y 12 x z σ z = c11ε z + c12 (ε x + ε y )
σ x = c11ε x + c12 (ε y + ε z )
τ = c 44 γ xy xy τ =c γ 44 yz yz τ zx = c 44 γ zx
= c 44 γ
= c 44 γ
xy
yz
τ
zx
= c 44 γ
zx
第三节 各向同性体中的弹性常数 当绕Z轴转一角度 α 时，即 x y
m1 = sin α
z ( z ')
z
n1 = 0 n2 = 0 n3 = 1
x
x'
y'
α
y
x′
y′
l1 = cos α
α
l2 = − sin α m2 = cos α l3 = 0 m3 = 0
c41 = c42 = c43 = 0 c51 = c52 = c53 = 0 c61 = c62 = c63 = 0 只能证9个数为0
第三节 各向同性体中的弹性常数 （2）沿任意两个相反的方向，弹性关系相同。 如只改变z轴方向，w和z的方向改变,则
γ yz
∂w ∂v = + = −γ yz′ ∂y ∂z

z
z
ϕLeabharlann ij m(7.2—13) (7.2—14)
ε = ϕ ⋅τ ,
xy
xy
ε = ϕ ⋅τ ,
yz
yz
ε zx = ϕ ⋅τ zx
如果认为在整个变形过程中材料不可压缩，泊松比ν = 0.5 ，则 K 0 = 0 ，式(7.2—13) 简化为：
ε ij = ϕ (σ ij − δ σij m ) = ϕ ⋅ sij
（7.1—10）
可见，服从广义胡克定律的各向同性线弹性材料，其应力莫尔圆与应变莫尔圆在几何
上是相似的，应力罗代参数 µ σ 等于应变罗代参数 µ ε 。等效应力与等效应变之间也有简 单关系。由等效应力定义式得：
σ= 1 2
(σ 1
−σ
)2
2
+ (σ
2
−σ 3)2
+ (σ
3
−σ1)2
= 2G 2
(ε 1 − ε 2 ) 2 + (ε 2 − ε 3 ) 2 + (ε 3 − ε 1 ) 2
+
eP ij
+ δ ij ε m
=
1 2G
s ij
+
φ 2G
s ij
+ 1− 2ν E
δσ ij m
=
1+φ 2G
s ij
+ 1− 2ν E
δ ijσ m
(7.2—12)
令 1+φ 2G
=ϕ
， 1− 2ν E
=
K 0 ，式(7.2—12)可改写成汉基理论的常用表达式：
ε ij = ϕs ij + K 0 δ ij σ m
求解小弹塑性变形问题，等同于求解某一非线性弹性力学问题，因此获得了广泛的应用。

σy
解： （1）求应变εx, εy ,εz 根据广义胡克定律：
σx
O
= ε x
1 E
(σ
x
−
µσ
y
)
=
1 200 ×
109
(160
×
106
+
0.25
×
40
×
106
)
=
8.5 ×10−4
εy
=1 E
(σ
y
−
µσ x )
= 200
1 ×
109
(−40 × 106
−
0.25×160×106 )
=−4 × 10−4
例: 刚性块D=5.001cm凹座，内放d=5cm刚性
圆柱体，F=300kN, E=200GPa, µ = 0.3,无摩擦，
求圆柱体主应力。
解：
σ3
=− F A
=− π30×05×012043
=−153MPa
F
设圆柱体胀满凹座
ε2 = (5.001− 5) 5= 0.0002
由对称性，可设 σ1 = σ2 = −q
(2) 坐标系转动30o，求 ε γ 30, 30/120
解：（ii）由应力转轴公式
σ= 30
σx
+σ y
2
+
σx
−σ
2
y
cos 2 × 30
−τ x
sin 2 × 30
= 160 − 40 + 160 + 40 cos 60 = 110MPa
2
2
（应力单位：MPa）
τ 30
σ
x
−σ
2
y

P a
y
z
x
y 解：铜块上截面上的压应力为
yP A30 0 .1 1 20 3 0
y x
3M 0 Pa
x
(b) Z z
1[ ( )]0
x Ex
y
z
由
1[ ( )]0
z Ez
x
y
解得
x
z
(1 1 2
)
y
0.314-(01.3042.34)(30)
-15.5MPa
铜块的主应力为
σ 1 σ 2 1 .5 M 5 σ P 3 3 a M 0 ,P
体积应变和最大剪应力分别为
1 E 2(123 ) 1 .9 5 1 4 0
max 1 2(13)7.25MPa
例题9-8 壁厚 t =10mm , 外径 D=60mm 的薄壁圆筒, 在表面上 k 点 处与其轴线成 45°和135° 角即 x, y 两方向分别贴上应变片,然后在 圆筒两端作用矩为 m 的扭转力偶,如图 所示已知圆筒材料的弹性模 量为 E = 200GPa 和 = 0.3 ,若该圆筒的变形在弹性范围内,且 max = 80MPa , 试求k点处的线应变 x ,y 以及变形后的筒壁厚度。
在x y z同时存在时, y,z方向的线应变为
y E 1[y (z x)] z E 1[z (x y)]
(2)剪应变的推导 剪应变 xy , yz ,zx与剪应力xy ,yz ,zx之间的关系为
xy
xy G
yz
yz G
zx
zx G
公式的适用范围 : 在线弹性范围内, 小变形条件下, 各向同性材料。
右侧面
σx
τ xz x
前面
2、各向同性材料的广义胡克定

45
1 E
(
45
145
)
3.31104
例 5-2 对于各向同性材料，试证明：
G
E 2(1
)
证： 根据几何关系求45。
x
y
2
x
y
2
cos2
xy sin2
2
x y 0 xy / G
45
xy
2
2G
根据广义胡克定律求 45。
45
1 E
( 3
1 )
(1 )
E
比较
G E
2(1 )
87各向同性材料的应力应变关系广义胡克定律平面应力状态xyxy例51e70gpa0334514545451031mpa30mpa50sin2cos2sin305045mpampa5513545xympa80mpa24mpa80mpa24
§8-7 各向同性材料的应力应变关系 （广义胡克定律）
广义胡克定律（平面应力状态） 广义胡克定律（三向应力状态） 例题
解：
y
F a2
80
x
MPa
Ex
E
y
x
0
x
E
E
y
0
x y 24 MPa
1 0, 2 24 MPa, 3 80 MPa
广义胡克定律（平面应力状态）
x
x
E
y
E
x
y
y
E
x
E
y
x
1 E
(
x
y)
y
1 E
( y
xy
x
G
x
)
x
1
E
2
(
x
y

《弹塑性力学与有限元》
弹性应力-应变关系和单轴状态下材料 的特征、模型
弹性固体的应变能和余能密度
其中，W为单位体积的应变能或应变能密度，且δW为应变能密度的
增长率。
W ij ij
因为应变能W定义上讲只是ɛ的函数，所以微分形式为：
W
W
ij
ij
《弹塑性力学与有限元》
弹性应力-应变关系和单轴状态下材料 的特征、模型
引言
本章假设材料特性是与时间无关的。 本章假设材料特性忽略力学与热学过程的相互作用。 弹性模型能很好描述处于工作荷载水平下的许多工程材
料的性能，因此弹性本构关系是在不同的工程问题中得 到广泛应用的弹性理论基础。
《弹塑性力学与有限元》
弹性应力-应变关系和单轴状态下材料 的特征、模型
各向同性材料的线弹性应力-应变关系（广义Hooke定律）
上式是在简单拉伸试验中所测得的应力-应变线性相关性的简单推广，
因此常将上式称为广义胡克（hooke）定律。
《弹塑性力学与有限元》
弹性应力-应变关系和单轴状态下材料 的特征、模型
各向同性材料的线弹性应力-应变关系（广义Hooke定律）
由于σij和ɛij都是对称的，固有如下对称条：
Cijkl C jikl Cijlk C jilk ij Cijkl kl
量之间存在一种简洁的分离形式，即：ij k k ij 2 ij
3p 3 2kk 3 2Gkk
K
3
2
3
p Kkk kk
在线弹性范围内，体积应力只产生体应变，即只产生体积改变。
《弹塑性力学与有限元》
弹性应力-应变关系和单轴状态下材料 的特征、模型
各向同性材料的线弹性应力-应变关系（广义Hooke定律）

拉V LV GP
材料的力学性能 应力应变关系
1-2 轴向拉伸与压缩实验 低碳钢的拉伸试验 将试件装卡在材料试验机上进行常温、静载拉伸试验，直 到把试件拉断为止，试验机的绘图装置会把试件所受的拉力 F 与试件的伸长量 l 之间的关系自动记录下来，绘出一条曲线 F - l曲线，称为拉伸图。
IC LMV LV GP
材料的力学性能 应力应变关系
1-2 轴向拉伸与压缩实验 （1）低碳钢的拉伸试验
• 第二阶段——屈服（流动）阶段 （曲线bc段 ）
曲线最低点所对应的应力，称为材料的屈服点，用 s s 表示，
即
ss

Fs A
IC LMV LV GP
材料的力学性能 应力应变关系
1-2 轴向拉伸与压缩实验 （1）低碳钢的拉伸试验
除去尺寸因素， 变为 应力-应
变曲线。即 se 曲线。
IC LMV LV GP
材料的力学性能 应力应变关系
1-2 轴向拉伸与压缩实验 （1）低碳钢的拉伸试验 将试件装卡在材料试验机上进行常温、静载拉伸试验，直 到把试件拉断为止，试验机的绘图装置会把试件所受的拉力 F 与试件的伸长量 l 之间的关系自动记录下来，绘出一条曲线 F - l曲线，称为拉伸图。
分析曲线，有几个特征点，把曲线分成 四 部分，说明低碳
钢拉伸时，变形分为 四个阶段。
IC LMV LV GP
材料的力学性能 应力应变关系
1-2 轴向拉伸与压缩实验 （1）低碳钢的拉伸试验
• 第一阶段——弹性变形阶段 （曲线ob段 ） 在此阶段任一时刻时，将载荷慢慢减少（称卸载）为零，变 形会消失。b 点对应的应力称材料的弹性极限。即，材料处
IC LMV LV GP
材料的力学性能 应力应变关系

第四章 应力应变关系前一章引进了应力和应变的概念以及应力分析和应变分析的公式。

应力分析仅用到力的平衡概念，应变分析仅用到几何关系和位移的连续性。

这些都没有涉及到所研究物体的材料性质。

本章开始将研究材料的性质。

这些性质决定了各种材料特殊的应力－应变关系，显示出材料的力学性能。

下面将着重描述低碳钢的力学性能，介绍各向同性材料的广义胡克定律。

作为选读材料，将介绍各向异性的复合材料单层板的应力－应变关系。

§4-1 低碳钢的拉伸试验在分别考虑了应力和应变后，从直觉上知道这两个量是互相关联的。

事实上，在第一章的绪论里已经提到过应力应变之间的胡克定律。

它描述了很大一类材料在小变形范围，在简单拉伸（压缩）条件下所具有的线性弹性的力学性能。

低碳钢Q235是工程上常用的金属材料。

这一节着重介绍低碳钢的力学性能，然后简单介绍其他一些材料的性能。

有关材料性能的知识来自于宏观的材料试验，以及从这些试验得出的宏观的、唯象的理论。

固体物理学家一直在从原子和分子量级上研究这些力学性能的微观基础。

力学家也已开始从细观尺度来分析材料的力学性能，并已经取得了很大进展。

材料力学作为固体力学的入门课程，将只限于材料的宏观力学性能的描述。

为了确定应力与应变关系，最常用的办法是用单向拉伸（压缩）试验来测定材料的力学性质。

这种试验通常是在常温（室温）下对试件进行缓慢而平稳加载的静载试验。

805l d =一、低碳钢拉伸试验按照我国的国家标准 “金属拉伸试验试样” （GB6397－86），将试件按规定做成标准的尺寸。

图4－1所示是一根中间直径为d 的圆杆型试件，两端的直径比中间部分大，以便于在试验机夹头上夹持。

试件中间取一段长度为l 的等直部分作为标距。

对圆截面标准试件，规定标距l 与直径d 的关系为 ，或，分别称为10倍试件和5倍试件。

试件也可制成截面为矩形的平板型，平板试件的10倍与5倍试件的标距分别为10l d==l和l =，其中A 为试件的横截面面积。

的法线方向 称为该材料的主方向。
四：横向各向同性材料的应力-应 变关系
三个相互垂直的弹性对称面中有一个是各向同 性的，如单向纤维增强复合材料。
其应力-应变关系为：
独立弹性常数只有５ 个
五：各向同性材料的应力-应变关 系
具有无穷多个弹性对称面的材料称为各向同性材 料。这种材料对于三个相互垂直的弹性对称面 的弹性性能完全相同。刚度系数满足：
此课件下载可自行编辑修改，供参考！ 部分内容来源于网络，如有侵权请与我联系删除！
复合材料力学与结构
第二章各向异性材料的应力应变关系
２.１三维各向异性材料的应力-应 变关系
一：广义胡克定律
在弹性变形范围内，应力与应变成正比例关系，
其比例系数称为弹性量。（拉压模量、剪切模
量等）
ij C ijkl kl
应力与应变的 关系
S ij
ijkl (ki.lj.k.l=1.2.3)
则柔度系数与工程弹性常数关系为：
同理，沿 ２ 轴向和 ３ 轴向的 单向拉伸，还可得：
对于102面、203面和103面的纯剪切，可得：
式中E1,E2,E3和G12,G23,G13分 别为正交各向异性材料的拉压弹 性模量和剪切弹性模量； V12,V23,V13以及V21,V32,V31分 别为主泊松比和副泊松比
单对称材料的应力
则单对称材料的应力应变关系就可以表示为：
则其应变-应力关系可以表示为：
三：正交各向异性材料的应力-应 变关系
具有三个相互正交的弹性对称面的材料称为正交 各向异性材料。按单对称材料分析方法可得：
则应力-应变关系为：
应变-应力关系为：
独立弹性常数只有９个， 正交各向异性材料三个 相互垂直的弹性对称面

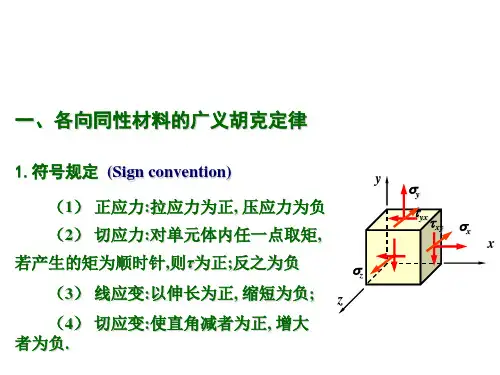
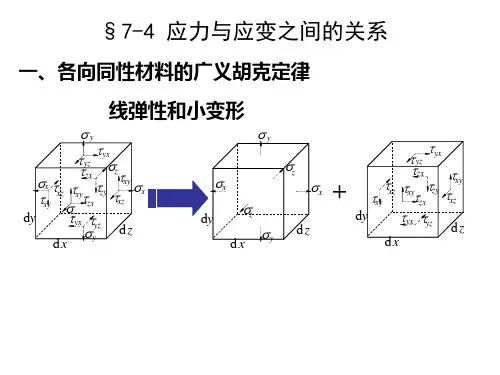
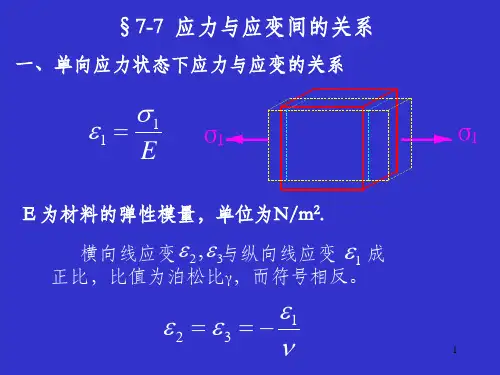
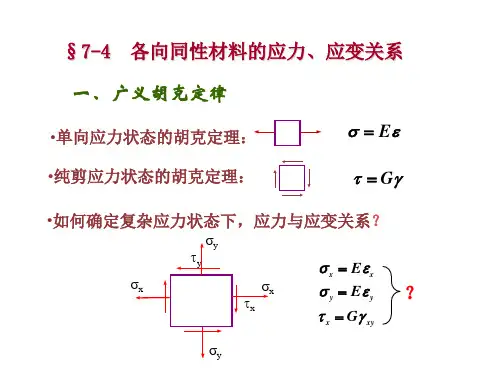
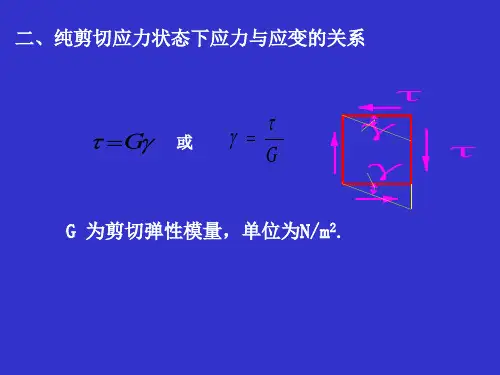
广义胡克定律广义胡克定律回顾：应力与应变的关系轴向拉压：轴向横向 广义胡克定律E σε=Eσεμ'=-简单应力状态下的胡克定律纯剪切：Gτγ=广义胡克定律复杂应力状态当一点处于平面应力状态或空间应力状态时，应力与应变间是什么关系呢？广义胡克定律一. 空间应力状态下的应力应变关系如图所示为受力构件内一点处最普通的单元体。

对于各向同性材料(线弹性小变形)，有如下结论：线应变只与正应力有关切应变只与切应力有关广义胡克定律叠加原理求x 方向线应变εx σx 单独存在时σz 单独存在时σy 单独存在时x x σεE '=y x σεμE ''=-z x σεμE '''=-三个切应力分量均与εx 无关。

广义胡克定律σx ,σy ,σz 同时存在时，x 方向的线应变εx 为1[()]x x y z εσμσσE=-+同理可得到y , z 方向的线应变分别为1[()]y y x z εσμσσE=-+1[()]z z y x εσμσσE=-+广义胡克定律切应力与切应变的关系xy xy G τγ=yzyz G τγ=zxzx Gτγ=与正应力无关广义胡克定律1[()]x x y z εσμσσE=-+1[()]y y x z εσμσσE=-+1[()]z z y x εσμσσE =-+xy xy G τγ=yz yz G τγ=zxzx Gτγ=广义胡克定律广义胡克定律主应力与主应变之间的关系123x y z σσσσσσ===0xy yz zx τττ===主单元体无切应变广义胡克定律11231[()]εσμσσE=-+22131[()]εσμσσE=-+33211[()]εσμσσE =-+主应力与主应变之间的关系ε1、ε2、ε3：主应变主应力与主应变的方向重合，一一对应广义胡克定律二. 平面应力状态下的应力应变关系假设σz = 0，τxz = 0，τyz = 0()()()11x x y y y x z x y xyxy EEE G εσμσεσμσμεσστγ=-=-=-+=εz ≠0广义胡克定律主应力与主应变之间的关系()()()11222131211EE E εσμσεσμσμεσσ=-=-=-+ε3≠0主应力与主应变的方向重合，一一对应ε1、ε2：主应变广义胡克定律例. 图示矩形截面简支梁，在梁的跨中受一集中力作用，测得中性层上点处沿45º方向的线应变为ε。

胡克定律的定义胡克定律的别称是弹性定律，适用的领域范围是现实世界中复杂的非线性现象。

下面是店铺给大家整理的胡克定律的定义，供大家参阅!胡克定律的定义与表达式胡克定律(Hooke's law)，又译为虎克定律，是力学弹性理论中的一条基本定律，表述为：固体材料受力之后，材料中的应力与应变(单位变形量)之间成线性关系。

满足胡克定律的材料称为线弹性或胡克型(英文Hookean)材料。

从物理的角度看，胡克定律源于多数固体(或孤立分子)内部的原子在无外载作用下处于稳定平衡的状态。

许多实际材料，如一根长度为L、横截面积A的棱柱形棒，在力学上都可以用胡克定律来模拟——其单位伸长(或缩减)量(应变)在常系数E(称为弹性模量)下，与拉(或压)应力σ成正比例，即：F=-k·x或△F=-k·Δx。

其中为总伸长(或缩减)量。

胡克定律用17世纪英国物理学家罗伯特·胡克的名字命名。

胡克提出该定律的过程颇有趣味，他于1676年发表了一句拉丁语字谜，谜面是：ceiiinosssttuv。

两年后他公布了谜底是：ut tensio sic vis，意思是“力如伸长(那样变化)”，这正是胡克定律的中心内容。

胡克定律的表达式为F=k·x或△F=k·Δx，其中 k是常数，是物体的劲度(倔强)系数。

在国际单位制中， F的单位是牛，x的单位是米，它是形变量(弹性形变)，k的单位是牛/米。

劲度系数在数值上等于弹簧伸长(或缩短)单位长度时的弹力。

弹性定律是胡克最重要的发现之一，也是力学最重要基本定律之一。

在现代，仍然是物理学的重要基本理论。

胡克的弹性定律指出：弹簧在发生弹性形变时，弹簧的弹力Ff和弹簧的伸长量(或压缩量)x成正比，即F= -k·x 。

k是物质的弹性系数，它由材料的性质所决定，负号表示弹簧所产生的弹力与其伸长(或压缩)的方向相反。

为了证实这一定律，胡克还做了大量实验，制作了各种材料构成的各种形状的弹性体。