间接式矩阵变换器的调制策略

格式：wps
大小：1.29 MB
文档页数：15

下载文档原格式

矩阵变换器空间矢量PWM过调制策略的研究

４０７）３０４
摘
要：针对矩阵变换器在实际应用中存在电压传输比较低的问题，于空间矢量Ｐ基ＷＭ研究了矩阵变换器的两种过调制策略。在过
调制策略中根据电压调制系数不同，出了参考电压矢量不同的调整策略，高电压传输比。在ＭｒＡ给以提ＡＺＢ下对过调制策略ｌ
为虚拟直流母
线电压，为期望输
出相电压矢量幅值。
当ｍ＝１时，出输相电压矢量轨迹为六边形的内切圆。当ｍ。，
＝
调制区域内，电压传输比的理想最大值只有８．％。针对矩阵６６变换器电压传输比低的问题，文研究了矩阵变换器空间矢量本
《气自化２１第３卷第４电动）１年３０期
控制理论及其应用
Ｃｏｔｈｏｙ＆ＩｐｉａｉｎｎｒＴｅｒｏＩｔＡｐｌｔｓｓｃｏ
矩阵变换器空间矢量ＰＷＭ过调制策略的研究
何红颜
（中光电技术研究所，华湖北武汉
ｖｌｅｔｎｆｒｎａｉｃｏｄｎｏｔｅｄｆｒｎｏｔｇｄｌｔｎｒｔｓＴｅｓｌｔｎｒｓａｃｆｏｅｍｏｕａｉｎｓｈｍｅｓｏｔｒｓｅｒｇｒｔａｃｒｉｇｔｉｅｅｔｖｌｅｍｏｕａｉａｉ．ｈｉａｉｅｅｒｈｏｖｒｄｌｔｃｅｓｉｇａａｉｏｈａｏｏｍｕｏｏｃｒｉｄｕｄｒＭＡＴＡＢＴｅｓｌｔｎｒｓｌｅｓｏｄｔａｈｒｐｓｄｓａｅｖｃｏｖｒｄｌｔｎｓｈｍｅａｆｃｉｅｙａｒｎｅｅＬ．ｈｉａｉｅｕｔａｈｗｅｈｔｔｅｐｏｏｅｐｃｅｔｒｏｅｍｏｕａｉｃｅｓｃｎｅｅｔｌｍｕｏｓｒｏｖ

矩阵变换器间接空间矢量逆变级过调制策略优化设计

矩阵变换器间接空间矢量逆变级过调制策略
优化设计
本文将介绍如何利用矩阵变换器间接空间矢量逆变级过调制策略进行优化设计。

以下是文章的主要内容：
一、矩阵变换器的基本原理
矩阵变换器是一种用于将输入信号进行线性变换的器件。

它通过矩阵乘法将输入信号变换到另一个向量空间中，从而实现信号处理和传输。

二、空间矢量逆变级的概念
空间矢量逆变级是一种将向量空间中的向量映射到其对偶空间中的线性变换。

它可以用于优化信号的传输和处理，提高系统性能和效率。

三、过调制策略的介绍
过调制策略是一种通过调制信号的幅值和相位来达到更高的信息传输速率和信噪比的方法。

它可以通过增加调制波的数量来提高传输速率，或通过调制波的相位差来提高信噪比。

四、矩阵变换器间接空间矢量逆变级过调制策略的优化设计
将矩阵变换器和空间矢量逆变级结合起来，可以实现更高效的信号处理和传输。

过调制策略可以通过优化矩阵变换器和逆变级的参数来实现最佳性能。

五、总结
矩阵变换器间接空间矢量逆变级过调制策略是一种有效的信号处理和传输方法。

它可以通过优化设计来实现更高的性能和效率，提高系统的稳定性和可靠性。

基于间接空间矢量调制的矩阵变换器控制策略仿真

一
式中：、、ｒ为对应开关矢量的作用时间，为开关周ｏ期。相应占空比可表示为：
ｌ＝／ｓ（。６）＝ｉ６一ｌｎ０ｖ
｛ｓ【／＝ｉ＝ｎ
＝１－一
式中：０眠：，ｕ） ≤ 。Ｕ ≤ （／１为输出相电压基波幅值，ｙｌｆｖ
中图分类号：Ｔ６Ｍ４
文献标识码Ａ
文章编号：１０ — ５９（００５０３— ２０７９９２１）１— ０１０
ＳｉｕｌｔｏｏａｒｘＣｏｖｒｅｓｄｎＩｍａｉｎｆＭｔｉｎｅｔｒｂａｅｏｎｄｉｅｔＳｒｃＶＰＷＭ
为直流侧电压均值。（）Ａ／Ｃ空间矢量调制原理－ＣＤ根据检测到的输入相电压空间矢量ｕ和设定的输入相位差可以确定希望得到的输入相电流空间矢量 ‘ 置。位对图ｌ的 “ 虚拟整流器 ”部分输入相电流进行矢量调制。根据输入相间不短路的约束，每一直流输出端只与一相交流输入端接通，从而有九种电流矢量开关组合状态，构成图２示输入相所
摘
一
２００）３６１
要：矩阵变换器因其具有的众多优良特性而受到人们关注。然而其所需功率开关众多，拓扑和控制都很复杂，在
定程度上限粕了它的发展。本文研究了基于虚拟直流环节的间接空间矢量调制策略结合四步换流控制策略，在仿真中验
证了该控制策略。仿真结果输出了正弦的交流电压和输入电流，取得了良好的效果。关键词：矩阵变换器；间接空问矢量调制（ＶＷＭ）ＳＰ；四步换流策略

间接式矩阵变换器的研制

间接式矩阵变换器的研制矩阵变换器是一种用于实现信号处理和控制系统的重要设备。

通过对输入信号进行矩阵变换，可以实现信号的调制、解调、滤波等功能。

在许多领域，如通信、电力系统、自动化控制等，矩阵变换器被广泛应用。

然而，传统的矩阵变换器存在一些问题，如复杂的硬件结构、高成本、信号失真等。

为了解决这些问题，研究人员提出了一种新型的矩阵变换器——间接式矩阵变换器。

间接式矩阵变换器采用了一种全新的工作原理。

它通过将输入信号转换为间接表示形式，然后通过一系列矩阵操作将其转换为输出信号。

这种间接表示形式可以是矩阵、向量或其他形式的数学表达式。

相比传统的直接式矩阵变换器，间接式矩阵变换器具有更简单的硬件结构和更低的成本。

研制间接式矩阵变换器的关键问题是设计合适的矩阵操作算法。

这些算法需要考虑输入信号的特性，如频率、幅值、相位等，以及所需的输出信号的特性。

通过数学建模和仿真实验，研究人员可以确定最佳的矩阵操作算法，并优化其参数。

除了算法设计，研制间接式矩阵变换器还需要考虑硬件实现。

在设计硬件电路时，需要选择合适的器件和元件，并考虑功耗、可靠性和成本等因素。

同时，还需要进行电路仿真和测试，以保证矩阵变换器的性能和稳定性。

最后，研制间接式矩阵变换器还需要进行系统集成和性能评估。

在集成过程中，需要将矩阵变换器与其他系统组件进行连接，并进行功能测试和性能测试。

通过实验数据的分析和对比，可以评估间接式矩阵变换器的性能并进行优化。

间接式矩阵变换器的研制为信号处理和控制系统的发展提供了一种新的解决方案。

它不仅可以提高系统的性能和稳定性，还可以降低系统的成本和复杂性。

未来，随着对矩阵变换器技术的深入研究，间接式矩阵变换器有望在更多领域得到应用，并为相关领域的发展带来新的机遇和挑战。

矩阵变换器过调制策略的研究

矩阵变换器过调制策略的研究鲁静;薛建设;蔡文君【摘要】In order to improve the voltage transfer ratio of matrix converter, the various over-modultion strategies are presented. The matrix converter is described to an equivalent circuit combining virtual rectifier and virtual inverter to realize the voltage modulation for the matrix converter. The over-modulation mode Ⅰ、Ⅱand single-mode over-modulation,the over-modulation based on Limit-Trajectory, the over-modulation based on ANN in virtual inverter are summarized to solve the problem that voltage transfer ratio is low. The advantages and disadvantages are analyzed. The different over-modulation methods are adopted in different matrix converter system.% 为了提高矩阵变换器的电压传输比，提出了多种过调制策略。

将矩阵变换器等效成虚拟的整流级和虚拟的逆变级，两者相结合完成对矩阵变换器的电压调制，在虚拟逆变级采用过调制策略可提高矩阵变换器的电压传输比。

对在虚拟逆变级采用的双模过调制模式Ⅰ、模式Ⅱ过调制策略，单模过调制策略，基于极限轨迹法的过调制策略，基于人工神经网络的过调制策略加以总结，并分析出各自的优点及缺点，针对不同矩阵变换器的系统要求，采用不同的过调制方法。

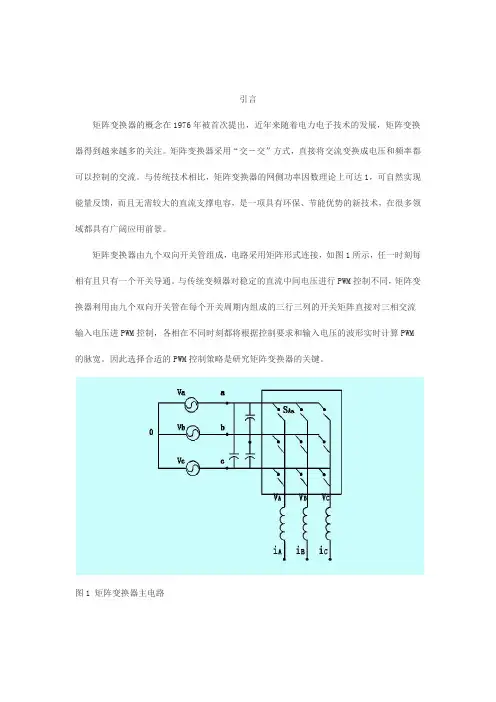
矩阵变换器空间矢量调制策略

引言矩阵变换器的概念在1976年被首次提出，近年来随着电力电子技术的发展，矩阵变换器得到越来越多的关注。

矩阵变换器采用“交－交”方式，直接将交流变换成电压和频率都可以控制的交流。

与传统技术相比，矩阵变换器的网侧功率因数理论上可达1，可自然实现能量反馈，而且无需较大的直流支撑电容，是一项具有环保、节能优势的新技术，在很多领域都具有广阔应用前景。

矩阵变换器由九个双向开关管组成，电路采用矩阵形式连接，如图1所示，任一时刻每相有且只有一个开关导通。

与传统变频器对稳定的直流中间电压进行PWM控制不同，矩阵变换器利用由九个双向开关管在每个开关周期内组成的三行三列的开关矩阵直接对三相交流输入电压进PWM控制，各相在不同时刻都将根据控制要求和输入电压的波形实时计算PWM 的脉宽。

因此选择合适的PWM控制策略是研究矩阵变换器的关键。

图1 矩阵变换器主电路本文正是对矩阵变换器调制策略进行研究，采用空间矢量调制法（SVM）对矩阵变换器进行控制，应用TI公司DSP TMS320F240实现调制策略，实验结果验证了这一方法的正确性和可行性。

矩阵变换器空间矢量调制策略（SVM）基本原理矩阵变换器空间矢量调制策略（SVM）的基本思想与应用在传统逆变器上的空间矢量调制法思想是相同的，但要比控制传统逆变器复杂的多，需要同时控制输出电压和输入电流两个矢量。

矩阵变换器三相输出线电压可表示为:——(1)因Vab、Vbc、Vca是正弦量且有120o相位差，因此上式可写成：——(2)其中Vol为输出线电压峰值，ωo为输出角频率。

同理输入电流空间矢量可以表示为：——(3)其中ii为输入相电流峰值,ωi为输入角频率，φi为输入滞后角。

在足够短的时间内，输出电压矢量可由一组由矩阵变换器产生的基本矢量来合成，如果足够短的时间是矩阵变换器的开关周期，那么下一个周期，输出电压矢量旋转到新的角度位置，将由另外一组新的矢量进行合成。

因而在整个周期，平均输出电压就会与参考给定电压十分接近。

矩阵变换器调制策略综述

增加了难度。而本文通过对最大电压传输比，开关的转换次数，输出行的，最后可以使得最大电压传输比达到０．８６６，由于应用的是矢量
电压和输入电流中包含的谐波含量惊醒了考察与比较进应用的结论。下面对于几种常见的调制策略进行分析。
２．１直接传递函数算法
论证了ＭＣ高频综合（ＨｉｇｈＦｒｅｑｕｅｎｃｙＳｙｎｔｈｅｓｉｚｅ）定理，找出了详细义输入侧的三相电压源为Ｕ、Ｕ、Ｕ，输入端的三相电流为ｉ、ｉ …ｉ所
的调制策略并应用于矩阵变换器的发展，慢慢引起了研究人员与学需的三相输出的电流为ｉＡｉ、ｉ，所需的三相输出的电压ｎＡＢ、ｕ瞰、ＵＣＡ。
而得
出所
调制的概念来实现对输出电压，输入来计算电流电压的瞬时占空比，所以
电流的控制，没有应用瞬时量当三相电压源不平衡时，间接
直接传递函数法是一种直接应用了数学方法的有效的一种方矢量２调．３制双策电略压略控显制不策足略。
法——调制占空比矩阵。按发展历程可分为ＡＶ（Ａｌｅｓｉｎａ—Ｖｅｎｔｕｒｉ— ｎｉ，ＡＶ）法与ＯＡｒ（ＯｐｔｉｍｕｍＡｌｅｓｉｎａ—Ｖｅｎｔｕｒｉｎｉ，ＯＡＶ）法。得矩
ｌ１．１
３ｒｎ２３ｍ３３ｌｌ／ｏ３ｌ
于其计算量小，计算简单，可以轻易的实现电网电压非正常情况下对输入电流的控制，但相比于空间矢量调制成的实现更为困难。（２）３结论
矩阵变换器被称为柔性（灵活）通用变换器，不仅指其变换功能
０
ｌ，Ｚ：１，２，３ｋ：１，２，３

间接式矩阵变换器简化调制型模型预测控制

间接式矩阵变换器简化调制型模型预测控制
齐火箭;徐海宾;王嘉宏;任志丹
【期刊名称】《电力电子技术》
【年(卷),期】2018(52)12
【摘要】针对传统调制型模型预测控制(CMMPC)整流级矢量选择方法,提出一种简化调制型模型预测控制(SMMPC).利用网侧参考电流相位求解出变换器输入侧参考电流矢量相位,然后根据变换器输入侧参考电流矢量在两相静止坐标系下的位置分布,直接选取整流级作用矢量.并对整流级矢量作用占空比进行修正,无需计算整流级调制比.该方法不存在网侧电流的多次预测和评估,有效降低了系统计算量.最后,通过实验验证了所提SMMPC的有效性.
【总页数】3页(P95-97)
【作者】齐火箭;徐海宾;王嘉宏;任志丹
【作者单位】国网冀北电力有限公司张家口供电公司,河北张家口 075000;国网冀北电力有限公司张家口供电公司,河北张家口 075000;国网冀北电力有限公司张家口供电公司,河北张家口 075000;国网冀北电力有限公司张家口供电公司,河北张家口 075000
【正文语种】中文
【中图分类】TM46
【相关文献】
1.基于输入电压的间接式矩阵变换器优化调制策略 [J], 孙军;聂子玲;朱俊杰;胡风革;张银锋;
2.基于间接式矩阵变换器的优化模型预测控制 [J], 朱维钧;朱伟江;周年光;刘海峰;范东海
3.双级式矩阵变换器的快速调制型模型预测 [J], 李发亮;刘国亮;何培东;郑钟
4.多输出间接矩阵变换器的简化模型预测控制方法 [J], 王闪闪; 徐彦
5.间接矩阵变换器-双异步电机调速系统的简化模型预测控制 [J], 梅杨;穆希旺因版权原因，仅展示原文概要，查看原文内容请购买。

矩阵变换器新型SVPWM调制策略的仿真研究

ｏｃｎｌｇＸｉａ０４Ｓａｎ，ｉａｆＴｅｈｏｏｙ， ’ ｎ７０８，ｈａｘｉＣｈｎ）１
Ａｂｓｒｃ：ｃｏｄｎｏｔｏｖｌａｒｎｓｅａｉｆｍａｒｘｃｎｖｒｅ，ａｋｎｉｉｅｎｄｒｃｐａｅｔａｔＡｃｒｉｇｔｈｅｌｗｏｔｇｅｔａｆｒｒｔｏｏｔｉｏｅｔｒｉｄｏｆｏｐｔｍｚｄｉｉｅｔｓｃｖｅｔｒｍｏｄａｔｏｔａｔｇｙ（ｖｌＳＶＰＷＭ）ｏｆｍａｒｘｃｎｖｒｅａｒｐｏｅ．Ｍｏｃｏｕｌｉｎｓｒｅｎｏｅｔｉｏｅｔｒｗｓｐｏｓｄｄｕｌｔｏｒｎｃｐｌｎｒａｉｎｐｉｉｅａｄｐｅ — ｆｒａｃｈｔａｅｎｒａｓｎｌａｒｓｅａｔｏｗａｎａｙｅｔｏｒｔｃｌｙｎｓｍｕａｉｏｌｏｍｎｅｏｆｔｅｓｒｔｇｙｏｎｉｃｅｉｇｖｏｔｇｅｔａｎｆｒｒｉｓａｌｚｄｈｅｅｉａｌａｄｉｌｔｏｎｍｄｅｗａｅｓｓｔｕｐ．ＴｈｅｅｉａｎｌｓｓｎｍｐｉｉａｉｕａｉｔｄｉｓｈｏｒｔｃｌａａｙｉａｄｅｒｃｌｓｍｌｔｏｎｓｕｅｓｏｗｈｎｈｉａａｎｗｔａｔｉｔｅｌｎｅｒｒｇｅｎｅＳＶＰＷＭｃｎｍａｅｔｅｖｔｅｔａｆｒｒｔｏｒｓｏ０．５５ｆｏｍ８６ｏｎｎｉｎａｎｄｉｅｔｓａｅｖｅｔｒｃｎｔｏｔａｔａｋｈｏｌａｇｒｎｓｅａｉｉｅｔ９ｒ０．６ｏｆｃｖｅｔｏｌｉｒｃｐｃｃｏｏｒｌｓｒ — ｅｙＯｕｐｕｔｖｔｇｅａｄｉｇ．ｔｏｌａｎｎｐｕｕｒｅｔｗａｅｏｒｓａｅｇｏ．Ｔｈｅｓｒｔｇｙｉｉｐｅｎｄｅｓｅｏｃｎｔｏｌｒａ— ｔｃｒｎｖｆｍｒｏｄｔａｅｓｓｍｌｒａａｉｒｔｏｒｅｌｔｍｅ，ｎｄｉｓｔｏｒｔｃｌｒｓａｃｖａｕｅａｄａｌｃｔｏｎｐｏｐｃｓｉａｔｈａｈｅｅｉａｅｅｒｈｌｎｐｐｉａｉｒｓｅｔ．Ｋｅｒｓ：ｎｄｉｅｔｓｃｃｏｒｍｏｄａｔｏｖｏｔｇｅｔａｆｒｒｉｏｉｉｅｙｗｏｄｉｒｃｐａｅｖｅｔｕｌｉｎ；ｌａｒｎｓｅａｔｏ；ｐｔｍｚｄ

基于MATLAB的司接式矩阵变换器的调制策略仿真研究

基于MATLAB的司接式矩阵变换器的调制策略仿真研究严肃
【期刊名称】《变频器世界》
【年(卷),期】2014(000)001
【摘要】作为一种新型矩阵变换器，间接矩阵变换器除了保留了传统矩阵变换器具有的无大体积储雏电容、输入输出电流为正弦波、可实现单位输入功率因数、能量可双向流动等优点外，还具有相对独立的整流侧和逆变侧，通过使用相对成熟的整流和逆变控制策略分别对其整流侧和逆变侧进行调制．仿真结果证实该控制策略设计可靠，控制过程得以简化，控制效果良好．给实际研究和设计提供方便。

【总页数】4页(P81-84)
【作者】严肃
【作者单位】西南交通大学电气工程学院
【正文语种】中文
【中图分类】TM464
【相关文献】
1.基于MATLAB的矩阵变换器空间矢量调制策略仿真 [J], 张大双;高海生
2.基于Matlab仿真模块的矩阵变换器空间矢量调制策略仿真研究 [J], 刘宏洋;杨庆江
3.两种矩阵变换器的调制策略比较仿真研究 [J], 黄伟;程启明;郭凯;徐聪
4.矩阵变换器新型SVPWM调制策略的仿真研究 [J], 李生民;邢新波;鲁静
5.矩阵变换器双空间矢量调制策略的仿真研究 [J], 曹佳佳;李俊贤
因版权原因，仅展示原文概要，查看原文内容请购买。

抑制间接矩阵变换器共模电压的调制策略

第51卷第18期电力系统保护与控制Vol.51 No.18 2023年9月16日Power System Protection and Control Sept. 16, 2023 DOI: 10.19783/ki.pspc.230272抑制间接矩阵变换器共模电压的调制策略马星河1,2，康志鹏1，赵军营1，潘玥1(1.河南理工大学电气工程与自动化学院，河南焦作 454003；2.河南省煤矿装备智能检测与控制重点实验室，河南焦作 454003)摘要：间接矩阵变换器在运行过程中会产生较大的共模电压，对电机系统造成严重的电磁干扰，影响系统正常运行。

针对这一问题，提出一种新的空间矢量调制策略降低共模电压大小，改善输出电压性能。

首先，将整流级空间矢量重新划分区域，根据参考电流矢量所在区域选择3个相邻的有效电流矢量，将有效矢量下的平均直流母线电压维持在一个恒定值，保证整流级的最大输出电压。

其次，逆变级采用无零矢量调制策略，通过使用3个有效电压矢量合成所需要的输出电压，将共模电压峰值抑制到输入相电压幅值的57.7%。

与传统调制策略相比，提出的调制策略不仅可以减轻系统计算负担，还可以减少系统输入输出谐波，改善输入输出波形质量。

最后，通过Matlab/Simulink和实验平台搭建相应模型，仿真和实验结果验证了所提出策略的有效性。

关键词：间接矩阵变换器；共模电压；空间矢量调制；整流级；参考电压Modulation strategy for suppressing the common-mode voltage of an indirect matrix converterMA Xinghe1, 2, KANG Zhipeng1, ZHAO Junying1, PAN Yue1(1. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454003, China;2. Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment, Jiaozuo 454003, China)Abstract: An indirect matrix converter will generate a large common mode voltage during operation, causing serious electromagnetic interference to the motor system and affecting the normal operation of the system. To address this issue, a new space vector modulation strategy is proposed to reduce the size of the common mode voltage and improve output voltage performance. First, the space vector of the rectifier stage is re-divided into regions, and three adjacent effective current vectors are selected based on the region where the reference current vector is located. The average DC bus voltage under the effective vector is maintained at a constant value to ensure the maximum output voltage of the rectifier stage.Second, the inverter stage adopts a ‘no zero vector’ modulation strategy, which suppresses the common mode voltage peak to 0.577 times the input phase voltage amplitude by synthesizing the required output voltage using three effective voltage vectors. Compared with traditional modulation strategies, the proposed modulation strategy not only reduces the computational burden of the system, but also reduces input and output harmonics, improving the quality of input and output waveforms. Finally, a corresponding model is built using Matlab/Simulink and an experimental platform, and the effectiveness of the proposed strategy is verified through simulation and experiment.This work is supported by the National Natural Science Foundation of China (No. U1404522).Key words: indirect matrix converter; common mode voltage; space vector modulation; rectifier side; reference voltage0 引言矩阵变换器(matrix converter, MC)被誉为“绿色变频器”，其具有正弦输入/输出电流波形、能量双向流动和输入功率因数可调等优点[1-5]。

矩阵变换器两种调制策略的比较与分析

矩阵变换器两种调制策略的比较与分析蔡巍;张晓锋;乔鸣忠;何必;朱鹏【期刊名称】《电力系统保护与控制》【年(卷),期】2013(000)010【摘要】对矩阵变换器的两种调制策略进行了分析比较，证明了两者占空比之间的相等关系，指出双电压调制法只是零矢量中置空间矢量调制法调换导通次序的另一种形式。

两种调制法均能实现在输入电压不平衡时的控制，且占空比计算都较为简单，但是采用空间矢量调制法可以完全消除窄脉冲，且能够较为方便地进行电压补偿操作。

分析了两种方法对开关损耗的影响。

由于空间矢量调制法为了消除窄脉冲、提高输出波形质量，在换流时的输出电压在大压差之间反复变化，造成了开关损耗大大上升，而双电压调制法在选通输入电压时均是按电压高低依次排列，因此双电压调制法的开关损耗较小。

故在选择消除窄脉冲和降低开关损耗之间，必须折衷考虑具体选择哪种调制顺序，也可以交替使用，兼有两者的优点。

%The space vector modulation (SVM) and double line voltage modulation (DLVM) for matrix converter are compared. The two modulations are proved to have the same duty-cycle. DLVM is a special modulation sequence of SVM which has one zero-vector in the middle of modulation sequence. Both two modulations can detect unbalanced input voltage real-time and generate balanced output voltage. But SVM with suitable zero vectors can further eliminate short PWM pulses and compensate output voltage at low modulation index. The switching loss of the two modulations is analyzed. The high differential voltage consists in the middle of the SVM modulationsubsequence which will cause high switching loss in the commutation before or after the high differential voltage. However, DLVM has lower switching loss than SVM because DLVM modulates according to the order of the magnitude of the input voltages. The choice between SVM and DLVM depends on request of eliminating short PWM pulses or reducing switching loss. The two modulations can be alternatively used to show both merits. <br> This work is supported by National Natural Science Foundation of China (No. 51007094).【总页数】7页(P111-117)【作者】蔡巍;张晓锋;乔鸣忠;何必;朱鹏【作者单位】海军潜艇学院，山东青岛 266042; 海军工程大学电气与信息工程学院，湖北武汉 430033;海军工程大学电气与信息工程学院，湖北武汉 430033;海军工程大学电气与信息工程学院，湖北武汉 430033;中船重工704所，上海200000;海军工程大学电气与信息工程学院，湖北武汉 430033【正文语种】中文【中图分类】TM464【相关文献】1.两种矩阵变换器的调制策略比较仿真研究 [J], 黄伟;程启明;郭凯;徐聪2.考虑不同调制策略的间接矩阵变换器输入电流谐波特性分析 [J], 梅杨;陈丽莎;王闪闪3.矩阵变换器间接空间矢量过调制策略分析与研究 [J], 夏益辉;乔鸣忠;张晓锋;魏永清4.输入非平衡条件下矩阵变换器两种电流偏置角调制策略的谐波分析 [J], 易灵芝;李志勇;朱建林;王根平;丁伟;唐广迪5.矩阵变换器空间矢量调制策略分析及基于DSP的设计 [J], 夏菲;金新民;童亦斌因版权原因，仅展示原文概要，查看原文内容请购买。

矩阵变换器调制策略的研究

矩阵变换器调制策略的研究矩阵变换器(Matrix Converter,简称MC)是一种直接变换型的交流-交流电力变换装置,具有很多优于传统交流电力变换装置的特性,如:无需大容量的储能元件、电能的双向流通、正弦输入和输出、可控的输入功率因数等。

MC因其诸多的优良性能,越来越受到广大研究人员的青睐,已成为近年来研究的一个热点。

MC的调制策略是其控制方法的核心部分,也是国内外学者一直以来的研究重点。

因此,本文针对3×3MC带三相平衡负载和3×4MC带三相不平衡负载的调制策略进行了研究。

MC控制策略的复杂性限制了其在实际中的应用。

针对3×3MC,在分析和比较现有调制策略的基础上,提出一种新型间接变换式调制策略。

该调制策略是基于3×3MC等效交-直-交拓扑上的,为方便逆变级的调制,使整流级调制输出平均值为常数且幅值最大的直流电压,同时为满足对电网无污染要求,使输入电流正弦且功率因数为1。

根据上述目标列写以占空比为变量的方程组并联立求解出整流级的占空比表达式。

对逆变级采用传统电压空间矢量调制,综合整流级和逆变级的调制得到新的调制策略。

将新调制策略与双空间矢量调制策略进行了比较,计算量上有所降低,具有重要的实际意义。

实际电网电压的非对称工况也是MC走出实验室、迈入工业应用之前所要考虑的。

在输入电压非对称情况下,分析了应用对称电压下调制策略对输出电压和输入电流的影响。

通过在整流级占空比中加入适当负序电压分量来改进调制策略,使得整流级输出的直流电压平均值仍然为恒定值,逆变级调制不作任何改变就能输出所期望的参考电压。

改进后的占空比可能出现负值,给出了一种负占空比的实现方法。

改进调制策略同时能消除输入电流中的低次谐波分量,对电流波形有所改善。

实际三相电源的负载不一定是平衡负载,所以常要求变换器电源具有对不平衡负载供电的能力,这就需要3×4MC。

为了将3×3MC的研究成果应用到3×4MC上,提出一种3×3MC到3×4MC调制策略的“增补”思想。

间接式矩阵变换器开路故障检测技术研究

间接式矩阵变换器开路故障检测技术研究间接式矩阵变换器(Indirect Matrix Converter,IMC)由直接式矩阵变换器(Direct Matrix Converter,DMC)衍生而来,IMC具有能量可双向流动、输入输出波形正弦、可四象限运行等特点。

此外,相比传统的两级式变频器,IMC摒弃中间储能环节,体积小,系统可靠性高,在工业领域具有良好的应用前景。

为了提高IMC在运行过程中的可靠性,研究其故障检测技术具有重要的意义。

然而,学术界目前还少有IMC故障检测相关的文献,也尚未完成IMC故障检测实验验证。

本文主要对IMC功率器件开路故障检测技术进行研究。

本文首先介绍了IMC 的基本拓扑结构及其数学模型,分析了广泛应用于IMC的空间矢量调制策略,并进一步总结了该调制算法的特点,为下文的电路分析奠定理论基础。

文中结合IMC实际电路结构,分析了功率器件开路故障的类型,并对故障状态下电流的续流回路展开了研究。

然后,本文详细分析了整流级单个双向开关开路故障下的电路特点、逆变级单个单向开关开路故障下的电路特点、开路故障下直流母线电压的特点。

在以上电路分析的基础上,针对发生在整流级上的开路故障和发生在逆变级上的开路故障,分别提出了整流级开路故障检测方法和逆变级开路故障检测方法。

在Matlab/Simulink环境里搭建了一个IMC故障检测仿真模型,仿真结果和故障状态下的电路分析相符,验证了所提故障检测方法的正确性和合理性。

最后,本文设计并搭建了一套IMC实验样机,文中详细介绍了系统的硬件电路设计和控制软件设计。

在此基础上,对所提IMC故障检测方法展开了实验研究与分析,实验结果验证了本文所提故障检测方法的可行性。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第2章间接式矩阵变换器的调制策略间接式矩阵变换器是一种新型矩阵变换器，除了保留了直接式矩阵变换器无大体积储能电容、输入输出电流为正弦波、可实现单位输入功率因数、能量可双向流动等优点外，由于具有相对独立的整流侧和逆变侧，因此可以用成熟的整流和逆变控制策略分别对其整流侧和逆变侧进行调制。

在本文中，对间接式矩阵变换器的整流侧采用PWM 调制，对逆变侧采用SVPWM 调制。

2.1 整流侧的PWM 调制设间接式矩阵变换器的三相输入相电压为()()()()()()i a a b im b im i c c i cos cos cos cos 120cos cos 120t u u U U t u t ωθθωθω⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥===-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦+⎣⎦⎣⎦i u(2-1)整流侧要求使中间直流电压dc 0U >。

为了充分提高电压传输比，按照如图2-1 所示的方法，在每个输入周期内将输入电压a u ，b u ，c u 平均划分为编号为1到6的6等份，每等份占/3π电角度，每一等份称为一个扇区。

1234561au bu cu图2-1 输入电压扇区划分如果按照图示的划分方法，则在每个扇区中，三相输入相电压都会有如下特点：一相电压的绝对值最大，另外两相电压与之反向。

例如，在第1扇区，a u 的绝对值最大，且为正值，b u 和c u 都为负值；在第2扇区，c u 的绝对值最大，且为负值，a u 和c u 都为正值。

假设在某个周期内，(),,k k a b c =相输入电压绝对值最大，l 和m 为与k 反向的另外两相电压，如果k 为正值，则在一个PWM 周期内，对照绪论中图1-4，整流侧双向开关kp S 始终导通，ln S 和mn S 轮流导通；如果k 为负值，则整流侧双向开关kn S 始终导通，lp S 和mp S 轮流导通。

例如在第6扇区，b U 的绝对值最大且为负值，则双向开关bn S 始终导通，ap S 和cp S 轮流导通。

当bn S 和ap S 导通时，输出直流电压dc a b ab U u u u =-=；当bn S 和cp S 导通时，输出直流电压dc c b cb U u u u =-=。

其他5个扇区的分析方法与第6扇区相同。

显然，在每个PWM 周期内，直流电压由两段构成，即直流侧按照一定的占空比输出两段相对较大的线电压。

例如在第6扇区，占空比计算为a abb ccb b u d u u d u ⎧=-⎪⎪⎨⎪=-⎪⎩(2-2) 当三相输入电压平衡时，ab cb 1d d +=，在第6扇区中一个PWM 调制周期内直流电压平均值为()imdc ab ab cb cb b 32cos U U d u d u θ=+=(2-3)其他五个扇区的占空比计算方法与第6扇区相同，其开关导通状态、输出直流电压、占空比见表2-1所示。

每个PWM 调制周期内的直流电压平均值为()imdc 32cos in U U θ=(2-4)其中im U 为输入相电压最大值，()()()()()a b c cos max cos ,cos ,cos in θθθθ=。

表2-1六扇区整流器的开关状态和直流电压扇区第一段第二段导通开关直流电压dc U占空比导通开关直流电压dc U占空比1 ap S 、bn S a b u u - b a /u u - ap S 、cn S a c u u - c a /u u -2 bp S 、cn S b c u u - b c /u u - ap S 、cn S a c u u - a c /u u -3 bp S 、cn S b c u u - c b /u u - bp S 、an S b a u u - a b /u u -4 cp S 、an S c a -u u c a /u u - bp S 、an S b a u u - b a /u u -5 cp S 、an S c a -u u a c /u u - cp S 、bn S c b -u u b c /u u - 6ap S 、bn Sa b u u -a b /u u -cp S 、bn Sc b -u uc b /u u -因此，间接式矩阵变换器整流侧的调制步骤包括确定输入电压所在扇区、确定合成直流电压的两个线电压、计算占空比、给开关器件触发脉冲。

2.2 逆变侧的SVPWM 调制由于逆变侧和交-直-交变频器的逆变侧一致，因此可以运用已经成熟的逆变侧调制策略对间接式矩阵变换器的逆变侧进行调制，包括正弦波脉宽调制(SPWM)、电流滞环跟踪法调制、电压空间矢量脉宽调制(SVPWM)等。

SPWM 调制运用载波和三角波比较的方式调制，目的是使得逆变器输出的电压波形尽量接近正弦波；电流滞环跟踪法调制则控制逆变器的输出电流，通过开关动作使输出电流逼近给定的正弦信号；而SVPWM 调制的目的是控制电机磁链为旋转圆形磁场，从而使得电机产生恒定的电磁转矩，因此这种方法又称为“磁链跟踪控制”。

SVPWM 方法适用于交流电机矢量控制调速系统，相对于SPWM 方法可改善变频器提供给交流电机的电能质量[67]，因此在本文中用SVPWM 方式对间接式矩阵变换器的逆变侧进行调制。

如图2-2所示，ABC 为交流电机定子绕组组成的一个静止坐标系，用加在各相绕组上的相电压定义为三个空间电压矢量A u ，B u 和C u ，其大小按照正弦规律变化，方向在各自相的轴线上，互相成120°。

设s u 为定子三相电压空间合成矢量，则=++s A B C u u u u 。

同理，定义s ψ为定子三相磁链空间合成矢量，s I 为定子三相电流空间合成矢量。

那么R =+s s s u I ψ (2-5)可以证明，当三相对称正弦电压给交流电机供电时，交流电机磁链幅值m ψ为定值，且磁链轨迹为圆形时，合成电压s u 的大小与输入电压频率成正比，方向磁链矢量s ψ正交，即与磁链轨迹的切线方向一致，这样即可将交流电机磁场轨迹的问题转化为空间电压矢量的问题[68]。

ABCωAu Bu Cu su图2-2 电压空间矢量间接式矩阵变换器的逆变侧模型如图2-3所示。

逆变侧一共有6个开关组成，其中A S 和A S '为A 相开关，B S 和B S '为B 相开关，C S 和C S '为C 相开关。

A S 、B S 和C S 为上桥臂开关，A S '、B S '和C S '为下桥臂开关。

BCAdcU +-dci AS AS 'B S 'CS 'CS BS图2-3 逆变侧的模型用数字“1”代表上桥臂导通，下桥臂关断；用数字“0”代表下桥臂导通，上桥臂关断。

将三个桥臂的开关状态分别按照A 、B 、C 相的顺序写成一个序列，则可用一组数代表整个逆变侧的一种开关状态。

例如，(101)代表A 相上桥臂、B 相下桥臂和C 相上桥臂导通，而A 相下桥臂、B 相上桥臂和C 相下桥臂关断。

根据开关状态的不同，逆变侧共有328=种工作状态，即8个空间矢量：(100)，(110)，(010)，(011)，(001)，(101)，(000)和(111)。

其中只有前六种空间矢量是有效的，而后两种空间矢量输出零电压，称为零矢量。

六个有效空间矢量的顶点构成一个正六边形[69]，如图2-4所示。

o123456()1100U ()2110U ()3010U ()4011U ()5001U ()6101U 07U U ，refU AU BU CU αβm md U n nd U refU SVθn U mUa) b)图2-4 空间电压矢量的划分如图2-4 a)所示，也将输出空间电压矢量也划分为6个扇区，输出电压矢量ref U 落在其中一个扇区内。

设ref U 为某一刻期望输出线电压空间矢量，与之相邻的两个有效空间矢量为m U 和n U ，ref U 与m U 的夹角为SV θ，则ref U 可由m U 和n U 合成，如图2-4 b)所示，即ref 00m m n n U d U d U d U =++ (2-6)m U ，n U 和0U （零矢量）的占空比计算公式为V SV V SV 0sin()sin(60)1m n m n d m d m d d dθθ=⎧⎪=-⎨⎪=--⎩(2-7) 其中V m 为逆变侧的调制系数()()lm lm V VV dc im2cos cos ,013in in U U m m m U U θθ''===≤≤ (2-8) 式中lm U 为输出线电压幅值，由于dc U 为一时变量，因此V m 也是一时变量，()cos in θ部分用来与直流电压波动相抵消，以保证输出线电压空间矢量幅值恒定。

由于输出相电压()om lm 3/3U U =⋅，由式(2-8)得间接式矩阵变换器的电压传输比为V V32G m '=(2-9) 当V1m '=时，间接式矩阵变换器的电压传输比达到其最大值0.866。

因此，间接式矩阵变换器逆变侧调制步骤包括确定所在扇区、确定相邻有效空间矢量、计算占空比、给开关器件触发脉冲。

2.4 本章小结本章介绍了矩阵变换器的调制策略，包括整流侧的PWM 调制和逆变侧的SVPWM 调制。

在调制策略的基础上，给出了仿真波形，并接阻感性负载进行了仿真。

仿真结果表明间接式矩阵变换器可以输出可调频率的电压，实现变频器的功能，输出电压电流波形为正弦波。

第3章永磁同步电机控制系统的设计永磁同步电机的转子是由永磁体制成的，具有结构简单、功率密度高、可靠性高、体积小等优点。

由于转子为永磁体，不需要额外的励磁绕组，因而控制方法比较简单，且电机转速与电机的输入频率严格成正比。

如今，永磁同步电机广泛应用于航空航天、机器人、数控机床等领域。

间接式矩阵变换器由于体积小、能量可双向流动、可实现单位输入功率、输入输出电流为正弦波、可分别对整流侧和逆变侧进行控制等优点，将间接式矩阵变换器与永磁同步电机进行结合，具有很好的应用前景。

本章设计基于间接式矩阵变换器的永磁同步电机控制系统。

3.1 坐标变换坐标变换是交流电机矢量控制重要的方法，可以将交流电机模型转化为直流模型，方便电机的控制。

坐标变换包括静止三相—两相变换(3s/2s 变换)、两相—两相旋转变换(2s/2r)、直角坐标—极坐标变换(K/T)，本文需要用到前两种。

3.1.1三相静止—两相静止变换(3s/2s 变换)电机定子绕组通以三相对称电流，在气隙中产生空间旋转的圆形磁场。

根据功率不变原则和磁动势相等的原则，如图3-1所示，可以将三相对称电流产生的旋转磁场等效为两相对称电流产生的旋转磁场。