高中数学 滚动训练9(无答案)苏教版

第3讲平面向量12021江苏兴化第一中学月考向量a=1,,b=-2,1,假设a⊥b,那么实数= 22021江苏南通中学期末化简:in13°co17°in17°co13°=32021江苏五校学情检测向量a=2,-6,b=-1,m,假设a∥b,那么实数m的值为4|a|=2,|b|=3,a与b的夹角为60°,那么|a-3b|=52021江苏宿迁期末假设in(α-π6)=13,其中π76(2π3-α)(α>0,|α|<π2)αα⃗⃗⃗⃗⃗⃗⃗⃗⃗ αα⃗⃗⃗⃗⃗⃗⃗⃗⃗ 0,ω>0的图象与直线=m的三个相邻交点的横坐标分别是π6,π3,2π3,那么实数ω的值为82021江苏南京多校段考向量a=coθ,inθ,b=2,-11假设a⊥b,求sinα-cosαsinα+cosα的值;2假设|a-b|=2,θ∈(0,π2),求in(α+π4)的值92021江苏盐城高三期中设直线=-π6是函数f=inaco的图象的一条对称轴1求函数f的最大值及取得最大值时的值;2求函数f在[0,π]上的减区间答案精解精析1答案 2解析 由a⊥b 得a·b=-2=0,那么=22答案 12解析 原式=in13°17°=in30°=123答案 3解析 由a∥b 得2m=6,解得m=34答案 √67解析 a·b=|a|·|b|co60°=3,那么|a-3b|=√(α-3α)2=√4-18+81=√675答案 -2√23解析 由π<α<7π6得5π6<α-π6<π, 又in (α-π6)=13,那么co (α-π6) =-√1-sin 2(α-π6)=-2√23, 那么in (2π3-α)=in [π2-(α-π6)] =co (α-π6)=-2√236答案 √3-4解析 由图象可得最小正周期T=12=2πα,即ω=π6,M1,2,N7,-2在图象上,那么f1=2in (π6+φ)=2,|φ|<π2,那么φ=π3,那么f=2in (π6x +π3),那么f2=2in 2π3=√3,f5=2in 7π6=-1,故P2,√3,Q5,-1,所以αα⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·αα⃗⃗⃗⃗⃗⃗⃗⃗⃗ =1,√3-2·-2,1=-2√3-2=√3-47答案 4解析 由题意可得该函数的最小正周期T=2π3-π6=π2,那么ω=2πα=48解析 1由a⊥b 可知,a·b=2coθ-inθ=0,所以inθ=2coθ,所以sin α-cos αsin α+cos α=2cos α-cos α2cos α+cos α=13 2由a-b=coθ-2,inθ1可得|a-b|=√(cos α-2)2+(sin α+1)2=√6-4cos α+2sin α=2,即1-2coθinθ=0①又co 2θin 2θ=1,且θ∈(0,π2),② 由①②可解得{sin α=35,cos α=45, 所以in (α+π4)=√22inθcoθ=√22×(35+45)=7√210 9解析 1∵直线=-π6是函数f 的图象的一条对称轴, ∴f (-π6+x )=f (-π6-x )对∈R 恒成立 ∴in (-π6+x )aco (-π6+x ) =in (-π6-x )aco (-π6-x ) 对∈R 恒成立,即a √3in=0对∈R 恒成立,得a=-√3从而f=in-√3co=2in (α-π3) 故当-π3=2ππ2∈Z,即=2π5π6∈Z 时,f 取得最大值2 2由2ππ2≤-π3≤2π3π2,解得2π5π6≤≤11π62π,∈Z 取=0,可得函数f 在[0,π]上的减区间为[5π6,π]。

CDBB C 1A1 13题图苏教版高二数学滚动练习8一、填空题1.已知点B 是点A （2，-3，5），关于平面xOy 的对称点，则=AB 2. 若圆心在x 的圆O 位于y 轴左侧，且与直线x+2y=0相切，则圆O 的方程是3. 已知双曲线x 2a 2－y 2b 2＝1的一条渐近线方程为y ＝43x ，则双曲线的离心率为4. 抛物线2y x =-上的点到直线4380x y +-=距离的最小值是5. 若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合，则p 的值为 6. 已知a 、b 是直线，α、β、γ是平面，给出下列命题：①若α∥β，a ⊂α，则a ∥β ②若a 、b 与α所成角相等，则a ∥b ③若α⊥β、β⊥γ，则α∥γ ④若a ⊥α, a ⊥β，则α∥β 其中正确的命题的序号是________________.7. 以等腰直角三角形ABC 斜边BC 上的高AD 为折痕，将△ABC 折成直二面角 时，在折成的图形中，△ABC 的形状为 .8. 如图所示,E ，F 分别是正方形SD 1DD 2的边D 1D ，DD 2的中点,沿 SE ,SF ,EF 将其折成一个几何体,使D 1,D ,D 2重合,记作D . 给出下列位置关系: ①SD ⊥面DEF ；②SE ⊥面DEF ； ③DF ⊥SE ； ④EF ⊥面SED . 其中成立的有: . 9. 如图，已知A （4，0）、B （0，4），从点P （2，0）射出的光线经直线AB 反向后再射到直线OB 上，最后经直线OB 反射后又回到P 点，则光线所经过的路程是10. 圆034222=-+++y x y x 上到直线x ＋y ＋1＝0的距离为2的点共有11. 若直线y x b =+与曲线3y =b 的取值范围是12. 已知12F F ，为双曲线22221(00)a b x y a b a b≠-=>>且，的两个焦点，P 为双曲线右支上异于顶点的任意一点，O 为坐标原点．下面四个命题①.12PF F △的内切圆的圆心必在直线x a =上；②.12PF F △的内切圆的圆心必在直线x b =上；③.12PF F △的内切圆的圆心必在直线OP 上；④.12PF F △的内切圆必通过点0a ()，．其中真命题的代号是（写出所有真命题的代号）．1213. 如图直三棱柱ABB 1-DCC 1中，∠ABB 1=90AB =4，BC =2，CC 1=1，DC 上有一动点P ， 则△APC 1周长的最小值是 .14. 如图，在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点．现将AFD ∆沿AF 折起，使平面ABD ⊥平面ABC ．在平面ABD 内过点D 作DK AB ⊥，K 为垂足．设AK t =，则t 的取值范围是 ．二、解答题15. 已知直线l 1：02=-+y x 和l 2：047=--y x ，过原点O 的直线与L 1、L 2分别交A 、B 两点,若O 是线段AB 的中点，求直线AB 的方程。

目录高考数学一轮复习基础夯滚天天练(1) 集合的基本运算高考数学一轮复习基础夯滚天天练(2) 命题和逻辑联结词高考数学一轮复习基础夯滚天天练(3) 充分条件和必要条件高考数学一轮复习基础夯滚天天练(4) 函数及其表示方法高考数学一轮复习基础夯滚天天练(5) 函数的解析式和定义域高考数学一轮复习基础夯滚天天练(6) 函数的值域和最值高考数学一轮复习基础夯滚天天练(7) 函数的单调性和奇偶性高考数学一轮复习基础夯滚天天练(8) 函数的图象高考数学一轮复习基础夯滚天天练(9) 二次函数高考数学一轮复习基础夯滚天天练(10) 函数的应用高考数学一轮复习基础夯滚天天练(11) 指数与对数高考数学一轮复习基础夯滚天天练(12) 幂函数、指数函数与对数函数高考数学一轮复习基础夯滚天天练(13) 函数与方程高考数学一轮复习基础夯滚天天练(14) 导数的概念及运算高考数学一轮复习基础夯滚天天练(15) 导数在研究函数中的简单应用高考数学一轮复习基础夯滚天天练(16) 同角三角函数的关系及诱导公式高考数学一轮复习基础夯滚天天练(17) 三角函数的图象高考数学一轮复习基础夯滚天天练(18) 三角函数的性质(1)高考数学一轮复习基础夯滚天天练(19) 三角函数的性质(2)高考数学一轮复习基础夯滚天天练(20) 和差倍角的三角函数高考数学一轮复习基础夯滚天天练(21) 正弦定理和余弦定理高考数学一轮复习基础夯滚天天练(22) 三角函数及解三角形高考数学一轮复习基础夯滚天天练(23) 一元二次不等式高考数学一轮复习基础夯滚天天练(24) 简单的线性规划高考数学一轮复习基础夯滚天天练(25) 基本不等式及其应用高考数学一轮复习基础夯滚天天练(26) 直线的斜率和直线的方程高考数学一轮复习基础夯滚天天练(27) 两条直线的位置关系高考数学一轮复习基础夯滚天天练(28) 圆的方程高考数学一轮复习基础夯滚天天练(29) 直线与圆、圆与圆的位置关系高考数学一轮复习基础夯滚天天练(30) 直线与圆的综合运用高考数学一轮复习基础夯滚天天练(31) 椭圆(1)高考数学一轮复习基础夯滚天天练(32) 椭圆(2)高考数学一轮复习基础夯滚天天练(33) 双曲线高考数学一轮复习基础夯滚天天练(34) 抛物线高考数学一轮复习基础夯滚天天练(35) 圆锥曲线高考数学一轮复习基础夯滚天天练(36) 向量的概念与线性运算高考数学一轮复习基础夯滚天天练(37) 平面向量的基本定理与坐标运算高考数学一轮复习基础夯滚天天练(38) 平面向量的数量积高考数学一轮复习基础夯滚天天练(39) 平面向量的应用高考数学一轮复习基础夯滚天天练(40) 复数的概念、几何意义及运算高考数学一轮复习基础夯滚天天练(41) 数列的概念高考数学一轮复习基础夯滚天天练(42) 等差数列高考数学一轮复习基础夯滚天天练(43) 等比数列高考数学一轮复习基础夯滚天天练(44) 等差数列与等比数列高考数学一轮复习基础夯滚天天练(45) 数列的通项与求和高考数学一轮复习基础夯滚天天练(46) 数列综合题高考数学一轮复习基础夯滚天天练(47) 平面的基本性质、空间两直线高考数学一轮复习基础夯滚天天练(48) 直线与平面的位置关系高考数学一轮复习基础夯滚天天练(49) 平面与平面的位置关系高考数学一轮复习基础夯滚天天练(50) 柱、锥、台、球的表面积与体积高考数学一轮复习基础夯滚天天练(51) 空间线面关系的判断、推证与计算高考数学一轮复习基础夯滚天天练(52) 抽样方法与总体估计高考数学一轮复习基础夯滚天天练(53) 算法的含义与流程图高考数学一轮复习基础夯滚天天练(54) 基本算法语句高考数学一轮复习基础夯滚天天练(55) 随机事件的概率、古典概型高考数学一轮复习基础夯滚天天练(56) 几何概型高考数学一轮复习基础夯滚天天练(57) 合情推理与演绎推理高考数学一轮复习基础夯滚天天练(58) 直接证明与间接证明高考数学一轮复习基础夯滚天天练(59) 热点知识练(1)高考数学一轮复习基础夯滚天天练(60) 热点知识练(2)参考答案121滴水穿石·数学一轮基础夯滚天天练>>>高考数学一轮复习基础夯滚天天练(1)集合的基本运算班级________姓名____________学号______成绩______日期____月____日一、填空题1. 已知集合A＝{0，1，2，3}，B＝{2，3，4，5}，则A∪B中元素的个数为________．2. 设集合M＝{m∈Z|－3<m<2}，N＝{n∈Z|－1≤n≤3}，则M∩N＝________________________________________________________________________.3. 已知全集U＝R，集合A＝{x|－2≤x≤3}，B＝{x|x<－1或x>4}，那么集合A∩∁U B ＝________．4. 已知全集U＝{0，1，2，3，4，5，6，7，8，9}，集合A＝{0，1，3，5，8}，集合B＝{2，4，5，6，8}，则∁U A∩∁U B＝________．5. 设集合S＝{x||x－2|>3}，T＝{x|a<x<a＋8}，S∪T＝R，则实数a的取值范围是________．6. 已知集合A＝{－1，2，2a＋1}，B＝{－4，3}，且A∩B＝{3}，则a＝________．7. 已知集合A＝{－3，x2，x＋1}，B＝{x－3，2x－1，x2＋1}，若A∩B＝{－3}，则A∪B ＝________________．8. 已知集合P＝{－1，2}与M＝{x|kx＋1＝0}满足P∪M＝P，则实数k的值所组成的集合是______________．9. 已知集合A ＝{x|y ＝log 2(x 2－1)}，B ＝⎩⎨⎧⎭⎬⎫y|y ＝⎝⎛⎭⎫12x －1，则A ∩B ＝______________．10. 集合B ＝{y ∈R |y ＝2x ，x ∈A }，则A ∩B ＝________．11. 定义集合运算：A*B ＝{z|z ＝x·y ，x ∈A ，y ∈B}．设A ＝{1，2}，B ＝{0，2}，则集合A*B 的所有元素之和为________．12. A ，B 是非空集合，定义A ×B ＝．若A ＝{x|y ＝x 2－3x}，B ＝{y|y ＝3x }，则A ×B ＝________．13. 若x ∈A ，且11－x∈A ，则称集合A 为“和谐集”．已知集合M ＝{－2，－1，－12，0，1，12，23，2，3}，则集合M 的子集中，“和谐集”的个数为________．14. 若集合{a ，b ，c ，d}＝{1，2，3，4}，且下列四个关系：①a ＝1；②b ≠1；③c ＝2；④d ≠4有且只有一个是正确的，则符合条件的有序数组(a ，b ，c ，d)的个数是________．二、 解答题15. 已知集合M ＝{x|2x －4＝0}，N ＝{x|x 2＋3x ＋m ＝0}．(1) 当m ＝2时，求M ∩N ，M ∪N ；(2) 若M ∩N ＝M ，求集合N.高考数学一轮复习基础夯滚天天练(2)命题和逻辑联结词班级________ 姓名____________ 学号______ 成绩______ 日期____月____日一、 填空题1. 命题的否定是____________________________．2. 已知命题“x ∈R ，使得x 2＋(a －1)x ＋1<0”是假命题，则实数a 的取值范围是________．3. 设命题p ：函数y ＝sin 2x 的最小正周期为π2；命题q ：函数y ＝cos x 的图象关于直线x ＝π2对称，则“p ∧q ”为________命题．(填“真”或“假”)4. 给出以下四个命题：①“若x ＋y ＝0，则x ，y 互为相反数”的逆命题；②“全等三角形的面积相等”的否命题；③“若q ≤－1，则x 2＋x ＋q ＝0有实根”的逆否命题；④“不等边三角形的三个内角相等”的逆否命题．其中真命题的序号为________．5. 已知命题p ：x ≤0，x 2＋2x －3≥0，则命题p 的否定是__________________________．6. 已知命题p ：x 2－2x －3<0；命题q ：1x －2<0.则x 的取值范围是________．7. 已知命题p ：“a ＝1”是“x>0，x ＋a x≥2”的充要条件；则下列命题正确的是________．(填序号)8. 命题“存在一个无理数，它的平方是有理数”的否定是________________________________________________________________________．9. 下列四个命题：①若一个命题的逆命题为真，则这个命题的逆否命题一定为真；②“a>b”与“a ＋c>b ＋c ”不等价；③“若a 2＋b 2＝0，则a ，b 全为0”的逆否命题是“若a ，b 全不为0，则a 2＋b 2≠0”； ④若一个命题的否命题为真，则这个命题的逆命题一定为真．其中不正确的是________．(填序号)10. 则a的取值范围是________．11. 则实数a的最小值为________．12. 如果不等式(a－2)x2＋2(a－2)x－4<0对于恒成立，那么a的取值范围为________．13. 若命题“,2x2－3ax＋9<0”为假命题，则实数a的取值范围为________________________________________________________________________．二、解答题14. 给定两个命题，p：对任意实数x，ax2＋ax＋1>0恒成立；q：关于x的方程x2－x＋a＝0有实数解．如果p与q中有且仅有一个为真命题，求实数a的取值范围．高考数学一轮复习基础夯滚天天练(3)充分条件和必要条件班级________ 姓名____________ 学号______ 成绩______ 日期____月____日一、 填空题1. 设x ∈R ，则“x >12”是“2x 2＋x －1>0”的____________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)2. “ac 2>bc 2”是“a>b”成立的____________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)3. “x<－1”是“x 2－1>0”的____________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)4. 已知向量a ＝(x －1，2)，b ＝(2，1)，则a ⊥b 的充要条件是________________．5. “M>N”是“log 2M>log 2N”成立的____________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)6. 若a ，b 为实数，则“0<ab<1”是“b<1a”的____________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)7. 方程x 2k ＋1＋y 2k －5＝1表示双曲线的充要条件是____________． 8. 设p ，q 是两个命题，若p 是q 的充分不必要条件，那么非p 是非q 的____________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)9. “a ＝1”是“函数f(x)＝2x －a 2x ＋a在其定义域上为奇函数”的____________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)10. “x<2”是“x 2－x －2<0”的____________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)11. 不等式1x －1<1的解集记为p ，关于x 的不等式x 2＋(a －1)x －a>0的解集记为q ，已知p 是q 的充分不必要条件，则实数a 的取值范围是________．12. 已知直线l 1：x ＋ay ＋6＝0和l 2：(a －2)x ＋3y ＋2a ＝0，则l 1∥l 2的充要条件是______________．13. 已知p ：12≤x ≤1，q ：(x －a)(x －a －1)>0，若p 是的充分不必要条件，则实数a的取值范围是________．14. 下列四个命题：①“，x 2－x ＋1≤0”的否定； ②“若x 2＋x －6≥0，则x >2”的否命题；③在△ABC 中,“A >30°”是“sin A >12”的充分不必要条件； ④“函数f (x )＝tan(x ＋φ)为奇函数”的充要条件是“φ＝k π(k ∈Z )”．其中真命题的序号是________．二、解答题15. 若f(x)是R上的减函数，且f(0)＝3，f(3)＝－1，设P＝{x||f(x＋t)－1|<2}，Q＝{x|f(x)<－1}．若“x∈Q”是“x∈P”的必要不充分条件，求实数t的取值范围．高考数学一轮复习基础夯滚天天练(4)函数及其表示方法班级________ 姓名____________ 学号______ 成绩______ 日期____月____日一、 填空题1. 有以下判断：其中判断正确的序号是________．①f(x)＝|x|x 与g(x)＝⎩⎪⎨⎪⎧1， x ≥0，－1， x<0表示同一函数； ②函数y ＝f(x)的图象与直线x ＝1的交点最多有1个；③f(x)＝x 2－2x ＋1与g(t)＝t 2－2t ＋1是同一函数；④若f(x)＝|x －1|－|x|，则f ⎝⎛⎭⎫f ⎝⎛⎭⎫12＝0.2. 下列四组中的f(x)，g(x)表示同一个函数的是________．(填序号)①f(x)＝1，g(x)＝x 0； ②f(x)＝x －1，g(x)＝x 2x－1； ③f(x)＝x 2，g(x)＝(x)4; ④f(x)＝x 3，g(x)＝3. 若f(x)＝x 2＋bx ＋c ，且f(1)＝0，f(3)＝0，则f(－1)＝________．4. 设函数f(x)＝⎩⎪⎨⎪⎧x 2＋1，x ≤1，2x， x>1，则f(f(3))＝________．5. 已知a ，b 为两个不相等的实数，集合M ＝{a 2－4a ，－1}，N ＝{b 2－4b ＋1，－2}，f ：x →x 表示把M 中的元素x 映射到集合N 中仍为x ，则a ＋b ＝________．6. 函数y ＝f(x)的图象与直线x ＝a(a 为常数)交点的个数为________．7. 已知f(x)是定义在R 上的奇函数，当x <0时f (x )＝log 2(2－x )，则f (0)＋f (2)的值为________．8. 已知函数f(x)＝⎩⎪⎨⎪⎧－x 2， x ≥0，x 2＋2x ， x<0，则不等式f(f(x))≤3的解集为____________．9. 已知函数f(x)的图象如图所示，则它的一个解析式是________________．10. 已知f(x)＝⎩⎪⎨⎪⎧x 2＋1，x ≥0，－2x ， x<0，若f(m)＝10，则m ＝________． 11. 已知f(2x ＋1)＝x 2－2x ，则f(3)＝________．12. 已知下列四组函数：①f(x)＝lg x 2，g(x)＝2lg x ；②f(x)＝x －2，g(x)＝x 2－4x ＋4；③f(x)＝1x －1，g(x)＝x ＋1x 2－1； ④f(x)＝x ，g(x)＝log a a x (a>0且a ≠1)．其中表示同一个函数的为________．(填序号)13. 已知映射f ：A →B ，其中A ＝B ＝R ，对应法则f ：x →y ＝－x 2＋2x ，对于实数k ∈B ，在集合A 中不存在元素与之对应，则k 的取值范围是________．二、 解答题14. 在边长为2的正方形ABCD 的边上有动点M ，从点B 开始，沿折线BCDA 向点A 运动，设点M 运动的距离为x ，△ABM 的面积为S.(1) 求函数S ＝f(x)的解析式、定义域和值域；(2) 求f(f(3))的值．高考数学一轮复习基础夯滚天天练(5)函数的解析式和定义域班级________ 姓名____________ 学号______ 成绩______ 日期____月____日一、 填空题1. 函数y ＝2x －x 2的定义域是________________．2. 函数y ＝16－x －x2的定义域是________________．3. 已知实数m ≠0，函数f(x)＝⎩⎪⎨⎪⎧3x －m ， x ≤2，－x －2m ， x>2，若f(2－m)＝f(2＋m)，则实数m 的值为________________．4. 若一系列函数的解析式相同，值域相同但定义域不同，则称这些函数为“孪生函数”．那么函数解析式为y ＝2x 2＋1，值域为{3，19}的“孪生函数”共有________种．5. 已知f(x)为一次函数，且f(f(x))＝4x －1，则函数f(x)的解析式为f(x)＝________________________________________________________________________.6. 已知二次函数y ＝f(x)满足条件f(x ＋1)－f(x)＝2x ，f(0)＝1，则f(x)的表达式为f(x)＝____________．7. 函数的定义域是________________．8. 函数y ＝x （x －1）＋x 的定义域是________________．9. 若定义在R 上的偶函数f (x )和奇函数g (x )满足f (x )＋g (x )＝e x ，则g (x )＝________．10. 已知函数y ＝f(x ＋1)的定义域是[－2，3]，则函数y ＝f(2x －1)的定义域为________．11. 函数f(x)＝lg (2x －3x )的定义域是________．12. 若函数y ＝f(x)的定义域是[0，8]，则函数g(x)＝f （2x ）ln x的定义域是________________________________________________________________________．13. 若函数f(x)＝x －4mx 2＋4mx ＋3的定义域为R ，则实数m 的取值范围是________．14. 已知二次函数y ＝f(x)(x ∈R )的图象过点(0，－3)，且f (x )>0的解集为(1，3)，则f (x )的解析式为f (x )＝________________．二、 解答题15. 如图所示，有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，且上底CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域．高考数学一轮复习基础夯滚天天练(6)函数的值域和最值班级________ 姓名____________ 学号______ 成绩______ 日期____月____日一、 填空题1. 函数y ＝x －x ＋1的值域为__________．2. 函数y ＝4－x 2的值域是________．3. 函数y ＝x 2＋3x ＋1的值域是____________________．4. 函数y ＝x －x 的值域为________．5. 函数f(x)＝2x －12x ＋1的值域为________．6. 已知函数y ＝x 2－2x ＋3⎝⎛⎭⎫0≤x ≤32，则函数的最大值和最小值的积是________．7. 函数f(x)＝⎩⎪⎨⎪⎧2x ， x ≤0，－x 2＋1， x>0的值域为________．8. 函数f(x)＝log 2(4－x 2)的值域为________．9. 设函数f(x)＝⎩⎨⎧2x ＋a ，x>2，x ＋a 2，x ≤2，若函数f(x)的值域为R ，则实数a 的取值范围是__________________．10. 函数f(x)＝⎩⎪⎨⎪⎧2x ， x ≥0，－2－x， x<0的值域是________________．11. 已知函数y ＝ax 2＋2x ＋1的值域为[0，＋∞)，则实数a 的取值范围是________．12. 已知函数f(x)＝x 2－1，g(x)＝－x ，令φ(x)＝max [f(x)，g(x)](即f(x)和g(x)中的较大者)，则φ(x)的最小值为________．13. 已知函数f(x)＝x ＋p x ＋1(x>－1，p 为正常数)，g(x)＝⎝⎛⎭⎫12－x 2＋2(x ∈R )有相同值域，则p ＝________．14. 下列几个命题：①函数f(x)＝(x)2与g(x)＝x表示的是同一个函数；②若函数f(x)的定义域为[1，2]，则函数f(x＋1)的定义域为[2，3]；③若函数f(x)的值域是[1，2]，则函数f(x＋1)的值域为[2，3]；④若函数f(x)＝x2＋mx＋1是偶函数，则函数f(x)的单调减区间为(－∞，0]；⑤函数f(x)＝lg(x2＋1＋x)既不是奇函数，也不是偶函数．其中正确的命题有________个．二、解答题15. 已知f(x)＝2＋log3x，x∈[1，9]，求函数y＝[f(x)]2＋f(x2)的值域．高考数学一轮复习基础夯滚天天练(7)函数的单调性和奇偶性班级________ 姓名____________ 学号______ 成绩______ 日期____月____日一、 填空题1. 在函数：①y ＝cos x ；②y ＝sin x ；③y ＝ln x ；④y ＝x 2＋1中，既是偶函数又存在零点的是________．(填序号)2. 已知定义在R 上的偶函数f (x )在[0，＋∞)上单调递增，且f (1)＝0，则不等式f (x －2)≥0的解集是________________．3. 函数y ＝1－x1＋x的单调减区间为________________．4. 已知函数f(x)＝2x 2－mx ＋3，当x ∈(－2，＋∞)时是增函数，当x ∈(－∞，－2)时是减函数，则f(1)＝________．5. 已知函数f(x)是减函数，且f(x)>0，则在函数：①y ＝1f （x ）；②y ＝2f(x)；③y ＝[f(x)]2；中为增函数的是________．(填序号)6. 设函数f(x)是定义在R 上的周期为2的偶函数，当x ∈[0，1]时，f (x )＝x ＋1，则f ⎝⎛⎭⎫32＝________．7. 若f(x)在区间(0，＋∞)上是减函数，则f(x 2＋x ＋1)和f ⎝⎛⎭⎫34的大小关系为______________．8. 已知函数f(x)是奇函数，且x ∈(0，＋∞)时的解析式是f(x)＝lg (x ＋1)，则x ∈(－∞，0)时，f(x)＝________________．9. 已知函数f(x)＝⎩⎪⎨⎪⎧e x －k ， x ≤0，（1－k ）x ＋k ， x>0是R 上的增函数，则实数k 的取值范围是________．10. 已知f(x)＝ax 2＋bx 是定义在[a －1，2a]上的偶函数，那么a ＋b 的值是________．11. 函数f(x)＝x 5＋sin x ＋1(x ∈R )，若f (a )＝2，则f (－a )＝________．12. 已知定义在R 上的奇函数f (x )满足f (x ＋4)＝f (x )，则f (8)的值为________．13. 已知y ＝log a (2－ax)在区间[0，1]上是关于x 的减函数，则a 的取值范围是________．14. 若f(x)＝ax ＋1x ＋2在区间(－2，＋∞)上是增函数，则a 的取值范围是________．二、 解答题15. 已知函数f(x)＝x 2＋ax(x ≠0，a ∈R )．(1) 判断函数f (x )的奇偶性；(2) 若函数f (x )在区间[2，＋∞)上是增函数，求实数a 的取值范围．高考数学一轮复习基础夯滚天天练(8)函数的图象班级________姓名____________学号______成绩______日期____月____日一、填空题1. 函数y＝x 43的图象大致是________．(填序号)①②③④2. 某班四个同学在同一坐标系中，作了两个函数的图象，其中能够作为函数y＝ax2＋bx与y＝ax＋b(a≠0，b≠0)的图象的是________．(填序号)①②③④3. 函数y＝a x－a(a>0，a≠1)的图象可能是________．(填序号)①②③④4. 函数y＝1－|1－x|的图象与x轴所围成的封闭图形的面积为________．5. 已知a>0且a≠1，函数y＝|a x－2|与y＝3a的图象有两个交点，则a的取值范围是____________．6. 若函数y＝4x＋a2x的图象关于原点对称，则实数a的值为________．7. 已知函数y＝log a(x＋b)的图象如图所示，则a b＝________．8. 函数y＝log2|x＋1|的图象关于直线________对称．9. 函数f(x)＝x|x＋a|＋b是奇函数的充要条件是________．10. 已知0<a<1，则函数f(x)＝a x －|log a x|的零点个数为________．11. 设函数f(x)＝⎩⎪⎨⎪⎧2x －4， x>0，－x －3， x<0.若f(a)>f(1)，则实数a 的取值范围是____________．12. 将函数y ＝2x 的图象向左平移一个单位长度，得到图象C 1，再将C 1向上平移一个单位长度得到图象C 2，则C 2的解析式为____________．13. 已知函数f(x)＝32x －(k ＋1)·3x ＋2，当x ∈R 时，函数f (x )恒为正值，则k 的取值范围是________________．二、 解答题14. 分别作出函数f(x)，g(x)的图象，并利用图象回答问题．(1) f(x)＝⎩⎪⎨⎪⎧4x －4， x ≤1，x 2－4x ＋3， x>1，g(x)＝log 2x ，求方程f(x)＝g(x)的解的个数；(2) f(x)＝x ＋1，g(x)＝log 2(－x)，求不等式f(x)>g(x)的解集．二次函数班级________姓名____________学号______成绩______日期____月____日一、填空题1. 若a，b，c成等比数列，则函数y＝ax2＋bx＋c的图象与x轴的交点的个数为________．2. 已知a，b为常数，若f(x)＝x2＋4x＋3，f(ax＋b)＝x2＋10x＋24，则5a－b＝________．3. 若函数y＝x2－2x＋a在区间[0，3]上的最小值是4，则a＝________；若最大值是4，则a＝________．4. 若函数y＝|x－a－3|＋b，x∈[a，b]的图象关于直线x＝3对称，则b＝________．5. 已知函数f(x)＝3(x－2)2＋5，且|x1－2|>|x2－2|，则f(x1)________f(x2)．(填“>”“<”或“＝”)6. 若函数y＝mx2＋x＋5在[－2，＋∞)上是增函数，则m的取值范围是________．7. 设x，y是关于m的方程m2－2am＋a＋6＝0的两个实根，则(x－1)2＋(y－1)2的最小值是________．8. 已知函数f(x)＝x2－4x，x∈[1，5]，则函数f(x)的值域是________．9. 已知函数f(x)＝x2－2x，x∈[a，b]的值域为[－1，3]，则b－a的取值范围是________．10. 若函数f(x)＝(a2－2a－3)x2＋(a－3)x＋1的定义域和值域都为R，则a的取值范围是________．11. 已知函数f(x)＝－4x2＋4ax－4a－a2在区间[0，1]上有一个最大值－5，则a＝________．12. 已知二次函数f(x)的二次项系数为a，且不等式f(x)>－2x的解集为(1，3)，又f(x)＋6a＝0有两个相等的根，则f(x)＝________________．13. 已知命题p：关于x的不等式x2＋(a－1)x＋a2≤0的解集为；命题q：函数y＝(2a2－a)x为增函数．若命题“p∨q”为真命题，则实数a的取值范围是________________________________________________________________________．二、解答题14. 已知函数f(x)＝x2＋ax＋3.(1) 当x∈R时，f(x)≥a恒成立，求a的取值范围；(2) 当x∈[－2，2]时，f(x)≥a恒成立，求a的取值范围．函数的应用班级________姓名____________学号______成绩______日期____月____日一、填空题1. 某出租车公司规定“打的”收费标准如下：3千米以内为起步价8元(即行程不超过3千米，一律收费8元)，若超过3千米，除起步价外，超过部分再按1.5元每千米收费计价，若某乘客与司机约定按四舍五入以元计费不找零钱，该乘客下车时乘车里程数为7.4千米，则乘客应付的车费是________元．2. 已知矩形的周长为1，它的面积S与矩形的长x之间的函数关系中，定义域为________．3. 某商场出售一种商品，每天可卖1 000件，每件可获利4元，据经验，若每件少卖0.1元，则每天可多卖出100件，为获得最好的经济利益每件单价应降低________元．4. 某厂生产中所需的一些配件可以外购，也可以自己生产．如果外购，每个价格是1.10元；如果自己生产，那么每月的固定成本将增加800元，并且生产每个配件的材料和劳力需0.60元，那么决定此配件外购还是自产的转折点是________件．(即生产多少件以上自产合算)5. 某产品的总成本y(万元)与产量x(台)之间的函数关系式是y＝3 000＋20x－0.1x2(0<x<240，x∈N)，若每台产品的售价为25万元，则生产者不亏本(销售收入不小于总成本)的最低产量是________台．6. 购买手机的“全球通”卡，使用时须付“基本月租费”(每月需交的固定费用)50元，在市内通话时每分钟另收话费0.40元；购买“神州行”卡，使用时不收“基本月租费”，但在市内通话时每分钟话费为0.60元．若某用户每月手机费预算为120元，则他购买________卡才合算．7. 如图，灌溉渠的横截面是等腰梯形，底宽2m，边坡的倾角为45°，水深h m，则横截面中有水面积S(m2)与水深h(m)的函数关系式为____________．8. 某企业生产的新产品必须先靠广告来打开销路，该产品的广告效益应该是产品的销售额与广告费之间的差．如果销售额与广告费的算术平方根成正比，根据对市场进行抽样调查的结果显示：每付出100元的广告费，所得的销售额是1 000元，那么该企业应该投入________元广告费，才能获得最大的广告效应．9. 某市的一家报刊摊点，从报社买进《晚报》的价格是每份0.20元，卖出价是每份0.30元，卖不掉的报纸可以以每份0.05元的价格退回报社．在一个月(以30天计)里，有20天每天卖出量可达400份，其余10天每天只能卖出250份，但每天从报社买进的份数必须相同，这个摊主每天从报社买进________份，才能使每月所获的利润最大．10. 一个工厂生产某种产品每年需要固定投资100万元，此外每生产1件该产品还需要增加投资1万元，年产量为x(x∈N*)件．当x≤20时，年销售总收入为(33x－x2)万元；当x>20时，年销售总收入为260万元．记该工厂生产并销售这种产品所得的年利润为y万元，则y(万元)与x(件)的函数关系式为__________________________________，该工厂的年产量为________件时，所得年利润最大．(年利润＝年销售总收入－年总投资)二、解答题11. 近年来，某企业每年消耗电费约24万元，为了节能减排，决定安装一个可使用15年的太阳能供电设备接入本企业电网．这种供电设备的安装费(单位：万元)与太阳能电池板的面积(单位：平方米)成正比，比例系数约为0.5.为了保证正常用电，安装后采用太阳能和电能互补供电的模式．假设在此模式下，安装后该企业每年消耗的电费C(单位：万元)与安装的这种太阳能电池板的面积x(单位：平方米)之间的函数关系是C(x)＝k20x ＋100(x ≥0，k 为常数)．记F 为该企业安装这种太阳能供电设备的费用与该企业15年共将消耗的电费之和．(1) 解释C(0)的实际意义，并建立F 关于x 的函数关系式； (2) 当x 为多少平方米时，F 取得最小值？最小值是多少万元？12. 随着机构改革工作的深入进行，各单位要裁员增效．有一家公司现有职员2a 人(140<2a<420，且a 为偶数)，每人每年可创利b 万元．据评估，在经营条件不变的前提下，每裁员1人，则留岗职员每人每年多创利0.01b 万元，但公司需付下岗职员每人每年0.4b 万元的生活费，并且该公司正常运转所需人数不得小于现有职员的34，为获得最大的经济效益，该公司应裁员多少人？高考数学一轮复习基础夯滚天天练(11)指数与对数一、 填空题 1.2. 计算：(log 32＋log 92)·(log 43＋log 83)＝________．3的值为________．4. 计算：lg 25＋lg 2·lg 50＋(lg 2)2＝________．5. 设则a ，b ，c 的大小关系是________．6. 方程log 3(x 2－10)＝1＋log 3x 的解是________．7. 设f(x)＝⎩⎪⎨⎪⎧2e x －1， x<2，lg （x 2－1）， x ≥2，则f(f(2))＝________．8. 计算：⎝⎛⎭⎫lg 14－lg 25÷＝________．9. 方程4x －2x ＋1－3＝0的解是________________．10. 关于x 的不等式的解集为________．11. 已知3a ＝5b ＝c ，且1a ＋1b ＝2，则c ＝________．12. 不等式log 2(2x －1)<log 2(－x ＋5)的解集为________．13. 给出下列结论，其中正确的是________．(填序号)①当a<0时，(a 2)32＝a 3；②na n ＝|a|(n>1，n ∈N *，n 为偶数)；③函数f (x )＝(x －2)12－(3x －7)0的定义域是⎩⎨⎧⎭⎬⎫x |x ≥2且x ≠73；④若2x＝16，3y＝127，则x＋y＝7.14. 已知函数f(x)＝2|x|－2，不等式x[f(x)＋f(－x)]>0的解集是________________________________________________________________________．二、解答题15. 求值或化简：(1) lg8＋lg125－lg2－lg5lg10·lg0.1；(2) ，求的值．16. 已知函数f(x)＝log a(a x－1)，a>0，a≠1.求证：(1) 函数f(x)的图象在y轴的一侧；(2) 函数f(x)图象上任意两点连线的斜率都大于0.高考数学一轮复习基础夯滚天天练(12)幂函数、指数函数与对数函数班级________ 姓名____________ 学号______ 成绩______ 日期____月____日一、 填空题1. 如果幂函数f(x)＝x a 的图象经过点(2，4)，那么函数f(x)的单调增区间为________．2. 函数f(x)＝ln x ＋1－x 的定义域为________．3. 若函数f(x)＝log a x(0<a<1)在区间[a ，2a]上的最大值是最小值的3倍，则a ＝________．4. 要使函数f(x)＝3x ＋1＋t 的图象不经过第二象限，则实数t 的取值范围为________．5. 若函数f(x)＝a x －1(a>0，a ≠1)的定义域和值域都是[0，2]，则实数a ＝________．6. 已知函数f(x)＝x 12，且f(2x －1)<f(3x)，则x 的取值范围是________．7. 若函数y ＝(log 0.5a)x 在R 上为增函数，则a 的取值范围是________．8. 设函数f(x)＝⎩⎪⎨⎪⎧－x ＋a ，x<1，2x ， x ≥1的最小值为2，则实数a 的取值范围是________．9. 函数f(x)＝的值域为________．10. 若log a 12a －1<1，则a 的取值范围是________．11. 在下列四个图象中，能够表示函数y ＝a x 与y ＝－log a x(a>0，a ≠1)在同一个平面直角坐标系的图象的可能是________．(填序号)①②③④12. 若函数f(x)＝log a (2x 2＋x)(a>0，a ≠1)在区间⎝⎛⎭⎫0，12内恒有f(x)>0，则函数f(x)的单调增区间是________．13. 函数y ＝a x －2＋1(a>0，a ≠1)恒过定点________．14. 若函数f(x)＝在[－1，1]上是单调增函数，则实数a 的取值范围是________________．二、 解答题15. 已知函数f(x)＝log a (3－ax)．(1) 当x ∈[0，2]时，函数f(x)恒有意义，求实数a 的取值范围；(2) 是否存在这样的实数a ，使得函数f(x)在区间[1，2]上为减函数，并且最大值为1？如果存在，求出a 的值；如果不存在，请说明理由．16. 已知函数f(x)＝x ⎝⎛⎭⎫13x －1＋12.(1) 判断该函数的奇偶性；(2) 求证：该函数在定义域上恒大于0.高考数学一轮复习基础夯滚天天练(13)函数与方程班级________ 姓名____________ 学号______ 成绩______ 日期____月____日 一、 填空题1. 已知函数f(x)的图象是连续不断的，x ，f(x)的对应关系如下表：则函数f(x)一定存在零点的区间有________．(填序号)①区间[1，2]；②区间[2，3]；③区间[3，4]；④区间[4，5]；⑤区间[5，6]．2. 已知函数f(x)＝ax ＋b 的零点是3，那么函数g(x)＝bx 2＋ax 的零点是________．3. 已知函数f(x)＝2mx ＋4，若存在x 0∈[－2，1]，使f(x 0)＝0，则实数m 的取值范围是________________．4. 已知函数f(x)＝ln x ＋x －2的零点所在的区间为(k ，k ＋1)(其中k 为整数)，则k 的值为________．5. 已知函数f(x)＝x 2＋x ＋a 在区间(0，1)上有零点，则实数a 的取值范围是________．6. 已知定义在R 上的函数f (x )＝(x 2－3x ＋2)g (x )＋3x －4，其中y ＝g (x )是一条连续曲线，则方程f (x )＝0在区间________范围内必有实数根．(填序号)①(0，1)；②(1，2)；③(2，3)；④(3，4)．7. 若函数f(x)＝⎩⎪⎨⎪⎧x 2－x －1，x ≥2或x ≤－1，1， －1<x<2，则函数g(x)＝f(x)－x 的零点为________．8. 函数f(x)＝2x ＋x 3－2在区间(0，1)上的零点的个数为________．9. 若对于任意的x ∈[a ，2a]，都有y ∈[a ，a 2]满足方程log a x ＋log a y ＝3，这时a 的取值的集合为________．10. 已知函数f(x)＝log 2x ＋a 在区间(2，4)上有零点，则实数a 的取值范围是________．11. 若函数y ＝x ＋5x －a在(－1，＋∞)上单调递减，则实数a 的取值范围是________．12. 若关于x 的方程lg (mx)·lg (mx 2)＝4的所有解都大于1，则实数m 的取值范围是________．13. 已知函数f(x)＝⎩⎪⎨⎪⎧2x ， x ≥2，（x －1）2， x<2， 若关于x 的方程f(x)＝k 有三个不同的实数根，则实数k 的取值范围为________．14. 若函数y ＝⎝⎛⎭⎫12|1－x|＋m 的图象与x 轴有公共点，则实数m 的取值范围是________．二、 解答题15. 已知关于x 的二次函数f(x)＝x 2＋(2t －1)x ＋1－2t. (1) 求证：对于任意t ∈R ，方程f (x )＝1必有实数根；(2) 若12<t <34，求证：方程f (x )＝0在区间(－1，0)及⎝⎛⎭⎫0，12上各有一个实数根．16. 已知函数f(x)＝log 4(4x ＋1)＋kx(x ∈R )是偶函数． (1) 求k 的值；(2) 若方程f (x )－m ＝0有解，求m 的取值范围．高考数学一轮复习基础夯滚天天练(14)导数的概念及运算班级________ 姓名____________ 学号______ 成绩______ 日期____月____日一、 填空题1. 已知函数f(x)＝1＋1x ，则f(x)在区间[1，2]，⎣⎡⎦⎤12，1上的平均变化率分别为________．2. 若f′(x)是函数f(x)＝13x 3＋2x ＋1的导函数，则f′(1)＝________．3. 函数f(x)＝x 2sin x 的导数为f′(x)＝________________．4. 函数f(x)＝cos x 在点⎝⎛⎭⎫π3，12处的切线方程为____________________．5. 已知曲线y ＝4x －x 2上两点A(4，0)，B(3，3)，若曲线上一点P 处的切线恰好与弦AB 平行，则点P 的坐标为________．6. 若直线y ＝12x ＋b 是曲线y ＝ln x(x>0)的一条切线，则实数b 的值为________．7. 函数y ＝x e x 在其极值点处的切线方程为________________．8. 过点(0，2)且与曲线y ＝－x 3相切的直线方程是________________．9. 若直线y ＝kx ＋1与曲线y ＝x 3＋ax ＋b 相切于点(1，3)，则b 的值为________．10. 设P 是曲线f(x)＝13x 3－x 2－3x －3上的一个动点，则过点P 的切线中斜率最小的切线的方程为________________．11. 曲线y ＝x －cos x 在点⎝⎛⎭⎫π2，π2处的切线方程为________________．12. 若曲线C 1：y 1＝ax 3－6x 2＋12x 在x ＝1处的切线与曲线C 2：y 2＝e x 在x ＝1处的切线垂直，则实数a 的值为________．二、 解答题13. 设函数f(x)＝ax －bx ，曲线y ＝f(x)在点(2，f(2))处的切线方程为7x －4y －12＝0.(1) 求函数f(x)的解析式；(2) 求证：曲线y ＝f(x)上任意一点处的切线与直线x ＝0和直线y ＝x 所围成的三角形的面积为定值，并求此定值．14. 设直线是曲线C：y＝ln xx在点(1，0)处的切线．(1) 求切线的方程；(2) 求证：除切点(1，0)之外，曲线C在直线的下方．。

高三单元滚动检测卷·数学考生留意：1．本试卷分第Ⅰ卷(填空题)和第Ⅱ卷(解答题)两部分，共4页．2．答卷前，考生务必用蓝、黑色字迹的钢笔或圆珠笔将自己的姓名、班级、学号填写在相应位置上． 3．本次考试时间120分钟，满分160分． 4．请在密封线内作答，保持试卷清洁完整．单元检测九 平面解析几何第Ⅰ卷一、填空题(本大题共14小题，每小题5分，共70分．请把答案填在题中横线上)1．当方程x 2＋y 2＋kx ＋2y ＋k 2＝0所表示的圆的面积最大时，直线y ＝(k －1)x ＋2的倾斜角α的值为________． 2．(2021·南京模拟)已知点P (x ，y )在以原点为圆心的单位圆上运动，则点Q (x ′，y ′)＝(x ＋y ，xy )的轨迹是__________．3．(2021·潍坊模拟)设F 是椭圆x 24＋y 2＝1的右焦点，椭圆上的点与点F 的最大距离为M ，最小距离是m ，则椭圆上与点F 的距离等于12(M ＋m )的点的坐标是__________．4．(2021·镇江模拟)已知双曲线x 24－y 212＝1的离心率为e ，抛物线x ＝2py 2的焦点为(e,0)，则p 的值为________．5．若AB 是过椭圆x 225＋y 216＝1中心的弦，F 1为椭圆的焦点，则△F 1AB 面积的最大值为________．6．(2021·武汉调研)已知O 为坐标原点，F 为抛物线C ：y 2＝42x 的焦点，P 为C 上一点，若PF ＝42，则△POF 的面积为________．7．(2022·北京海淀区期末练习)双曲线C 的左，右焦点分别为F 1，F 2，且F 2恰好为抛物线y 2＝4x 的焦点，设双曲线C 与该抛物线的一个交点为A ，若△AF 1F 2是以AF 1为底边的等腰三角形，则双曲线C 的离心率为________．8．已知P (x ，y )是圆x 2＋(y －1)2＝1上任意一点，欲使不等式x ＋y ＋c ≥0恒成立，则实数c 的取值范围是____________．9．(2021·福州质检)已知F 1，F 2是双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左，右焦点，若双曲线左支上存在一点P 与点F 2关于直线y ＝bxa对称，则该双曲线的离心率为______．10．设抛物线y 2＝2x 的焦点为F ，过点M (3，0)的直线与抛物线相交于A 、B 两点，与抛物线的准线相交于点C ，BF ＝2，则△BCF 与△ACF 的面积之比S △BCFS △ACF＝________.11．已知动点P (x ，y )在椭圆C ：x 225＋y 216＝1上，F 是椭圆C 的右焦点，若点M 满足|M F →|＝1且M P →·M F →＝0，则|PM →|的最小值为________．12．若双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的一条渐近线的倾斜角为2π3，离心率为e ，则a 2＋e 22b 的最小值为________．13．(2021·南通模拟)已知椭圆C ：x 29＋y 24＝1，点M 与C 的焦点不重合．若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则AN ＋BN ＝________.14．设A ，B 为双曲线x 2a 2－y 2b 2＝λ(a >0，b >0，λ≠0)同一条渐近线上的两个不同的点，已知向量m ＝(1,0)，|AB →|＝6，AB →·m |m |＝3，则双曲线的离心率为________．第Ⅱ卷二、解答题(本大题共6小题，共90分．解答时应写出文字说明、证明过程或演算步骤)15．(14分)(2021·安徽六校联考)如图，在平面直角坐标系xOy 中，点A (0,3)，直线l ：y ＝2x －4，设圆C 的半径为1，圆心在l 上．(1)若圆心C 也在直线y ＝x －1上，过点A 作圆C 的切线，求切线的方程； (2)若圆C 上存在点M ，使MA ＝2MO ，求圆心C 的横坐标a 的取值范围．16．(14分)(2021·扬州模拟)已知中心在原点，焦点在x 轴上的椭圆C 的离心率为12，其一个顶点是抛物线x 2＝－43y 的焦点． (1)求椭圆C 的标准方程；(2)若过点P (2,1)的直线l 与椭圆C 在第一象限相切于点M ，求直线l 的方程和点M 的坐标．17.(14分)如图所示，离心率为12的椭圆Ω：x 2a 2＋y 2b 2＝1(a >b >0)上的点到其左焦点的距离的最大值为3，过椭圆Ω内一点P 的两条直线分别与椭圆交于点A ，C 和B ，D ，且满足AP →＝λPC →，BP →＝λPD →，其中λ为常数，过点P 作AB 的平行线交椭圆于M ，N 两点．(1)求椭圆Ω的方程；(2)若点P (1,1)，求直线MN 的方程，并证明点P 平分线段MN .18．(16分)(2021·连云港模拟)设抛物线C ：y 2＝2px (p ＞0)的焦点为F ，准线为l ，M ∈C ，以M 为圆心的圆M 与l 相切于点Q ，Q 的纵坐标为3p ，E (5,0)是圆M 与x 轴除F 外的另一个交点． (1)求抛物线C 与圆M 的方程；(2)已知直线n ：y ＝k (x －1)(k ＞0)，n 与C 交于A ，B 两点，n 与l 交于点D ，且F A ＝FD ，求△ABQ 的面积．19.(16分)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点为F (c,0)．(1)若双曲线的一条渐近线方程为y ＝x 且c ＝2，求双曲线的方程；(2)以原点O 为圆心，c 为半径作圆，该圆与双曲线在第一象限的交点为A ，过A 作圆的切线，斜率为－3，求双曲线的离心率．20．(16分)(2021·青岛质检)已知椭圆C 1的中心为原点O ，离心率e ＝22，其一个焦点在抛物线C 2：y 2＝2px 的准线上，若抛物线C 2与直线l ：x －y ＋2＝0相切． (1)求该椭圆的标准方程；(2)当点Q (u ，v )在椭圆C 1上运动时，设动点P (2v －u ，u ＋v )的运动轨迹为C 3.若点T 满足：O T →＝M N →＋2OM→＋O N →，其中M ，N 是C 3上的点，直线OM 与ON 的斜率之积为－12，试说明：是否存在两个定点F 1，F 2，使得TF 1＋TF 2为定值？若存在，求F 1，F 2的坐标；若不存在，请说明理由．答案解析1.3π4解析 若方程x 2＋y 2＋kx ＋2y ＋k 2＝0表示圆， 则有k 2＋4－4k 2＞0，解得0≤k 2＜43，而此时圆的半径r ＝12k 2＋4－4k 2＝12－3k 2＋4，要使圆的面积最大，只需r 最大，即当k ＝0时，r 取得最大值1，此时直线方程为y ＝－x ＋2， 由倾斜角与斜率的关系知，k ＝tan α＝－1，又由于α∈[0，π)，所以α＝3π4.2．抛物线解析 设P 在以原点为圆心，1为半径的圆上，则P (x 0，y 0)，有x 20＋y 20＝1，∵Q (x ′，y ′)＝(x ＋y ，xy )，∴⎩⎪⎨⎪⎧x ′＝x 0＋y 0，y ′＝x 0·y 0. ∴x ′2＝x 20＋y 20＋2x 0y 0＝1＋2y ′， 即Q 点的轨迹方程为y ′＝12x ′2－12，∴Q 点的轨迹是抛物线． 3．(0，±1)解析 据题意可知椭圆上的点到右焦点F 的最大距离为椭圆长轴的左端点到F 的距离． 故M ＝a ＋c ＝2＋3，最小距离为椭圆长轴的右端点到F 的距离， 即m ＝a －c ＝2－3，故12(M ＋m )＝12(2＋3＋2－3)＝2， 易知点(0，±1)满足要求． 4.116解析 依题意得双曲线中a ＝2，b ＝23， ∴c ＝a 2＋b 2＝4，∴e ＝c a ＝2，抛物线方程为y 2＝12p x ，故18p ＝2，得p ＝116. 5．12解析 如图，设A 的坐标为(x ，y )， 则依据对称性得B (－x ，－y )，则△F 1AB 面积S ＝12×OF 1×|2y |＝c |y |.∴当|y |最大时，△F 1AB 面积最大，由图知，当A 点在椭圆的顶点时，其△F 1AB 面积最大，则△F 1AB 面积的最大值为cb ＝25－16×4＝12. 6．23解析 由于抛物线C ：y 2＝42x 的准线方程是x ＝－2，所以由PF ＝42得x p ＝32， 代入抛物线方程得y p ＝±26， 所以△POF 的面积为 12·OF ·|y p |＝12×2×26＝2 3. 7．1＋2解析 依题意可知，点A (1，±2)，F 1(－1,0)，F 2(1,0)，AF 1＝22＋22＝22，AF 2＝F 1F 2＝2， 双曲线C 的离心率为e ＝F 1F 2AF 1－AF 2＝222－2＝2＋1.8．[2－1，＋∞)解析 欲使不等式x ＋y ＋c ≥0恒成立， 则c ≥(－x －y )max .令t ＝－x －y ，由题意知，当直线y ＝－x －t 与圆相切时，t 可取到最大值． 由数形结合可知，圆心到直线的距离为d ＝|1＋t |2＝1，解得t ＝±2－1，所以t ＝2－1时，取得最大值． 即c ≥2－1. 9.5解析 记线段PF 2与直线y ＝bax 的交点为M ，依题意，直线y ＝ba x 是已知双曲线的一条渐近线，M 是PF 2的中点，且PF 2＝2MF 2＝2b ；又点O 是F 1F 2的中点，因此有PF 1＝2OM ＝2a ；由点P 在双曲线的左支上得PF 2＝PF 1＋2a ＝4a ＝2b ，b ＝2a ，该双曲线的离心率是e ＝ 1＋(ba)2＝ 5.10.45解析 如图，过A ，B 作准线l ：x ＝－12的垂线，垂足分别为A 1，B 1，由于F 到直线AB 的距离为定值． ∴S △BCF S △ACF ＝BCAC. 又∵△B 1BC ∽△A 1AC ，∴BC AC ＝BB 1AA 1，由抛物线定义BB 1AA 1＝BF AF ＝2AF ，由BF ＝BB 1＝2知x B ＝32，y B ＝－3，∴AB ：y －0＝33－32(x －3)，把x ＝y 22代入上式，求得y A ＝2，x A ＝2，∴AF ＝AA 1＝52.故S △BCF S △ACF ＝BF AF ＝252＝45. 11.3解析 由题意可得F P →·FM →＝|FM →|2＝1，所以|PM →|＝|FM →－F P →|＝1＋|F P →|2－2＝|F P →|2－1≥(5－3)2－1＝3，当且仅当点P 在右顶点时取等号，所以|PM →|的最小值是 3. 12.233解析 由题意，ba＝3，∴b ＝3a ，∴c ＝2a ，e ＝2，a 2＋e 22b ＝a 2＋423a ＝a 23＋23a ≥233(当且仅当a ＝2时取等号)，则a 2＋e 22b 的最小值为233.13．12解析 取MN 的中点G ，G 在椭圆上，由于点M 关于C 的焦点F 1，F 2的对称点分别为A ，B ， 故有GF 1＝12AN ，GF 2＝12BN ，所以AN ＋BN ＝2(GF 1＋GF 2)＝4a ＝12. 14．2或233解析 设AB →与m 的夹角为θ， 则AB →·m |m |＝6cos θ＝3，所以cos θ＝12.所以双曲线的渐近线与x 轴成60°角，可得ba ＝ 3.当λ>0时，e ＝ca ＝1＋(ba )2＝2；当λ<0时，e ＝cb＝1＋(a b )2＝233.15．解 (1)由⎩⎪⎨⎪⎧y ＝2x －4，y ＝x －1得圆心C (3,2)，∵圆C 的半径为1，∴圆C 的方程为(x －3)2＋(y －2)2＝1， 明显切线的斜率确定存在，设所求圆C 的切线方程为y ＝kx ＋3， 即kx －y ＋3＝0，∴|3k －2＋3|k 2＋1＝1，∴|3k ＋1|＝k 2＋1，∴2k (4k ＋3)＝0，∴k ＝0或k ＝－34，∴所求圆C 的切线方程为y ＝3或y ＝－34x ＋3，即y ＝3或3x ＋4y －12＝0.(2)∵圆C 的圆心在直线l ：y ＝2x －4上， ∴设圆心C 为(a,2a －4)，则圆C 的方程为(x －a )2＋[y －(2a －4)]2＝1. 又∵MA ＝2MO ，∴设M (x ，y ), 则x 2＋(y －3)2＝2x 2＋y 2， 整理得x 2＋(y ＋1)2＝4，设为圆D ，∴点M 既在圆C 上又在圆D 上，即圆C 和圆D 有交点，∴2－1≤a 2＋[(2a －4)－(－1)]2≤2＋1， 解得a 的取值范围为[0，125]．16．解 (1)设椭圆C 的方程为 x 2a 2＋y 2b 2＝1(a ＞b ＞0)，由题意得b ＝3，c a ＝12，解得a ＝2，c ＝1.故椭圆C 的标准方程为x 24＋y 23＝1.(2)由于过点P (2,1)的直线l 与椭圆C 在第一象限相切，所以直线l 的斜率存在， 故可设直线l 的方程为y ＝k (x －2)＋1(k ≠0)． 由⎩⎪⎨⎪⎧x 24＋y 23＝1，y ＝k (x －2)＋1得(3＋4k 2)x 2－8k (2k －1)x ＋16k 2－16k －8＝0.① 由于直线l 与椭圆C 相切，所以Δ＝[－8k (2k －1)]2－4(3＋4k 2)(16k 2－16k －8)＝0. 整理，得96(2k ＋1)＝0，解得k ＝－12.所以直线l 的方程为y ＝－12(x －2)＋1＝－12x ＋2.将k ＝－12代入①式，可以解得M 点的横坐标为1，故切点M 的坐标为(1，32)．17．解 (1)由题意得e ＝c a ＝12，a ＋c ＝3，联立a 2＝b 2＋c 2，解得a ＝2，b ＝3，c ＝1， ∴椭圆方程为x 24＋y 23＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，由AP →＝λPC →可得C (1－x 1λ＋1，1－y 1λ＋1)．∵点C 在椭圆上，故(1＋λ－x 1)24λ2＋(1＋λ－y 1)23λ2＝1，整理得712(1＋λ)2－16(1＋λ)(3x 1＋4y 1)＋(x 214＋y 213)＝λ2，又点A 在椭圆上可知x 214＋y 213＝1，故有712(1＋λ)2－16(1＋λ)(3x 1＋4y 1)＝λ2－1.①由BP →＝λPD →，同理可得712(1＋λ)2－16(1＋λ)(3x 2＋4y 2)＝λ2－1.②②－①得3(x 1－x 2)＋4(y 1－y 2)＝0，即k AB ＝－34.又AB ∥MN ，故k MN ＝－34，∴直线MN 的方程为y －1＝－34(x －1)，即3x ＋4y －7＝0. 由⎩⎪⎨⎪⎧x 24＋y 23＝1，3x ＋4y －7＝0可得21x 2－42x ＋1＝0⇒x M ＋x N ＝2＝2x p ， ∴P 是MN 的中点，即点P 平分线段MN .18．解 (1)由抛物线的定义知，圆M 经过焦点F (p2，0)，Q (－p2，3p )，点M 的纵坐标为3p ，又M ∈C ，则M (3p2，3p )，MF ＝2p .由题意，M 是线段EF 的垂直平分线上的点， 故3p 2＝p 2＋52，解得p ＝2. 故抛物线C ：y 2＝4x ，圆M ：(x －3)2＋(y －23)2＝16.(2)由⎩⎪⎨⎪⎧y ＝k (x －1)，x ＝－1得y ＝－2k ，则D (－1，－2k )，由⎩⎪⎨⎪⎧y 2＝4x ，y ＝k (x －1) 得ky 2－4y －4k ＝0(k ＞0)，即y ＝2＋21＋k 2k 或y ＝2－21＋k 2k .∵F A ＝FD ，则A 的纵坐标为2＋21＋k 2k，且2＋21＋k 2k ＝2k ，解得k ＝ 3.∴A (3,23)，B (13，－233)，直线n ：y ＝3(x －1)，Q (－1,23)，则AB ＝163，点Q 到直线n 的距离d ＝23， △ABQ 的面积S ＝12·AB ·d ＝1633.19．解 (1)∵双曲线x 2a 2－y 2b 2＝1的渐近线方程为y ＝±ba x ，由双曲线的一条渐近线方程为y ＝x ， 可得ba ＝1，解之得a ＝b ，∵c ＝a 2＋b 2＝2，∴a ＝b ＝ 2. 由此可得双曲线方程为x 22－y 22＝1.(2)设A 的坐标为(m ，n )，可得直线AO 的斜率满足k ＝n m ＝－1－3，即m ＝3n .①∵以点O 为圆心，c 为半径的圆的方程为x 2＋y 2＝c 2， ∴将①代入圆的方程，得3n 2＋n 2＝c 2， 解得n ＝12c ，m ＝32c ，将点A (32c ，12c )代入双曲线方程，得(32c )2a 2－(12c )2b 2＝1，化简得34c 2b 2－14c 2a 2＝a 2b 2，∵c 2＝a 2＋b 2，∴b 2＝c 2－a 2代入上式，化简整理得 34c 4－2c 2a 2＋a 4＝0， 两边都除以a 4，整理得3e 4－8e 2＋4＝0， 解之得e 2＝23或e 2＝2，∵双曲线的离心率e >1，∴该双曲线的离心率e ＝2(舍负)．20．解 (1)由⎩⎨⎧y 2＝2px ，x －y ＋2＝0⇒y 2－2py ＋22p ＝0，∵抛物线C 2：y 2＝2px 与直线l ：x －y ＋2＝0相切， ∴Δ＝4p 2－82p ＝0⇒p ＝2 2. ∴抛物线C 2的方程为y 2＝42x ， 其准线方程为x ＝－2，∴c ＝ 2.∵离心率e ＝c a ＝22，∴a ＝2，b 2＝a 2－c 2＝2，故椭圆的标准方程为x 24＋y 22＝1.(2)设M (x 1，y 1)，N (x 2，y 2)，P (x ′，y ′)，T (x ，y )，则⎩⎪⎨⎪⎧x ′＝2v －u ，y ′＝u ＋v⇒⎩⎨⎧u ＝13(2y ′－x ′)，v ＝13(x ′＋y ′).∵点Q (u ，v )在椭圆C 1上，∴u 24＋v 22＝1⇒[13(2y ′－x ′)]2＋2[13(x ′＋y ′)]2＝4 ⇒x ′2＋2y ′2＝12，∴点P 的轨迹方程为x 2＋2y 2＝12. 由O T →＝M N →＋2OM →＋O N →得(x ，y )＝(x 2－x 1，y 2－y 1)＋2(x 1，y 1)＋(x 2，y 2) ＝(x 1＋2x 2，y 1＋2y 2)， x ＝x 1＋2x 2，y ＝y 1＋2y 2.设k OM ，k ON 分别为直线OM ，ON 的斜率， 由题设条件知k OM ·k ON ＝y 1y 2x 1x 2＝－12，因此x 1x 2＋2y 1y 2＝0.∵点M ，N 在椭圆x 2＋2y 2＝12上，∴x 21＋2y 21＝12，x 22＋2y 22＝12， 故x 2＋2y 2＝(x 21＋4x 22＋4x 1x 2)＋2(y 21＋4y 22＋4y 1y 2) ＝(x 21＋2y 21)＋4(x 22＋2y 22)＋4(x 1x 2＋2y 1y 2) ＝60＋4(x 1x 2＋2y 1y 2)． ∴x 2＋2y 2＝60，从而可知点T 是椭圆x 260＋y 230＝1上的点．∴存在两个定点F 1，F 2，且为椭圆x 260＋y 230＝1的两个焦点，使得TF 1＋TF 2为定值，其坐标为F 1(－30，0)，F 2(30，0)．。

滚动练习二十1．函数)32sin(π-=x y 的周期是______ __．2．函数)621cos(ππ--=x y 的周期是______ __． 3．函数))(2125sin(Z k k x y ∈++=π的周期是______ __． 4．函数)3sin(2)(π+=kx x f 与函数)6tan(3)(π-=kx x g 的周期之和为π2，则正实数k 的值为 5．定义在R 上的函数)(x f 既是偶函数又是周期函数.若)(x f 的最小正周期是π，且当]2,0[π∈x 时，x x f sin )(=，则)35(πf = 6．若函数)3cos(3πω+=x y 的周期为T ，且T∈(2，3)，则正整数ω是______ __． 7.的值为，则最小正整数的最小正周期不大于k k kx x f 1)0)(35sin(3)(≠+= . 8．已知函数()f x 对任意x ∈R ,有(5)()f x f x +=,且()()f x f x -=-,若(3)1f -=,则(13)______.f =9.函数)7(,10)5(12)(f f T x f 则，且为偶函数，若的周期=== . 10．设f(x)是定义域为R ，最小正周期为23π的函数，已知⎪⎩⎪⎨⎧<≤<≤-=)0(sin )02(cos )(ππx x x x x f 则 )415(π-f = .请把答案写在下列横线上1. _______________2. _______________3. _______________4.______ _________5. _______________6._______________7. _______________8. _______________9._______________10. _______________11．求函数)35sin(3)(π+=x k x f )0(≠k 的周期，并求最小的正整数k ，使它的周期不大于１．12 . 求证：（1）x x y 2sin 2cos +=的周期为π；（2）.2|cos ||sin |π的周期为x x y +=。

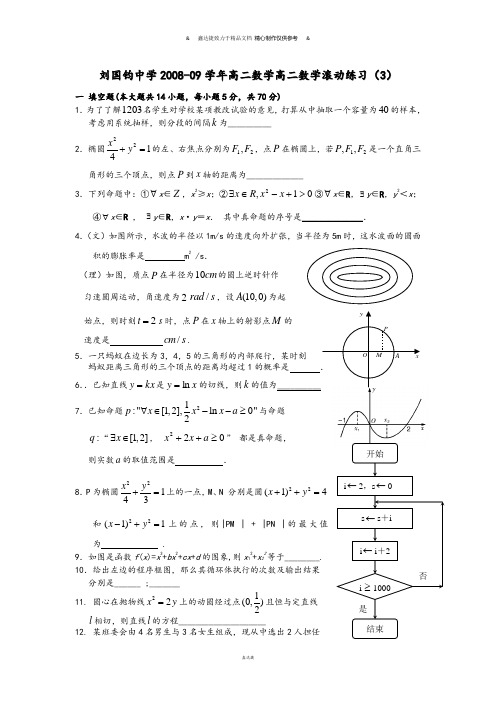
刘国钧中学2008-09学年高二数学高二数学滚动练习（3）一 填空题(本大题共14小题，每小题5分，共70分) 1．为了了解1203名学生对学校某项教改试验的意见，打算从中抽取一个容量为40的样本， 考虑用系统抽样，则分段的间隔k 为__________2．椭圆1422=+y x 的左、右焦点分别为21,F F ，点P 在椭圆上，若21,,F F P 是一个直角三 角形的三个顶点，则点P 到x 轴的距离为_____________3．下列命题中：①∀x ∈Z ，x 2≥x ；②01,2>+-∈∃x x R x ③∀x ∈R ，∃y ∈R ，y 2＜x ；④∀x ∈R ， ∃y ∈R ，x ·y ＝x ． 其中真命题的序号是______________．4．（文）如图所示，水波的半径以1m/s 的速度向外扩张，当半径为5m 时，这水波面的圆面积的膨胀率是 m 2/s ．（理）如图，质点P 在半径为10cm 的圆上逆时针作 匀速圆周运动，角速度为2/rad s ，设(10,0)A 为起始点，则时刻2t =s 时，点P 在x 轴上的射影点M 的 速度是 /cm s .5．一只蚂蚁在边长为3，4，5的三角形的内部爬行，某时刻蚂蚁距离三角形的三个顶点的距离均超过1的概率是 ． 6．．已知直线kx y =是x y ln =的切线，则k 的值为__________ 7．已知命题21:"[1,2],ln 0"2p x x x a ∀∈--≥与命题 :q “[1,2]x ∃∈， 022≥++a x x ” 都是真命题，则实数a 的取值范围是 ．8．P 为椭圆22143x y +=上的一点，M 、N 分别是圆22(1)4x y ++=和22(1)1x y -+=上的点，则|PM | + |PN |的最大值为 .9．如图是函数f (x )=x 3+bx 2+cx +d 的图象,则x 12+x 22等于________. 10．给出左边的程序框图，那么其循环体执行的次数及输出结果 分别是______ ;_______11. 圆心在抛物线y x 22=上的动圆经过点)21,0(且恒与定直线l 相切，则直线l 的方程____________________12. 某班委会由4名男生与3名女生组成，现从中选出2人担任xyOPMA 否是 开始i ←2，s ←0s ←s ＋i i ←i ＋2i ≥1000结束正、副班长，至少有1名女生当选的概率为 _____________13. 为了了解高三学生的身体状况．抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前3个小组的频率之比为1︰2︰3，第2小组的频数为12，则抽取的男生人数是 ．14．下表是某厂1～4月份用水量（单位：百吨）的一组数据，是（用最小二乘法求线性回归方程a bx y+=ˆ系数公式121()()()niii nii x x y y b x x ==--=-∑∑，a y bx =-．）二 解答题(本大题共6小题，共90分．解答时应写出文字说明、证明过程或演算步骤.) 15. 集合⎭⎬⎫⎩⎨⎧<+-=011|x x x A ,{}a b x x B <-=|||，若 “1=a ”是 “φ≠⋂B A ”的充分条件，求实数b 的取值范围．16. 某城市现有人口总数为100万人，如果年自然增长率为1.2%，解答下列问题：⑴ 写出该城市人口数y （万人）与经过年数x 的函数关系式； ⑵ 用伪代码及流程图表示计算10年以后该城市人口总数的算法； ⑶ 用伪代码及流程图表示如下算法：计算大约多少年以后该城市人口将达到120万人。

刘国钧中学2008-09学年高二数学滚动练习（1）一 填空题（本大题共14小题，每小题5分，共70分．）1．命题：“若ab 0≠，则,a b 都不为零”的逆否命题是 ______________________ 2．在如下程序框图中，输入0()cos f x x =，则输出的是___ ____3．下边程序执行的是求和03696022222++++，请填写空余部分：① 。

②______________4. 已知样本9,10,11,,x y 的平均数是10，标准差是2， 则xy =___ ____5. 甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为a ， 再由乙猜甲刚才所想的数字，把乙猜的数字记为b ,{},0,1,2,,9a b ∈，若1a b -≤，就称甲乙“心有灵犀”， 那么两人“心有灵犀”的概率为6. 甲，乙两人约定在1时到2时之间在某处会面，并约定先到者应等候另一个人10分钟，过时即可离去，则两人能会面的概率为 。

7. 某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户.为了调查社会购买力的某项指标，要从中抽取1个容量为100户的样本，记作①；某学校高一年级有12名女排运动员，要从中选出5人调查学习负担情况，记作②.那么完成上述两项调查宜采用的抽样方法分别是 ① ；② ___________________ 8. 已知函数qx px x x f --=23)(的图象与x 轴切于点)0,1(，则)(x f 的极大值、极小值依 次为 __ ； _______9. 为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－１８岁的男生体重(kg) ,得到频率分布直方图如下：根据下图可得这100名学生中〔56.5,64.5〕的学生人数是_____________10 如图定点N （1，0），动点A 、B 分别在图中抛物线24y x = 及椭圆22143x y += 的 实线部分上运动，且AB ∥x 轴，则=++BN AB AN 211 已知真命题“a b c d ≥⇒>”和“a b e f <⇔≤”，则“c d ≤”是“e f ≤”的__________条件12 已知21F F 、是两个定点，点P 是以21F F 、为公共焦点的椭圆和双曲线的一个交点，并且21PF PF ⊥,21e e 、分别是椭圆和双曲线的离心率，则=+222111e e __________ 13 已知)5)(4)(3)(2)(1()(-----=x x x x x x x f ，则=)1('f ___________14. 已知函数1)1(3)(223+--+=k x k x x f 在区间(0,4)上是减函数，则实数k 的取值范 围是______________二解答题（本大题共6小题，共90分，解答应写出必要的文字说明、证明过程或演算步骤)S ←1For i ①② End For Print Sy x O A NB第10 题15．已知,R m ∈且,0≠m 命题p ：“方程221y x m+=表示椭圆”, 命题q ：“函数324()2(43)3f x x mx m x m =-+--在（－∞，＋∞）上单调递增”，若p ∧q 是假命题，p ∨q 是真命题，求m 的范围.16．已知函数f （x ）＝x 3＋ax 2＋bx ＋c 在x ＝－23与x ＝1时都取得极值 ⑴ 求a 、b 的值与函数f （x ）的单调区间 ⑵ 若对[1,2]x ∈-都有3()f x c< 恒成立，求c 的取值范围17．一次口试，每位考生在8道口试题中随机抽出2道题回答，若答对其中1题即为及格。

刘国钧中学2008-09学年高二数学滚动练习（2）一 填空题（本大题共14小题，每小题5分，共70分）1. 在长为10cm 的线段AB 上任取一点P ，并以线段AP 、BP 为相邻两边作矩形，这个矩形的面积介于21cm 2与24cm 2之间的概率为_________2. 设P 是双曲线()222109x y a a -=>上的一点，双曲线的一条渐近线方程为320x y +=，12,F F 分别为双曲线的左右焦点，若13PF =，则2PF 等于3. 已知样本32,32,3221+++n x x x 的方差为2; 平均数是15， 则样本1,,1,121+++n x x x 的平均数、标准差分别为 _ ;____________4. 右边算法语句的输出结果是___________5. 如右图是一个容量为200的样本的频率 分布直方图,根据图中数据填空:样本 数据落在范围［5,9)的频数为_______.6. 执行右上的程序框图，若0.8p =，则输出的n =7. 设集合{12}{123}A B ==，，，，，分别从集合A 和B 中随机取一个数a 和b ，确定平面上的点()P a b ，，记“点()P a b ，落在直线x y n +=上”为事件(25)n C n n ∈N ≤≤，，若事件n C 的概率最大，则n 的可能值为__________8. 已知曲线x y cos =上一点)0,2(πP 处的切线分别交x 轴、y 轴于A ，B 两点，O 为坐标原点，则△OAB 的面积为9. 甲、乙、丙、丁四位女生玩传手绢游戏，拿到手绢的人立即传给其他3人中的一个，现从甲开始传手绢，经过三次传递后，手绢仍回到甲手中的概率是___ ____ 10．若命题“∀[]1,1p ∈-，()2330px p x +-->”为真，则实数x 的范围为11． 某小卖部为了了解热茶销量y （杯）与气温C x 0之间的关系，随机统计了某4天卖出的热茶杯数与当天气温，并制作了对照表：气温/ 0C 18 13 10 -1 杯数24343864由表中数据得线性回归方程a bx yˆ+=中2b -=，预测当气温为C 50-时，热茶销量约为______ _杯12．已知抛物线mx y =2)0(≠m 的准线与椭圆12622=+y x 的右准线重合，则实数m 的值是 。

滚动训练六一、填空题：1．若{}{}1,3,5,,1A B x ==，且B A ⊆，则x 的值为 ．2．若2829,log 3x y ==，则2x y +的值为 ． 3．1sin()24y x π=+的周期为 ．4．221333121(),(),()252a b c ===，则a 、b 、c 的大小关系为 ．（用“>”连接） 5．函数[]()3sin 20,3y x x ππ⎛⎫=-∈ ⎪⎝⎭的单调减区间是 ． 6．已知函数))(22()(1R x a x x f x x ∈⋅+=-+是偶函数，则实数a 的值为 ；7．已知函数()2log 2f x x x =+-的零点在区间()(),1n n n Z +∈内，则n = .8．如图是函数()sin(),(0,0,||)2f x A x A πωϕωϕ=+>><在一个周期内的图象，则其解析式是______ ______.9．已知()()3,10,5,10.n n f n f f n n -≥⎧⎪=⎨+<⎡⎤⎪⎣⎦⎩则()7f =_10．已知f (x )是定义在(,)-∞+∞上的奇函数，当0x >时，2()2f x x x =-，若函数f (x )在区间[-1，t ]上的最小值为-1，则实数t 的取值范围是 .请将答案填到下面的横线上：1、 2、 3、 4、5、 6、 7、 8、9、 10、二、解答题11．函数()sin()(0,||)2f x x πωϕωϕ=+><在它的某一个周期内的单调减区间 是511[,]1212ππ. （1） 求()f x 的解析式；（2） 将()y f x =的图象先向右平移6π个单位，再将图象上所有点的横坐标变为原来的12倍（纵坐标不变），所得到的图象对应的函数记为()g x ，求函数()g x 在3[,]88ππ上的最大值和最小值.12．已知21log 25622≥≤x x 且，求函数f(x)=2log 2log 22x x ⋅的值域.。

第9讲立体几何的综合问题<0,若p且q为真,则x的取值范围是.1.已知p:x2-2x-3<0;q:-2.已知△ABC的三边长分别为a,b,c且a2+b2-c2=ab,则∠C=.3.若存在实数x,使得x2-4bx+3b<0成立,则实数b的取值范围是.4.(2018苏州学业阳光指标调研)如图,两座建筑物AB,CD的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°,则这两座建筑物AB和CD的底部之间的距离BD= m.5.(2017无锡普通高中调研)在平行四边形ABCD中,AB=4,AD= ,∠A=,M为DC的中点,N为平面ABCD内一点,若|-|=|-|,则·= .6.(2018江苏高考信息预测)如图,在平行四边形ABCD中,E,F分别在BC,CD上,且BE=BC,DF=FC,AE与BF 交于点H,设=a,=b,且=xa+yb(x,y∈R),则x-y= .7.(2018江苏扬州中学高三模拟)如图,四棱锥P-ABCD中,四边形ABCD为菱形,PA⊥平ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.(1)求证:FG∥平面PBD;(2)求证:BD⊥FG.8.(2018江苏盐城中学高三期末)如图,在△ABC中,B=,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.(1)若△BCD的面积为,求CD的长;(2)若ED=,求角A的大小.答案精解精析1.答案 (-1,2)解析 解不等式x 2-2x-3<0得-1<x<3,所以p 真时,x 的取值范围是(-1,3);解不等式- <0,得x<2,所以q是真命题时,x 的取值范围是(-∞, ).所以若p 且q 为真,则x 的取值范围是(-1,2). 2.答案 0°解析 因为a 2+b 2-c 2=2abcosC=ab,所以cosC=,∠C= 0°.3.答案 (-∞,0)∪4, ∞解析 Δ=(-4b)2-12b>0⇒b<0或b>4. 4.答案 18解析 过点A 作CD 的垂线AE,垂足是E,设∠EAD=α,∠EAC=β,BD=xm,则tan α=,tan β=,tan45°=tan(α+β)=tan tan -tan t an =-54=1,解得x=18(舍负),即BD=18m.5.答案 6解析 解法一:由| - |=| - |得| |=| |,则点N 在线段AM 的垂直平分线上,取AM 的中点E,则EN⊥AM.又 = +,则| |2==| |2+ · +4| |2=4+ ×4× + 4× = ,所以 · = ·( + )= · =| |2=6.解法二:以点A 为坐标原点,AB 所在直线为x 轴,过点A 且垂直于AB 的直线为y 轴,建立平面直角坐标系,则D(1, ),M(3, ),线段AM 的垂直平分线方程为y=- x+2 ,由| - |=| - |得| |=| |,则点N 在线段AM 的垂直平分线上,设N(x,y),则 · =3x+ y=6. 6.答案4解析 分别延长BF,AD 交于点O,由题设,得DO=BC=AD. 又∵BE∥AO,∴AH∶HE=AO∶BE= ∶ , ∴ = 4 =4( + )=4( +)= 4 + =4a+b.又∵ =xa+xb(x,y∈R),a 与b 不共线, ∴x=4,y=,x-y= 4- =4.7.证明 (1)连接PE,因为G 、F 分别为EC 和PC 的中点, ∴FG∥PE.又FG ⊄平面PBD,PE ⊂平面PBD,所以FG∥平面PBD.(2)因为四边形ABCD 是菱形,所以BD⊥AC,又PA⊥平面ABCD,BD ⊂平面ABCD,所以BD⊥PA,因为PA ⊂平面PAC,AC ⊂平面PAC,且PA∩AC=A,∴BD⊥平面PAC,∵FG ⊂平面PAC,∴BD⊥FG. 8.解析 (1)由已知得S △BCD =BC·BD·sinB=,又B=,BC= ,∴BD=.在△BCD 中,由余弦定理得CD 2=BC 2+BD 2- BC·BD·cosB= ,∴CD=.(2)在△CDE 中,sin∠ =sin∠.∵AD=DC, ∴∠A=∠DCE,∴CD=AD= sin = sin .在△BCD 中 sin∠ =sin , 又∠BDC= ∠A,∴ sin =sin,∴CD=sin , ∴CD=sin =sin ,解得cosA=,所以A=4.。