数学---陕西省西安中学2016-2017学年高二下学期期中考试普通班(理)

2016-2017学年陕西省西北大学附中高二（下）期中数学试卷（理科）一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是最符合题目要求的）1．（3分）“x≠1”是“x2﹣3x+2≠0”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件2．（3分）若p∧q是假命题，则（）A．p是真命题，q是假命题B．p、q均为假命题C．p、q至少有一个是假命题D．p、q至少有一个是真命题3．（3分）用数学归纳法证明等式1+2+3+…+（n+3）＝时，第一步验证n＝1时，左边应取的项是（）A．1B．1+2C．1+2+3D．1+2+3+4 4．（3分）（e x+2x）dx等于（）A．1B．e﹣1C．e D．e+15．（3分）若曲线y＝x4的一条切线l与直线x+4y﹣8＝0垂直，则l的方程是（）A．4x﹣y﹣3＝0B．x+4y﹣5＝0C．4x﹣y+3＝0D．x+4y+3＝0 6．（3分）把语文、数学、物理、历史、外语这五门课程安排在一天的五节课里，如果数学必须比历史先上，则不同的排法有（）A．48B．24C．60D．1207．（3分）中心在原点的双曲线，一个焦点为，一个焦点到最近顶点的距离是，则双曲线的方程是（）A．B．C．D．8．（3分）已知A（﹣1，﹣2，6），B（1，2，﹣6）O为坐标原点，则向量与的夹角是（）A．0B．C．πD．9．（3分）设（2﹣x）5＝a0+a1x+a2x2…+a5x5，那么的值为（）A．﹣B．﹣C．﹣D．﹣110．（3分）函数f（x）＝x3﹣ax+1在区间（1，+∞）内是增函数，则实数a的取值范围是（）A．a＜3B．a＞3C．a≤3D．a≥3二、填空题（本大题共5小题，每小题4分，共20分，把答案填在题中横线上．）11．（4分）若a+bi＝i2，其中a、b∈R，i为虚数单位，则a+b＝．12．（4分）在（2x﹣1）5的展开式中，x2的系数为．13．（4分）由直线x＝，x＝3，曲线y＝及x轴所围图形的面积是．14．（4分）将侧棱相互垂直的三棱锥称为“直角三棱锥”，三棱锥的侧面和底面分别叫直角三棱锥的“直角面和斜面”；过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”．已知直角三角形具有性质：斜边长等于斜边的中线长的2倍．类比上述性质，直角三棱锥具有性质：．15．（4分）已知椭圆x2+ky2＝3k（k＞0）的一个焦点与抛物线y2＝12x的焦点重合，则该椭圆的离心率是．三、解答题（本大题共4题，50分，请写出必要的解答过程）．16．（10分）求直线l1：（t为参数）和直线l2：x﹣y﹣2＝0的交点P的坐标，及点P与Q（1，﹣5）的距离．17．（12分）已知函数f（x）＝．（1）求函数f（x）的导数；（2）求曲线y＝f（x）在点M（π，0）处的切线方程．18．（14分）如图，在四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD＝DC，E，F分别是AB、PB的中点．（Ⅰ）求证：EF⊥CD；（Ⅱ）在平面P AD内求一点G，使GF⊥平面PCB，并证明你的结论；（Ⅲ）求DB与平面DEF所成角的正弦值．19．（14分）已知椭圆C：＝1（a＞b＞0）的焦距为2，椭圆C上任意一点到椭圆两个焦点的距离之和为6．（Ⅰ）求椭圆C的方程；（Ⅱ）设直线l：y＝kx﹣2与椭圆C交于A，B两点，点P（0，1），且|P A|＝|PB|，求直线l的方程．附加题：（本大题共3题，20分，请写出必要的解答过程）20．（5分）如图，在杨辉三角形中，斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”的数列：1，3，3，4，6，5，10，…，记此数列的前n项之和为S n，则S21的值为（）A．66B．153C．295D．36121．（5分）已知f（x）为一次函数，且f（x）＝x+2，则f（x）＝．22．（10分）已知函数f（x）＝ax3+bx2﹣3x在x＝±1处取得极值（1）求函数f（x）的解析式；（2）求证：对于区间[﹣1，1]上任意两个自变量的值x1，x2，都有|f（x1）﹣f（x2）|≤4；（3）若过点A（1，m）（m≠﹣2）可作曲线y＝f（x）的三条切线，求实数m的范围．2016-2017学年陕西省西北大学附中高二（下）期中数学试卷（理科）参考答案与试题解析一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是最符合题目要求的）1．（3分）“x≠1”是“x2﹣3x+2≠0”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【解答】解：由x2﹣3x+2≠0，得x≠1且x≠2，能够推出x≠1，而由x≠1，不能推出x≠1且x≠2；因此前者是后者的必要不充分条件．故选：B．2．（3分）若p∧q是假命题，则（）A．p是真命题，q是假命题B．p、q均为假命题C．p、q至少有一个是假命题D．p、q至少有一个是真命题【解答】解：根据复合命题与简单命题真假之间的关系可知，若p∧q是假命题，则可知p，q至少有一个为假命题．故选：C．3．（3分）用数学归纳法证明等式1+2+3+…+（n+3）＝时，第一步验证n＝1时，左边应取的项是（）A．1B．1+2C．1+2+3D．1+2+3+4【解答】解：在等式中，当n＝1时，n+3＝4，而等式左边起始为1的连续的正整数的和，故n＝1时，等式左边的项为：1+2+3+4故选：D．4．（3分）（e x+2x）dx等于（）A．1B．e﹣1C．e D．e+1【解答】解：∵（e x+x2）′＝e x+2x，∴═＝（e+1）﹣（1+0）＝e，故选：C．5．（3分）若曲线y＝x4的一条切线l与直线x+4y﹣8＝0垂直，则l的方程是（）A．4x﹣y﹣3＝0B．x+4y﹣5＝0C．4x﹣y+3＝0D．x+4y+3＝0【解答】解：设与直线x+4y﹣8＝0垂直的直线l为：4x﹣y+m＝0，即曲线y＝x4在某一点处的导数为4，而y′＝4x3，∴y＝x4在（1，1）处导数为4，将（1，1）代入4x﹣y+m＝0，得m＝﹣3，故l的方程为4x﹣y﹣3＝0．故选：A．6．（3分）把语文、数学、物理、历史、外语这五门课程安排在一天的五节课里，如果数学必须比历史先上，则不同的排法有（）A．48B．24C．60D．120【解答】解：因为数学必须比历史先上，顺序固定，是安排除数学和历史之外的三门课，共有＝60（种）．故选：C．7．（3分）中心在原点的双曲线，一个焦点为，一个焦点到最近顶点的距离是，则双曲线的方程是（）A．B．C．D．【解答】解：∵中心在原点的双曲线，一个焦点为F（0，），∴其焦点在y轴，且半焦距c＝；又F到最近顶点的距离是﹣1，∴a＝1，∴b2＝c2﹣a2＝3﹣1＝2．∴该双曲线的标准方程是y2﹣＝1．故选：A．8．（3分）已知A（﹣1，﹣2，6），B（1，2，﹣6）O为坐标原点，则向量与的夹角是（）A．0B．C．πD．【解答】解：∵A（﹣1，﹣2，6），B（1，2，﹣6）O为坐标原点，∴向量＝（﹣1，﹣2，6），＝（1，2，﹣6），∴cos＜＞＝＝﹣1，∴向量与的夹角为π．故选：C．9．（3分）设（2﹣x）5＝a0+a1x+a2x2…+a5x5，那么的值为（）A．﹣B．﹣C．﹣D．﹣1【解答】解：在（2﹣x）5＝a0+a1x+a2x2…+a5x5中，令x＝1可得a0+a1+a2+…+a5 ＝1 ①，令x＝﹣1可得a0﹣a1+a2﹣…﹣a5 ＝35②．由①②求得a0+a2+a4＝122，a1+a3+a5 ＝﹣121，∴＝﹣，故选：B．10．（3分）函数f（x）＝x3﹣ax+1在区间（1，+∞）内是增函数，则实数a的取值范围是（）A．a＜3B．a＞3C．a≤3D．a≥3【解答】解：f′（x）＝3x2﹣a，令f′（x）＝3x2﹣a＞0即x2＞，当a＜0时，x∈R，函数f（x）＝x3﹣ax+1在区间R内是增函数，从而函数f（x）＝x3﹣ax+1在区间（1，+∞）内是增函数；当a≥0时，解得x＞，或x＜﹣；因为函数在区间（1，+∞）内是增函数，所以≤1，解得0≤a≤3，综上所述，所以实数a的取值范围是a≤3．故选：C．二、填空题（本大题共5小题，每小题4分，共20分，把答案填在题中横线上．）11．（4分）若a+bi＝i2，其中a、b∈R，i为虚数单位，则a+b＝﹣1．【解答】解：∵a+bi＝i2＝﹣1，∴a＝﹣1，b＝0，则a+b＝﹣1．故答案为：﹣1．12．（4分）在（2x﹣1）5的展开式中，x2的系数为﹣40．【解答】解：（2x﹣1）5的展开式中含x2的项是C52（2x）2（﹣1）3＝﹣40x2所以x2的系数是40．故答案为：﹣40．13．（4分）由直线x＝，x＝3，曲线y＝及x轴所围图形的面积是2ln3．【解答】解：如图，直线x＝，x＝3，曲线y＝及x轴所围图形的面积S＝dx＝lnx＝ln3﹣ln＝2ln3，故答案为：2ln3．14．（4分）将侧棱相互垂直的三棱锥称为“直角三棱锥”，三棱锥的侧面和底面分别叫直角三棱锥的“直角面和斜面”；过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”．已知直角三角形具有性质：斜边长等于斜边的中线长的2倍．类比上述性质，直角三棱锥具有性质：斜面的中面面积等于斜面面积的四分之一．【解答】解：由于直角三角形具有以下性质：斜边的中线长等于斜边边长的一半，故对于“直角三棱锥”，具有以下性质：斜面的中面面积等于斜面面积的四分之一．故答案为：斜面的中面面积等于斜面面积的四分之一．15．（4分）已知椭圆x2+ky2＝3k（k＞0）的一个焦点与抛物线y2＝12x的焦点重合，则该椭圆的离心率是．【解答】解：抛物线y2＝12x的焦点（3，0）方程可化为．∵焦点（3，0）在x轴上，∴a2＝3k，b2＝3，又∵c2＝a2﹣b2＝9，∴a2＝12，解得：k＝4．＝故答案为：．三、解答题（本大题共4题，50分，请写出必要的解答过程）．16．（10分）求直线l1：（t为参数）和直线l2：x﹣y﹣2＝0的交点P的坐标，及点P与Q（1，﹣5）的距离．【解答】解：把直线代入直线，解得t＝2，∴交点P的坐标为（1+2，1）．再由Q（1，﹣5），可得点P与Q（1，﹣5）的距离为＝4．17．（12分）已知函数f（x）＝．（1）求函数f（x）的导数；（2）求曲线y＝f（x）在点M（π，0）处的切线方程．【解答】解：（1）．（2）由（1）得在点M（π，0）处的切线的斜率k＝f′（π）＝﹣，所以在点M（π，0）处的切线方程为y﹣0＝﹣（x﹣π），即y＝﹣+1．18．（14分）如图，在四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD＝DC，E，F分别是AB、PB的中点．（Ⅰ）求证：EF⊥CD；（Ⅱ）在平面P AD内求一点G，使GF⊥平面PCB，并证明你的结论；（Ⅲ）求DB与平面DEF所成角的正弦值．【解答】解：以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系（如图），设AD＝a，则D（0，0，0）、A（a，0，0）、B（a，a，0）、C（0，a，0）、E（a，，0）、F（，，）、P（0，0，a）．（1）∵＝（﹣，0，），＝（0，a，0），∴•＝（﹣，0，）•（0，a，0）＝0，∴⊥∴EF⊥DC．﹣﹣﹣﹣﹣﹣﹣（4分）（2）设G（x，0，z），则G∈平面P AD．＝（x﹣，﹣，z﹣），•＝（x﹣，﹣，z﹣）•（a，0，0）＝a（x﹣）＝0，∴x＝；•＝（x﹣，﹣，z﹣）•（0，﹣a，a）＝+a（z﹣）＝0，∴z＝0．∴G点坐标为（，0，0），即G点为AD的中点．﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）（3）设平面DEF的法向量为＝（x，y，z）．由得：取x＝1，则y＝﹣2，z＝1，∴＝（1，﹣2，1）．cos＜，＞＝＝＝，∴DB与平面DEF所成角的正弦值的大小为﹣﹣﹣﹣﹣﹣（12分）19．（14分）已知椭圆C：＝1（a＞b＞0）的焦距为2，椭圆C上任意一点到椭圆两个焦点的距离之和为6．（Ⅰ）求椭圆C的方程；（Ⅱ）设直线l：y＝kx﹣2与椭圆C交于A，B两点，点P（0，1），且|P A|＝|PB|，求直线l的方程．【解答】解：（Ⅰ）由椭圆的定义可得2a＝6，2c＝2，解得a＝3，c＝，所以b2＝a2﹣c2＝3，所以椭圆C的方程为+＝1．（Ⅱ）由得（1+3k2）x2﹣12kx+3＝0，由于直线与椭圆有两个不同的交点，所以△＝144k2﹣12（1+3k2）＞0解得．设A（x1，y1），B（x2，y2）则，，，所以，A，B中点坐标E（，），因为|P A|＝|PB|，所以PE⊥AB，即k PE•k AB＝﹣1，所以•k＝﹣1解得k＝±1，经检验，符合题意，所以直线l的方程为x﹣y﹣2＝0或x+y+2＝0．附加题：（本大题共3题，20分，请写出必要的解答过程）20．（5分）如图，在杨辉三角形中，斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”的数列：1，3，3，4，6，5，10，…，记此数列的前n项之和为S n，则S21的值为（）A．66B．153C．295D．361【解答】解：从杨辉三角形的生成过程，可以得到你的这个数列的通项公式a（n）．n为偶数时，a（n）＝（n+4）/2，n为奇数时，1＝c20＝C22，3＝C31＝C32，6＝C42，10＝C53＝C52，…a（n）＝C（n+3）/22＝（n+3）（n+1）/8．然后求前21项和，偶数项和为75，奇数项和为[（22+42+62+…+222）+2（2+4+6…+22）]/8＝[（22×4×23）+11×24]/8＝286，最后S（21）＝361故选：D．21．（5分）已知f（x）为一次函数，且f（x）＝x+2，则f（x）＝x ﹣1．【解答】解：∵f（x）为一次函数，且，∴设f（x）＝x+b则b＝2∫01（x+b）dx＝2（x2+bx）|01＝2（+b）解得：b＝﹣1∴f（x）＝x﹣1故答案为：x﹣122．（10分）已知函数f（x）＝ax3+bx2﹣3x在x＝±1处取得极值（1）求函数f（x）的解析式；（2）求证：对于区间[﹣1，1]上任意两个自变量的值x1，x2，都有|f（x1）﹣f（x2）|≤4；（3）若过点A（1，m）（m≠﹣2）可作曲线y＝f（x）的三条切线，求实数m的范围．【解答】解：（1）f′（x）＝3ax2+2bx﹣3，依题意，f′（1）＝f′（﹣1）＝0，解得a＝1，b＝0．∴f（x）＝x3﹣3x（2）∵f（x）＝x3﹣3x，∴f′（x）＝3x2﹣3＝3（x+1）（x﹣1），当﹣1＜x＜1时，f′（x）＜0，故f（x）在区间[﹣1，1]上为减函数，f max（x）＝f（﹣1）＝2，f min（x）＝f（1）＝﹣2∵对于区间[﹣1，1]上任意两个自变量的值x1，x2，都有|f（x1）﹣f（x2）|≤|f max（x）﹣f min（x）||f（x1）﹣f（x2）|≤|f max（x）﹣f min（x）|＝2﹣（﹣2）＝4（3）f′（x）＝3x2﹣3＝3（x+1）（x﹣1），∵曲线方程为y＝x3﹣3x，∴点A（1，m）不在曲线上．设切点为M（x0，y0），切线的斜率为（左边用导数求出，右边用斜率的两点式求出），整理得2x03﹣3x02+m+3＝0．∵过点A（1，m）可作曲线的三条切线，故此方程有三个不同解，下研究方程解有三个时参数所满足的条件设g（x0）＝2x03﹣3x02+m+3，则g′（x0）＝6x02﹣6x0，由g′（x0）＝0，得x0＝0或x0＝1．∴g（x0）在（﹣∞，0），（1，+∞）上单调递增，在（0，1）上单调递减．∴函数g（x0）＝2x03﹣3x02+m+3的极值点为x0＝0，x0＝1∴关于x0方程2x03﹣3x02+m+3＝0有三个实根的充要条件是，解得﹣3＜m＜﹣2．故所求的实数m的取值范围是﹣3＜m＜﹣2．。

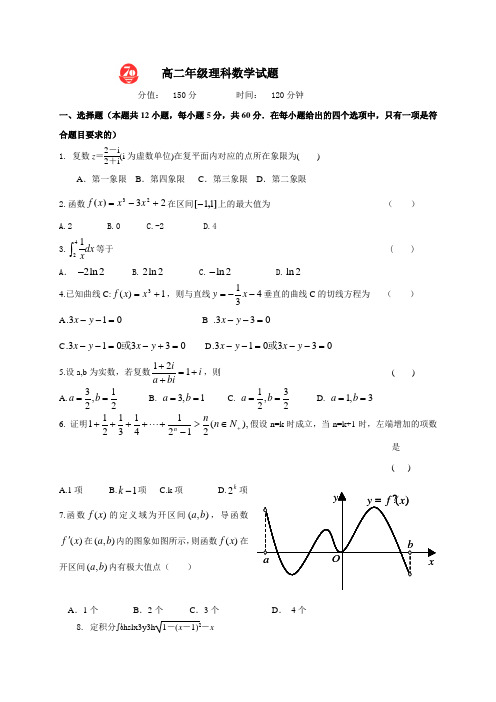
高二年级理科数学试题分值： 150分 时间： 120分钟一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1. 复数z ＝2－i 2＋i (i 为虚数单位)在复平面内对应的点所在象限为( ) A ．第一象限 B ．第四象限 C ．第三象限 D ．第二象限2.函数2323+-=x x x f )(在区间],[11-上的最大值为 （ ）A.2B.0C.-2D.43.421dx x⎰等于 ( ) A ． 2ln2- B.2ln 2 C.ln 2- D.ln 2 4.已知曲线C:1)(3+=x x f ，则与直线431--=x y 垂直的曲线C 的切线方程为 （ ） A 013.=--y x B 033.=--y xC 033013.=+-=--y x y x 或D 033013.=--=--y x y x 或5.设a,b 为实数，若复数i bia i +=++121，则 ( ) A.31,22ab == B. 3,1a b == C. 13,22a b == D. 1,3a b == 6. 证明),(21214131211+∈>-+++++N n n n 假设n=k 时成立，当n=k+1时，左端增加的项数是( )A.1项B.1-k 项C.k 项D.k 2项7.函数)(x f 的定义域为开区间),(b a ，导函数)(x f '在),(b a 内的图象如图所示，则函数)(x f 在开区间),(b a 内有极大值点（ ）A ．1个B ．2个C ．3个D ． 4个8. 定积分ʃ10hslx3y3h 1－(x －1)2－x a b xy )(x f y ?=O由S 3＝a 1＋a 2＋a 3＝12⎝ ⎛⎭⎪⎫a 3＋1a 3， 得a 23＋22a 3－1＝0，所以a 3＝3－ 2.(2)猜想a n ＝n －n －1(n ∈N ＋).证明：①当n ＝1时，a 1＝1－0＝1，命题成立；②假设n ＝k (k ≥1，k ∈N ＋)时，a k ＝k －k －1成立，则n ＝k ＋1时，a k ＋1＝S k ＋1－S k＝12⎝⎛⎭⎪⎫a k ＋1＋1a k ＋1－12⎝ ⎛⎭⎪⎫a k ＋1a k ， 即a k ＋1＝12⎝ ⎛⎭⎪⎫a k ＋1＋1a k ＋1 －12⎝ ⎛⎭⎪⎫k －k －1＋1k －k －1 ＝12⎝ ⎛⎭⎪⎫a k ＋1＋1a k ＋1－k ， 所以a 2k ＋1＋2ka k ＋1－1＝0.所以a k ＋1＝k ＋1－k ，则n ＝k ＋1时，命题成立.则①②知，n ∈N ＋，a n ＝n －n －1.22.（14分）解：（1）()f x 的定义域是(0,+∞),22222()1.a x ax f x x x x -+'=+-= 设2()2g x x ax =-+,二次方程()0g x =的判别式28a ∆=-.① 当280a ∆=-<，即0a <<时，对一切0x >都有()0f x '>,此时()f x 在(0,)+∞上是增函数。

2016-2017学年陕西省西安一中高二（下）第二次月考数学试卷（理科）一、选择题（本大题共12小题，每小题3分，共36分）1．（3分）用数字1，2，3，4，5组成的无重复数字的四位偶数的个数为（）A．8B．24C．48D．1202．（3分）把3封信投到4个信箱，则不同的投法共有（）A．24种B．4种C．43种D．34种3．（3分）设随机变量ξ服从正态分布N（0，1），P（ξ＞1）＝p，则P（﹣1＜ξ＜0）等于（）A．p B．1﹣p C．1﹣2p D．﹣p4．（3分）对标有不同编号的6件正品和4件次品的产品进行检测，不放回地依次摸出2件．在第一次摸出正品的条件下，第二次也摸到正品的概率是（）A．B．C．D．5．（3分）表中提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对应数据．根据下表提供的数据，求出y关于x的线性回归方程为＝0.7x+0.35，那么表中t的值为（）A．3B．3.15C．3.5D．4.56．（3分）通过随机询问110名性别不同的大学生是否爱好某项运动，得到如表的列联表：参考公式：K2＝，其中n＝a+b+c+d参照附表，得到的正确结论是（）A．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”B．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”C．有99%以上的把握认为“爱好该项运动与性别有关”D．有99%以上的把握认为“爱好该项运动与性别无关”7．（3分）已知随机变量ξ+η＝8，若ξ～B（10，0.6），则Eη，Dη分别是（）A．6和2.4B．2和2.4C．2和5.6D．6和5.68．（3分）已知f（x）＝|x+2|+|x﹣4|的最小值为n，则二项式展开式中x2项的系数为（）A．15B．﹣15C．30D．﹣309．（3分）将10个相同的小球装入3个编号为1，2，3的盒子（每次要把10个球装完），要求每个盒子里球的个数不少于盒子的编号数，这样的装法种数是（）A．9B．12C．15D．1810．（3分）用五种不同的颜色，给图中的（1）（2）（3）（4）的各部分涂色，每部分涂一种颜色，相邻部分涂不同颜色，则涂色的方法有（）种．A．240B．120C．60D．18011．（3分）式子﹣2∁n1+4∁n2﹣8∁n3+…+（﹣2）n∁n n等于（）A．（﹣1）n B．（﹣1）n﹣1C．3n D．3n﹣112．（3分）设曲线C的参数方程为（θ为参数），直线l的方程为x﹣3y+2＝0，则曲线C上到直线l距离为的点的个数为（）A．1B．2C．3D．4二、填空题（本大题共5小题，每小题4分，共20分）13．（4分）6个人坐到9个座位的一排位置上，则恰有3个空位且3个空位互不相邻的概率为．14．（4分）若ξ的分布列为：其中p∈（0，1），则Eξ＝，Dξ＝．15．（4分）P为曲线C1：，（θ为参数）上一点，则它到直线C2：（t 为参数）距离的最小值为．16．（4分）形如45132的数称为“波浪数”，即十位数字，千位数字均比与它们各自相邻的数字大，则由1，2，3，4，5可构成不重复的五位“波浪数”的个数为．17．（4分）设f（x）是（x2+）6展开式的中间项，若f（x）≤mx在区间[，]上恒成立，则实数m的取值范围是．三、解答题（本大题共4小题，共44分）18．（10分）某网站点击量等级规定如表：统计该网站4月份每天的点击数如下表：（1）若从中任选两天，则点击数落在同一等级的概率；（2）从4月份点击量低于100万次的天数中随机抽取3天，记这3天点击等级为差的天数为随机变量X，求随机变量X的分布列与数学期望．19．（10分）在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρcos（）＝1，M，N分别为C与x轴，y轴的交点．（1）写出C的直角坐标方程，并求M，N的极坐标；（2）设MN的中点为P，求直线OP的极坐标方程．20．（12分）某市职教中心组织厨师技能大赛，大赛依次设基本功（初赛）、面点制作（复赛）、热菜烹制（决赛）三个轮次的比赛，已知某选手通过初赛、复赛、决赛的概率分别是，，且各轮次通过与否相互独立．（Ⅰ）设该选手参赛的轮次为ξ，求ξ的分布列和数学期望；（Ⅱ）对于（I）中的ξ，设“函数f（x）＝3sinπ（x∈R）是偶函数”为事件D，求事件D发生的概率．21．（12分）设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ＝0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ＝1．（1）求概率P（ξ＝0）；（2）求ξ的分布列，并求其数学期望E（ξ）．2016-2017学年陕西省西安一中高二（下）第二次月考数学试卷（理科）参考答案与试题解析一、选择题（本大题共12小题，每小题3分，共36分）1．（3分）用数字1，2，3，4，5组成的无重复数字的四位偶数的个数为（）A．8B．24C．48D．120【解答】解：由题意知本题需要分步计数，2和4排在末位时，共有A21＝2种排法，其余三位数从余下的四个数中任取三个有A43＝4×3×2＝24种排法，根据由分步计数原理得到符合题意的偶数共有2×24＝48（个）．故选：C．2．（3分）把3封信投到4个信箱，则不同的投法共有（）A．24种B．4种C．43种D．34种【解答】解：第1封信投到信箱有4种方法，第2封信投到信箱有4种方法，第3封信投到信箱有4种方法，由分步计数原理可知共有43种方法．故选：C．3．（3分）设随机变量ξ服从正态分布N（0，1），P（ξ＞1）＝p，则P（﹣1＜ξ＜0）等于（）A．p B．1﹣p C．1﹣2p D．﹣p【解答】解：∵随机变量ξ服从正态分布N（0，1），∴正态曲线关于ξ＝0对称，∵P（ξ＞1）＝p，∴P（ξ＜﹣1）＝p，∴P（﹣1＜ξ＜0）＝﹣p．故选：D．4．（3分）对标有不同编号的6件正品和4件次品的产品进行检测，不放回地依次摸出2件．在第一次摸出正品的条件下，第二次也摸到正品的概率是（）A．B．C．D．【解答】解：设“第一次摸出正品”为事件A，“第二次摸出正品”为事件B，则事件A和事件B相互独立，在第一次摸出正品的条件下，第二次也摸到正品的概率为：P（B|A）＝＝＝．故选：D．5．（3分）表中提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对应数据．根据下表提供的数据，求出y关于x的线性回归方程为＝0.7x+0.35，那么表中t的值为（）A．3B．3.15C．3.5D．4.5【解答】解：∵由回归方程知＝，解得t＝3，故选：A．6．（3分）通过随机询问110名性别不同的大学生是否爱好某项运动，得到如表的列联表：参考公式：K2＝，其中n＝a+b+c+d参照附表，得到的正确结论是（）A．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”B．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”C．有99%以上的把握认为“爱好该项运动与性别有关”D．有99%以上的把握认为“爱好该项运动与性别无关”【解答】解：由题意知本题所给的观测值，X2＝≈7.8∵7.8＞6.635，∴这个结论有0.010的机会说错，即有99%的把握认为“爱好该项运动与性别有关．故选：C．7．（3分）已知随机变量ξ+η＝8，若ξ～B（10，0.6），则Eη，Dη分别是（）A．6和2.4B．2和2.4C．2和5.6D．6和5.6【解答】解：∵ξ～B（10，0.6），∴Eξ＝10×0.6＝6，Dξ＝10×0.6×0.4＝2.4，∵ξ+η＝8，∴Eη＝E（8﹣ξ）＝2，Dη＝D（8﹣ξ）＝2.4故选：B．8．（3分）已知f（x）＝|x+2|+|x﹣4|的最小值为n，则二项式展开式中x2项的系数为（）A．15B．﹣15C．30D．﹣30【解答】解：∵已知f（x）＝|x+2|+|x﹣4|的最小值为n，而由绝对值的意义可得|x+2|+|x﹣4|表示数轴上的x对应点到﹣2和4对应点的距离之和，它的最小值为6，故n＝6．则二项式＝的展开式的通项公式为T r+1＝•x6﹣r•（﹣1）r•x﹣r＝（﹣1）r ••x6﹣2r，令6﹣2r＝2，求得r＝2，故展开式中x2项的系数为＝15，故选：A．9．（3分）将10个相同的小球装入3个编号为1，2，3的盒子（每次要把10个球装完），要求每个盒子里球的个数不少于盒子的编号数，这样的装法种数是（）A．9B．12C．15D．18【解答】解：根据题意，先在编号为2、3的三个盒子中分别放入1、2个小球，编号为1的盒子里不放；再将剩下的7个小球放入3个盒子里，每个盒子里至少一个，分析可得，7个小球排好，有6个空位，在6个空位中任选2个，插入挡板，共C62＝15种放法，即可得符合题目要求的放法共15种，故选：C．10．（3分）用五种不同的颜色，给图中的（1）（2）（3）（4）的各部分涂色，每部分涂一种颜色，相邻部分涂不同颜色，则涂色的方法有（）种．A．240B．120C．60D．180【解答】解：由题意知本题是一个分步计数问题，第一步先给（3）涂色共有5种结果，第二步再给（1）（2）涂色共有4×3种结果，第三步给（4）涂色有4种结果，∴由分步计数原理知共有5×4×3×4＝240故选：A．11．（3分）式子﹣2∁n1+4∁n2﹣8∁n3+…+（﹣2）n∁n n等于（）A．（﹣1）n B．（﹣1）n﹣1C．3n D．3n﹣1【解答】解：﹣2∁n1+4∁n2﹣8∁n3+…+（﹣2）n＝（1﹣2）n﹣1＝（﹣1）n﹣1故选：B．12．（3分）设曲线C的参数方程为（θ为参数），直线l的方程为x﹣3y+2＝0，则曲线C上到直线l距离为的点的个数为（）A．1B．2C．3D．4【解答】解：曲线C的参数方程为（θ为参数），化为普通方程为圆C：（x﹣2）2+（y﹣1）2＝9，圆心为（2，1），半径为3．则圆心到直线的距离d＝＝．则直线与圆相交，则由3﹣＞，故在直线x﹣3y+2＝0的上方和下方各有两个，共4个．故选：D．二、填空题（本大题共5小题，每小题4分，共20分）13．（4分）6个人坐到9个座位的一排位置上，则恰有3个空位且3个空位互不相邻的概率为．【解答】解：6个人坐到9个座位的一排位置上，基本事件总数n＝，恰有3个空位且3个空位互不相邻包含的基本事件个数m＝，∴恰有3个空位且3个空位互不相邻的概率p＝＝．故答案为：．14．（4分）若ξ的分布列为：其中p∈（0，1），则Eξ＝q，，Dξ＝pq．【解答】解：Eξ＝0×p+1×q＝qDξ＝（0﹣q）2×p+（1﹣q）2×q＝pq故答案为：q；pq．15．（4分）P为曲线C1：，（θ为参数）上一点，则它到直线C2：（t 为参数）距离的最小值为1．【解答】解：将曲线C1化成普通方程是（x﹣1）2+y2＝1，圆心是（1，0），直线C2化成普通方程是y﹣2＝0，则圆心到直线的距离为2，∴曲线C1上点到直线的距离为1，该点为（1，1），故答案为：1．16．（4分）形如45132的数称为“波浪数”，即十位数字，千位数字均比与它们各自相邻的数字大，则由1，2，3，4，5可构成不重复的五位“波浪数”的个数为16．【解答】解：此“波浪数”中，十位数字，千位数字必有5、另一数是3或4；是4时“波浪数”有A22A33＝12；另一数3时4、5必须相邻即45132；45231；13254；23154．四种．则由1，2，3，4，5可构成数字不重复的五位“波浪数”个数为16．故答案为：16．17．（4分）设f（x）是（x2+）6展开式的中间项，若f（x）≤mx在区间[，]上恒成立，则实数m的取值范围是[5，+∞）．【解答】解：由题意可得f（x）＝•x6•＝•x3．由f（x）≤mx在区间[，]上恒成立，可得m≥x2在区间[，]上恒成立，由于x2在区间[，]上的最大值为5，故m≥5，即m的范围为[5，+∞），故答案为：[5，+∞）．三、解答题（本大题共4小题，共44分）18．（10分）某网站点击量等级规定如表：统计该网站4月份每天的点击数如下表：（1）若从中任选两天，则点击数落在同一等级的概率；（2）从4月份点击量低于100万次的天数中随机抽取3天，记这3天点击等级为差的天数为随机变量X，求随机变量X的分布列与数学期望．【解答】解：（1）折点击数落在同一等级的为事件A概率：，即点击数落在同一等级的概率为．（2）X的可能取值为0、1、2、3，，，，，随机变量X的分布列为数学期望．19．（10分）在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρcos（）＝1，M，N分别为C与x轴，y轴的交点．（1）写出C的直角坐标方程，并求M，N的极坐标；（2）设MN的中点为P，求直线OP的极坐标方程．【解答】解：（Ⅰ）由从而C的直角坐标方程为即θ＝0时，ρ＝2，所以M（2，0）（Ⅱ）M点的直角坐标为（2，0）N点的直角坐标为所以P点的直角坐标为，则P点的极坐标为，所以直线OP的极坐标方程为，ρ∈（﹣∞，+∞）20．（12分）某市职教中心组织厨师技能大赛，大赛依次设基本功（初赛）、面点制作（复赛）、热菜烹制（决赛）三个轮次的比赛，已知某选手通过初赛、复赛、决赛的概率分别是，，且各轮次通过与否相互独立．（Ⅰ）设该选手参赛的轮次为ξ，求ξ的分布列和数学期望；（Ⅱ）对于（I）中的ξ，设“函数f（x）＝3sinπ（x∈R）是偶函数”为事件D，求事件D发生的概率．【解答】解：（I）ξ可能取值为1，2，3．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）记“该选手通过初赛”为事件A，“该选手通过复赛”为事件B，则P（ξ＝1）＝P（）＝1﹣＝；P（ξ＝2）＝P（）＝P（A）P（）＝＝；P（ξ＝3）＝P（AB）＝P（A）P（B）＝＝﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）ξ的分布列为：ξ的数学期望Eξ＝1×+2×+3×＝﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（7分）（Ⅱ）当ξ＝1时，f（x）＝3sin（）＝3cos，∴f（x）为偶函数；当ξ＝2时，f（x）＝3sin（）＝﹣3sin，∴f（x）为奇函数；当ξ＝3时，f（x）＝3sin（），∴f（x）为偶函数；∴事件D发生的概率是．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）21．（12分）设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ＝0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ＝1．（1）求概率P（ξ＝0）；（2）求ξ的分布列，并求其数学期望E（ξ）．【解答】解：（1）若两条棱相交，则交点必为正方体8个顶点中的一个，过任意1个顶点恰有3条棱，∴共有8对相交棱，∴P（ξ＝0）＝．（2）若两条棱平行，则它们的距离为1或，其中距离为的共有6对，∴P（ξ＝）＝，P（ξ＝1）＝1﹣P（ξ＝0）﹣P（ξ＝）＝．∴随机变量ξ的分布列是：∴其数学期望E（ξ）＝1×+＝．。

2016-2017学年陕西省西安八十三中高二（下）期中数学试卷（理科）一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．复数z=﹣2+i，则复数z在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限2．n个连续自然数按规律排成表：根据规律，从2016到2018，箭头的方向依次为（）A．↓→ B．→↑ C．↑→ D．→↓3．已知函数f（x）=x3+ax2+（a+6）x+1有极大值和极小值，则实数a的取值范围是（）A．﹣1＜a＜2 B．﹣3＜a＜6 C．a＜﹣3或a＞6 D．a＜﹣1或a＞24．由直线x=1，x=2，曲线y=x2及x轴所围图形的面积为（）A．3 B．7 C．D．5．已知函数y=xf′（x）的图象如图所示（其中f′（x）是函数f（x）的导函数），下面四个图象中，y=f（x）的图象大致是（）A．B．C．D．6．用数学归纳法证明“当n 为正奇数时，x n+y n能被x+y整除”，在第二步时，正确的证法是（）A．假设n=k（k∈N*），证明n=k+1命题成立B．假设n=k（k为正奇数），证明n=k+1命题成立C．假设n=2k+1（k∈N*），证明n=k+1命题成立D．假设n=k（k为正奇数），证明n=k+2命题成立7．观察（x2）′=2x，（x4）′=4x3，（cosx）′=﹣sinx，由归纳推理可得：若定义在R 上的函数f（x）满足f（﹣x）=f（x），记g（x）为f（x）的导函数，则g（﹣x）=（）A．﹣g（x）B．f（x）C．﹣f（x）D．g（x）8．函数f（x）=3x﹣4x3（x∈）的最大值是（）A．1 B．C．0 D．﹣19．曲线y=ln（2x﹣1）上的点到直线2x﹣y+3=0的最短距离是（）A．B．2 C．3 D．010．已知二次函数f（x）=ax2+bx+c的导数为f′（x），f′（0）＞0，对于任意实数x都有f（x）≥0，则的最小值为（）A．3 B．C．2 D．二、填空题（本大题共5小题，每小题4分，共20分．请将答案写在答题卡相应位置）11．若三角形的内切圆半径为r，三边的长分别为a，b，c，则三角形的面积S=r （a+b+c），根据类比思想，若四面体的内切球半径为R，四个面的面积分别为S1、S2、S3、S4，则此四面体的体积V=．12．已知函数f（x）=x3+ax2+bx+c在x=﹣2处取得极值，并且它的图象与直线y=﹣3x+3在点（1，0）处相切，则函数f（x）的表达式为．13．下列是关于复数的类比推理：①复数的加减法运算可以类比多项式的加减法运算法则；②由实数绝对值的性质|x|2=x2类比得到复数z的性质|z|2=z2；③已知a，b∈R，若a﹣b＞0，则a＞b．类比得已知z1，z2∈C，若z1﹣z2＞0，则z1＞z2；④由向量加法的几何意义可以类比得到复数加法的几何意义．其中推理结论正确的是．14．=．15．在如下数表中，已知每行、每列中的数都成等差数列，那么，位于下表中的第n行第n+1列的数是．第1列第2列第3列…第1行123…第2行246…第3行369………………三、解答题（本大题共4小题，每小题10分，共40分．请将答案写在答题卡相应位置）16．已知复数z=m（m﹣1）+（m2+2m﹣3）i；当实数m取什么值时，复数z是：（1）实数（2）虚数（3）纯虚数（4）零．17．已知函数f（x）=x3﹣ax2﹣3x．（1）若f（x）在上单调递减，在（﹣∞，﹣10，10，11，+∞）上是增函数，求实数a的取值范围．（2）若x=3是f（x）的极值点，求f（x）的单调区间及极值．【考点】6B：利用导数研究函数的单调性；6D：利用导数研究函数的极值．【分析】（1）对函数f（x）=x3﹣ax2﹣3x进行求导，转化成f′（x）在1，+∞）上是增函数，∴f′（x）在1，+∞）上恒成立．则必有≤1且f′（1）=﹣2a≥0，∴a≤0；实数a的取值范围是（﹣∞，0hslx3y3h．（2）∵f（x）=x3﹣ax2+3x．∴f′（x）=3x2﹣2ax+3．由题意有f′（3）=0，解得a=5，故f（x）=x3﹣5x2+3x，∴f′（x）=3x2﹣10x+3=（3x﹣1）（x﹣3）令f′（x）＞0，解得：x＞3或x＜，令f′（x）＜0，解得：＜x＜3，故f（x）在（﹣∞，）递增，在（，3）递减，在（3，+∞）递增，=，f（x）极小值=f（3）=﹣9．故f（x）极大值=f（）18．已知a，b，c是互不相等的实数，求证：由y=ax2+2bx+c，y=bx2+2cx+a，y=cx2+2ax+b 确定的三条抛物线至少有一条与x轴有两个不同的交点．【考点】FD：反证法的应用．【分析】本题是一个至少性问题，可以利用反证法证明，其步骤为：①否定命题的结论，即假设“任何一条抛物线与x轴没有两个不同的交点”成立→②根据函数的性质可以得到三个函数对应方程的△≤0均成立→③利用不等式的性质，同向不等式求和→④得到的式子与实数的性质相矛盾→⑤故假设不成立，原结论成立．【解答】解：假设题设中的函数确定的三条抛物线都不与x有两个不同的交点（即任何一条抛物线与x轴没有两个不同的交点），由y=ax2+2bx+c，y=bx2+2cx+a，y=cx2+2ax+b得△1=（2b）2﹣4ac≤0，△2=（2c）2﹣4ab≤0，△3=（2a）2﹣4bc≤0．同向不等式求和得，4b2+4c2+4a2﹣4ac﹣4ab﹣4bc≤0，∴2a2+2b2+2c2﹣2ab﹣2bc﹣2ac≤0，∴（a﹣b）2+（b﹣c）2+（c﹣a）2≤0，∴a=b=c，这与题设a，b，c互不相等矛盾，因此假设不成立，从而命题得证．19．已知函数f（x）满足f（x）=f′（1）e x﹣1﹣f（0）x+x2；（1）求f（x）的解析式及单调区间；（2）若，求（a+1）b的最大值．【考点】6K：导数在最大值、最小值问题中的应用；6B：利用导数研究函数的单调性．【分析】（1）对函数f（x）求导，再令自变量为1，求出f′（1）得到函数的解析式及导数，再由导数求函数的单调区间；（2）由题意，借助导数求出新函数的最小值，令其大于0即可得到参数a，b 所满足的关系式，再研究（a+1）b的最大值【解答】解：（1）f（x）=f'（1）e x﹣1﹣f（0）x+⇒f'（x）=f'（1）e x﹣1﹣f（0）+x令x=1得：f（0）=1∴f（x）=f'（1）e x﹣1﹣x+令x=0，得f（0）=f'（1）e﹣1=1解得f'（1）=e故函数的解析式为f（x）=e x﹣x+令g（x）=f'（x）=e x﹣1+x∴g'（x）=e x+1＞0，由此知y=g（x）在x∈R上单调递增当x＞0时，f'（x）＞f'（0）=0；当x＜0时，有f'（x）＜f'（0）=0得：函数f（x）=e x﹣x+的单调递增区间为（0，+∞），单调递减区间为（﹣∞，0）（2）f（x）≥﹣（a+1）x﹣b≥0得h′（x）=e x﹣（a+1）①当a+1≤0时，h′（x）＞0⇒y=h（x）在x∈R上单调递增，x→﹣∞时，h（x）→﹣∞与h（x）≥0矛盾②当a+1＞0时，h′（x）＞0⇔x＞ln（a+1），h'（x）＜0⇔x＜ln（a+1）得：当x=ln（a+1）时，h（x）min=（a+1）﹣（a+1）ln（a+1）﹣b≥0，即（a+1）﹣（a+1）ln（a+1）≥b∴（a+1）b≤（a+1）2﹣（a+1）2ln（a+1），（a+1＞0）令F（x）=x2﹣x2lnx（x＞0），则F'（x）=x（1﹣2lnx）∴F'（x）＞0⇔0＜x＜当x=时，F（x）max=即当a=时，（a+1）b的最大值为2017年6月29日。

2016-2017学年陕西省西安七十中高二（下）期中数学试卷（理科）一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）复数（i为虚数单位）在复平面内对应的点所在象限为（）A．第一象限B．第二象限C．第三象限D．第四象限2．（5分）f（x）＝x3﹣3x2+2在区间[﹣1，1]上的最大值是（）A．﹣2B．0C．2D．43．（5分）dx等于（）A．﹣2ln2B．2ln2C．﹣ln2D．ln24．（5分）已知曲线C：f（x）＝x3+1，则与直线垂直的曲线C的切线方程为（）A．3x﹣y﹣1＝0B．3x﹣y﹣3＝0C．3x﹣y﹣1＝0或3x﹣y+3＝0D．3x﹣y﹣1＝0或3x﹣y﹣3＝0 5．（5分）设a，b为实数，若复数，则（）A．B．a＝3，b＝1C．D．a＝1，b＝36．（5分）证明1++…+（n∈N*），假设n＝k时成立，当n＝k+1时，左端增加的项数是（）A．1项B．k﹣1项C．k项D．2k项7．（5分）函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值点（）A．1个B．2个C．3个D．4个8．（5分）定积分[﹣x]dx等于（）A．B．﹣1C．D．9．（5分）设f′（x）是函数f（x）的导函数，将y＝f（x）和y＝f′（x）的图象画在同一个直角坐标系中，不可能正确的是（）A．B．C．D．10．（5分）已知函数f（x）在R上满足f（x）＝2f（2﹣x）﹣x2+8x﹣8，则曲线y＝f（x）在点（1，f（1））处的切线方程是（）A．y＝2x﹣1B．y＝x C．y＝3x﹣2D．y＝﹣2x+3 11．（5分）设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则，类比这个结论可知：四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4，内切球半径为R，四面体S﹣ABC的体积为V，则R＝（）A．B．C．D．12．（5分）若0＜x＜，则2x与3sin x的大小关系（）A．2x＞3sin x B．2x＜3sin xC．2x＝3sin x D．与x的取值有关二、填空题（本题共5小题，每小题5分，共25分）13．（5分）复数z＝1+i，为z的共轭复数，则＝．14．（5分）设函数，其中，则导数f′（1）的取值范围是．15．（5分）已知f（x）＝x3+ax2+（a+6）x+1有极大值和极小值，则a的取值范围为．16．（5分）已知a1＝3，a n﹣a n a n+1＝1（n∈N+），A n表示数列{a n}的前n项之积，则A2010＝．17．（5分）f（n）＝1+++…+（n∈N*），计算f（2）＝，f（4）＞2，f（8）＞，f（16）＞3，f（32）＞，推测当n≥2时，有．三．解答题（共65分）18．（12分）设复数z＝，若z2+az+b＝1+i，求实数a，b的值．19．（13分）已知函数f（x）＝x2+lnx．（1）求函数f（x）的单调区间；（2）求证：当x＞1时，x2+lnx＜x3．20．（13分）已知a＞0，求证：﹣≥a+．21．（13分）在各项为正的数列{a n}中，数列的前n项和S n满足S n＝（a n+），（1）求a1，a2，a3；（2）由（1）猜想数列{a n}的通项公式，并用数学归纳法证明你的猜想．22．（14分）已知函数f（x）＝x﹣．（1）讨论f（x）的单调性．（2）若f（x）在区间（1，2）上单调递减，求实数a的取值范围．2016-2017学年陕西省西安七十中高二（下）期中数学试卷（理科）参考答案与试题解析一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）复数（i为虚数单位）在复平面内对应的点所在象限为（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：∵＝＝﹣i∴复数在复平面对应的点的坐标是（，﹣）∴它对应的点在第四象限，故选：D．2．（5分）f（x）＝x3﹣3x2+2在区间[﹣1，1]上的最大值是（）A．﹣2B．0C．2D．4【解答】解：f'（x）＝3x2﹣6x＝3x（x﹣2），令f'（x）＝0可得x＝0或2（2舍去），当﹣1＜x＜0时，f'（x）＞0，当0＜x＜1时，f'（x）＜0，∴当x＝0时，f（x）取得最大值为f（0）＝2．故选：C．3．（5分）dx等于（）A．﹣2ln2B．2ln2C．﹣ln2D．ln2【解答】解：∵（lnx）′＝∴＝lnx|24＝ln4﹣ln2＝ln2故选：D．4．（5分）已知曲线C：f（x）＝x3+1，则与直线垂直的曲线C的切线方程为（）A．3x﹣y﹣1＝0B．3x﹣y﹣3＝0C．3x﹣y﹣1＝0或3x﹣y+3＝0D．3x﹣y﹣1＝0或3x﹣y﹣3＝0【解答】解：设切点M（x0，y0）∵切线与直线垂直∴切线的斜率为3，∴曲线在点M处的导数y′＝3x02＝3，即x0＝±1．当x0＝1时，y0＝2，利用点斜式得到切线方程：3x﹣y﹣1＝0；当x0＝﹣1时，y0＝0，利用点斜式得到切线方程：3x﹣y+3＝0．综上所述：切线的方程为3x﹣y﹣1＝0或3x﹣y+3＝0．故选：C．5．（5分）设a，b为实数，若复数，则（）A．B．a＝3，b＝1C．D．a＝1，b＝3【解答】解：由可得1+2i＝（a﹣b）+（a+b）i，所以，解得，，故选：A．6．（5分）证明1++…+（n∈N*），假设n＝k时成立，当n＝k+1时，左端增加的项数是（）A．1项B．k﹣1项C．k项D．2k项【解答】解：当n＝k时不等式为：成立当n＝k+1时不等式左边为则左边增加2k+1﹣2k＝2k项．故选：D．7．（5分）函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值点（）A．1个B．2个C．3个D．4个【解答】解：由图象得：导函数f′（x）＝0有3个根，只有在b附近的根满足根的左边为负值，根的右边为正值，故函数只有1个极小值点，故选：A．8．（5分）定积分[﹣x]dx等于（）A．B．﹣1C．D．【解答】解：dx表示以（1，0）为圆心，半径r＝1的圆的面积的四分之一，故dx＝，xdx＝|＝，故定积分[﹣x]dx＝﹣，故选：A．9．（5分）设f′（x）是函数f（x）的导函数，将y＝f（x）和y＝f′（x）的图象画在同一个直角坐标系中，不可能正确的是（）A．B．C．D．【解答】解析：检验易知A、B、C均适合，不存在选项D的图象所对应的函数，在整个定义域内，不具有单调性，但y＝f（x）和y＝f′（x）在整个定义域内具有完全相同的走势，不具有这样的函数，故选：D．10．（5分）已知函数f（x）在R上满足f（x）＝2f（2﹣x）﹣x2+8x﹣8，则曲线y＝f（x）在点（1，f（1））处的切线方程是（）A．y＝2x﹣1B．y＝x C．y＝3x﹣2D．y＝﹣2x+3【解答】解：∵f（x）＝2f（2﹣x）﹣x2+8x﹣8，∴f（1）＝2f（1）﹣1∴f（1）＝1∵f′（x）＝﹣2f′（2﹣x）﹣2x+8∴f′（1）＝﹣2f′（1）+6∴f′（1）＝2根据导数的几何意义可得，曲线y＝f（x）在点（1，f（1））处的切线斜率k＝f′（1）＝2∴过（1，1）的切线方程为：y﹣1＝2（x﹣1）即y＝2x﹣1故选：A．11．（5分）设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则，类比这个结论可知：四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4，内切球半径为R，四面体S﹣ABC的体积为V，则R＝（）A．B．C．D．【解答】解：设四面体的内切球的球心为O，则球心O到四个面的距离都是R，所以四面体的体积等于以O为顶点，分别以四个面为底面的4个三棱锥体积的和．则四面体的体积为∴R＝故选：C．12．（5分）若0＜x＜，则2x与3sin x的大小关系（）A．2x＞3sin x B．2x＜3sin xC．2x＝3sin x D．与x的取值有关【解答】解：设g（x）＝2x﹣3sin x，则g′（x）＝2﹣3cos x，当0＜x＜arccos时，g′（x）＜0，g（x）是减函数，g（x）＜g（0）＝0，∴2x＜3sin x；当arccos＜x＜时，g'（x）＞0，g（x）是增函数，但g（arccos）＜0，g （）＞0，∴在区间[arccos，）有且仅有一点θ使g（θ）＝0；当arccos≤x＜θ时，g（x）＜g（θ）＝0，2x＜3sin x；当θ＜x＜时，g（x）＞g（θ）＝0，2x＞3sin x；∴当0＜x＜θ时，2x＜3sin x；当x＝θ时，2x＝3sin x；当θ＜x＜时，2x＞3sin x．故选：D．二、填空题（本题共5小题，每小题5分，共25分）13．（5分）复数z＝1+i，为z的共轭复数，则＝﹣i．【解答】解：∵复数z＝1+i，为z的共轭复数∴＝1﹣i∴＝（1+i）（1﹣i）﹣（1+i）﹣1＝2﹣1﹣i﹣1＝﹣i故答案为：﹣i14．（5分）设函数，其中，则导数f′（1[，2]．【解答】解：∵，∴f'（x）＝sinθx2+cosθx∴f′（1）＝sinθ+cosθ＝2sin（θ+）∵，∴θ+∈[，]∴sin（θ+）∈[，1]∴f′（1）∈[，2]故答案为：[，2]．15．（5分）已知f（x）＝x3+ax2+（a+6）x+1有极大值和极小值，则a的取值范围为a＜﹣3或a＞6．【解答】解：函数f（x）＝x3+ax2+（a+6）x+1，所以函数f′（x）＝3x2+2ax+（a+6），因为函数有极大值和极小值，所以方程f′（x）＝0有两个不相等的实数根，即3x2+2ax+（a+6）＝0有两个不相等的实数根，∴△＞0，∴（2a）2﹣4×3×（a+6）＞0，解得：a＜﹣3或a＞6故答案为：a＜﹣3或a＞616．（5分）已知a1＝3，a n﹣a n a n+1＝1（n∈N+），A n表示数列{a n}的前n项之积，则A2010＝1．【解答】解：∵a1＝3，a n﹣a n a n+1＝1（n∈N+），∴3﹣3a2＝1，∴，，∴，，a4＝3，∴数列{a n}是周期为3的数列，且a1•a2•a3＝，∵2010＝670×3，∴A2010＝（a1•a2•a3）670＝（﹣1）670＝1．故答案为：1．17．（5分）f（n）＝1+++…+（n∈N*），计算f（2）＝，f（4）＞2，f（8）＞，f（16）＞3，f（32）＞，推测当n≥2时，有f（2n）≥．【解答】解：观察已知中等式：得f（2）＝，即f（21）＝f（4）＞2，即f（22）＞f（8）＞，即f（23）＞f（16）＞3，即f（24）＞f（32）＞，即f（25）＞…则f（2n）≥（n∈N*）故答案为：f（2n）≥三．解答题（共65分）18．（12分）设复数z＝，若z2+az+b＝1+i，求实数a，b的值．【解答】解：z＝＝＝＝＝1﹣iz2+az+b＝（1﹣i）2+a（1﹣i）+b＝a+b﹣（a+2）i＝1+i∴解得19．（13分）已知函数f（x）＝x2+lnx．（1）求函数f（x）的单调区间；（2）求证：当x＞1时，x2+lnx ＜x3．【解答】（1）解：依题意知函数的定义域为{x|x＞0}，∵f′（x）＝x +，∴f′（x）＞0，∴f（x）的单调增区间为（0，+∞）．（2）证明：设g（x ）＝x3﹣x2﹣lnx，∴g′（x）＝2x2﹣x﹣，∵当x＞1时，g′（x ）＝＞0，∴g（x）在（1，+∞）上为增函数，∴g（x）＞g（1）＝＞0，∴当x＞1时，x2+lnx＜x3．20．（13分）已知a＞0，求证：﹣≥a +．【解答】证明：要证﹣≥a +，只要证明+2≥a++．∵a＞0，∴只要证明（+2）2≥（a ++）2，只要证明2≥（a +），只要证明≥2，显然成立，∴﹣≥a +．21．（13分）在各项为正的数列{a n}中，数列的前n项和S n满足S n ＝（a n +），（1）求a1，a2，a3；（2）由（1）猜想数列{a n}的通项公式，并用数学归纳法证明你的猜想．第11页（共13页）【解答】解：（1）易求得（3分）；（2）猜想（5分）证明：①当n＝1时，，命题成立②假设n＝k时，成立，（8分）则n＝k+1时，＝＝，所以，，∴．即n＝k+1时，命题成立．由①②知，n∈N*时，．（12分）22．（14分）已知函数f（x）＝x﹣．（1）讨论f（x）的单调性．（2）若f（x）在区间（1，2）上单调递减，求实数a的取值范围．【解答】解：（1）由题意得，函数f（x）的定义域是（0，+∞），且f′（x）＝1+﹣＝设g（x）＝x2﹣ax+2，二次方程g（x）＝0的判别式△＝a2﹣8，①当△＝a2﹣8＜0，即0＜a＜2时，对一切x＞0都有f′（x）＞0，此时f（x）在（0，+∞）上是增函数；②当△＝a2﹣8＝0，即a＝2时，仅对x ＝有f′（x）＝0，对其余的x＞0，都有f′（x）＞0，此时f（x）在（0，+∞）上也是增函数．③当△＝a2﹣8＞0，即a＞2时，g（x）＝x2﹣ax+2＝0有两个不同的实根，，由f′（x）＞0得，0＜x ＜或x＞，由f'（x）＜0得，＜x ＜，第12页（共13页）此时f（x）在（0，），（，+∞）上单调递增，在（，）是上单调递减，（2）解：f′（x）＝1+﹣＝，依题意f'（x）≤0（等零的点是孤立的），即x2﹣ax+2≤0在（1，2）上恒成立，令g（x）＝x2﹣ax+2，则有，解得a≥3，故实数a的取值范围为[3，+∞）．第13页（共13页）。

参考答案一、选择题：(5分×12=60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A D C B A D A C C B B C 二、填空题(5分×4=20分)13．123 14．4 15．10 16．[34，＋∞)三、解答题(本大题共6小题，共70分)17. 证明 (1)当n ＝1时，左边＝12×1×2×1＋2＝18，右边＝141＋1＝18，左边＝右边，所以等式成立．-----------3分(2)假设n ＝k (k ∈N ＋)时等式成立，即有12×4＋14×6＋16×8＋…＋12k 2k ＋2＝k4k ＋1，----------5分则当n ＝k ＋1时，12×4＋14×6＋16×8＋…＋12k 2k ＋2＋12k ＋1[2k ＋1＋2]＝k4k ＋1＋14k ＋1k ＋2＝k k ＋2＋14k ＋1k ＋2＝k ＋124k ＋1k ＋2＝k ＋14k ＋2＝k ＋14k ＋1＋1.---------8分所以当n ＝k ＋1时，等式也成立，----------9分由(1)(2)可知，对于一切n ∈N ＋等式恒成立．---------10分18. 解 (1)因为当x ＝5时，y ＝11，所以a2＋10＝11，a ＝2.-----3分(2)由(1)可知，该商品每日的销售量为y ＝2x －3＋10(x －6)2.所以商场每日销售该商品所获得的利润为f (x )＝(x －3)[2x －3＋10(x －6)2]＝2＋10(x －3)(x －6)2,3<x <6.----------7分从而，f ′(x )＝10[(x －6)2＋2(x －3)(x －6)]＝30(x －4)(x －6)．-------9分于是，当x 变化时，f ′(x )，f (x )的变化情况如下表： x (3,4) 4 (4,6)f ′(x ) ＋ 0 －f (x ) 单调递增 极大值42 单调递减由上表可得，当x ＝4时，函数f (x )取得极大值，也是最大值．所以，当x ＝4时，函数f (x )取得最大值且最大值等于42.---------12分19. 证明 (1)∵a >0，b >0,2c >a ＋b ≥2ab ，∴c >ab ，平方得c 2>ab .---------5分(2)要证c －c 2－ab <a <c ＋c 2－ab ，只要证－c 2－ab <a －c <c 2－ab ，即证|a －c |<c 2－ab ，即(a －c )2<c 2－ab .∵(a －c )2－c 2＋ab ＝a (a ＋b －2c )<0成立，∴原不等式成立．---------12分20.解 (1)因为f (x )＝a (x －5)2＋6ln x ，所以f ′(x )＝2a (x －5)＋6x .令x ＝1，得f (1)＝16a ，f ′(1)＝6－8a ，所以曲线y ＝f (x )在点(1，f (1))处的切线方程为y －16a ＝(6－8a )(x －1)，----4分由点(0,6)在切线上，可得6－16a ＝8a －6，故a ＝12.----5分所以，切线方程是y=2x+6--------6分(2)由(1)知，f (x )＝12(x －5)2＋6ln x (x >0)，f ′(x )＝x －5＋6x ＝x －2x －3x .-------7分令f ′(x )＝0，解得x ＝2或3.当0<x <2或x >3时，f ′(x )>0，故f (x )在(0,2)，(3，＋∞)上为增函数；当2<x <3时，f ′(x )<0，故f (x )在(2,3)上为减函数.-------10分由此可知f (x )在x ＝2处取得极大值f (2)＝92＋6ln 2，在x ＝3处取得极小值f (3)＝2＋6ln 3. 综上，f (x )的极大值为92＋6ln 2，极小值为2＋6ln 3.----12分21.解 (1)由已知|AB |＝52|BF |， 即a 2＋b 2＝52a ，4a 2＋4b 2＝5a 2,4a 2＋4(a 2－c 2)＝5a 2，∴e ＝c a ＝32.-----5分(2)由(1)知a 2＝4b 2，∴椭圆C ：x 24b 2＋y2b 2＝1.设P (x 1，y 1)，Q (x 2，y 2)，直线l 的方程为y －2＝2(x －0)，即2x －y ＋2＝0.由⎩⎪⎨⎪⎧2x －y ＋2＝0，x 24b 2＋y 2b 2＝1消去y ，得x 2＋4(2x ＋2)2－4b 2＝0，即17x 2＋32x ＋16－4b 2＝0.---------7分Δ＝322＋16×17(b 2－4)>0，解得b >21717.x 1＋x 2＝－3217，x 1x 2＝16－4b217.∵OP ⊥OQ ，∴OP →·OQ →＝0，即x 1x 2＋y 1y 2＝0，x 1x 2＋(2x 1＋2)(2x 2＋2)＝0，5x 1x 2＋4(x 1＋x 2)＋4＝0.从而516－4b 217－12817＋4＝0，---------10分解得b ＝1，满足b >21717.----------11分∴椭圆C 的方程为x 24＋y 2＝1.------12分22.解：(1)因为f (x )＝a 2ln x －x 2＋ax ，其中x >0，所以f ′(x )＝a 2x －2x ＋a ＝－x －a 2x ＋ax .---------2分当a >0，所以f (x )的增区间为(0，a )，减区间为(a ，＋∞).当a<0，所以f (x )的增区间为(0，-a/2)，减区间为(-a/2，＋∞).---------6分(2)由题意得f (1)＝a －1≥e－1，即a ≥e.------7分由(1)知f (x )在[1，e]内单调递增，要使e －1≤f (x )≤e 2对x ∈[1，e]恒成立.只要⎩⎪⎨⎪⎧ f 1＝a －1≥e－1，f e ＝a 2－e 2＋a e≤e 2，---------11分解得a ＝e.----------12分。

参考答案一、选择题：(5分×12=60分)二、填空题(5分×4=20分)13． 49π 14. 201 15．e - 16．16 三、解答题(本大题共6小题，共70分)17.解: 由⎩⎨⎧ y ＝x ，y ＝2－x 得交点A (1,1)；由⎩⎪⎨⎪⎧y ＝2－x ，y ＝－13x 得交点B (3，－1). 故所求面积S ＝ʃ10⎝⎛⎭⎫x ＋13x d x ＋ʃ31⎝⎛⎭⎫2－x ＋13x d x 32123201211()|(2)|363x x x x =++-＝23＋16＋43＝136. 18.解: (1)-1+i(2)由|(x －2)＋y i|＝3，得(x －2)2＋y 2＝3，此方程表示如图所示的圆C ，则y x的最大值为切线OP 的斜率． 由|CP |＝3，|OC |＝2，得∠COP ＝π3，∴切线OP 的斜率为 3 19.解: (1)分三类:第一类有4个红球,则有10644=C C 种取法; 第二类有3个红球,则有241634=C C 种取法; 第三类有2个红球,则有902624=C C 种取法;各根据加法原理共有1+24+90=115种不同的取法.(2)若总分不少于7,则可以取4红1白,或3红2白,或2红3白,共3类,取法总数为+1644C C +2634C C 18620615463624=⨯+⨯+=C C 种不同的取法.20.解: (1)当a ＝1时，f (x )＝1x ＋ln x －1，x ∈(0，＋∞)，所以f ′(x )＝－1x 2＋1x ＝x －1x 2， x ∈(0，＋∞).因此f ′(2)＝14，即曲线y ＝f (x )在点(2，f (2))处的切线斜率为14.又f (2)＝ln 2－12， 所以曲线y ＝f (x )在点(2，f (2))处的切线方程为y －(ln 2－12)＝14(x －2)， 即x －4y ＋4ln 2－4＝0.(2)因为f (x )＝a x ＋ln x －1，所以f ′(x )＝－a x 2＋1x ＝x －a x 2.令f ′(x )＝0，得x ＝a . ①若a ≤0，则f ′(x )>0，f (x )在区间(0，e]上单调递增，此时函数f (x )无最小值.②若0<a <e ，当x ∈(0，a )时，f ′(x )<0，函数f (x )在区间(0，a )上单调递减，当x ∈(a ，e]时，f ′(x )>0，函数f (x )在区间(a ，e]上单调递增，所以当x ＝a 时，函数f (x )取得最小值ln a .③若a ≥e ，当x ∈(0，e]时，f ′(x )≤0，函数f (x )在区间(0，e]上单调递减，所以，当x ＝e 时，函数f (x )取得最小值a e. 综上可知，当a ≤0时，函数f (x )在区间(0，e]上无最小值；当0<a <e 时，函数f (x )在区间(0，e]上的最小值为ln a ；当a ≥e 时，函数f (x )在区间(0，e]上的最小值为a e. 21.解: (1)当n ＝1时，f (1)＝1，g (1)＝1，所以f (1)＝g (1)；当n ＝2时，f (2)＝98，g (2)＝118，所以f (2)<g (2)； 当n ＝3时，f (3)＝251216，g (3)＝312216，所以f (3)<g (3)． (2)由(1)，猜想f (n )≤g (n )，下面用数学归纳法给出证明．①当n ＝1,2,3时，不等式显然成立，②假设当n ＝k (k ≥3，k ∈N ＋)时不等式成立，即1＋123＋133＋143＋…＋1k 3<32－12k 2.那么，当n ＝k ＋1时，f (k ＋1)＝f (k )＋1（k ＋1）3<32－12k 2＋1 k ＋1 3. 因为12（k ＋1）2－[12k 2－1（k ＋1）3]＝k ＋32（k ＋1）3－12k 2＝－3k －12（k ＋1）3k 2<0， 所以f (k ＋1)<32－12（k ＋1）2＝g (k ＋1)．由①②可知，对一切n ∈N ＋，都有f (n )≤g (n )成立． 22.解:（Ⅰ）2()ln 1h x ax x x =--+，2121()2x ax h x a x x x -+-'=--=， 由()h x 在()0,1递减，所以()0h x '≤恒成立，而0x >，所以2210x ax -+-≤恒成立，即12a x x ≤+恒成立，而12x x +≥x =时，等号成立，所以a ≤a 的取值范围是(-∞。

西安市第三中学2016-2017学年度第二学期期中考试高二数学（理）试题命题人：王群娜 审题人：王钢一、选择题（本大题共10个小题，每小题4分，共40分）1．复数11212i i+-+-的虚部是（ ） A ．15i B ．15C ．15i -D ．15- 2．函数()322f x x ax bx a =--+，在1x =时有极值10，则a 、b 的值为（ ）A ．3a =，3b =-，或4a =-，11b =B ．4a =-，11b =C ．3a =，3b =-D ．以上都不正确3．函数()()3x f x x e =-的单调递增区间是（ ）A ．()2-∞，B ．()03，C ．()14，D ．()2+∞，4．如图所示，在边长为1的正方形OABC 上任取一点P ，则点P 恰好取自阴影部分的概率为（ ）A ．14B ．15C ．16D ．17 5．已知空间三点()202A -，，，()112B -，，，()304C -，，，设a A B = ，b AC = 。

若向量ka b + 与2ka b - 互相垂直，则k 的值是（ ）A ．2B ．52-C ．52或2-D ．52-或2 6．曲线21x y e -=+在点()02，处的切线与直线0y =和y x =围成的三角形的面积为（ ） A ．13B ．12C ．23D ．17．已知正四棱柱1111ABCD A B C D -中，2AB =，1CC =E 为1CC 的中点，则直线1AC 与平面BED 的距离为（ ）A．2 B C D ．18．设()f x ，()g x 分别是定义在R 上的奇函数和偶函数，当0x ＜时，()()()()0f x g x f x g x ''+＞，且()30g -=，则不等式()()0f x g x ＜的解集是（ ）A ．()()303-+∞ ，，B ．()()3003- ，， C ．()()303-∞- ，， D ．()()33-∞-+∞ ，， 9．已知函数()f x 在R 上满足()()22288f x f x x x =--+-，则曲线()y f x =在点()()11f ，处的切线方程是（ ） A ．21y x =-B ．y x =C ．32y x =-D ．23y x =-+10．已知函数()213ln 22f x x x =-+在其定义域内有一个子区间()11a a -+，内不是单调函数，则实数a 的取值范围是（ ）A ．1322⎛⎫- ⎪⎝⎭，B ．514⎡⎫⎪⎢⎣⎭，C ．312⎛⎫ ⎪⎝⎭，D ．312⎡⎫⎪⎢⎣⎭，二、填空题（本大题共5个小题，每小题4分，共20分） 11．在四面体O ABC -中，OA a = ，OB b = ，OC c = ，E 为ABC △的重心，则OE = _______（用a 、b 、c 表示）。

2017-2018学年陕西西安高二下学期期中考试理科数学试题考试时间：120分钟第I 卷（选择题）一、单选题（每小题5分，共60分））1．设是虚数单位，Z 错误！未找到引用源。

表示复数错误！未找到引用源。

的共轭复数.若i i Z )3(+=错误！未找到引用源。

，则1-i Z=错误！未找到引用源。

( ) A.B.C.D.2．已知复数iiZ +=12错误！未找到引用源。

(为虚数单位)，则Z = ( ) A. 3 B. 2 C. D.3．用数学归纳法证明不等式11112321n n ++++<- (*n N ∈，且1n >）时，第一步应证明下述哪个不等式成立（ ） A. 12< B. 111223++< C. 1122+< D. 1123+< 4．观察下列各式：,,则( )A. 18B. 29C. 47D. 765．函数23ln 2x x y -=错误！未找到引用源。

的单调增区间为( ) A. )33,0()33,( --∞错误！未找到引用源。

B. )33,0(),0,33(- 错误！未找到引用源。

C. )33,0(错误！未找到引用源。

D. ),33(+∞错误！未找到引用源。

6．用反证法证明命题：“三角形的内角中至少有一个不大于”时，假设正确的是（ ）A. 假设三内角都不大于B. 假设三内角都大于C. 假设三内角至多有一个大于D. 假设三内角至多有两个大于7．已知函数223)(a bx ax x x f +++=错误！未找到引用源。

在处取极值10，则（ ）A. 4或B. 4或C. 4D.8．利用数学归纳法证明不等式()()*11112,2321n f n n n N ++++<≥∈- 的过程中，由n k =到1n k =+时，左边增加了（ ） A. 1项 B. k 项 C. 21k -项 D. 2k 项9．设函数)(x f 错误！未找到引用源。

在上可导，其导函数为，且函数的图象如图所示，则下列结论中一定成立的是（ ）A. 函数)(x f 错误！未找到引用源。

2016-2017学年陕西省西安中学普通班高二（下）期中数学试卷（理科）一.选择题：（共12小题，每题5分，共60分，每题只有一个正确答案）. 1．（5分）复数z=的共轭复数是（）A．2+i B．2﹣i C．﹣1+i D．﹣1﹣i2．（5分）定积分（2x+e x）dx的值为（）A．e+2 B．e+1 C．e D．e﹣13．（5分）设f（x）=ax3+3x2+2，若f′（﹣1）=4，则a的值等于（）A．B．C．D．4．（5分）王刚同学衣服上左、右各有一个口袋，左边口袋里装有30个英语单词卡片，右边口袋里装有20个英语单词卡片，这些英语单词卡片都互不相同，则从两个口袋里任取一张英语单词卡片，不同取法的种数为（）A．20 B．30 C．50 D．6005．（5分）用反证法证明命题：“若a，b∈Z，ab能被5整除，则a，b中至少有一个能被5整除”，那么假设的内容是（）A．a，b都能被5整除B．a，b都不能被5整除C．a，b有一个能被5整除D．a，b有一个不能被5整除6．（5分）已知函数f（x）=2x3﹣6x2+3，则函数f（x）在[﹣2，2]上的最小值为（）A．﹣37 B．﹣29 C．﹣5 D．以上都不对7．（5分）如图，函数y=f（x）的图象在点P处的切线方程是y=﹣x+8，则f（5）+f′（5）=（）A．B．1 C．2 D．08．（5分）有甲、乙、丙、丁四位学生参加数学竞赛，其中只有一名学生获奖，有其他学生问这四个学生的获奖情况，甲说：“是乙或丙获奖”，乙说：“甲、丙都没有获奖”，丙说：“我获奖了”，丁说：“是乙获奖了”，四位学生的话有且只有两个的话是对的，则获奖的学生是（）A．甲B．乙C．丙D．丁9．（5分）设f（x）=x（ax2+bx+c）（a≠0）在x=1和x=﹣1处有极值，则下列点中一定在x轴上的是（）A．（a，b） B．（a，c） C．（b，c） D．（a+b，c）10．（5分）用1，2，3，4，5这5个数字，组成无重复数字的三位数，其中奇数有（）A．12种B．24种C．36种D．48种11．（5分）已知函数y=xf′（x）的图象如图所示（其中f′（x）是函数f（x）的导函数），下面四个图象中，y=f（x）的图象大致是（）A．B．C．D．12．（5分）设f（x），g（x）在[a，b]上可导，且f′（x）＞g′（x），则当a＜x＜b时有（）A．f（x）+g（a）＞g（x）+f（a）B．f（x）＜g（x）C．f（x）＞g（x）D．f（x）+g（b）＞g（x）+f（b）二.填空题（共4题，每题5分，共20分）.13．（5分）复数z=（m2﹣1）+（m+1）i，（m∈R）为纯虚数，则实数m=．14．（5分）已知f（x）=x3+ax2+（a+6）x+1有极大值和极小值，则a的取值范围为．15．（5分）dx=．16．（5分）现将如图所示的5个小正方形涂上红、黄两种颜色，其中3个涂红色，2个涂黄色，若恰有两个相邻的小正方形涂红色，则不同的涂法种数共有．（用数字作答）三.解答题：（共6小题，共70分，要求写出解答或证明过程）.17．（10分）现有5幅不同的国画，2幅不同的油画，7幅不同的水彩画．（1）从中任选一幅画布置房间，有几种不同的选法？（2）从这些国画、油画、水彩画中各选一幅布置房间，有几种不同的选法？（3）从这些画中选出两幅不同种类的画布置房间，有几种不同的选法？18．（12分）已知复数z满足|z|=，z2的虚部为2．（Ⅰ）求z；（Ⅱ）设z，z2，z﹣z2在复平面对应的点分别为A，B，C，求△ABC的面积．19．（12分）已知函数f（x）=；（1）求函数f（x）图象在x=1处切线l的方程；（2）求由曲线y=，直线l及y轴围成图形的面积．20．（12分）已知x=2是函数f（x）=（x2+ax﹣2a﹣3）e x的一个极值点（I）求实数a的值；（II）求函数f（x）在的最大值和最小值．21．（12分）观察下列等式：13=12，13+23=32，13+23+33=62，13+23+33+43=102…；（1）根据上述规律，写出第n个等式；（2）用数学归纳法证明（1）中所写的等式．22．（12分）设函数f（x）=2lnx﹣ax，（a∈R，a＞0）；（1）求函数f（x）的单调区间；（2）求函数f（x）在x∈[1，2]上的最大值．2016-2017学年陕西省西安中学普通班高二（下）期中数学试卷（理科）参考答案与试题解析一.选择题：（共12小题，每题5分，共60分，每题只有一个正确答案）. 1．（5分）复数z=的共轭复数是（）A．2+i B．2﹣i C．﹣1+i D．﹣1﹣i【解答】解：复数z====﹣1+i．所以复数的共轭复数为：﹣1﹣i．故选：D．2．（5分）定积分（2x+e x）dx的值为（）A．e+2 B．e+1 C．e D．e﹣1【解答】解：（2x+e x）dx=（x2+e x）|=（1+e）﹣（0+e0）=e．故选：C．3．（5分）设f（x）=ax3+3x2+2，若f′（﹣1）=4，则a的值等于（）A．B．C．D．【解答】解：f′（x）=3ax2+6x，∴f′（﹣1）=3a﹣6=4，∴a=故选：D．4．（5分）王刚同学衣服上左、右各有一个口袋，左边口袋里装有30个英语单词卡片，右边口袋里装有20个英语单词卡片，这些英语单词卡片都互不相同，则从两个口袋里任取一张英语单词卡片，不同取法的种数为（）A．20 B．30 C．50 D．600【解答】解：根据题意，分两类情况讨论：第一类从左口袋有取一张有30张不同取法，第二类从右口袋有取一张有20张不同取法，根据分类计数原理，共有30+20=50种．故选：C．5．（5分）用反证法证明命题：“若a，b∈Z，ab能被5整除，则a，b中至少有一个能被5整除”，那么假设的内容是（）A．a，b都能被5整除B．a，b都不能被5整除C．a，b有一个能被5整除D．a，b有一个不能被5整除【解答】解：由于反证法是命题的否定的一个运用，故用反证法证明命题时，可以设其否定成立进行推证．命题“a，b∈Z，如果ab可被5整除，那么a，b至少有一个能被5整除．”的否定是“a，b都不能被5整除”．故选：B．6．（5分）已知函数f（x）=2x3﹣6x2+3，则函数f（x）在[﹣2，2]上的最小值为（）A．﹣37 B．﹣29 C．﹣5 D．以上都不对【解答】解：函数f（x）=2x3﹣6x2+3，的导数f′（x）=6x2﹣12x=6x（x﹣2），当x∈[0，2]时，f′（x）＜0，即有f（x）在区间[0，2]上递减，f（﹣2）=﹣16﹣24+3=﹣37可得f（2）=16﹣24+3=﹣5．函数的最小值为：﹣37．故选：A．7．（5分）如图，函数y=f（x）的图象在点P处的切线方程是y=﹣x+8，则f（5）+f′（5）=（）A．B．1 C．2 D．0【解答】解：f′（5）=﹣1将x=5代入切线方程得f（5）=﹣5+8=3，所以f（5）+f′（5）=3+（﹣1）=2，故选：C．8．（5分）有甲、乙、丙、丁四位学生参加数学竞赛，其中只有一名学生获奖，有其他学生问这四个学生的获奖情况，甲说：“是乙或丙获奖”，乙说：“甲、丙都没有获奖”，丙说：“我获奖了”，丁说：“是乙获奖了”，四位学生的话有且只有两个的话是对的，则获奖的学生是（）A．甲B．乙C．丙D．丁【解答】解：若甲是获奖的，则都说假话，不合题意．若乙是获奖的，则甲、乙、丁都说真话，丙说假话，不符合题意．若丁是获奖的，则甲、丙、丁说假话，乙说真话，不符合题意．故丙获奖．故选：C．9．（5分）设f（x）=x（ax2+bx+c）（a≠0）在x=1和x=﹣1处有极值，则下列点中一定在x轴上的是（）A．（a，b） B．（a，c） C．（b，c） D．（a+b，c）【解答】解：∵f（x）=x（ax2+bx+c）=ax3+bx2+cx，∴f′（x）=3ax2+2bx+c，∵f（x）在x=1和x=﹣1处有极值，∴1，﹣1是方程3ax2+2bx+c=0的两根，∴1+（﹣1）=﹣，=﹣1，故b=0，c=﹣3a≠0；可排除B、C、D．故选：A．10．（5分）用1，2，3，4，5这5个数字，组成无重复数字的三位数，其中奇数有（）A．12种B．24种C．36种D．48种【解答】解：从1，3，5中选一个为个位数字，再从剩下的4个数字选2个排在前2位，共有C31A42=36，故选：C．11．（5分）已知函数y=xf′（x）的图象如图所示（其中f′（x）是函数f（x）的导函数），下面四个图象中，y=f（x）的图象大致是（）A．B．C．D．【解答】解：由图象看出，﹣1＜x＜0，和x＞1时xf′（x）＞0；x≤﹣1，和0≤x≤1时xf′（x）≤0；∴﹣1＜x≤1时，f′（x）≤0；x＞1，或x≤﹣1时，f′（x）≥0；∴f（x）在（﹣1，1]上单调递减，在（﹣∞，﹣1]，（1，+∞）上单调递增；∴f（x）的大致图象应是B．故选：B．12．（5分）设f（x），g（x）在[a，b]上可导，且f′（x）＞g′（x），则当a＜x＜b时有（）A．f（x）+g（a）＞g（x）+f（a）B．f（x）＜g（x）C．f（x）＞g（x）D．f（x）+g（b）＞g（x）+f（b）【解答】解：设F（x）=f（x）﹣g（x），∵在[a，b]上f'（x）＞g'（x），F′（x）=f′（x）﹣g′（x）＞0，∴F（x）在给定的区间[a，b]上是增函数．∴当x＞a时，F（x）＞F（a），即f（x）﹣g（x）＞f（a）﹣g（a）即f（x）+g（a）＞g（x）+f（a）故选：A．二.填空题（共4题，每题5分，共20分）.13．（5分）复数z=（m2﹣1）+（m+1）i，（m∈R）为纯虚数，则实数m=1．【解答】解：∵z=（m2﹣1）+（m+1）i，（m∈R）为纯虚数，∴，解得m=1，故答案为：1．14．（5分）已知f（x）=x3+ax2+（a+6）x+1有极大值和极小值，则a的取值范围为a＜﹣3或a＞6．【解答】解：函数f（x）=x3+ax2+（a+6）x+1，所以函数f′（x）=3x2+2ax+（a+6），因为函数有极大值和极小值，所以方程f′（x）=0有两个不相等的实数根，即3x2+2ax+（a+6）=0有两个不相等的实数根，∴△＞0，∴（2a）2﹣4×3×（a+6）＞0，解得：a＜﹣3或a＞6故答案为：a＜﹣3或a＞615．（5分）dx=π．【解答】解：令y=，画出图象：由微积分基本定理的几何意义可得：=π．故答案为π．16．（5分）现将如图所示的5个小正方形涂上红、黄两种颜色，其中3个涂红色，2个涂黄色，若恰有两个相邻的小正方形涂红色，则不同的涂法种数共有6．（用数字作答）【解答】解：当涂红色两个相邻的小正方形在两端时是有=4，当涂红色两个相邻的小正方形在不在两端时是有=2，则不同的涂法种数共有4+2=6种．故答案为：6．三.解答题：（共6小题，共70分，要求写出解答或证明过程）.17．（10分）现有5幅不同的国画，2幅不同的油画，7幅不同的水彩画．（1）从中任选一幅画布置房间，有几种不同的选法？（2）从这些国画、油画、水彩画中各选一幅布置房间，有几种不同的选法？（3）从这些画中选出两幅不同种类的画布置房间，有几种不同的选法？【解答】解：（1）根据题意，共有5幅不同的国画，2幅不同的油画，7幅不同的水彩画，共有5+2+7=14幅画，从中任选一幅画布置房间，有14种选法，（2）分三步完成，第一步选国画有5种，第二步选油画有2种，第三步选水彩画有7种，根据分步计数原理得，共有5×2×7=70种．（2）根据题意，分三类情况讨论：第一类，选国画和油画共有5×2=10种，第二类，选国画和水彩画共有5×7=35种，第三类，选油画和水彩画共有2×7=14种，根据分类计数原理共有10+25+14=59种．18．（12分）已知复数z满足|z|=，z2的虚部为2．（Ⅰ）求z；（Ⅱ）设z，z2，z﹣z2在复平面对应的点分别为A，B，C，求△ABC的面积．【解答】解：（I）设Z=x+yi（x，y∈R）由题意得Z2=（x﹣y）2=x2﹣y2+2xyi∴故（x﹣y）2=0，∴x=y将其代入（2）得2x2=2∴x=±1故或故Z=1+i或Z=﹣1﹣i；（II）当Z=1+i时，Z2=2i，Z﹣Z2=1﹣i所以A（1，1），B（0，2），C（1，﹣1）∴当Z=﹣1﹣i时，Z2=2i，Z﹣Z2=﹣1﹣3i，A（﹣1，﹣1），B（0，2），C（﹣1，﹣3）S△ABC=×1×2=1．19．（12分）已知函数f（x）=；（1）求函数f（x）图象在x=1处切线l的方程；（2）求由曲线y=，直线l及y轴围成图形的面积．【解答】解：（1）f′（x）=，f（1）=1，f′（1）=，故切线方程是：y﹣1=（x﹣1），即；（2）由，解得：，故直线l及y轴围成图形的面积：S=[（（x+1）﹣]dx=（x2+x+c）﹣=．20．（12分）已知x=2是函数f（x）=（x2+ax﹣2a﹣3）e x的一个极值点（I）求实数a的值；（II）求函数f（x）在的最大值和最小值．【解答】解：（I）由f（x）=（x2+ax﹣2a﹣3）e x可得∴f′（x）=（2x+a）e x+（x2+ax﹣2a﹣3）e x=[x2+（2+a）x﹣a﹣3]e x∵x=2是函数f（x）的一个极值点，∴f′（2）=0∴（a+5）e2=0，解得a=﹣5；（II）由（I）知，f′（x）=（x﹣2）（x﹣1）e x，∴函数在x=1或2处取极值∵f（1）=3e，f（2）=e2，f（3）=e3，∴函数f（x）在的最小值为f（2）=e2；最大值为e3．21．（12分）观察下列等式：13=12，13+23=32，13+23+33=62，13+23+33+43=102…；（1）根据上述规律，写出第n个等式；（2）用数学归纳法证明（1）中所写的等式．【解答】解：（1）根据上述规律，写出第n个等式；或13+23+33+…+n3=（1+2+3+…+n）2（2）证明如下，①当n=1时，左边=1，右边=（1+1）2=1，∴等式成立，②假设当n=k时，等时成立，即13+23+33+…+k3=k2（k+1）2．那么，当n=k+1时，有13+23+33+…+k3+（k+1）3=k2（k+1）2+（k+1）3，=（k+1）2•（+k+1）=（k+1）2•=═（k+1）2（k+1+1）2．这就是说，当n=k+1时，等式也成立，根据①②，可知对n∈N*等式成立．22．（12分）设函数f（x）=2lnx﹣ax，（a∈R，a＞0）；（1）求函数f（x）的单调区间；（2）求函数f（x）在x∈[1，2]上的最大值．【解答】解：（1）f（x）=2lnx﹣ax，（a＞0），f′（x）=，x∈（0，）时，f′（x）＞0，f（x）递增，x∈（，+∞）时，f′（x）＜0，f（x）递减；（2）当≥2，0＜a≤1时，由（1）得f（x）在[1，2]递增，f（x）max=f（2）=2ln2﹣2a，当1＜＜2，即1＜a＜2时，由（1）得f（x）在[1，）递增，在（，2]递减，f（x）max=f（）=2ln2﹣2lna﹣2，当≤1即a≥2时，由（1）得f（x）在[1，2]递减，故f（x）max=f（1）=a，综上，f（x）max=．。