弹性波理论
- 格式:doc
- 大小:809.50 KB
- 文档页数:13



弹性波场理论基本概念介绍引言测绘是一门数学性很强的学科,许多数学的理论在测绘中应用非常的普遍。
如最小二乘法,最小范数法,回归分析法,各种曲线拟合法,蒙特卡罗法,模拟退火法,遗传算法,等等。
只要是在数学领域可以应用的方法,在测绘的实际应用中同样可以。
同时,测绘学科也是一门与地球物理紧密相关的学科,在地球物理中的很多理论方法在解决测绘问题中都起到了非常重要的作用。
如流体力学的应用,弹性力学的应用,等等。
本文主要是介绍一下地球物理学的关于弹性波场的理论,最后做了简要的展望。
弹性波场就是在弹性介质中传播的波。
弹性介质在外力或扰动的作用下会发生体积和形状的变化(称为形变),产生所谓应变。
应变可分为纵向(或胀缩)应变和横向(或剪切)应变。
这些应变用弹性常数来表示。
当一扰动作用于均匀各向同性完全弹性介质时,在弹性介质内有胀缩应变的纵向位移形式向前传播的纵波存在,同时也有以剪切横向位移形式向前传播的横波存在。
纵波传播速度比横放传播速度快,在地震时纵波比横波先到。
地震波的实质就是地下岩石中传播的弹性波。
在地震波传播范围内绝大部分岩石都可以 近似地看成理想弹性体或完全弹性体。
因此弹性力学的许多理论和概念可以引人地震勘查中 来。
在这里我们重复了一些弹性力学的概念,是为了将它们引伸到地震勘查范围中来,着眼点是从地震勘查的角度描述这些基本概念。
一 应力和应变(一)应力当弹性体在外力作用下发生形变时,总有一种阻止弹性体形变,欲恢复弹性体原状的内力,这种内力称为内应力,简称应力。
应力可定义为单位面积上的内力。
注意,应力的量纲不是力的量纲而是单位面积上力的量纲,因此有的书将应力称为“胁强”。
根据力的分解定理,可将弹性体内任意方向的应力分解为垂直于单位面积的法向应力和 相切于单位面积的剪切应力。
描述弹性体内某一点M 的应力,在直角坐标系中常取一小平行六面体、六面体的每个面都垂直坐标轴(图1),考虑这些面上的应力,可得九个应力分量,即法向应力xx σ,yy σ,zz σ剪切应力xy σ,xz σ,yx σ,yz σ,zx σ,zy σ。

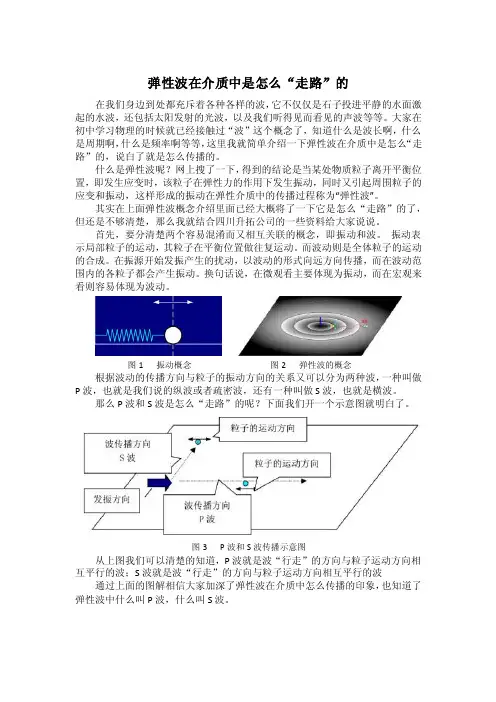
弹性波在介质中是怎么“走路”的在我们身边到处都充斥着各种各样的波,它不仅仅是石子投进平静的水面激起的水波,还包括太阳发射的光波,以及我们听得见而看见的声波等等。
大家在初中学习物理的时候就已经接触过“波”这个概念了,知道什么是波长啊,什么是周期啊,什么是频率啊等等,这里我就简单介绍一下弹性波在介质中是怎么“走路”的,说白了就是怎么传播的。
什么是弹性波呢?网上搜了一下,得到的结论是当某处物质粒子离开平衡位置,即发生应变时,该粒子在弹性力的作用下发生振动,同时又引起周围粒子的应变和振动,这样形成的振动在弹性介质中的传播过程称为“弹性波”。
其实在上面弹性波概念介绍里面已经大概将了一下它是怎么“走路”的了,但还是不够清楚,那么我就结合四川升拓公司的一些资料给大家说说。
首先,要分清楚两个容易混淆而又相互关联的概念,即振动和波。
振动表示局部粒子的运动,其粒子在平衡位置做往复运动。
而波动则是全体粒子的运动的合成。
在振源开始发振产生的扰动,以波动的形式向远方向传播,而在波动范围内的各粒子都会产生振动。
换句话说,在微观看主要体现为振动,而在宏观来看则容易体现为波动。
图1 振动概念图2 弹性波的概念根据波动的传播方向与粒子的振动方向的关系又可以分为两种波,一种叫做P波,也就是我们说的纵波或者疏密波,还有一种叫做S波,也就是横波。
那么P波和S波是怎么“走路”的呢?下面我们开一个示意图就明白了。
图3 P波和S波传播示意图从上图我们可以清楚的知道,P波就是波“行走”的方向与粒子运动方向相互平行的波;S波就是波“行走”的方向与粒子运动方向相互平行的波通过上面的图解相信大家加深了弹性波在介质中怎么传播的印象,也知道了弹性波中什么叫P波,什么叫S波。

弹性波场理论基本概念介绍引言测绘是一门数学性很强的学科,许多数学的理论在测绘中应用非常的普遍。
如最小二乘法,最小范数法,回归分析法,各种曲线拟合法,蒙特卡罗法,模拟退火法,遗传算法,等等。
只要是在数学领域可以应用的方法,在测绘的实际应用中同样可以。
同时,测绘学科也是一门与地球物理紧密相关的学科,在地球物理中的很多理论方法在解决测绘问题中都起到了非常重要的作用。
如流体力学的应用,弹性力学的应用,等等。
本文主要是介绍一下地球物理学的关于弹性波场的理论,最后做了简要的展望。
弹性波场就是在弹性介质中传播的波。
弹性介质在外力或扰动的作用下会发生体积和形状的变化(称为形变),产生所谓应变。
应变可分为纵向(或胀缩)应变和横向(或剪切)应变。
这些应变用弹性常数来表示。
当一扰动作用于均匀各向同性完全弹性介质时,在弹性介质内有胀缩应变的纵向位移形式向前传播的纵波存在,同时也有以剪切横向位移形式向前传播的横波存在。
纵波传播速度比横放传播速度快,在地震时纵波比横波先到。
地震波的实质就是地下岩石中传播的弹性波。
在地震波传播范围内绝大部分岩石都可以 近似地看成理想弹性体或完全弹性体。
因此弹性力学的许多理论和概念可以引人地震勘查中 来。
在这里我们重复了一些弹性力学的概念,是为了将它们引伸到地震勘查范围中来,着眼点是从地震勘查的角度描述这些基本概念。
一 应力和应变(一)应力当弹性体在外力作用下发生形变时,总有一种阻止弹性体形变,欲恢复弹性体原状的内力,这种内力称为内应力,简称应力。
应力可定义为单位面积上的内力。
注意,应力的量纲不是力的量纲而是单位面积上力的量纲,因此有的书将应力称为“胁强”。
根据力的分解定理,可将弹性体内任意方向的应力分解为垂直于单位面积的法向应力和 相切于单位面积的剪切应力。
描述弹性体内某一点M 的应力,在直角坐标系中常取一小平行六面体、六面体的每个面都垂直坐标轴(图1),考虑这些面上的应力,可得九个应力分量,即法向应力xx σ,yy σ,zz σ剪切应力xy σ,xz σ,yx σ,yz σ,zx σ,zy σ。





《连续介质⼒学》期末复习提纲--弹性波理论部分<连续介质⼒学> 期末复习提纲—弹性波理论部分1、⽆界线弹性体中的波传播(1)Helmholtz 定理 a. 定理内容b. 位移场的分解---⽆旋部分与⽆散部分(1)(2u u u =+ ,其中(1)0u ??= ,(2)0u ??=c. 转动向量与体积膨胀率的位移场表⽰(2)21122u ωψ=??=-?, (1)2u θφ=??=?(2)⽆界线弹性体中的P 波与S 波a. 体积膨胀率与转动向量满⾜的波动⽅程(★)2212211112,f c c c λµθθρ+?+??==222222211,2f c c c µωωρ+==b. Helmholtz 势满⾜的波动⽅程222222221211,b B c t c tφφφψ+=?+=??c. 位移场⽆旋部分与⽆散部分满⾜的波动⽅程2(1)(1)2(2)(2)221211,u b u u B u c c ?+?=?+??= d. 纵波与横波的相速度及其⽐值(★)21121221222)21c c c c c c c c ν??=- ===??=-??2、⽆界线弹性体中的平⾯波(1)波阵⾯、平⾯波与球⾯波(2)⼀般平⾯波及其描述(★)a. ⼀般平⾯波位移场的形式(★)(,)()u x t f x n ct d =?-b. 纵横波满⾜的条件及相速度公式(★)20()()()0d n n d c c P wave S wavec d n d n µρλµ?=±?=---++?=c. ⼀般平⾯波的能量密度与能通量密度向量(★)①平⾯纵波的情况(★)能量密度:[][][]222211112211112211()()22()p ij ij i i e uu c f x n c t c f x n c t c f x n c t ετρρρρ=+''=?-+?-'=?- 能通量密度向量:[]2311()p ij i j ue n cf x n c t ?τρ'=-=?- ⼆者关系: 1p p c n ?ε=②平⾯横波的情况(★)能量密度:[][][]222221212221112211()()22()s ij ij i i e uu c f x n c t c f x n c t c f x n c t ετρρρρ=+''=-+-'=- 能通量密度向量:[]2321()s ij i j u e n c f x n c t ?τρ'=-=?- ⼆者关系: 2s s c n ?ε=(2)平⾯简谐波及其描述(★) a. 描述平⾯简谐波的物理量(★) kc ω=,2T πω=,12T ωαπ==,22c cT kππωΛ===2k n n c ωπ==Λ, 222i i k k k k k c ω?===A c T k k x n -ct k ωα--Λ-?振幅 -相速度周期-波数-圆频率波长()-相位-频率-波数向量b. 平⾯简谐波的位移场形式(★)[]()()c o s ()R e R e i k x n c ti k x tu A d k x n c t A d e A d e ω?-?-=?-??c. 平⾯简谐波的能量密度与能通量密度向量及波的强度(★)①平⾯简谐纵波的情形(★)能量密度:1122p ij ij i i e uu ετρ=+ 能通量密度向量:p ij i j u e ?τ=-⼆者的关系: 1p p c n ?ε=平⾯简谐纵波的强度:1T pp dt T ??=?②平⾯简谐横波的情形(★)能量密度:1122s ij ij i i e uu ετρ=+ 能通量密度向量:s ij i j ue ?τ=-⼆者的关系: 2s s c n ?ε=平⾯简谐横波的强度:01T s s dt T=d. ⾮均匀平⾯简谐波位移场满⾜的条件(★)''()k x i k x t u Ade e ω'-??-=?2220k k kk k c k k ω?''''''?-?=='''?=?e. ⾮均匀平⾯简谐波的传播特征。
弹性波的散射与反散射问题的理论与应用研究弹性波的散射与反散射问题是物理领域中的一个重要研究课题。
弹性波是一种能够在固体和液体介质中传播的波动现象,常见的弹性波包括声波、横波和纵波等。
在许多不同的领域,如地震学、声学、非破坏性检测以及材料科学等方面,弹性波的散射与反散射问题都具有重要的理论与应用价值。
确定实验的目的是进行研究散射与反散射问题,首先需要了解关于弹性波的基本定律。
其中,最基本的定律之一是弹性波的传播速度与介质的弹性常数和密度有关。
弹性波传播的速度可以通过声速、剪切波速和纵波速来衡量。
此外,利用波动方程可以描述弹性波的传播过程。
根据波动方程,弹性波的传播可以通过求解波动方程来推导。
为了研究弹性波的散射与反散射问题,实验准备是非常重要的一步。
首先,需要设计一个合适的实验装置来产生弹性波。
常见的实验装置包括声源、振动器、超声波发生器以及激光器等设备。
在实验过程中,应该根据实际需要选择适合的波源和探测器。
接下来,在进行实验时需要选择合适的实验参数,如频率、振幅以及入射角度等。
这些参数将直接影响到弹性波的传播效果以及散射行为。
根据具体的研究目标,可以通过调整实验参数来探究不同的散射与反散射现象。
在实验进行中,我们需要实时监测和记录实验数据,以便后续的数据分析与处理。
常见的实验数据记录方式包括振幅随时间的变化曲线、波速以及强度等参数的测量。
通过对实验数据的分析与处理,可以获得关于散射与反散射问题的定量信息,如反射系数、折射系数以及散射幅度等。
弹性波的散射与反散射问题在实际应用中有着广泛的应用价值。
在地震学研究中,通过对地震波的散射与反散射行为的研究,可以对地下地质结构进行探测和刻画。
声学领域中,对声波的散射与反散射问题的研究可以应用于声学隔离材料的设计与优化。
此外,在非破坏性检测中,利用弹性波的散射与反散射行为可以实现对材料缺陷、损伤以及结构健康状态的评估和监测。
除了应用领域外,弹性波的散射与反散射问题也在物理理论研究中具有重要意义。
地震波交错网格高阶差分数值模拟研究摘要: 地震波数值模拟技术是勘探地球物理学中的重要组成部分,研究通过弹性波一阶速度——应力方程,采用交错网格高阶有限差分法实现了地震波在各向同性介质中的高精度的数值模拟,并采用完全匹配层( PML) 吸收边界来消除边界反射,可取得较好的效果。
通过模型的正演计算和复杂模型的处理结果表明,交错网格高阶有限差分法数值模拟是一种快速有效的地震波数值模拟方法。
关键词: 地震勘探; 交错网格; 有限差分; 数值模拟引言地震数值模拟是模拟地震波在介质中传播的一种数值模拟技术,随着地震波理论在天然地震和地震勘探中的应用,地震模拟技术便应运而生,并随着地震波理论和计算机技术的发展,地震数值模拟技术自20世纪60年代以来也得到了飞速发展,形成了目前具有有限差分法、有限元法、虚谱法和积分方程法等各种数值模拟方法的现代地震数值模拟技术。
有限差分法是偏微分方程的主要数值解法之一。
在各种地震数值模拟方法中,最早出现的数值模拟方法是有限差分法。
Alterman和Karal(1968)首先将有限差分法应用于层状介质弹性波传播的数值模拟中。
此后,Boore(1972)又将有限差分法用于非均匀介质地震波传播的模拟。
Alford等(1974)研究了声波方程有限差分法模拟的精确性。
Kelly等(1976)研究了用有限差分法制作人工合成地震记录的方法。
Virieux(1986)提出了应用速度——应力一阶方程交错网格有限差分法模拟P——SV波在非均匀介质中的传播。
交错网格方法提高了地震模拟的精度和稳定性,并消除了部分假想。
有限元法也是偏微分方程的数值解法之一。
Lysmer和Drake(1972)最早将有限元法应用于地震数值模拟。
Marfurt(1984)研究对比了模拟弹性波传播的有限差分法和有限元法的精度。
Seron等(1990,1996)给出了弹性波传播有限元模拟方法。
Padovani等(1994)研究了地震波模拟的低阶和高阶有限元法。
Sarma等(1998)给出了三维声波模拟的虚谱法。
积分方程法是建立在波动方程的积分表达式的基础上的,其理论基础是惠更斯原理。
积分方程法也是有限元法之后发展起来的一种地震数值模拟方法。
Pao 和Varatharajulu(1976)提出了弹性波散射的积分表达式。
Bennett和Mieras(1981)给出了流体目标声波散射的时间域积分方程解。
Bouchon(1987)给出了裂隙或孔洞弹性波绕射的离散波数法模拟方法。
Bouchon等(1989)研究了具有不规则界面的多层介质中波传播的边界积分方程——离散波数法。
Bakamjian(1992)给出了三维地震波传播模拟的边界积分方程法。
符力耘和牟永光(1994)提出了弹性波正演模拟的边界元法。
符力耘等(1997)提出了非线性Fredholm积分方程的正演问题。
符力耘(2003)给出了含起伏地表的广义Lipmann—Schwinger积分方程的数值模拟方法。
射线追踪方法是建立在波动方程的高频近似基础上的一种地震数值模拟方法(cerveny等,1977)。
这种方法实际只计算了最奇异部分的解,即旅行时和振幅函数的特征曲线,它们分别是程函方程和传播方程的解。
这种方法计算效率高。
但是,一些复杂的本构方程由于积分方程法和射线追踪法不满足假设条件而限制了这些方法的应用。
上述这些地震数值模拟方法各有优缺点。
对于复杂构造、复杂地质体和复杂岩性地震模拟而言,交错网格高阶有限差分法其综合性能(占内存大小、模拟精度、计算效率和并行算法实现)最好,是实用性最好的方法。
在声波方程正演的数值模拟中,由于有限的计算空间区域无形之中引入了人为边界,不可避免的需要对在数值网格边界上产生的反射或回绕能量进行合适的处理,否则这些人为产生的反射或回绕能量会在很大程度上扭曲真正的波动传播信号,使模拟剖面变得模糊不清,不利于对地层构造信息进行解释。
为了消除这些人为产生的边界反射或回绕能量,人们发展了多种方法,其中最常见的主要有以下几种:一是最简单的扩展边界法,即在需要计算的数值网格外增加一些额外的网格数目,这样可以使人为边界反射效应远离所需要的计算网格,但是这种方法带来的负面效应是所需要的网格数目大大增加,因而也大大增加了计算量,对计算机的计算速度和存储能力提出了更高的要求,所以这种方法并没有得到很好的推广;二是海绵吸收法,即在计算网格的边界区域设置一定宽度的阻尼带,利用某些衰减函数对数值模拟波场进行逐步衰减;三是反周期扩展法,即利用正反周期函数极性相反的特点消除回绕波场;四是傍轴近似法,即利用波动方程的傍轴近似条件来消除计算边界上的反射。
如何选择合适的边界吸收是一个值得研究的问题。
数值模拟基本原理各向同性介质是最基本的一种介质模型,目前地震勘探中大多都是基于这种介质模型,根据弹性介质位移,应力和应变之间的关系,可以推导出各向同性介质中的弹性波方程,在二维介质情况下为:(1)式中x V ———质点位移速度的水平分量;z V ———质点位移速度的垂直分量; xx σ———X 方向正应力; zz σ———Z 方向正应力; xz σ———切应力分量; λ,μ———拉梅系数。
一阶声波方程交错网格差分方程的建立1)一阶声波方程时间导数的2M 阶差分精度算法在计算机中进行数值计算时,需要对连续函数离散化,即对方程(1)中的微(2)(2)()x xx xzxz z zz xx x z x zz z xz x z v t x z v t x zv v t x z v v t z x v v t z x σσσσσσσρρλμλλμλμ∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂⎧=+⎪=+⎪⎪=++⎨⎪=++⎪⎪=+⎩分用有限差分来代替。
设函数f(t)单值连续且存在任意阶导数,则其Taylor 展开式为:232323111222!23!2!2()()()()...+()+()m mf f f f mm t t t t t t m t t t f t f t O t ∂∂∂∂∆∆∆∆∆∂∂∂∂+=++++∆232323111222!23!2!2-(-)()-()()...+(-)+()m mf f ff mm tt t t t t m t t t f t f t O t ∂∂∂∂∆∆∆∆∆∂∂∂∂=++∆将以上两式相减,得到2M 阶精度的时间差分近似式为:2-12-12-11(2m-1)!=12222*()*+()=(-)+2*()m m Mfm t m M tt t f t f t O t ∂∂∆∆∆+∆∑(2)Δt 为时间步长,在采用交错网格技术解声波方程时,速度场在2+tt ∆ 时刻计算,而应力场在t +Δt 时刻计算。
当M =1时,对方程(1)中的时间微分进行数值离散,可得2阶时间差分近似为:22(+)=(-)+[]xx xz t t t x x x z v t v t σσρ∂∂∆∆∆∂∂+22(+)=(-)+[]xz zz tt tz z xzv t v t σσρ∂∂∆∆∆∂∂+(+)=()+[(2)]x zv v xx xx xz t t t t σσλμλ∂∂∂∂∆∆++ (+)=()+[(2)]xzv v zz zz x z t t t t σσλλμ∂∂∂∂∆∆++(+)=()+[]x z v v xz xz xzt t t t σσμμ∂∂∂∂∆∆+对于时间高阶差分,计算2-12-1m m f t ∂∂时将涉及较多的时间层,需要大量的存储空间因此利用一阶弹性波方程中的速度-应力关系式,将速度对时间的任意奇数阶高阶导数用应力对空间的导数代替,而应力对时间的任意奇数阶高阶导数用速度对空间的导数代替,这样,在计算一个时间层上的速度或应力场时,只需要前一个时刻的速度或应力场以及两时间层之间的应力或速度场,不需要过多的时间层,从而节省了内存(董良国,2000)。
2)一阶弹性波方程空间导数的2N 阶差分精度算法为了提高计算精度,空间导数也要采用高阶差分近似。
在交错网格技术中,对空间变量的导数是在相应的空间变量网格点之间的半程上计算,对于空间函数f (x),假设其存在2N +1阶导数,则f (x)在2-102=n x x x ±∆处的2N +1阶Taylor展开式为:2-122+1()(i)2+22-10002!=1()=()+()+O(),n=1,2,...,N i n N N n i i f x x f x f x x ±±∆∆∑(3)由于交错网格一阶导数2N 阶精度差分近似式可表示为:()(2N+1)2+12(+1)+12-12-100022==1={[+]-[-]}+e ()+()Nf x N N n n n N x x xn xc f x x f x x f x x O x ∂∂∆∆∆∆∆∑ (4)其中,n c 为差分系数,N e 为误差系数; 将(3)式代入(4)式中,化简得到:2+12+12+1-1(2n-1)(2n-1)(1)(1)(2i+1)2+1(2N+1)0000(2+1)!(2+1)!=1=1=1=12(+1)+1()=(2n-1)()+()+()+() i i N NN N Nx N n n ni N n n i n N xf x c xf x c fx c x f x O x ∆∆∆∆∆∑∑∑∑5()根据上式,可得差分系数由下面的方程确定:1113322-12-1113(2N-1)013(2N-1)=013(2N-1)N N N c c c ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 求出差分系数n c 之后,则可得到空间导数的2N 阶精度差分近似:()22-12-1122=1={[+]-[-]}+()Nf x N n n n xx n c f x x f x x O x ∂∂∆∆∆∆∑ (6)3)一阶弹性波方程差分格式图1 精度为O(24+tx ∆∆)的交错网格示意图(据Levander 1988)如图1所示,水平速度x V 定义在网格点(i,j),垂直速度z V 定义在网格点1122(i+,j+)正应力xx σ,zz σ都定义在网格点12(i+,j),剪切应力xz σ定义在网格点12(i,j+)。
速度分量x V 、z V 均定义在时间层12-k ,12+k ,应力分量xx σ,zz σ,xz σ均定义在时间层k ,k+1。
设+12+12,+12,+12+12,+12,,+12,,,,k k k k ki j i j i j i j i j U V P Q S 分别为质点速度分量x V 、z V 和应力分量xx σ,zz σ,xz σ的离散值,ρ,λ,μ的离散值分别为,,,,,i j i j i j l m ρ,水平与垂直方向网格间距均为Δx 。