卫星轨道动力学数值计算

人造地球卫星推算公式
人造地球卫星的轨道是由许多因素决定的，包括地球引力、大气阻力、太阳引力等。

为了推算卫星的轨道，需要运用一些数学公式。

其中，最基本的公式是牛顿万有引力定律，它描述了两个物体之间的引力大小和方向。

对于地球和卫星之间的引力，可以用以下公式表示：
F =
G * M1 * M2 / r^2
其中，F表示引力大小，G为万有引力常数，M1和M2分别表示
地球和卫星的质量，r为地球和卫星之间的距离。

根据牛顿第二定律，物体的加速度等于受到的力除以物体的质量。

因此，我们可以得到卫星在轨道上的加速度公式：
a = F / m
其中，a表示卫星在轨道上的加速度，m为卫星的质量。

根据牛顿运动定律，物体的运动状态是由它的初速度、加速度和时间决定的。

因此，我们可以推算出卫星在轨道上的速度和位置：
v = v0 + at
r = r0 + vt + 1/2at^2
其中，v表示卫星的速度，v0为卫星的初速度，r表示卫星的位置，r0为卫星的初始位置，t为时间。

除了上述基本公式，还需要考虑到大气阻力、太阳引力等因素对卫星轨道的影响。

因此，在实际应用中，还需运用更加复杂的公式进行推算。

关于卫星的运动3关于卫星的运动支配卫星运动的力遵循平方反比律，即F∝1／r，即卫星做圆周运动所需的向心力由万有引力f=GMm／r提供。

一、线速度与轨道半径的关系设地球的质量为M，卫星质量为m，卫星在半径为r的轨道上运行，其线速度为v，则 22GMm／r＝mv／r，从而 v＝22，即v∝1／。

可见，卫星在轨道上运动的线速度与轨道半径的平方根成反比。

也由此可知，卫星的环绕线速度79km／s是所有人造卫星中的最大线速度。

二、动能与轨道半径的关系卫星运动的动能为 Ek＝GMm／2r，即Ek∝1／r。

可见，卫星的动能与轨道半径成反比。

三、运动周期与轨道半径的关系对卫星而言，T＝2πr／v，将v与r的关系式代入，得T=4πr／GM，即T∝r。

该式即为开普勒第三定律，解题时可以直接使用。

四、能量与轨道半径的关系运动物体的能量等于其动能与势能之和，即E＝Ek+Ep 。

对卫星来说，若轨道半径为r，取距地球无穷远处势能为零，则Ep＝-GMm／r。

卫星动能为Ek＝GMm／2r，故E＝Ek+Ep＝-GMm／2r，可知E ＜0 。

上式可写成 22323即可见，卫星的轨道半径与它在该轨道上的能量的乘积不变。

由于描述运动规律的各物理量都是轨道半径r的函数，故各个物理量之间的关系都可以通过r这个桥梁来相互转化，一个量变化，其他各量都随之变化。

[例]卫星做圆周运动，由于大气阻力的作用，其轨道的高度将逐渐变化(由于高度变化很缓慢，变化过程中的任一时刻，仍可认为卫星满足匀速圆周运动的规律)，下述关于卫星运动的一些物理量的变化情况正确的是: A．线速度减小B．轨道半径增大C．向心加速度增大D．周期增大[ 解析] 假设轨道半径不变，由于大气阻力使线速度减小，因而需要的向心力减小，而提供向心力的万有引力不变，故提供的向心力大于需要的向心力，卫星将做向心运动而使轨道半径减小，由于卫星在变轨后的轨道上运动时，满足v∝1／确。

和T∝r，故v增大而t减小，又a＝F引／m＝GM／r，故a 增大，则选项C正232思考与练习近地人造卫星沿轨道运动时由于受大气摩擦作用，卫星的运动状况发生怎样的改变? (摩擦力做负功，使卫星的动能减小，从而速度减小。

测绘技术中的导航卫星轨道参数计算方法导航卫星轨道参数计算是测绘技术中的重要环节，它为全球定位系统（GPS）、北斗导航系统、伽利略导航系统等提供了精准的卫星定位和导航服务。

在这篇文章中，我将介绍测绘技术中常用的导航卫星轨道参数计算方法。

我国的北斗导航系统是目前世界上发展最为迅猛的卫星导航系统之一。

为了保证北斗卫星系统的精准定位和导航能力，需要准确计算卫星的轨道参数。

在测绘技术中，常用的导航卫星轨道参数计算方法有“数值积分法”和“天文方法”。

数值积分法是导航卫星轨道参数计算中常用的一种方法。

它基于牛顿第二定律和万有引力定律，通过对卫星的运动轨迹进行数值计算来得到卫星的位置和速度。

数值积分法的优点是计算结果准确，适用范围广。

但是，它的计算过程比较复杂，需要大量的计算资源和时间。

另一种常用的导航卫星轨道参数计算方法是“天文方法”。

天文方法是通过观测卫星在天空中的位置和运动轨迹，利用天文学的知识和方法来计算导航卫星的轨道参数。

天文方法的优点是计算过程相对简单，无需大量的计算资源。

然而，它的准确度受到观测条件和天气等因素的限制，可能存在一定的误差。

除了这两种方法外，还有其他一些导航卫星轨道参数计算方法被广泛应用于测绘技术中。

例如，基于差分定位技术的轨道参数计算方法可以通过对接收机接收到的卫星信号进行处理，进而计算出卫星的轨道参数。

这种方法的优点是计算过程简单快捷，适用于现场实时测量。

此外，还有一些高级的计算方法被应用于导航卫星轨道参数的计算中。

比如，卡尔曼滤波方法、最小二乘法和粒子滤波方法等。

这些方法通过对测量值和预测值进行迭代运算，逐步优化计算结果，提高了轨道参数计算的精度和稳定性。

当然，这些方法的计算过程相对复杂，需要较高的专业知识和技术。

综上所述，导航卫星轨道参数计算是测绘技术中不可或缺的一环。

不同的计算方法各有优劣，适用于不同的应用场景。

如何选择合适的方法，并在实际应用中准确计算出导航卫星的轨道参数，是测绘技术工作者需要不断探索和研究的课题。

卫星轨道动力学数值计算卫星轨道动力学是研究卫星在其运动过程中受到的引力和运动的规律的一门学科，而卫星轨道动力学数值计算则是十分重要的卫星运动计算的一种方法。

在这篇文章中，我们将分步骤地为您讲解卫星轨道动力学数值计算的相关内容。

第一步，确定初始条件。

卫星轨道动力学数值计算中，第一个重要的步骤就是要确定卫星的初位置和速度。

卫星的速度和位置确定后，就可以开始根据物理定律计算轨道的变化。

第二步，建立动力学模型。

在计算卫星的轨道时，需要建立完整的动力学模型，该模型包含了卫星的力学特性以及环境因素对运动的影响。

模型的建立需要对卫星的运动因素进行细致的分析，准确地描述卫星受到的力和运动的规律。

第三步，选择计算方法。

在卫星轨道动力学数值计算中，需要根据实际的运动情况选择合适的计算方法。

目前常见的计算方法有欧拉方法、龙格-库塔法、雅各比-克劳兹方法等。

第四步，编写计算程序。

编写程序是卫星轨道动力学数值计算过程中的重要一环。

程序语言的选择与计算方法密切相关，而编写好的程序可以更好地帮助科研人员完成有关卫星运动的计算。

第五步，计算轨道的变化。

通过上述过程，就可以进行轨道动力学的数值计算了。

计算结果可以帮助科研人员更好地了解卫星的运动特性，从而进行更准确的卫星运动控制和轨道设计等相关研究。

总之，卫星轨道动力学数值计算是一项复杂的科学工作，在具体实践中需要考虑到许多因素。

通过不断的研究和实践，科研人员可以逐渐完善计算方法和程序，更好地适应实际的卫星运动控制需求。

卫星定轨ksg积分
卫星定轨是一项非常重要的任务，它涉及到卫星的精确控制和监测。

KSG 积分是一种非常有效的卫星定轨算法，它通过模拟卫星的运动过程来计算卫星的位置和速度。

这种算法具有很高的精度和可靠性，因此在卫星定轨领域得到了广泛的应用。

KSG积分算法基于卫星轨道动力学模型，通过数值积分方法对卫星的运动方程进行离散化求解。

它能够准确地模拟卫星的运动轨迹，并根据观测数据不断修正卫星轨道参数。

这种算法不仅具有很高的计算效率，而且能够处理大量的观测数据，为卫星定轨提供了强有力的支持。

在卫星定轨过程中，需要不断优化卫星轨道参数，以使得模拟的卫星运动轨迹与实际观测数据尽可能吻合。

KSG积分算法采用迭代优化方法,如最小二乘法、卡尔曼滤波等，不断调整和优化卫星轨道参数。

这种优化方法能够快速收敛，并得到最优的卫星轨道参数，为卫星的精确控制和监测提供了可靠的保障。

总之，KSG积分是一种非常有效的卫星定轨算法，它基于卫星动力学模型进行模拟和计算，利用观测数据和优化算法不断修正卫星轨道参数,最终得到精确的卫星轨道。

这种算法具有高精度、高可靠性、高计算效率和迭代优化等特点，因此在卫星定轨领域具有广泛的应用前景。

目录1星历计算的时间和坐标系统 (3)1.1 有关的时间系统与坐标系统 (3)1.1.1 时间系统及其换算 (3)1.1.2 坐标系统及其换算 (5)1.2 计算单位和有关常数 (10)2 轨道动力学计算的基本数学模型 (17)2.1 二体问题 (17)2.2 地球非球形引力摄动 (18)2.3 日、月摄动 (21)2.4 太阳直接辐射压摄动 (22)2.5 地球固体潮摄动 (26)2.6 大气阻力摄动 (26)2.7 Y轴偏差加速度摄动 (27)2.8 巡航姿态控制动力摄动 (28)2.9 其它摄动影响 (29)附录：日月位置计算 (29)3 轨道计算方法 (34)3.1 Runge_Kutta积分法 (35)3.2 Adams_Cowell积分 (36)3.3 轨道计算 (39)3.4 星历的快速插值 (40)4 轨道根数与位置矢量、速度矢量的关系 (45)4.1 由位置矢量和速度矢量计算轨道根数 (45)4.2 由轨道根数计算位置矢量和速度矢量 (46)1星历计算的时间和坐标系统1.1 有关的时间系统与坐标系统轨道计算过程重要涉及到不同的时间系统和坐标系统，下面将空间战场环境系统中所涉及到的时间系统和坐标系统进行定义，并说明各系统之间的相互关系。

一般情况下，仿真系统采用的是TDT 时间系统和J2000地心惯性坐标系。

1.1.1 时间系统及其换算在轨道计算中，时间是独立变量。

但是，在计算不同的物理量时，却使用不同的时间系统。

例如：在计算恒星时用世界时UT1；定位解算时采用GPS 时GPST ；岁差和章动量的计算采用TDB 时等。

所以必须清楚各时间系统的定义和各时间系统之间的转换，下面给出各种时间系统的定义及它们之间的转换公式。

格林尼治恒星时格林尼治恒星时为春分点对格林尼治平天文子午面的时角。

由于岁差、章动原因，它由格林尼治真恒星时（GAST ）和平恒星时（GMST ）之分。

两者的关系是：εψcos ∆+=GMST GAST其中：εψcos ∆为赤经章动3521062.0093104.0)876600812866.8640184(54841.67310u s u s u h s s T T T GMST -⨯-+++=u T 为自)0.2451545(0.2000JD J 起算至观测1UT 时刻的儒略世纪数，即.365250.2451545)1(-=UT JD T u 世界时1UT1UT 是以平北极（国际习惯用原点）为统一标准的观测世界时，是反映地球实际自转的时间，恒星时计算与此有关。

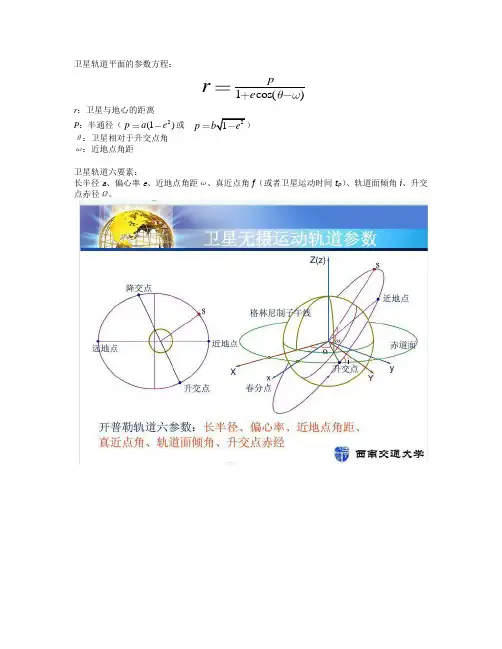
卫星轨道平面的参数方程：1cos()p e rr ：卫星与地心的距离P ：半通径（2(1)p a e 或21p b e ） θ：卫星相对于升交点角 ω：近地点角距卫星轨道六要素：长半径a 、偏心率e 、近地点角距ω、真近点角f （或者卫星运动时间t p ）、轨道面倾角i 、升交点赤径Ω。

OXYZ─赤道惯性坐标系，X轴指向春分点T ；ON─卫星轨道的节线（即轨道平面与赤道平面的交线），N为升交点；S─卫星的位置；P─卫星轨道的近地点；f─真近点角，卫星位置相对于近地点的角距；ω─近地点幅角，近地点到升交点的角距；i─轨道倾角，卫星通过升交点时，相对于赤道平面的速度方向；Ω─升交点赤经，节线ON与X轴的夹角；e─偏心率矢量，从地心指向近地点，长度等于e；W─轨道平面法线的单位矢量，沿卫星运动方向按右旋定义，它与Z轴的夹角为i；a─半长轴；α，δ─卫星在赤道惯性坐标系的赤经、赤纬。

两个坐标系：地心轨道坐标系、赤道惯性坐标系。

地心轨道坐标系Ox0y0z0：以ee1为x0轴的单位矢量，以W为z0轴的单位矢量，y0轴的单位矢量可以由x0轴的单位矢量与z0轴的单位矢量确定，它位于轨道平面内。

赤道惯性坐标系：OXYZ,X轴指向春分点。

由地心轨道坐标系到赤道惯性坐标系的转换：1.先将地心轨道坐标绕W旋转角（-ω），旋转矩阵为R Z(-ω)；2.绕节线ON旋转角（-i），旋转矩阵为R X(-i)；3.最后绕Z轴旋转角（-Ω），旋转矩阵为R Z(-Ω)；经过三次旋转后，地心轨道坐标系和赤道惯性坐标系重合。

在地心轨道坐标系中，卫星的位置坐标是：0 0 0cos sin 0x r f y r fz地心轨道坐标系到赤道惯性坐标系的转换关系是：000()()()cos cos sin cos sin sin cos cos cos sin sin sin cos =cos sincos cos sin sin sincos cos cos sin cos sin sin cos sin cos z x z x x y R R i R y z z i i i r f i i i i ii2sin 0cos sin()sin sin()cos(1)=sin cos()cos sin()cos 1cos sin()sin r f f f i a e f f ie ff i赤道惯性坐标系下的坐标确定后，可与r 、α、δ联系起来，关系式如下：1222()2arctan arctan(1)1cos 1cos y xz x y p a e re fe f若卫星六要素都已知，则可以解出α、δ。

卫星轨道动⼒学数值计算⽬录1星历计算的时间和坐标系统 (2)1.1 有关的时间系统与坐标系统 (2)1.1.1 时间系统及其换算 (2)1.1.2 坐标系统及其换算 (4)1.2 计算单位和有关常数 (7)2 轨道动⼒学计算的基本数学模型 (12)2.1 ⼆体问题 (12)2.2 地球⾮球形引⼒摄动 (12)2.3 ⽇、⽉摄动 (15)2.4 太阳直接辐射压摄动 (16)2.5 地球固体潮摄动 (19)2.6 ⼤⽓阻⼒摄动 (19)2.7 Y轴偏差加速度摄动 (20)2.8 巡航姿态控制动⼒摄动 (20)2.9 其它摄动影响 (21)附录：⽇⽉位置计算 (21)3 轨道计算⽅法 (24)3.1 Runge_Kutta积分法 (24)3.2 Adams_Cowell积分 (25)3.3 轨道计算 (27)3.4 星历的快速插值 (28)4 轨道根数与位置⽮量、速度⽮量的关系 (32)4.1 由位置⽮量和速度⽮量计算轨道根数 (32)4.2 由轨道根数计算位置⽮量和速度⽮量 (33)1星历计算的时间和坐标系统1.1 有关的时间系统与坐标系统轨道计算过程重要涉及到不同的时间系统和坐标系统，下⾯将空间战场环境系统中所涉及到的时间系统和坐标系统进⾏定义，并说明各系统之间的相互关系。

⼀般情况下，仿真系统采⽤的是TDT 时间系统和J2000地⼼惯性坐标系。

1.1.1 时间系统及其换算在轨道计算中，时间是独⽴变量。

但是，在计算不同的物理量时，却使⽤不同的时间系统。

例如：在计算恒星时⽤世界时UT1；定位解算时采⽤GPS 时GPST ；岁差和章动量的计算采⽤TDB 时等。

所以必须清楚各时间系统的定义和各时间系统之间的转换，下⾯给出各种时间系统的定义及它们之间的转换公式。

格林尼治恒星时格林尼治恒星时为春分点对格林尼治平天⽂⼦午⾯的时⾓。

由于岁差、章动原因，它由格林尼治真恒星时（GAST ）和平恒星时（GMST ）之分。

卫星轨道动力学数值计算
卫星轨道动力学数值计算是一种重要的技术手段，用于研究卫星在空间中的运动轨迹和动力学特性。

该技术主要基于牛顿力学和开普勒定律，通过数值计算模拟卫星在地球轨道上的运动状态，为卫星的设计、发射和运行提供重要的理论支持。

卫星轨道动力学数值计算的基本原理是利用牛顿第二定律和万有引力定律，建立卫星在地球引力场中的运动方程，然后通过数值计算方法求解该方程，得到卫星在轨道上的位置、速度和加速度等动力学参数。

具体来说，该技术主要包括以下几个方面：
1. 轨道参数计算：根据卫星的轨道高度、倾角、偏心率等参数，计算出卫星在地球轨道上的轨道参数，如轨道周期、轨道速度、轨道倾角等。

2. 轨道预报：根据卫星的轨道参数和初始状态，预测卫星在未来一段时间内的运动轨迹和位置，为卫星的运行和控制提供重要的参考。

3. 轨道设计：根据卫星的任务需求和运行要求，设计出最优的轨道参数和轨道类型，以实现卫星的最佳运行效果和任务完成能力。

4. 轨道控制：根据卫星的实际运行情况和任务需求，对卫星的轨道进行调整和控制，以保证卫星的稳定运行和任务完成能力。

卫星轨道动力学数值计算是一种重要的技术手段，为卫星的设计、
发射和运行提供了重要的理论支持。

随着卫星技术的不断发展和应用，该技术的应用范围和研究深度也将不断扩大和深化。

卫星轨道动力学数值计算
1.轨道参数：卫星轨道计算需要确定卫星的轨道参数，如半长轴，轨道倾角，近地点角，升交点赤经等。

这些参数必须根据历元计算出来，以确定卫星在指定历元的轨道位置。

2.运动方程：对于卫星的运动，除了已知的轨道参数外，还需要建立一个基本的运动方程，用来描述卫星的运动。

3.动力学模型：动力学模型是用来描述卫星在太空中的运动方程的，可以根据引力加速度来建立运动方程，通过改变模型来模拟不同的太空环境。

4.时间序列：卫星轨道动力学数值计算时，还需要指定一定的时间序列，用来记录卫星在每个时刻的轨道位置，以及卫星在一段时间内的运动过程。

5.计算系统：所有这些参数和模型都需要一个程序来实现，该程序由运算程序和辅助程序组成，根据输入的轨道参数及时间序列，建立动力学模型，计算出卫星在指定时间内的轨道位置。

本文介绍了卫星轨道动力学数值计算方法的基本原理。

卫星轨道动力学中的Hansen系数一、概述随着航天科技的飞速发展，卫星轨道动力学成为一个备受关注的研究领域。

在卫星的设计、轨道调整、轨道预测等方面，都需要深入了解卫星轨道的动力学特性。

而Hansen系数作为一种描述卫星轨道摄动效应的重要参数，对于理解和预测卫星轨道具有重要意义。

二、Hansen系数的基本概念Hansen系数最早由丹麦天文学家Peter Andreas Hansen在19世纪提出，并被广泛应用于描述卫星轨道摄动效应。

Hansen系数可用于描述太阳、月球、其他星球等天体对卫星轨道产生的摄动效应，它是一种数学函数，能够描述这些天体对卫星轨道参数的影响。

在卫星轨道动力学模拟中，Hansen系数的计算及应用至关重要。

三、Hansen系数的计算方法Hansen系数的计算涉及复杂的数学方法和物理模型。

一般来说，可以通过天体力学的基本理论和数值方法进行计算。

在实际的卫星轨道动力学仿真中，人们往往需要考虑多种摄动效应，因此需要综合考虑各种因素对Hansen系数的影响。

四、Hansen系数在卫星轨道动力学中的应用Hansen系数在卫星轨道动力学中具有广泛的应用价值，主要体现在以下几个方面：1. 卫星轨道设计：通过计算Hansen系数，可以帮助设计更稳定和可靠的卫星轨道，减小摄动效应对卫星轨道的影响。

2. 轨道调整：在卫星发射后，由于各种外部因素的影响，可能会导致卫星轨道偏离设计轨道，此时可以通过调整卫星轨道参数来重新计算Hansen系数，以实现轨道调整的目的。

3. 轨道预测：在卫星运行过程中，需要不断对卫星轨道进行预测和修正，Hansen系数的计算可以帮助提高轨道预测的准确性。

五、Hansen系数的发展与未来随着卫星技术的不断发展，Hansen系数的研究也在不断深入。

未来，人们将不断完善Hansen系数的计算方法，提高其精度和适用范围，为卫星轨道动力学的研究和应用提供更加有力的支持。

六、结语Hansen系数作为描述卫星轨道摄动效应的重要参数，在卫星轨道动力学中具有重要意义。

行星轨道动力学的数值模拟行星轨道动力学是天体力学的分支之一，研究的是行星在引力场中的运动规律。

通过运用数学方法对这些规律进行模拟，可以更好地理解和预测行星的运动。

本文将介绍行星轨道动力学数值模拟的基本原理和方法，并探讨其应用领域和局限性。

1. 数值模拟的基本原理行星轨道动力学数值模拟主要基于牛顿力学和引力定律。

根据牛顿第二定律F=ma，行星在引力场中受到合外力的作用会产生加速度，进而改变其速度和位置。

而根据万有引力定律F=G*m1*m2/r^2，行星之间的相互作用是基于其质量和距离的。

为了模拟行星轨道的运动，需要对行星的位置和速度进行数值计算。

通常将运动轨迹离散化，将连续的运动过程划分为多个时间步长。

通过迭代计算每一个时间步长内行星的位置和速度，可以逼近实际的运动轨迹。

数值模拟可以通过多种方法实现，其中常用的有欧拉法、改进的欧拉法、四阶龙格-库塔法等。

2. 数值模拟的方法（1）欧拉法欧拉法是行星轨道动力学数值模拟中最简单的方法之一。

该方法通过将时间步长分割为若干小段，根据当前位置和速度计算出下一个时间步长内的位置和速度。

然而，欧拉法有一定的局限性，因为它只考虑了当前状态的影响，未能充分考虑到加速度的变化。

（2）改进的欧拉法为了解决欧拉法的局限性，改进的欧拉法引入了中间状态的计算。

它在每一个时间步长内先计算一次当前位置和速度的中间状态，然后再计算下一个时间步长内的最终状态。

改进的欧拉法能更好地逼近真实轨道，但仍存在一定的误差。

（3）四阶龙格-库塔法四阶龙格-库塔法是行星轨道动力学数值模拟中最常用的方法之一，通过计算多个中间状态来逼近真实轨道。

该方法对每一个时间步长内的位置和速度进行四次计算，并通过加权平均获得最终结果。

相比于欧拉法和改进的欧拉法，四阶龙格-库塔法的精度更高，误差更小。

3. 应用领域和局限性行星轨道动力学的数值模拟在多个领域有重要的应用价值。

首先，它可以帮助研究人员更好地理解太阳系中行星的运动规律，揭示宇宙的奥秘。