“电路原理”第1-6章作业
- 格式:doc
- 大小:1.47 MB
- 文档页数:18
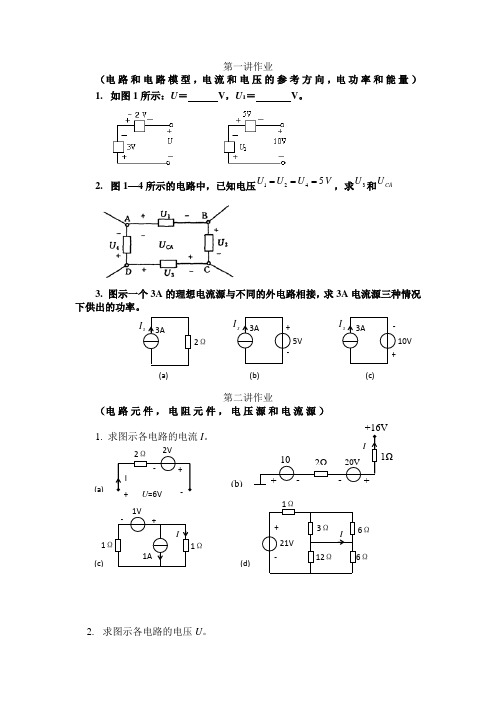
第一讲作业(电路和电路模型,电流和电压的参考方向,电功率和能量) 1. 如图1所示:U = V ,U 1= V 。
2. 图1—4所示的电路中,已知电压1245U U U V===,求3U 和CAU3. 图示一个3A 的理想电流源与不同的外电路相接,求3A 电流源三种情况第二讲作业(电路元件,电阻元件,电压源和电流源)I 。
2. 求图示各电路的电压U 。
3. 图示各电路,求:(1) 图(a)中电流源S I 产生功率S P 。
(2) 图(b)中电流源S U 产生功率S P第三讲作业(受控电源,电路基本定律(VAR 、K CL 、K VL ))1. 图示某电路的部分电路,各已知的电流及元件值已标出在图中,求I 、s U 、R 。
2. 图示电路中的电流I = ( )。
3. 图示含受控源电路,求:(1) 图(a)中电压u 。
(2) 图(b)中2Ω电阻上消耗的功率R P 。
第四讲作业(电路的等效变换,电阻的串联和并联,电阻的Y形联结和△形连结的等效变换)1.图示电路中的acb支路用图支路替代,而不会影响电路其他部分的电流和电压。
2.电路如图,电阻单位为Ω,则R ab=_________。
3. 求图示各电路中的电流I 。
第五讲作业(电压源和电流源的串联和并联,实际电源的两种模型及其等效变换,输入电阻)1. 求图示电路中的电流I 和电压U ab 。
2. 用等效变换求图示电路中的电流I 。
.3. 求图示各电路ab 端的等效电阻ab R 。
第三章作业3-1、某电路有n 结点,b 支路,其树枝数为 ,连枝数为 ,基本回路数为 ;独立的KCL 方程有 个,独立的KVL 方程有 个,独立的KCL 和KVL 方程数为 。
3-2、电路的图如图,以2、3、4为树枝,请写出其基本回路组。
3-3、电路如图,用支路电流法列方程。
3-4、电路见图,用网孔分析法求I 。
3-5、用网孔电流法(或回路电流法)求解图2电路中电流I及电压U 。


第1章 直流电路习题一、单项选择题1.图示电阻元件R 消耗电功率10W ,则电压U 为( )。
A )-5V B )5V C )20VU+题1图2.图示电路中,A 点的电位V A 为( )。
A )2 V B )-4 V C ) -2 V- 2 k 7 k ΩΩ题2图3.图示电路中,U 、I 的关系式正确的是( )。
A )U = (I S + I )R 0 B )U = (I S -I )R 0 C )U = (I - I S )R 0R L题3图I 2题4图4.图示电路中电流I 2为( )。
A )7AB )3AC )-3A5.理想电流源的外接电阻越大,则它的端电压( )。
A )越高 B )越低 C )不能确定6.把图1所示的电路改为图2的电路,其负载电流I 1和I 2将( )。
A )增大B )不变C )减小221Ω2V 2A图 1图 2+题6图7.图示电路中,供出功率的电源是( )。
A )理想电压源 B )理想电流源 C )理想电压源与理想电流源8.在图示电路中,各电阻值和U S 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ,需列出独立的电流方程数和电压方程数分别为( )。
A )4和3 B )3和3 C )3和4I RU 2A 14VSS1Ω1Ω..+题7图R R R R R I U 1234GGS....+题8图9.在计算线性电阻电路的电压和电流时,用叠加原理。
在计算线性电阻电路的功率时,加原理( )。
A )可以用 B )不可以用 C )有条件地使用10.在图示电路中,已知U S =12V ,I S =2A 。
A 、B 两点间的电压U AB 为( )。
A )-18VB )18VC )-6VU I ABSSΩ3+题10图.-6V SA.1k 1k ΩΩ题11图11.在图示电路中,当开关S 闭合时A 点的电位V A ( )。
A ) -3V B )3V C )0V12.图示电路中,理想电流源I S1发出的电功率P 为( )。




2010年《电工学》习题(上)解答 第1章 电路定律及分析方法习题解答一、单项选择题1.图示电阻元件R 消耗电功率10W ,则电压U 为( A )。
A )-5V B )5V C )20VUR 题1图2.在图示的电路中,A 点的电位V A 为( C )。
A )2 V B )-4 V C ) -2 V- 2 k 7 k ΩΩ题2图3.在图示电路中,U 、I 的关系式正确的是( B )。
A )U = (I S + I )R 0 B )U = (I S -I )R 0 C )U = (I - I S )R 0R L题3图I 2题4图4.图示电路中电流I 2为( C )。
A )7AB )3AC )-3A5.理想电流源的外接电阻越大,则它的端电压( A )。
A )越高 B )越低 C )不能确定6.图示电路中,用一个等效电源代替,应该是一个( B )。
A )2A 的理想电流源 B )2V 的理想电压源 C )不能代替,仍为原电路2 V题6图7.把图1所示的电路改为图2的电路,其负载电流I 1和I 2将( B )。
A )增大B )不变C )减小221Ω2V 2A图 1图 2+题7图8.图示电路中,供出功率的电源是( A )。
A )理想电压源 B )理想电流源C )理想电压源与理想电流源U4VS题8图S题9图9.在图示电路中,各电阻值和U S 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ,需列出独立的电流方程数和电压方程数分别为( B )。
A )4和3 B )3和3 C )3和410.在计算线性电阻电路的电压和电流时,用叠加原理。
在计算线性电阻电路的功率时,加原理( B )。
A )可以用 B )不可以用 C )有条件地使用11.在图示电路中,已知U S =12V ,I S =2A 。
A 、B 两点间的电压U AB 为( A )。
A )-18VB )18VC )-6VU I SS+题11图SA题12图12.在图示电路中,当开关S 闭合时A 点的电位V A ( C )。




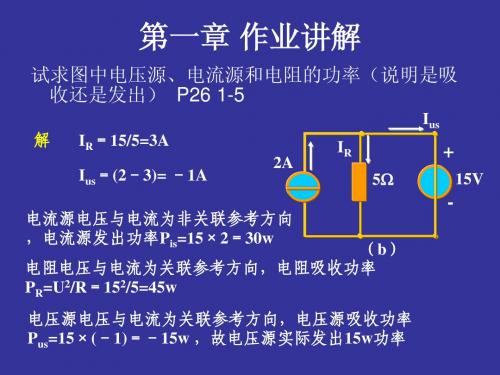


4. 图示电路中电流12为( A ) 7A B ) 3A5. 理想电流源的外接电阻越大,则它的端电压7•图示电路中,供出功率的电源是( )。
A )理想电压源B )理想电流源C )理想电压源与理想电流源&在图示电路中,各电阻值和U s 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ,需列出独立的电流方程数和电压方程数分别为 ( )。
A )4 和 3B )3 和 3C )3 和 4第1章直流电路习题、单项选择题 R 消耗电功率10W ,则电压U 为( )。
B ) 5V C ) 20V I 1.图示电阻元件 A ) 5V R—U + 2 A题i 图 2.图示电路中,A 点的电位V A 为()。
A ) 2 V B ) 4 V C ) 2 V —6V12V ・ _._匚二I ------2 k A 7 k 题2图 3.图示电路中,U 、丨的关系式正确的是()。
A ) U= (I s + I )R oB ) U = (I s — I )R oC ) U = (II s )R o丨 1- 7||-^-|| 1—1 2SR o UR LM 卜I +4题3图)。
C ) 3AA )越高B )越低 6.把图1所示的电路改为图A )增大B )不变C )不能确定2的电路,其负载电流 C )减小I 1和I 2将( )。
2AAG2A )18V B ) 18V C ) 6VA )可以用B )不可以用C )有条件地使用10.在图示电路中,已知U s =12V ,I S =2A 。
A 、B 两点间的电压U AB 为(B 题10图11. 在图示电路中,当开关A )3V12. 图示电路中,A ) 3WB ) 3V 理想电流源 B ) 21WS 闭合时A 点的电位V A (C ) 0VI S1发出的电功率P 为( C ) 3W)°12图题13图13.图示电路中,电流I 是(A ) 3AB ) 0A)°C ) 6A二、分析计算题1.1 (1 )试求如图所示电路中的 ,I 3 ,U 4 °(2)求如图所示电路中 A 点电位。

第一章 电路模型和电路定律电路理论主要研究电路中发生的电磁现象,用电流 i 、电压 u 和功率 p等物 理量来描述其中的过程。
因为电路是由电路元件构成的,因而整个电路的表现 如何既要看元件的联接方式,又要看每个元件的特性,这就决定了电路中各支 路电流、电压要受到两种基本规律的约束,即:( 1)电路元件性质的约束。
也称电路元件的伏安关系( VCR ),它仅与元件 性质有关,与元件在电路中的联接方式无关。
( 2)电路联接方式的约束(亦称拓扑约束) 。
这种约束关系则与构成电路的 元件性质无关。
基尔霍夫电流定律( KCL )和基尔霍夫电压定律( KVL )是概括 这种约束关系的基本定律。
掌握电路的基本规律是分析电路的基础。
1-1 说明图( a ), (b )中, (1)u,i的参考方向是否关联?( 2) ui 乘积表示什 么功率?( 3)如果在图( a )中 u 0,i 0;图( b )中u 0,i 0,元件实际发 出还是吸收功率?解:(1)当流过元件的电流的参考方向是从标示电压正极性的一端指向负极 性的一端, 即电流的参考方向与元件两端电压降落的方向一致, 称电压和电流的 参考方向关联。
所以( a )图中u,i的参考方向是关联的;(b )图中u,i的参考方 向为非关联。
(2)当取元件的 u,i参考方向为关联参考方向时,定义 p ui为元件吸收的 功率;当取元件的 u,i参考方向为非关联时,定义 p ui为元件发出的功率。
所 以( a )图中的 ui 乘积表示元件吸收的功率; ( b )图中的 ui 乘积表示元件发出的 功率。
(3)在电压、电流参考方向关联的条件下,带入 u, i数值,经计算,若p ui 0,表示元件确实吸收了功率;若 p 0,表示元件吸收负功率,实际是发出功率。
(a )图中,若 u 0,i 0 ,则 p ui 0,表示元件实际发出功率在 u,i参考方向非关联的条件下,带入 u,i数值,经计算,若 p ui 0,为正值,表示元件确实发出功率;若p 0,为负值,表示元件发出负功率,实际是吸收功率。
第一章“电路模型和电路定律”练习题1-1说明题1-1图(a )、(b )中:(1)u 、i 的参考方向是否关联?(2)ui 乘积表示什么功率?(3)如果在图(a )中u >0、i <0;图(b )中u >0、i >0,元件实际发出还是吸收功率?(a ) (b )题1-1图解:(1)图(a )中电压电流的参考方向是关联的,图(b )中电压电流的参考方向是非关联的。
(2)图(a )中由于 电压电流的参考方向是关联的,所以ui 乘积表示元件吸收的功率。
图(b )中电压电流的参考方向是非关联的,所以ui 乘积表示元件发出的功率。
(3)图(a )中u >0、i <0,所以ui <0。
而图(a )中电压电流参考方向是关联 的,ui 乘积表示元件吸收的功率,吸收的功率为负,所以元件实际是发出功率;图(b )中电压电流参考方向是非关联的,ui 乘积表示元件发出的功率,发出的功率为正,所以元件实际是发出功率。
1-4 在指定的电压u 和电流i 的参考方向下,写出题1-4图所示各元件的u 和i 的约束方程(即VCR )。
(a ) (b ) (c )(d ) (e ) (f )题1-4图解:(a )电阻元件,u 、i 为关联参考方向。
由欧姆定律u=Ri=104 i (b )电阻元件,u 、i 为非关联参考方向,由欧姆定律u = - R i = -10 i (c )理想电压源与外部电路无关,故 u = 10V (d )理想电压源与外部电路无关,故 u = -5V(e )理想电流源与外部电路无关,故 i=10×10-3A=10-2A(f )理想电流源与外部电路无关,故i=-10×10-3A=-10-2A1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a ) (b ) (c )题1-5图解:(a )由欧姆定律和基尔霍夫电压定律可知各元件的电压、电流如解1-5图(a )故 电阻功率10220WR P u i ==⨯=吸(吸收20W )电流源功率 I 5210WP ui ==⨯=吸(吸收10W ) 电压源功率U 15230WP ui ==⨯=发(发出30W )(b )由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(b )故 电阻功率12345WR P =⨯=吸(吸收45W ) 电流源功率 I 15230WP =⨯=发(发出30W ) 电压源功率U 15115WP =⨯=发(发出15W )(c )由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(c )故 电阻功率15345WR P =⨯=吸(吸收45W )电流源功率 I 15230WP =⨯=吸(吸收30W ) 电压源功率U 15575WP =⨯=发(发出75W )1-16 电路如题1-16图所示,试求每个元件发出或吸收的功率。
I 1(a ) (b )题1-16图解:(1)题1-16图(a )中,应用KVL 可得到方程20.520U U -+⨯+= 解得 1U V=-电流源电压U 与激励电流方向非关联,因此电流源发出功率为=0.510.50.5S I P U W W ⨯=-⨯=-发(实际吸收0.5W )电阻功率为2=0.520.5R P W W ⨯=VCVS 两端电压2U 与流入电流方向关联,故吸收功率为=20.51SU P U W ⨯=-吸(实际发出功率1W )显然,=+P SS IU R P P 发吸(2)题1-16图(b )中,在结点A 应用KCL,可得211123I I I I =+=再在左侧回路应用KVL ,可得到112+3=2I I 解得1=0.4A I 根据各电压,电流方向的关联关系,可知,电压源发出功率为120.8SU P I W ==发CCCS 发出功率为113230.420.4=0.96SCP I I W W =⨯=⨯⨯⨯发2Ω电阻消耗功率为12120.32R P I W =⨯= 1Ω电阻消耗功率为 221(3)1 1.44R P I W =⨯=显然 12S S U C R R P P P P +=+发发 。
1-20 试求题1-20图所示电路中控制量u 1及电压u 。
u 1题1-20图解:设电流i ,列KVL 方程3131110001010102101010i i u u i u ⎧+⨯+=⎪⎨=⨯+⎪⎩得:120200u V u V==第二章“电阻电路的等效变换”练习题2-1电路如题2-1图所示,已知u S =100V ,R 1=2k Ω,R 2=8k Ω。
试求以下3种情况下的电压u 2和电流i 2、i 3:(1)R 3=8k Ω;(2)R 3=∞(R 3处开路);(3)R 3=0(R 3处短路)。
题2-1图2-5用△—Y 等效变换法求题2-5图中a 、b 端的等效电阻:(1)将结点①、②、③之间的三个9Ω电阻构成的△形变换为Y 形;(2)将结点①、③、④与作为内部公共结点的②之间的三个9Ω电阻构成的Y 形变换为△形。
ab③题2-5图解:(1)变换后的电路如解题2-5图(a )所示。
因为变换前,△中Ω===9312312R R R(2)变换后的电路如图2-5图(b )所示。
因为变换前,Y 中1439R R R ===Ω所以变换后,1443313927R R R ===⨯=Ω故144331//(//3//9)ab R R R R =+Ω=72-11 利用电源的等效变换,求题2-11图所示电路的电流i 。
10V4Ω题2-11图解解2-5图2R 3R ③①②①③④31R 43R 14R2-13 题2-13图所示电路中431R R R ==,122R R =,CCVS 的电压11c 4i R u =,利用电源的等效变换求电压10u 。
u SR 4题2-13图解:由题意可等效电路图为解2-13图。
解解2-11图解2-13图2-14 试求题2-14图(a )、(b )的输入电阻ab R 。
1(a ) (b )题2-14图解:(1)由题意可设端口电流i 参考方向如图,于是可由KVL 得到,21111,ab u R i uu u R i μ=-+=11221121(1)ab u R i R i R i R i β=+=++第三章“电阻电路的一般分析”练习题3-1 在以下两种情况下,画出题3-1图所示电路的图,并说明其结点数和支路数:(1)每个元件作为一条支路处理;(2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。
(a ) (b )题3-1图解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解3-1图(a1)和(b1)。
图(a1)中节点数6=n ,支路数11=b 图(b1)中节点数7=n,支路数12=b(2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图(a)和图(b)所示电路的图分别为题解图(a2)和(b2)。
图(a2)中节点数4=n ,支路数8=b 图(b2)中节点数15=n,支路数9=b3-2 指出题3-1中两种情况下,KCL 、KVL 独立方程各为多少?解:题3-1中的图(a)电路,在两种情况下,独立的KCL 方程数分别为 (1)5161=-=-n (2)3141=-=-n独立的KVL 方程数分别为 (1)616111=+-=+-n b (2)51481=+-=+-n b图(b)电路在两种情况下,独立的KCL 方程数为 (1)6171=-=-n (2)4151=-=-n独立的KVL 方程数分别为(1)617121=+-=+-n b (2)51591=+-=+-n b3-7题3-7图所示电路中Ω==1021R R ,Ω=43R ,Ω==854R R ,Ω=26R ,V 20S3=u ,V 40S6=u ,用支路电流法求解电流5i 。
u题3-7图解:由题中知道4n =,6b = , 独立回路数为16413l b n =-+=-+= 由KCL 列方程:对结点① 1260i i i ++= 对结点② 2340i i i -++= 对结点③4660i i i -+-=由KVL 列方程: 对回路Ⅰ 642281040i i i --=-对回路Ⅱ 1231010420-i i i ++=-对回路Ⅲ 45-488203i i i ++=联立求得 0.956A5i =-3-8 用网孔电流法求解题3-7图中电流5i 。
解:可设三个网孔电流为11i 、2l i 、3l i ,方向如题3-7图所示。
列出网孔方程为246122436211232333413234533()()()l l l s l l l s l l l s R R R i R i R i u R i R R R i R i u R i R i R R R i u++--=-⎧⎪--++-=-⎨⎪--+++=⎩ 12312312320108401024420842020l l l l l l l l l i i i i i i i i i --=-⎧⎪-+-=-⎨⎪--+=⎩ 行列式解方程组为3-11 用回路电流法求解题3-11图所示电路中电流I 。
5V题3-11图u题3-7图解:由题已知,1I 1A l =其余两回路方程为()()123123555303030203020305l l l l l l I I I I I I -+++-=⎧⎪⎨--++=-⎪⎩代人整理得2322334030352A305015 1.5Al l l l l l I I I I I -==⎧⎧⇒⎨⎨-+==⎩⎩ 所以232 1.50.5A l l II I =-=-=3-12 用回路电流法求解题3-12图所示电路中电流a I 及电压o U 。
I a题3-12图解:由题可知12312331(415 2.5) 2.51502.5(8 2.52)2141.4l l L l l L L a a l I I I I I I I I I I ⎧++--=⎪⎪-+++-=-⎨⎪==⎪⎩ 解得123517l a l L I I A I A I A ⎧==⎪=⎨⎪=⎩得1230152242l l l U I I I V =--+=-3-15 列出题3-15图(a )、(b )所示电路的结点电压方程。
G i S7ii R(a ) (b )题3-15图题3-4图(b)③(a)④s i i解:图(a)以④为参考结点,则结点电压方程为:()231223321n n n s s G G u G u G u i i +--=-()2124252n n s s G u G G u i i -++=- ()3136375n ns s G u G G u i i -++=-图(b)以③为参考结点,电路可写成由于有受控源,所以控制量i 的存在使方程数少于未知量数,需增补一个方程,把控制量i 用结点电3-21 用结点电压法求解题3-21图所示电路中电压U 。