小学高年级数学竞赛奥数培训班 (62)

奥数综合训练：差倍问题（专项训练）小学四年级数学竞赛通用版全解析一．解答题（共17小题）1．同学们去参观历史博物馆，三年级比二年级多去了60人，三年级去的人数是二年级的3倍，两个年级分别去了多少人？2．路灯队第一天比第二天多运进电线杆120根，第一天运进的根数是第二天运进根数的3倍，两天各运进电线杆多少根？3．一个分数如果分子加上1，就等于1；如果分母加上1，就等于．原来这个分数是多少？4．饲养场鹅的只数比鸭的只数多82，鹅的只数比鸭的只数的4倍多1只．鹅有多少只？5．学校举行冬季跳踢比赛．参加跳绳比赛的人数比踢毽子人数的3倍少12人．跳绳人数比踢毽子人数多148人．参加跳绳和踢毽子比赛的各有多少人？6．有大小两个桶原来水一样多，如果从小桶倒8千克水到大桶，则大桶中水是小桶的3倍，求原来大桶有水多少千克？7．甲桶里的油比乙桶里的油的2倍多40千克，若甲、乙两桶里的油各倒出20千克，则甲桶里的油是乙桶里油的4倍，甲、乙两桶原来各有油多少千克？8．一桶油连桶重19千克，用了一半油以后，再连桶一称，共重12千克．求原来油和桶各重多少？9．已知两个数的商是4，而这两个数的差是39，那么这两个数中较小的一个是多少？10．用一个杯子向空瓶里倒牛奶，如果倒进去2杯牛奶，连瓶共重450克；如果倒进去5杯牛奶，连瓶共重750克．一杯牛奶和一个空瓶各重多少克？11．甲、乙两瓶油同样重，如果从乙瓶中倒50千克油到甲瓶中，那么甲瓶的油是乙瓶的3倍，甲瓶原有多少千克油？12．甲、乙两数的差是7.92，把乙数的小数点向右移动一位正好等于甲，甲、乙两个数各是多少？13．如图所示，EF＝20厘米，DE＝14厘米，三角形CDE的面积比三角形ABC的面积大30平方厘米，求AB的长度．14．零售店运来两桶酒，大桶有酒120千克，小桶有酒90千克，卖出同样多的酒后，大桶剩的酒刚好是小桶剩的酒的4倍，小桶卖出多少酒？15．把数字9写到一个三位数的左边，得到一个四位数，再把这个四位数加上这个三位数，所得的和是原三位数的17倍，求原三位数是多少？16．四年级三个班开展读好书活动．二班比一班多读20本书，三班读的书比二班的2倍多3本，比一班多读56本书，三个班一共读多少本书？17．袋子里有红、黑两种球，红球比黑球的3倍多2个，每次从袋子里取出4个红球和2个黑球，若干次后，袋子里剩下12个红球和2个黑球，袋子里黑球原有多少个？奥数综合训练：差倍问题（专项训练）小学四年级数学竞赛通用版全解析参考答案与试题解析一．解答题（共17小题）1．同学们去参观历史博物馆，三年级比二年级多去了60人，三年级去的人数是二年级的3倍，两个年级分别去了多少人？【分析】三年级去的人数是二年级的3倍，那么三年级比二年级多去的60人，就相当于二年级人数的（3﹣1）倍，用除法求出二年级人数，再进一步求出三年级去的人数即可．【解答】解：60÷（3﹣1）＝60÷2＝30（人）30×3＝90（人）答：二年级去了30人，三年级去了90人．2．路灯队第一天比第二天多运进电线杆120根，第一天运进的根数是第二天运进根数的3倍，两天各运进电线杆多少根？【分析】第一天比第二天多运进电线杆120根，即数量差是120根，相当于第二天运进根数的3﹣1＝2倍，由此用除法即可求出第二天运进根数，再进一步解答即可．【解答】解：120÷（3﹣1）＝120÷2＝60（根）60+120＝180（根）答：第一天运进180根，第二天运进60根．3．一个分数如果分子加上1，就等于1；如果分母加上1，就等于．原来这个分数是多少？【分析】根据题意，分子+1与分母相等，即分母比分子多1，分母加上1，此时分母比分子多2，分数为，分母比分子多1份，所以每份为2，对应的分子为16，分母为18，然后分母﹣1可以求出原分母．【解答】解：根据题意（1+1）÷（9﹣8）＝2÷1＝22×9﹣1＝1717﹣1＝16所以原分数是．4．饲养场鹅的只数比鸭的只数多82，鹅的只数比鸭的只数的4倍多1只．鹅有多少只？【分析】由题意知：82﹣1＝81只正好是鸭的3倍，这样可求出鸭的只数，之后便可求得鹅的只数．【解答】解：（82﹣1）÷（4﹣1）＝27（只）82+27＝109（只）答：鹅有109只．5．学校举行冬季跳踢比赛．参加跳绳比赛的人数比踢毽子人数的3倍少12人．跳绳人数比踢毽子人数多148人．参加跳绳和踢毽子比赛的各有多少人？【分析】由“参加跳绳比赛的人数比踢毽子人数的3倍少12人．跳绳人数比踢毽子人数多148人”得出：跳绳的比踢毽子的多148人再加上12人的话，正好是踢毽子人数的3﹣1＝2倍，这样便可求出踢毽子的人数，进而再求得跳绳人数．【解答】解：（148+12）÷（3﹣1）＝80（人）80+148＝228（人）答：参加跳绳比赛的有228人，踢毽子比赛的有80人．6．有大小两个桶原来水一样多，如果从小桶倒8千克水到大桶，则大桶中水是小桶的3倍，求原来大桶有水多少千克？【分析】由题意知，当从小桶倒8千克水到大桶，此时大桶里的水比小桶的多8+8＝16千克，进而得知“16千克是小桶此时有水的3﹣1＝2倍”，至此便可求出此时小桶有水16÷2＝8千克，然后再加上倒出的8千克就是小桶原来水的千克数，当然也是大桶原来有水的千克数．【解答】解：（8+8）÷（3﹣1）＝8（千克）8+8＝16（千克）答：原来大桶有水16千克．7．甲桶里的油比乙桶里的油的2倍多40千克，若甲、乙两桶里的油各倒出20千克，则甲桶里的油是乙桶里油的4倍，甲、乙两桶原来各有油多少千克？【分析】由题意，中两次减少的都是40千克，两桶的和不变，是和倍问题，求出乙桶占两桶总数的比例，可得两桶总数及原来两桶总数，即可得出结论．【解答】解：先将乙桶倒出40 千克，则甲桶是乙桶的 2 倍；此时乙桶占两桶总数的＝；再将甲、乙两桶里的油各倒出20千克，则甲桶里的油是乙桶里油的4倍；此时乙桶占两桶总数的＝；则两桶总数为20÷（）＝150 千克，原来两桶总数是150+40＝190 千克；最后乙桶是150×＝30 千克，甲桶是150﹣30＝120 千克；原来甲桶是120+20＝140 千克，乙桶是190﹣140＝50 千克．答：甲、乙两桶原来各有油140 千克、50千克8．一桶油连桶重19千克，用了一半油以后，再连桶一称，共重12千克．求原来油和桶各重多少？【分析】一桶油连桶重19千克，用去一半油后连桶重12千克，则油的一半为19﹣12＝7千克，那么用7乘2就是油的总重量，因此桶重＝连桶重19千克﹣油的总重量，据此解答即可．【解答】解：（19﹣12）×2＝7×2＝14（千克）；19﹣14＝5（千克）；答：原来桶里有油14千克，油桶重5千克．9．已知两个数的商是4，而这两个数的差是39，那么这两个数中较小的一个是多少？【分析】两个数的商是4，即大数是较小数的4倍，因为这两个数的差是39，即较小数的（4﹣1）倍是39，根据已知一个数的几倍是多少，求这个数，用除法即可求出较小数．【解答】解：39÷（4﹣1）＝39÷3＝13，答：较小数是13；故答案为：13．10．用一个杯子向空瓶里倒牛奶，如果倒进去2杯牛奶，连瓶共重450克；如果倒进去5杯牛奶，连瓶共重750克．一杯牛奶和一个空瓶各重多少克？【分析】由题意可知3杯牛奶的重量是750﹣450＝300克，由此可以求出一杯牛奶的重量，进而求出一个空瓶的重量．【解答】解：（750﹣450）÷（5﹣2）＝100（克）450﹣100×2＝250（克）答：一杯牛奶的重量是100克，一个空瓶的重量是250克．11．甲、乙两瓶油同样重，如果从乙瓶中倒50千克油到甲瓶中，那么甲瓶的油是乙瓶的3倍，甲瓶原有多少千克油？【分析】由“甲、乙两瓶油同样重，如果从乙瓶中倒50千克油到甲瓶中”说明这时甲瓶比乙瓶多了50×2＝200千克油；再结合“甲瓶的油是乙瓶的3倍”得知“100千克油是乙瓶油的3﹣1＝2倍”，这样可求出此时乙瓶中有油50千克，之后再加上倒出的50千克就是乙瓶原有油的千克数，这也是甲瓶原有油的千克数．【解答】解：50×2÷（3﹣1）＝50（千克）50+50＝100（千克）答：甲瓶原来有100千克油．12．甲、乙两数的差是7.92，把乙数的小数点向右移动一位正好等于甲，甲、乙两个数各是多少？【分析】把乙数的小数点向右移动一位正好等于甲，说明甲是乙的10倍，根据甲、乙两数的差是7.92，可得结论．【解答】解：乙数：7.92÷（10﹣1）＝0.88甲数：0.88×10＝8.8答：甲数是8.8，乙数是0.88．13．如图所示，EF＝20厘米，DE＝14厘米，三角形CDE的面积比三角形ABC的面积大30平方厘米，求AB的长度．【分析】三角形CDE的面积比三角形ABC的面积大30平方厘米，即长方形BDEF的面积比三角形AEF的面积大30平方厘米，然后根据长方形和三角形的面积公式解答即可．【解答】解：（20×14﹣30）×2÷20＝500÷20＝25（厘米）答：AB的长是25厘米．14．零售店运来两桶酒，大桶有酒120千克，小桶有酒90千克，卖出同样多的酒后，大桶剩的酒刚好是小桶剩的酒的4倍，小桶卖出多少酒？【分析】由题意知，两桶的差120﹣90＝30千克一直没变；由“卖出同样多的酒后，大桶剩的酒刚好是小桶剩的酒的4倍“可知，30千克是卖后小桶酒的4﹣1＝3倍，这样便可求出此时小桶里酒的千克数为30÷3＝10千克，这说明小桶卖掉了90﹣10＝80千克．【解答】解：（120﹣90）÷（4﹣1）＝10（千克）90﹣10＝80（千克）答：小桶卖出了80千克．15．把数字9写到一个三位数的左边，得到一个四位数，再把这个四位数加上这个三位数，所得的和是原三位数的17倍，求原三位数是多少？【分析】根据题意，把数字9写到一个三位数的左边，得到一个四位数，即相当于原来这个三位数+9000+原来这个三位数＝原来的三位数×17，因此这个三位数＝9000÷（17﹣2）＝600，据此回答．【解答】解：根据题意得9000÷（17﹣1﹣1）＝9000÷15＝600答：原来这个数是600．16．四年级三个班开展读好书活动．二班比一班多读20本书，三班读的书比二班的2倍多3本，比一班多读56本书，三个班一共读多少本书？【分析】根据“二班比一班多读20本书，三班读的书比一班多读56本书”可得三班读的书比二班多读56﹣20＝36本书，那么36﹣3＝33本相当于二班的2﹣1＝1倍，然后根据差倍公式数量：差÷（倍数﹣1）＝较小数进一步解答即可．【解答】解：（56﹣20﹣3）÷（2﹣1）＝33（本）33﹣20＝13（本）33×2+3＝69（本）33+13+69＝115（本）答：三个班一共读115本书．17．袋子里有红、黑两种球，红球比黑球的3倍多2个，每次从袋子里取出4个红球和2个黑球，若干次后，袋子里剩下12个红球和2个黑球，袋子里黑球原有多少个？【分析】运用倒推的方法，即可得出结论．【解答】解：由题意，12+4+4＝20，2+2+2＝6，20÷6＝3…2，即取2次后，袋子里剩下12个红球和2个黑球，所以袋子里黑球原有6个．答：袋子里黑球原有6个．。

小学数学兴趣班的类型有哪些在当今的教育环境中，小学数学兴趣班如雨后春笋般涌现，为孩子们提供了丰富多样的学习选择。

这些兴趣班不仅能够帮助孩子们巩固数学知识，提高学习成绩，还能培养他们的数学思维和解决问题的能力。

那么，小学数学兴趣班究竟有哪些类型呢？一、奥数班奥数班可以说是最为常见的小学数学兴趣班之一。

奥数注重培养孩子的逻辑思维、创新能力和解题技巧，通过一系列具有挑战性的数学问题，激发孩子对数学的兴趣和探索欲望。

在奥数班中，孩子们会接触到比学校课程更深入、更复杂的数学知识，例如数论、组合数学、几何等。

这些知识的学习需要孩子们具备较强的抽象思维和推理能力。

然而，奥数班并非适合所有孩子。

对于那些对数学有浓厚兴趣、学有余力的孩子来说，奥数班能够提供很好的拓展和提升机会。

但对于数学基础较弱或者对数学不太感兴趣的孩子，可能会感到压力过大，甚至产生厌学情绪。

二、数学思维拓展班数学思维拓展班侧重于培养孩子的数学思维方式和方法。

通过各种有趣的数学游戏、活动和案例，引导孩子从不同的角度思考问题，培养他们的观察力、分析力和判断力。

比如，通过拼图游戏培养孩子的空间想象力，通过逻辑推理游戏锻炼孩子的逻辑思维能力。

这种类型的兴趣班更注重培养孩子的综合素质和思维能力，而不仅仅是知识的传授。

数学思维拓展班通常采用启发式教学方法，鼓励孩子们自主思考和探索，培养他们独立解决问题的能力。

对于大多数孩子来说，这种兴趣班能够有效地提高他们的数学学习兴趣和能力。

三、数学应用实践班数学应用实践班将数学知识与实际生活紧密结合，让孩子们在实践中感受数学的魅力和用途。

例如，通过组织孩子们进行市场调查、统计分析等活动，让他们运用数学知识解决实际问题；或者通过制作数学模型、进行数学实验等方式，加深孩子们对数学概念的理解。

这种类型的兴趣班能够让孩子们明白数学并非只是书本上的枯燥公式和定理，而是与生活息息相关的实用工具。

它有助于培养孩子们的实践能力和应用意识，提高他们运用数学知识解决实际问题的能力。

国子学数学竞赛班型一、国子学数学竞赛简介国子学数学竞赛，简称“国数赛”，是我国一项具有较高声誉和影响力的数学竞赛活动。

旨在激发青少年学生对数学的兴趣与热爱，培养学生的逻辑思维、创新能力和综合素质。

该项竞赛自创办以来，吸引了众多优秀学子积极参与，成为了检验数学实力的重要平台。

二、国子学数学竞赛班型分类为了更好地满足不同学生的需求，国子学数学竞赛培训班分为以下三种班型：1.常规班：针对数学基础较好，希望提高数学素养和应试能力的同学。

课程设置注重基础知识的巩固与拓展，培养学生的解题技巧和思维能力。

2.提高班：针对数学成绩优异，有较强自学能力和应试压力的同学。

课程旨在帮助学生巩固基础知识，提高解题速度和准确率，冲击竞赛奖项。

3.精英班：针对数学特长生，课程设置更具挑战性和针对性。

通过高难度的题目训练，提升学生的数学素养和竞赛水平，助力夺取高分奖项。

三、各班级特点及适用对象1.常规班：适用于数学基础较好，希望提高数学素养和应试能力的中小学生。

课程内容丰富，既有基础知识的学习，也有解题技巧的传授。

2.提高班：适用于数学成绩优异，有较强自学能力的中小学生。

课程注重培养学生的解题速度和准确率，助力在数学竞赛中取得优异成绩。

3.精英班：适用于数学特长生，课程极具挑战性和针对性。

通过高难度的题目训练，提升学生的数学素养和竞赛水平。

四、国子学数学竞赛培训效果与优势国子学数学竞赛培训班凭借丰富的教学经验和专业的师资团队，为学生提供优质的教学服务。

培训效果显著，历年来学员在国数赛中成绩斐然，获奖人数众多。

此外，培训班还具备以下优势：1.针对性教学：根据学生实际需求，制定合适的教学计划和课程内容。

2.优质师资：拥有一支经验丰富、专业素质高的教师队伍，为学生提供个性化辅导。

3.高效辅导：注重培养学生的解题技巧和思维能力，提高学习效率。

4.全方位服务：提供课后答疑、学习资料等辅助服务，确保学生学习效果。

五、报名与咨询渠道有兴趣参加国子学数学竞赛培训班的同学及家长，可通过以下渠道了解报名详情并进行咨询：1.官网：访问国子学数学竞赛官方网站，了解赛事信息和培训班详情。

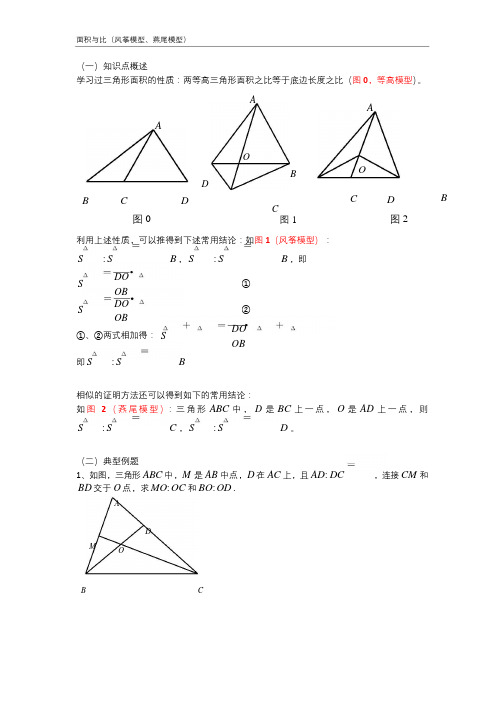
（一）知识点概述学习过三角形面积的性质：两等高三角形面积之比等于底边长度之比（图0，等高模型）。

AAAOOBDB C D图0 C图1C D图2B利用上述性质，可以推得到下述常用结论：如图1（风筝模型）：S : S B，S : S B，即S S D OOBD OOB①②①、②两式相加得：S D OOB即S : S B相似的证明方法还可以得到如下的常用结论：如图 2 （燕尾模型）：三角形ABC 中，D 是BC 上一点，O 是AD 上一点，则S : S C ，S : S D 。

（二）典型例题1、如图，三角形ABC 中，M 是AB 中点，D 在AC 上，且AD: DC ，连接CM 和 BD 交于O 点，求MO:OC 和BO:OD .ADM OB C2、如图，三角形ABC 中，D 、E 分别在BC 和AB 上，连接AD 、CE 交于O 点，BD ，O 是EC 中点，求AE : EB和AO:OD.AEOB D C3、如图，三角形ABC 中，D 、E 分别在AB 、AC 上，连接BE 、CD 交于O 点，且BO ，CO:OD ，求AD: DB 和AE : EC.AD EOB C4、如图，长方形ABCD中，E 、F 分别在AB 、BC 上，且满足EB ，BF ，连接BD 、EF 交于O 点，求：（1）EO:OF ；（2）三角形BOF 是长方形ABCD面积的几分之几.E BAO FD C5、如图，长方形ABCD中，E 、F 分别在CD和BC 上，且满足DE : EC ，连接AF 、 BE 交于O 点，如果AO:OF ，求BF : FC.BAOFD EC6、如图，三角形ABC 中，D 在AC 上，且满足AD: DC ，E 、F 是BC 上的两个三等分点，连接BD 、AE 、AF ，AE 、AF 分别与BD 交于M 、N ，三角形AMN 占三角形ABC 面积的几分之几？AM N DB E FC7、如图，三角形ABC 中，D 、E 、F 分别在AB 、BC 、CA 上，且满足3AD ，3BE ，3CF ，连接AE 、BF 、CD，三条线段两两交于P 、Q 、R 三点，求（1）：AP : PQ :QE ；（2）三角形PQR 是三角形ABC 面积的几分之几？AD PFQ RB E C【思考题】如图，E 是平行四边形ABCD外一点，且满足S : S : S ，且三角形EBD 的面积是12，那么四边形ADCE 的面积是多少？EA BD C。

全国奥数培训品牌排名哪家⽐较好奥数能够很好地提升学⽣的思维能⼒，对学⽣的学习帮助很⼤，下⾯⼩编为⼤家总结整理了全国奥数机构的排名情况，供⼤家参考。

全国⽐较好的奥数品牌有哪些1学⽽思师资⼒量：A机构资质：正规资源指标：A++规模指标：A++企业成长性：B+班级体系：集训队-超A班-超常班-尖⼦班-提⾼班点评：沪上最⼤规模⼩奥机构，上市公司，市场服务意识强，但⽼师多以年轻⼤学⽣担纲，名师流失⾃⽴门户较多，适合打基础。

2四季师资⼒量：A+机构资质：正规资源指标：A++规模指标：A+企业成长性：A班级体系：创新班-实验班-⾦牌班-精英班点评：沪上⽼牌培训机构，市场份额较⼤。

但⽬前名师流失严重，教学质量不断下降。

著名杯赛亚太杯主办⽅。

3新东⽅泡泡师资⼒量：B+机构资质：正规资源指标：A++规模指标：A++企业成长性：B+班级体系：思维训练班+专项提⾼班点评：有很强的品牌知名度和规模，奥数体系⼀直在完善中。

4昂⽴少⼉师资⼒量：B机构资质：正规资源指标：A++规模指标：A+企业成长性：B+班级体系：数理资优-竞赛培训-数学精品-思维拓展点评：沪上本⼟综合实⼒派，但奥数兼职⽼师为主。

5新贝师资⼒量：B机构资质：正规资源指标：A++规模指标：A+企业成长性：B+班级体系：考证班-奥数提⾼班点评：市场营销强悍，各种杯赛关键字均为其买断的。

奥数兼职⽼师为主，没有标准化的体系，围绕着杯赛⼀直在做⽂章。

6新⾈师资⼒量：A+机构资质：正规资源指标：A++规模指标：A企业成长性：A+班级体系：光明顶-竞赛班-精英班-提⾼班-基础班点评：浦东地区⽼牌培训机构，浦东地区市场份额较⼤。

传背后有⼤资⾦⼊驻，近期将向全市发展。

7尚品：师资⼒量：B++机构资质：正规资源指标：A+规模指标：A企业成长性：B++班级体系：精英班-提⾼班-基础班点评：沪上⽼牌机构，上海⾛美杯举办⽅，资源渠道丰富，若不是近年教师流失⾮常严重，值得关注！8乐在四季师资⼒量：B+机构资质：正规资源指标：A++规模指标：A企业成长性：B++班级体系：⾦牌班-精英班-优等⽣班点评：闵⾏区业数就放在其校区可见其资源渠道的实⼒，稍微⽋缺的就是师资⼒量。

南昌云轩奥数收费标准南昌云轩奥数是一家专业的奥数培训机构，致力于为学生提供优质的数学辅导服务。

为了让家长和学生更好地了解南昌云轩奥数的收费标准，我们将详细介绍我们的收费政策。

首先，南昌云轩奥数的收费标准根据学生的年级和课程类型进行区分。

针对小学生、初中生和高中生，我们提供了不同的课程体系，并且针对不同年级的学生，我们也设计了相应的收费标准。

对于小学生来说，我们的奥数课程主要分为基础班和提高班两种类型。

基础班主要针对一年级到四年级的学生，课程内容主要围绕数学基础知识的巩固和提高；提高班主要针对五年级到六年级的学生，课程内容更加深入，涉及到奥数的基本概念和解题技巧。

针对小学生的奥数课程，收费标准为每学期2000元，包括教材费和学杂费。

对于初中生和高中生来说，我们的奥数课程更加注重数学思维能力和解题技巧的培养。

我们设有初中奥数强化班和高中奥数提高班两种类型的课程。

针对初中生，收费标准为每学期2500元，针对高中生，收费标准为每学期3000元，同样包括教材费和学杂费。

此外，南昌云轩奥数还提供了一对一的个性化辅导服务，针对学生的个别需求和学习特点，我们将制定专属的学习计划和课程内容。

一对一辅导的收费标准为每小时200元，学生可以根据自己的学习需求和时间安排自由选择上课时间。

总的来说，南昌云轩奥数的收费标准是相对合理和透明的。

我们致力于为学生提供高质量的奥数课程，帮助他们在数学学习中取得更好的成绩。

同时，我们也注重与家长的沟通和反馈，确保家长对我们的收费标准和课程内容有清晰的了解。

在南昌云轩奥数，我们相信每个学生都有潜力成为数学的高手，我们将竭诚为他们提供最好的学习环境和服务。

希望通过我们的努力，能够帮助更多的学生在数学学习中取得成功。

海淀最热门的奥数机构和班型介绍
1.海淀最热门的奥数机构：
（1）海淀嘉华奥数中心：海淀嘉华教育集团旗下的小学、初中、高
中等专业教育机构，以教育学校、培训机构和奥数中心三位一体构成，在
海淀多家分校提供奥数培训和多种课程；
（2）海淀智思教育项目：智思教育致力于根植海淀本土，拓展北京
十六区，引领全国乃至世界教育服务，专注从小学到大学的教育服务，以
及提供小学和初中奥数培训；
（3）海淀柠蜻蜓教育：柠蜻蜓教育集团的核心业务是提供一体化的
服务，从青少年成长到小学、初中，以及高中奥数培训，针对不同年龄段
的孩子进行全方位的辅导。

2.海淀最热门的奥数班型介绍：
（1）小学班：小学奥数班包括小学数学、奥数、竞赛课程三大板块，采取一对一教学模式，提供专业知识和辅导，助孩子们在数学和奥数素养
上提高；
（2）初中班：初中奥数班包括数学、物理、化学、生物四大学科，
采取小班授课模式，配合系统有效的变式训练，助孩子们在以上四大学科
课程和奥数思维深入探究；
（3）高中班：高中奥数班包括高中数学、奥数、竞赛课程三大板块，采取一对一教学模式，结合竞赛模拟题等训练，助孩子们在高中。

呦鸣教育浅水湾奥数
在青岛市崂山区有一家名为呦鸣教育的培训机构，位于美丽的浅水湾附近，专门为学生提供奥数辅导。

奥数，即奥林匹克数学，是一种培养学生逻辑思维能力和数学解决问题能力的数学学科。

呦鸣教育浅水湾奥数班以其优质的师资和教学模式，备受家长和学生的青睐。

呦鸣教育浅水湾奥数班的师资力量非常强大。

这里的老师都是经过严格筛选和培训的优秀教师，他们不仅具有扎实的数学知识，更重要的是能够激发学生对数学的兴趣和热爱。

老师们耐心细致地讲解数学知识，引导学生掌握解题技巧，帮助他们建立正确的数学思维方式。

无论是基础知识的巩固还是奥数竞赛题的讲解，老师们都能够给予学生及时有效的指导和帮助。

呦鸣教育浅水湾奥数班的教学模式独具特色。

在这里，学生不仅仅是被动接受知识，更是被激发思考和实践的主体。

教师们会根据学生的实际情况和学习需求制定个性化的学习计划，针对性地进行教学。

课堂上除了讲解知识点，还会引导学生进行实际操作和解题训练，培养他们的数学思维和解决问题的能力。

通过多种形式的教学活动，学生们能够在轻松愉快的氛围中提高自己的数学水平。

呦鸣教育浅水湾奥数班还注重与家长的沟通与合作。

教师们会定期与家长进行沟通，了解学生的学习情况和问题所在，共同制定有效
的解决方案。

家长们也能够及时了解孩子在学校的学习情况，与教师共同关心和指导孩子的成长。

这种良好的家校合作氛围有助于孩子们更好地发展自己的潜力，取得更好的学习成绩。

2014年春季浓度问题2（暑假会继续学习）浓度问题2★方程法解浓度问题（基本上是根据溶质不变列方程；）寻找不变量列方程求解；▲十字交叉法了解并熟练掌握三个浓度：两个初始一个混合；三个质量：混合前两个初始溶液质量和混合后混合溶液质量（对应三个浓度）▲混合溶液浓度求解.相同质量的两种溶液混合，混合浓度是两种溶液浓度的平均数。

混合浓度介于初始两种浓度之间，大于小浓度，小于大浓度。

1.甲、乙两只装有糖水的桶，甲桶有糖水60千克，含糖率为4%，乙桶有糖水40千克，含糖率为20%，两桶互相交换多少千克才能使两桶糖水的含糖率相等？2.有浓度为85%和45%两种酒，现要配制含酒精60%的酒400克，应当从这种酒中各取多少克？3.甲种酒精溶液中有酒精6千克，水9千克；乙种酒精溶液中有酒精9千克，水3千克；要配制成50%的酒精溶液7千克，问两种酒精溶液各需多少千克？4.有3个一样大的桶，一个装有浓度60%的酒精100升，一个装有水100升，还有一个桶是空的.现在要配置成浓度为36%的酒精，只有5升和3升的空桶各一个可以作为量具，并且桶上无其他刻度.如果每一种量具最多用4次，那么最多能配制成36%的酒精多少升？5.甲容器有浓度为2％的盐水 180克，乙容器中有浓度为9％的盐水若干克，从乙取出240克盐水倒入甲.再往乙倒入水，使两个容器中有一样多同样浓度的盐水.问：现在甲容器中食盐水浓度是多少？6.甲种酒精纯酒精含量为72%，乙种酒精纯酒精含量为58%，混合后纯酒精含量为62%．如果每种酒精取的数量比原来都多取15升，混合后纯酒精含量为63.25%．第一次混合时，甲、乙两种酒精各取了多少升？7.纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%．如果每种酒精都多取20克，混合后纯酒精的含量变为45%．求甲、乙两种酒精原有多少克？8.在一个奇怪的动物村庄里住着猫、狗和其他一些动物．有20%的狗认为它们是猫；有20%的猫认为它们是狗．其余动物都是正常的．一天，动物村的村长小猴子发现：所有的猫和狗中，有32%认为自己是猫．如果这个奇怪的动物村庄里有狗比猫多180只．那么狗的数目是多少只？。