(16)有向无环图及其应用分析
- 格式:ppt
- 大小:1.10 MB
- 文档页数:35
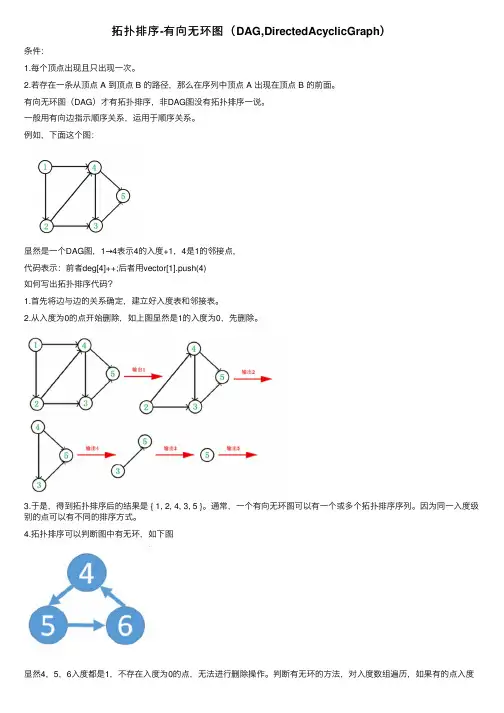
拓扑排序-有向⽆环图(DAG,DirectedAcyclicGraph)条件:1.每个顶点出现且只出现⼀次。
2.若存在⼀条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前⾯。
有向⽆环图(DAG)才有拓扑排序,⾮DAG图没有拓扑排序⼀说。
⼀般⽤有向边指⽰顺序关系,运⽤于顺序关系。
例如,下⾯这个图:显然是⼀个DAG图,1→4表⽰4的⼊度+1,4是1的邻接点,代码表⽰:前者deg[4]++;后者⽤vector[1].push(4)如何写出拓扑排序代码?1.⾸先将边与边的关系确定,建⽴好⼊度表和邻接表。
2.从⼊度为0的点开始删除,如上图显然是1的⼊度为0,先删除。
3.于是,得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。
通常,⼀个有向⽆环图可以有⼀个或多个拓扑排序序列。
因为同⼀⼊度级别的点可以有不同的排序⽅式。
4.拓扑排序可以判断图中有⽆环,如下图显然4,5,6⼊度都是1,不存在⼊度为0的点,⽆法进⾏删除操作。
判断有⽆环的⽅法,对⼊度数组遍历,如果有的点⼊度不为0,则表明有环。
例题+代码拓扑排序(⼀)-Hiho-Coder1174描述由于今天上课的⽼师讲的特别⽆聊,⼩Hi和⼩Ho偷偷地聊了起来。
⼩Ho:⼩Hi,你这学期有选什么课么?⼩Hi:挺多的,⽐如XXX1,XXX2还有XXX3。
本来想选YYY2的,但是好像没有先选过YYY1,不能选YYY2。
⼩Ho:先修课程真是个⿇烦的东西呢。
⼩Hi:没错呢。
好多课程都有先修课程,每次选课之前都得先查查有没有先修。
教务公布的先修课程记录都是好多年前的,不但有重复的信息,好像很多都不正确了。
⼩Ho:课程太多了,教务也没法整理吧。
他们也没法⼀个⼀个确认有没有写错。
⼩Hi:这不正是轮到⼩Ho你出马的时候了么!⼩Ho:哎??我们都知道⼤学的课程是可以⾃⼰选择的,每⼀个学期可以⾃由选择打算学习的课程。
唯⼀限制我们选课是⼀些课程之间的顺序关系:有的难度很⼤的课程可能会有⼀些前置课程的要求。



有向无环图的最优路径有向无环图(Directed Acyclic Graph,简称DAG)是一种图论中常见的数据结构,其中的有向边没有闭环。
在计算机科学和应用程序设计中,有向无环图的最优路径是一个重要的问题,它在许多领域都有广泛的应用,例如优化问题、动态规划和调度算法等。
在有向无环图中,最优路径是指从起始节点到目标节点的路径,使得路径上的权重之和最小或最大。
最优路径的选择取决于具体的应用场景和问题要求。
在本文中,我们将讨论求解有向无环图最优路径的算法和技巧。
一、拓扑排序拓扑排序是解决有向无环图最优路径问题的一种重要算法。
它通过对图的节点进行排序,使得任何一条边的起始节点都排在终止节点之前。
拓扑排序可以用来处理依赖关系,例如任务调度和编译器优化等问题。
在实现拓扑排序算法时,可以使用深度优先搜索(DFS)或广度优先搜索(BFS)等方法。
具体步骤如下:1. 初始化一个栈,用于存储已经访问过的节点。
2. 选择一个未访问的节点作为起始节点,将其标记为已访问。
3. 对于起始节点的每个未访问的邻接节点,递归调用拓扑排序算法。
4. 将当前节点入栈。
5. 重复步骤3和步骤4,直到所有节点都被访问。
6. 从栈顶到栈底的顺序即为拓扑排序的结果。
拓扑排序算法可以求解有向无环图的最优路径,例如,最长路径和最短路径等问题。
在实际应用中,我们可以根据具体需求选择不同的路径计算方法。
二、动态规划动态规划是解决有向无环图最优路径问题的另一种常用方法。
它通过将问题分解为子问题,并用一个表格来存储子问题的解,从而逐步构建出最优解。
在使用动态规划算法求解有向无环图最优路径时,可以使用以下步骤:1. 定义状态:将问题表示为一个状态集合,其中每个状态和图中的一个节点对应。
2. 定义状态转移方程:通过递推关系式来定义状态之间的转移关系,以得到最优路径。
3. 计算最优解:根据状态转移方程,从起始节点开始计算每个节点的最优路径值,并记录路径信息。


有向无环图有向无环图(DAG)是一种重要的图形数据结构,在计算机科学、网络和算法分析等领域中都有广泛的应用。
它与普通无向图有所不同,因为它会在连接时增加一个方向,这就意味着它可以表示有序的数据。
有向无环图被广泛应用于计算机科学领域,比如拓扑排序、分布式处理、编译器设计等等。
概念有向无环图是由一些顶点和一些有序的边组成,它将数据结构中的每个顶点连接起来。
每条边都有一个方向,这就决定了图中的有序性,也决定了如何遍历图中的每个顶点。
它只有在没有重复出现的边时,才能保证从一个顶点开始,能够遍历到整个图中的每个顶点。
另外一个特点是,它不能有环,也就是说,从一个顶点出发,不能回到该顶点本身。
拓扑排序有向无环图是一种很强大的数据结构,它可以用来实现拓扑排序(Topological Sorting)。
拓扑排序是一种重要的技术,可以根据有向边的方向,对顶点进行排序,以便给定时序性任务分配排序方式。
比如,在建筑工程中,需要用到拓扑排序,比如地基建完再搭框架,搭框架后再安装门窗等等。
拓扑排序能保证输出的顺序和输入的顺序一致,也可以用于求解最短路径问题,比如求解从一个城市到另外一个城市的最短路径。
分布式处理有向无环图也可以用来实现分布式处理(Distributed Processing),它可以把任务分解成一些独立的子任务,然后把它们连接起来,形成有向无环图,这样每一个子任务可以在不同的处理器上完成。
分布式处理可以使用有向无环图的拓扑排序算法,实现对任务的排序,从而保证任务的正确执行。
同时,由于它不存在环路,因此也可以保证它是安全的,不会出现死锁的情况,这样也就可以保证流程的有序性。
编译器设计有向无环图也可以用于编译器设计(Compiler Design)。
编译器是计算机科学中一种重要的应用,它可以把高级语言翻译成机器语言,从而可以让计算机处理高级语言编写的程序。
有向无环图可以用来构建编译器,因为它可以实现对语句的排序,这样可以保证编译器在编译过程中符合语法规则,并且能够正确翻译,从而使程序能够正确执行。

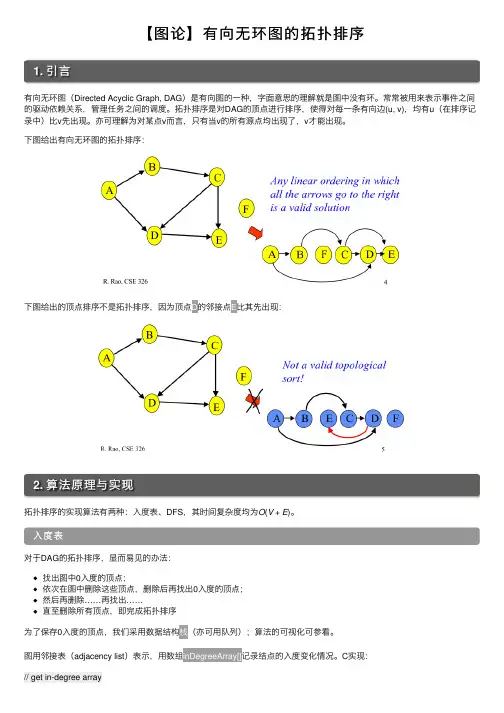
【图论】有向⽆环图的拓扑排序1. 引⾔有向⽆环图(Directed Acyclic Graph, DAG)是有向图的⼀种,字⾯意思的理解就是图中没有环。
常常被⽤来表⽰事件之间的驱动依赖关系,管理任务之间的调度。
拓扑排序是对DAG的顶点进⾏排序,使得对每⼀条有向边(u, v),均有u(在排序记录中)⽐v先出现。
亦可理解为对某点v⽽⾔,只有当v的所有源点均出现了,v才能出现。
下图给出有向⽆环图的拓扑排序:下图给出的顶点排序不是拓扑排序,因为顶点D的邻接点E⽐其先出现:2. 算法原理与实现拓扑排序的实现算法有两种:⼊度表、DFS,其时间复杂度均为O(V+E)。
⼊度表对于DAG的拓扑排序,显⽽易见的办法:找出图中0⼊度的顶点;依次在图中删除这些顶点,删除后再找出0⼊度的顶点;然后再删除……再找出……直⾄删除所有顶点,即完成拓扑排序为了保存0⼊度的顶点,我们采⽤数据结构栈(亦可⽤队列);算法的可视化可参看。
图⽤邻接表(adjacency list)表⽰,⽤数组inDegreeArray[]记录结点的⼊度变化情况。
C实现:// get in-degree arrayint *getInDegree(Graph *g) {int *inDegreeArray = (int *) malloc(g->V * sizeof(int));memset(inDegreeArray, 0, g->V * sizeof(int));int i;AdjListNode *pCrawl;for(i = 0; i < g->V; i++) {pCrawl = g->array[i].head;while(pCrawl) {inDegreeArray[pCrawl->dest]++;pCrawl = pCrawl->next;}}return inDegreeArray;}// topological sort functionvoid topologicalSort(Graph *g) {int *inDegreeArray = getInDegree(g);Stack *zeroInDegree = initStack();int i;for(i = 0; i < g->V; i++) {if(inDegreeArray[i] == 0)push(i, zeroInDegree);}printf("topological sorted order\n");AdjListNode *pCrawl;while(!isEmpty(zeroInDegree)) {i = pop(zeroInDegree);printf("vertex %d\n", i);pCrawl = g->array[i].head;while(pCrawl) {inDegreeArray[pCrawl->dest]--;if(inDegreeArray[pCrawl->dest] == 0)push(pCrawl->dest, zeroInDegree);pCrawl = pCrawl->next;}}}时间复杂度:得到inDegreeArray[]数组的复杂度为O(V+E);顶点进栈出栈,其复杂度为O(V);删除顶点后将邻接点的⼊度减1,其复杂度为O(E);整个算法的复杂度为O(V+E)。

一、无向图:方法1:如果存在回路,则必存在一个子图,是一个环路。
环路中所有顶点的度〉=2。
n算法:第一步:删除所有度<=1的顶点及相关的边,并将另外与这些边相关的其它顶点的度减一。
第二步:将度数变为1的顶点排入队列,并从该队列中取出一个顶点重复步骤一。
如果最后还有未删除顶点,则存在环,否则没有环。
n算法分析:由于有m条边,n个顶点。
i)如果m〉=n,则根据图论知识可直接判断存在环路。
(证明:如果没有环路,则该图必然是k棵树 k>=1.根据树的性质,边的数目m = n-k.k〉=1,所以:m<n)ii)如果m〈n 则按照上面的算法每删除一个度为0的顶点操作一次(最多n次),或每删除一个度为1的顶点(同时删一条边)操作一次(最多m次).这两种操作的总数不会超过m+n。
由于m〈n,所以算法复杂度为O(n).注:该方法,算法复杂度不止O(V),首先初始时刻统计所有顶点的度的时候,复杂度为(V + E),即使在后来的循环中E>=V,这样算法的复杂度也只能为O(V + E)。
其次,在每次循环时,删除度为1的顶点,那么就必须将与这个顶点相连的点的度减一,并且执行delete node from list[list[node]],这里查找的复杂度为list[list[node]]的长度,只有这样才能保证当degree[i]=1时,list[i]里面只有一个点。
这样最差的复杂度就为O(EV)了.方法2:DFS搜索图,图中的边只可能是树边或反向边,一旦发现反向边,则表明存在环。
该算法的复杂度为O(V).方法3:摘自:http:///lzrzhao/archive/2008/03/13/2175787。
aspxPS:此方法于2011—6-12补充假定:图顶点个数为M,边条数为E遍历一遍,判断图分为几部分(假定为P部分,即图有 P 个连通分量)对于每一个连通分量,如果无环则只能是树,即:边数=结点数-1只要有一个满足边数 > 结点数-1原图就有环将P个连通分量的不等式相加,就得到:P1:E1=M1-1P2:E2=M2—1.。

有向无环图的最优路径有向无环图(Directed Acyclic Graph,简称DAG)是一种图的数据结构,它定义了一组有向边,并且不存在任何环路。
在此基础上,我们将讨论有向无环图的最优路径问题。
一、什么是最优路径在有向无环图中,最优路径指的是从图中的某一起点到终点的最短路径或者最长路径,其长度可根据具体情况来决定。
这里我们将重点讨论求解最短路径的问题。
二、最优路径的应用最优路径在许多领域都有广泛的应用。
例如,在交通规划中,我们希望找到最短路径以减少行程时间和交通拥堵。
在电信网络中,最短路径算法使得数据能够高效地传输。
另外,最优路径还可以应用于任务调度、路径规划等领域。
三、有向无环图的最优路径算法有向无环图的最优路径可以通过动态规划算法来求解。
下面介绍两种较为常用的算法:迪杰斯特拉算法和贝尔曼-福特算法。
1. 迪杰斯特拉算法迪杰斯特拉算法是一种典型的单源最短路径算法,适用于有向无环图。
它的基本思想是从起点开始,逐步确定到达各个顶点的最短路径。
算法步骤如下:(1)初始化:将起点的最短路径设置为0,其他顶点的最短路径设置为无穷大。
(2)选择:选择一个未被访问过的顶点,使得当前被访问的顶点到该顶点的路径长度最短。
(3)更新:通过比较当前路径长度和新路径长度的大小,更新到达其他未被访问过的顶点的最短路径。
(4)重复:重复选择和更新步骤,直到所有顶点都被访问过。
2. 贝尔曼-福特算法贝尔曼-福特算法是一种通用的最短路径算法,适用于一般的有向图,包括带有负权边的图。
算法步骤如下:(1)初始化:将起点的距离设置为0,其他顶点的距离设置为无穷大。
(2)迭代:重复对所有边进行松弛操作,即通过比较当前路径和新路径的长度,更新距离数组中的值。
(3)判断负权环:若经过上述迭代,距离数组仍然在更新,则存在负权环,无法求解最短路径。
四、最优路径的应用举例以城市之间的交通规划为例,假设我们已经构建了一个有向无环图,其中城市之间的道路表示为有向边,而道路的长度表示为边的权重。

给定一个包含n个点m条边的有向无环图一、重要概念1. 图、简单图、图的同构、度序列与图序列、补图与自补图、两个图的联图、两个图的积图、偶图图:一个图是一个有序对<V, E>,记为G=(V, E),其中:1) V是一个有限的非空集合,称为顶点集合,其元素称为顶点或点。
用|V|表示顶点数;2) E是由V中的点组成的无序对构成的集合,称为边集,其元素称为边,且同一点对在E中可以重复出现多次。
用|E|表示边数注:图G 的顶点集记为V(G),边集记为E(G)。
图G 的顶点数(或阶数)和边数可分别用符号n(G)和m(G)表示简单图:无环无重边的图称为简单图。
(除此之外全部都是复合图)注:点集与边集均为有限集合的图称为有限图。
只有一个顶点而无边的图称为平凡图。
边集为空的图称为空图图的同构:设有两个图G1=(V1, E1)和G2=(V2, E2),若在其顶点集合间存在双射,使得边之间存在如下关系:设u1↔u2, v1↔v2,u1, v1∈V1,u2, v2∈V2;u1v1∈E1当且仅当u2v2∈E2,且u1v1与u2v2 的重数相同。
称G1与G2同构,记为G1≌G2 图的度序列:一个图G的各个点的度d1, d2,…, dn构成的非负整数组(d1, d2,…, dn)称为G的度序列注:非负整数组(d1, d2,…., dn)是图的度序列的充分必要条件是:∑di 为偶数。
度序列的判定问题为重点!图的图序列:一个非负数组如果是某简单图的度序列,称它为可图序列,简称图序列补图:对于一个简单图G=(V, E),令集合E1={uv|u≠v, u, v ∈V},则图H=(V,E1\E)称为G的补图自补图:若简单图G与其补图同构,则称G为自补图注:自补图的性质(1)若n阶图G是自补的,即那么有联图:设G1,G2是两个不相交的图,作G1+G2,并且将G1中每个顶点和G2中的每个顶点连接,这样得到的新图称为G1与G2的联图。
图论:有向图和⽆向图,有环和⽆环
有向⽆环图:为什么不能有环,有环会导致死循环。
检查⼀个有向图是否存在环要⽐⽆向图复杂。
(有向图为什么⽐⽆向图检查环复杂呢?)
现实中管⽹会存在环吗?管⽹是有⽅向的,理论上也是⽆环的。
arcgis有向⽆环图最短路径。
有向⽆环图和⼆叉树的关系:如何确定⽗节点和⼦节点[没有⽗节点的就是⽗节点,没有⼦节点的就是叶⼦节点] 有向⽆环图并不⼀定能转化成树【那能不能把有向⽆环图劈开成多棵树】
⼀个⽆环的有向图称做有向⽆环图(Directed Acyclic Graph)。
简称DAG 图。
DAG 图是⼀类较有向树更⼀般的特殊有向图,如图给出了有向树、DAG 图和有向图的例⼦。
虽然DAG图是更⼀般的有向图,但是依然可以使⽤树的判断公式来判断复杂度。
判断是否有环:
1. 起点编码和终点编码是否相等
从OBJECTID为1的开始遍历:下⼀个点是否与OBJECTID为1的相等。
如果相等,则回到起点,为环。
>>性质:有向⽆环图的⽣成树个数等于⼊度⾮零的节点的⼊度积。
有向⽆环图⽣成树:
(百度百科上不是说有向⽆环图不⼀定能转换成树吗?严格意义上,树的叶⼦节点只有⼀个⽗节点)
DAG(有向⽆环图)能否转化为树?:
如果说⼀个叶⼦节点有两个⽗节点,会怎么样
有向⽆环图不⼀定能只⽣成⼀棵树,但是可以⽣成多棵树。
但是这样就破坏了什么信息呢?。
一、无向图:方法1:∙如果存在回路,则必存在一个子图,是一个环路。
环路中所有顶点的度>=2。
∙ n算法:第一步:删除所有度<=1的顶点及相关的边,并将另外与这些边相关的其它顶点的度减一。
第二步:将度数变为1的顶点排入队列,并从该队列中取出一个顶点重复步骤一。
如果最后还有未删除顶点,则存在环,否则没有环。
∙ n算法分析:由于有m条边,n个顶点。
i)如果m>=n,则根据图论知识可直接判断存在环路。
(证明:如果没有环路,则该图必然是k棵树k>=1。
根据树的性质,边的数目m = n-k。
k>=1,所以:m<n)ii)如果m<n 则按照上面的算法每删除一个度为0的顶点操作一次(最多n次),或每删除一个度为1的顶点(同时删一条边)操作一次(最多m次)。
这两种操作的总数不会超过m+n。
由于m<n,所以算法复杂度为O(n)。
∙注:该方法,算法复杂度不止O(V),首先初始时刻统计所有顶点的度的时候,复杂度为(V + E),即使在后来的循环中E>=V,这样算法的复杂度也只能为O(V + E)。
其次,在每次循环时,删除度为1的顶点,那么就必须将与这个顶点相连的点的度减一,并且执行delete node from list[list[node]],这里查找的复杂度为list[list[node]]的长度,只有这样才能保证当degree[i]=1时,list[i]里面只有一个点。
这样最差的复杂度就为O(EV)了。
方法2:DFS搜索图,图中的边只可能是树边或反向边,一旦发现反向边,则表明存在环。
该算法的复杂度为O(V)。
方法3:摘自:/lzrzhao/archive/2008/03/13/2175787.aspx PS:此方法于2011-6-12补充假定:图顶点个数为M,边条数为E遍历一遍,判断图分为几部分(假定为P部分,即图有P 个连通分量)对于每一个连通分量,如果无环则只能是树,即:边数=结点数-1只要有一个满足边数> 结点数-1原图就有环将P个连通分量的不等式相加,就得到:P1:E1=M1-1P2:E2=M2-1...PN:EN>MN-1所有边数(E) > 所有结点数(M) - 连通分量个数(P)即: E + P > M 所以只要判断结果 E + P > M 就表示原图有环,否则无环.实例代码如下:1.#include<iostream>2.#include<malloc.h>ing namespace std;4.#define maxNum 100 //定义邻接举证的最大定点数5.int visited[maxNum];//通过visited数组来标记这个顶点是否被访问过,0表示未被访问,1表示被访问6.int DFS_Count;//连通部件个数,用于测试无向图是否连通,DFS_Count=1表示只有一个连通部件,所以整个无向图是连通的7.int pre[maxNum];8.int post[maxNum];9.int point;//pre和post的值10.11.//图的邻接矩阵表示结构12.typedef struct13.{14.char v[maxNum];//图的顶点信息15.int e[maxNum][maxNum];//图的顶点信息16.int vNum;//顶点个数17.int eNum;//边的个数18.}graph;19.void createGraph(graph *g);//创建图g20.void DFS(graph *g);//深度优先遍历图g21.void dfs(graph *g,int i);//从顶点i开始深度优先遍历与其相邻的点22.void dfs(graph *g,int i)23.{24.//cout<<"顶点"<<g->v[i]<<"已经被访问"<<endl;25. cout<<"顶点"<<i<<"已经被访问"<<endl;26. visited[i]=1;//标记顶点i被访问27. pre[i]=++point;28.for(int j=1;j<=g->vNum;j++)29. {30.if(g->e[i][j]!=0&&visited[j]==0)31. dfs(g,j);32. }33. post[i]=++point;34.}35.36.void DFS(graph *g)37.{38.int i;39.//初始化visited数组,表示一开始所有顶点都未被访问过40.for(i=1;i<=g->vNum;i++)41. {42. visited[i]=0;43. pre[i]=0;44. post[i]=0;45. }46.//初始化pre和post47. point=0;48.//初始化连通部件数为049. DFS_Count=0;50.//深度优先搜索51.for(i=1;i<=g->vNum;i++)52. {53.if(visited[i]==0)//如果这个顶点为被访问过,则从i顶点出发进行深度优先遍历54. {55. DFS_Count++;//统计调用void dfs(graph *g,int i);的次数56. dfs(g,i);57. }58. }59.}60.void createGraph(graph *g)//创建图g61.{62. cout<<"正在创建无向图..."<<endl;63. cout<<"请输入顶点个数vNum:";64. cin>>g->vNum;65. cout<<"请输入边的个数eNum:";66. cin>>g->eNum;67.int i,j;68.//输入顶点信息69.//cout<<"请输入顶点信息:"<<endl;70.//for(i=0;i<g->vNum;i++)71.// cin>>g->v[i];72.//初始画图g73.for(i=1;i<=g->vNum;i++)74.for(j=1;j<=g->vNum;j++)75. g->e[i][j]=0;76.//输入边的情况77. cout<<"请输入边的头和尾"<<endl;78.for(int k=0;k<g->eNum;k++)79. {80. cin>>i>>j;81. g->e[i][j]=1;82. g->e[j][i]=1;//无向图对称83. }84.}85.int main()86.{87. graph *g;88. g=(graph*)malloc(sizeof(graph));89. createGraph(g);//创建图g90. DFS(g);//深度优先遍历91.//连通部件数,用于判断是否连通图92. cout<<"连通部件数量:";93. cout<<DFS_Count<<endl;94.if(DFS_Count==1)95. cout<<"图g是连通图"<<endl;96.else if(DFS_Count>1)97. cout<<"图g不是连通图"<<endl;98.//各顶点的pre和post值99.for(int i=1;i<=g->vNum;i++)100. cout<<"顶点"<<i<<"的pre和post分别为:"<<pre[i]<<" "<<post[i]<<endl;101.//cout<<endl;102.//判断无向图中是否有环103.if(g->eNum+DFS_Count>g->vNum)104. cout<<"图g中存在环"<<endl;105.else106. cout<<"图g中不存在环"<<endl;107.int k;108. cin>>k;109.return 0;110.}111./*112.输入:113.正在创建无向图...114.请输入顶点个数vNum:10115.请输入边的个数eNum:9116.请输入边的头和尾117.1 2118.1 4119.2 5120.2 6121.4 7122.5 9123.6 3124.7 8125.9 10126.*/注意:有向图不能使用此方法。