平行四边形和梯形各部分的名称

四年级数学平行四边形和梯形知识点大全四年级数学平行四边形和梯形知识点一垂直与平行1认识平行和垂直①同一平面内的两条直线的位置关系只有两种：相交和不相交。

相交又有成直角的和不成直角的两种情况。

_“同一平面”是确定两条直线平行关系的前提，如果不在同一平面内，即便不相交，也不能称为互相平行。

②平行线：在同一个平面内不相交的两条直线叫做平行线，也可以说这两条直线互相平行。

平行的表示方法：a//b，读作a平行于b。

生活中平行的例子：窗户相对的框，黑板相对的两条边，公路上的斑马线......③垂直：如果两条直线相交成直角，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。

垂直的表示方法：ab生活中垂直的例子：三角尺上的两条直角边互相垂直......④三条直线的特殊关系：a//b，b//c,那么a//c：在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线互相平行ab，bc，那么a//c：在同一平面内，如果两条直线都和第三条直线垂直，那么这两条直线互相平行。

2垂线的画法和性质①过直线上和直线外一点怎样画这条直线的垂线：把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺，使三角尺的顶点和直线上的已知点重合;从直角的顶点起，沿着另一条直角边画出一条直线，这条直线就是已知直线的垂线。

②过直线外一点怎样画这条直线的垂线：把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺，使三角尺的另一条直角边与直线外的一点重合;沿着三角尺的另一条直角边画一条直线③垂线的性质：从直线外一点到这条直线所画的垂直线段最短，它的长度叫做这点到直线的距离。

3平行线的画法及运用①平行线的画法：固定三角尺，沿一条直角边先画一条直线;用直尺紧靠三角尺的另一条直角边，固定直尺，然后平移三角尺;再沿第一步中的直角边画出另一条直线。

②检验两条直线是否平行的方法：把三角尺的一条直角边与其中的一条直线重合;用直尺紧靠三角尺的另一条直角边，固定直尺，然后平移三角尺;如果第一步的三角尺的直角边与另一条直线完全重合，这两条直线就互相平行，如果不完全重合，这两条直线就不平行。

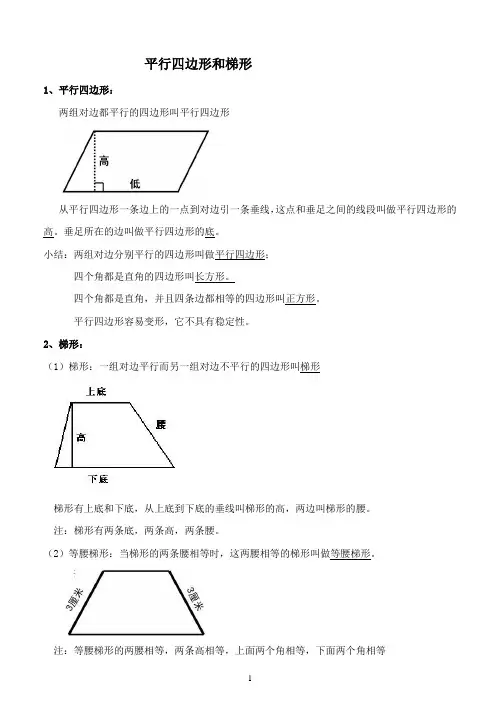
平行四边形和梯形1、平行四边形：两组对边都平行的四边形叫平行四边形从平行四边形一条边上的一点到对边引一条垂线，这点和垂足之间的线段叫做平行四边形的高。

垂足所在的边叫做平行四边形的底。

小结：两组对边分别平行的四边形叫做平行四边形；四个角都是直角的四边形叫长方形。

四个角都是直角，并且四条边都相等的四边形叫正方形。

平行四边形容易变形，它不具有稳定性。

2、梯形：（1）梯形：一组对边平行而另一组对边不平行的四边形叫梯形梯形有上底和下底，从上底到下底的垂线叫梯形的高，两边叫梯形的腰。

注：梯形有两条底，两条高，两条腰。

（2）等腰梯形：当梯形的两条腰相等时，这两腰相等的梯形叫做等腰梯形。

注：等腰梯形的两腰相等，两条高相等，上面两个角相等，下面两个角相等一、填空。

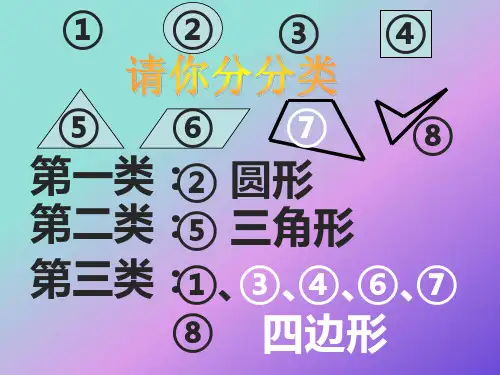
1、我们学过的四边形有（）、（）、（）和（）。

2、两条直线相交成（）度时，这两条直线互相垂直。

3、平行四边形具有（）。

4、长方形相邻的两条边互相（）。

相对的两条边互相（）。

5、以平行四边形的一条边为底，能作出（）条高，这些高的长度都（）。

6、在同一平面内，（）的两条直线叫做平行线。

7、（）和（）都是特殊的平行四边形。

8、等腰梯形（）一组对边平行。

9、平行四边形（）轴对称图形。

10、任意四边形的内角和都是（）度。

二、选择。

1、互相垂直的两条直线可以相交成4个（）。

A、锐角B、直角C、钝角D、平角2、从平行四边形的一条边上的一点到对边可以引（）垂线。

A、一条B、两条C、无数条3、两个完全一样的三角形一定可以拼成一个（）。

A、平行四边形B、梯形C、长方形4、下面图形中，不是轴对称图形的是（）。

A、长方形B、圆形C、平行四边形D、等腰梯形5、右图中有（）个梯形。

A、5B、7C、96、长方形中有（）组对边平行。

A、1B、2C、4三、判断。

1、两个梯形可以拼成一个平行四边形。

（）2、有四个角是直角的图形一定是长方形。

（）3、过一点可以画一条直线。

（）4、只有一组对边平行的四边形一定是梯形。

---------------------------------------------------------------最新资料推荐------------------------------------------------------人教版四年级上册数学第五单元《平行四边形和梯形》全单元教材分析及归纳总结第五单元平行四边形和梯形一、教学内容 1．平行与垂直。

2．平行四边形和梯形。

与实验教材的主要区别：三点。

细节变化在介绍中体现二、教学目标三、具体内容（一）平行与垂直 1．例 1：认识平行与垂直。

教材去掉了情境引入，直接通过学生在平面上画任意两条直线来引入，这样编排可引导学生体会在同一平面内两条直线位置关系有相交和不相交两种情况，就能比较好地回避了重合这种情况。

分别教学平行和垂直，重点更突出、线索更清楚。

教材第一次给出了平行的记法与读法，不但可以培养学生的符号意识，而且体现了数学的简洁之美，能够与第三学段的学习做好对接。

后面量一量的活动意在通过测量，引导学生发现两条直线相交的两种情况，认识到垂直是在相交的一种特殊的位置关系，从而在感知与体验中建构垂直的概念。

教材呈现了三组不同方向的垂直情况图，加深对垂直特征的理1/ 7解，帮助学生建立垂直的表象。

2．例 2：画垂线。

本套教材删去了平行线的画法，但保留了垂线的画法，因为后边画高要用到画垂线的知识。

首先呈现了用两把三角尺或量角器来画垂线，意在尊重学生已有的知识和经验，放手让学生自己来探索画法。

接下来，通过三幅连续的动态图画已知直线的垂线的方法，重点突出了画的过程。

3．例 3：点到直线的距离和平行线间的距离相等。

首先自主尝试，亲身经历画、量、比、想的过程，从而发现点到直线间垂线段最短的这一性质，培养学生的观察与发现的能力。

然后让学生在两条平行线间画垂线。

画、测量、发现平行线间的距离相等这一特点。

做一做以生活中走斑马线为素材，使学生体验数学与生活的密切联系。

【导语】平⾏四边形和梯形是四年级学习中的⼀个重点知识章节。

以下是⽆忧考为⼤家精⼼整理的内容，欢迎⼤家阅读。

【篇⼀】⼈教版四年级上册数学《平⾏四边形和梯形》知识点 ⼀、垂直与平⾏ 1、认识平⾏和垂直 ①同⼀平⾯内的两条直线的位置关系只有两种：相交和不相交。

相交⼜有成直⾓的和不成直⾓的两种情况。

*“同⼀平⾯”是确定两条直线平⾏关系的前提，如果不在同⼀平⾯内，即便不相交，也不能称为互相平⾏。

②平⾏线：在同⼀个平⾯内不相交的两条直线叫做平⾏线，也可以说这两条直线互相平⾏。

平⾏的表⽰⽅法：a//b，读作a平⾏于b。

⽣活中平⾏的例⼦：窗户相对的框，⿊板相对的两条边，公路上的斑马线...... ③垂直：如果两条直线相交成直⾓，就说这两条直线互相垂直，其中⼀条直线叫做另⼀条直线的垂线，这两条直线的交点叫做垂⾜。

垂直的表⽰⽅法：ab ⽣活中垂直的例⼦：三⾓尺上的两条直⾓边互相垂直...... ④三条直线的特殊关系： a//b，b//c,那么a//c：在同⼀平⾯内，如果两条直线都和第三条直线平⾏，那么这两条直线互相平⾏ ab，bc，那么a//c：在同⼀平⾯内，如果两条直线都和第三条直线垂直，那么这两条直线互相平⾏。

2、垂线的画法和性质 ①过直线上和直线外⼀点怎样画这条直线的垂线：把三⾓尺的⼀条直⾓边与已知直线重合；沿着直线移动三⾓尺，使三⾓尺的顶点和直线上的已知点重合；从直⾓的顶点起，沿着另⼀条直⾓边画出⼀条直线，这条直线就是已知直线的垂线。

②过直线外⼀点怎样画这条直线的垂线：把三⾓尺的⼀条直⾓边与已知直线重合；沿着直线移动三⾓尺，使三⾓尺的另⼀条直⾓边与直线外的⼀点重合；沿着三⾓尺的另⼀条直⾓边画⼀条直线 ③垂线的性质：从直线外⼀点到这条直线所画的垂直线段最短，它的长度叫做这点到直线的距离。

3、平⾏线的画法及运⽤ ①平⾏线的画法：固定三⾓尺，沿⼀条直⾓边先画⼀条直线；⽤直尺紧靠三⾓尺的另⼀条直⾓边，固定直尺，然后平移三⾓尺；再沿第⼀步中的直⾓边画出另⼀条直线。

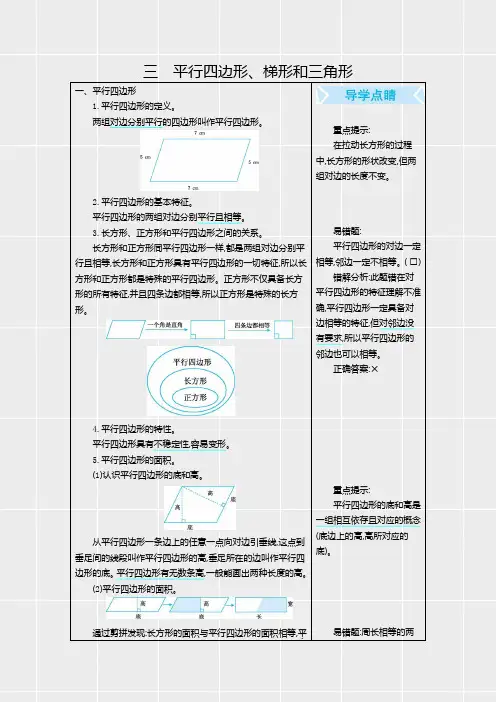
三平行四边形、梯形和三角形一、平行四边形1.平行四边形的定义。

两组对边分别平行的四边形叫作平行四边形。

2.平行四边形的基本特征。

平行四边形的两组对边分别平行且相等。

3.长方形、正方形和平行四边形之间的关系。

长方形和正方形同平行四边形一样,都是两组对边分别平行且相等,长方形和正方形具有平行四边形的一切特征,所以长方形和正方形都是特殊的平行四边形。

正方形不仅具备长方形的所有特征,并且四条边都相等,所以正方形是特殊的长方形。

4.平行四边形的特性。

平行四边形具有不稳定性,容易变形。

5.平行四边形的面积。

(1)认识平行四边形的底和高。

从平行四边形一条边上的任意一点向对边引垂线,这点到垂足间的线段叫作平行四边形的高,垂足所在的边叫作平行四边形的底。

平行四边形有无数条高,一般能画出两种长度的高。

(2)平行四边形的面积。

通过剪拼发现:长方形的面积与平行四边形的面积相等,平．重点提示:在拉动长方形的过程中,长方形的形状改变,但两组对边的长度不变。

易错题:平行四边形的对边一定相等,邻边一定不相等。

( )错解分析:此题错在对平行四边形的特征理解不准确,平行四边形一定具备对边相等的特征,但对邻边没有要求,所以平行四边形的邻边也可以相等。

正确答案:✕重点提示:平行四边形的底和高是一组相互依存且对应的概念(底边上的高,高所对应的底)。

易错题:周长相等的两行四边形的底等于长方形的长．．．．．．．．．．．．．;．平行四边形的高等于长方形的．．．．．．．．．．．．．宽．。

长方形的面积=长×宽平行四边形的面积=底×高如果用S表示平行四边形的面积,a和h分别表示平行四边形的底和高,那么平行四边形的面积的字母公式为S=ah。

二、梯形1.梯形的定义。

只有一组对边平行的四边形叫作梯形。

2.平行四边形和梯形的异同点。

相同点:都是四边形;都有平行的对边。

不同点:平行四边形的两组对边分别平行且相等;梯形只有一组对边平行,且平行的这组对边不相等。