反常积分敛散性的导数自比法

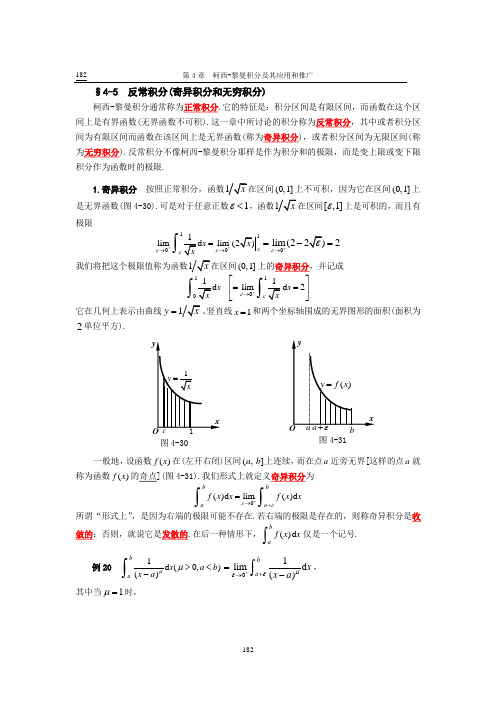
第4章柯西-黎曼积分及其应用和推广182§4-5 反常积分(奇异积分和无穷积分)柯西-黎曼积分通常称为正常积分.它的特征是：积分区间是有限区间，而函数在这个区间上是有界函数(无界函数不可积).这一章中所讨论的积分称为反常积分，其中或者积分区间为有限区间而函数在该区间上是无界函数(称为奇异积分)，或者积分区间为无限区间(称为无穷积分).反常积分不像柯西-黎曼积分那样是作为积分和的极限，而是变上限或变下限积分作为函数时的极限.1.奇异积分按照正常积分，函数在区间]1,0(上不可积，因为它在区间]1,0(上是无界函数(图4-30).可是对于任意正数1ε<，函数在区间[,1]ε上是可积的，而且有极限1100lim limxεεεε++→→=⎰0lim(22ε+→=-=我们将把这个极限值称为函数]1,0(上的奇异积分，并记成1x⎰1lim2xεε+→⎡⎤==⎢⎥⎣⎦⎰它在几何上表示由曲线y=竖直线1=x和两个坐标轴围成的无界图形的面积(面积为2单位平方).一般地，设函数)(xf在(左开右闭)区间],(ba上连续，而在点a近旁无界[这样的点a就称为函数)(xf的奇点](图4-31).我们形式上就定义奇异积分为()d lim()db ba af x x f x xεε+→+=⎰⎰所谓“形式上”，是因为右端的极限可能不存在.若右端的极限是存在的，则称奇异积分是收敛的；否则，就说它是发散的.在后一种情形下，()dbaf x x⎰仅是一个记号.例201d(0,)()bax a bx aμμ><-⎰01lim d()baxx aμεε++→=-⎰，其中当1μ=时，图4-31图4-30§4-5 反常积分（奇异积分和无穷积分）1831d ln()ln()ln (0)bb a a x x a b a x aεεεε+++=-=--→+∞→-⎰当1μ>时，111d ()()1bb a a x x a x a μμεεμ-++=---⎰111()(0)1b a μμεεμ--+⎡⎤=--→+∞→⎣⎦- 当1μ<时，111d ()()1bb a a x x a x a μμεεμ-++=---⎰111()1b a μμεμ--⎡⎤=--⎣⎦-1()(0)1b a μεμ-+-→→-综上所述：当1<μ时，奇异积分1d ()ba x x a μ-⎰收敛； 当1≥μ时，奇异积分1d ()bax x a μ-⎰发散.【注】当0≤μ时，1d ()bax x a μ-⎰是正常积分.计算正常积分的牛顿—莱布尼茨公式、换元积分法和分部积分法等，都可以转移到奇异积分上来.例如，若函数)(x f 在区间],(b a 上连续(a 是奇点)，)(x F 是它的一个原函数，则有()d ()()()bb aaf x x F x F b F a +==-⎰其中)(lim )(x F a F ax +→+=. 而且，当有极限)(lim )(x F a F ax +→+=时，奇异积分收敛；当没有极限)(lim )(x F a F ax +→+=时，奇异积分发散.因此，例20就可以做成1d ()ba x x a μ-⎰(1)1d ln()bb aaxx a x aμ++=====--⎰ln()()b a =---∞=+∞(*)1d ()bax x a μ-⎰(1)111d ()1()bbaaxx a x a μμμμ++≠-====---⎰11()(1)1()(1)1b a b a μμμμμμ--⎧->+∞=+∞⎪-⎪=⎨-⎪<⎪-⎩事实上，奇异积分与正常积分是相通的．．．．．．．．．．．．．，因为有时奇异积分经过换元会变成正常积分，反过来也是如此.例如，(*)在扩充实数系中，规定±∞=±∞+)(x .第4章 柯西-黎曼积分及其应用和推广1841x ⎰(奇异积分)1[212d 1t t t +⎰(正常积分)同样，若函数)(x f 在(左闭右开)区间),[b a 上连续且点b 是奇点(图4-32)，则也可形式上定义奇异积分()d lim()d bb aaf x x f x x εε+-→=⎰⎰而且它的收敛性也是根据右端是否有极限来确定.像例20 那样，可以证明奇异积分1d ()()bax a b b x μ<-⎰当1<μ时收敛，而当1≥μ时发散. 积分的上下限可能同时都是被积函数的奇点，当奇异积分收敛时，就可以像正常积分那样去计算.例如111arcsin arcsin 1arcsin(1)x x--==--⎰22ππ⎛⎫=--=π ⎪⎝⎭,或111022arcsin x x x-==⎰⎰2arcsin 10=-=π,(偶函数的积分)或12[sin ]12d x t x t t ππ=--π-π=======π⎰⎰⎰.(换元积分法)函数的奇点也可能出现在积分区间的内部.譬如，若点),(b a c ∈是函数)(x f 的奇点，而且函数)(x f 在区间),[c a 和],(b c 上连续，则可形式上定义奇异积分()d ()d ()d bcbaacf x x f x x f x x =+⎰⎰⎰请注意，只有当右端两个奇异积分都收敛时，才能说左端的奇异积分是收敛的.换句话说，只要右端至少有一个积分是发散的，则左端的积分就是发散的.因为奇异积分实际上是函数的极限，所以有下面的结论：⑴若奇异积分()d ba f x x ⎰和()d bag x x ⎰都收敛，则[]()()d baf xg x x αβ±⎰也收敛，且有[]()()d ()d ()d bbb aaaf xg x x f x x g x x αβαβ±=±⎰⎰⎰(线性运算性质)⑵若奇异积分()d baf x x ⎰和()d bag x x ⎰中有一个收敛，另一个发散，则[]()()d baf xg x x ±⎰必发散.图4-32§4-5 反常积分（奇异积分和无穷积分）185但是请读者注意，若奇异积分()d ba f x x ⎰和()d ba g x x ⎰都发散时，则[]()()d baf xg x x ±⎰有可能收敛.在许多理论问题中，只需要知道一个奇异积分是否收敛，而不需要知道它收敛时的积分值(甚至有时就根本求不出它的积分值).在这种情形下，就需要下面的柯西判别法.柯西判别法 设函数)(x f 在区间],(b a 上连续(a 是奇点).若有某个正数1<μ和某个正数A ，使()()()A f x a x b x a μ≤<≤- (4-22)则奇异积分()d baf x x ⎰收敛；相反，若有某个1μ≥和某个正数A ，使()()()A f x a x b x a μ≥<≤- (4-23)则奇异积分()d baf x x ⎰发散.证 当满足条件(4-22)时，则有μμμ)(2)()()()(0a x A a x A x f a x A x f -≤-+≤-+≤)(b x a ≤<于是，对于任意正数a b -<ε，根据积分单调性，有10()d 2d ()()bba a Af x x A x x a x a μμεε++⎡⎤≤+≤⎢⎥--⎣⎦⎰⎰112()2d 1()baA b a Ax M x a --≤==--⎰μμμ其中右端是与ε无关的正常数，即作为ε的函数()()d ()ba Ag f x x x a μεε+⎡⎤=+⎢⎥-⎣⎦⎰)0(a b -<<ε有上界； 又当+→0ε时，函数)(εg 是增大的，所以有极限(单调有界原理)0lim ()g εε+→=lim ()d ()ba A f x x x a μεεε+→+⎡⎤+⎢⎥-⎣⎦⎰()d ()baAf x x x a μ⎡⎤=+⎢⎥-⎣⎦⎰)1(<μ 因此，也有极限0lim()d ba f x x εε+→+⎰lim ()d ()()ba A A f x x x a x a μμεε+→+⎧⎫⎡⎤⎪⎪=+-⎨⎬⎢⎥--⎪⎪⎣⎦⎩⎭⎰ lim()d ()ba Af x x x a μεεε+→+⎡⎤=+⎢⎥-⎣⎦⎰0lim d ()ba A x x a μεε+→+--⎰()d ()baA f x x x a μ⎡⎤=+⎢⎥-⎣⎦⎰d ()baA x x a μ--⎰即奇异积分()d baf x x ⎰收敛.其次，当条件(4-23)满足时，函数)(x f 不变号[因为)(x f 是连续函数]，不妨认为第4章 柯西-黎曼积分及其应用和推广186 ()0f x >)(b x a ≤<.根据例20，则有()d lim()d bbaa f x x f x x εε+→+=⎰⎰(1)1lim d ()ba A x x a μμεε+≥→+⎡⎤≥====+∞⎢⎥-⎣⎦⎰即奇异积分()d baf x x ⎰发散.我们当然可以把上面的结论及其证明类比到上限b 是奇点的情形.作为习题，请你证明下面的柯西判别法：设函数()f x 在区间),[b a 上连续(b 是奇点).若有某个正数1<μ和某个正数A ，使()()()Af x a x b b x μ≤≤<- 则奇异积分()d baf x x ⎰收敛；相反，若有某个1μ≥和某个正数A ，使()()()A f x a x b b x μ≥≤<-则奇异积分()d baf x x ⎰发散.例21研究奇异积分10x ⎰的敛散性.解 点0和点1都是奇点.为了研究它的敛散性，需要把它分成两个积分，使每一个积分只含有一个奇点，即1x =⎰1/2x +⎰11/2x ⎰（0是奇点） （1是奇点）在右端第一个积分中，因为102x ⎛⎫=≤<≤ ⎪⎝⎭根据柯西判别法，所以右端第一个积分收敛；在右端第二个积分中，因为112x ⎛⎫=≤≤< ⎪⎝⎭（注意上限1是奇点） 根据柯西判别法，所以右端第二个积分也收敛.因此，奇异积分1x ⎰收敛.2.无穷积分 在计算某些几何量或物理量时，有时会遇到无限区间上的“积分”，即()d af x x +∞⎰，或()d bf x x -∞⎰，或()d f x x +∞-∞⎰它们都不是正常积分中那种积分和的极限，而是变上(下)限积分(看作函数时)的极限.例如图4-33中那个由曲线21y x =与O x 轴和直线1x =围成的无界图形的面积，规定为极限§4-5 反常积分（奇异积分和无穷积分）187211d x x +∞=⎰211limd bb xx →+∞⎰11lim bb x →+∞⎛⎫=- ⎪⎝⎭1lim 11b b →+∞⎛⎫=-= ⎪⎝⎭(单位平方) 是合理的.再如放置在原点O 处带有正电量q 的点电荷，在它周围产生有静电场(图4-34).今有单位正电荷，它到原点的距离为a ，并在电场力的作用下移动的距离为r 时，电场力所做的功为211d a raqx q a a r x μμ+⎛⎫=- ⎪+⎝⎭⎰因为通常把无穷远处的电位看作零，所以点a 处的电位是211()limd lim a rr r aqq U a x q a a r a x μμμ+→+∞→+∞⎛⎫==-=⎪+⎝⎭⎰还有，当用换元积分法计算正常积分时，经过换元有时也会遇到无穷积分.例如，tan 2212d d 1sin (1)x t x t xt ⎡⎤=⎢⎥π+∞⎣⎦=====++⎰⎰]d 12d ,12[sin 22t tx tt x +=+=因此，我们有必要来定义无穷积分.虽然这种积分不是用积分和的极限定义的正常积分，但是它与正常积分是相通的.设函数)(x f 在区间),[+∞a 上连续.形式上就定义无穷积分为()d lim()d bb aaf x x f x x +∞→+∞=⎰⎰所谓“形式上”，是因为右端的极限可能不存在.若右端的极限是存在的，则称无穷积分是收敛的；否则，就说它是发散的.在后一种情形下，()d af x x +∞⎰仅是一个记号.类似地，也可形式上定义无穷积分()d lim()d bba af x x f x x →-∞-∞=⎰⎰和()d lim()d lim()d ()d ()d cb c a b accf x x f x x f x x f x x f x x +∞+∞→-∞→+∞-∞-∞=+=+⎰⎰⎰⎰⎰并且规定：图4-33O· q · a a +r· x图4-34第4章 柯西-黎曼积分及其应用和推广188+∞-∞⎰()d f x x 是收敛的，当且仅当-∞⎰()d cf x x 和+∞⎰()d cf x x 都是收敛的.请读者注意，不能把其中的无穷积分()d f x x +∞-∞⎰理解为极限()d lim()d aa af x x f x x +∞→+∞-∞-=⎰⎰因为右端极限存在时，而左端的无穷积分有可能不收敛.例如li ms i n d 0aa a xx -→+∞=⎰，但s i n d x x +∞-∞⎰不收敛.例22ed limed limd (e)b bxxxb b x x x x x +∞---→+∞→+∞==-⎰⎰⎰lim e e b x x b x --→+∞⎡⎤=--⎣⎦lim e e 10011b bb b --→+∞⎡⎤=--+=++=⎣⎦ 注意，其中()lim e (0)0b b b -→+∞-∞⋅=是根据洛必达法则.计算正常积分的牛顿—莱布尼茨公式，也可以转移到无穷积分上来.若函数)(x f 在区间),[+∞a 上连续，)(x F 为它的一个原函数，则()d ()()()aaf x x F x F F a +∞+∞==+∞-⎰其中记号)(lim )(x F F x +∞→=+∞.若有极限)()(lim +∞=+∞→F x F x ，则无穷积分()d af x x +∞⎰是收敛的；否则，它就是发散的.因此，例22就可以直接做成ed ed [e e ]1xxx x x x x xx +∞+∞+∞----==--=⎰⎰其中原函数在上限的值当然是指它在无穷远处．．．．．．)(+∞的极限．．．.类似地，像下面这样的演算也是合法的，即2211d d arctan 2211x xxx x+∞+∞+∞-∞-∞-∞ππ⎛⎫===--=π ⎪++⎝⎭⎰⎰ 或222111d 2d 2d 111x x xx x x+∞+∞+∞-∞==+++⎰⎰⎰02arctan 22x+∞π==⋅=π（偶函数的积分）正常积分中的换元积分法和分部积分法，也可以转移到无穷积分上来.例如，若函数()f x 和()g x 都有连续导数，则有()d ()()()()d ()aaaf xg x f x g x g x f x +∞+∞+∞=-⎰⎰因此，例22也可以做成§4-5 反常积分（奇异积分和无穷积分）189ed d (e)[e](e )d xxxx x x x x x +∞+∞+∞+∞----=-=---⎰⎰⎰e1x+∞-=-=例23 在含参数μ的无穷积分1d (0)ax a xμ+∞>⎰中，若1μ>，则11111d 11x x aax xaxμμμμμ+∞=+∞--===--⎰；若1μ≤，则1(1)ln 1d 1(1)1x x a x ax a x x x x μμμμμ=+∞+∞==+∞-=⎧==+∞⎪=⎨<=+∞⎪-⎩⎰因此，当1μ>时，它收敛；当1≤μ时，它发散.因为无穷积分实际上也是函数的极限，根据函数极限的运算性质，所以有下面的结论：⑴ 若无穷积分()d a f x x +∞⎰和()d a g x x +∞⎰都收敛，则[]()()d af xg x x αβ+∞±⎰也收敛，且有[]()()d ()d ()d aaaf xg x x f x x g x x αβαβ+∞+∞+∞±=±⎰⎰⎰(线性运算性质)⑵ 若无穷积分()d a f x x +∞⎰和()d ag x x +∞⎰中有一个收敛，另一个发散，则[]()()d af xg x x +∞±⎰必发散.但是请读者注意，若无穷积分()d a f x x +∞⎰和()d ag x x +∞⎰都发散时，则[]()()d af xg x x +∞±⎰有可能收敛.在许多理论问题中，只需要知道一个无穷积分是否收敛，而不需要知道它收敛时的积分值(甚至有时就根本求不出它的积分值).在这种情形下，像奇异积分那样，就需要下面的柯西判别法.柯西判别法 设函数)(x f 在区间),[+∞a 上连续(0)a >.若有某个正数1>μ和某个正数A ，使)0()(+∞<≤<≤x a xA x f μ(4-24)则无穷积分()d af x x +∞⎰收敛；相反，若有某个正数1μ≤和某个正数A ，使()(0)A f x a x x μ≥<≤<+∞ (4-25)则无穷积分()d af x x +∞⎰发散.第4章 柯西-黎曼积分及其应用和推广190 证 当满足条件(4-24)时，有μμμxA xA x f xA x f 2)()(0≤+≤+≤ )0(+∞<≤<x a于是，对于a b >，根据积分单调性，有110()d 2d 2d bbaaaA f x x A x Ax x x x μμμ+∞⎡⎤≤+≤≤⎢⎥⎣⎦⎰⎰⎰121Aa M μμ-==-(常数)即作为上限b 的函数()()d baA g b f x x x μ⎡⎤=+⎢⎥⎣⎦⎰)0(+∞<<<b a 有上界； 又当+∞→b 时，函数)(b g 是增大的(因为被积函数是非负的)，所以有极限(单调有界原理)lim ()limb b g b →+∞→+∞=()d baA f x x x μ⎡⎤+=⎢⎥⎣⎦⎰()d aA f x x x μ+∞⎡⎤+⎢⎥⎣⎦⎰因此，也有极限lim()d limbb b af x x →+∞→+∞=⎰()d b aA A f x x x x μμ⎧⎫⎡⎤+-⎨⎬⎢⎥⎣⎦⎩⎭⎰lim()d b b aA f x x x μ→∞⎡⎤=+⎢⎥⎣⎦⎰lim d bb aA x xμ→+∞-⎰)1(>μ()d aA f x x x μ+∞⎡⎤=+⎢⎥⎣⎦⎰d aA x xμ+∞-⎰【因为右端两个积分都是收敛的】即无穷积分()d af x x +∞⎰收敛.其次，当条件(4-25)满足时，函数)(x f 不变号，不妨认为)(0)(a x x f ≥>.于是有1()d lim()d lim d bbb b aaaf x x f x x Ax x μ+∞→+∞→+∞⎡⎤=≥⎢⎥⎣⎦⎰⎰⎰1d aA x xμ+∞==+∞⎰（例23）即无穷积分()d af x x +∞⎰发散.例24 研究积分2e d x x +∞--∞⎰的收敛性.解 见图4-35，在概率论中称函数2()e x x ϕ-=为标准正态分布的密度函数.为了讨论无穷 积分2ed x x +∞--∞⎰的收敛性，需把它分成两个积分，即2ed x x +∞--∞⎰2ed x x --∞=+⎰2e d x x +∞-⎰在右端第二个积分中，根据不等式e 1(0)xx x ≥+≥，则有22e 1xx ≥+，所以图4-35§4-5 反常积分（奇异积分和无穷积分）191222110e 1ex x x-≤=≤+因此，对于任意0b >，有222110ed d d 11bbx x x x xx+∞-≤≤≤++⎰⎰⎰arctan 2x+∞π==注意到积分2e d bx x -⎰关于上限b 是单调增大的，根据函数极限的单调有界原理，必有极限22limed e d bx x b x x +∞--→+∞=⎰⎰即2e d x x +∞-⎰收敛.又积分2ed x x --∞⎰2()ed t x t t +∞=--====⎰2e d x x +∞-⎰所以2ed x x --∞⎰也收敛.因此，2e d x x +∞--∞⎰收敛.因为概率论中用到无穷积分2e d x x +∞--∞⎰，所以称它为概率积分(历史上称它为欧拉—泊松积分).在节后的附录中，进一步证明了2e d x x +∞--∞=⎰.【注】概率论中用到的是下面的结论.设函数()t ϕ在任意有限区间上可积分，且无穷积分()d xt t ϕ-∞⎰对任意(,)x ∈-∞+∞都收敛，则在概率论中就用()()d xF x t t ϕ-∞=⎰定义连续型随机变量的分布函数.等读者学习到§5-1时，就能够像正常积分那样证明：⑴函数()F x 是连续函数；⑵若()t ϕ在点x 是连续的，则()F x 在点x 可微分且()()F x x ϕ'=.3.绝对收敛和条件收敛 在正常积分中，若函数()f x 在[,]a b 上可积，则()f x 在[,]a b 上也可积(相反的结论不成立).可是在反常积分中，结论恰好相反.譬如在奇异积分中，若()d baf x x ⎰收敛（*），则()d baf x x ⎰也收敛(相反的结论不成立).这个结论的证明与柯西判别法的证明是一样的.事实上，不妨设a 为函数()f x 的奇点.因为0()()2()f x f x f x ≤+≤，所以作为ε的函数()()()d b a g f x f x x +⎡⎤=+⎣⎦⎰εε(0)b a <<-ε当0+→ε时单调增大有上界，因此有极限00lim ()lim()()d ()()d b b a ag f x f x x f x f x x ++→→+⎡⎤⎡⎤=+=+⎣⎦⎣⎦⎰⎰εεεε（*）有时称函数()f x 在[,]a b 上绝对可积。

内蒙古财经大学本科学年论文反常积分敛散性的判定方法作者陈志强学院统计与数学学院专业数学与应用数学年级2012级学号122094102指导教师魏运导师职称教授最终成绩75分目录摘要..............................................................。

(1)关键词………………………………………………。

.……。

….…………。

.1引言-—--—-———-———--——----—---————-------——-—--———-—-—-—--—---—--—-—-—-----————-—--————--—--—2一、预备知识......................................。

...。

. (2)1.无穷限反常积分…………………………。

.…….…。

…………….。

22.瑕积分........................。

..........。

(3)3。

反常积分的性质........................。

...........。

(3)二、反常积分的收敛判别法.....................................。

.. (4)1无穷积分的收敛判别 (4)（1)。

定义判别法......................。

......。

...................。

(4)（2）。

比较判别法.....................。

............................。

(4)（3）。

柯西判别法.....................。

.. (5)(4)阿贝尔判别法。

…………………..……。

…。

……………。

6（5)。

狄利克雷判别法.............................。

. (7)2瑕积分的收敛判别......................。

........................... ...。

§6.2反常积分判敛法复习：1．反常积分⎪⎩⎪⎨⎧无界函数的反常积分无穷限的反常积分2．P 积分⎰∞+ apxdx 当1>p 时收敛；当1≤p 时发散。

3. q 积分⎰-baqa x dx )(及)()( b a x b dx baq<-⎰当1<q 时收敛；当1≥q 时发散。

6.2.1无穷区间反常积分判敛法定理1(比较判别法)设),[)( ),(+∞∈a C x g x f ，且)()(0x g x f ≤≤（),[+∞∈a x ）， 则（1）当⎰∞+ )(a dx x g 收敛时，⎰∞+ )(a dx x f 也收敛； （2）当⎰∞+ )(adxx f 发散时，⎰∞+ )(adxx g 也发散。

证明：设⎰∞+ )(adxx g 收敛A 于，∵)()(0x g x f ≤≤，∴a b ≥∀，有A dx x g dx x g dx x f b I ababa=≤≤=⎰⎰⎰∞+ )()()()(∵0)()(≥='b f b I ，∴)(b I 单调不减且有上界， 故⎰+∞→+∞→=bab b dxx f b I )(lim)(lim 存在，即⎰∞+ )(adxx f 收敛。

（2）用反证法由（1）即得。

例1．判别反常积分的敛散性： （1）dxex⎰∞+-12解：∵xxee--<<20，而eedx ex x111=-=∞+-∞+-⎰，∴dxex⎰+∞-1收敛，故dxex⎰∞+-12也收敛， （2）⎰∞++0sin 1xx dx解：∵011sin 11>+≥+xxx ，而+∞=+=+∞+∞+⎰)1ln(1x xdx ，∴⎰∞++01xdx 发散，故⎰∞++0sin 1xx dx 也发散。

由于反常积分)0( >⎰∞+a xdx ap当1>p 时收敛；当1≤p 时发散。

因此在定理1中取pxx g 1)(=，即可得反常积分的极限判别法。

定理2(极限判别法)设),[)(+∞∈a C x f ，0)(≥x f ，且l x f x p x =+∞→)(lim ，则当（1）当1>p ，+∞<≤l 0时，⎰∞+ )(a dx x f 收敛； （2）当1≤p ，+∞≤<l 0时，⎰∞+ )(adxx f 发散。

反常积分敛散性的导数自比法作者：吴旻诚来源：《科技传播》2012年第24期摘要本文给出了利用导函数性质判别反常积分敛散性的导数自比法，不但对形式作了推广，也对精度作了推广，最后将结论类比到无穷级数。

关键词反常积分；敛散性；导数；无穷级数中图分类号O17 文献标识码A 文章编号1674-6708（2012）81-0120-02在反常积分的比较判别法中，如何找寻恰当的函数与所要研究的函数进行比较是最关键的，而有时这也是最难的。

所以，能否有一种判别法，无需自己寻找比较的函数而恰当利用被积函数自身的性质，就能简便判别反常积分的敛散性成为本文的主要讨论内容。

又因为无穷级数与无穷积分的敛散性密切相关，故将无穷积分的结论推广到无穷级数中也是必要的。

1 无穷积分的导数自比法定理 1 设函数为定义在上的正值一阶可导函数，若存在常数及使得当时有，则无穷积分收敛；反之，若存在常数使得当时有，则无穷积分发散。

该定理有如下极限形式：设为定义在上的正值函数，且，则无穷积分：1）当时收敛；2）当时发散。

下面对极限形式给出证明，一般形式证明类似。

证明当时，对，存在，当时，有，即，两边积分有（是与有关的常数），化简得；而无穷积分当时收敛，从而收敛。

由比较判别法知收敛，即原无穷积分收敛。

当时，可特取，亦可证原无穷积分收敛。

当时，对，存在，当时，有，即，两边积分有（是与有关的常数），化简得，而无穷积分当时发散，从而发散。

由比较判别法知发散，即原无穷积分发散。

导数自比法不仅能因比式的形式化简一些相对较复杂的题目，而且能处理符合该判别法的抽象函数。

因篇幅所限，笔者就不举例了。

此外，定理1还有如下等价形式：推论1 设函数为定义在上的正值一阶可导函数，且，则无穷积分：1）当时收敛；2）当时发散。

2 高阶导数自比法在定理1中，若为恒正无穷小量，且存在常数及使得当时有，则由洛必达（L’Hospital）法则和极限存在的保序性，可得.以此类推，我们可以得到一般的结论：推论2 设为定义在上的正值n阶可导函数，且，若存在常数及使得当时有，其中表示的n 阶导函数。