最新届高考数学立体几何(理科)专题01-线面角
- 格式:doc
- 大小:1.40 MB
- 文档页数:13

线面角的三种求法1.直接法 :平面的斜线与斜线在平面内的射影所成的角即为直线与平面所成的角。
通常是解由斜线段,垂线段,斜线在平面内的射影所组成的直角三角形,垂线段是其中最重要的元素,它可以起到联系各线段的作用。
例1 ( 如图1 )四面体ABCS 中,SA,SB,SC 两两垂直,∠SBA=45°, ∠SBC=60°, M 为 AB 的中点,求(1)BC 与平面SAB 所成的角。
(2)SC 与平面ABC 所成的角。
解:(1) ∵SC ⊥SB,SC ⊥SA,BMHSCA图1∴SC ⊥平面SAB 故 SB 是斜线BC 在平面SAB 上的射影, ∴∠SBC 是直线BC 与平面SAB 所成的角为60°。
(2) 连结SM,CM ,则SM ⊥AB,又∵SC ⊥AB,∴AB ⊥平面SCM, ∴面ABC ⊥面SCM过S 作SH ⊥CM 于H, 则SH ⊥平面ABC ∴CH 即为 SC 在面ABC 内的射影。
∠SCH 为SC 与平面ABC 所成的角。
sin ∠SCH=SH /SC∴SC 与平面ABC 所成的角的正弦值为√7/7 (“垂线”是相对的,SC 是面 SAB 的垂线,又是面 ABC 的斜线. 作面的垂线常根据面面垂直的性质定理,其思路是:先找出与已知平面垂直的平面,然后一面内找出或作出交线的垂线,则得面的垂线。
) 2. 利用公式sin θ=h /ι其中θ是斜线与平面所成的角, h 是 垂线段的长,ι是斜线段的长,其中求出垂线段的长(即斜线上的点到面的距离)既是关键又是难点,为此可用三棱锥的体积自等来求垂线段的长。
例2 ( 如图2) 长方体ABCD-A 1B 1C 1D 1 , AB=3 ,BC=2, A 1A= 4 ,求AB 与面 AB 1C 1D 所成的角的正弦值。
A 1C 1D 1H4C123BAD解:设点 B 到AB 1C 1D 的距离为h, ∵V B ﹣AB 1C 1=V A ﹣BB 1C 1∴1/3 S △AB 1C 1·h= 1/3 S △BB 1C 1·AB ,易得h=12/5设AB 与 面 A B 1C 1D 所成的角为θ,则sin θ=h /AB=4/5图23. 利用公式cos θ=cos θ1·cos θ2已知,如图,AO 是平面α的斜线,A 是斜足,OB 垂直于平面α,B 为垂足,则直线AB 是斜线在平面α内的射影。

2018届高考数学立体几何(理科)专题01-线面角------------------------------------------作者xxxx2018届高考数学立体几何(理科)专题01 线面角1.如图,等腰梯形ABCD 中, //AB CD , DE AB ⊥于E , CF AB ⊥于F ,且2AE BF EF ===, 2DE CF ==,将AED 和BFC 分别沿DE CF 、折起,使A B 、两点重合,记为点M ,得到一个四棱锥M CDEF -,点,,G N H 分别是,,MC MD EF 的中点。
(Ⅰ)求证: //GH 平面DEM ;(Ⅱ)求证: EM CN ⊥;(Ⅲ)求直线GH 与平面NFC 所成的角的大小。
2.如图,在直角梯形ABCP 中, 1,,22CP AB CP CB AB BC CP ⊥===, D 是CP 的中点,将PAD 沿AD 折起,使得PD CD ⊥。
(Ⅰ)若E 是PC 的中点,求证: AP 平面BDE ;(Ⅱ)求证:平面PCD ⊥平面ABCD ;(Ⅲ)求二面角A PB C --的大小。
3.如图,在矩形ABCD中,4∆向上AD=, E是CD的中点,以AE为折痕将DAEAB=, 2折起, D变为'D,且平面'D AE⊥平面ABCE.(Ⅰ)求证:'⊥;AD EB(Ⅱ)求二面角'--的大小.A BD E4.如图,在四棱锥P。
ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=22,BC=42,PA=2。
(1)求证:AB⊥PC;(2)在线段PD上,是否存在一点M,使得二面角MAC.D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.5.如图1,在△中,,分别为,的中点,为的中点,,.将△沿折起到△的位置,使得平面平面,如图2.(Ⅰ)求证:;(Ⅱ)求直线和平面所成角的正弦值;(Ⅲ)线段上是否存在点,使得直线和所成角的余弦值为?若存在,求出的值;若不存在,说明理由.6.已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形。
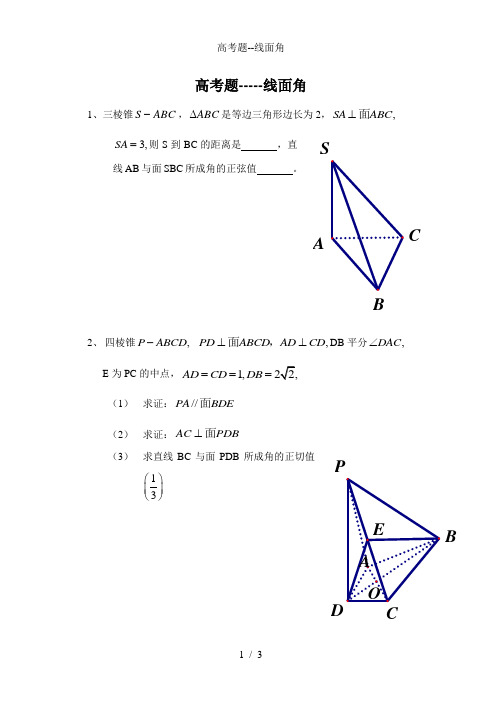
高考题-----线面角1、三棱锥S ABC -,ABC ∆是等边三角形边长为2,,SA ABC ⊥面3,SA =则S 到BC 的距离是 ,直线AB 与面SBC 所成角的正弦值 。
2、 四棱锥,P ABCD - ,PD ABCD AD CD ⊥⊥面,DB 平分,DAC ∠ E 为PC的中点,1,AD CD DB === (1) 求证://PA BDE 面 (2) 求证:AC PDB ⊥面(3) 求直线BC 与面PDB 所成角的正切值13⎛⎫ ⎪⎝⎭ACBSO E DCA BP3、,//,DC ABC EB DC ⊥面 22,AC BC EB DC ====0120,ACB ∠=P 、Q 分别为AE 、AB 的中点。
(1) 求证://PQ ACD 面(2) 求AD 与面ABE所成角的正弦值⎝⎭4、四棱锥,P ABCD -ABCD 为矩形,,1,AD PD BC ⊥= 0120,PDC ∠= 2,PD CD ==(提示:01cos1202=-)(1) 求异面直线PA 与BC 所成角的正切值。
(2) 求证:面PDC ⊥面ABCD(3) 求直线PB 与面ABCD 所成角的正弦值D C ABPQP C BDEA5、 四棱锥,S ABCD -//,,AB CD BC CD ⊥侧面SAB 是等边三角形,2,1,AB BC CD SD ====(1) 求证:SD SAB ⊥面 (2)求AD 与面SDB6、四棱锥,P ABCD -ABCD 是平行四边形,045,1,ADC AD AC ∠=== O 是AC 中点,PO=2PO ABCD M PD ⊥面,,为中点, (1) 求证://PB ACM 面 (2)求证:AD PAC ⊥面(3)求AM 与面ABCD7、 PO 垂直于圆O所在平面,PO AB 为直径,AB=2,点C 在圆上,030,CAB D AC ∠=为中点,(1) 求证:AC POD ⊥面(2)求直线OC 与面PAC所成角的正弦值3DC ABS MO DCABP AP。

1
一、解答题
1.如图所示,四棱锥中,底面,,,,,,为的中点.
(1)求证:平面; (2)求直线与平面所成角的正弦值. 2.如图,面,面,,,是的中点,
(1)求直线与所成角的大小; (2)求直线与平面所成角的余弦值。
3.如图,在直三棱柱中, 分别是棱的中点,点在线段上(包括两个端点......
)运动.
(1)当为线段的中点时,
①求证:;②求平面与平面所成锐二面角的余弦值;
(2)求直线与平面所成的角的正弦值的取值范围.
4.如图,已知三棱锥的侧棱两两垂直,且,,是的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线A E和平面OBC的所成角.
5.如图,三棱柱中,,,.
(Ⅰ)证明:;
(Ⅱ)若平面平面,,求直线与平面所成角的正弦值.
6.在菱形中,且,点分别是棱的中点,将四边形沿着转动,使得与重合,形成如图所示多面体,分别取的中点.
(Ⅰ)求证:平面;
(Ⅱ)若平面平面,求与平面所成的正弦值.
2
3。


空间角求法题型(线线角、线面角、二面角)空间角能比较集中的反映学生对空间想象能力的体现, 也是历年来高考命题者的热点, 几乎年年必考。
空间角是线线成角、线面成角、面面成角的总称。
其取值范围分别是:0° < 90°、0°< < 90°、0° < 180°。
空间角的计算思想主要是转化:即把空间角转化为平面角,把角的计算转化到三角形边角关系或是转 化为空间向量的坐标运算来解。
空间角的求法一般是:一找、二证、三求解,手段上可采用:几何法(正 余弦定理)和向量法。
下面举例说明。
一、异面直线所成的角:例1如右下图,在长方体 ABCD A i BiGD i 中,已知AB 4 , AD 3, AA 2。
E 、F 分别是线段AB 、BC 上的点,且EB FB 1。
求直线EC i 与FD i 所成的角的余弦值。
思路一:本题易于建立空间直角坐标系,uuu uuu把EC i 与FD i 所成角看作向量 EC 与FD 的夹角,用向量法求 解。
思路二:平移线段C i E 让C i 与D i 重合。
转化为平面角,放到 三角形中,用几何法求解。
(图I )uuu uju umr解法一:以A 为原点,ABAD'AA 分别为x 轴、y 轴、z 轴的•••直线EC i 与FD i 所成的角的余弦值为 --- I4解法二: 延长 BA 至点 E i ,使 AE i =I ,连结 E i F 、DE i 、D i E i 、DF , 有D i C i //E i E , D i C i =E i E ,则四边形 D i E i EC i 是平行四边形。
则 E i D i //EC i 于是/ E i D i F 为直线EC i 与FD i 所成的角。
在 Rt △ BE i F 中, E i F -J E i F 2 BF 2「5 2 i 2 「‘莎。
2018届高考数学立体几何(理科)专题01 线面角1.如图,等腰梯形ABCD 中, //AB CD , DE AB ⊥于E , CF AB ⊥于F ,且2AE BF EF ===,2DE CF ==,将AED V 和BFC V 分别沿DE CF 、折起,使A B 、两点重合,记为点M ,得到一个四棱锥M CDEF -,点,,G N H 分别是,,MC MD EF 的中点.(Ⅰ)求证: //GH 平面DEM ; (Ⅱ)求证: EM CN ⊥;(Ⅲ)求直线GH 与平面NFC 所成的角的大小.2.如图,在直角梯形ABCP中,1,,22CP AB CP CB AB BC CP⊥===P, D是CP的中点,将PADV沿AD折起,使得PD CD⊥.(Ⅰ)若E是PC的中点,求证: AP P平面BDE; (Ⅱ)求证:平面PCD⊥平面ABCD;(Ⅲ)求二面角A PB C--的大小.3.如图,在矩形ABCD 中, 4AB =, 2AD =, E 是CD 的中点,以AE 为折痕将DAE ∆向上折起, D 变为'D ,且平面'D AE ⊥平面ABCE .(Ⅰ)求证: 'AD EB ⊥; (Ⅱ)求二面角'A BD E --的大小.4.如图,在四棱锥PABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=22,BC=42,PA=2.(1)求证:AB⊥PC;(2)在线段PD上,是否存在一点M,使得二面角MACD的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.5.如图1,在△中,,分别为,的中点,为的中点,,.将△沿折起到△的位置,使得平面平面,如图2.(Ⅰ)求证:;(Ⅱ)求直线和平面所成角的正弦值;(Ⅲ)线段上是否存在点,使得直线和所成角的余弦值为?若存在,求出的值;若不存在,说明理由.6.已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)M 为AB 中点,在线段CB 上是否存在一点P ,使得//MP 平面1CNB ?若存在,求出BP 的长;若不存在,请说明理由;(2)求二面角11C NB C --的余弦值.2018届高考数学立体几何(理科)专题01 线面角(教师版)1.如图,等腰梯形ABCD 中, //AB CD , DE AB ⊥于E , CF AB ⊥于F ,且2AE BF EF ===, 2DE CF ==,将AED V 和BFC V 分别沿DE CF 、折起,使A B 、两点重合,记为点M ,得到一个四棱锥M CDEF -,点,,G N H 分别是,,MC MD EF 的中点.(Ⅰ)求证: //GH 平面DEM ; (Ⅱ)求证: EM CN ⊥;(Ⅲ)求直线GH 与平面NFC 所成的角的大小. 【答案】(1)见解析(2)见解析(3)π4试题解析:证明:(Ⅰ)连结,NG EN ,因为,N G 分别是,MD MC 的中点,所以1//,2NG CD NG CD =, 因为H 是EF 的中点, //EF CD , EF CD =,所以1//,2EH CD EH CD =,所以//,NG EH NG EH =, 所以四边形ENGH 是平行四边形,所以//GH EN ,又GH ⊄平面DEM , EN ⊂平面DEM ,所以//GH 平面DEM .以H 为原点,以,,HM HF HP 为坐标轴建立空间直角坐标系, 则()()()310,1,0,3,0,0,0,1,2,,,12E MC N ⎛⎫-- ⎪ ⎪⎝⎭,所以()333,1,0,,,12EM NC ⎛⎫==- ⎪ ⎪⎝⎭u u u u v u u u v ,所以333101032EM NC⎛⎫⋅=⨯-+⨯+⨯=⎪⎪⎝⎭u u u u v u u u v,所以EM NC⊥.解:(Ⅲ)()()310,1,0,0,0,0,,,132F H G⎛⎫⎪⎪⎝⎭,所以()3133,,1,0,0,2,,,13232HG PC NC⎛⎫⎛⎫===-⎪ ⎪⎪ ⎪⎝⎭⎝⎭u u u v u u u v u u u v,所以2cos,2n HGn HGn HG⋅==⋅u u u vvu u u vvu u u vv,所以直线GH与平面NFC所成角的正弦值为22,所以直线GH与平面NFC所成角为π4.2.如图,在直角梯形ABCP中,1,,22CP AB CP CB AB BC CP⊥===P, D是CP的中点,将PADV沿AD折起,使得PD CD⊥.(Ⅰ)若E是PC的中点,求证: AP P平面BDE;(Ⅱ)求证:平面PCD⊥平面ABCD;(Ⅲ)求二面角A PB C--的大小.【答案】(1)见解析(2)见解析(3)23π(Ⅱ)由已知可得,,AD PD AD CD⊥⊥又因为,,PD CD D PD CD⋂=⊂平面,PCD所以AD⊥平面,PCD因为AD⊂平面,ABCD所以平面PCD⊥平面.ABCD解:(Ⅲ)由(Ⅱ)知, AD⊥平面,PCD所以AD PD⊥,又因为,,PD CD AD CD D⊥⋂=所以PD⊥平面.ABCD 所以以D为原点,以,,DA DC DP所在的直线分别为x轴, y轴, z轴,建立如图所示的空间直角坐标系D xyz-,所以()2,0,2AP =-u u u v ,()0,2,0AB =u u u v ,()()2,0,0,0,2,2BC PC =-=-u u u v u u u v .设平面APB 的法向量为(),,m x y z =v, 所以0,{ 0.m AP m AB ⋅=⋅=u u uv v u u u v v 即20,{220.y x z =-+=令1x =,解得()1,0,1m =v. 设平面PBC 的法向量为(),,n a b c =v ,所以0,{0.n CP n BC ⋅=⋅=u u u v v u u u v v 即220,{ 20.b c a -=-=令1b =,解得()0,1,1n =v. 所以1001111cos ,222n m ⨯+⨯+⨯〈〉==⋅v v. 由图可知,二面角A PB C --为钝角,所以二面角A PB C --的大小为23π. 3.如图,在矩形ABCD 中, 4AB =, 2AD =,E 是CD 的中点,以AE 为折痕将DAE ∆向上折起, D 变为'D ,且平面'D AE ⊥平面ABCE . (Ⅰ)求证: 'AD EB ⊥;(Ⅱ)求二面角'A BD E --的大小.【答案】(Ⅰ)证明见解析;(Ⅱ) 90o .试题解析:(Ⅰ)证明:∵AE BE 22==, AB 4=,∴222AB AE BE =+,∴AE EB ⊥,取AE 的中点M ,连结MD ',则AD D E 2MD AE ''==⇒⊥,∵ 平面D AE '⊥平面ABCE ,∴MD '⊥平面ABCE ,∴MD '⊥ BE ,从而EB ⊥平面AD E ',∴AD EB '⊥ (Ⅱ)如图建立空间直角坐标系,设()2n x y z =u u v,,为平面BD E '的法向量,则22n BE 220{ n BD'320x y x y z ⋅=-=⇒⋅=-+=u u v u u u vu u v u u u v可以取2n (1,12=-u u v ,) 因此, 12n n 0⋅=u u v u u v ,有12n n ⊥u u v u u v ,即平面ABD ' ⊥平面BD E ',故二面角A BD E -'-的大小为90o.4.如图,在四棱锥P ABCD 中,PA ⊥平面ABCD ,AD ∥BC ,AD ⊥CD ,且AD =CD =22,BC =42,(2)在线段PD上,是否存在一点M,使得二面角MACD的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.【答案】(1)见解析(2)26【解析】所以∠BAC=90°,即AB⊥AC,因为PA⊥平面ABCD,所以PA⊥AB,又PA∩AC=A,所以AB⊥平面PAC,所以AB⊥PC.(2)存在,理由如下:取BC的中点E,则AE⊥BC,以A为坐标原点,AE,AD,AP所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,则A(0,0,0),C(2,2,0),D(0,2,0), P(0,0,2),B (2,-2,0),=(0,2,-2),=(2,2,0).设=t (0<t<1),则点M的坐标为(0,2t ,2-2t),所以=(0,2t,2-2t).设平面MAC的法向量是n=(x ,y ,z),则即令x=1,得y=-1,z=,则n=.又m=(0,0,1)是平面ACD的一个法向量,所以|cos〈m,n〉|===,5.如图1,在△中,,分别为,的中点,为的中点,,.将△沿折起到△(Ⅲ)线段上是否存在点,使得直线和所成角的余弦值为?若存在,求出的值;若不存在,说明理由.【答案】(Ⅰ)见解析.(Ⅱ).(Ⅲ).【解析】试题分析:第一问根据等腰三角形的特征,可以得出,再结合面面垂直的性质定理,可以得出平面,再根据线面垂直的性质,可以得出以,之后根据面面垂直的性质和线面垂直的性质得出结果;第二问根据题中的条件,建立空间直角坐标系,利用空间向量求得结果;第三问关于是否存在类问题,都是假设其存在,结合向量所成角的余弦值求得结果.所以平面,所以.(Ⅱ)取的中点,连接,所以.由(Ⅰ)得,.如图建立空间直角坐标系.由题意得,,,,.所以,,.设平面的法向量为,则即令,则,,所以.设直线和平面所成的角为,则.所以 直线和平面所成角的正弦值为.所以.令, 整理得.解得,舍去.所以 线段上存在点适合题意,且.6.已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)M 为AB 中点,在线段CB 上是否存在一点P ,使得//MP 平面1CNB ?若存在,求出BP 的长;若不存在,请说明理由;(2)求二面角11C NB C --的余弦值.【答案】(1)存在1BP =;(2)3.()()()()()()114,0,00,0,00,0,44,4,00,8,00,8,4A B C N B C 、、、、、.(1)设平面1CNB 的法向量(),,n x y z =v ,∵()()14,4,4,4,4,0NC NB =--=-u u u v u u u u v ,∴1·4440{ ·440NC n x y z NB n x y =--+==-+=u u u v v u u u u v v ,∴令1x =,可解得平面1CNB 的一个法向量()1,1,2n =v,设()()0,0,04P a a ≤≤,由于()2,0,0M ,则()2,0,PM a =-u u u u v ,又∵//MP 平面1CNB ,∴·220PM n a =-=u u u u v v ,即1a =,∴在线段CB 上存在一点P ,使得//MP 平面1CNB ,此时1BP =;∴令1x =,可解得平面11C NB 的一个法向量()1,1,0m =v ,∴·3cos ,·36?2m n m n m n ===v v v v v v . 由图可知,所求二面角为锐角,即二面角11C NB C --余弦值为33.。