山东省烟台市2017-2018学年高三下学期高考适应性练习(一)数学(理)试题 Word版含答案

山东省烟台市2017-2018学年高考适应性练习(一)理综物理试题二、选择题(本题包括7小题，每小题给出的四个选项中，有的只有一个选项正确，有的有多个选项正确，全部选对的得6分，选对但不全的得3分，有选错或不答的得0分)14.【题文】如图所示，滑块穿在水平横杆上并可沿杆左右滑动，它的下端通过一根细线与小球相连，小球受到水平向右的拉力F的作用，此时滑块与小球处于静止状态．保持拉力F始终沿水平方向，将其大小缓慢增大，细线偏离竖直方向的角度将增大，这一过程中滑块始终保持静止，则A.滑块对杆的压力增大B.滑块受到杆的摩擦力增大C.小球受到细线的拉力大小不变D.小球所受各力的合力增大【答案】B【解析】本题主要考查共点力平衡条件以及力的合成与分解；选项A，对于滑块与小球的整体受力分析可知，竖直方向滑块对杆的压力大小等于整体的重力，因此压力不变，选项A错误；选项B，对整体分析，水平方向拉力错误！未找到引用源。

等于摩擦力，由于拉力增大，则摩擦力增大，选项B正确；选项C，有图可知，错误！未找到引用源。

，由于错误！未找到引用源。

增大，使得错误！未找到引用源。

增大，又因为错误！未找到引用源。

，故绳子拉力错误！未找到引用源。

增大，选项C错误；选项D，小球始终静止，合外力一直为零，故选项D错误；本题正确选项为B。

【题型】单选题【备注】【结束】15.【题文】如图所示，光滑水平面上有一矩形长木板，木板左端放一小物块，已知木板质量大于物块质量，t=0时两者从图中位置以相同的水平速度v0向右运动，碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来，运动过程中物块一直未离开木板，则关于物块运动的速度v随时间t变化的图象可能正确的是【答案】A【解析】本题主要考查牛顿第二定律以及速度时间图像；在木板与挡板碰撞前，物块与木板一起匀速运动，碰撞之后，物块受到木板向左的摩擦力，开始做匀减速运动直至速度减为零，之后在向左的摩擦力作用下，开始向左加速，最终与木板共速，一起向左匀速运动，故选项A正确。

山东省烟台市2017届高三数学适应性练习试题（二）理（扫描版）2017年高考适应性练习（二）理科数学参考答案一、 选择题C A C A C B B CD B 二、填空题: 11.1712. -1513. 414.215. 2 三、解答题:16．解：（1） ()2(f x =++m n)m =m m n213sin 1cos 2222x x x =+++ ………………………1分 ()331cos 22x x =-++)33x π=-+ ………………………3分令 322232k x k πππππ+≤-≤+，得5112266k x k ππππ+≤≤+， 所以()f x 的单调减区间为5112,266k k ππππ⎡⎤++⎢⎥⎣⎦，k ∈Z ． …………… 6分所以函数()y g x =图象的对称中心为(2,3)3k π+，k ∈Z . ……………12分17．（1）证明：设AB 的中点为F ，连结,DF CF ，因为ABC ABD ∆∆、为等腰直角三角形，,AC BC AD BD ==所以,AB DF AB CF ⊥⊥，又 DFCF F =，所以AB ⊥平面CFD ， ……………………2分 因为平面ABC ⊥平面ABD ，平面ABC平面ABD AB =，DF ⊂平面ABC ，,⊥DF AB所以 DF ⊥平面,ABC又EC ⊥平面ABC ，所以//DF EC .所以DF EC 、可确定唯一确定的平面ECFD . ………………………………4分 又DE ⊂平面ECFD ,DE AB ∴⊥. ……………………………6分 （2）以F 为坐标原点，建立如图所示的空间直角坐标系，则 ()2,0,0B ，()0,2,1E ，()0,0,2D ，()2,0,0A -，()4,0,0AB =，()221BE =-，，，()2,02BD =-，. ………………………………8分 00AB BE ==n n ，即设平面DBE 的法向量00BE BD ==m m ，即………………………………设二面角D BE -55m n m n=，所以二面角D BE A --的余弦值为5． ……………………………12分 18. 解：（1）设学生甲得分X 的所有取值为15,0,15,30-，03643101(15)30C C P X C =-==， 12643103(0),10C C P X C ===21643101(15)2C C P X C === ，30643101(30)6C C P X C ===. ……………………4分所以甲得分的分布列为13115)0153012301226EX =⨯+⨯+⨯+⨯=（-1. …………………………6分 （2）记事件A :“甲得分不少于15分”，记事件B :“乙得分不少于15分”．112()(15)(30)263P A P X P X ==+==+=，22333321220()()()33327P B C C =⨯⨯+⨯=. ……………………10分所以甲、乙两人中至少有一人得分大于等于15分的概率为71741()1(1())(1())1=27381P P A B P A P B =-⋅=---=-⨯. …………12分19.解：（1）由 2132n n n a a a ++=-，得2112()n n n n a a a a +++-=-，又11a =，23a =，所以212a a -=所以{}1n n a a +-是首项为2，公比为2的等比数列． …………………3分所以12nn n a a +-=，所以()()1211211122221n n n n n a a a a a a --=+-++-=++++=-.…………………6分（2）21n n a =-,()24log 2113n n b ∴=-++43n =+，()()()()()()11112121211212121212121n n n n n n n n n n c ++++---===-------，…………………8分 记数列(){}11nn n b b +-的前n 项和为n S ，则212233445()()n S b b b b b b b b =-++-+212221()n n n n b b b b -+++-+()()2222422()8411833256.2n n n b b d b b b n n n n +=+++=⨯=++=+…………………10分记数列{}n c 的前n 项和为n T ，则2122n n T c c c =+++=122321222111111111 (212121212121212)1n n n n -+⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-+- ⎪ ⎪ ⎪ ⎪--------⎝⎭⎝⎭⎝⎭⎝⎭121112121n +=---211121n +=--. ……………11分 所以数列(){}11nn n n b b c +-+的前n 项和为22113256121n n n +++--. ………12分20解：（1）()()()21111'()0x x a a x ax a f x x a x x x x--+--+-=+-==>，令()()()110h x x x a =--+=，得11x =，21x a =-，当11a ->，即2a >时，在()0,1,()1,a -+∞上，()0f x '>，在()1,1a -上()0f x '<，此时，()f x 的增区间为()0,1,()1,a -+∞，减区间为()1,1a -；当11a -=，即2a =时，在()0,+∞上()0f x '>，此时，()f x 的增区间为()0,+∞； 当011a <-<，即12a <<时，在()0,1,a -()1,+∞上()0f x '>，在()1,1a -上()0f x '<，此时，()f x 的增区间为()0,1,a -()1,+∞，减区间为()1,1a -；当10a -≤，即1a ≤时，在()1,+∞上()0f x '>，在()0,1()0f x '<，此时，()f x 的增区间为()1,+∞上单增，减区间为()0,1.…………………………5分（2）21()ln ()ln 2g x x f x a x x ax =+=+-， ()2()0a x ax ag x x a x x x -+'∴=+-=>，()g x 有两个极值点12,x x ，12,x x ∴是方程()200x ax a x -+=>的两个不相等实根，∴240a a ∆=->，且12120,0x x a x x a +=>=>， …………………………7分由()()()1212g x g x x x λ+<+，得221112221211(ln )(ln )()22a x x ax a x x ax x x λ+-++-<+，整理得 ()()()()212121212121ln 2a x x x x x x a x x x x λ++--+<+，将1212,x x a x x a +==代入得 221ln 2a a a a a a λ+--<，因为4a >，所以1ln 12a a λ>-- 于是1ln 12a a λ>--对4a ∀>恒成立， ……………………………………10分 令()1ln 12a a a ϕ=--，则()()11'42a a a ϕ>->，所以 ()'0a ϕ<，()1ln 12a a a ϕ=--在()4,+∞单减，所以 ()ln 421ln 43a ϕ<--=-,因此 ln 43λ≥-. ……………………………………13分 21. 解：（1）由题意4CP QC QP QC QF CF =+=+=>=∴点Q 的轨迹是以点,C F为焦点，焦距为4的椭圆，所以2,1a c b ===，所以点Q 的轨迹方程是2214x y += ……………………4分 （2）①设1l 的方程为(2)y k x =-， 联立方程()22142x y y k x ⎧+=⎪⎨⎪=-⎩，得2222(14)161640k x k x k +-+-=，设1l 与椭圆除()2,0A 外的另一个交点11(,)M x y ，则212164214k x k -=+，2128214k x k -=+，代入1l 的方程得12414ky k -=+，所以222824,1414k k M k k ⎛⎫-- ⎪++⎝⎭， ………………6分 因为12,l l 倾斜角互补，所以2l 的方程为1y kx =-+，联立方程组22141x y y kx ⎧+=⎪⎨⎪=-+⎩，得22(14)80k x kx +-=，设2l 与椭圆除()0,1B 外的另一个交点22(,)N x y ，则228014k x k +=+，22814kx k =+， 代入2l 的方程得2221414k y k -=+，所以222814,1414k k N k k ⎛⎫- ⎪++⎝⎭， …………………8分∴直线MN 的斜率为212112MN y y k x x -==-. ………………9分②设直线MN 的方程为12y x b =+,联立方程221412x y y x b⎧+=⎪⎪⎨⎪=+⎪⎩，得222220x bx b ++-=,由()()2222422840b b b ∆=-⨯-=->得b <<……………10分设()()1122,,,M x y N x y ，则212122,22x x b x x b +=-=-，∴12MN x =-==……11分设12,d d 分别为点,A B 到直线MN 的距离,则12d d ==()1212AMN BMN S S S MN d d ∆∆=+=+=(11b b =++-+， (12)分 当1b <<S ()20,2==,当11b -≤≤时，S 2,⎡=⎣,当1b <-时，S ()20,2=-=，∴S 的取值范围为(0,. …………………………………14分。

山东省烟台市2017届高三数学适应性练习试题（二）文（扫描版)2017年高考适应性练习（二)文科数学参考答案一、 选择题B DC A C BD B A B 二、填空题:11.17 12。

120 13. =。

①② 三、解答题:16．解:（1）由表可知，既参加跳绳又参加踢毽的同学9人,只参加踢毽的同学4人，只参加跳绳的同学7人，所以至少参加上述一项活动的同学有20人. 设“该同学至少参加上述一项活动”为事件A ，则()201402P A ==． ……4分 （2）设5名男同学为甲,1,2，3，4；4名女同学为乙，5，6,7。

所有可能的结果有:（甲，乙）,（甲，5），(甲,6），（甲,7），（1，乙)，（1,5）,（1，6），(1,7）,（2，乙),（2，5），（2，6），（2,7），（3,乙）,（3,5)，（3,6），（3，7），（4，乙），（4,5)，（4,6），（4，7），共计20种． ………………………………8分 记“男同学甲未被选中且女同学乙被选中"为事件B,则B 共包含（1,乙）,（2，乙），（3，乙），（4，乙）,共4个结果． …………10分()41205P B ∴==． ………………………………12分17。

解：（1)()f x =222cos 1x x --，2cos22x x =--2sin 226x π⎛⎫=-- ⎪⎝⎭， ……………………2分令222262k x k πππππ-≤-≤+，得,63k x k k ππππ-≤≤+∈Z ，所以()f x 的单调增区间是,,63k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z 。

…………………4分 令26x k ππ-=，可得1,122x k k ππ=+∈Z ， 所以函数()f x 的对称中心为1,2(122k k ππ⎛⎫+-∈⎪⎝⎭Z).……………6分 (2)∵(A)f =2sin 2206A π⎛⎫--= ⎪⎝⎭，∴sin 216A π⎛⎫-= ⎪⎝⎭，OAB CD EFH∵()0,A π∈∴112(,)666A πππ-∈-，2,623A A πππ∴-==， …………8分1sin 1,2ABC S bc A b ∆====4c ∴=。

2017年高考适应性练习(一)理科数学注意事项：1．本试题满分150分，考试时间为120分钟．2．使用答题纸时，必须使用0.5毫米的黑色签字笔书写，要字迹工整，笔迹清晰．超出答题区书写的答案无效；在草稿纸、试题卷上答题无效．3．答卷前将密封线内的项目填写清楚．一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个选项符合题目要求．1．设复数z 满足3iz i =-+(i 为虚数单位)，则z 的虚部为 A ．1- B ．1 C ．3 D ．3i2．已知集合{}{}26021A x x x B x x A B =-->=->⋂=，集合，则 A ．()1,3- B ．()3,1- C ．()(),32,-∞-⋃+∞ D ．()3,2-3．命题2:2,:log 0xxap e e q a b b-+>>>0>命题若，则．下列命题正确的是 A ．pB ．p q ∧C ．q p ⌝∧D ．p q ⌝∧4．在一次高中生英语口语比赛中，8名评委为学生小张打出的分数的茎叶图如右图所示，去掉一个最高分和一个最低分，所剩数据的中位数和平均数分别为A ．84.5，85B ．84，85C ．84.5，85．5D ．84，85.55．已知函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π，为了得到函数()sin g x x ω=的图象，只要将()y f x =的图象A ．向左平移4π个单位长度 B ．向右平移4π个单位长度 C ．向左平移8π个单位长度 D ．向右平移8π个单位长度6．执行右图所示的程序框图，输出的最后一组(),x y 为 A ．()27,6- B ．()27,8- C ．()81,8-D ．()243,10-7．已知两个向量a ，b 的夹角为30,a b =为单位向量，()1c ta t b b c =+-⊥，若，则实数t 的值为A ． C ．2 D ．2-8.已知函数()()()()()()()1213,1,,ln ,1x e x f x f x f x f x f f x f x x x ⎧≤====⎨>⎩，记()()2f f x …，则()2017f e 等于A ．eB ．2C ．1D ．09．过平面区域20.20,20,x y x y y +-≤⎧⎪--≥⎨⎪+≥⎩内一点P 作圆22:1O x y +=的两条切线，切点分别为A ，B ，则cos APB ∠的最大值为 A.12B.910C.1920D.1010．设函数()y f x =的定义域为D ，若对于任意1212,2x x D x x a ∈+=、当时，恒有()()122f x f x b +=，则称点(),a b 为函数()y f x =图象的对称中心．研究函数()sin 2f x x x π=+-的某一个对称中心，并利用对称中心的上述定义，可得到1234032403320172017201720172017f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值为 A ．4033- B ．4033 C ．8066- D ．8066二、填空题：本大题共有5个小题，每小题5分，共25分． 11．若()()22,xf x e f x dx -==⎰则12．从1～6这六个数字中任取4个不同数字，分别填入右图a ，b ，c ，d 表示的四个区域中，其中a 区域中的数字最大的填法种数为13．三棱柱111ABC A B C -的侧棱垂直于底面，且1,2AB BC AB BC AA ⊥===，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为14．若函数()xf x kx x e -=--没有零点，则实数k 的取值范围为15．已知双曲线()222210,0x y a b a b-=>>的左右焦点分别是12F F ，，若该双曲线顶点到渐近线的距离为1d ，焦点到渐近线的距离为2d ，且双曲线右支上总存在一点P ，使得112221sin sin d PF F d PF F ∠=∠，则离心率e 的取值范围是 三、解答题：本大题共6个小题，共75分． 16．(本小题满分12分)已知ABC ∆的内角A ，B ，C 所对的边分别是a ，b ，c ，向量(),m a b c =-与(),n a c a b =-+共线．(1)求角B 的值；(2)求函数()()4cos cos 04f x x x B π⎡⎤=-⎢⎥⎣⎦在，上的值域．17．(本小题满分12分)如图所示的几何体中，ABC ∆是边长为2的正三角形，1AA BM 、垂直于平面ABC ，且11,2BM AA N AB =为的中点． (1)求证：1A N CN ⊥；(2)若1AA =1M AC N --的余弦值．18．(本小题满分12分)某中学对高三学生开设了“职业规划”、“心理健康”、“艺术欣赏”三门校本选修课程，供学生自由选修．因课程要求不同，选修“职业规划”、“心理健康”、“艺术欣赏”可分别获得1，2，3个校本选修学分．某学生甲三门课程选修与否相互独立，选修“职业规划”、“心理健康”、“艺术欣赏”的概率依次为111234，，． (1)求学生甲至少选修两门校本选修课程的概率； (2)求学牛甲获得校本选修学分布列和数学期望．19．(本小题满分12分)设n S 为数列{}n a 的前n 项和，且()233n n S a n N *=-∈．(1)求数列{}n a 的通项公式；(2)数列{}n b 的通项公式为()41n b n n N*=+∈，若将数列{}{}nna b 与的公共项按它们在原来数列中的先后顺序排成一个新数列{}n c ，求数列9921log log n n c c +⎧⎫⎨⎬⎩⎭的前n 项和n T ．20．(本小题满分13分)已知椭圆()2222:10x y C a b a b+=>>的焦距为12,A A 为椭圆的左右顶点，点M为椭圆上不同于12,A A 的任意一点，且满足1214A M A M k k ⋅=-． (I)求椭圆C 的方程：(2)已知直线l 与椭圆C 相交于P ，Q(非顶点)两点，且有11A P A Q ⊥． (i)直线l 是否恒过一定点?若过，求出该定点；若不过，请说明理由． (ii)求2PA Q ∆面积S 的最大值．21．(本小题满分14分) 已知函数()()()ln ,af x xg x x a R x==+∈． (1)设()()()()[]1,F x f x g x x x e =+-，若F 在上的最小值为32，求实数a 的值： (2)若对任意[)()()1,x f x g x ∈+∞≤，恒成立，求实数a 的取值范围； (3)当()2n n N *≥∈时，求证：ln 2ln 3ln 1341n n n⋅⋅⋅⋅⋅⋅<+．。

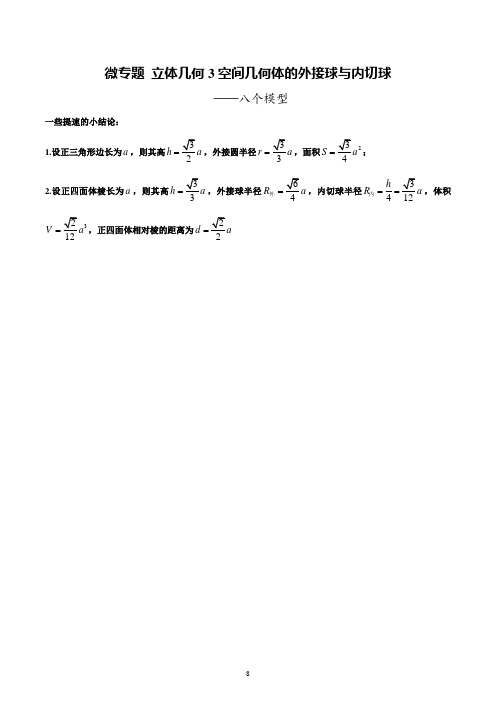
微专题 立体几何3空间几何体的外接球与内切球——八个模型一些提速的小结论：1.设正三角形边长为a ，则其高h =，外接圆半径r a =，面积2S =；2.设正四面体棱长为a ，则其高h =，外接球半径R =外，内切球半径4h R ==内，体积312V a =，正四面体相对棱的距离为2d =模型一 墙角模型模型解读：类似于三角形有且仅有唯一一个外接圆，将三角形补成平行四边形，则该平行四边形外接圆与三角形外接圆是同一个外接圆；三菱锥有且仅有一个外接球，特殊情况下，将其补成一个长方体，则该长方体与三棱锥有共同的外接球。

根据对称性，长方体体对角线即为外接球的直径。

模型公式：2222)2(c b a R ++=或2222c b a R ++=； 秒杀公式：()222S a b c π=++，()222222V ab c a b c π=++++适用情况：几何体中有三条两两垂直的棱时（非必要条件，见图3）。

（柱体适应模型1）c abCP A Babc 图2PCBAabc 图3CBPAa bc PCO 2BA典型例题例1、已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ C ） A ．π16 B ．π20 C ．π24 D ．π32例2、若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 9π 例3、若三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是 29π跟踪练习1、已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为2、若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（ A ） A.3B.6C.36D.93、（2018宝鸡模拟）已知底面边长为12的正四棱柱的各顶点均在同一个球面上，则该球的体积为（ D ）32.3A π .4B π .2C π 4.3D π4、（广东省汕头市达濠华桥中学2017-2018学年期末）《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥P ABC -为鳖臑， PA ⊥平面ABC ， 2,4PA AB AC ===，三棱锥P ABC -的四个顶点都在球O 的球面上，则球O 的表面积为（ C ）A. 8πB. 12πC. 20πD. 24π5、（2020·安徽高三（理））已知一个正方体的各顶点都在同一球面上，现用一个平面去截这个球和正方体，得到的截面图形恰好是一个圆及内接正三角形，若此正三角形的边长为a ，则这个球的表面积为（ D ）． A ．234a πB ．23a πC ．26a πD ．232a π6、（2020延安高考模拟）刘徽《九章算术•商功》中将底面为长方形，两个三角面与底面垂直的四棱锥叫做阳马．如图，是一个阳马的三视图，则其外接球的体积为（ B ）A ．B ．C ．D ．7、（2020菏泽高三模拟）已知直三棱柱的底面为直角三角形，且两直角边长分别为1和，此三棱柱的高为，则该三棱柱的外接球的体积为（ C ） A ．B ．C ．D ．8、（2020届·厦门市五月质量检测理6）某三棱锥的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的外接球的表面积为（ B ） A.9π B.27π C.81π D.108π9、已知一个三棱锥的三视图如图，其中俯视图是斜边长为2的等腰直角三角形，该三棱锥的外接球的半径为2，则该三棱锥的体积为（C ）（A ）2 （B ）43 （C ）23（D ）2210、（2017云南第二次统一检测）已知体积为6的长方体的八个顶点都在球O 的球面上，在这个长方体经过同一个顶点的三个面中，如果有两个面的面积分别为343O 的体积等于（ A ） A ．323π B ．73π C ．332πD ．1172π11、（2017江西赣州模拟）在四面体SABC 中，SA ⊥平面ABC ，∠ABC =90°，SA =AC =2，AB =1，则该四 面体的外接球的表面积为 . 8π提升练习1、在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥，若侧棱3SA =三棱锥ABC S -外接球的表面积是 。

2017-2018学年 理科数学一、选择题：本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1.已知i 是虚数单位，若复数z 满足2zi i=-，则||z =（ ）A ．2B 2.设全集U R =，若集合22{|log (4)}A x y x ==-，集合{|21,}xB y y x R ==-∈，则集合()U C AB =（ ）A ．(1,2)-B ．[1,2)-C ．(,1][2,)-∞-+∞D ．(,1)[2,)-∞-+∞3.为估测某校初中生的身高情况，现从初四.二班的全体同学中随机抽取10人进行测量，其身高数据如图所示，则这组数据的众数和中位数分别为（ ） A ．172,172 B ．172,169 C ．172,168.5 D ．169,1724.若:P x R ∀∈，不等式20x a -+>恒成立，:q x R ∀∈，不等式|1||1|x x a -++>恒成立，则p ⌝是q 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件 5.某程度框图如图所示，则输出的S 的值为（ ）A ．0 D ．6.已知,a b 为空间两条不重合的直线，,αβ为空间两个不重合的平面，则以下结论正确的是（ ）A ．若,a αβα⊥⊂，则a β⊥B ．若,a αββ⊥⊥，则//a αC ．若,//a a αβ⊂，则//αβD ．若,a a αβ⊂⊥，则αβ⊥7.若函数()f x 在定义域内满足条件：①()()0f x f x +-=；②()()0f x f x t -+<（其中0t >），则函数()f x 的解析式可以是（ ）A ．1y x x =+B ．tan y x =C ．2y x= D ．3y x = 8.已知,x y 满足线性约束条件2040240x y x y x y -≤⎧⎪+-≤⎨⎪+-≥⎩，则目标函数12x z y +=+的最小值为（ ）A ．16 B ．1110 C ．1314 D ．10119.椭圆22221(0)x y a b a b+=>>的左右焦点分别为12,F F ，若椭圆上存在一点P 使得1290F PF ∠=，且1||PF 是2||PF 和12||F F 的等差中项，则椭圆的离心率e 为（ ）A ．57 B ．23 C ．45 D ．410.设函数()f x 的定义域为R ，若不等式|()|||f x x ≤对任意的实数x 均成立，则称函数()f x 为“T ”函数，给出下列四个函数：①2122()1x f x x =+；②2()sin f x x x =；③23()ln(1)f x x =+；④4()1xxe f x e =+. 其中，“T ”函数的个数是（ ） A ．1 B ．2 C ．3 D ．4二、填空题（每题5分，满分20分，将答案填在答题纸上）11.若0sin a xdx π=⎰，则8()a x x-的展开式中的常数项为 .（用数字作答） 12.已知函数()cos(2)f x x ϕ=+的图象关于点2(,0)3π对称，若将函数()f x 的图象向右平移(0)m m >个单位得到一个偶函数的图象，则实数m 的最小值为 .13.给定两个单位向量,OA OB ，它们的夹角为60，点C 在以O 为圆心的圆弧AB 上运动，若OC xOA yOB =+，其中,x y R ∈，则xy 的最大值为 .14.已知圆22:(2)(3)1C x y -+-=，若过点(0,3)且斜率为k 的直线l 与圆C 有两个不同的交点,M N ，且845OM ON ∙=，则实数k 的值为 . 15.设定义在R 上的函数()f x 满足：1(tan )cos 2f x x=，则111()()()(0)(2)(2015)(2016)201620152f f f f f f f ++++++++= . 三、解答题 （本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.）16. （本小题满分12分）在ABC ∆中，内角,,A B C 所对的边分别为,,a b c ，b c ≠，且22sin sin cos cos C B B B C C -. （1）求角A 的大小；（2）若34a C ==，求ABC ∆的面积.17. （本小题满分12分） 已知函数()21x f x x =+，数列{}n a 的前n 项和为n S ，若112a =，1()n n S f S += *()n N ∈. （1）求数列{}n a 的通项公式；（2）设22212n nT S S S =+++，当2n ≥时，求证：142n T n<-. 18. （本小题满分12分）如图，菱形ABCD 的棱长为2，60BAD ∠=，CP ⊥底面ABCD ，E 为边AD 的中点. （1）求证：平面PBE ⊥平面BCP ；（2）当直线AP 与底面ABCD 所成的角为30时，求二面角A PB C --的余弦值.19. （本小题满分12分）甲乙两人进行象棋比赛，约定每局胜者得1分，负者得0分，若其中的一方比对方多得2分或下满5局时停止比赛，设甲在每局中获胜的概率为23，乙在每局中获胜的概率为13，且各局胜负相互独立.（1）求没下满5局甲即获胜的概率；（2）设比赛停止时已下局数为ξ，求ξ的分布列和数学期望E ξ. 20. （本小题满分12分）已知点1(,24是等轴双曲线2222:1x y C a b -=上一点，抛物线22(0)x py p =>的焦点与双曲线C 的一个焦点重合. （1）求抛物线的方程；（2）若点P 是抛物线上的动点，点,A B 在x 轴上，圆22(1)1x y +-=内切于PAB ∆，求PAB ∆面积的最小值.21. （本小题满分14分）已知函数2()ln(1)(1)f x a x b x =+-+图象上点(1,(1))P f 处的切线方程为32ln 21y x =-+-.（1）求,a b 的值，并判断()f x 的单调性；（2）若方程()0f x t -=在1[1,1]e e--内有两个不等实数根，求实数t 的取值范围（其中e 为自然对数的底数， 2.71828e =）；（3）设2()21g x x x m =-++-，若对任意的(1,2)x ∈-，()()f x g x ≤恒成立，求实数m 的取值范围.高三适应性练习（一）数学理科参考答案及评分标准一、选择题D C B B C D D A A C 二、填空题 11. 1120 12. 12π 13. 13 14.1215. 1三、解答题16．解：（1）由题意得1cos 21cos 2sin 222222C B B C ---=-, …………2分整理得112cos 22cos 22222B B C C -=-即sin(2)sin(2)66B C ππ-=-， …………………………………4分由b c ≠，得B C ≠，又(0,)B C π+∈，得2266B C πππ-+-=，故sin sin()sin cos cos sin B A C A C A C =+=+1324=+⨯=…………………………………10分 所以ABC ∆的面积为1139sin 22232S ac B ==⨯=.…12分17. 解（1）由题意可知，121n n n S S S +=+，两边取倒数得：121112n n n nS S S S ++==+， 即1112n n S S +-=，又112S =， 所以数列1{}nS 是首项为2，公差为2的等差数列，………………………………3分故122(1)2n n n S =+-=，所以12n S n =， ………………………5分当2n ≥时，111122(1)2(1)n n n a S S n n n n -=-=-=---，……………………7分 所以1,121,22(1)n n a n n n ⎧=⎪⎪=⎨⎪-≥-⎪⎩. ………………………8分（2）由（1）可知，2214n S n=， 当2n ≥时，21144(1)n n n <-， ………………………10分所以111111(11)42231n T n n <+-+-++--L 即142n T n<-， ……………………………………………………………12分18.解：（1）连接BD ，因为四边形ABCD 为棱长为2的菱形，=60BAD ∠o， 所以ABD ∆为等边三角形，又E 为边AD 的中点，所以BE AD ⊥，而//AD BC ，故BE BC ⊥； …………………………………………2分 因为CP ABCD ⊥底面，BE ABCD ⊂底面，所以BE PC ⊥，BC CP C =I ，故BE BCP ⊥平面，…………………………4分 又BE ⊂平面PBE ，所以平面PBE ⊥平面BCP . ………………5分 （2）连接AC ，因为CP ABCD ⊥底面，所以PAC ∠就是直线AP 与底面ABCD 所成的角，故=30PAC ∠o ，在t ACP ∆R 中，tan tan 30CP PAC AC ∠===o ，可得2CP =， 建立空间直角坐标系C xyz -如图，此时30BCy ∠=o ， ………………6分可得(0,0,0),(0,0,2),(1C P B A ，(1(0,0,2),(2,0,0),CB CP BA ===u u r u u r u u r………8分(1,BP =-u u r ，设(,,)x y z =n 为平面PBC 的一个法向量，则有0,0CB CP ==n n u u r u u rg g ，即020x z ⎧+=⎪⎨=⎪⎩，令y =(=-n ，同理可得平面PAB 的一个法向量=m ， ………………………10分cos ,||||7<>===m n m n m n g ，所以二面角A PB C --的余弦值为……………………………………………12分 19. 解：（1）没打满5局甲获胜有两种情况： ①是两局后甲获胜，此时1224339P =⨯=， …………………………………2分 ②是四局后甲获胜，此时122212216()333381P C =⨯⨯⨯=，……………………4分 所以甲获胜的概率124165298181P P P =+=+=. ……………………5分 （2）依题意知，ξ的所有可能值为2，4，5. ……………………6分 设前4局每两局比赛为一轮，则该轮结束时比赛停止的概率为:22215()()339+=． ……………………7分 若该轮结束时比赛还将继续，则甲、乙在该轮中必是各得一分，此时，该轮比赛结 果对下轮比赛是否停止没有影响．从而有: 5(2)9P ξ==， 4520(4)()()9981P ξ===， 2416(5)()981P ξ===， ……………………10分所以ξ的分布列为：故520162502459818181E ξ=⨯+⨯+⨯=． ……………………12分20.解：（1）将1()42代入双曲线可得，2231184a a -=，解之，218a =，22214c a a =+=， ……………………2分 由题意可知，122P =，1P =, 所以抛物线方程为22x y =. ……………………4分 （2）设00(,),(,),(,0)P x y A a o B b ，不妨设b a >． 直线PA 的方程:00()y y x a x a=--， 化简得000()0y x a x y ay +--=． ……………………6分 又圆心(0,1)到PA 的距离为1，1= ，上式化简得22200000(2)20y y a x y a y -+-=，同理有22200000(2)20y y b x y b y -+-=． ……………………8分 所以00020002222x y x a b y y y --+==--，200200022y y ab y y y --==--，则22200020448()(2)x y y a b y +--=-． ……………………10分 因00(,)P x y 是抛物线上的点，有2002x y =，则22204()(2)y a b y -=-，易知02y >，所以0022y b a y -=-． 所以00000014()(2)4222PBC y S b a y y y y y ∆=-⋅=⋅=-++--48≥+=． ……………………12分当20(2)4y -=时，上式取等号，此时004,y x ==±因此PBC S ∆的最小值为8． ……………………13分 21.解：（1）由题意可知，(1,)x ∈-+∞，()2(1)1a f x b x x '=-++，(1)4,(1)ln 242af b f a b '=-=-， 可得，432ab -=-，ln 242ln 24a b -=-， 解得：2,1a b == ……………………………………3分此时222(2)()2(1)11x x f x x x x -+'=-+=++， 因为(1,)x ∈-+∞，当(1,0)x ∈-，()0f x '>，()f x 单调递增，当(0,)x ∈+∞，()0f x '<，()f x 单调递减. …………………5分 （2）依题意，22ln(1)(1)t x x =+-+，由（1）可知， 当1(1,0)ex ∈-， ()f x 单调递增，当(0,e 1)x ∈-， ()f x 单调递减， …………………6分而(0)1f =-，211(1)2eef -=--，2(e 1)2e f -=-， 因为2222112(2e )e 40e e ----=-->， …………………8分所以1(1)(e 1)ef f ->-，要使方程()0f x t -=在1[1,e 1]e--内有两个不等实数根，只需2121e t --≤<-，所以2121et --≤<-. …………………10分（3）由()()f x g x ≤可得，222ln(1)(1)21x x x x m +-+≤-++-， 即22ln(1)3x x x m ++-≤在(1,2)x ∈-上恒成立，令2()2ln(1)3h x x x x =++-， …………………11分2221(21)(1)()23111x x x x h x x x x x --+-'=+-==+++， 当1(1,)2x ∈--时，()0h x '>，单增，1(,1)2x ∈-，()0h x '<，单减， (1,2)x ∈时，()0h x '>，单增， 又17()2ln 224h -=-，(2)2ln 32h =-， …………………13分 115()(2)2ln 6024h h --=->， 所以max 17()()ln 224h x h =-=-，所以7ln 24m ≥-. …………………14分。

2018年：高考、模拟分项专题8 农业【2018年高考题】（2018·江苏卷）二十世纪六十年代以来，我国蔗糖产业的重心从台湾不断西移，1993年后，广西甘蔗种植面积和蔗糖产量稳居全国首位。

广西地跨北回归线，其东部、北部和西北部为山地，中南部是平原。

图12为“2016年广西蔗糖产量分布示意图”。

据此回答1～2题。

（双选）1．我国蔗糖产业重心西移的主要原因是A．东部地区产业升级B．东部地区环境退化C．广西生产成本较低D．广西消费市场广阔2．广西中南部成为甘蔗种植集中区域的主要影响因素是A．技术B．资金C．地形D．气候（2018·海南卷）荷兰位于欧洲西部，利用温室无土栽培方式种植花卉、蔬菜，技术先进。

山东某蔬菜生产企业在荷兰投资兴建蔬菜生产基地，同样采用温室种植。

据此完成3～4题。

3．荷兰吸引山东蔬菜生产企业投资兴建蔬菜生产基地的优势条件是A．生产技术先进B．交通运输便捷C．自然条件优越D．生产成本低廉4．山东蔬菜生产企业在荷兰兴建蔬菜生产基地的根本目的是A．满足国内需求B．拓展国际市场C．提高研发水平D．增强国际影响（2018·天津卷）5．（21分）读图文材料，回答问题。

《京津冀协同发展规划纲要》明确了京、津、冀在协同发展中的战略定位。

（如图12文字所示）河北省为落实“京津冀生态环境支撑区”的定位，因地制宜采取了相应措施。

为保护生态环编，河北省的山区和平原地区在农业方面应分别采取何种措施？（6分）【2018年高考模拟题】(【全国百强校】宁夏银川唐徕回民中学2018届高三下学期第四次模拟考)青海省共和县塔拉滩（图甲）以戈壁沙丘为主，是黄河上游风沙危害最严重地区之一。

2011～2017年，塔拉滩地区大力发展光伏产业，建成数十个光伏企业集聚的产业园。

光伏产业发展促进了生态改善，植被不断恢复，沙丘移动明显减缓。

但植被恢复对光伏发电效率产生了不利影响，为此园区引入牧羊业（图乙），形成了良性循环。

2018届山东省烟台市高三高考适应性练习（一）试题（数学理）（含答案解析）2018年高考适应性练习（一）理科数学参考答案一、选择题BCCBCDAAADBC二、填空题 13.814.12-15.14[,]4316.①②④ 三、解答题17.解：（1）由已知可得，⎩⎨⎧=+=51221111b a b a b a ，…………………………………2分即⎩⎨⎧=⋅++=52)1(1111111b a b a b a ， 解之得⎩⎨⎧==1111b a ，……………………………………4分 {}n a 的公差为1=d ，{}n b 的公比2=q ，所以n a n =，12-=n n b ()n N *∈，……………………………………6分（2）n n n n an n b c n 2)1(2log 2log 2122-=⋅==-)(N n ∈，…………………8分 n n c c c T +⋅⋅⋅++=21n n 2)1(23222432-+⋅⋅⋅+⨯+⨯+=，15432)1(232222+-+⋅⋅⋅+⨯+⨯+=n n n T ，两式相减得，14322)1(2222+--+⋅⋅⋅+++=-n n n n T ，211222(1)24(2)212n n n n n ++-⨯=--=-+--……………………………11分 1(2)24n n T n +=-+()n N *∈.………………………………………12分18.解：（1）证明：∵平面BDFE ⊥平面ABCD ，平面BDFE ∩平面ABCD =BD ，AC ⊂平面ABCD ，AC BD ⊥，∴AC ⊥平面BDFE .………………………………………………3分又AC AFC ⊂平面,∴平面AFC ⊥平面BFE .………………………………4分（2）设AC ∩BD =O ，∵四边形ABCD 为等腰梯形，AC ⊥BD ，AB =2CD =，∴OD =OC =1，OB =OA =2，∵//FE OB 且FE OB =，∴四边形FEBO 为平行四边形，∴//OF BE ，且2OF BE ==，又∵BE ⊥平面ABCD ，∴OF ⊥平面ABCD .以O 为原点，向量,,OA OB OF 的方向分别为x 轴，y 轴，z 轴的正方向，建立如图所示的空间直角坐标系，……………………………6分则(020)B ，，，(0,1,0)D -，(0,0,2)F ，(100)C ﹣，，，(0,1,2)DF =，(1,1,0)CD =-，(0,2,2)BF =-，…………………8分设平面DFC 的一个法向量为(,,)x y z =n ， 有00DF CD ⎧=⎪⎨=⎪⎩n n ，即200y z x y +=⎧⎨-=⎩，不妨设1z =，得2x y ==-.取(2,2,1)=--n ，……………………………………10分于是cos ,2BF <>==n . 设BF 与平面DFC 所成角为θ，则sin |cos ,|2BF θ=<>=n ． ∴BF 与平面DFC所成角的正弦值为2．……………………………………12分 19.解：（1）树高在225235cm 之间的棵数为：10010.0053+0.015+0.020+0.025+0.0110=15⨯⨯⨯[-（）].……………1分树高的平均值为：0.05190+0.15200+0.2210+0.25220+0.15230+⨯⨯⨯⨯⨯0.1240+0.05250+0.05260=220.5⨯⨯⨯，……………………………………3分方差为：22220.05190220.5+0.15200220.5+0.2210220.5+0.25220220.5⨯-⨯-⨯-⨯-（）（）（）（）2+0.15230220.5+⨯-（）220.1240220.5+0.05250220.5⨯-⨯-（）（）2+0.05260220.5=304.75305⨯-≈（），…………………………………5分（2）由（1）可知，树高为优秀的概率为：0.1+0.05+0.05=0.2，由题意可知ξ的所有可能取值为0,1,2,3，033(0)0.80.512P C ξ===，123(1)0.80.20.384P C ξ==⨯=，223(2)0.80.20.096P C ξ==⨯=，333(3)0.20.008P C ξ===，……………………8分故ξ的分布列为：所以=30.20.6E ξ⨯=…………………………………………………10分（3）由（1）的结果，结合参考数据，可知=220.5μ，=17.45σ所以10.9544(255.4)(2)10.97722P X P X μσ-≤=≤+=-=.……………………12分 20.解：（1）由题意可知c =1122(,),(,)A x y B x y ，代入椭圆可得：22221122222211x y x y a b a b+=+=，，两式相减并整理可得， 2221221112y x y y b y x x x a-+⋅=--+，即22AB OD b k k a ⋅=-.……………………………2分 又因为12AB k =，12OD k =-，代入上式可得，224a b =. 又2222,3a b c c =+=，所以224,1a b ==，故椭圆的方程为2214x y +=.…………………………………………4分 （2）由题意可知，(F ，当MN 为长轴时，OP 为短半轴，此时21115=+1=||||44MN OP +；…………………………………………5分 否则，可设直线l 的方程为(y k x =+，联立2214(x y y k x ⎧+=⎪⎨⎪=⎩，消y 可得，2222(1+4)1240k x x k ++-=，则有：2121221241+4kx x x xk-+==，………………………………7分所以21124+4|||1+4kMN x xk =-=…8分设直线OP方程为1y xk=-，联立22141xyy xk⎧+=⎪⎪⎨⎪=-⎪⎩，根据对称性，不妨得(P，所以||OP==……………………10分故2222222111+41+445==+=||||4+44+44+44k k kMN OP k k k++，综上所述，211||||MN OP+为定值54.……………………………12分21.解：（1）22()(2)e(1)e((2)1)ex x xf x x a x ax x a x a'=++++=++++(1)(1)e xx x a=+++，……………………1分因为函数()f x在R上没有极值点，所以有11a--=-，解得0a=，此时2()(1)e xf x x=+，…………………………………………2分则22()ln()(1)ln(1)(1)ln(1)g x f x m x x x m x mx x=+-=+++-=++，22222()11x mx x mg x mx x++'=+=++，(i)当0m=时，在(,0)-∞上()0g x'<，单调递减，在(0,)+∞上()0g x'>，单调递增，…………………………………3分（ii）当0m≠时，令方程220mx x m++=的2440m∆=-≤，解得1m≥或1m≤-①当1m≥时，在R上()0g x'>，函数单调递增，②当1m≤-时，在R上()0g x'<，函数单调递减，……………………4分当0∆>，即11m -<<且0m =时，方程220mx x m ++=，③当01m <<>x ∈，()0g x '<，()g x 单调递减；当()x ∈-∞+∞时，()0g x '>，()g x 单调递增，………………………………………5分④当10m -<<时，11m m -+--<，当11(,)x m m--∈，()0g x '>，()g x 单调递增；当11(,),()x m m---∈-∞+∞时，()0g x '<，()g x 单调递减.……………………………………………………6分综上所述：当1m ≥或0m =时，()g x 在R 上单调递增；当1m ≤-时，()g x 在R 上单调递减；当01m <<时，()g x 在()-∞+∞单调递增，单调递减；当10m -<<时，()g x 在()-∞+∞单调递减，在单调递增.………………………………………………………………7分（2）解：令()e 1xh x x =--，令()e 10x h x '=-=，可得0x =， 当(,0)x ∈-∞时，()0h x '<，单调递减，当(0,)x ∈+∞，()0h x '>，单调递增，所以()(0)0h x h >=，即e 1x x >+，………………………………………8分因为(1,)x ∈-+∞，所以10x +>， 又当1(2,)2a ∈-时，2()10r x x ax =++>，事实上2min ()()1024a a r x r =-=->. 要证原不等式成立，只需证明不等式21x ax a ++>，即210x ax a ++->.……9分事实上，令2()1,(1,)x x ax a x ϕ=++-∈-+∞.因为12a <，二次函数()x ϕ的对称轴为1124a x =->->-，所以2min ()()124a a x a ϕϕ=-=--+， 令221()1(2)244a t a a a =--+=-++，()t a 关于a 在1(2,)2-上单调递减，所以17()()0216t a t >=>.所以min ()0x ϕ>. 所以，当122a -<<时，对于任意的(1,)x ∈-+∞， 不等式()(1)f x a x >+恒成立.…………………………12分22.解：（1）直线l 的参数方程为⎩⎨⎧α+=α+=sin 2cos 3t y t x ， 普通方程为sin cos 2cos 3sin 0x y αααα-+-=，……………………2分将x ρθρ==代入圆C 的极坐标方程θ=ρcos 2中, 可得圆的普通方程为0222=-+x y x ，………………………………4分（2）解：直线l 的参数方程为⎩⎨⎧α+=α+=sin 2cos 3t y t x 代入圆的方程为0222=-+x y x 可得： 07)sin 4cos 4(2=+α+α+t t （*），且由题意)sin (cos 421α+α-=+t t ，721=⋅t t ,………………………5分 ||||||||||1||1MB MA MB MA MB MA ⋅+=+12124|sin cos |7t t t t αα+==+.………7分 因为方程（*）有两个不同的实根，所以028)sin (cos 162>-α+α=∆，即|sin cos |2αα+>，………………………………………………8分又sin cos )[4πααα+=+∈，………………………9分所以|sin cos |(2αα+∈.因为|sin cos |αα+∈，所以4|sin cos |77αα+∈所以724||1||1772≤+<MB MA .…………………………………………10分 23.解：（1）当1=a 时，()12112+++=+++=x x x a x x f ，()⇒≤1x f 1121≤+++x x ，……………………………………1分所以⎩⎨⎧≤-----≤11211x x x 或⎪⎩⎪⎨⎧≤--+-<<-1121211x x x 或⎪⎩⎪⎨⎧≤+++-≥112121x x x ， 即⎩⎨⎧-≥-≤11x x 或⎪⎩⎪⎨⎧-≥-<<-1211x x 或⎪⎩⎪⎨⎧-≤-≥3121x x ，……………………………3分 解得1-=x 或211-<<-x 或11.23x -≤<-． 所以原不等式的解集为1{|1}3x x -≤≤-．……………………………4分 （2）因为P ⊆⎥⎦⎤⎢⎣⎡--41,1，所以当⎥⎦⎤⎢⎣⎡--∈41,1x 时，不等式()21f x x ≤-+， 即2121x a x x +++≤-+在⎥⎦⎤⎢⎣⎡--∈41,1x 上恒成立，……………………5分 当⎥⎦⎤⎢⎣⎡--∈21,1x 时，1212+-≤--+x x a x ，即2≤+a x ， 所以22≤+≤-a x ，x a x -≤≤--22在⎥⎦⎤⎢⎣⎡--∈21,1x 恒成立 所以min max )2()2(x a x -≤≤--，即251≤≤-a ……………………7分 当⎥⎦⎤⎢⎣⎡--∈41,21x 时，1212+-≤+++x x a x 即x a x 4-≤+ 所以x a x x 44-≤+≤，x a x 53-≤≤在⎥⎦⎤⎢⎣⎡--∈41,21x 恒成立 所以min max )5()3(x a x -≤≤，即4543≤≤-a ……………………9分 综上，a 的取值范围是⎥⎦⎤⎢⎣⎡-45,43.…………………………………10分。

（文数第6题图片）参考答案一、选择题B C D C B C C B A A A B二、填空题13. 6π 14. 7 15. 122n n +--16. 3 三、解答题17.解:(1)由正、余弦定理得222222223a c b a b c abc abc c+-+-+=， ………………2分即2223a abc c= ……………………………………………………4分整理得：b =……………………………………………………5分（2）由cos 2.B B =得2sin()26B π+=，即sin(+=16B π）， (0,)B π∈62B ππ∴+=3B π∴=. ……………………………………7分 2222cos b a c ac B =+- 2232a c ac ac ac ac ∴=+-≥-=3ac ∴≤（当且仅当a c == ……………………………10分11sin 32224S ac B ∴=≤⨯⨯= 所以ABC ∆ ……………………………12分18.证明:（1）取BD 中点O ，连接,OM OE ，因为,O M 分别为,BD BC 中点， 所以//OM CD 且 ………………………1分 由已知//EF AB 且12EF AB =，又在菱形ABCD 为菱形中，AB 与CD 平行其相等，所以//EF CD 且12EF CD =. ……………………………3分 于是所以EF OM //且EF OM =, 所以四边形OMEF 为平行四边形，所以//MF OE . …………………4分 又OE ⊂平面BDE 且MF ⊄平面BDE ，所以//MF 平面BDE . ……………………………6分（2）由（1）得//FM 平面BDE ，所以F 到平面BDE 的距离等于M 到平面BDE 的距离． ……………7分取AD 的中点H ，因为EA ED =，所以EH AD ⊥，因为平面ADE ⊥平面ABCD ，平面ADE 平面ABCD AD =，EH ⊂平面ADE ，所以EH ⊥平面ABCD . ………………………………………9分由已知，可得EH =BE ==所以等腰三角形BDE ∆的面积12BDE S ∆=⨯=.又因为111(44222BDM BCD S S ∆∆==⨯⨯⨯= 设F 到平面BDE 的距离为h ，由E BDM M BDE V V --=得1133BDM BDE S EH S h ∆∆⋅⋅=⋅⋅, ………………………11分即1133h ⨯=⨯⨯解得h =,即F 到平面BDE ． ………………………12分 19. 解：（1）因为参加社会实践活动的时间在)2,0[内的有1人，对应的频率为：05.02025.0=⨯, 所以样本容量1200.05n ==. …………………………2分根据频率分布直方图，该校学生每周参加社会实践活动时间的平均值为:)11025.09075.07125.0515.031.01025.0(2⨯+⨯+⨯+⨯+⨯+⨯⨯8.5=小时. ……………………………………4分（2）由题意得“不经常参加社会实践”的学生有：10.12205+⨯⨯=，所以完整的列联表：……………………………………6分所以2K 的观测值：220(41213) 5.934 3.841713155k ⨯-⨯=≈>⨯⨯⨯. …………………8 分所以能在犯错误的概率不超过0.05的前提下可以认为青少年科技创新大赛成绩优秀与经常参加社会实践活动有关系. ……………………………………9 分（3）由（2）可知不经常参加社会实践活动的有5人，其中成绩优秀的有1人，不妨设编号为1，成绩一般的学生有4人，编号依次为,,,a b c d .所有参加培训的情况有： (1,),(1,),(1,),(1,),(,),a b c d a b (,),(,),(,),(,),(,)a c a d b c b d c d ，共10种.…………………………10 分恰好一人成绩优秀的情况有(1,),(1,),(1,),(1,)a b c d ,共4种. ………………11 分 所以由古典概型计算公式得：42105=. ………………………12分 20. 解：（1）由题意可知c =1122(,),(,)A x y B x y ，代入椭圆可得：22221122222211x y x y a b a b+=+=，，两式相减并整理可得， 2221221112y x y y b y x x x a-+⋅=--+，即22AB OD b k k a ⋅=-. ……………………………2分 又因为12AB k =，12OD k =-，代入上式可得，224a b =. 又2222,3a b c c =+=，所以224,1a b ==， 故椭圆的方程为2214x y +=. …………………………4分 （2）由题意可知，(F ，当MN 为长轴时，OP 为短半轴，此时21115=+1=||||44MN OP +； ……………………………………………5分 否则，可设直线l的方程为(y k x =+，联立2214(x y y k x ⎧+=⎪⎨⎪=⎩，消y 可得，2222(1+4)1240k x x k ++-=， 设1122(,),(,)M x y N x y ，则有：22121222124,1+41+4k x x x x k k -+=-=， ………………………………7分所以21124+4|||1+4k MN x x k =-= ………………………………8分设直线OP 方程为1y x k =-，联立22141x y y x k ⎧+=⎪⎪⎨⎪=-⎪⎩，根据对称性，不妨令(P ，于是||OP == ……………………10分故2222222111+41+445=+=||||4+44+44+44k k k MN OP k k k ++， 综上所述，211||||MN OP +为定值54. …………………………………12分 21. 解：（1）当0b =时，()cos f x x a x =-.由题意，()1sin 0f x a x '=+≥对任意(0,)x ∈+∞恒成立. ……………2分 若0a =，不等式显然成立；若0a <，()max 1sin ,(0,)x x a ≤-∀∈+∞，所以10a -≤<；若0a >，()min sin ,(0,)x x a≥-∀∈+∞，所以01a <≤； 综上，a 的取值范围是[1,1]-. ………………………………………5分（2）若0b ≥，()1sin b f x a x x '=++10b ba x x>-+>≥，于是()f x 在(0,)+∞单增， 与存在12,x x 满足12()()f x f x =矛盾. 所以0b <. ……………………7分 因为12()()f x f x =，所以111222cos ln cos ln x a x b x x a x b x -+=-+, 所以()()212121ln ln cos cos b x x x x a x x --=---．不妨设120x x <<，由（1）知cos y x x =-在(0,)+∞单调递增， 所以2211cos cos x x x x ->-，即2121cos cos x x x x -<-.所以()()()21212121ln ln cos cos (1)b x x x x a x x a x x --=--->--． 又01a <<，所以212101ln ln x x b a x x ->>--． ……………………………9分下面证明2121ln ln x x x x ->-21x t x =，则1t >．于是证明上述不等式等价于证明1ln t t ->ln 0t <．事实上，设)()ln 1g t t t =>，则()210g t -'=<在(1,)+∞恒成立． 所以()g t 在(1,)+∞单调递减，故()()10g t g <=，从而ln 0t <得证．于是21211ln ln x x b a x x ->>-- ………………………12分 22. 解：（1）直线l 的参数方程为⎩⎨⎧α+=α+=sin 2cos 3t y t x ，普通方程为sin cos 2cos 3sin 0x y αααα-+-=， ……………………2分将ρθρ==代入圆C 的极坐标方程θ=ρcos 2中,可得圆的普通方程为0222=-+x y x ， ………………………………4分（2）解：直线l 的参数方程为⎩⎨⎧α+=α+=sin 2cos 3t y t x 代入圆的方程为0222=-+x y x 可得：07)sin 4cos 4(2=+α+α+t t （*），且由题意 )sin (cos 421α+α-=+t t ，721=⋅t t , ………………………5分||||||||||1||1MB MA MB MA MB MA ⋅+=+12124|sin cos |7t t t t αα+==+. ………7分 因为方程（*）有两个不同的实根，所以028)sin (cos 162>-α+α=∆，即|sin cos |αα+> ………………………………………………8分又sin cos )[4πααα+=+∈， ………………………9分所以|sin cos |αα+∈.因为|sin cos |αα+∈，所以4|sin cos |7αα+∈ 所以724||1||1772≤+<MB MA . …………………………………………10分 23. 解：（1）当1=a 时，()12112+++=+++=x x x a x x f ，()⇒≤1x f 1121≤+++x x ， ………………………………1分所以 ⎩⎨⎧≤-----≤11211x x x 或⎪⎩⎪⎨⎧≤--+-<<-1121211x x x 或⎪⎩⎪⎨⎧≤+++-≥112121x x x ， 即⎩⎨⎧-≥-≤11x x 或⎪⎩⎪⎨⎧-≥-<<-1211x x 或⎪⎩⎪⎨⎧-≤-≥3121x x ， ……………………………3分解得1-=x 或211-<<-x 或11.23x -≤<-．所以原不等式的解集为1{|1}3x x -≤≤-． ……………………………4分（2）因为P ⊆⎥⎦⎤⎢⎣⎡--41,1，所以当⎥⎦⎤⎢⎣⎡--∈41,1x 时，不等式()21f x x ≤-+，即2121x a x x +++≤-+在⎥⎦⎤⎢⎣⎡--∈41,1x 上恒成立， ……………………5分当⎥⎦⎤⎢⎣⎡--∈21,1x 时，1212+-≤--+x x a x ，即2≤+a x ，所以22≤+≤-a x ，x a x -≤≤--22在⎥⎦⎤⎢⎣⎡--∈21,1x 恒成立所以min max )2()2(x a x -≤≤--，即251≤≤-a ……………………7分 当⎥⎦⎤⎢⎣⎡--∈41,21x 时，1212+-≤+++x x a x 即x a x 4-≤+ 所以x a x x 44-≤+≤，x a x 53-≤≤在⎥⎦⎤⎢⎣⎡--∈41,21x 恒成立 所以min max )5()3(x a x -≤≤，即4543≤≤-a ……………………9分 综上，a 的取值范围是⎥⎦⎤⎢⎣⎡-45,43. …………………………………10分。