第六章 容器计量的计算方法综述
- 格式:ppt
- 大小:174.00 KB
- 文档页数:41
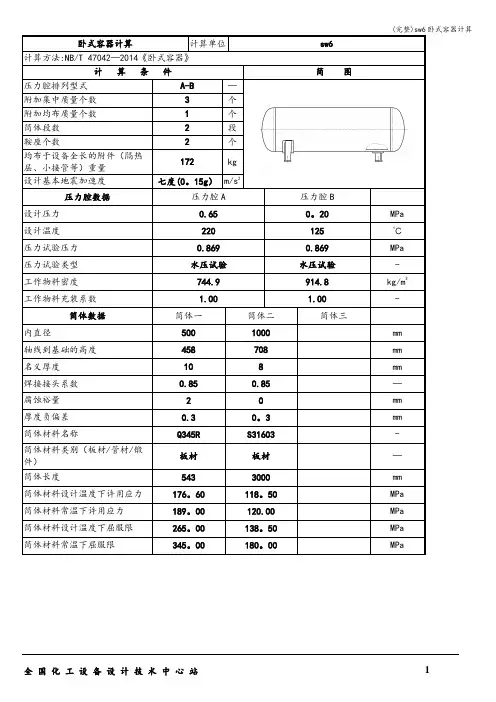
卧式容器计算计算单位sw6
计算方法:NB/T 47042—2014《卧式容器》
计算条件简图
压力腔排列型式A-B—
附加集中质量个数3个
附加均布质量个数1个
筒体段数2段
鞍座个数2个
均布于设备全长的附件(隔热
172kg
层、小接管等)重量
设计基本地震加速度七度(0。
15g)m/s2
压力腔数据压力腔A压力腔B
设计压力0.650。
20MPa 设计温度220125℃压力试验压力0.8690.869MPa 压力试验类型水压试验水压试验-工作物料密度744.9914.8kg/m3工作物料充装系数 1.00 1.00-筒体数据筒体一筒体二筒体三
内直径5001000mm 轴线到基础的高度458708mm 名义厚度108mm 焊接接头系数0.850.85—腐蚀裕量20mm 厚度负偏差0.30。
3mm 筒体材料名称Q345R S31603-
筒体材料类别(板材/管材/锻
板材板材—件)
筒体长度5433000mm 筒体材料设计温度下许用应力176。
60118。
50MPa 筒体材料常温下许用应力189。
00120.00MPa 筒体材料设计温度下屈服限265。
00138。
50MPa 筒体材料常温下屈服限345。
00180。
00MPa
a。

卧式储罐储液存量计算对于lng的计量我们采用静态计量的方法,就是通过测量储罐的液位等数据后确定其体积,再测量温度和压强的数据计算密度,然后根据体积密度与质量的关系得出储罐中储液的存量。
一、储罐中储液体积计算在计算储液体积时我们可以把储罐分成封头部分和筒体部分分别计算求和1、筒体储液体积计算要计算筒体储液体积只需计算筒体横截面(如图2)储液面积再乘以筒体计算长度即可。
(1)、筒体的横截面为一个圆形,其中储液平面为圆形水平截出的一个圆弓形(如图2)把截面置于平面直角坐标系中可得圆的方程为:S扇形=R3603°三角形ABC面积:S三角形=2√h(D−h)(R−h)2化简:S三角形=√h(D−h)(R−h 所求弓形面积为:S弓形=2arcsin√h(D−h)RπR²360−√h(D−h)(R−h)所求储液体积: V 筒= L [2arcsin√h (D−h )RπR²360−2如图3可拼成一个椭圆球体。
求液位从0到H 点的体积。
1°如图6(x−R )²R²+y²b²+z²R²=12°过x 其方程为:y²b²+z²R²=1- -(x−R )²R²整理得:y²b²(1− −(x−R )²R²)+z²R²(1− −(x−R )²R²)=1由椭圆面积公式:S = πab可得:S(x)= π√b²(1− −(x−R)²R²)*√R²(1− −(x−R)²R²)=πbR(2Rx−x²)根据积分法则求椭圆球体体积:V 封=∫S(x)dx H=πb R ∫(2Rx−x²)dx H=πb R [RH²- -13H³]3、对筒体部分储液体积和封头部分储液体积求和得出储罐储液总体积:V 总=L[2arcsin√h(D−h)RπR²360−√h(D−h)(R−h)] + πbR[RH²- -13H³]二、储罐中储液密度计算。
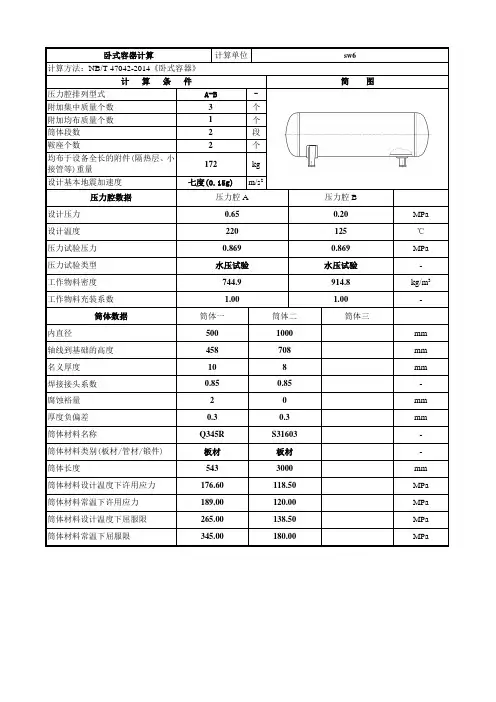
卧式容器计算计算单位sw6
计算方法:NB/T 47042-2014《卧式容器》
计算条件简图
压力腔排列型式A-B -
附加集中质量个数 3 个
附加均布质量个数1个
筒体段数2段
鞍座个数 2 个
均布于设备全长的附件(隔热层、小
172kg
接管等)重量
设计基本地震加速度七度(0.15g) m/s2
压力腔数据压力腔A压力腔B
设计压力0.65 0.20 MPa 设计温度220 125 ℃压力试验压力0.869 0.869 MPa 压力试验类型水压试验水压试验- 工作物料密度744.9 914.8 kg/m3工作物料充装系数 1.00 1.00 - 筒体数据筒体一筒体二筒体三
内直径500 1000 mm 轴线到基础的高度458 708 mm 名义厚度10 8 mm 焊接接头系数0.85 0.85 - 腐蚀裕量 2 0 mm 厚度负偏差0.3 0.3 mm 筒体材料名称Q345R S31603 - 筒体材料类别(板材/管材/锻件) 板材板材- 筒体长度543 3000 mm 筒体材料设计温度下许用应力176.60 118.50 MPa 筒体材料常温下许用应力189.00 120.00 MPa 筒体材料设计温度下屈服限265.00 138.50 MPa 筒体材料常温下屈服限345.00 180.00 MPa
注: 带#的材料数据是设计者给定的,下同。
a。
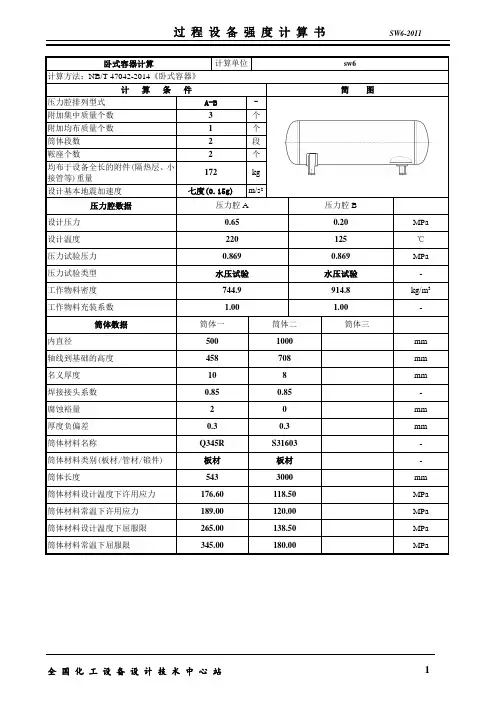
卧式容器计算计算单位sw6
计算方法:NB/T 47042-2014《卧式容器》
计算条件简图
压力腔排列型式A-B -
附加集中质量个数 3 个
附加均布质量个数1个
筒体段数2段
鞍座个数 2 个
均布于设备全长的附件(隔热层、小
172kg
接管等)重量
设计基本地震加速度七度(0.15g) m/s2
压力腔数据压力腔A压力腔B
设计压力0.65 0.20 MPa 设计温度220 125 ℃压力试验压力0.869 0.869 MPa 压力试验类型水压试验水压试验- 工作物料密度744.9 914.8 kg/m3工作物料充装系数 1.00 1.00 - 筒体数据筒体一筒体二筒体三
内直径500 1000 mm 轴线到基础的高度458 708 mm 名义厚度10 8 mm 焊接接头系数0.85 0.85 - 腐蚀裕量 2 0 mm 厚度负偏差0.3 0.3 mm 筒体材料名称Q345R S31603 - 筒体材料类别(板材/管材/锻件) 板材板材- 筒体长度543 3000 mm 筒体材料设计温度下许用应力176.60 118.50 MPa 筒体材料常温下许用应力189.00 120.00 MPa 筒体材料设计温度下屈服限265.00 138.50 MPa 筒体材料常温下屈服限345.00 180.00 MPa
a。

容器设计的数学建模计算【摘要】本题目属于在一定条件下求最优解的问题。
具体到题目是求不同形状的容器在容积一定容器表面积最小的情况下,求容器的各项参数(圆锥台的高h,上下底面半径r, R, L;圆柱高H)之间的比值,并将解的精确度进行优化的问题。
求解的大体步骤为先建立简化模型,以便于计算且使结论具有一定普遍性。
使用Autocad2007绘图软件绘制图形。
建立容器各项参数与表面积、体积的正确的的函数关系式,并使容器表面积达到最小,求出此时各项参数间的比值。
解答过程中,因出现较为复杂的函数关系式,我们将借助数学软件LINGO9.0进行编程计算,调整输出数据的精确度的有效位数,得到最优解。
【关键词】优化最小值比值理想模型1、问题重述容器的设计问题:(1).要设计一个无盖的圆锥台形状的容器,上半径为R,下半径为r<R,高为h。
求容积在一个正常数的条件下,使该容器的表面积达到最小时的两个比值r/R , h/R的精确值(用整数的有限次四则运算及根式运算的最简形式表示)及它们精确到20位有效数字的近似值。
(2).要设计一个无盖的容器,是一个半径为R,高为H的圆柱面放在一个圆锥台上组成的。
圆锥台的半径为R,下半径为r<R,高为h.求容积在一个正常数的条件下,使该容器的表面积达到最小时的三个比值r/R, h/R, H/R的精确值(意义同(1))及它们精确到20位有效数字的近似值。
(3).要设计一个无上盖的容器,是一个高为H,上半径为L,下半径为R<L的圆锥台放在高为h,上半径为R,下半径为r<R的圆锥台组成的。
求容积为一整常数的条件下,使该容器的表面积达到最小时的四个比值h/L, H/L, r/L, R/L的精确到20位有效数字的值。
2、模型假设及符号说明这虽然是一道有关容器设计的实际应用问题,而在实际生产实践中,容器是具有一定的厚度的,而因种类、工艺、功能等原因,不同的容器对厚度的要求也不尽相同,例如从原始的陶器到现代的不锈钢容器,从生活中的碗到工业炼铁的高炉,它们的厚度都不尽相同,甚至同一容器在不同部位的厚度也有所差异(如啤酒瓶的侧壁薄而底厚)。

卧式容器计算1.卧式容器的强度计算 1.1支座反力按下式计算:2mgF =式中:F —每个支座的反力,N ;m —容器质量(包括容器自身质量、充满水或充满介质的质量、所有附件质量及隔热层等质量),Kg ;g —重力加速度,取g=9.812/s m 1.2圆筒轴向应力 1.2.1 圆筒轴向弯矩计算圆筒轴向最大弯矩位于圆筒中间截面或鞍座平面上。
圆筒中间横截面上的轴向弯矩,按下式计算:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-+=L A L h L h R FL M i i a 4341)(2142221式中:1M —圆筒中间处的轴向弯矩,mm N ⋅; F —每个支座的反力,N ; L —封头切线间的距离,mm ; a R —圆筒的平均半径,2/n i a R R δ+= i h —封头曲面深度,mm ;A —鞍座底板中心线至封头切线的距离,mm鞍座平面上的轴向弯矩,按下式计算:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+---=L h AL h R L A FA M ii a 341211222式中:2M —支座处圆筒的轴向弯矩,mm N ⋅; F —每个支座的反力,N ;A —鞍座底板中心线至封头切线的距离,mm ; L —封头切线间的距离,mm ;a R —圆筒的平均半径,2/n i a R R δ+= i h —封头曲面深度,mm ; 1.2.2圆筒轴向应力计算1.2.2.1圆筒中间横截面上,由压力及轴向弯矩引起的轴向应力,按下面两式计算: 1)最高点处:ea e a c R M R p δδσ21114.32-=式中:1σ—圆筒中间处横截面内最高点的轴向应力,MPa ; c p —计算压力,MPa ;a R —圆筒的平均半径,2/n i a R R δ+= e δ—圆筒有效厚度,mm ;A —鞍座底板中心线至封头切线的距离,mm ; 1M —圆筒中间处的轴向弯矩,mm N ⋅; 2)最低点处:ea e a c R M R p δδσ21214.32+=由上面可得: 1.2.2.2鞍座平面上,由压力及轴向弯矩引起的轴向应力,按下面两式计算: 1)当圆筒在鞍座平面上或靠近鞍座处有加强圈或被封头加强(即2/a R A ≤)时,轴向应力3σ位于横截面最高点处;当圆筒未被加强时,3σ位于靠近水平中心线处:ea e a c R K M R p δδσ212314.32-=式中:3σ—支座处圆筒横截面内最高点出的轴向应力,MPa ; c p —计算压力,MPa ;a R —圆筒的平均半径,2/n i a R R δ+= e δ—圆筒有效厚度,mm ;2M —支座处圆筒的轴向弯矩,mm N ⋅;1K —系数,由JB/T4731-2005钢制卧式容器表7-1查得:1K =1)在横截面最低点处的轴向应力4σ: ea e a c R K M R p δδσ212414.32+=由上面可得: 1.2.3圆筒轴向应力的校核 对于操作状态下应满足下条件:1)计算得到41~σσ,取出最大拉应力(最大正值): {}[]t σφσσσσ≤4321,,,m a x 式中:φ—焊缝接头系数,此处取φ=[]tσ—设计温度下壳体材料的许用应力,MPa ;2)计算得到41~σσ,取出最大压应力(最小负值):}[]tac σσσσσ≤4321,,,min式中:[]tac σ—设计温度下壳体材料的轴向许用压缩应力,取[]tσ、B 中较小 者,MPa ; 对于操作状态下应满足下条件:1) 充满水未加压时计算得到41~σσ,取出最大压应力(最小负值): {}[]ac T T T T σσσσσ≤4321,,,min式中:[]ac σ—常温下容器壳体材料的轴向许用压缩应力,取0.9)(2.0p el R R 、0B 中 较小者,MPa ;2) 加压状态下计算得到41~σσ,取出最大拉应力(最大正值): {})(9.0,,,m a x 2.04321P el T T T T R R φσσσσ≤ 式中:φ—焊缝接头系数,此处取φ=)(2.0p el R R —圆筒材料在试验温度下的屈服强度或0.2%规定非比例延伸强 度,MPa ; 1.3切向剪应力1.3.1圆筒切向剪应力计算在圆筒支座处横截面上的剪应力,按下面两式计算。

根据液体体积计算方法总结
液体体积的计算是在很多实际情况中都需要进行的一项工作。
以下总结了一些常用的液体体积计算方法:
1.直接测量法
直接测量法是最简单的液体体积计算方法。
通过使用体积标尺、量杯或注射器等工具,直接测量液体的体积。
这种方法适用于较小
的液体容量。
具体步骤如下:
1.准备一个标有刻度的,如量杯。
2.将液体慢慢倒入中,使其达到所需的体积刻度。
3.读取液面高度并记录下来,即可获得液体的体积。
2.几何形状法
当液体存放在形状特殊的中时,直接测量法可能不容易实施。
这时可以利用的几何形状计算液体体积。
具体方法如下:
1.观察的形状,确定其几何特征,如圆柱体、圆锥体、矩形等。
2.根据的几何特征,使用相应的公式计算液体的体积。
3.根据的尺寸和液面高度,代入公式计算液体的体积。
3.等量代换法
等量代换法在一些特殊情况下适用,例如液体溢出或难以直接
测量的情况。
具体方法如下:
1.将中的液体全部倒入一个已知体积的中。
2.记录已知中的液体体积,设为V1.
3.将液体从已知倒回原,直到液面高度与原中的液面高度相同。
4.记录已知中剩余的液体体积,设为V2.
5.利用等量代换原理,计算原中的液体体积为V1 - V2.
以上是几种常用的液体体积计算方法。
在实际应用中,根据具
体情况选择合适的方法,并注意测量的准确性和精度。


容量初步如何用容器进行容量的比较和测量容量是一个物体所能容纳的物质的数量或容积的大小。
在日常生活中,我们经常需要进行容量的比较和测量,以便更好地掌握物质的使用和管理。
在本文中,我们将讨论容量的比较和测量的方法以及如何使用容器进行这些操作。
一、容量的比较方法容量的比较可以通过两种主要的方法进行,即直接比较和间接比较。
1. 直接比较直接比较是指将两个容器的物质量或容积直接进行对比。
在进行直接比较时,我们需要保证两个容器所测量的物质处于相同的状态,如相同的温度和压力条件下。
可以通过倾倒、倒入或逐个对比方法进行直接比较。
2. 间接比较间接比较是指使用一个已知容量的容器与另一个容器进行比较。
我们可以用一个已知容量的容器将待测量的物质逐个转移进去,然后记录所转移的次数,从而间接获得待测量物质的容量大小。
二、容量的测量方法容量的测量需要使用一些常见的工具和设备,如容器、量杯和容积瓶等。
下面介绍几种常用的测量方法。
1. 量杯测量法量杯是一种常见的容器,通常具有刻度线。
在使用量杯进行容量测量时,我们只需要将待测物质逐渐倒入量杯中,然后读取刻度线上所示的物质高度即可。
需要注意的是,读取时要保持视线与刻度线垂直,以减少误差。
2. 比重法测量容积对于一些液体物质,我们可以使用比重法来测量其容积。
这种测量方法是基于液体具有可调整比重的特性。
通过将待测物质与其他已知比重的液体混合,根据混合物的比重来间接测量物质的容积。
3. 容积瓶测量法容积瓶是用于较精确测量物质容量的一种设备。
容积瓶通常具有较窄的高颈和精确的刻度线。
在测量时,我们只需要将物质缓慢地注入容积瓶中,直到物质恰好接触刻度线为止,然后读取刻度线上所示的容量数值。
三、使用容器进行容量比较和测量的要点在进行容量比较和测量时,需要注意以下几个要点:1. 温度和压力的影响温度和压力会对容量的比较和测量结果产生影响。
因此,在进行比较和测量时,需要保持相同的温度和压力条件,以减少误差。

五种计量基准方法容量重量一、引言计量基准方法是衡量容量和重量的一种方法,它对于各个领域的应用都非常广泛。
本文将介绍五种常见的计量基准方法,包括体积、容量、质量、重力和密度。
通过深入探讨这些方法,我们可以更好地理解它们的原理和应用。
二、体积2.1 体积的定义体积是指物体所占据的三维空间的大小。
它是计量基准方法中最基本的一种,常用单位有立方米、立方厘米等。
2.2 体积的测量方法测量体积的方法有很多种,常见的有直接测量法、容器法和几何法。
直接测量法是指通过测量物体各个边长并进行计算来得到体积;容器法是指将物体放入一个已知容积的容器中,通过容器的体积变化来计算物体的体积;几何法是指通过物体的形状和尺寸来计算其体积。
2.3 体积的应用体积的应用非常广泛,例如在工程中,我们需要测量建筑物的体积以确定所需材料的数量;在化学实验中,我们需要测量溶液的体积以确定反应物的浓度;在生物学研究中,我们需要测量细胞的体积以了解其结构和功能。
三、容量3.1 容量的定义容量是指容器所能容纳的物质的量。
它是计量基准方法中用于衡量液体、气体等流体的一种方法,常用单位有升、毫升等。
3.2 容量的测量方法测量容量的方法主要有直接测量法和比较法。
直接测量法是指直接将液体或气体倒入已知容量的容器中进行测量;比较法是指将待测液体或气体与已知容量的容器进行比较来确定容量。
3.3 容量的应用容量的应用非常广泛,例如在食品加工中,我们需要测量原料的容量以确定配料的比例;在医学实验中,我们需要测量药物的容量以确定剂量;在环境监测中,我们需要测量大气中的容量以了解空气质量。
四、质量4.1 质量的定义质量是指物体所具有的惯性和重力作用下所表现出的属性。
它是计量基准方法中用于衡量物体重量的一种方法,常用单位有千克、克等。
4.2 质量的测量方法测量质量的方法有很多种,常见的有天平法、弹簧测力计法和电子秤法。
天平法是指通过比较待测物体和已知质量的物体之间的平衡状态来确定质量;弹簧测力计法是指通过测量物体所受弹簧的伸缩量来确定质量;电子秤法是指通过电子秤测量物体所受重力的大小来确定质量。

体积法立管压力法体积法和立管压力法是两种常用的测量液体体积的方法。
它们广泛应用于化学、生物、医药和科学研究等领域,具有高精度和可靠性的特点。
本文将分别介绍体积法和立管压力法的原理、应用以及优缺点,并对两种方法进行比较。
一、体积法体积法是一种通过测量液体体积的方法。
它基于物质的体积不变性原理,即在一定温度和压力下,物质的体积保持不变。
在实际应用中,常用的体积法包括滴定法、容量测量法和比重瓶法等。
滴定法是一种通过加入滴定液直至与待测液体完全反应,并根据滴定液的体积来确定待测液体体积的方法。
滴定法可以用于测定化学反应中的滴定剂的浓度、氧化还原反应中活性氧化剂和还原剂的摩尔比以及含量等。
容量测量法是一种通过利用容器的容积特性来确定待测液体体积的方法。
常用的容量测量器包括皮尔斯皿、烧瓶、量筒和容积管等。
容量测量法较为简单,精度较高,广泛应用于科学实验和生产中。
比重瓶法是一种通过测量液体密度来确定液体体积的方法。
它基于物质的密度与质量之间的关系,通过测量质量、容器容积以及液体密度的比值来确定液体体积。
比重瓶法适用于各种固体和液体的密度测量。
体积法具有测量快速、操作简单、精度高等优点,适用于大多数液体体积的测量。
但是,体积法在实际应用中也存在一些问题,比如操作难度较大、仪器设备要求较高以及测量液体性质的限制等。
二、立管压力法立管压力法又称作差压法,是一种通过测量液体在立管中的压力差来确定液体体积的方法。
它基于液体在重力作用下的压力差与液体高度之间的关系,通过测量液体的压力差,再结合相关的公式来计算液体体积。
立管压力法适用于各种液体的体积测量,无需考虑液体的性质。
常用的立管压力计包括水银压力计、酒精压力计和压电传感器等。
立管压力法具有测量快速、操作简单、精度高等优点,并且无需特殊的仪器设备。
然而,立管压力法也存在一些限制,比如需要考虑液体的表面张力、温度对密度的影响以及压力的误差等。
此外,立管压力法对于气体和不易流动的液体的测量有一定的限制。
学习计量新方法——读文献综述自己在求学时期尤其是读博士期间,从文献综述中受益良多。
我的博士学位论文选题方向是贫困地区农户借贷行为实证研究,读到一篇文献:Martin Petrick, Empirical Measurement of Credit Rationing in Agriculture: A Methodological Survey, Agricultural Economics, Vol.33, Issue 2, 2005。
说到这里,懂行的人一定能理解我当时看到这篇文献的兴奋和喜悦。
现在,不管是博士生还是研究生写点实证论文,都要整点数据,做一些计量分析。
很显然,掌握必要的计量方法是必要的。
这里,向大家推荐一种学计量的方法——读文献综述。
在我看来,读文献综述,学计量方法,有这么几个好处。
好处一:能够更为全面了解和认识所想要学习的计量方法。
针对某个具体方法的文献综述,会涉及多个研究领域,考虑到了内容和实施的方方面面。
通过这样的文献综述,可以了解到具体研究过程中的某个具体问题的多种形式、不同原因和多种解决思路。
举个例子,王宇和李海洋在《管理学研究中的内生性问题及修正方法》中将内生性问题的来源归为5类:遗漏变量偏差、选择偏差、双向因果、动态面板偏差、测量误差。
这种读文献综述的学习方法,避免了只看和自己研究有关的文献,开阔了视野,也为自己寻找更多思路和方法提供了“弹药”。
好处二:能够跟踪某个计量方法的最新前沿发展。
与教科书和手册不同,文献综述一般都会将最新的文章纳入进来。
读近期的文献综述,有助于把握方法技术发展的新动向。
这同时也表明,要与时俱进地学习新的方法技术,就得紧跟近期的文献综述。
好处三:能够从理论逻辑和具体运用两个方面来认识和理解所想要学习的计量方法。
一般的文献综述都会运用一些论文实例来讲解计量方法。
相对于教科书里讲的计量方法,文献综述里讲的计量方法更加“鲜活”,也更加具体。
我个人更加偏爱于一些有过计量分析实战经验的研究者所撰写的文献综述。
《测量体积》容器与体积,关联大发现在我们的日常生活和科学研究中,测量物体的体积是一项非常重要的任务。
无论是计算液体的容量、固体的空间大小,还是了解物体的密度,都离不开对体积的准确测量。
而在这个测量的过程中,容器扮演着至关重要的角色。
容器,简单来说,就是能够容纳物质的器具。
它的形状、大小和材质多种多样,从常见的杯子、瓶子、箱子,到实验室里的量筒、量杯、容量瓶等等。
不同的容器有着不同的用途和特点,也适用于不同的测量场景。
让我们先从最简单的容器——杯子说起。
杯子是我们日常生活中最常见的容器之一,我们用它来喝水、泡茶。
然而,如果我们想要用杯子来精确测量液体的体积,就会发现存在一定的困难。
因为杯子通常没有刻度,而且其形状也不一定规则,所以很难准确得出液体的体积。
相比之下,量筒和量杯则是专门为测量液体体积而设计的容器。
量筒的刻度通常比较精确,而且它的形状是细长的圆柱形,这样可以减少测量误差。
量杯的刻度则相对较粗,但它的容量较大,适合测量较多的液体。
在使用量筒和量杯测量液体体积时,我们需要将液体平稳地倒入容器中,使液面与刻度线平齐,同时视线要与刻度线保持水平,这样才能得到准确的测量结果。
除了液体,我们在测量固体的体积时也经常会用到容器。
比如,当我们要测量一个不规则形状的石头的体积时,可以先将一个装满水的量筒放在一个大容器中,然后将石头放入量筒中,石头会排出一部分水。
我们只要测量出排出水的体积,就可以知道石头的体积。
这种方法被称为“排水法”,它巧妙地利用了容器和水来测量固体的体积。
在实验室中,还有一种特殊的容器叫做容量瓶。
容量瓶是一种非常精确的测量容器,通常用于配制一定浓度的溶液。
它的体积是固定的,而且刻度非常精确,可以准确地配制出所需浓度的溶液。
除了这些常见的容器,还有一些特殊的容器用于特定的测量需求。
比如,在测量气体体积时,我们会用到气体摩尔体积测定装置;在工业生产中,会使用大型的储罐来测量和储存液体或气体的体积。
容器贮液量的准确计算
Poddar,T;张立奎
【期刊名称】《化工装备技术》
【年(卷),期】1994(015)006
【摘要】当容器的截面积沿线性长度不变的时候,其容积的准确计算是相当容易的;当它的截面积不是这样的时候,容积的准确计算是复杂而又费时的。
本文提供一个既简单又合理的精确方法,即使用一种常数表来计算许多此类容器的容积。
在化学工业中,所遇到最疑难容器具有代表类型的是...
【总页数】2页(P47-48)
【作者】Poddar,T;张立奎
【作者单位】不详;不详
【正文语种】中文
【中图分类】TQ051.302
【相关文献】
1.核工程贮液容器的工程抗震计算 [J], 张征明;何树延
2.椭圆形封头卧式容器中贮液量计算 [J], 张凤仙;薛长礼
3.圆形贮液容器的动水压力及其地震反应的计算 [J], 胡正顶
4.圆柱形弹性贮液容器基频近似计算法 [J], 翁智远;杨建中
5.用DYTRAN程序计算贮液容器液面晃动 [J], 杨龙;于溯源
因版权原因,仅展示原文概要,查看原文内容请购买。