- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
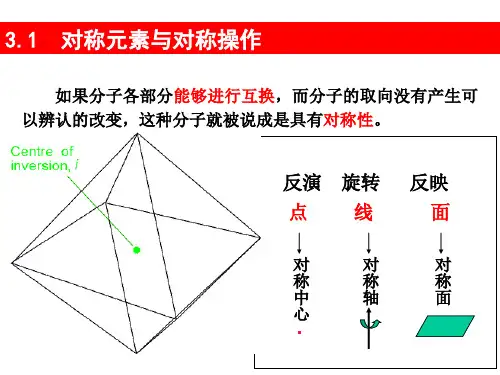
点线
面
对
对
对
称
称
称
中
轴
面
心.
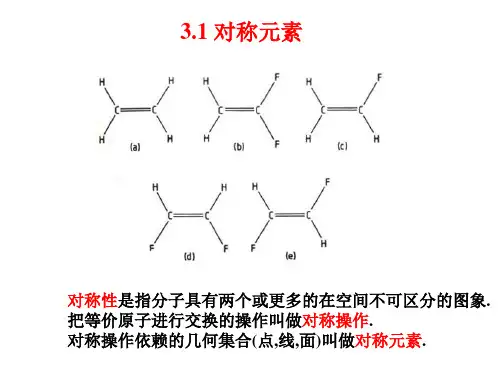
(1)旋转轴(Cn ) 和旋转操作 =2/n
分子中若存在一条轴线,绕此轴旋转2/n的角度能 使分子复原,就称此轴为旋转轴, 符号为Cn . 旋转可以实 际进行,为真操作;相应地,旋转轴也称为真轴. n-轴次
Cˆn
H2O2中的C2
• 定义:在具有多个旋转轴的分子中,轴次最高的旋 转轴叫主轴。AX3分子的主轴是C3。
熊夫利斯记号隐含了该点群中代表性的对称元素符 号。
例如:H2O分子,有1个C2轴,2个v反映面,所以属于
C2v点群,SO2,H2S也属于此点群;
NH3分子,它有1个C3轴和3个v反映面,属于C3v
点群,类似的如CHCl3,NF3等。
3.2.2 主要点一群些化学中重要的点群
点群 对 称 元 素(未包括恒等元素)
找出Re2Cl82-离子的对称元素
Re-Re连线是一根C4轴,它同时 也是C2轴; 两根通过棱柱相对的垂直边中
Cl
Cl 心的二重轴C2,
两根通过相对的垂直面中心的
Cl
Cl
二重轴C2’’ 平分Re-Re键和全部垂直边的对
Re
称面σh
Re Cl
两个包含相对垂直边的平面
Cl
σv’σv’’ 两个切割相对垂直面中心的平
面用σd 表示
试找出分子中的镜面
重叠式C2H6
对称面的性质
• 通过对称面连续进行两次反映,分子中所 有原子均回到起始位置,得到起始构型的 恒等构型,即σ2=E。由此推得,σ2n=σ2=E, σ2n+1=σ,n为整数。
(3) 对称中心(i )与反演操作
分子中若存在一点,将每个原子通过这一点引连线并延 长到反方向等距离处而使分子复原,这一点就是对称中心i, 通过对称中心使分子复原的操作叫反演.反演操作用i 表示。
进行反映,产生一个不可分辨的构型,那么这个轴就是n重旋转 -反映轴,称作映轴,相应的对称元素称为映轴Sn 。
Sn = σ Cn 复合操作. 旋转、反映的两步操作顺序可以反过来. Sn是虚轴. 对于Sn,若n等于奇数,则Cn和与之垂直的σ都独立存在;若 n等于偶数,则有Cn/2与Sn共轴,但Cn和与之垂直的σ并不一定独 立存在.
正四面体 正六面体 正八面体 正十二面体 正二十面体
群 Td
Oh
Oh
Id
Ih
1) Td群 (正四面体构型的分子)
对称元素:3个C2,4个C3,3个S4 , 6个d
Td Eˆ,3Cˆ2,4Cˆ3,4Cˆ32,3Sˆ41,3Sˆ43,6ˆd
24阶群
C3
C2 (S4)
CH4
P4
d
CH4、P4、GeH4、SO42-、ClO4-、CrO4-、MnO4-
C4 h
SF6
立方烷
C3
d
UF6、SF6、CoF63-、Mn(OH2)62+、Fe(CN)64-、Co(CO)6
5. 线性分子 Cv 无对称中心
CO,HCN,NO,HCl,N2O
元素:C 和无穷个v
Dh 有对称中心 CO2,O2,N2,C2H2
元素:C 和无穷个v 、无穷个垂直于C 的C2, h ,i
C2H4, N2O4 D2h
C6H6 D6h
重叠式C2H6 D3h
Cl
Cl
Cl Cl
Re
Re Cl Cl
Cl
Cl
PCl5
属于什么点群?
3) Dnd群 Dn+nd d :平分相邻两个C2轴之间的夹角
H C2
H
H
H
H
H
反式乙烷
D3d
D3d : 乙烷交错型
4. 高对称群—含有二个以上高次轴Cn(n2) Td, Oh, Ih
属于什么点群?
2. 单轴群—仅含一个Cn轴或Sn轴的群
如 Cn,Cnv,Cnh,Sn群
1) Cn群 对称元素:E, Cn n 阶群
Cl C2
H
Cl
{Eˆ , Cˆ2} C2 群 H
H
H
{Eˆ , Cˆ3 , Cˆ32}
C3
群
1,3,5-三甲基苯 部分交错式
2) Cnv群
对称元素:E, Cn, nv 阶数:2n
3.恒等元素:群中必含一恒等元素E,它和群中任一元 素的乘积即为该元素本身。 例如,aE=Ea=a。
4.逆元素:群中任一元素a必有一逆元素a-1,元素a与 其逆元素a-相乘等于恒等元素 E:aa-1=a-1a=E。
以H2O分子为例,看C2v群的性质:
1.封闭性
O
O
O
C2
v
H
H
1
2
2)Oh群:(正八面体分子)
元素:3C4,4C3,6C2, 3 h, 6d,3S4,4S6,i
Oh
Eˆ ,3Cˆ41,3Cˆ43,3Cˆ2 ,4Cˆ31,4Cˆ32 ,6Cˆ2 ',3ˆ h ,6ˆ d ,
3Sˆ41,3Sˆ43,4Sˆ61,4Sˆ65 , iˆ
48阶群
E
v
v
E
v
C2 C2 E
v v E
v
v
E
EE E
C2、σv、σv′和E的逆元素就是它们本身。
一个分子所具有的对称操作(点对称操作)的完全集 合构成一个点群(Point Group)。每个点群具有一个特定 的符号,国际上通用的分子点群符号叫SchÖnflies(熊夫 利斯)记号。
SiFClBrI
H2O2, PPh3 H2O, NH3 反-N2F2 CO,HCN Cr(C2O4)33- BF3,PtCl42- H2, Cl2
Dnd Dn的对称元素、再加一套平分每一C2轴的垂直镜面 Sn 有唯一对称元素(Sn映轴) Td 正四面体分子或离子,4C3、3C2、3S4和6d
B2Cl4,交错C2H6
CH4中的映轴S4与旋转反映操作
• 注意: C4和与之垂直的σ都不独立存在
在交错构型的乙烷分子中就有一根与C3轴重合的S6轴
对于Sn,若n等于奇数,则Cn和与之垂直的σ都独立存在
重叠型二茂铁具有S5, 所 以, C5和与之垂直的σ也都 独立存在;
S1 h ; S2 i ; S3 C3 h ; S4独立,包含C2 ; S5 C5 h ; S6 C3 i
船式环已烷
N2H4
Mn(CO)5I
属于什么点群?
3) Cnh 群: 对称元素:E, Cn, h , (Sn) 阶数:2n
F
H
CC
H
F
H O
H
B
O
O
H
C2h 群
C3h 群
C2
· H i Cl
Cl
H
σh
属于什么点群?
4) Sn群
只具有一个Sn轴
n 4, S1 Cs S2 Ci S3 C3h
等价构型 Cnn、 i2、σ2=E,恒等操作
作产生的结果和两个或多个其他操作 连续作用的结果相同,通常称这一操作为其他操 作的乘积。
Example满其足结于果分关相子系当具于A有B对A,分BC子, C,单 , D独即 施对等行分对子C称先操操后作作施,,行则若称B其和C中为A某操A些作和操,B作 的乘积。
C6H6
D6h
三角双锥 PCl5
D3h
结构
分子
点群
正四面体 CH4
Td
正八面体 SF6
Oh
夹心化合物
重叠型
S4
1,3,5,7-四甲基环辛四烯
3. 二面体群(D群) —有一个Cn轴和n个垂直于Cn的C2轴
Dn,Dnh,Dnd 1) Dn群 对称元素: E,nC2Cn 阶数:2n
C2 Cn
C2
C2
C2
D2
[Co(dien)2]3+
C2
D3
[Co(en)3]3+
2) Dnh群
对称元素: E,Cn,nC2,h, (nv, Sn) 阶数:4n
• 旋转2π/n的操作以Cn表示,每次旋转2π/n,连续完 成m次的旋转,用符号Cmn表示, 旋转角为m*2π/n。
BCl3分子有1C3、3C2
Cn的性质
• n次Cn, 共生成n个操作:Cn, C2n, …,Cnn , 旋转角度依次为:2π/n, 2*2π/n,…, n*2π/n=2π。Cnn的效果为不动,得到恒等 构型。不动操作亦即恒等操作,通常以E 表示,故Cnn=E.
(5) 恒等操作E
对分子不作任何动作构成恒等操作。一切分子都 具有这个对称元素。因为对分子不作任何动作, 这个分子的状况是不会改变的。似乎这个元素是 个毫无价值的对称元素,但因群论计算中要涉及 它,所以必须包括。
恒等操作与等价操作
恒等操作是分子恒等不变,各原子的位置与最 初完全相同;
其他对称操作中,经过一次操作以后分子取向 复原,称为等价操作,但并不是跟原来完全相同。
H
H
2
1
H
H
1
2
σv′
2.结合律
vC2
v
C2
v
v v v E
C2 v v C2C2 E
则有
C2
v
v C2
v v
3.恒等元素
4.逆元素
EC2 C2 E C2
E v v E v
C2
O
H