公开课菱形的性质 ppt课件

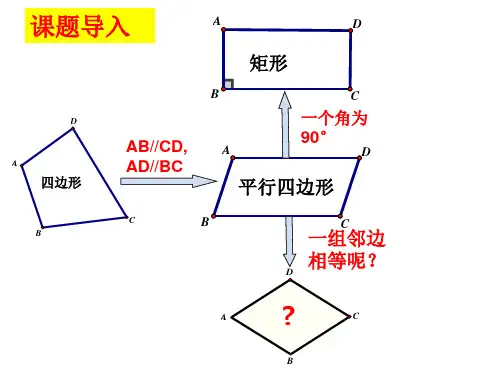
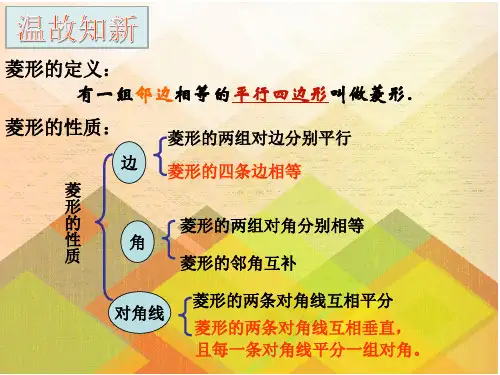
1.理解菱形的概念，了解它与平行四边形之间的关系.2.经历菱形性质定理的探索过程.（重点）3.能够用综合法证明菱形的性质定理.（难点）下面几幅图中都含有一些平行四边形.观察这些平行四边形，你能发现它们有什么样的共同特征吗？知识点1 菱形的定义由上图中的这些平行四边形，你能发现它们有什么共同点吗？从边的角度想一想。

平行四边形菱形菱形的定义：有一组邻边相等的平行四边形叫做菱形.归纳做一做用菱形纸片折一折，回答下列问题：（1）菱形是轴对称图形吗？如果是，它有几条对称轴？对称轴之间有什么位置关系？知识点2 菱形的性质（2）菱形中有哪些相等的线段？探索菱形的性质通过上面的折纸活动，我们可以发现：（1）菱形是轴对称图形，有两条对称轴.（2）菱形四条边都相等.（3）菱形的对角线互相垂直.证明菱形的性质已知：如图，在菱形ABCD中，AB=AD，对角线AC 与BD相交于点O.求证:(1）AB = BC = CD =AD；（2）AC⊥BD.A BC DO证明：（1）∵四边形ABCD是菱形，∴AB = CD，AD = BC（菱形的对边相等）. 又∵AB=AD，∴AB = BC = CD =AD.证明菱形的性质已知：如图，在菱形ABCD中，AB=AD，对角线AC 与BD相交于点O.求证:(1）AB = BC = CD =AD；（2）AC⊥BD.A BC DO（2）∵AB=AD，∴△ABD是等腰三角形.又∵四边形ABCD是菱形，∴OB=OD.在等腰三角形ABD中，∵OB=OD，∴AO⊥BD，即AC⊥BD.如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，∠BAD=60°，BD=6，求菱形的边长AB 和对角线AC 的长.解：∵四边形ABCD 是菱形，∴ AB = BD (菱形的四条边相等)，∴ AC ⊥BD (菱形的对角线互相垂直)， OB =OD = BD = ×6=3(菱形的对角线互相平分).在等腰三角形ABC 中，∵∠BAD =60°，1212A C DOB如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，∠BAD=60°，BD=6，求菱形的边长AB 和对角线AC 的长.A C D OB ∴△ABD 是等边三角形.∴AB = BD = 6.在Rt ΔAOB 中，由勾股定理，得OA 2+OB 2=AB 2，∴ OA = = = ∴ AC = 2OA = （菱形的对角线互相平分）.22AB O B -2263-3 3.63菱形是特殊的平行四边形，它除具有平行四边形的所有性质外，还有平行四边形所没有的特殊性质.对称性：是轴对称图形.边：四条边都相等.对角线：互相垂直. 角：对角相等，邻角互补.边：对边平行且相等.对角线：相交并相互平分.1.菱形具有而一般平行四边形不具有的性质是 （ ）A.对角相等B.对边相等C.对角线互相垂直D.对角线相等C2.如图，在菱形ABCD 中，对角线AC 与BD 相交 于点O . 已知AB =5cm，AO =4cm，求BD 的长.解：∵四边形 ABCD 是菱形，∴AC ⊥BD （菱形的对角线互相垂直）.在Rt△AOB 中，由勾股定理，得OA 2 + OB 2 = AB 2，∴BO = .-=-=2222543AB AO∵四边形ABCD 是菱形，∴BD =2BO = 2×3=6（菱形的对角线互相平分）.∴BD 的长为 6 cm.2.如图，在菱形ABCD 中，对角线AC 与BD 相交 于点O . 已知AB =5cm，AO =4cm，求BD的长.3.已知：如图，在菱形ABCD 中，∠BAD=2∠B.求证：△ABC是等边三角形.证明：∵四边形ABCD是菱形∴AD∥BC，∴∠BAD+∠B=180°.又∵∠BAD=2∠B, ∴∠B=60°.∵AB=BC，∴△ABC是等边三角形.4.已知：如图，在菱形ABCD中，对角线AC与BD相交于点O.求证：AC，CA分别平分∠BAD和∠BCD，BD，DB分别平分∠ABC和∠ADC.证明：∵四边形ABCD是菱形，∴AB=AD ，BO=DO，∴AC⊥BD，AC平分∠BAD，同理：CA平分∠BCD，BD，DB分别平分∠ABC和∠ADC.1.从课后习题中选取；2.完成练习册本课时的习题.。