晶格振动的模式密度
- 格式:doc
- 大小:125.50 KB
- 文档页数:4

晶格振动模式密度研究王晴晴;宫昊;程荣龙;葛立新【摘要】晶格振动模式密度(声子态密度)即单位频率间隔内的模式数,是反映声子在波矢空间分布疏密程度的物理量.为了准确地求出品格热容量随温度的变化关系,必须用较精确的办法计算出晶格振动的模式密度,进而掌握材料的热力学性质.一般教材中对该部分的讲解晦涩难懂,本文从品格振动的物理意义开始,分析说明并推导一维、二维、三维不同体系的晶格振动模式密度公式,进而求出德拜模型下不同体系晶格热容公式.【期刊名称】《大学物理》【年(卷),期】2018(037)008【总页数】4页(P4-7)【关键词】晶格振动;声子态密度;德拜模型;晶格热容【作者】王晴晴;宫昊;程荣龙;葛立新【作者单位】蚌埠学院理学院,安徽蚌埠233030;蚌埠学院理学院,安徽蚌埠233030;蚌埠学院理学院,安徽蚌埠233030;蚌埠学院理学院,安徽蚌埠233030【正文语种】中文【中图分类】O481晶格振动模式密度,也称为频谱密度、声子态密度、简正模式密度、频率分布函数等,是在解决晶格热容随温度的变化关系过程中提出来的,一般用g(ω)表示,黄昆先生的《固体物理学》[1]教材中给出的定义式为(1)其中dn表示在ω→ω+dω频率间隔内晶格振动模式的数目.最初对晶格振动模式密度的计算是为了准确求出晶格热容随温度的变化关系,而晶格热容的大小直接反映了固体材料的热力学性质.后来发现,计算晶格振动模式密度对研究晶体的某些电学性质和光学性质也非常有用.但是教材中对于晶格振动模式密度的计算这部分讲解晦涩难懂,特别是对于一般本科院校的学生很难完全理解如何计算和应用.本文将以通俗的语言从晶格振动的物理意义开始,引入一维、二维、三维不同体系格波分布密度和等频率面间的体积,然后举例讲解如何计算晶格振动模式密度,并获得计算通用公式,最后在德拜模型下推导不同体系的晶格热容公式.1 晶格振动模式晶体中原子的排列是具有周期性的,而其排列的具体形式即称为晶格,格子的位置代表了原子的平衡位置.晶体的一些宏观性质如导电性、导热性等就是因为晶体中电子和原子的运动造成的,而晶格振动即晶体中原子在其平衡位置附近的振动,温度越高振动越激烈,温度达到熔点附近则原子将脱离格点的束缚而发生相变.在简谐近似即温度不太高的小振动过程中,研究发现晶格振动中所有原子都以相同的振动频率参与振动,且振动的模式具有波的形式,一般把体系中所有原子一起参与的共同振动叫做一个振动模式.振动模式具有波的形式又叫做格波,格波的能量量子叫声子,声子是一种假想的能量量子.原则上只要找到了体系的振动模式或格波的运动方程,就能方便的求解薛定谔方程,解决相应的问题.振动模式具有波的形式,需要描述体系格波的特性,如格波方程、格波波长、格波波矢等参数.由于晶格具有周期性,只需讨论一个周期内的特性就可反映整个晶体的特性,因此引入了布里渊区的概念.第一布里渊区即倒格子空间的维格纳-赛兹原胞,是倒格子空间的最小周期性单元.在求解晶格振动模式密度的过程中比较关注的就是格波波矢q与频率ω之间的关系即色散关系式ω(q)(又称为晶格振动谱)[2].研究发现一维单原子链一个波矢q对应一个频率ω,而二维、三维体系中一个波矢q对应多个频率ω,即一个波矢将对应多个振动模式.2 晶格振动模式密度的计算2.1 格波分布密度不管是一维、二维还是三维体系都存在边界问题,在求解所有原子的联立方程过程中,很难求出格波解的形式,因此所有体系都要在玻恩-卡曼边界条件下进行,即其中N=N1·N2·N3为总的原胞个数,α1、α2、α3为晶格的三个基矢,h1、h2、h3为一组整数.即波矢q不是连续的,而是q空间均匀分布的量子化的点,点的个数正好为h1·h2·h3个.格波分布密度就是单位体积中的量子化点的个数,所以不同体系的格波分布密度计算公式如下.1) 三维体系q空间的体积为格波分布密度为其中V0=α1·(α2×α3)为原胞的体积,V为晶体的体积.2) 二维体系q空间的面积为格波分布密度为其中A0=|α1×α2|为二维体系原胞的面积,A为二维晶面的面积.3) 一维体系q空间的长度为格波分布密度为其中α为一维体系原胞的间距,L为一维原子链的长度.2.2 晶格振动模式密度计算特例根据晶格振动模式密度的定义,其中dn表示ω→ω+dω频率间隔内晶格振动模式的数目,若能求出ω→ω+dω等频率面(ω(q)=常数对应的q空间中的面)间的体积,则dn=格波频率密度×等频率间体积1) 三维体系,以等频率面是球面为例.图1 三维体系等频率面等频率面间的体积为其中忽略(dq)2项和(dq)3项.ω→ω+dω频率间隔内晶格振动模式的数目为晶格振动模式密度为(2)若可以通过实验的方法获得体系的晶格振动谱ω(q),就可直接求出g(ω)的值.2) 二维体系,以等频率线是圆形为例.等频率线间的面积为π(q+dq)2-πq2≈2πqdq其中忽略(dq)2项.ω→ω+dω频率间隔内晶格振动模式的数目为晶格振动模式密度为(3)3) 一维体系等频率点间距可直接为2dqω→ω+dω频率间隔内晶格振动模式的数目为晶格振动模式密度为(4)2.3 晶格振动模式密度一般表达式实际三维晶体的等频率面一般很复杂,不能用简单的球形来代表.若用dS表示等频率曲面上的面积元,dq为q空间频率ω→ω+dω的垂直距离,则表示第j个模式等频率面的梯度.(假设体系包含n个原子,则三维体系共有3n支格波,其中3支声学波,(3n-3)支光学波;二维体系共有2n支格波,其中2支声学波,(2n-2)支光学波;一维体系共有n支格波,其中1支声学波,(n-1)支光学波.)晶格振动模式密度的一般表达式如下:1) 三维体系:∬2) 二维体系:3) 一维体系:3 实验与理论计算方法求解晶格振动模式密度(声子态密度)的关键在于晶格振动谱的具体表达式.实验上一般采用Raman散射获得晶格振动谱:即将特定频率的光波照射待测样品表面,光子会与声子发生碰撞并散射,若能测定散射前后粒子的频率与波长的改变,就可以根据能量守恒和动量守恒公式确定声子的频率和波矢的关系.另外也可以采用布里渊散射、中子非弹性散射、X射线散射等实验手段确定晶格振动谱.对于晶格振动谱比较简单的体系,可以近似的描述等频率面的形状并求出等频率面间体积,直接用上文中的公式计算声子态密度.对于晶格振动谱复杂的体系,不能单纯的通过公式计算求解,可用Raman振动谱的积分面积和拟合峰高来定性描述声子态密度,若积分面积和拟合峰高比较大,说明声子态密度大,反之则声子态密度小[3].理论模拟计算中,一般采用基于密度泛函理论的第一性原理计算分析[4-6],如利用Materials Studio中的CASTEP程序软件包、Quantum-ESPRESSO软件的PWscf软件包均可以画出声子态密度曲线.4 德拜模型下由声子态密度求解晶格热容材料的热力学性质与其内部的晶格振动有很大关系,基于密度泛函理论的第一性原理可通过较小的计算量获得布里渊区内声子谱,从而求出相应的热力学参数.德拜模型提出将格波看成弹性介质波(长声学波),而热容是原子的各种频率(0到极大值ωD,ωD为德拜频率)振动贡献的总和.即德拜模型下三维体系包括一支纵声学波、两支横声学波,二维体系包括一支纵声学波、一支横声学波,一维体系包括一支纵声学波.弹性波色散关系式可简单写成:纵波:ωL=vLq;横波:ωT=vTq(5)其中vL、vT分别为纵声学波和横声学波的传播速度.将式(5)分别带入式(2)、式(3)、式(4)可得声子态密度.三维体系:二维体系:一维体系:假设体系包含N个原胞,根据式(1)即声子态密度的定义式:1) 三维体系g(ω)dω=3N⟹(6)2) 二维体系g(ω)dω=2N⟹(7)3) 一维体系g(ω)dω=N⟹(8)根据晶格热容的量子理论,晶体内能和晶格热容公式分别为:(9)(10)分别将式(6-8)带入式(9)、式(10)计算得:1) 三维体系2) 二维体系3) 一维体系其中为德拜温度,表征了原子间结合力的一重要物理量,不同材料的德拜温度不同,熔点高,即材料原子健结合力强,则德拜温度越高[7,8].根据德拜温度的定义它是一个跟温度无关的物理量,但实验证实德拜温度随着温度的变化而变化[9],这因为德拜模型忽略了晶体的各向异性及光学波、高频声学波对热容的贡献[10].实际晶格热容随温度的变化曲线直接反映了声子态密度的整体行为[11].而热容是固体原子热运动在宏观性质上的最直接体现.因此研究和分析实际固体的声子态密度具有重大的意义.【相关文献】[1] 黄昆. 固体物理学[M]. 韩汝琦,改.北京:高等教育出版社, 1988.[2] 田强, 洪馥男. 具有在位势的一维双原子链晶格振动的色散关系[J].大学物理, 2006, 25(4):17-17.[3] 苏方宁, 邓再德. 声子态密度对掺稀土玻璃材料上转换发光强度的影响[J]. 玻璃与搪瓷, 2007,35(2):1-5.[4] 郭连权, 林琳, 马贺,等. Mg2Si的声子谱与力热性能的第一性原理计算[J]. 沈阳工业大学学报, 2015, 37(3):294-298.[5] 蒋文灿, 陈华, 张伟斌. TATB晶体声子谱及比热容的第一性原理研究[J]. 物理学报, 2016,65(12):216-224.[6] 付佳琦. 第一性原理研究纤锌矿结构AIN和InN的声子及热力学性质[D]. 内蒙古大学, 2015.[7] 程本培, 虞炳西. 用测定德拜温度的方法判断合金中原子间结合力的变化[J]. 物理测试,1991(5):6-11.[8] 文潮, 孙德玉, 关锦清,等. 用X射线衍射强度测定纳米金刚石的德拜特征温度和熔点[J]. 高压物理学报, 2003, 17(3):199-203.[9] 刘洋. 纳米材料德拜温度、体膨胀系数及热容的尺寸效应[D]. 吉林大学, 2008.[10] 高钦翔, 田强. 光频支格波对晶格热容的贡献[J]. 大学物理, 2002, 21(7):16-17.[11] 王晓旭, 赵琉涛, 成海霞,等. La3Co29-xFexSi4B10的择优占位、电子结构和晶格振动性质的理论研究[J]. 物理学报, 2016, 65(5):266-272.。



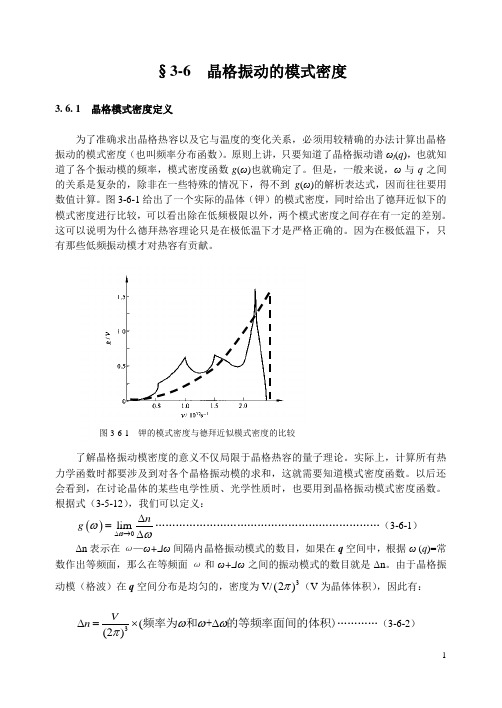
§3-6 晶格振动的模式密度3. 6. 1 晶格模式密度定义为了准确求出晶格热容以及它与温度的变化关系,必须用较精确的办法计算出晶格振动的模式密度(也叫频率分布函数)。
原则上讲,只要知道了晶格振动谱ωj (q ),也就知道了各个振动模的频率,模式密度函数g (ω)也就确定了。
但是,一般来说,ω与q 之间的关系是复杂的,除非在一些特殊的情况下,得不到g (ω)的解析表达式,因而往往要用数值计算。
图3-6-1给出了一个实际的晶体(钾)的模式密度,同时给出了德拜近似下的模式密度进行比较,可以看出除在低频极限以外,两个模式密度之间存在有一定的差别。
这可以说明为什么德拜热容理论只是在极低温下才是严格正确的。
因为在极低温下,只有那些低频振动模才对热容有贡献。
了解晶格振动模密度的意义不仅局限于晶格热容的量子理论。
实际上,计算所有热力学函数时都要涉及到对各个晶格振动模的求和,这就需要知道模式密度函数。
以后还会看到,在讨论晶体的某些电学性质、光学性质时,也要用到晶格振动模式密度函数。
根据式(3-5-12),我们可以定义:()0limng ωωω∆→∆=∆…………………………………………………………(3-6-1)Δn 表示在ω—ω+Δω间隔内晶格振动模式的数目,如果在q 空间中,根据ω (q )=常数作出等频面,那么在等频面ω和ω+Δω之间的振动模式的数目就是Δn 。
由于晶格振动模(格波)在q 空间分布是均匀的,密度为V/3(2)π(V 为晶体体积),因此有:3((2)Vn ωωωπ∆=⨯∆频率为和+的等频率面间的体积)…………(3-6-2) 图3-6-1 钾的模式密度与德拜近似模式密度的比较如图3-6-2所示,等频面间的体积可表示成对体积元dsdq 在面上的积分:3(2)Vn dsdq π∆=⎰…………………………………………………(3-6-3) 其中dq 表示两等频率面间的垂直距离,ds 为面积元,显然()q dq q ωω∇=∆因为()q q ω∇表示沿法线方向频率的改变率。

晶格振动模式密度定义晶格振动模式密度(Phonon Density of States,简称PDOS)是描述晶体中原子振动模式的一种物理量。
晶体中的原子在平衡位置附近以小振幅做简谐振动,这些简谐振动构成了晶体的振动模式。
PDOS给出了不同频率的振动模式在能量空间中的分布情况,反映了晶体各种振动模式的丰度和分布情况。
PDOS对于研究晶体的热力学性质、热传导、声学性质等都具有重要意义。
它是计算晶体热容、热导率、声子散射等性质的基础。
此外,PDOS还可以用于研究晶体的相变、物理化学性质以及材料的设计和优化。
PDOS的具体定义如下:设晶体中的原子总数为N,晶格振动模式的总数为M,则PDOS可以定义为每单位频率范围内单位原子数的平均数,即:PDOS(ω) = (1/ N) * ∑(m=1 to M) δ(ω - ω_m)其中,δ(ω-ω_m)为狄拉克函数,当ω等于ω_m时取值为1,否则取值为0。
PDOS可以分为各向同性的PDOS和各向异性的PDOS。
各向同性PDOS是指晶体中各个晶向上的振动模式在一些频率范围内的分布情况,它是晶体的各向同性介质的特征。
各向异性PDOS是指晶体中不同晶向上的振动模式在一些频率范围内的分布情况,它反映了晶体的各向异性效应,比如晶体的声子色散关系。
在实际计算中,PDOS通常通过量子力学计算或者分子动力学模拟得到。
对于固体材料,计算PDOS是一个复杂的过程,需要考虑晶胞、原子的排列方式、晶格常数等诸多因素。
目前,常用的计算方法包括密度泛函理论(DFT)、哈密顿动力学模拟(HMD)等。
根据计算得到的PDOS,可以进一步研究晶体的声子态密度(Phonon Density of States,简称PhDOS),PhDOS是PDOS的积分,表示在一些频率以下的所有振动模式的能量状态密度。
总结起来,晶格振动模式密度(PDOS)是指描述晶体中不同频率的振动模式在能量空间中的分布情况。
它是了解晶体物理、热学以及声学性质的重要指标,可以通过理论计算或者模拟得到。
§3-6 晶格振动的模式密度
3. 6. 1 晶格模式密度定义
为了准确求出晶格热容以及它与温度的变化关系,必须用较精确的办法计算出晶格振动的模式密度(也叫频率分布函数)。
原则上讲,只要知道了晶格振动谱ωj (q ),也就知道了各个振动模的频率,模式密度函数g (ω)也就确定了。
但是,一般来说,ω与q 之间的关系是复杂的,除非在一些特殊的情况下,得不到g (ω)的解析表达式,因而往往要用数值计算。
图3-6-1给出了一个实际的晶体(钾)的模式密度,同时给出了德拜近似下的模式密度进行比较,可以看出除在低频极限以外,两个模式密度之间存在有一定的差别。
这可以说明为什么德拜热容理论只是在极低温下才是严格正确的。
因为在极低温下,只有那些低频振动模才对热容有贡献。
了解晶格振动模密度的意义不仅局限于晶格热容的量子理论。
实际上,计算所有热力学函数时都要涉及到对各个晶格振动模的求和,这就需要知道模式密度函数。
以后还会看到,在讨论晶体的某些电学性质、光学性质时,也要用到晶格振动模式密度函数。
根据式(3-5-12),我们可以定义:
()0lim
n
g ωωω
∆→∆=∆…………………………………………………………(3-6-1)
Δn 表示在ω—ω+Δω间隔内晶格振动模式的数目,如果在q 空间中,根据ω (q )=常数作出等频面,那么在等频面ω和ω+Δω之间的振动模式的数目就是Δn 。
由于晶格振动模(格波)在q 空间分布是均匀的,密度为V/3
(2)π(V 为晶体体积),因此有:
3
((2)
V
n ωωωπ∆=
⨯∆频率为和+的等频率面间的体积)…………(3-6-2) 图3-6-1 钾的模式密度与德拜近似模式密度的比较
如图3-6-2所示,等频面间的体积可表示成对体积元dsdq 在面上的积分:
3(2)
V
n dsdq π∆=
⎰…………………………………………………(3-6-3) 其中dq 表示两等频率面间的垂直距离,ds 为面积元,显然
()q dq q ωω∇=∆
因为()q q ω∇表示沿法线方向频率的改变
率。
因此
3(2)q V
dS
n ωπω
⎡⎤
∆=∆⎢
⎥∇⎢⎥⎣
⎦
⎰
………(3-6-4) 从而得到模式密度的一般表达式
()()
()3
2q
V dS
g q ωωπ=
∇⎰………(3-6-5)
3. 6. 2 一维单原子链的模式密度
对于一维情况,q 空间的密度约化为L /2π,L =Na 为单原子链的长度,其中a 为原子间距,N 为原子数目。
则在q 空间内振动模式数目为2L
dq π。
d ω频率间隔内的振动模式数目为:
22L dq n d d ωπω
∆=⨯
⋅…………………………………………………………(3-6-6) 等式右边的因子2来源于ω(q )具有中心反演对称,q>0和q<0区间的完全等价的。
从而有
()1
L g d dq
ωωπ=
…………………………………………………………(3-6-7) 这是公式(3-6-7)在一维情况时的简化形式。
对于一维单原子链,只计入最近邻原子之间的相互作用时,有
(
)11
sin 22
m q aq aq ωω=
= 其中m ω为最大频率。
代入(3-6-7)式可以得到:
图3-6-2 等频面示意图
()122
2
2()m
N
g ωωωπ
-
=
-…………………………………………(3-6-8)
3. 6. 3 分析ω=c 2q 的模式密度
首先回顾一下德拜近似的模式密度,德拜近似的核心是假定频率正比于q 。
即 c ω=q
代入(3-6-5)式,容易得到:
()()
23
231422V
V
g c c c
ωωπωππ⎛⎫=
= ⎪⎝⎭…………………………………(3-6-9) 下面,我们以色散关系为ω=c 2q 为例,分析其三维、二维及一维情况下的模式密度。
(1) 三维情况模式密度 对于三维情况,
ω=c 2q ……………………………………………(3-6-10) 在q 空间等频率面为球面,半径为:
q =
在球面上,
()22q d q Cq dq ωω∇=
==是一个常数,且球面积分为:2
4ds q π=⎰
,因此:
()()()()()2
123
33232111422222q q V
ds V V V g ds q cq c
ωπωωωππππ=
===∇∇⎰
⎰ ……………………………………………(3-6-11)
(2)二维情况模式密度
对于二维情况,q 空间也约化为二维空间,其等频面实际为一个圆,圆半径为:
q =
二维情况下的q 空间中的密度为:A/(2π)2
,(这里A 为二维晶格的面积),而且有:
()222q d q Cq dq dL q
ωωπ∇=
===⎰所以对于ω=c 2q ,二维情况的模式密度为:
2
2
2()(2)(2)24()q dn A dL A q A
g d Cq C
q πωωπππω=
=
==∇⎰
…………………(3-6-12) (3)一维情况
同理,在一维情况下,q 空间有两个等频点+q 和-q 。
仿上面的方法可以得到:
1()2(2)(2)2()q dn L dq L g d Cq q ωωππω=
==⨯=
∇⎰……………(3-6-13) 总之,色散关系为ω=c 2q 的形式时,在三维、二维和一维情况下,模式密度分别与频率ω的½,0,-½次方成比例。
3. 6. 4 模式密度的范霍夫奇点
从(3-6-5)式可以看出,在()q ω对q 的梯度为零的地方,g (ω)应显示出某种奇异性,我们称()0q q ω∇=的点为范霍夫奇点,也称为临界点。
例:一维单原子链的范霍夫奇点
对于一维单子链,模式密度
为
()g ω=
显然:当ω→m
ω(或q=±π/a 时,g(ω)→∞,即m ω为一维单原子情况的范霍夫奇点,如图3-6-3所示。
,。