一维双原子链晶格振动光学支与声学支频隙宽度

色散关系（频率与波矢的关系）
一维单原子链动力学方程的一般解 得到：
l 0, 1, 2,
Gl
表示同一格波，所以可以将 q e的取iN值aqq 限制1在第一N布a里q渊区：2 ,
n 1,2,3, N
l 0,1,2,
当两个原子的振动位相差为2 Aei(qx t )
的整数倍时，两个原子q的振动2位移l相,
m
d 2un dt 2
(un1
un1
2un
)
强行者有志。
胸有凌云志，无高不可攀。 贫困教会贫困者一切。 贫穷是一切艺术职业的母亲。
得到： m 2u eiaqu eiaqu 2u
n
n
n
n
学做任何事得按部就班，急不得。
壮志与毅力是事业的双翼。
立志是事业的大门，工作是登门入室的旅程。 褴褛衣内可藏志。 人若有志，万事可为。 志，气之帅也。
将动力学方程的一般解
un
u(na,t)
i( 2nat )
Ae
Aei(naqt)
人 志无之志所向 趋， ，和 无迷 远途 勿的 届盲 ，人穷一 山样 复。 海不能代限也入;志动之所力向学，无方坚程不摧，。
鸟不展翅膀难高飞。 穷人的孩子早当家。 人之所以异于禽者，唯志而已矣! 志坚者，功名之柱也。登山不以艰险而止，则必臻乎峻岭。
等，晶体原子振动以格波在晶体中传
l 0,1,2
播。
2、相邻间距为d 的两个原子的恢复力系数为
; Na
3、相邻间距为(a-d)的两个原子的恢复力系数为 2
u2 (na, t) 格波圆频率具有中心反演对称性： 若格波波长 比晶体原子间距离大得多，即
由于 q
a
a

—— ω 与q之间存在着两 种不同的色散关系 —— 一维复式格子存在 两种独立的格波
2 − 2β B mω + —— 光学波 ( )+ = − A 2β cos aq
2 B mω − − 2β —— 声学波 ( )− = − A 2 β cos aq
05/ 20
q的取值 M和 m原子振动方程 相邻原胞之间位相差 波矢 q的值
2 ω− =β
(m + M ) 4mM {1 − [1 − sin 2 aq ]2 } mM ( m + M )2
1 (m + M ) 4mM {1 + [1 − sin 2 aq ] 2 } mM (m + M )2
1
2 ω+ =β
—— A、 B有非零的解，系数行列式为零
1
2 ω− =β
1 (m + M ) 4mM {1 − [1 − sin 2 aq] 2 } mM (m + M )2
33一维双原子链声学波和光学波一维复式格子的情形一维无限长链两种原子m和m构成一维复式格子m原子位于2n12n12n3同种原子间的距离2a晶格常数系统有n个0120n个原胞有2n个独立的方程两种原子振动的振幅a和b一般来说是不同的第2n1个m原子的方程第2n个m原子的方程方程解的形式iaqiaqiaqiaqab有非零的解系数行列式为零第2n1个m原子第2n个m原子方程的解aqaqmmaqmmmmaqmmmmaqmm与q之间存在着两种不同的色散关系一维复式格子存在两种独立的格波光学波声学波0520mmaqmmmmaqmm光学波声学波mmaqmm相邻原胞之间位相差aqm和m原子振动方程q的取值布里渊区大小2aq第一布里渊区允许的q值的数目晶体中的原胞数目对应一个q有两支格波

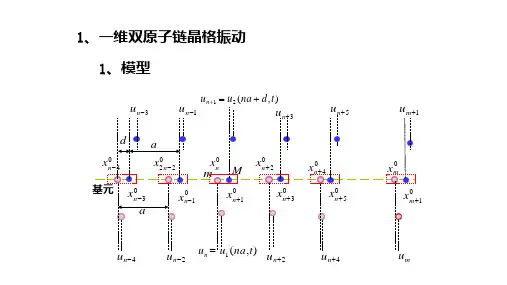
固体物理题目总汇填空题1、根据固体材料中原子排列的方式可以将固体材料分为晶体、非晶体和准晶体。

2、晶体结构=点阵+基元3、晶体的比热包括晶格比热和电子比热。

4、结晶学中，属于立方晶系的布拉维晶胞有简单立方、体心立方和面心立方三种。

5、密堆结构有两种：六方密堆积和立方密堆积。

6、原子电负性在一个周期内由左到右不断升高，周期表由上到下，负电性逐渐降低。

7、限定波矢q的取值范围在第一布里渊区8、金属的未满能带叫价带或导带。

1、人们利用某射线衍射测定晶体结构。

3、晶体的热学性质，如比热、热膨胀和热传导等就与晶格振动密切有关。

4、声子是一种准粒子，不具有通常意义下的动量，常把q称为声子的准动量。

5、根据晶体缺陷在空间延伸的线度晶体缺陷可分为点缺陷~线缺陷、面缺陷和体缺陷。

6、V心是F心的反型体。

1、晶体的基本结构单元称为基元2、面心立方晶胞的晶格常数为a，其倒格子原胞的体积等于323/a33、布拉维空间点阵共有14种，归为7种晶系。

5、一维双原子链的色散关系中频率较低的一支叫声学支（声频支），它很像单原子链中的声学支，；频率较高的一支则叫光学支（光频支）。

6、面缺陷有堆垛层错、小角晶界和晶粒间界三种主要形式。

8、一般情况下晶体电子的近似质量是张量，自由电子的惯性质量是标量。

9、对复式晶格，格波可分为声学波和光学波。

1、体心立方结构的第一布里渊区是菱形十二面体。

2、已知某晶体的基矢取为a1、a2、a3，某一晶面在三个基矢上的截距分别为3，2，-1，则该晶面的晶面指数为2363、倒格矢体现了晶面的面间距和法向。

8、晶体中的载流子是电子和空穴2、正格子原胞体积与倒格子原胞体积之积为233、金刚石晶体的基元含有2个原子，其晶胞含有8个碳原子。

6、准晶是介于周期性晶体和非晶玻璃之间的一种新的固体物质形态。

8、晶格振动的简化模型主要有爱因斯坦模型和德拜模型。

1、面心立方结构的第一布里渊区是十四面体。

2、代表基元中的几何点称为格点。

的声子所用的
对应电磁波的能量和波长
EO max
0.442 eV
2.8 m
E v 2 2c T
—— 要激发的声子所用的电磁波波长在近红外线波段 （Near Infrared）(NIR)
1 2
)i
本征态函数 ni (Qi )
i
exp(
2
2
)
H
ni
(
)
m d 2n
dt 2
(n1 n1 2n )
(n 1, 2, 3 , N )
得到
2 4 sin2( aq)
m
2
§3.3 一维双原子链 声学波和光学波 一维复式格子的情形 —— 一维无限长链 —— 两种原子m和M _( M > m) ____ 构成一维复式格子 —— M原子位于2n-1， 2n+1， 2n+3 …… —— m原子位于2n， 2n+2， 2n+4 …… —— 同种原子间的距离2a____晶格常数
4) 如果用电磁波激发光学波，要激发的声子所用的电磁波
波长在什么波段？
1) 声学波的最大频率
A max
3 1014
rad / s
光学波的最大频率
O max
5
2
M
6.7 1014
rad / s
光学波的最小频率
O min
2
m
6 1014 rad / s
2）相应声子的能量
EA max
0.198 eV
EO max
0.442 eV
EO min
0.396 eV
3) 某一特定谐振子具有激发能
的几率
根据归一化条件
归一化常数

4mM (m M )2
sin2
1
aq
2
独立的格波：
• 声学波（频率较低）
• 光学波（频率较高）
2 m
• 频率的禁带区
2
• 命名主要根据两种格波在长
M
波极限 ( q→0 ) 的性质
一维双原子链模型
声学波的长波极限
• 频率 q 0,
2 sin(aq) a
mM
2 q
mM
• 两种原子振幅比值
• 慢中子的能量：0.02~0.04 eV，与声子的能量同数量级； 中子的德布罗意波长：2~3×10-10 m（2~3 Å），与晶格常 数同数量级；可直接准确地给出晶格振动谱的信息
• 局限性：不适用于原子核对中子有强俘获能力的情况
典型晶格振动谱
Pb
Cu
典型晶格振动谱
Si GaAs
典型晶格振动谱
一维双原子链模型
一维双原子链模型
• 两种原子m和M (M > m) 构成一维复式格子
• M原子位于2n-1, 2n+1, 2n+3 … m原子位于2n, 2n+2, 2n+4…
• 晶格常数、同种原子间的距离：2a
• 第2n+1个M原子的方程
M
d 22n1
dt 2
(22n1 2n2
2n )
• 第2n个m原子的方程
• 离子晶体中光学波的共振能引 起对远红外光的强烈吸收，可
应用于红外光谱学
• 晶格振动谱可以利用中子、可见光光子或X光光子受晶格的 非弹性散射来测定。
• 中子（或光子）与晶格的相互作用即中子（或光子）与晶 体中声子的相互作用。中子（或光子）受声子的非弹性散 射表现为中子吸收或发射声子的过程。

m2 2 2 cos aq
在长波极限下， q 0
2 max
2
(M Mm
m)
2
B ( A)
m
2
2
2 cosqa
m M
表明：长波光学模中原胞内两原子作相对振动，而且原胞
质心保持不动。这一点很重要，例如离子晶体中，原胞内正、 负离子振动方向相反，产生迅速变化的电偶极矩，与光波耦 合必然影响其光学性质，这就是为什么称为光学模的原因。
2 min
m 2
m
2
(
B A)
m2 2 2 cos aq
B ( A)
m2 2 2 cosqa
0
表明基元中相邻原子作相对振动，这是光 学模的振动特点。
东北师范大学物理学院
3 – 3 一维双原子链
第三章 晶格振动与晶体的热学性质
相邻原子的运动情况
（声学支Acoustic branches）
24516710gmk???maxoeminoemaxaemino?15nm??maxo?4mm?maxa?41510dyncm?第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院1声学波的最大频率14max310arads???光学波的最大频率光学波的最小频率14610rads??max2am???4mm?15nm??max2o????02mmmmm????14max256710oradsm?????min2om???cmgs2m???radsgdyncm第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院max0442oeev?min0396oeev?max0198aeev?2相应声子的能量minminooe??min2om???maxmaxooe??max2o????max2am???maxmaxaae??第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院6周期性边界条件periodicboundarycondition表明

固体物理的思考题1.解理⾯是⾯指数低的晶⾯还是⾯指数⾼的晶⾯，为什么？答：解理⾯是指⾯与⾯之间的相互作⽤⼒⽐较弱，容易解离的⾯，若⾯间距⽐较⼤，则容易形成解理，晶⾯指数越⼤，⾯间距越⼩，晶⾯指数越⼩，⾯间距越⼤，所以是⾯指数低的晶⾯容易解离。

2.⾼指数的晶⾯族与低指数的晶⾯族相⽐，对于同级衍射，那⼀晶⾯族衍射光弱？为什么？答：由布拉格衍射公式，其中θ为⼊射x射线的掠射⾓，⾼指数的晶⾯族晶⾯间距d⽐较⼩，对于同级衍射，d越⼤，则越⼩，光的透射能⼒就越弱，此时形成的衍射光就⽐较弱。

也可以从另⼀⽅⾯考虑，晶⾯指数越⼤，晶⾯间距越⼩，原⼦密度也越⼩，此时对⼊射光的反射作⽤就⽐较弱，所以⾼指数晶⾯组的衍射光弱。

3.对于x射线衍射，可否将⼊射光改为可见光？答：不可以，主要由于原⼦的间距在?的数量级，根据布拉格衍射公式，可知⼊射光波的波长也应在?的数量级，然⽽可见光的波长⼀般为⼏百nm所以不可以改为可见光⼊射，常⽤的⼊射光⼀般为Cu的线1.54?。

4.在⼀般的单式格⼦中是否存在强烈的红外吸收，为什么？答：在离⼦晶体中的长光学⽀格波有特别重要的作⽤，因为不同离⼦间的相对振动产⽣电偶极矩，从⽽可以和电磁波相互作⽤，长光学波与红外光波的共振，引起对⼊射波的强烈吸收，但是对于单式格⼦（简单晶格）⽽⾔，由于是只包含单个原⼦，并不存在光学⽀格波，所以不会引起对红外光波的强烈吸收。

5.⾊散曲线中，能否判断哪知格波的模式密度⽐较⼤，是光学⽀格波还是声学⽀格波？答：在⾊散曲线中，光学⽀格波的⾊散曲线⽐较平缓，⽽声学⽀的⾊散曲线⽐较陡峭，模式密度表⽰在频率ω附近单位频率间隔内的格波数，由于光学⽀格波⾊散曲线变化平缓，对应⼩的ω区间就具有了较⼤的波⽮q的变化，所以光学⽀格波的模式密度⽐较⼤。

6.拉曼散射中光⼦会不会产⽣倒逆散射？答：拉曼散射是长光学波声⼦与光⼦（红外光）的相互作⽤，长光学波声⼦的波⽮很⼩，响应的动量⼩，产⽣倒逆散射的条件要求波长⼩，波⽮⼤，散射⾓⼤，拉曼散射不满⾜条件所以不会产⽣倒逆散射。

v h v h2 v h3 v 1. q = 1 b + b2 + b3, h、h2、h3 ∈Z 1 1 N1 N2 N3 v q点占据的体积： 平均一个 点占据的体积：示意图 v v v 3 3 b2 b3 1 (2π ) b 1 (2π ) 1 ⋅ × = ⋅ Ω* = ⋅ = N N N N1 2 N Ω V 3 1 V v v q的分布密度（单位体积 q点的数目）： 3 = 的分布密度（ 中 点的数目）： (2π ) (2π )3 V v q被限制在第一布里渊区
M 设 > m，则：
2β ω2min = m 2β (m+ M) ω 2m = ax mM
色散曲线
ω(q)为周期函数，周期为 ←倒易原胞长度 为周期函数，
a
π
π π + 将q限制在－ ， ←第一布里渊区 2a 2a
周期性边界条件
N 设晶体中有 个原胞 x1 = x2N+1 ⇒ Aei(ωt−qa) = Aei[ωt −q(2N+1)a] ⇒e−i 2qNa =1 ∴2qNa = 2π ⋅ l(l ∈Z) ⇒ q =
表示所有原子均以频 率ω振动，波矢为q。
− mω2 A = β eiqa + e−iqa B − 2βA ⇒ 2 iqa −iqa − Mω B = β e + e A− 2βB
( (
) )
2β − mω2 A−[2β cos(qa)]B = 0 −[2β cos(qa)]A+ 2β − Mω2 B = 0
一般情况下原子的振动方向既不平行也不垂直于q格波前进方向只在一些特殊方向通常是布里渊区的对称轴方向格波才可以分解成两个频率简并的横波振动方向与格波行进方向垂直和一个纵波振动方向与格波行进方向垂直支声学波而无光学波

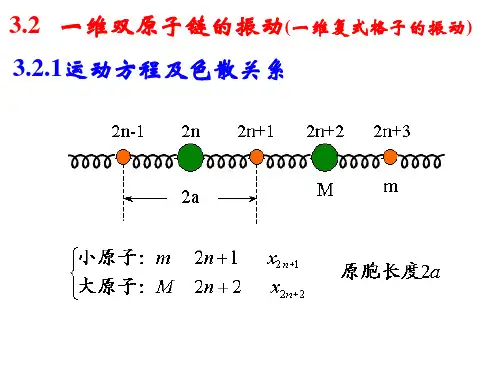
一维双原子链声学波和光学波1.双原子链模型一维双原子链模型是近代物理学中非常重要的模型之一，它可以用来研究固体中原子之间的相互作用及其导致的声学波与光学波的传播。

在双原子链模型中，两个原子之间由劲度系数$k$连接，两个原子之间的距离为$a$，另外一个原子的质量可以看作是无穷大，即它不参与振动。

因为只有一维，所以每个原子只能向左或向右振动。

2.声学波与光学波的区别声学波和光学波是通过双原子链模型分析得到的两种不同类型的波动。

声学波是一种可以在固体内部自由传播的机械波，它的传播需要原子之间的相互作用。

在双原子链模型中，声学波的速度为$\sqrt{\frac{k}{m}}$，其中$k$表示劲度系数，$m$表示质量。

光学波则是一种电磁波动，在固体内的传播需要原子中的电子参与，因此它的速度和谐振器中的电磁波速度相近。

在双原子链模型中，光学波的速度为$\sqrt{\frac{2k}{m}}$。

3.声学波与光学波的特征由于声学波和光学波的速度不同，它们在固体中的传播也存在差异。

当固体内没有缺陷时，声学波和光学波的传播是分离的。

当一个声学波到达固体表面时，它会被反射成相同的声学波，而当一个光学波到达固体表面时，它会被反射成相反的光学波。

此外，声学波可以在固体内部的任何位置传播，而光学波则不能。

在一个均匀无缺陷的双原子链中，只有声学波是存在的，光学波是不存在的。

4.应用双原子链模型和声学波与光学波的理论分析对于材料科学领域中的材料表征、纳米结构研究和器件设计等方面有很重要的应用价值。

例如，在纳米结构研究中，声学波能够帮助我们研究纳米材料的结构特征，而光学波则可以用来研究这些材料的光学性质。

总之，双原子链模型中的声学波和光学波不仅在理论上有很重要的应用价值，也在实践中发挥了重要作用。

对一维双原子链晶格振动的讨论祖春燕 06科教一班 指导教师：陈敬艳摘要：在固体物理中，一维原子链晶格振动是晶格振动理论的基础。

本文研究了一维双原子链晶格振动的色散关系，讨论了一维双原子链晶格振动的特点，并总结了几种不同情况的一维双原子链振动的色散关系。

关键词：晶格振动，色散关系，光学模，声学模一维双原子链晶格的振动是研究晶格振动理论的基础,它包含了晶格振动的主要性质，是固体物理教科书中不可缺少的内容。

但在固体物理教科书中对该现象的理论分析及总结并不完备,本文试图从一维双原子链晶格振动出发总结出各种讨论的情况，以弥补教科书中的不足。

为了简化问题，我们选择自由一维双原子链，并且考虑最近邻原子的相互作用。

1.一维双原子链的色散关系考虑一般的一维双原子链,即在一条直线上相间地排列着质量为m 、M 的原子（m<M ）,相邻原子之间的平衡距离为a,即原胞的大小为2a,以x 2n 表示第n 个原胞内质量为m 的原子离开平衡位置的位移,以x 2n+1表示第n 个原胞内质量为M 的原子离开平衡位置位移,假设只有相邻原子间存在相互作用，力常数为β,则第n 原胞内两个原子的运动方程为)2()2(1222212212122+++-+-+=-+=n n n n n n n n x x x xM x x x xm ββ其中,n=0,±1,±2，……这是一个无穷多个方程联立的方程组,该方程组有行波解，))12((12)2(2aq n t i n naq t i n Bex Ae x +-+-==ωω代入运动方程得到：BA e eB M A B e e A m iaqiaqiaq iaq ββωββω2)(2)(22-+=--+=---以A 、B 为未知数的线性齐次方程：M2n-22n-12n 2n+12n+2 2n+3)2(cos 20cos 2)2(22=-+=---B M aqA aqB A m βωβββω若 A 、B 有非零的解，系数行列式满足02cos 2cos 2222=--βωβββωM aq aqm非零解条件，利用求根公式，可解得如下形式解：⎭⎬⎫⎩⎨⎧+-±+=±aq m M Mm Mm m M 222sin )(411βω即一维双原子链的色散关系2.讨论一维双原子链晶格振动特点(1)存在两支w(q)与单原子链相比，双原子链情况存在着两支ω(q)关系。

确定声子的波矢:
确定声子的频率:
非弹性X-射线散射
• X 射线是在同振动着的晶格发生作用，因此除了衍射 现象外，电磁波还会和晶格发生能量的交换，入射波 吸收或者发射一个声子而发生能量和波矢的变化，这 就是X射线的非弹性散射。 • 由于X 射线频率（ 10 eV ）远大于声子频率（0.03eV）
确定波矢: 确定频率:
q0
sin 2 qa / 2 0

2
2
q
2 sin qa / 2 1 a
2
2
M m 2 2 [1 1] Mm Mm M m M m [1 1] 0 Mm M m M m 2 1 Mm M m m M m M m 2 1 Mm M m M
光子散射法
辐射波 X射线 可见光 声子 能量 （eV） 约10 几个 10-2 波矢 （cm-1） 108 105 108
• X射线能量太高，波矢（108 cm-1）和布里渊区接近。 • 激光可见光源的能量降低了，但波矢（105 cm-1）也降低了，和 晶体的布里渊区比小了。 • 因而，光散射只能和长波声子，即接近布里渊区心的声子发生 相互作用，涉及光学声子的称Raman 散射，涉及声学声子的称 Brilouin散射。 • 远红外和红外吸收光谱也只能测光学声子。 • 测定的晶格振动谱只是长波附近很小的一部分声子。
一、三维晶格振动 – 边界条件
一、三维晶格振动 – 边界条件
补充：关于波矢q （1）一维 m 2 b, q m, q
Na
Na
N
m = 0 , ±1 , ±2 ...
一个 m 值对应一个q 点，波矢取分离值，均匀分布相 邻 q 点 “距离”为 2 ，一个 q 点的“长度”为 2 q 空间中波矢q 的密度 =

3s
q
q i
dS
(3-48)
(3-45)
（四）格波的态密度函数
格波的态密度函数g()，又称为模式密度 数，其定义为
对于第 i 支格波，在频率 到 ＋ d 之间的 格波数，就等于在 q 空间频率为 到 ＋ d 这两个等频率面之间所包含的q点数，即
在附近单位频率间隔内的格波总数。
V g i d＝ 3 2
允许的波矢数＝晶体的初基元胞数 格波总数＝晶体振动的总自由度数
以后可以看到，此结论对三维晶体也是 适用的。
(二) .长波极限
当|q∣→0, λ→∞时, 相邻元胞间的振动相位差qa→0。 利用 cosqa ≈1 －（1/2）（qa）2 （1－x）1/2 ≈1－(x/2) （x为小量）， 式（3－24）可简化为
对声学支 A2＝A1
iqd d＜＜a , A2≈A1 e当
由于q→π/a，相邻元胞运动的相位差 qa→π。
声学支格波仍描述元胞内原子的同相整体运动
光学支格波仍描述元胞内原子的反相运动。
三 、三维晶格振动
设实际三维晶体沿基矢 a1、a2、a3 方向的初基 元 胞 数 分 别 为 N1、N2、N3， 即 晶 体 由 N＝ N1〃 N2〃 N3初基元胞组成，每个初基元胞内 含s个原子。 1 .原子振动方向 一维情况下，波矢 q 和原子振动方向相同， 所以只有纵波。 三维情况下，有纵波也有横波。
q＝2πm/Na m：整数 (3-27) 在第一布里渊区内，可取的q点数为
2 / a N 2 / Na
注意:

这里的N为一维晶格的初基元胞数。每个q对 应两个频率（ωA和ω0），则共有2N组（ω,q）， 所以一维双原子链有2N个格波，或说有2N个 简正模式。晶体中任何一原子的运动，为这 2N个格波所确定的谐振动的线性叠加。这时， 晶体的总自由度数也为2N，推广的结论：

一、名词解释1.晶态--晶态固体材料中的原子有规律的周期性排列，或称为长程有序。

2.非晶态--非晶态固体材料中的原子不是长程有序地排列，但在几个原子的范围内保持着有序性，或称为短程有序。

3.准晶--准晶态是介于晶态和非晶态之间的固体材料，其特点是原子有序排列，但不具有平移周期性。

4.单晶--整块晶体内原子排列的规律完全一致的晶体称为单晶体。

5.多晶--由许多取向不同的单晶体颗粒无规则堆积而成的固体材料。

6.理想晶体（完整晶体）--内在结构完全规则的固体，由全同的结构单元在空间无限重复排列而构成。

7.空间点阵（布喇菲点阵）--晶体的内部结构可以概括为是由一些相同的点子在空间有规则地做周期性无限重复排列，这些点子的总体称为空间点阵。

8.节点（阵点）--空间点阵的点子代表着晶体结构中的相同位置，称为节点（阵点）。

9.点阵常数（晶格常数）--惯用元胞棱边的长度。

10.晶面指数—描写布喇菲点阵中晶面方位的一组互质整数。

11.配位数—晶体中和某一原子相邻的原子数。

12.致密度—晶胞内原子所占的体积和晶胞体积之比。

13.原子的电负性—原子得失价电子能力的度量；电负性＝常数（电离能＋亲和能）14.肖特基缺陷—晶体内格点原子扩散到表面，体内留下空位。

15.费仑克尔缺陷--晶体内格点原子扩散到间隙位置，形成空位－填隙原子对。

16.色心--晶体内能够吸收可见光的点缺陷。

17.F心--离子晶体中一个负离子空位，束缚一个电子形成的点缺陷。

18.V心--离子晶体中一个正离子空位，束缚一个空穴形成的点缺陷。

19.近邻近似--在晶格振动中，只考虑最近邻的原子间的相互作用。

20.Einsten模型--在晶格振动中，假设所有原子独立地以相同频率ωE振动。

21.Debye模型--在晶格振动中，假设晶体为各向同性连续弹性媒质,晶体中只有3支声学波，且ω=vq 。

22.德拜频率ωD── Debye模型中g(ω)的最高频率。

23.爱因斯坦频率ωE──Einsten模型中g(ω)的最可几频率。

一维双原子链晶格振动光学支与声学支频隙宽度
一维双原子链是指由两种不同原子组成的线性排列，其晶格振动可以分为光学支和声学支两种模式。

光学支和声学支的频率随着波矢的变化而变化，且在一定波矢范围内存在频隙。

频隙是指在该波矢范围内，晶格振动不允许出现某些频率的波动。

光学支和声学支的频隙宽度受到多种因素的影响，包括原子间相互作用力的强度、原子质量、晶格常数等。

一维双原子链的光学支和声学支频隙宽度可以通过计算其声子频率来获得。

声子是指晶格中的一种元激发，其频率与晶格振动的频率相同。

在计算声子频率时，可以采用线性近似的方法，即将原子间相互作用力近似为线性势能，并将晶格振动分解为离散的几何位移。

然后，可以通过分别求解光学支和声学支波动方程，得到其频率随波矢的变化曲线。

通过分析曲线的特征，可以确定光学支和声学支的频隙宽度。

总的来说，一维双原子链的光学支和声学支频隙宽度是由其晶格结构和原子相互作用力等因素决定的。

通过计算其声子频率，可以获得光学支和声学支的频率随波矢的变化曲线，并从中获得频隙宽度。

原子的运动方程应是
即
求格波解，令
，
代入运动方程，可导出线性方程组为：
令 ，从A，B有非零解的系数行列式等于零的条件可得
可解出
色散关系见下图
时， ， ，
时， ， ，
3.6．在一维双原子链中，如 ，求证
[证]由书中（3.22）式知，双一维原子链声学支
， 由近似式 ，
得
，
对 ，由于 ，
3.7在一维双原子晶格振动情况中，证明在布里渊区边界 处，声学支格波中所有轻原子m静止，而光学支格波中所有重原子M静止。画出这时原子振动的图象。
1.8若基失a，b，c构成正交晶系，求证：晶面族（hkl）的面间距为
答：根据晶面指数的定义，平面族（hkl）中距原点最近平面在三个晶轴a1，a2，a3上的截距分别为 ， ， 。该平面（ABC）法线方向的单位矢量是
这里d是原点到平面ABC的垂直距离，即面间距。
由|n|=1得到 故
1.9用波长为0.15405nm的X射线投射到钽的粉末上，得到前面几条衍射谱线的布拉格角θ如下
用正交关系式
求出倒易点阵初基矢量b1，b2。设
由
得到下面四个方程式
（1）
（2）
（3）
（4）
由（1）式可得： 由（2）式可得： 由（3）式可得： 由（4）式可得：
于是得出倒易点阵基矢
第三章习题答案
3.1试求由5个原子组成的一堆单原子晶格的格波频率，设原子质量m＝8.35×10－27kg，恢复力常数β＝15N·m－1
（4）对于六方密堆积一个晶胞有两个原子，其坐标为（000）（1/3，2/3，1/2），在理想的密堆积情况下，密排六方结构中点阵常数与原子半径的关系为a=2r，因此θ= =
（5）对于金刚石结构Z=8 那么 = .

[mω2－（β1＋β2）]A1＋（β1e-iqa＋β2）eiqdA2＝0 （β1eiqa＋β2）e-iqdA1＋[mω2－（β1＋β2）]A2＝0
（3－22）
注意:该代数方程组与n无关。 A1、A2有非零 解的条件是其系数行列式为零：
mω2 －(β1＋β2) (β1e-iqa＋β2）eiqd ＝0 （β1eiqa＋β2）e-iqd mω2－(β1＋β2)

声学支格波仍描述原胞内原子的同相整体运动 光学支格波仍描述原胞内原子的反相运动。
三 、三维晶格振动
设实际三维晶体沿基矢 a1、a2、a3 方向的初基 原 胞 数 分 别 为 N1、N2、N3， 即 晶 体 由 N＝ N1·N2·N3初基原胞组成，每个初基原胞内含 s个原子。 1 .原子振动方向 一维情况下，波矢 q 和原子振动方向相同， 所以只有纵波。 三维情况下，有纵波也有横波。
当q→π/a时， 因 β2 >β1， 由式（3－23） ωO2 =（β1＋β2）/m+(β12＋β22＋2β1β2cosqa)1/2 /m 可得对于光学支格波
2 2 0＝ m
12
(3-32)
对于声学支格波,由(3-23)式 ωA2=（β1＋β2）/m (β12＋β22＋ 2β1β2cosqa)1/2 /m
2 / a N 2 / Na
注意:

这里的N为一维晶格的初基原胞数。每个q对 应两个频率（ωA和ω0），则共有2N组ω,q）， 所以一维双原子链有2N个格波，或说有2N个 简正模式。晶体中任何一原子的运动，为这 2N个格波所确定的谐振动的线性叠加。这时， 晶体的总自由度数也为2N，推广的结论：
允许的波矢数＝晶体的初基原胞数 格波总数＝晶体振动的总自由度数

收稿日期:2001-10-24　基金项目:教育部高等学校骨干教师资助计划项目　作者简介:田强(1962—),男,陕西西安人,北京师范大学物理系教授,博士,主要从事固体物理学教学、凝聚态非线性输运和半导体量子点实验研究.第22卷第2期大　学　物　理Vol.22No.22003年2月COLL EGE PHYSICS Feb.2003不同边界条件下一维双原子链的晶格振动田　强,张启义(北京师范大学物理系,北京　100875)摘要:在自由边界条件和驻波边界条件下,讨论分析了一维双原子链晶格振动的振动模和色散关系,并与周期性边界条件下的结果进行了比较;明确了在不同边界条件下讨论实际原子链晶格振动的振动模和色散关系,其结果是相同的.关键词:晶格振动;边界条件;振动模;色散关系 中图分类号:O 481 文献标识码:A 文章编号:100020712(2003)022******* 晶格振动的振动模和色散关系,通常都是在波恩-卡曼周期性边界条件下分析得到的;在周期性边界条件下,晶格振动的方程组具有一定的对称性,便于数学求解.但是,求解得到的振动模和色散关系是否依赖于周期性边界条件,在其他的边界条件下晶格振动的振动模和色散关系是否会有所不同,这些一直是固体物理教学中关注的问题.本文讨论在自由边界条件和驻波边界条件下,一维双原子链晶格振动的振动模和色散关系,并与周期性边界条件下的结果进行比较分析.1　波恩-卡曼周期性边界条件下的振动模和色散关系 考虑一般的由N 个原胞组成的一维双原子链,即在一条直线上相间地排列着质量为m 与M 的原子(m<M ),相邻原子之间的平衡距离为a ,即原胞的大小为2a.以u 2n -1表示第n 个原胞内质量为M 的原子离开平衡位置(2n -1)a 的位移,以u 2n 表示第n 个原胞内质量为m 的原子离开平衡位置2na 的位移,n =1,2,3,…,N.在简谐近似和最近邻近似下,考虑波恩-卡曼周期性边界条件[1],原子链的运动方程为:M d 2u 1d t 2=β(u 2N +u 2-2u 1)(1a )m d 2u 2d t 2=β(u 3+u 1-2u 2)(1b ) ……Md 2u 2n -1d t 2=β(u 2n +u 2n -2-2u 2n -1)(1c )m d 2u 2n d t 2=β(u 2n +1+u 2n -1-2u 2n )(1d )……Md 2u 2N -1d t 2=β(u 2N +u 2N -2-2u 2N -1)(1e )m d 2u 2N d t 2=β(u 1+u 2N -1-2u 2N )(1f )β是相邻原子之间的力常数.为了分析晶格振动的振动模,即形式为u s (t )～exp[i (qsa -ωt )]　s =1,2,3, (2)(2)波矢为q 、频率为ω的格波特解[2],将试探解:u 2n -1=B e i [q(2n -1)a -ωt ](3a )u 2n =A e i(q 2na -ωt )(3b )代入方程组(1),以确定振动模的波矢q 和相应的频率ω;其中由于一维双原子链包含有两种不同的原子,这两种不同原子的振幅一般也是不同的[3],故在上式表示的振动模(q ,ω)中小原子和大原子的振幅分别记为A 和B.正是由于采用了周期性边界条件,使方程组(1)具有很好的对称性,将试探解(3)代入方程组(1),只得到两个独立的方程: -M ω2B =β(e i qa +e -i qa )A -2βB (4a ) -m ω2A =β(e i qa +e -i qa )B -2βA (4b )由此得到色散关系:ω2±=β1m M(m +M )±(M -m )·1+4m M cos 2(qa )(M -m )21/2(5)这是大家熟知的一维双原子链晶格振动的色散关系,分为声频支和光频支.若取M =2m,上式可写为E ±=32±12[1+8cos 2(qa )]1/2(6)其中令E =mβω2.一维双原子链晶格振动的色散关系如图1所示.图1　一维双原子链(M =2m )的色散关系示意图同时,由周期性边界条件,有u 2n =u 2N +2n(7)得到振动模波矢q 的取值是分立的,为q l =2π2N al (l 为整数)(8)由进一步关于布里渊区的知识,可知振动模的波矢q l 取值的数目等于原子链的原胞数N ,相应的频率ω或E 取值数目为2N ,等于组成原子链的原子数.2　自由边界条件和驻波边界条件下的振动模和色散关系 上述的晶格振动色散关系和振动模波矢q 分立取值的分析讨论,都直接与边界条件有关,而对于实际的有限晶体,周期性边界条件是假想的[1].为了分析振动模和色散关系对边界条件的依赖性,下面改变边界条件,分别在自由边界条件和驻波边界条件下分析一维双原子链的振动模和色散关系.对于有限长一维双原子链,边界上的两个原子的运动方程与方程组(1)不同,没有周期性边界条件假想的原子的相互作用;边界上原子在自由边界条件和驻波边界条件下的运动方程分别为:自由边界条件下,M d 2u 1d t 2=β(u 2-u 1)(9a )m d 2u 2N d t 2=β(u 2N -1-u 2N )(9b )驻波边界条件下,令u 1(t )=u 2N (t )=0,有m d 2u 2d t 2=β(u 3-2u 2)(10a )Md 2u 2N -1d t 2=β(u 2N -2-2u 2N -1)(10b )其余原子的运动方程均与方程组(1)相同.为了分析晶格振动的振动模(q ,ω),将试探解(3)代入新的方程组;由于新的方程组没有了方程组(1)的对称性,给数学上确定解析解带来了困难;下面进行数值求解和分析.为了方便数值求解,且便于与图1比较,这里仍取M =2m ,E =mβω2.将试探解写为u s =Q q (s )e -i ωt s =1,2,3, (2)(11)代入运动方程组,得到关于Q q (s )的线性齐次方程组,下面分别对自由边界条件和驻波边界条件下的情况进行分析和求解.2.1　自由边界条件下的情况在自由边界条件下,关于Q q (s )的线性齐次方程组为1-2E-1-12-E-1-12-2E-1ω-12-2E-1-11-EQ q (1)Q q (2)Q q (3)　⁝Q q (2N -1)Q q (2N )=0(12)该线性齐次方程组有解的条件是其系数行列式为零,由此可以得到E 的2N 个可能取值,即得到一维双原子链晶格振动模频率ω的2N 个可能取值;对不同的E ,进一步由该线性齐次方程组,可以得到振动模的实空间振动曲线Q q (s )(s =1,2,3,…,2N ),由振动曲线可以确定振动模相应的波矢q.图2给出了几种不同情况下的计算结果.图中(a )、(b )、(c )分别是N =10、N =50和N =100的一维双原子链振动曲线,图中“.”表示大质量原子,“ ”表示小质量原子;各图中的E 都是方程组(12)系数行列式为零的解,各图中的两条振动曲线分别对应于E 的一个较小值E A 和一个较大值E O ;显然E A 振动模为原胞质心的振动,为声学模,E O 振动模为原子相对于质心的振动,为光学模.8大　学　物　理 第22卷图2　自由边界条件下振动模的振动曲线由图2所示的各个E 的振动曲线,通过确定声学模原胞质心的位移,或光学模中原子相对质心的位移,确定各个E 对应的波矢q ,可以得到色散关系E -q.2.2　驻波边界条件下的情况在驻波边界条件下,u 1(t )=u 2N (t )=0,即Q q (1)=Q q (2N )=0(13)关于Q q (s )的线性齐次方程组为2-E -1-12-2E-1ω-12-2EQ q (2)Q q (3)⁝Q q (2N -1)=0(14)由线性齐次方程组(14)的系数行列式为零,可得到E 的2(N -1)个可能取值,即得到驻波边界条件下振动模频率ω的2(N -1)个可能取值;对不同的E ,由该线性齐次方程组可以得到振动模的振动曲线Q q (s )(s =2,3,…,2N -1),通过振动曲线可以确定振动模相应的波矢q.图3给出了(a )N =10,E A =0.3068,E O =2.9199;(b )N =50,E A =0.0027,E O =2.9973;(c )N =100,E A =0.6340,E O =2.9893三种情况下的声学模和光学模的振动曲线.图3　驻波边界条件下振动模的振动曲线通过振动曲线,可确定声学模原胞质心的位移,或光学模中原子相对质心的位移,从而确定各个E 的振动模相应的波矢q ,得到色散关系E -q.驻波边界条件下晶格振动的色散关系如图4所示,自由边界条件下晶格振动的色散关系与之基本相同.9第2期 田　强等:不同边界条件下一维双原子链的晶格振动图4　驻波边界条件下一维双原子链(M=2m)的色散关系3　结果分析和讨论3.1　结果分析一维双原子链的晶格振动,在周期性边界条件下得到[1]:晶格振动频率的数目=晶体的自由度数晶格振动波矢的数目=晶体原胞数本文在自由边界条件和驻波边界条件下,得到了同样的结论.由N个原胞组成的一维双原子链,有2N 个原子;在自由边界条件和驻波边界条件下,通过原子振动的线性齐次方程组的系数行列式为零,分别得到2N和2(N-1)个振动模频率,由于驻波边界条件下实际参与振动的原子数为2(N-1),所以不同边界条件下振动模的数目都等于晶体的自由度数,与边界条件的选取无关.在自由边界条件和驻波边界条件下的数值计算表明,一维双原子链晶格振动分为声频支和光频支两支,由自由边界条件的2N个振动模频率和驻波边界条件的2(N-1)个振动模频率,分别得到N和N-1个波矢q,都等于晶体原胞数(在驻波边界条件下实际参与振动的原胞数为N-1).所以,对于周期性边界条件下的上述结论,在其他边界条件下具有同样的结论;上述结论与边界条件无关.在自由边界条件和驻波边界条件下,数值计算得到一维双原子链晶格振动的色散关系,随着原胞数的增多,色散关系逐渐趋于准连续的两支,与周期性边界条件下的结果相同.3.2　讨论晶格振动的色散关系,通常是在周期性边界条件下分析得到的,同时,已经在实际的晶体中得到了中子非弹性散射等实验的验证;换句话说,周期性边界条件下得到的晶格振动色散关系,是与边界条件无关的.实际的晶体大小总是有限的,存在着与体内原子环境不同的少数边界原子;在晶格振动的分析中,为了数学处理的简便,周期性边界条件中假想存在无穷多个相同的晶体,由于原子间互作用主要是短程的,实际的有限晶体中只有边界上极少数原子的运动才受到相邻的假想晶体的影响;对于一维原子链,通常晶体的原子线密度为107cm-1,边界上的原子只有两个,晶体中绝大部分原子的运动实际上不会受到这些假想晶体的影响.本文在自由边界条件和驻波边界条件下,讨论一维双原子链晶格振动的振动模和色散关系,得到了与周期性边界条件相同的结果,说明了周期性边界条件的合理性.参考文献:[1]　方俊鑫,陆栋.固体物理学[M].上海:上海科学技术出版社,1980.109～111.[2]　李正中.固体理论[M].北京:高等教育出版社,1985.25～26.[3]　方俊鑫,陆栋.固体物理学[M].上海:上海科学技术出版社,1980.104～105.(下转30页)焦距f与转动角速度ω的关系,从而求得凹面镜焦距与角速度的经验公式,能培养实验者分析现象和处理数据的能力.4)使用半导体激光器为光源,利用其单色、方向性和扩束小等特点,使实验测量精确度提高,使学生体会半导体激光器在物理实验中的作用.总之,通过这样一个实际综合性设计实验,有利于培养学生的创新能力和实验能力,是值得推荐的好实验.参考文献:[1]　贾起民,郑永令.力学　上册[M].上海:复旦大学出版社,1989.116～117.[2]　章志鸣,沈元华,陈惠芬.光学[M].北京:高等教育出版社,1995.[3]　谷超豪,数学词典[M].上海:上海辞书出版社,1992.182～183.A ne w kind of rotating liquid experiment———Introducing a kind of researchf ul physical experimentBAO Y i2liang,HUAN G Ji,L U Shen2long(Department of Physics,Fudan University,Shanghai,200433,China)Abstract:A new kind of rotating liquid experiment is introduced,through which,we can observe the phenomenon of centrifugal force,measure the acceleration due to gravity,investigate the linking of the focal distance in the optical system of the rotating liquid and the angular speedω,and observe the linking of the image produced by this system and the speed of rotation.K ey w ords:rotating liquid;centrifugal force;rotating parabolic surface;acceleration due to grav2 ity;optical system(上接10页)The lattice vibration of one2dimensional diatomic chain underdifferent boundary conditionsTIAN Qiang,ZHAN G Qi2yi(Department of Physics,Beijing Normal University,Beijing,100875,China) Abstract:The lattice vibration of one2dimensional diatomic chain is analyzed under the free bound2 ary condition and the stationary2wave boundary condition.The vibrational mode and dispersion relation are the same with those under the periodic boundary condition.In conclusion,the results of lattice vi2 bration under the periodic boundary condition are also true for other boundary conditions.K ey w ords:lattice vibration;boundary condition;vibrational mode;dispersion relation(上接22页) 1994,13(4):30～31.[3]　奥齐西克M N.热传导[M].北京:高等教育出版社,1983.663～678.[4]　郭忡衡.张量[M].北京:科学出版社,1988.142.An analysis of thermal diff usivity in anisotropic materialsXIN G Jin2hua(Department of Physics,Changshu College,Changshu,Jiangsu,215500,China) Abstract:The thermal diffusivity of anisotropic materials is analyzed.The relation between ther2 mal diffusivity to heat diffusion along arbitrary direction and principal thermal diffusicity is derived.A method to determine thermal diffusivity to heat diffusion along arbitrary direction is presented.K ey w ords:anisotropic sample;thermal diffusivity;principal axes。