下载文档原格式
用心 爱心 专心 三角形的内角和（一）教学目标：1.理解三角形的内角和定理的证明过程。
2.会按角的大小对三角形进行分类。
3.会初步运用内角和定理及推论1和方程思想进行简单计算。
教材分析教学重点：三角形内角和定理及其应用。
教学难点：三角形内角和定理证明中辅助线的添置。
教学过程： 1．猜想定理（1）三角形中三边满足什么关系？答：两边之和大于第三边，两边之差小于第三边。
（2）三角形的三个内角有什么关系呢？你有什么办法说明你的答案是正确的？ 答：用量角器量出三个内角的度数，计算得出三角形的内角和等于180度。
（3）度量有误差，无法得出准确答案，如何排除误差干扰呢？（根据学生回答可以运用拼图的方法得到证明方法.） 2.推导定理(1)分析证明思路：见下面图形A. 如图3.3(1)延长一边，延长BC 到D.B.如图3.3(2)过点A 作CE ∥BA.C.如图3.3(3)过点C 作CD ∥BA.D.如图3.3(4)过BC 上的一点D 作DE ∥AC 交AB 于E ，作DF ∥BA 交AC 于F.AB CD图3.3(1)AB图3.3(2)BB图3.3(3)图3.3(4)用心 爱心 专心教师根据任选一种方法进行证明，重点分析辅助线的作法目的，并板书其中的一种的详细证明过程，得到三角形内角和定理。
2.分析定理的内容、作用和变式形式. ①∠A=180°— ；②∠A+∠B=180°— ；③21∠A+21∠B+21∠C= ； ④21∠A=90°— ； ⑤21（∠A+∠B ）= ； 3.应用定理对三角形分类问题1：利用三角形的内角和定理判断，在一个三角形的三个内角中，能有几个钝角？能有几个直角？问题2：三角形中锐角的个数能有几个？还有其他情况吗？ 根据学生回答的情况小结：直角三角形锐角三角形 三角形斜三角形钝角三角形 练习1：判断对错(1)三角形的三个内角中，最多有一个角是钝角； (2)三角形的三个内角中，至少有两个角是锐角； (3)等腰三角形的底角一定是锐角； (4)等腰三角形的顶角一定是锐角； (5)直角三角形的两个锐角互余； 例1.在△ABC 中，⑴ ∠A=52°，∠B=118°，求∠C ；⑵ ∠A 是∠B 的2倍，∠C 比∠A+∠B 大12°，判断△ABC 的形状； ⑶ ∠C=90°，∠A 与∠B 差为20°，求∠B ；用心 爱心 专心⑷ ∠A ：∠B ：∠C=1：2：3，判断△ABC 的形状；⑸ ∠A=∠B 有一角是50°，求另两角；若有一角是110°呢？例2.如图3.3(5)，在△ABC 中，∠C=∠ABC ∠=2∠A ，BD 是AC 边上的高，求 ∠DBC 的度数例3.如图3.3(6)，AB ∥CD ，AD 和BC 交于E ，∠D=45°，∠CED=100°， ∠2=2∠1，求∠1和∠3的度数。
第4课时课题：三角形的内角和（1）教学目标通过实践活动，理解三角形三个内角的和等于180o，理解直角三角形的两锐角互余的性质。
了解三角形的分类教学重点、难点三角形三个内角和等于180o的性质。
教学过程1．合作学习：①请每个学生利用手中的三角形（已备），把三角形的三个角撕（或剪）下来，然后把这三个角拼起来，然后观察这三个角拼成了一个什么角？②请学生归纳这一结论，教师板书：三角形的三个内角的和等于180O③你能证明这个结论吗？（可以把角B平移到点C使点B和点C重合）2、三角形内角和性质的应用①口答：△ABC中，∠A=45O，∠B=60O，求∠C②△ABC中，∠A=57O18，，∠B=46O49，。
求∠C③△ABC中，∠A=∠B，∠C=110O，求∠A，∠B④△ABC中，∠A：∠B：∠C=1：2：3，求这个三角形的三个内角。
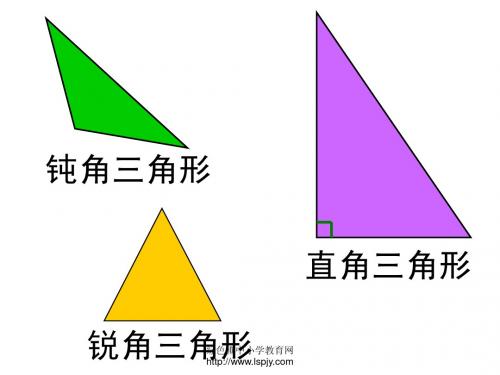
3、由上题练习得出图中三角形的形状①②得出的三角形的三个角都是锐角，这样的三角形称之为锐角三角形③得出的三角形有一个角是钝角，这样的三角形称之为钝角三角形④得出的三角形有一个角是直角，这样的三角形称之为直角的三角形钝角三角形和锐角三角形合称为斜三角形。
4、直角三角形（1）直角三角形的表示方法：Rt△；直角三角形ABC表示成Rt△ABC。
读作——（2）直角三角形的边：直角边；斜边。
（3）等腰三角形、等腰直角三角形的概念：（4）直角三角形的两锐角有什么关系？学生讨论后小结：直角三角形的两锐角互为余角。
若一个三角形为Rt△，那么它的其余两个锐角互余。
5、做一做：P125练习1、2、3题6：小结与探究：①三角形的内角和性质；三角形的分类。
②三角形的内角和是1800，任意四边形、五边形、六边形的内角和是多少呢？第5课时课题：三角形的内角和（2）教学目标理解三角形的一个外角等于和它不相邻的两个内角的和，一个外角大于任何一个和它不相邻的内角，三角形的外角和3600的性质。
运用三角形的内角和外角和的性质简单的几何问题。
