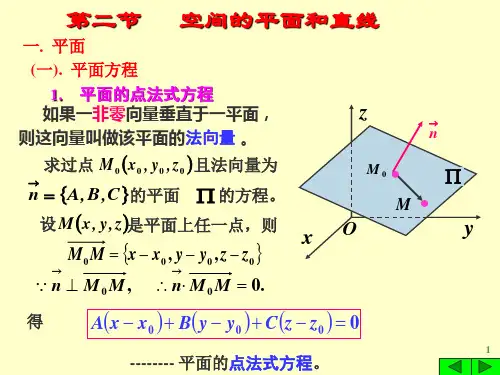
《高等数学》(北大第二版 )5-3空间中平面及直线的方程

空间图形的基本关系与公理__________________________________________________________________________________ __________________________________________________________________________________理解和掌握平面的性质定理，能合理运用；掌握直线与直线、直线与平面、平面与平面的位置关系； 会判断异面直线、掌握异面直线的求法；会用图形语言、符号语言表示点、线、面的位置关系．一、平面1.平面的概念：平面是一个不加定义，只需理解的原始概念．立体几何里所说的的平面是从现实生活中常见的平面抽象出来的．常见的桌面、平静的水面等都给我们以平面的部形象．平面是理想的、绝对的平且无大小，无厚度，不可度量． 2.平面的表示方法：(1)一个平面： 当平面是水平放置的时候，通常把平行四边形的锐角 画成45o，横边画成邻边的2倍长，如右图． (2)两个相交平面：画两个相交平面时，通常要化出它们的交线，当一个平面的一部分被另一个平面遮住，应把被遮住部分的线段画成虚线或不画（如下图）3. 运用集合观点准确使用图形语言、符号语言和文字语言空间图形的基本元素是点、直线、平面从运动的观点看，点动成线，线动成面，从而可以把直线、平面看成是点的集合，因此还可借用集合中的符号语言来表示点、线、面的基本位置关系如下表所示：αBAβαABαβαβBAAβαBA a ∈ 点A 在直线a 上A a ∉ 点A 不在直线a 上A α∈ 点A 在平面α内A α∉ 点A 不在平面α内a b A =I 直线a 、b 交于A 点a α⊂直线a 在平面α内a α=∅I 直线a 与平面α无公共点a A α=I直线a 与平面α交于点Al αβ=I 平面α、β相交于直线l二、平面的基本性质1. 公理1 如果一条直线的两点在一个平面内，那么这条直线上的_____都在这个平面内推理模式：A AB B ααα∈⎫⇒⊂⎬∈⎭． 如图示： 或者：∵,A B αα∈∈，∴AB α⊂ 公理1的作用：①判定直线是否在平面内；②判定点是否在平面内； ③检验面是否是平面．2. 公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的______推理模式：A A l A ααββ∈⎫⇒∈=⎬∈⎭I 如图示： 或者：∵,A A αβ∈∈，∴,l A l αβ=∈I 公理2的作用：(1)判断两个平面是否相交及交线位置； (2)判断点是否在线上今后所说的两个平面(或两条直线),如无特殊说明,均指不同的平面(直线)．(1)以上是确定平面的四个不同的条件，是判断两个平面重合的依据，是证明点线共面的依据，也是作截面、辅助面的依据．(2)有且只有一个”的含义要准确理解．这里的“有”是说图形的存在，“只有一个”是说图形唯一．因此，在证明有关这类语句的命题时，要从“存在性”和“唯一性”两方面来论证． 3. 公理3____________________________________________推理模式：,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合或者：∵,,A B C 不共线，∴存在唯一的平面α，使得,,A B C α∈. 推论1：经过一条直线和这条直线外的一点，有且只有一个平面； 推论2：经过两条相交直线，有且只有一个平面； 推论3：经过两条平行直线，有且只有一个平面．(1)以上是确定平面的四个不同的条件，是判断两个平面重合的依据，是证明点线共面的依据，也是作截面、辅助面的依据．(2)“有且只有一个”的含义要准确理解．这里的“有”是说图形的存在，“只有一个”是说图形唯一．因此，在证明有关这类语句的命题时，要从“存在性”和“唯一性”两方面来论证． 三、空间两直线的位置关系四、平行直线 1. 公理4 平行公理__________________________________________推理模式：//,////a b b c a c ⇒．(1)它是判断空间两条直线平行的依据； (2)它说明平行关系具有传递性 2.等角定理如果一个角的两边和另一个角的两边分别平行，且方向相同，那么这两个角_______． 由球的半径R 计算球表面积的公式：S 球＝4πR 2.即球面面积等于它的大圆面积的4倍． 五、异面直线 1. 定义：不在任何一个平面内的两条直线叫做异面直线(1)异面直线既不平行，也不相交，永远不存在一个平面能同时包含这两直线； (2)不能把异面直线误认为：分别在不同平面内的两条直线为异面直线 (3)异面直线一般是对两条直线而言的，没有三条异面直线的说法． 2．异面直线的画法画异面直线时，为了充分显示不共面的特点，常常需要以辅助平面为衬托，以加强直观性．ba αbaαβbaα3．异面直线判定定理过平面内一点与平面外一点的直线，和这个平面内不经过该点的直线是异面直线推理模式：l A B B L ααα⊂⎫⎪∉⎪⇒⎬∈⎪⎪∉⎭直线AB 与直线l 是异面直线六、异面直线所成的角 1. 定义：已知a ，b 是两条异面直线，经过空间任意一点O 作直线//,//a a b b ''，我们把直线a '和b '所成的锐角（或直角）叫做异面直线a ，b 所成的角．(1)异面直线所成的角与O 点的位置无关．(2)如果两条异面直线所成角是直角，则说这两条异面直线互相垂直，记作a b ⊥． (3)异面直线所成角的范围是______． 2. 求异面直线所成角的步骤（1）恰当选点，由平移构造出一个交角； （2）证平行关系成立；（3）把角放入三角形或其它平面图形中求出；（4）作结论：若求出的角是锐角或直角，则它就是所求异面直线所成的角；若求出的角是钝角，则它的补角才是所求异面直线所成的角． 七、直线、平面的位置关系1．空间直线与平面的位置关系有以下三种：(1)直线在平面内：如果一条直线a 与平面α有两个不同的公共点，那么这条直线就在这个平面内，记作a ⊂α.(2)直线与平面相交：直线a 与平面α只有一个公共点A ，叫做直线与平面相交，记作a ∩α＝A ，公共点A 叫做直线a 与平面α的交点．(3)直线与平面平行：如果一条直线a 与平面α没有公共点，叫做直线与平面平行，记作a ∥α. 2.两个平面的位置关系有且只有一下两种： (1)两个平面平行---没有交点 (2)两个平面相交---有一条公共直线3.顺次连接不共面的四点A 、B 、C 、D 所构成的图形，叫做空间四边形．这四个点中的各个点叫做空间四边形的顶点；所连接的相邻顶点间的线段叫做空间四边形的边；连接不相邻的顶点的线段叫做空间四边形的对角线．类型一 平面及其性质例1：(2014·邵阳一中月考)对下图的几何图形，下列表示错误的是( )A ．l ∈αB ．P ∉lC ．l ⊂αD ．P ∈α练习1：判断下列说法是否正确，并说明理由．（1）平面的形状是平行四边形（ ） （2）任何一个平面图形都可以表示平面（ ） （3）平面ABCD 的面积为10㎡（ ） （4）空间图形中，后引的辅助线是虚线（ ） 练习2：1、下列说法正确的个数（ ）①铺的很平的一张纸是一个平面；②可以一个长20cm 、宽30cm 的平面；③通常300页的书要比10页的书厚一些，那么300个平面重合在一起时一定比10个平面重合在一起厚．A 、0个B 、1个C 、2个D 、3个 练习3：若点Q 在直线b 上，b 在直线平面β内，则,,Q b β之间的关系可记作（ ）A 、Q b β∈∈B 、Q b β∈⊂C 、Q b β⊂⊂D 、Q b β⊂∈例2：如右图，已知,,,E F G H 分别为空间四边形ABCD 各边,,,AB AD BC CD 上的点，且EF GH P =I ，求证：,,B D P 共线．练习1：已知l 与三条平行线,,a b c 都相交，求证：l 与,,a b c 共面． 练习2：两个不重合的平面有公共点，则公共点的个数是（ ）A 、2个B 、有无数个且在一条直线上C 、一个或无数个D 、1个练习3：下列命题：①公理1可用集合符号叙述为：若,A l B l ∈∈且,A B αα∈∈，则必有l α∈；②四边形的两条对角线必交于一点；③用平行四边形表示的平面，以平行四边形的四边作为平面边界线；④梯形是平面图形．其中正确的命题个数为（ ）A 、1B 、2C 、3D 、4 类型二 直线及其位置关系例3：(2014·甘肃嘉峪关市一中高一期末测试)若a 、b 是异面直线，直线c ∥a ，则c 与b 的位置关系是( ) A ．相交 B ．异面 C ．平行 D ．异面或相交练习1：在长方体ABCD －A 1B 1C 1D 1中，E 、F 分别是BD 和CD 的中点，长方体的各棱中与EF 平行的有( )A ．1条B ．2条C ．3条D ．4条 练习2：空间四边形ABCD 中，给出下列说法：①直线AB 与CD 异面； ②对角线AC 与BD 相交； ③四条边不能都相等；④四条边的中点组成一个平行四边形． 其中正确说法的个数是( ) A ．1个 B ．2个 C ．3个 D ．4个PH GF EDC BA练习3：a 、b 、c 是空间中三条直线，下面给出几种说法：①若a ∥b ，b ∥c ，则a ∥c ；②若a 与b 相交，b 与c 相交，则a 与c 也相交；③若a 、b 分别在两个相交平面内，则这两条直线不可能平行． 上述说法中正确的是________(仅填序号)．例4：已知正方体1111ABCD A B C D -,E 、F 分别为1AA 、1CC 的中点，求证:1//BF ED 练习1：已知棱长为a 正方体1111ABCD A B C D -,M 、N 分别为CD 、AD 的中点， 求证:四边形11MNA C 是梯形练习2：已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点，若AE AB ＝AH AD ＝12，CF CB ＝CG CD ＝13，则四边形EFGH 形状为________． 例5：已知E 、1E 分别是正方体1111ABCD A B C D -的棱AD 、11A D 的中点． 求证：111BEC B E C ∠=∠练习1：如右图，111,,AA BB CC 不共面，且1111//,//BB AA CC AA ,求证：△ABC ≌△111A B C练习2：在平行六面体ABCD －A 1B 1C 1D 1中，M 、N 、P 分别是CC 1、B 1C 1、C 1D 1的中点．求证：∠NMP ＝∠BA 1D .例6：如右图，已知不共面的直线,,a b c 相交于O 点，M 、P 是直线a 上 两点，N 、Q 分别是直线b 、c 上一点．求证：MN 和PQ 是异面直线． 练习1：两条异面直线是指（ ）A 、空间没有公共点的两条直线B 、分别位于两个平面内的直线C 、平面内的一条直线与平面外的一条直线D 、既不平行也不相交的两条直线练习2：下列说法正确的有__________．c ba OQP NM①两直线无公共点，则两直线平行；②两直线若不是异面直线，则必相交或平行；③过平面外一点与平面内一点的连线，与平面内的任一直线均构成异面直线；④和两条一面直线都相交的直线的两直线必是异面直线．练习3：已知,,a b a b A αββ=⊂=I I 且,//c c a α⊂，求证：b ，c 为异面直线．例7：正四面体A BCD -的棱长为a ，E 、F 分别为棱AD 、BC 的中点，求异面直线AF 和CE 所成角的余弦值．练习1：已知m 、n 为异面直线，m α⊂，n β⊂，l αβ=I ，则直线l （ ）A 、与m 、n 都相交B 、与m 、n 至少一条相交C 、与m 、n 都不相交D 、至多与m 、n 中的一条相交练习2：在棱长为1的1111ABCD A B C D -中，M 和N 分别为11A B 和1BB 的中点，那么直线AM 与CN 所成角的余弦值是（ ）ABC 、35D 、25练习3：如右图，等腰直角三角形ABC中，90,,A BC DA AC DA AB ∠==⊥⊥o,若1DA =，且E 为DA 的中点．求异面直线BE 与CD 所成角的余弦值．1．在空间内，可以确定一个平面的条件是（ ）A 、两两相交的三条直线B 、三条直线，其中的一条与另外两条直线分别相交C 、三个点D 、三条直线，它们两两相交，但不交于同一点E 、两条直线 2．分别和两条异面直线都相交的两条直线的位置关系是( )A ．异面B ．相交C ．平行D ．异面或相交3．一条直线与两条平行线中的一条是异面直线，那么它与另一条的位置关系是（ ）A 、相交B 、异面C 、平行D 、相交或异面4．从空间一点P 分别向BAC ∠的两边,AB AC 作垂线,PE PF ，垂足分别为,E F ，则EPF ∠与BAC ∠的关系为（ ）A 、互补B 、相等C 、互补或相等D 、以上都不对5．在正四面体A BCD -中，E 为AD 的中点，则AB 与CE 所成角的余弦值为_______．_________________________________________________________________________________ _________________________________________________________________________________基础巩固1. 空间有四个点，其中无三点共线，可确定_______个平面；若将此四点两两相连，再以所得线段FE D CBA中点为顶点构成一个几何体，则这个几何体至多有_______个面． 2、三个两两相交的平面最多可把空间分为_______个部分． 3、下面6个命题：①四边相等的四边形是菱形；②两组对边相等的四边形是平行四边形；③若四边形有一组对角相等，则该四边形是圆内接四边形；④在空间，过已知直线外一点，引该直线的平行线，可能不只一条；⑤四条直线两两平行，无三线共面，它们共可确定6个平面．其中正确命题的个数是（ ）A 、0B 、1C 、2D 、34. 在正方体1111ABCD A B C D 中，与1AD 成60o 的面对角线共有（ ）A 、4条B 、6条C 、8条D 、10条5. 已已知棱长为a 的正方体ABCD －A ′B ′C ′D ′中，M 、N 分别为CD 、AD 的中点，则MN 与A ′C ′的位置关系是________．能力提升6. (2014·山东泰安肥城高一期末测试)如图，点P 、Q 、R 、S 分别在正方体的四条棱上，且是所在棱的中点，则直线PQ 与RS 是异面直线的一个图是________．7. 若直线a 、b 与直线l 相交且所成的角相等，则a 、b 的位置关系是( )A ．异面B ．平行C ．相交D ．三种关系都有可能8. 如图，在长方体ABCD －A 1B 1C 1D 1中，A 1C 1∩D 1B 1＝O ，E 、F 分别是B 1O 和C 1O 的中点，则在长方体各棱中与EF 平行的有________条．9. 如图，a ∥α，A 是α的另一侧的点，B ，C ，D ∈a ，线段AB ，AC ，AD 分别交平面α于E ，F ，G ，若BD ＝4，CF ＝4，AF ＝5，则EG ＝________.10. 如右图，正方体1111ABCD A B C D 中，求AC 与1A D 所成角的大小课程顾问签字： 教学主管签字：F ED 1C 1B 1A 1DCBA。

习题5・31•指出下列平面位置的特点：(1)5x - 3z +1 = 0(2)x + 2y - 7z = 0(3)y + 5 = 0(4)2)，- 9z = 0(5)x-y-5 = 0(6)x = 0. 解⑴平行于屛由.⑵过原点.⑶平行于平面.⑷ 过兀轴.(5)平行于z轴•⑹0〃平面.2.求下列各平面的方程：⑴平行于y轴且通过点(1,-5,1)和(3,2,-2);(2)平行于O私平面且通过点(5,2,-8);(3)垂直于平面兀-4y + 5z = 1且通过点(-2,7,3)及(0,0,0);⑷垂直于Oyz平面且通过点(5,-4,3)及(-2,1,8).1j k解⑴—(0 ,l,0),* = (2,7,-3),n= 0 1 0 =(-3,0,-2).27-3_3O_1)_2(Z_1)=0,3JC +2Z_5=0.⑵y = 2.i j k(3)a = (1,-4,5), 6 = (-2,7,3),n = 1 -4 5 = (-47,-13,-1).-2 7 347x+13y+ 1 = 0.i j k(4)“ = (1,0,0),〃 = (-7,5,5),〃= 1 0 0 =(0,-5,5) = 5(0, -1,1).-7 5 5_(y + 4) + (z_3) = 0,y_z + 7 = 0.3.求通过点A(2,4,8), B(-3,1,5)及C(6,—2,7)的平面方程.解 a = (一5, —3,—3),〃 = (4,-6,-1).i j kn= -5 -3 -3 =(-15,-17,42),4 -6 -1一15(兀一2) —17(y — 4) + 42(z — 8) = 0,15x + 17y —42z + 238 = 0.4.设一平而在各坐标轴上的截距都不等于零并相等,且过点(5, -7, 4),求此平而的方程.解—+ —+ — = 1, —H—+ — = l,a = 2, x + y + z — 2 = 0.a, a a a a a5已知两点4(2,-1,-2)及〃(8,7,5),求过B且与线段AB垂直的平面.解〃 =(6, & 7).6(x-8) + 8(y-7) + 7(z-5) = 0,6x + 8y + 7z-139 = 0.6.求过点(2,0, -3)且与2兀-2y + 4z + 7 = 0,3x+y-2z + 5二0垂直的平面方程.i j k解 n= 2 -24 =(0,16,8) = 8(0,2,l).2y + (z + 3) = 0,y + z + 3 = 0. 3 1 -27.求通过兀轴且与平面9兀-4y-2z + 3 = 0垂直的平面方程. 解 By + Cz=0,—4B —2C = 0,取B = 1,C = —2,y —2z = 0.8•求通过直纟划:｛；；工：二5地:仁鳥平行的平面方程. i j ki j k 解a = 1 0 2 = (-6,1,3), 6 = 1 -1 0= (1,1,1), 0 3-10 1 -1 i j kn - -6 13 =(-2,9,-7).用z ()= 0代入厶的方程，得x° =4,>\} =-8/3.1 1 1 -2(x-4) + 9(^ + 8/3)-7(z) = 0,-2x + 9y-7z + 32 = 0.x = 3r + 89.求直线厶：* +彳=•' +1 = __与直线/ ：< y = f + l 的交点坐标,3 24 _ 小， z = + 6并求通过此两直线的平面方程.解求两条直线交点坐标：3r + 8 + 3 / + 1 + 1 2/ + 6 —2 \\ t t A 163 24 3 2 23 i j kn= 3 2 4 = (0,6, -3) = 3(0,2, -l).2(y +1) - (z - 2) = 0,2y - z + 4 = 0.3 1 2 10•求通过两直线厶=^ = 凹和厶：土 = □=三的平面方程. 1 2 -1 1 -4 2 -2i j k解 两直线平行•平面过点(1,-1,-1)和(-2,2,0).川=2 — 1 1 = (—4,—5,3).-33 1一4(兀一 l)-5(y + l) + 3(z + l) = 0,-4x — 5y + 3z + 2 = 0.11证明两直线厶：口和是异面直线*-121 - 0 1 -2证首先，两直线的方向向量(-1,2,1)和(0,1,-2)不平行.x 二 _2l 2< y 二1+t —―二匕〜 力+ 3J = 5』= 0,矛盾.故两直线无公共点.-1 2 1 X Q = 一& 儿=一一牛交点(一8占弓)两-直线不平行，又无交点，故是异面直线. 12.将下列直线方程化为标准方程及参数方程：[2x+y-z + l = 0 [x-3z + 5 = 0(1* ⑵彳[3x - y + 2z - 8 = 0; [y - 2z + 8 = 0.i j k解(1)〃= 2 1 -1 =(1,-7,-5).3-12V — 7 + 1 = 0⑴中令兀0=0,{ 解Z得儿=6,Zo=7・-y+ 2z-8 = 0;标准方程—q・1 -7 -5x = t参数方程：< y = 6-lt,-oo <t < +oo.z = l-5ti j k(2)(1加=1 0 -3 =(3,2,1).0 1 -2⑵中令z° = 0,直接得x° = -5, y Q = -8.标准方程出二凹二工3 2 1x ——5 + 3t参数方程：* >' = -8 + 2r,-co<t < +oo.z = t13•求通过点(32-5)及乂轴的平面与平面3x-y-7z + 9 = 0的交线方程・ ■I j k解地第一个平面的法向量〃二1 0 0 =(0,5,2), 3 2 -5平面方程5y + 2z = 0.直线方程严+ 2*°[3 兀-y-7z + 9 = 0.i j k直线的方向向量a =0 5 2 =(一336-15) = 3(-112-5)・3 -1 -7直线方程:r 匕14 •当D 为何值时,直线产？ £弓与0z 轴相交?[x + 4y-z + D = 0解直线F ：y + 2z-6弓与Oz 轴相交O 存在(0,0,勺)在此直线上，[x + 4y-z + £> = 0f2z o -6 = O <=> < u> £> =知=3. Ho+o=o15.试求通过直线人：£一2"：弓并与直线Z. = 2平行的平面方程.[3y — z + 8 = 0 *•匕 _y + 6 = 0i J k解厶的方向向&a = 1 0 -2 =(6丄3).0 3-1i J 平面的法向量/i =6 1 1 1 Q 在的方程中令z ()二0得X 。

82 第五章 向量代数与空间解析几何§5.1 向量代数(甲)内容要点内容要点一、空间直角坐标系一、空间直角坐标系 二、向量概念二、向量概念®a ＝®i x +®j y +®k z坐标()z y x ,,模®a ＝222z y x ++ 方向角g b a ,,方向余弦g b a cos ,cos ,cosa cos ＝222zy x x ++ ；b cos ＝222zy x y ++ ；g cos ＝222zy x z ++三、向量运算三、向量运算设®a ()11,1,z y x ；®b ()22,2,z y x ；®c ()33,3,z y x 1． 加（减）法加（减）法®a ±®b ＝()2121,21,z z y y x x ±±± 2． 数乘数乘 ()111,,z y x a l l l l =®3． 数量积（点乘）（ⅰ）定义®a ·®b =®a®b ÷øöçèæ®®Ðb a ,cos （ⅱ）坐标公式®a ·®b =21x x +21y y +21z z （ⅲ）重要应用®a ·®b =0Û®a ^®b4．向量积（叉乘）（ⅰ）定义®a ´®b ＝®®ba ÷øöçèæ®®Ðb a ,sin ®a ´®b 与®a 和®b 皆垂直，且®a ，®b ，®a ´®b 构成右手系构成右手系83（ⅱ）坐标公式®a ´®b =222111z y x z y x k j i®®®（ⅲ）重要应用®a ´®b =®0Û®a ，®b 共线共线5、混合积、混合积 （ⅰ）定义（ⅰ）定义（®a ，®b ，®c ）＝（®a ´®b ）·®c （ⅱ）坐标公式（®a ，®b ，®c ）=333222111z y x z y x z y x （ⅲ）÷øöçèæ®®®c b a ,,表示以®a ，®b ，®c 为棱的平行六面体的体积为棱的平行六面体的体积§5.2 平面与直线（甲）内容要点（甲）内容要点一、一、 空间解析几何空间解析几何1 空间解析几何研究的基本问题。