当前位置：文档之家 › 空间直线及其方程ppt课件

空间直线及其方程ppt课件

  • 格式：ppt
  • 大小：340.00 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

高等数学 第5讲 空间直线及其方程

高等数学 第5讲 空间直线及其方程


与直线
2 3
x x

2 8
y y

z z

23 18

0 0
的夹角的余弦为__________；
3、 直
线

x x

y y

3z 0 z0
和平面
x

y

z

1

0
在平
面 x 2 y z 1 0上的夹角为___________；
4、点(1 , 2 , 0 )在平面x 2 y z 1 0上的投影为
设直线 L 的方向向量为 s (m, n, p) 平面 的法向量为 n (A, B,C )
则直线与平面夹角 满足
︿ sin cos( s , n )
ns L

sn sn

Am Bn C p m2 n2 p2 A2 B2 C2
特别有:
(1) L

D1 D2
0 0
对称式
参数式

x y

x0 y0
m n
t t
z z0 p t
(m2 n2 p2 0)
2. 线与线的关系
直线
L1：x
x1 m1

y
y1 n1

z
z1 p1
,
直线
L2：x
x2 m2

y
y2 n2

z
z2 p2
,
L1 L2
比例，所以对于任何一个 值，方程(3)的系数：
A1 A2、B1 B2、C1 C2不全为零，从而方程(3)表示
空间直线方程PPT课件

空间直线方程PPT课件

空间直线的一般方程25直线的点向式方程其中方向向量26两直线的夹角公式求上半球与圆柱体的公共部分在2121xoy公共部分体在坐标面的投影为圆面xoz公共部分体在坐标面的投影为37页习题84282121axxoyxoz求上半球与圆柱体的公共部分在2121消去参数xoz消去参数30定义直线和它在平面上的投影直线的夹cpbnamsincos32直线与平面的位置关系
i
j k
3i 4 j k
2 1 3 1 3 2
ijk
s2 n3 n4 2 2 1
38 1
2 1 2 1 2 2
i 8
j 13
k 13
8 10i 5 j 10k
第22页/共64页
s1 s2 cos( L1 , L2 ) s1 s2
30 20 10
0.
9 16 1 100 25 100
y3
z4
1
1
2
的解。
2x y z 6 0
利用直线的参数方程求解更简便
第39页/共64页
设 x2 y3 z4 t
1
1
2
x 2 t, y 3 t, z 4 2t
代入题中平面方程 2 x y z 6 0
中得：4 2t 3 t 4 2t 6 0
t 1
代入参数方程中得： x 1, y 2, z 2
注：
x
同一条直线的方向向量有无穷多个。
有单位向量，还有一般的向量。
第5页/共64页
下面导出直线的点向式方程
z
s
L
M0( x0, y0, z0 ), s (m, n, p),
M L, M ( x, y, z),
M M0
o
y
M0M// s
空间直线方程 ppt课件

空间直线方程 ppt课件


y0
2 1.5
交线在xoz坐标面的投影
1 0.5
-02
消去参数y,
z
2
a2
ax
y 0 PPT课件
-1 0 1
2
30
四、直线与平面的夹角
定义 直线和它在平面上的投影直线的夹
角 称为直线与平面的夹角．
0 .
2
L : x x0 y y0 z z0 , sr (m, n, p),
:
m
n
p
s1 s2
cos(L1, L2 ) ur ur
s s 1PPT课件2
20
281
2
cos(L1 , L2 )
. 1 16 1 4 4 1 2
所以两直线的夹角为 . 4
PPT课件
21
练习
求直线
5x 3y 3z 9 0
3x
2y
z
1
0
与
直线
2x
3
x
2 8 uur
y y
z z
PPT课件
9
从空间直线的一般方程到对称式方程
L
:
A1 A2
x x
B1 B2
y y
C1z C2z
D1 D2
0 0
先在直线上任取一点。再求直线的方向向量。 uur
1 : A1 x B1 y C1z D1 0 nuu1r (A1, B1,C1) 2 : A2 x B2 y C2z D2 0 n2 ( A2 , B2 ,C2 )
代入题中平面方程 2 x y z 6 0
x x0 y y0 z z0 直线的对称式方程
m
n
p
PPT课件
7
下面得出直线的参数方程
第六节 空间直线及其方程.ppt

第六节 空间直线及其方程.ppt


其中系数 A1、B 1、C 1 与 A 2、B 2 、C 2 不成比例. 方程
A1x B1y C1z D1 A2x B2 y C2z D2 0
表示通过直线 L 的平面束(通过直线L 的平面的全体), 其中 是任意常数.
例6
求直线
x y z1 0
A2 B2 C 2 m2 n2 p2
| 1 2 (1) (1) 2 2 | 7 .
6 9
36
arcsin 7 为所求夹角．
36
五、平面束
设直线 L 的方程为

A1x A2 x

B1 y B2 y
C1z D1 0, C2z D2 0
y0
z0 2 0 , 3z0 6 0
解得 y0 0, z0 2
点坐标 (1,0,2),
因所求直线与两平面的法向量都垂直
取
s

n1

n2

{4,1,3},
对称式方程 x 1 y 0 z 2 , 4 1 3
x 1 4t
(s^,n)
2
(s^,n)
2
sin

cos
2



cos
2
.
sin
| Am Bn Cp | A2 B2 C 2 m2 n2 p2
直线与平面的夹角公式
直线与平面的位置关系：
(1)
L

A B C. mn p
第六节 空间直线及其方程
空间直线方程 空间直线和直线，直线和平面的
夹角
第8章第6节空间直线及其方程

第8章第6节空间直线及其方程

第六节 空间直线及其方程
一、空间直线的一般方程 二、空间直线的对称式方程与参数方程 三、两直线的夹角 四、直线与平面的夹角
五 平面束
六、小结及作业
1
一、空间直线的一般方程
定义 空间直线可看成两平面的交线．
1 : A1 x B1 y C1z D1 0 z
2 : A2 x B2 y C2z D2 0
23
内容小结
1. 空间直线方程
一般式

A1x A2 x

B1 B2
y y

C1z C2 z

D1 D2
0 0
对称式
参数式

x y

x0 y0
m n
t t
z z0 p t
(m2 n2 p2 0)
24
2. 线与线的关系
直线
L1：x
x1 m1
例8. 求过点(1,－2 , 4) 且与平面
垂
直的直线方程.
解: 取已知平面的法向量 n (2, 3, 1)
n
为所求直线的方向向量.
则直线的对称式方程为
x 1 y 2 z 4 2 3 1
19
例 9 设直线 L : x 1 y z 1，平面 2 1 2
: x y 2z 3，求直线与平面的夹角. 解 n {1,1, 2}, s {2,1, 2},
x 1 4t
参数方程

y

t
.
z 2 3t
9
例 3 一直线过点A(2,3,4)，且和 y 轴垂直相
交，求其方程.
解 因为直线和 y轴垂直相交,
《空间直线的方程》课件

《空间直线的方程》课件


3
总结
总结不同表达方式，及其转换关系和平面与直线的关系。
参
《线性代数》第二版
《空间直线的方程》PPT 课件
学习空间直线的方程，在三维坐标系中计算直线的参数方程、一般式和对称 式等形式。
空间直线的定义与表示
空间直线的定义
描述了空间中无限延申的直线，由无数个点组 成。
参数式与点向式的转换
通过转换公式可以互相转换参数式和点向式的 表示。
空间直线的表示
可以用点向式、参数式、对称式和一般式等多 种形式来表示。
直线的一般式及其性质
一般式是直线及其性质
直线的对称式
对称式是直线的一种表示形式， 便于求解直线与平面的关系。
对称式与参数式的相互转化 平面与直线的关系
通过转换公式可以互相转换对称 式和参数式的表示。
直线可在平面内或平面外，与平 面有不同的相交关系。
基础知识回顾
1 三维坐标系
空间直线的表示依赖于三维坐标系的概念与运算。
2 向量的表示和运算
向量在计算空间直线的方程中起到了重要的作用。
3 两点之间的距离公式
计算直线参数方程和一般式时需要用到两点之间的距离公式。
实例解析与练习
1
实例解析
通过具体实例来深入理解空间直线的方程。
2
练习题
进行一些练习题，加深对空间直线方程的掌握。
空间直线的一般方程.ppt

空间直线的一般方程.ppt


y0 y0
z0 2 0 , 3z0 6 0
解得 y0 0, z0 2
点坐标 (1,0,2),
因所求直线与两平面的法向量都垂直
取
s

n1

n2

{4,1,3},
对称式方程 x 1 y 0 z 2 , 4 1 3
x 1 4t
第八节 空间直线及其方程
一、空间直线的一般方程
定义 空间直线可看成两平面的交线．
1 : A1 x B1 y C1z D1 0
z 1
2 : A2 x B2 y C2z D2 0
2

A1 A2
x x

B1 B2
y y

C1z C2z

D1 D2
直线方程为：x x1 y y1 z z1 x2 x1 y2 y1 z2 z1
例1 用对称式方程及参数方程表示直线
x y z 2x y
1 0 3z 4
. 0
解 在直线上任取一点 ( x0 , y0 , z0 )
取
x0
1


例 6 设直线L : x 1 y z 1，平面 2 1 2
: x y 2z 3，求直线与平面的夹角. 解 n {1,1, 2}, s {2,1, 2},
sin
| Am Bn Cp |
A2 B2 C 2 m2 n2 p2
又已知平面的法向量 n {1,4,8}.
由题设知
cos 4

nnnn11
(1 ) 1 5 (4) (1 ) (8)
空间直线及其方程 PPT

空间直线及其方程 PPT


大家好
8
三、两直线的夹角
定义 两直线的方向向量的夹角称之.（锐角）
直线 L1 : 直线 L2 :
xx1yy1zz1,
m1
n1
p1
xx2yy2zz2,
m2
n2
p2
^ cL o 1 ,L 2 s ) (m 1 2 |m n 1 1 2 m 2 p 1 2 n 1 n 2 m 2 2 p 1 p n 2 2 |2 p 2 2
6 9
36
arcsi7n 为所求夹角．
36
大家好
15
例6 求 过 点 (3,2,5)且 与 两 平 面 x4z3和 2xy5z1的 交 线 平 行 的 直 线 方 程 .
解 设所求直线的方向向量为 sr(m ,n,p),
根据题意知 sn1, sn2, 取 s n 1n 2(4,3,1),
所求直线的方程 x3y2z5. 4 31
大家好
10
例3. 求以下两直线的夹角
L1:
x1yz3 1 4 1
L2:2 xy22z1
解:直线 L 1的方向向量为 s1(1,4,1)
直线
L 2 的方向向量为
r s2(2,2,1)
二直线夹角 的余弦为
cos 1 2 ( 4 ) ( 2 ) 1 ( 1 ) 2
12(4)212 22(2)2(1)2 2
(2) L// A B m C n 0 .p
大家好
14
例5设 直 线 L:x1yz1， 平 面 2 1 2
:xy2z3， 求 直 线 与 平 面 的 夹 角 . 解 n r(1,1,2), sr(2,1,2),
sin |A m B C n|p
A 2B 2 C 2 m 2 n 2p 2
高等数学 第5讲 空间直线及其方程

高等数学 第5讲 空间直线及其方程


与直线
2 3
x x

2 8
y y

z z

23 18

0 0
的夹角的余弦为__________；
3、 直
线

x x

y y

3z 0 z0
和平面
x

y

z

1

0
在平
面 x 2 y z 1 0上的夹角为___________；
4、点(1 , 2 , 0 )在平面x 2 y z 1 0上的投影为
o
y
空间直线的一般方程 x
2. 对称式方程 方向向量的定义：
如果一非零向量平行于 一条已知直线，这个向量称 为这条直线的方向向量．
一般用s (m, n, p)表示.
z s
L
M
M0
o
y
M0( x0 , y0 , z0 ), M( x, y, z), x
M L,

M0M// s
s (m, n, p), M0M ( x x0 , y y0 , z z0 )
x y z 1 (x y z 1) 0
即
从中选择 使其与已知平面垂直：
得 1, 从而得投影直线方程
xy
z y
1 z

0 0
这是投影平面
内容小结
1. 空间直线方程
一般式

A1x A2 x

B1 B2
y y


C1z C2 z
故所求直线方程为 x 1 y 2 z 1 3 2 5
方法2 利用所求直线与L2 的交点 .
8-7空间直线及其方程-PPT精品文档

8-7空间直线及其方程-PPT精品文档


4. 空间直线的两点式方程
设直线 L 过点 M ( x , y , z ) 与 M ( x , y , z ) ， 1 1 1 1 2 2 2 2 x x y y z z 1 1 1 则其方程为 x x y z 2 1 y 2 1 z 2 1
直线的两点式方程
例1 用对称式方程及参数方程表示直线 xyz 1 0 . 2 xy 3 z 4 0 x ,y ,z ) ， 解 在直线上任取一点 ( 5 0 0 0 x x y 1 0 3 令 z 0 ， ， 解得 , 2x y40 y2 52 3 故直线过点 ( , ,0 ) ， 33 因所求直线与两平面的法向量都垂直， i j k 取 s n n { 4 , 1 , 3 } ， 1 1 1 1 2
x 2 y 3 z 4 由两点式方程，所求直线方程为 . 2 0 4 2 x z 0 或 . y 3
二、两直线的夹角
定义 两直线方向向量间的夹角，称为两直线的夹角．
(一般取锐角) x x y z 1 y 1 z 1 直线 L ： ， s m , n , p ， 1 1 1 1 1 m n p 1 1 1
m n p 1 1 1 s s . L L ( 2 ) 1 // 2 // 2 1 m n p 2 2 2 例如， 直线 L1 : s { 1 , 4 , 0 } ， 1 直线 L2 : s { 0 , 0 , 1 } ， 2 s s ， s s 0 ， 即 L L . 1 2 1 2 1 2
x 1 y 5 z 8 例4 设有直线 L ： 及 1 1 2 1 x y 6 ， 直线 L ： 则 L 与 L 的夹角 [ ． ( 19 ) C] 2 1 2 2 y z 3 ，
空间的直线方程PPT课件

空间的直线方程PPT课件

ijk 2 3 1 (1, 5, 13).
3 2 1
第8页/共44页
现求一定点. 将联立方程组 2x 3y z 7
3x 2y z 1
令x = 1得 y= 1, z =2, 得一定点(1, －1, 2). 故得对称式
x 1 y 1 z 2 1 5 13
第9页/共44页
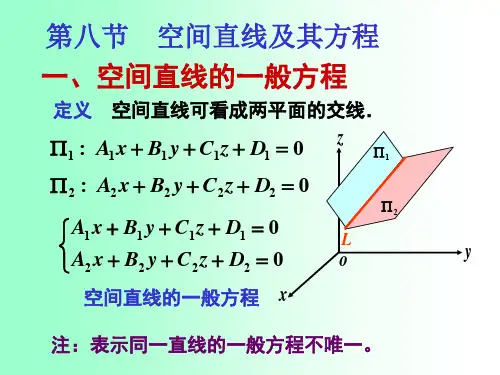
二 两直线的位置关系
（A）平行平面π
（C）在平面π上
（B）垂直平面π
（D）与平面π斜交
解： 直线l的方向向量 s为：
ij k
s 1 3 2 28i 14 j 7k {28,14, 7}
2 1 10
s {4,- 2,1}
又因为平面的法向量为{4,- 2,1}
所以直线l与平面垂直，故选择（B） 第20页/共44页
2 abc
b2c2 a2c2 a2b2
第30页/共44页
本节综合习题
【1】求过点M0(3, 3, 0)且与直线 l1:
x 1
y 1
z 2
垂直相交的直线 l 的方程.
解：
设所求直线 l 与 l2 与交点
M0•
l1 为M1(x1, y1, z1).
则
M1
M0M1 s1 = (1, 1, 2).
2 1 3
(4, 1, 3).
第5页/共44页
现求一定点. 将联立方程组 x y z 1 0,
2x y 3z 4 0
相加:
3x 4z 5 0.
令z = 1得 x = 3, y=1,
得一定点(3, 1, 1). 故得对称式
x 3 y 1 z 1. 4 1 3
第6页/共44页
有： sin
| Am Bn Cp |
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

t
, 则直线的方程变成：
x x 0 mt
y y 0 nt
z
z
0
pt
（t为参数） ----------空间直线L的参 数式方程
4
例1、过点（-1，2，0.8）且以rs
r 3i
r 0.2 j
r 10k
为方向向量
的直线的标准式方程和参数式方程。
解： 直线的标准式方程：
x 1 3
y2 0.2
8
当ur两条ur 直线 L1 、L2相交时，设两条直线的夹角为 ，而方向 向量s1 、s 2 的夹角为 ，则 或
2、直线与平面的位置关系
设直线L的方程为：
xx0 m
yy0 n
zz0 p
平面 的方程为：Ax By Cz D 0
则有：L //
儍
rr sn
rr
L 儍 s // n
故（1.-1.0）为直线上一点 .
rr r
r ur uur i j k
rr
r
s n1 n2 2 3 1 5i 7 j 11k
3 1 2
直线的标准式方程：x51
y 1 7
z 11
7
练习
将直线L的一般方程
x2 z50
化成标准式方程.
y6 z70
二、直线与直线、直线与平面间的关系
建立了直线与平面的方程，就可以通过方程来讨论直线 与直线、直线与平面的位置关系.
即 x 13 y 10 z 5 0
x12t
例3、求 平行于两直线
y 2
（t为参数）及
z0
x2 3
直线过两点 M 1( x1. y1. z1) M 2( x 2. y 2. z 2) , 则直线的两点式
方程为：
xx1 x2x1
y y1 y 2 y1
zz1 z 2z1
4、直线的一般方程
一条直线可以看成是过此直线的两个平面的交线， 故直线方程可以用两个平面方程联立起来表示。
设两个相交的平面方程为：
A2 x B 2 y C 2 z D 2 0 A1 x B1 y C 1 z D1 0
则它们的交线L的方程为：
A1 x B1 yC 1 z D10 A2 x B 2 yC 2 z D 20
-------空间直线的一般方程
6
例
将直线L的一般方程
2
x3
y
z
50
化成标准式方程.
3x y2 z20
解 令z 0代入原方程组， 得
2 x3 y5
3x y2
解此方程组得 x 1 y 1
第六节 空间直线及其方程
本节内容提要 一、空间直线的几种形式 二、直线与直线、直线与平面间的关系 三、利用直线与平面其间的关系，求解综合题
1
教学目的： 使学生了解空间直线的几种形式，并会其间的 转换，会根据所给条件求直线方程，了解直线 与直线、直线与平面间的关系，会利用直线与 平面间的关系求解综合性题目。
mA nB pC 0
m A
n B
p C
当直线 L 和平面 相交时，直线 L 与它在平面上的投影线
之间的夹角
（0
2
）称为直线
L与平面
的夹角。
如图
9
设直线的方向向量 rs与平面法向量 nr的夹角为 ，则：
2
（或
2
）
rr
sn
因此 sin cos r r
mAnB pC
sn
m2 n2 p2 A2 B2 C2
例
求直线L：x12
y3 1
z4 2
与平面 ：2 x
y
z
6
0的夹角
解： 设直线L与平面 的夹角 为，则：
sin
uur r co（ s s、n）
212 6 6
1 2
6
三、利用直线与平面其间的关系，求解综合题
例1、求过点（-3.2.5）且与两平面 x 4 y 3 和 2x y 5z 1 的交线平行的直线方程。
L：x 3 2
y 1
z2 1
的平面方程。
解： 由直线 L 的方程可知：
11
直线直L的线方上向一向点M量rs （0 2..r-1.r2）r ，平面的法向量垂直于MuuuMuur0
及
r uuuuur ur i j k
r
r
r
n MM 0 S 1 3 4 i 13 j 10k
3 1 1
所求的平面方程为 x1 +13 y-2 +10 z+2 =0
1、直线与直线的位置关系
设直线L1 和直线L2 的方程分别为：
L1 :
xx1 m1
y y1 n1
zz1 p1
L2
:
xx2 m2
yy2 n2
zz2 p2
则：L1 // L2
儍
uur uur S 1 // S 2
ur ur L1 L2 儍 s1 s2
m1 m2
n1 n2
p1 p2
m1m2 n1n2 p1 p 2 0
(1)
------直线的标准式方程（或点向式方程）
注：因为 sr 0 ，所以 m、n、p 中可以有一个或两个数为
零，规定（1）式中若分母为零，则其相应的分子也为零。
如：m 0 ，则直线L的方程为： y y 0 z z 0
n
p
x x 0 0
2、直线的参数式方程
令 xx0
m
yy0 n
zz0 p
重点、难点：求空间直线方程 教学方法： 启发式教学法 教学手段： 多媒体课件和面授讲解相结合 教学时数： 2课时
2
一、空间直线的几种形式
过一点做一条且仅做一条与一条已知直线平行的直线，我 们利用这一点建立直线方程.
1、直线的标准式方程
定线L义的：方若向一向非量零，向一量般与用一sr条表直示线。L由平定行义，可则知称直该线向的量方为向直
z 0.8 10
x13t
直线的参数式方程：
y20.2t
（t为参数）
z 0.810t
例2、求过点（1.1.-2）且垂直于平面2x 3z 0 的直线方程。
解：因为所求直线垂直于平面，所以这个平面的法向量可
以做为所求直线的方向向量，即
r s
2.0.3
x 1 2
y 1 0
z2 3
5
3、直线的两点式方程
向量不唯一。
已知直线L上一点 M（0 x0，y0.z0）和直线L的方向向
量 sr m.n. p，建立该直线L的方程.
在uuu直uuur线L上任取一点M（x.y.z）
M 0 M x x 0，y y 0，z-z0
因为sr // L
，所以sr
//
uuuuuur M 0M
3
xx0 m
yy0 n
zz0 p
10
解：设所求直线的方向向量为
r s
因为所求直线与两平面的交线平行，所以
r s
垂直于两平
面的法向量。 r r r
r ur uur i j k
r rr
s n1 n2 1 0 4 4i 3 j k
2 1 5
所求直线为：
x3 4
y2 3
z5 1
即
x3 4
y2 3
z5 1
例2、求通过点M（1.2.-2）且通过直线