当前位置：文档之家 › 平面直线的方程ppt课件

平面直线的方程ppt课件

  • 格式：ppt
  • 大小：628.00 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

线性代数：平面与直线方程

线性代数：平面与直线方程


从代数上看，即方程组
A1 x B1 y C1z D1 0
A2
x
B2
y
C2z
D2
0
*
有没有解？有多少解？
2020/12/12
14
14
(1) 1 // 2
A1 B1 C1 D1 A2 B2 C2 D2
方程组*系数矩阵的秩 与增广矩阵的秩不等
Ax By Cz D 0 *
D ( Ax0 By0 Cz0 )
注： (1) 三元一次方程* 一一对应空间中的平面, 此即三元一次方程的几何意义.
(2) 以上5种形式的方程可相互转化
2020/12/12
6
6
例：求经过点 A(1, 2, 3)，B(1, 4, 2)，C(0, 1, 1)
n M0M
n M0M 0
A( x x0 ) B( y y0 ) C(z z0 ) 0
2020/12/12
2
2
2 点位式方程
给定M0，和两个不共线的向量，， 那么过M0且平行于，的平面可唯一确定.
称向量，为平面 的方位向量 M0
设M0 ( x0 , y0 , z0 )，
M
{ X1,Y1, Z1}， { X2 ,Y2 , Z2 }
M( x, y, z) M0M,, 共面
x x0 y y0 z z0
(M0M,, ) 0 X1
Y1
Z1 0
2020/12/12
3
X2
Y2
Z2 3
3 三点式方程
M1( x1 , y1 , z1 )
M2( x2 , y2 , z2 ) M3 ( x3 , y3 , z3 )，
从几何上看，它们可能是相交、平行、重合.
直线和平面平行的判定定理ppt课件

直线和平面平行的判定定理ppt课件

直线和平面平行的判定 定理ppt课件
2024/1/28
1
目录
2024/1/28
• 直线与平面平行基本概念 • 判定定理一：斜率相等法 • 判定定理二：向量共线法 • 判定定理三：距离相等法 • 综合应用与拓展 • 总结回顾与课堂互动
2
直线与平面平行基
01
本概念
2024/1/28
3
直线与平面定义
及特殊情况的处理。
15
判定定理三：距离
04
相等法
2024/1/28
16
距离相等法原理
直线与平面平行时，直线上任意一点 到平面的距离都相等。
利用这一性质，可以通过比较直线上 不同点到平面的距离是否相等来判断 直线与平面是否平行。
2024/1/28
17
点到直线距离公式
点$P(x_0, y_0, z_0)$到平面 $Ax + By + Cz + D = 0$的距 离公式为
2024/1/28
$d = frac{|Ax_0 + By_0 + Cz_0 + D|}{sqrt{A^2 + B^2 + C^2}}$
其中，$A, B, C$是平面方程中 的系数，$D$是常数项。
18
实例分析与讨论
实例1
已知直线$l$的方程为$frac{x-1}{2} = frac{y-2}{3} = frac{z-3}{4}$，平 面$pi$的方程为$x + y + z = 6$， 判断直线$l$与平面$pi$是否平行。
解
在直线$m$上任取两点$Q_1(-1,2,0)$和$Q_2(0,1,1)$，分别计算它们到平面 $alpha$的距离$d_3$和$d_4$。根据点到平面的距离公式，有
直线的方程_PPT课件

直线的方程_PPT课件


（1）l1： x y 0,
l2：3x 3y 10 0 ; 相交
（2）l1：3x y 4 0, l2：6x 2y 1 0; 平行
（3）l1：3x 4y 5 0, l2：6x 8y 10 0.重合
知识探究
1、方程 m(3x 4 y 2) n(2 x y 2) 0 （m，n不同时为0）表示什么图形？
A1 A2
B1 B2
l1与l2相交
8、两条直线的位置关系
已知 : 直线 l1 ：A1x+B1y+C1= 0 直线 l2 ： A2x+B2y+C2= 0
A1B2 A2 B1且 A1C 2 A2C1 l1、 l2平 行 A1 A2 B1B2 0 l1 l2 A1B2 A2 B1 l1、 l2相 交
知识回顾
判断直线与直线的位置关系
（1）直线2x+y-1=0与直线2x+y+1=0 （2）直线3x+4y-2=0与直线2x+y+2=0
知识探究
怎样确定直线l1:3x+4y-2=0与 直线l2:2x+y+2=0的交点坐标？
y P
o
x
l1
l2
知识探究
一般地，若直线l1:A1x+B1y+C1=0和 l2:A2x+B2y+C2=0相交，如何求其交 点坐标？
知识探究
2、方程 3x 4 y 2 (2 x y 2) 0 表示的直线包括过交点 M（-2，2） 的所有直线吗？
知识探究
一般地，经过两相交直线 l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的 交点的直线系方程可怎样表示？
《直线与方程》课件

《直线与方程》课件

《直线与方程》PPT课件
欢迎来到《直线与方程》PPT课件！在本课程中，我们将一起探索直线和方程 的基础概念、方程的各种形式和应用。让我们开始这个充满趣味和深入的旅 程吧！
基础概念
直线的定义和性质
我们将探索直线的定义，了解直线的性质以 及直线与其他几何概念的关系。
直线的一般式和点斜式
探索直线的一般式和点斜式表示法，学习如 何根据已知条件写出直线的方程。
直线的斜率和截距的概念
学习直线的斜率和截距的概念以及它们在方 程中的作用和应用。
直线的垂线、平行线和夹角定理
了解直线之间的垂线、平行线关系以及夹角 定理的概念和性质。
直线的方程
点斜式的推用点斜式解决 问题。
一般式的推导和使 用
推导直线的一般式，了解一 般式的特点和应用场景。
拓展知识和应用场景
提供一些拓展知识和应用场景，让你了解直线与 方程的更多应用领域。
截距式的推导和使 用
学习使用截距式表示直线的 方程，探索截距在几何和实 际问题中的作用。
直线的应用
1 两点距离公式的推导和应用
了解如何使用两点距离公式计算直线上两点之间的距离，以及它在几何和实际问题中的 应用。
2 直线与圆的交点和切点
研究直线与圆相交的情况，探索交点和切点的性质以及它们的几何意义。
3 直线和平面的交点和夹角
学习直线与平面相交的情况，研究交点和夹角的概念，并探索它们的应用。
练习题
1
练习题和解答
通过练习题加深对直线与方程的理解，并提供详细的解答，帮助你巩固所学知识。
2
自主思考题
通过自主思考题，激发你的思考能力，挑战你的直线与方程的理解。
总结
直线与方程的重点概括
总结直线与方程的核心概念和重要知识点，帮助 你回顾和复习所学内容。
《平面方程教学》课件

《平面方程教学》课件

极坐标形式的优缺点
极坐标形式可以更方便地描述圆和椭圆等形状，但有时候需要转换为直角坐标 形式进行计算或分析。
平面方程的矩阵形式
矩阵形式
平面方程可以表示为矩阵形式，其中矩阵元素表示x、y、z等坐标值，通常用于 描述复杂的几何形状和变换。
矩阵形式的优缺点
矩阵形式可以更方便地描述复杂的几何形状和变换，但有时候需要转换为其他形 式进行计算或分析。
04
平面方程的拓展知识
平面方程的参数形式
参数形式
平面方程可以表示为参数方程，其中 x、y是参数t的函数，通常用于描述 曲线的轨迹。
参数方程的优缺点
参数方程可以更直观地描述曲线的形 状和变化趋势，但有时候参数t的物理 意义不明确，导致理解困难。
平面方程的极坐标形式
极坐标形式
平面方程可以表示为极坐标形式，其中r为半径，θ为角度，通常用于描述圆和 椭圆等形状。
03
平面方程的应用
平面几何中的应用
确定点与平面的关系
通过平面方程，可以判断一个点是否在平面上。
计算平面上的距离
利用平面方程，可以计算点到平面的垂直距离。
求解平面几何问题
平面方程是解决平面几何问题的重要工具，如求两平面的交线等。
解析几何中的应用
01
02
03
描述平面上的点
平面方程可以用来描述平 面上的任意一点。
平面方程的基本性质
平面的法线向量是 (A, B, C)， 即平面方程中系数 A、B、C 所 对应的向量。
平面的法线向量与平面垂直， 并且方向由系数 A、B、C 的正 负号决定。
平面的法线向量与平面上的任 意一点连线的向量与平面的法 线向量垂直，即它们的点积为 零。
02
课件：平面和直线方程及点线面的位置关系

课件：平面和直线方程及点线面的位置关系


是异面直线, 并求出它们之间的距离及 公垂线的方程.
第 3 章 几何向量
§3.4 平面和直线
3. 在特殊位置的平面.
(1)过原点的平面: Ax+By+Cz = 0.
(2)平行于x轴的平面: By+Cz+D = 0.
平行于y轴的平面: Ax+Cz+D = 0.
平行于z轴的平面: Ax+By+D = 0.
(3)平行于xoy面的平面: Cz+D = 0.
§3.4 平面和直线
z
L
·P
·P0
s
xO
y
x = x0+lt, y = y0+mt, z = z0+nt.
2. 标准(对称)方程.
xx0 l
=
yy0 m
=
zz0 n
第 3 章 几何向量
3. 一般方程.
§3.4 平面和直线
A1x+B1y+C1z+D1 = 0 A2x+B2y+C2z+D2 = 0
4. 两点式方程.
注: 也可以利用混合积的 几何意义来理解上述
s1s2
P2
s2
公式.
S = || s1s2 ||, d |(P1 P2 )s1s2 |
V = (s1s2)·P1P2 d = V/S.
P1
s1
第 3 章 几何向量
§3.4 平面和直线
例4 求证
l1:
x
4
3
=
y3 1
=
z+1 1
l2:
x 2
=
y 0
z+2 = 1
平面与直线

平面与直线


例 18 求过三点 A( 2,−1,4)、 B( −1,3,−2) 和
C (0,2,3)的平面方程.
解
AB = { −3, 4,−6}
AC = { −2, 3,−1}
取 n = AB × AC = {14, 9,−1}, 所求平面方程为 14( x − 2) + 9( y + 1) − ( z − 4) = 0, 化简得 14 x + 9 y − z − 15 = 0.
n1 = { A1 , B1 , C1},
Π1
n2 = { A2 , B2 , C 2 },
按照两向量夹角余弦公式有
cosθ =
| A1 A2 + B1B2 + C1C2 | A + B + C ⋅ A2 + B2 + C2
2 1 2 1 2 1 2 2 2
两平面位置特征： 两平面位置特征：
两平面夹角余弦公式
因所求直线与两平面的法向量都垂直 取
s = n1 × n2 = {4,−1,−3},
x −1 y −0 z + 2 对称式方程 , = = 4 −1 −3 x = 1 + 4t . 参数方程 y = − t z = −2 − 3t
3、两直线的夹角 定义 两直线的方向向量的夹角称之 （锐角） 两直线的方向向量的夹角称之.（锐角）
1
o x
y
由所求平面与已知平面平行得 （向量平行的充要条件） a = b = c , 向量平行的充要条件）
1
1
6
1
6
1 1 1 1 1 1 = = , 令 = = 化简得 =t 6a b 6c 6a b 6c 1 1 1 ⇒a= , b= , c= , 6t 6t t
直线的方程ppt

直线的方程ppt


（2）经过点B（3，-1），斜率是 2 ； y 1 2(x 3)
（3）经过点C（- 2
，2），倾斜角是30°y； 2
3 3
x
2
（4）经过点D（0，3），倾斜角是0°； y 3 0
（5）经过点E（4，-2），倾斜角是120°； y 2 3x 4
答案
不能,因为斜率可能不存在. 因此,在具体运用时应根据情况分类讨论,避免遗漏. 从严治校 科学管理
1、直线方程的点斜式和斜截式 高素质·高技能·高能力·高就
问题3： 已知直线的斜率为业K，与Y轴的交点是P（0，b），
求直线L的方程？
说明：纵截距：直线L与Y轴交点的纵坐标。
横截距：直线L与X轴交点的横坐标。
直线的倾斜角高 业和素质斜·高率技能·高能力·高就
在平面直角坐标系中，对于一条与x 轴相交的直线，如果把x轴绕着交点按逆 时针方向旋转到和直线重合时所转的最
小正角记为 ，那么 就叫做直线的倾
斜角。
倾斜角不是90°的直线，它的倾斜角的 正切叫做这条直线的斜率，常用K表示。
从严治校 科学管理
高素质·高技能·高能力·高就
x y 1 a0且b0 ab
3、直线方程的一般形式 高素质·高技能·高能力·高就
①直线方程有几种形式？指明它业 们的条件及应用范围.
直线名称 已知条件
直线方程
使用范围 示意图
k存在 点斜式 P(x1,y1)及k y y1 k(x x1 )
斜截式 k及b y kx b k存在
从严治校 科学管理
3、直线方程的高一素质般·高形技能式·高能力·高就 业
探究1：方程Ax+By+C=0 (A、B不全为0) 总表示直线吗？
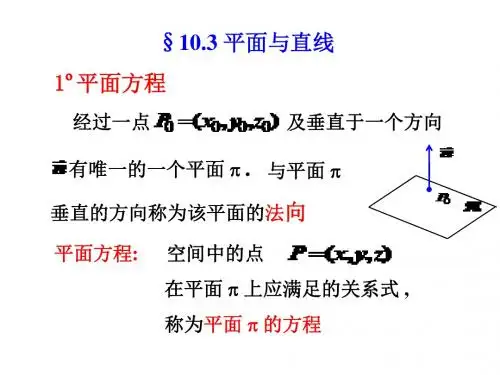
10.3 平面与直线(1-52)

10.3 平面与直线(1-52)

(5) 由于其法向量 平面 同理可知: 表示一平行于 y 轴的平面 表示一平行于 z 轴的平面 在 yoz 平面上 , x轴
(2) 若 (4) 式中的 A , B , C 0
(a) 若 D = 0 , 则 平面 经过原点 (b) 若 D 0 , 则 (4) 式可以表示为 (6) 其中 即为平面 在 x , y ,
(2) 截距式方程 (6) ( 反映平面与各坐标轴的截距 ) (3) 法式方程 (7) ( 反映平面与原点 O 的距离 ) 它们都分别刻画了平面 (4) 的一些重要特征
例 试求经过点 P1=(1 , 2 , 1) , P2=( 2 , 3 , 1 ) ,
P3=( 1 , 0 , 4 ) 的平面 的方程 解 构造 取 经过的点 P0=P3=( 1 , 0 , 4 )
距离:
例： 求过点P (2,1,9)且与直线
x 1 y 1 z L1 : 垂直相交的直线 L的方程. 3 2 1
解 : 过点 P 且垂直于L1 的平面
3( x 2) 2( y 1) ( z 9) 0
求 与 L1 的交点 L1 的参数方程 x 3t 1, y 2t 1, z t ,
的投影平面 ) , 则
下面考虑 L 关于 的投影平面
过 L 的平面束方程:
(5) 说明: 平面 而且 是经过直线 L 的 , 其中 除平面 , 外
包含了经过 L 的所有平面 于是在 中寻找一使 的平面即为 , 即求 使
L关于平面 的投影平面
例 求直线 L :
上的投影直线
解 过 L 的平面束方程
即
例 求通过 x 轴和点( 4, – 3, – 1) 的平面方程. 解: 因平面通过 x 轴 , 故 A D 0 By Cz 0 设所求平面方程为 代入已知点 (4 , 3 , 1) 得
直线的方程ppt课件

直线的方程ppt课件

详细描述
斜截式方程的一般形式为y=kx+b，其中k为该直线的斜率，b为截 距。
求解步骤
根据已知的斜率k和截距b，代入斜截式方程中即可求得直线方程 。
两点式方程的求解
总结词
两点式方程是直线方程的一种形式，它表示了直线上任意一点与两 个已知点之间的位置关系。
详细描述
两点式方程的一般形式为(y-y1)/(y2-y1)=(x-x1)/(x2-x1)，其中(x1, y1)和(x2, y2)为直线上两个已知点。
求直线的截距
1 2
截距定义
直线的截距是指直线与x轴或y轴的交点坐标，反 映了直线在x轴或y轴上的位置。
截距计算
根据已知直线方程，可以分别计算出直线与x轴 和y轴交点的横坐标和纵坐标。
3
截距与直线斜率
截距为0表示直线与y轴平行，截距不为0表示直 线与x轴垂直。
解决相关问题
01
直线方程的应用范围广泛，包括但不限于解决几何问
05
直线方程的转化
点斜式方程与斜截式方程的转化
01
总结词：点斜式方程是直线方程的一种表示形式，它包含 了直线的斜率和通过的一个点。斜截式方程表示直线与y 轴的交点（截距）和直线的斜率。两者可以通过以下步骤 相互转化
02
给出点斜式方程 y - y1 = k(x - x1)
03
斜截式方程 y = kx + b
向量形式
向量方向
直线的方向向量可以表示为$\overrightarrow{v} = (x_2 - x_1, y_2 - y_1)$，其 中(x1, y1)和(x2, y2)为已知的直线上的两点。
向量法
直线可以表示为$\overrightarrow{P_1P_2} = \lambda\overrightarrow{v}$， 其中$\overrightarrow{P_1P_2}$是从点P1到点P2的向量，$\lambda$为比例系 数。
高数课件 10.3 平面与直线

高数课件 10.3 平面与直线


||
三元一次方程
D
Ax By Cz D 0 称为 平面的一般方程，
并且法向量 n {A, B, C} ．
一些特殊的三元一次方程的图形特征: (1) D=0, Ax+By+Cz=0 表示通过原点的平面; 缺常数项 (2) C=0, Ax+By+D=0 表示平行于z轴的平面; 缺z项
B=0, Ax+Cz+D=0 表示平行于y轴的平面; 缺y项 A=0, By+Cz+D=0 表示平行于x轴的平面; 缺x项 (3) C=D=0, Ax+By=0 表示含z轴的平面; 缺z项和常数项 B=D=0, Ax+Cz=0 表示含y轴的平面; 缺y项和常数项 A=D=0, By+Cz=0 表示含x轴的平面; 缺x项和常数项 (4) A=B=0, Cz+D=0 表示平行于xoy面的平面; 缺x,y项
各种平面的画法
❖ 平行于各坐标面的平面(含坐标面) ❖ 平行于各坐标轴的平面 ❖ 过各坐标轴的平面 ❖ 过原点的平面 ❖ 与三轴都相交的平面
三. 两平面的夹角
n2
n1
定义 两平面法线向量的夹角 , 称为两平面的夹角(0 )．
2
2
设平面 1：A1 x B1 y C1z D1 0
1
化简为
14x 9 y z 15 0
注意：不共线的三点才唯一地 确定一平面 ．
例 3. 一平面通过两点M1 (1, 1, 1)和M2 (0, 1, 1)且垂直于平面
x y z 0，求它的方程．
解 由于所求平面与 x y z 0 垂直，
则又M其1法, M向2在量该n平与面上n1，则{1,n1, 1M} 垂1M直2，，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
y. x0 , y0
直线与y轴垂直时，斜率为0，
o
x 直线方程为y=y0
10
1、求满足下列条件直线的方程 （1）过点A（3，-1），且垂直于x轴 （2）过点A（3，-1），且平行于x轴 2、你能说出x轴所在的直线方程吗？
Y轴呢？
11
k存在
方程：y-y 0
k(x
x0 )
过点（x 0，y0）的 直线方程
（2）过原点，斜率k
(1)解：x 0
3,
y0
1, k
1
由直线的点斜式y-y 0
k(x
x0 )
得：直线的方程为y-(-1)=-1(x-3)
即：y 1 (x 3)
7
你真的掌握了吗？ 1. 直线l经过点P(-2,3),且倾斜角α=45°, 求直线l的点斜式方程 2 .已知直线过两点A(2,1),B(3,-1),
3.垂直于y轴的直线斜率是 ___0____
4.垂直于x轴的直线斜率__不__存__在____
3
问题1：过一点P（1，2）有多少条直线？ 问题2：过一点P（1，2）且倾斜α=45°
的直线有多少条？ 问题3: 确定一条直线需要哪些条件？
答：平面上的两个点或平面上的一点和它的斜率
4
问题4:
直线 l 过点P(2，1)，且斜率为3， 点Q(x,y)是 l 上不同于P的一点，则x、
y满足怎样的关系式？
y 1 3 x2
5
相信这个也难不倒你
直线l经过点 P0(x0,y0) ,且斜率为k，点 P(x,y)为直线l上不同于P0的任意一点，则x、
y满足的关系式是__y__y_0__k__x__x_0 _
点斜式方程
6
例1 求满足下列条件的直线的方程
（1）过点A（3，-1），斜率为-1
点斜式
k不存在 方程：x x0
注意：x轴所在直线方程为y=0 y轴所在直线方程为x=0
12
学而不思则罔
回
课 后
头 一 看
作，
业我
想
说
：
学习指导用书11页 1，(1)(3) (5) 2, (2) (3)
13
作业
学习指导用书11页 1，(1) (3) (5) 2, (2) (3)
14
15
课堂小测验 求满足下列条件的直线的方程
求其方程
8
尝试写出满足下列条件的直线的方程 （1）经过点A（4，1），B(-3, 1) （2）经过点A（2，5），B(2, 4)
9
问题5:
直角坐标系上任意直线都可以用直
线的点斜式方程表示吗?
. y
P0 x0, y0 直线与x轴垂直时，斜率不存在，
o
. .P1 x0,0
P2 x0 , y2
直线方程为x=x0
（1）过点A（-2，1），斜率为-2 （2）直线l经过点P(2,1),且倾斜角α=60°,
（3）直线过两点A(2,1),B(3,-1), （4）经过点A（2，3），与x轴垂直 （5）经过点A（-2，1），且与y轴垂直
16
1
1.直线的倾斜角α与斜率k的关系是 ___k___ta_n___
2.过点A(x1,y1)、B (x2,y2)的直线的斜
y2 y1
率k＝__x_2 _x_1__ （x1 x2）
2
1.已知直线l的倾斜角为 ，则斜率为__3___
3 2.过点A（2，3）和B（1，2）的直线l的斜
1
率为 ____3___