最优化控制 线性二次型最优控制问题
- 格式:ppt
- 大小:1.48 MB
- 文档页数:93






最优控制问题的线性系统方法最优控制是应用数学和控制理论中的一个重要分支,旨在寻找系统最优行为以满足特定的性能指标。
在线性系统中,最优控制问题可以通过线性规划和线性二次型问题来表示和解决。
本文将探讨基于线性系统的最优控制问题,并介绍常见的线性系统方法。
一、线性系统基础线性系统是指系统的行为遵循线性关系的动态系统。
它可以用线性微分方程来描述,具有以下形式:$$\dot{x}(t)=Ax(t)+Bu(t)$$$$y(t)=Cx(t)+Du(t)$$其中$x(t)$是系统的状态向量,$u(t)$是输入向量,$y(t)$是输出向量,$A$是系统矩阵,$B$是输入矩阵,$C$是输出矩阵,$D$是直接传递矩阵。
线性系统的状态和输出可以通过系统的初始状态$x(0)$、输入$u(t)$和系统矩阵来确定。
二、最优控制问题的目标和约束最优控制问题旨在寻找满足特定性能指标的最优控制策略。
通常,我们定义一个性能指标函数$J$,它量化了系统的性能表现。
最优控制问题的目标是最小化或最大化$J$,同时满足系统动态方程和约束条件。
常见的性能指标函数包括最小化控制误差、最小化能量消耗、最小化响应时间等。
约束条件可以是状态约束、输入约束或输出约束,用于限制系统的操作范围。
三、线性规划方法线性规划是一种常见的最优控制方法,基于线性系统模型和线性约束条件。
最优控制问题可以通过线性规划的方法进行建模和求解。
线性规划问题的一般形式如下:$$\min_{u(t)} J = \int_{t_0}^{t_f} \left( q(t)x^T(t)Qx(t)+r(t)u^T(t)Ru(t) \right) dt$$$$\text{subject to} \quad \dot{x}(t)=Ax(t)+Bu(t)$$$$y(t)=Cx(t)+Du(t)$$$$x(t_0)=x_0$$$$x(t_f)=x_f$$其中$Q$和$R$是正定矩阵,$q(t)$和$r(t)$是正权重函数。

最优控制课后习题答案最优控制课后习题答案最优控制是现代控制理论中的重要分支,它研究如何在给定约束条件下,使系统的性能指标达到最优。
在最优控制的学习过程中,课后习题是巩固理论知识、培养解决问题能力的重要环节。
本文将为大家提供一些最优控制课后习题的答案,希望能对大家的学习有所帮助。
1. 线性二次型最优控制问题考虑一个线性时不变系统,其状态方程和性能指标分别为:$$\begin{align*}\dot{x}(t) &= Ax(t) + Bu(t) \\J(u) &= \int_{0}^{T} (x^T(t)Qx(t) + u^T(t)Ru(t))dt\end{align*}$$其中,$x(t)$为系统的状态向量,$u(t)$为控制输入向量,$A$和$B$为系统矩阵,$Q$和$R$为正定矩阵,$T$为最优控制的时间段。
求解该问题的最优控制输入$u^*(t)$。
答案:根据最优控制的原理,最优控制输入$u^*(t)$满足以下的最优性条件:$$\begin{align*}\frac{\partial J}{\partial u}(u^*(t)) &= 2R u^*(t) + 2B^T P(t)x(t) = 0 \\\dot{P}(t) &= -PA - A^T P - Q + PBR^{-1}B^T P\end{align*}$$其中,$P(t)$为状态向量的共轭变量矩阵。
通过求解上述的代数方程和微分方程,可以得到最优控制输入$u^*(t)$和状态向量的共轭变量矩阵$P(t)$。
2. 非线性最优控制问题考虑一个非线性系统,其状态方程和性能指标分别为:$$\begin{align*}\dot{x}(t) &= f(x(t), u(t)) \\J(u) &= \int_{0}^{T} g(x(t), u(t)) dt\end{align*}$$其中,$f(x(t), u(t))$为非线性函数,$g(x(t), u(t))$为性能指标函数。


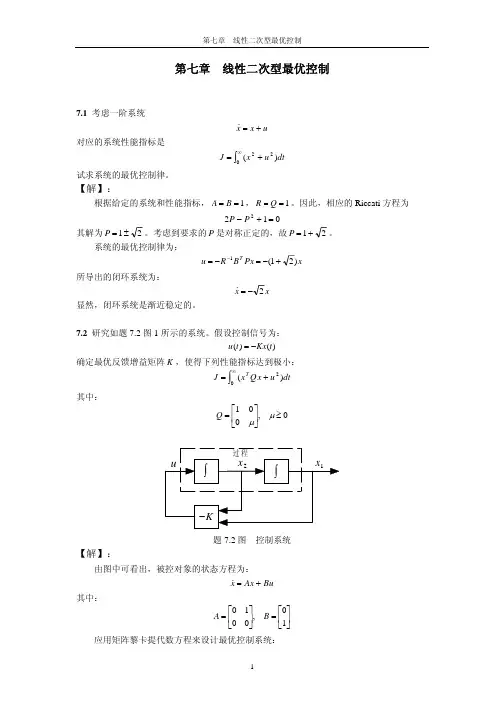

许多控制问题可以转化为线性二次型问题;其最优解可以写成统一的解析表达式,理论比较成熟第四章 线性二次型性能指标的最优控制问题4.1概述如果所研究的系统为线性,所取的性能指标为状态变量与控制变量的二次型函数,则这种动态系统的最优控制问题,称为线性二次型问题。
设线性时变系统的状态方程为()()()()(),()()()xt A t x t B t u t y t c t x t =+=在工程实际中,希望:系统输出y(t)尽量接近某一理想输出y r (t) 定义误差:e(t)= y r (t)- y(t)求最优控制u *(t),使下列性能指标极小:11()()[()()()()()()]22ft T T T f f t J e t Fe t e t Q t e t u t R t u t dt =++∫F 为对称非负定常阵,Q(t)为对称非负定时变矩阵,R(t)为对称正定时变矩阵,t 0,t f 固定。
上式中系数21是为了简化计算。
指标的物理意义:使系统在控制过程中的动态误差与能量消耗,以及控制结束时的系统稳态误差综合最优。
(1) 状态调节器问题若c(t) = I, y r (t) = 0, 则有e(t)= - y(t)= - x(t)11()()[()()()()()()]22f t T TT f f t J x t Fx t x t Q t x t u t R t u t dt =++∫此时系统可归纳为:当系统受扰动偏离平衡零状态时,要求产生一控制向量,使系统状态x(t)保持在零状态附近。
(2) 输出调节器若 y r (t) = 0, 则有e(t)= - y(t)11()()[()()()()()()]22ft T T T f f t J y t Fy t y t Q t y t u t R t u t dt =++∫ 此时系统可归纳为:当系统受扰动偏离平衡零状态时,要求产生一控制向量,使系统输出y(t)保持在零状态附近。
线性二次型最优控制问题2. 线性二次型最优控制问题如果所研究系统为线性,所取性能指标为状态变量与控制变 量的二次型函数,称这种动态系统最优化问题为线性二次型最概念优控制问题.问题的提法 设线性时变系统的状态方程为:x ( t ) = A( t ) x ( t ) + B( t )u( t ) y( t ) = C ( t ) x ( t )假设控制向量u(t)不受约束 ,用yr(t)表示期望输出,则误差向量为e( t ) = yr ( t ) − y( t )求最优控制u*(t) ,使下列二次型性能指标极小。
1 T 1 tf e ( t f )Fe ( t f ) + ∫ [e T ( t )Q( t )e( t ) + u( t )T R( t )u( t )]dt 2 2 t0 F —半正定 q × q常数矩阵 , Q ( t ) —半正定 q × q时变矩阵 J ( u) =R ( t ) —正定 p × p时变矩阵 t 0 及 t f 固定NORTHWESTERN POLYTECHNICAL UNIVERSITYNWPU线性二次型最优控制问题2. 线性二次型最优控制问题各项指标物理意义1 T 1 tf T J ( u) = e ( t f )Fe ( t f ) + ∫ [e ( t )Q( t )e( t ) + u( t )T R( t )u( t )]dt 2 2 t0(1) 第一积分过程项 0.5∫ttf0[e T ( t )Q ( t )e( t )]dt 是对动态跟踪误差加权平方和的积分要求,是系统在运动过程中动态跟踪误差的总度量. t (2) 第二积分过程项 0.5∫t [u( t )T R( t )u( t )]dt 表示系统在控制过程中对系统加权f 0后的控制能量消耗的总度量. (3) 末值项 0.5eT (t f )Fe( t f ) 表示末态跟踪误差向量与希望的零向量之间的距 离加权平方和. 整个性能指标物理意义: 使系统在控制过程中的动态误差与能量消耗,以及控制结束时的系统 终端跟踪误差综合最优。