电流峰值控制boost电路数学模型
- 格式:docx
- 大小:332.92 KB
- 文档页数:7


电流模式控制Boost变换器论文:电流模式控制Boost变换器分岔及其控制【中文摘要】电流模式控制Boost变换器是一种电压转换装备,相比较电压模式控制,电流模式控制的Boost变换器具有增益大、动态反应快、输出电感相对小、补偿电路相对简化且易于均流等众多优点,其广泛运用在各类用电设备上。
由于其电路结构的优势,在有源功率因数校正领域发挥重要作用,这些都是不争的事实。
但是这种电路有它自身的缺点,电流模式控制Boost变换器系统是一个强非线性系统,工作中易因电路参数选择不当或者外部干扰而是系统运行出现不稳定现象,严重地影响了其在各类用电设备的正常使用,所以其不稳定问题成为限制这类系统应用的重要瓶颈之一。
电流模式控制分为峰值电流控制和平均电流控制。
当采用峰值电流控制且占空比大于50%时,系统开环不稳定,容易产生次谐波振荡,其抗干扰能力差,特别当电感中纹波电流成分很少时,这种情况更严重。
目前工程上大都采用斜坡补偿法,利用斜坡信号叠加在电感电流上,从而得到控制系统稳定的作用。
但目前这种方法的参数选择(斜率m的取值)主要靠经验和重复实验,不能形象、客观地观察到系统运行规律。
在初期研究DC-DC变换器中混沌现象主要是通过数值仿真的方法,经过求解描述这些系统的微分方程得到系统运动的轨迹。
利用非线性理论研究非线性电路领域是目前较为前沿的研究手段,本文采用混沌等非线性理论研究电流模式控制Boost变换器。
针对Boost变换器的稳定性控制,目前已有很多的控制手段,总体可分为反馈控制和非反馈控制方法,非反馈控制方法的实用性很高,且这一方法比较成熟,目前采用比较多,但其也存在控制效率低、适用面窄、控制精度难以掌握等许多固有的缺陷。
工程上经常采用斜坡控制方法,但目前还是凭靠经验,不断地调整控制参数,这样大大增加了设计的工作量以及操作难度,因此限制了这一方法的推广应用。
本文将采用非反馈控制方法,分析研究电流模式控制Boost变换器在扰动强度及扰动相位共同作用下的系统二维分岔图,使我们更容易地观察以及总结到在两者控制下的电流模式控制Boost变换器系统的运行规律,从而便于工程人员在了解系统运行规律的前提下选择更精确的控制参数,减少设计过程的工程量以及操作难度。

滨江学院学年论文题目峰值电流控制的单相BOOST PFC变换器工作原理分析院系滨江学院^专业电气工程与自动化学生姓名徐小松学号061指导教师毛鹏职称讲师二O一一年二月十八日{峰值电流控制的单相BOOST PFC变换器工作原理分析徐小松南京信息工程大学滨江学院电气工程与自动化,南京210044摘要:传统的电压型控制是一种单环控制系统,是一种有条件的稳定系统。
因而出现了双环控制系统即电流型控制系统。
从原理、应用方面系统地论述了单相PFC变换器中电流型控制的发展,阐述了各种控制方法的优缺点。
峰值和平均电流型控制是单相PFC中应用最频繁的两种电流控制方法。
因而对这两种方法的讨论得出一些结论。
…关键词:BOOST变换器,功率因数PFC,峰值电流控制,平均电流控制1 引言峰值电流模式控制简称电流模式控制。
它的概念在60年代后期来源于具有原边电流保护功能的单端自激式反激开关电源。
在70年代后期才从学术上作深入地建模研究。
直至80年代初期,第一批电流模式控制PWM集成电路(UC3842、UC3846)的出现使得电流模式控制迅速推广应用,主要用于单端及推挽电路。
近年来,由于大占空比时所必需的同步不失真斜坡补偿技术实现上的难度及抗噪声性能差,电流模式控制面临着改善性能后的电压模式控制的挑战。
误差电压信号送至PWM比较器后,并不是象电压模式那样与振荡电路产生的固定三角波状电压斜坡比较,而是与一个变化的其峰值代表输出电感电流峰值的三角状波形或梯形尖角状合成波形信号UΣ比较,然后得到PWM脉冲关断时刻。
因此(峰值)电流模式控制不是用电压误差信号直接控制PWM脉冲宽度,而是直接控制峰值输出侧的电感电流大小,然后间接地控制P WM脉冲宽度。
2Boost变换器及其工作原理|工程中常用的升压(Boost)变换器的原理图如图1所示[5][6],其中Vi为输入直流电源,Q为功率开关管,在外部脉冲信号的激励下工作于开关状态,Q导通,输入电流流经电感L和开关管Q,电感L储能;开关管Q 截止时,二极管D 导通,直流电源Vi 和电感L 同时向负载R 供电,输入电流经电感L 、二极管D 流向负载R ,同时给电容C 充电,电感L 释放能量,在理 想情况下,该电路输出电压:()i out v dv -=11ViLR Vout图1 BOOST 变换器式中D 为Boost 变换器的占空比,因为占空比D<1,所以V (out )>Vi ,故称升压式换器。


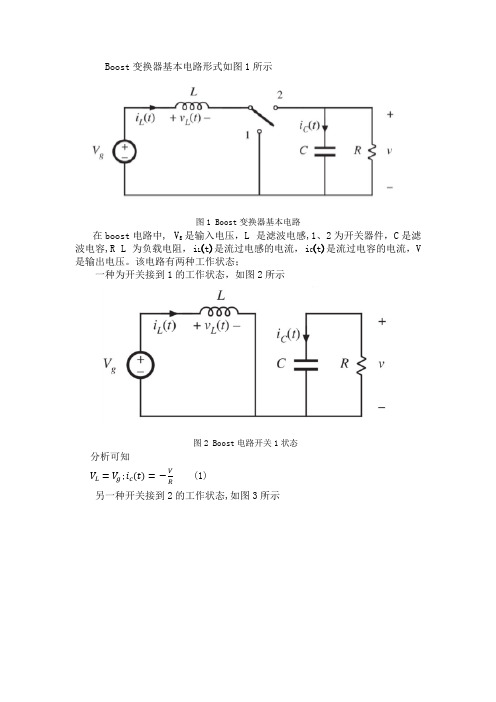
Boost 变换器基本电路形式如图1所示图1 Boost 变换器基本电路在boost 电路中, g V 是输入电压,L 是滤波电感,1、2为开关器件,C 是滤波电容,R L 为负载电阻,)(t i L 是流过电感的电流,)(t i C 是流过电容的电流,V 是输出电压。
该电路有两种工作状态;一种为开关接到1的工作状态,如图2所示图2 Boost 电路开关1状态分析可知; (1)另一种开关接到2的工作状态,如图3所示图3 Boost 电路开关2状态其中(2)根据电压定理作)(t V L 与时间的函数关系,如图4所示图4 电感电压与时间的函数关系S g S g S L T D V V DT V T 0dt t V ')()(-+⨯=⎰ 即 )()(''S S S g T VD T D DT V 0-++⨯=可得 D11D 1V V D M g -===')( (3) 根据电流定理作)(t i C 与时间的函数关系,如图6所示图6 电容电流与时间的函数关系S L S S C T D R V i DT R V dt T 0t i ')()()(-+⨯-=⎰即 L S S S i T D T D DT RV 0⨯++⨯-='')()( 可得;RD 1Vg i 2L )(-= (4) 通过对理想Boost 变换器在一个开关周期内两个工作阶段的分析,得到电感电压的分段函数:()()⎥⎦⎤⎢⎣⎡+=⎰⎰ττττd V d V T 1V S T D L D 0L S L (5) 用平均变量代替瞬时变量,化简得()()V V D 1DV V g g L --+= (6)又因为()()dtt di L d V T 1V L T 0L L S==⎰ττ (7) 将上式带入(5)得电感电压平均值的表达式()()V D 1V dtt di L g L --= (8) 同理可得电容电流平均值的分段表达式()()()RV t i D 1dt t dv C L --= (9) 为了将上式非线性问题线性化,找到变换器的静态工作点,对上面式子分离扰动,表示为直流分量和小信号分量之和,直流分量描述变换器的稳态解,交流小信号分量描述变换器在静态工作点处的动态性能。
基于峰值控制的交错 Boost变换器建模与设计阎昌国;龚仁喜;刘小雍【摘要】交错Boost变换器作为中大功率开关电源前级PFC技术的核心部分,其数学建模对开关电源的设计至关重要。
本文基于峰值电流控制技术,提出了一种交错Boost变换器的建模与设计方案。
运用时间平均等效原理,导出了该方案的完整交流小信号模型,设计了控制器补偿网络,并制作了一台800 W的实验样机。
测试结果表明,该方案具有峰值限流好、动态响应快、输出电压波动小等优点。
%Interleaved Boost converts are the core of the former PFC in the high-power switching power supply , its mathematical modeling is very important for switching power supply design .A new modeling and design method for interleaved boost convert with the peak current control is proposed in this paper .Firstly its whole AC small-sig-nal model is derived based on time averaging equivalent principle .Secondly its controller compensating network is designed ,Finally a 800 W prototype is made .The experimental result show this method has good peak current limit-ing, fast dynamic response and small output voltage fluctuation .【期刊名称】《科学技术与工程》【年(卷),期】2017(017)002【总页数】5页(P44-48)【关键词】交错Boost;开关电源;峰值电流;小信号模型【作者】阎昌国;龚仁喜;刘小雍【作者单位】遵义师范学院工学院1,遵义 563002;广西大学电气工程学院2,南宁530004;遵义师范学院工学院1,遵义 563002【正文语种】中文【中图分类】TM615电工技术随着电力电子控制技术的高速发展,开关电源已逐步向高频化、大功率化与集成化发展。
• 28•峰值电流型Boost变换器斜坡补偿分析咸阳职业技术学院汽车学院 习 璐中海油节能环保服务有限公司 陈文奎咸阳职业技术学院汽车学院 吴 珊本文以峰值电流型PFC Boost 变换器为基础,在输入电压正弦变化的条件下,推导出参考电流和电感电流平均值的时变表达式,进一步分析采取固定斜坡补偿时功率因数降低和过零死区出现的原因。
1.引言PFC Boost 变换器是目前有源功率因数校正电路中应用最广的一种电路结构,由于非线性电子元器件如功率开关和乘法器等在该电路中的使用,虽然能起到提高电路功率因数的作用,但同时给系统带来很强的非线性,即出现了分岔和混沌等不稳定现象(C K Tse.Circuit theory of power factor correction in switch-ing converters:International Journal of Circuit Theory and Ap-plica-tion,2003,31(2):157-198;O Dranga,C K Tse,H C H IU.Bifurcation behavior of a power-factor-correction Boost converter:International Journal of Bifurcation and Chaos,2003,13(10):3107-3114;马西奎,刘伟增,张浩.快时标意义下Boost PFC 变换器中的分岔与混沌现象分析:中国电机工程学报,2005,25(5):61-67)。
通常通过斜坡补偿的方法解决分岔和混沌,从而削弱不稳定现象范围(邹建龙,马西奎.功率因数校正Boost 变换器中快时标分岔的实验研究:中国电机工程学报,2008,28(12):38-43;任海鹏,刘丁.基于Matlab 的PFC Boost 变换器仿真研究和实验验证:电工技术学报,2006(5):29-35;黄家成.峰值电流控制模式PFC Boost 变换器中的斜坡补偿:合肥:安徽大学,2010:34-43)。
峰值电流型控制Boost 等效功率级的小信号传递函数
普高(杭州)科技开发有限公司 张兴柱 博士
Boost 变换器在峰值电流型控制下的等效功率级小信号传递函数(CCM ): )
1)(1()1()1()(220n n p p zc a vc vc s Q s s s s G s G ωωωωω++++−′≈′ )1)(1()1)(1()(220
n n p p zc a vg vg s Q s s s s G s G ωωωωω++++′+′≈′ )
1()1()(0p zc out s s R s Z ωω++′≈′ 其中:10F D R R G i vc ′=′,120F F L RT G s vg =′,1
0F R R =′ 11F RC p =ω,L R D a 2′=ω,)5.0(1−′=D m Q c p π,C R c zc 1=ω,s
n T πω= a a D F ωω×′=′22,)]5.0(21[231−′+=c s m D L RT F ,]5.0[22−′+′′=D m RT D L D F c s
n e c S S m +=1,i g n R L
V S ×=
Boost 的峰值电流控制等效功率级小信号传递函数,与Buck 的差别是在控制电压到输出电压这个小信号传递函数中增加了一个右半平面零点,其它的特性很类似,但由于其极点数少了一阶,所以相比于电压型控制而言,它的补偿电路也是比较容易设计的。
1。
BOOST电路设计介绍0 引言在实际应用中经常会涉及到升压电路的设计,对于较大的功率输出,如70W以上的DC/DC升压电路,由于专用升压芯片内部开关管的限制,难于做到大功率升压变换,而且芯片的价格昂贵,在实际应用时受到很大限制。
考虑到Boost升压结构外接开关管选择余地很大,选择合适的控制芯片,便可设计出大功率输出的DC/DC 升压电路。
UC3S42是一种电流型脉宽调制电源芯片,价格低廉,广泛应用于电子信息设备的电源电路设计,常用作隔离回扫式开关电源的控制电路,根据UC3842的功能特点,结合Boost拓扑结构,完全可设计成电流型控制的升压DC/DC电路,且外接元器件少,控制灵活,成本低,输出功率容易做到100W以上,具有其他专用芯片难以实现的功能。
1 UC3842芯片的特点UC3842工作电压为16~30V,工作电流约15mA。
芯片内有一个频率可设置的振荡器;一个能够源出和吸入大电流的图腾式输出结构,特别适用于MoSFET的驱动;一个固定温度补偿的基准电压和高增益误差放大器、电流传感器;具有锁存功能的逻辑电路和能提供逐个脉冲限流控制的PWM比较器,最大占空比可达100%。
另外,具有内部保护功能,如滞后式欠压锁定、可控制的输出死区时间等。
由UC3842设计的DC/DC升压电路属于电流型控制,电路中直接用误差信号控制电感峰值电流,然后间接地控制PWM脉冲宽度。
这种电流型控制电路的主要特点是:1)输入电压的变化引起电感电流斜坡的变化,电感电流自动调整而不需要误差放大器输出变化,改善了瞬态电压调整率;2)电流型控制检测电感电流和开关电流,并在逐个脉冲的基础上同误差放大器的输出比较,控制PWM脉宽,由于电感电流随误差信号的变化而变化,从而更容易设置控制环路,改善了线性调整率;3)简化了限流电路,在保证电源工作可靠性的同时,电流限制使电感和开关管更有效地工作;4)电流型控制电路中需要对电感电流的斜坡进行补偿,因为,平均电感电流大小是决定输出大小的因素,在占空比不同的情况下,峰值电感电流的变化不能与平均电感电流变化相对应,特别是占空比,50%的不稳定性,存在难以校正的峰值电流与平均电流的误差,即使占空比<50%,也可能发生高频次谐波振荡,因而需要斜坡补偿,使峰值电感电流与平均电感电流变化相一致,但是,同步不失真的斜坡补偿技术实现上有一定的难度。
Boost 变换器基本电路形式如图1所示
图1 Boost 变换器基本电路
在boost 电路中, g V 是输入电压,L 是滤波电感,1、2为开关器件,C 是滤波电容,R L 为负载电阻,)(t i L 是流过电感的电流,)(t i C 是流过电容的电流,V 是输出电压。
该电路有两种工作状态;
一种为开关接到1的工作状态,如图2所示
图2 Boost 电路开关1状态
分析可知
; (1)
另一种开关接到2的工作状态,如图3所示
图3 Boost 电路开关2状态
其中
(2)
根据电压定理作)(t V L 与时间的函数关系,如图4所示
图4 电感电压与时间的函数关系
S g S g S L T D V V DT V T 0
dt t V ')()(-+⨯=⎰ 即 )()(''S S S g T VD T D DT V 0-++⨯=
可得 D
11D 1
V V D M g -===')( (3) 根据电流定理作)(t i C 与时间的函数关系,如图6所示
图6 电容电流与时间的函数关系
S L S S C T D R V i DT R V dt T 0t i ')()()(-+⨯-=⎰
即 L S S S i T D T D DT R
V 0⨯++⨯-='')()( 可得;
R
D 1Vg i 2L )(-= (4) 通过对理想Boost 变换器在一个开关周期内两个工作阶段的分析,得到电感电压的分段函数:
()()⎥⎦
⎤⎢⎣⎡+=⎰⎰ττττd V d V T 1V S T D L D 0L S L (5) 用平均变量代替瞬时变量,化简得
()()V V D 1DV V g g L --+= (6)
又因为
()()dt
t di L d V T 1
V L T 0L L S
==⎰ττ (7) 将上式带入(5)得电感电压平均值的表达式
()()V D 1V dt
t di L g L --= (8) 同理可得电容电流平均值的分段表达式
()()()R
V t i D 1dt t dv C L --= (9) 为了将上式非线性问题线性化,找到变换器的静态工作点,对上面式子分离扰动,表示为直流分量和小信号分量之和,直流分量描述变换器的稳态解,交流小信号分量描述变换器在静态工作点处的动态性能。
)()(_____t v V t v g g g ∧
+=
)()(____t i I t i ∧
+=
)()(____t v V t v ∧
+=
(10) )(t d 中含有同频交流分量,所以
)()(t d D t d ∧
+= 将(10)式代入(8)式和(9)式,得交流小信号的状态方程:
)()()()()()('t v t d t d V t v D t v dt
t i d L g ∧∧∧∧∧∧
++-= (11) )()()()()()('t v t d t d I R t v t i D dt t v d C ∧∧∧∧
∧
∧---= (12) 将上式中二阶微分项与直流分量从等式中略去,可得
)()()()('t v t d V t v D dt
t i d L g ∧∧∧∧
++-= (13) )()()()('t d I R t v t i D dt t v d C ∧∧
∧∧--= (14) 取()()L c i s i s = (15)
以上方程经拉式变换,得
()()()()L g sLi s v s D v s Vd s '=-+ (16) ()()()()v s sCv s D i s Id s R
'=-- (17) ()()g L i s i s = (18)
采用电流控制一阶模型,将式(15)代入式(16),得 ()()()()c g sLi s v s D v s Vd s '=-+ (19)
解出占空比
()()()()c g sLi s D v s v s d s V
'+-= (20) 将式(15)和式(20)带入式(17),得 ()()()()()()c g v s sLi s D v s v s sCv s D i s I R V
'+-'=-- (21) 令()g v s =0,得控制输出传递函数
2()2vc RD sL G s sCRD D '-=''
+ (22) PWM 调制器传递函数为
1()m m
G s V = 反馈分压网络传递函数为
212
()R H s R R =+ 代入得原始回路增益函数
()()()()o vc m G s G s G s H s ==64.4*100.73330.0076520
s s --++
幅值裕度为64.8,相角裕度为无穷大,系统稳定。
考察动态性能
闭环函数阶跃响应无法达到1,系统存在静差。
进行pi调节
选择K
p =32.7,K
i
=1.893*10-5,调节后阶跃响应与bode图如图,幅值裕度为
34.5,相角裕度为66.5,系统稳定;带宽为5855.6,调节时间为2.3*10-4s,超调量为5.36%。