三角函数与向量习题(快)

专题33 三角函数与向量问题专题知识梳理平面向量与三角函数是高中数学的两个重要分支，内容繁杂，且平面向量与三角函数交汇点较多，向量的平行、垂直、夹角、数量积等知识都可以与三角函数进行交汇.不论是哪类向量知识与三角函数的交汇命题，都会出现交汇问题中的难点，对于此类问题的解决方法就是利用向量的知识将条件“脱去外衣”转化为三角函数中的“数量关系”，再利用三角函数的相关知识进行求解.考点探究【例1】 (2017·江苏卷)已知向量a ＝(cos x ，sin x )，b ＝(3，－3)，x ∈[0，π].(1)若a ∥b ，求x 的值；(2)记f (x )＝a ·b ，求f (x )的最大值和最小值以及对应的x 的值.【例2】 (2018·南京模拟)已知向量a ＝(2cos α，sin 2α)，b ＝(2sin α，t )，α∈⎝⎛⎭⎫0，π2，t 为实数. (1)若a －b ＝⎝⎛⎭⎫25，0，求t 的值；(2)若t ＝1，且a ·b ＝1，求tan ⎝⎛⎭⎫2α＋π4的值.题组训练1.(2018·苏、锡、常、镇调研)已知向量m ＝⎝⎛⎭⎫3sin x 4，1，n ＝⎝⎛⎭⎫cos x 4，cos 2x 4. (1)若m ·n ＝1，求cos ⎝⎛⎭⎫2π3－x 的值；(2)记f (x )＝m ·n ，在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且满足(2a －c )cos B ＝b cos C ，求f (A )的取值范围.2. (2018·南通、扬州等六市调研)在平面直角坐标系xOy 中，设向量a ＝(cos α，sin α)，b ＝(－sin β，cos β)，c ＝⎝⎛⎭⎫－12，32. (1)若|a ＋b |＝|c |，求sin(α－β)的值；(2)设α＝5π6，0＜β＜π，且a ∥(b ＋c )，求β的值.3.（2019·扬州中学月考）已知向量(2,1),(sin ,cos()),2A m nBC =-=+u r r 角,,A B C 为ABC ∆的内角，其所对的边分别为,,.a b c（1）当.m n u r r 取得最大值时，求角A 的大小；（2）在（1）成立的条件下，当a =22b c +的取值范围.4.（2018·南京三模）已知向量a ＝(2cos α，sin 2α)，b ＝(2sin α，t )，α∈(0，π2)． （1）若a －b ＝(25，0)，求t 的值； （2）若t ＝1，且a • b ＝1，求tan(2α＋π4)的值．5.在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知向量m ＝(sin A 2，cos A 2)，n ＝(cos A 2，－cos A 2)，且2m ·n ＋|m |＝22，AB →·AC →＝1.(1)求角A 的大小；(2)求△ABC 的面积S .6.已知向量m ＝(3sin x 4，1)，n ＝(cos x 4，cos 2x 4)． (1)若m·n ＝1，求cos(2π3－x )的值； (2)记f (x )＝m·n ，在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且满足(2a －c )cos B ＝b cos C ，求f (A )的取值范围．。

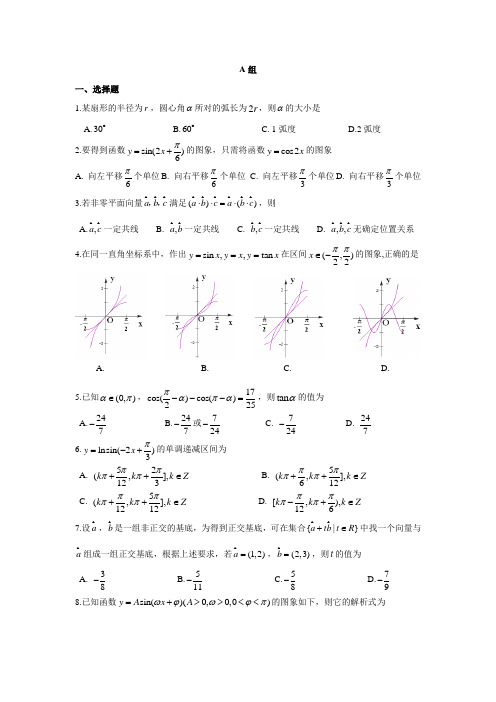
A 组一、选择题1.某扇形的半径为r ，圆心角α所对的弧长为2r ，则α的大小是A.30B.60C. 1弧度D.2弧度 2.要得到函数sin(2)6y x π=+的图象，只需将函数cos2y x =的图象A. 向左平移6π个单位B. 向右平移6π个单位 C. 向左平移3π个单位D. 向右平移3π个单位3.若非零平面向量 a b c ，，满足()()a b c a b c ⋅⋅=⋅⋅，则 A.,a c一定共线 B. ,a b一定共线 C. ,b c一定共线 D. ,,a b c无确定位置关系 4.在同一直角坐标系中，作出sin ,,tan y x y x y x ===在区间(,)22x ππ∈-的图象,正确的是5.已知(0,)απ∈，17cos()cos()225παπα---=，则tan α的值为A.247-B.247-或724-C. 724-D. 2476.lnsin(2)3y x π=-+的单调递减区间为A. 52(,],123k k k Z ππππ++∈ B. 5(,],612k k k Z ππππ++∈ C. 5(,],1212k k k Z ππππ++∈ D. [,),126k k k Z ππππ-+∈7.设a ，b 是一组非正交的基底，为得到正交基底，可在集合{|}a tb t R +∈中找一个向量与a 组成一组正交基底，根据上述要求，若(1,2)a = ，(2,3)b =，则t 的值为A. 38-B.511-C.58-D.79- 8.已知函数sin()(0,0,0)y A x A ωϕωϕπ=+>><<的图象如下，则它的解析式为A.D.C.B.A.52sin()126y x ππ=+B.2sin()66y x ππ=+ C.2sin()126y x ππ=+ D.2sin()66y x ππ=+或52sin()126y x ππ=+ 9.已知函数()cos (0)f x x ωω=>，其图象关于点6(,0)7M π对称，且在区间[0,]2π是单调函数，则ω的值为A.74 B. 78 C.74或712 D. 71210.已知α为第三象限角，化简1sin 1sin 1sin 1sin αααα+---+的结果为 .11.在ABC ∆中，D 是BC 上一点，2DC DB =-，若||2,||3AB AC == ，则||AD的取值范围为 .12.给出下列4个命题： ①保持函数sin(2)3y x π=+图象的纵坐标不变，将横坐标扩大为原来的2倍，得到的图象的解析式为sin()6y x π=+.②在区间[0,)2π上，0x 是tan y x =的图象与c o s y x =的图象的交点的横坐标，则064x ππ<<.③在平面直角坐标系中，取与x 轴、y 轴正方向相同的两个单位向量 i ,j作为基底，则四个向量 2i j + ，2 3i j + ，3 2i j - ，2 i j -的坐标表示的点共圆. ④方程33cos sin 1x x -=的解集为{|2,}2x x k k Z ππ=-∈.其中正确的命题的序号为 .13. 已知||1a = ，||2b =，a 与b 的夹角为60 . （1）求a b + 与a的夹角的余弦值；（2）当||a tb +取得最小值时，试判断a tb + 与b 的位置关系，并说明理由.第8题A 组参考答案 题号 1 2 3 4 5 6 7 8 9答案 DBAAADCBC10． αt a n 2- 11. )37,31( 12. ○2○313．已知1||=a ，2||=b ，a 与b 的夹角为60. （1）求b a +与a 的夹角的余弦.（2）当||b t a +取得最小值时，试判断b t a +与b 的位置关系，说明理由. 解：（1）设b a +与a 的夹角为θ，于是160cos ||||=⋅=⋅ b a b a ，72)(||222=+⋅+=+=+b b a a b a b a ，于是77272||||)(cos ==⋅+⋅+=a b a a b a θ. （2）令43)41(4124||22++=++=+t t t b t a ，当且仅当41-=t 时，取得最小值，此时04)(=+⋅=⋅+t b a b b t a ，所以b b t a ⊥+)(.B 组1．边长为1的等边三角形ABC 中，设AB c = ，BC a = ，CA b = ，则ab bc ca ⋅+⋅+⋅=（ ）A ．23 B ．23- C ．21 D ．21- 2．已知O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足()OP OA AB AC λ=++，[)0,λ∈+∞，则点P 的轨迹一定通过ABC ∆的（ ）A ．内心B ．外心C ．垂心D ．重心3．已知20a b =≠，且关于x 的方程0||2=⋅++b a x a x 有两个不同的实数根，则b a 与的夹角范围为（ ）A ．]32,3(ππ B ．],3(ππ C ．)6,0[π D ．],6(ππ4．已知1cos sin =+αα，则=-ααcos sin ．5．已知平面向量,a b，且满足1,2a b == ，则a b + 的取值范围 ．6．如图，有以下命题：设P 、Q 是线段AB 的三等分点，则有OB OA OQ OP +=+把此命题推广，设点1321,,-n A A A A 是线段AB 的n 等分点),3(*N n n ∈≥，则有)_____(1321OB OA OA OA OA OA n +=+++-7．如图，在ΔOAB 中，已知︒=∠==90,32||,2||AOB OB OA ，单位圆O 与OA 交于C ，)1,0(,∈=λλAB AD ，P 为单位圆O 上的动点。

三角函数与平面向量题型归类解析1.考查三角函数的化简或求值2.考查三角函数中的求角问题3. 考查三角形的边长或角的运算4. 考查三角函数的最值与向量运算5. 考查三角函数解析式的求法一、结合向量的数量积,考查三角函数的化简或求值 【例1】（2007年高考安徽卷）已知04πα<<，β为()cos(2)8f x x π=+的最小正周期，(tan(),1),(cos ,2),4a b a b m βαα=+-=⋅=，求22cos sin 2()cos sin ααβαα++-的值．【解答】因为β为()cos(2)8f x x π=+的最小正周期，故βπ=．因为a b m ⋅=，又cos tan()24a b βαα⋅=⋅+-，故cos tan()24m βαα⋅+=+．由于04πα<<，所以22cos sin 2()cos sin ααβαα++=-22cos sin(22)cos sin ααπαα++-22cos sin 2cos sin αααα+=-2cos (cos sin )cos sin ααααα+=-1tan 2cos 1tan ααα+=⋅-cos tan()24m βαα=⋅+=+．【评析】 合理选用向量的数量积的运算法则构建相关等式，然后运用三角函数中的和、差、半、倍角公式进行恒等变形，以期达到与题设条件或待求结论的相关式，找准时机代入求值或化简。

题型二：结合向量的夹角公式，考查三角函数中的求角问题 【例2】 （2006年高考浙江卷）如图，函数2sin(),y x x R πϕ=+∈（其中02πϕ≤≤）的图像与y 轴交于点（0，1）。

（Ⅰ）求ϕ的值；（Ⅱ）设P 是图像上的最高点，M 、N 是图像与x 轴的交点，求PM 与PN 的夹角。

【解答】（I ）因为函数图像过点(0,1)， 所以2sin 1,ϕ=即1sin .2ϕ= 因为02πϕ≤≤，所以6πϕ=.（II ）由函数2sin()6y x ππ=+及其图像，得115(,0),(,2),(,0),636M P N -- 所以11(,2),(,2),22PM PN =-=-从而cos ,||||PM PNPM PN PM PN ⋅<>=⋅1517=，故,PM PN <>=15arccos 17.【评析】 此类问题的一般步骤是：先利用向量的夹角公式：cos ,a b a b a b⋅=⋅求出被求角的三角函数值，再限定所求角的范围，最后根据反三角函数的基本运算，确定角的大小；或者利用同角三角函数关系构造正切的方程进行求解。

一、选择题1．（全国1文理）已知向量(5,6)a =- ，(6,5)b =，则a 与bA ．垂直B ．不垂直也不平行C ．平行且同向D ．平行且反向 2、（山东文5）已知向量(1)(1)n n ==-，，，a b ，若2-a b 与b 垂直，则=a （ ） A ．1BC ．2D ．43、（广东文4理10）若向量,a b满足||||1a b ==，,a b的夹角为60°，则a a a b ⋅+⋅=______；4、（天津理10） 设两个向量22(2,cos )a λλα=+- 和(,sin ),2m b m α=+ 其中,,m λα为实数.若2,a b = 则mλ的取值范围是( )A.[6,1]-B.[4,8]C.(,1]-∞D.[1,6]-5、（山东理11）在直角ABC ∆中，CD 是斜边AB 上的高，则下列等式不成立的是（A ）2AC AC AB =⋅ （B ） 2BC BA BC =⋅（C ）2AB AC CD =⋅（D ） 22()()AC AB BA BC CD AB⋅⨯⋅=6、（全国2 理5）在∆ABC 中，已知D 是AB 边上一点，若=2，=λ+31,则λ=(A)32(B)31(C) -31(D) -32 7、（全国2文6）在ABC △中，已知D 是AB 边上一点，若123AD DB CD CA CB λ==+，，则λ=（ ）A ．23B ．13C ．13-D ．23-8（全国2文9）把函数e xy =的图像按向量(2)=，0a 平移，得到()y f x =的图像，则()f x =（ ）A ．e 2x+B ．e 2x-C ．2ex -D ．2ex +9、（北京理4）已知O 是ABC △所在平面内一点，D 为BC 边中点，且2OA OB OC ++=0，那么（ ）Ａ．AO OD =Ｂ．2AO OD =Ｃ．3AO OD =Ｄ．2AO OD =10、（上海理14）在直角坐标系xOy 中，,i j分别是与x 轴，y 轴平行的单位向量，若直角三角形ABC 中，2AB i j =+ ，3AC i k j =+，则k 的可能值有A 、1个B 、2个C 、3个D 、4个 11、（福建理4文8）对于向量，a 、b 、c 和实数错误！未找到引用源。

()21.,,2sin 2cos 22sin 1.22B ABC a b c A B C m B B n m n π⎛⎫⎛⎫=-=+⊥ ⎪ ⎪⎝⎭⎝⎭△中，，，分别是角的对边，向量，，，，121.B a b c ==（）求角的大小；（）若，求的值()()2.,,cos cos //.ABC a b c A B C m a B n b A m n m n ==≠ △中，，，分别是角的对边，向量，，，，，12sin sin .ABC A B +（）求证：△是直角三角形；（）求的取值范围()()()2123.,,331,,221cos 1sin cos 02231.2O A B C OC OA OB A B C A x B x x x f x OA OC m AB m π=+⎡⎤⎛⎫+∈=⋅-+⋅ ⎪⎢⎥⎣⎦⎝⎭ 在平面直角坐标系中，是坐标原点，三点满足（）求证：三点共线；（）已知，，，，，，的最小值为，求实数的值4.3cos -cos -0.1cos 22ABC a B b C ccsoB B BA BC b a c=⋅== 在△中，有（）求；（）若，且，)()()()()()()15.sin sin 0021221.66a x x b x f x a b b f x f x x f x ωωωωπωππ==>=+⋅-⎡⎤∈-⎢⎥⎣⎦若，，，，其中，记函数（）若的图象中两条相邻对称轴间的距离为，求及的单调减区间；（）在（）的条件下，且，，求的最大值)()()2226..1tan -tan 1tan tan 2sin ,13,cos 2.ABC c a b ab A B A B B m A n A m n =+-=+⋅==⋅ 在△中，有（）若，求；（）设，，试求的最大值()()()()[]()17.cos 4cos 2cos 21204.a x xb x x f x a b k k R f x x f x k π⎛⎫===⋅+∈ ⎪⎝⎭∈ 若向量，，，函数（）求的单调增区间；（）若，时，的最大值为，求())()8.sin cos 110.212cos 24cos sin .a A A b a b A A f x x A x π⎛⎫==-⋅=∈ ⎪⎝⎭=+ 若向量，，，，且，（）求；（）求函数的值域9.cos ,sin cos ,sin .22223712.2C C C C a b c ABC A B C m n m n C c ABC S a b π⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭==+ 设，，分别为△的内角，，的对边，，，与的夹角为（）求角的大小；（）已知，△的面积的值()()()()()10.2cos 1cos 2.1221.2f x m n m x n x x x R f x ABC f A b ABC ABC R =⋅==∈== 设函数，其中向量，，，（）求的最小正周期和单调递减区间；（）在△中，已知，，△的外接圆半径()(211.2sin cos 22cos 1.2121.ABC B ABC m A C n B m n B b ABC S ⎛⎫=+=- ⎪⎝⎭= △在锐角△中，已知，，，且，共线（）求角的大小；（）如果，求△的面积的最大值(()2212.1cos sin 1.11sin 223tan .sin cos A B C ABC m n A A m n A B C B B==⋅=-+=- 已知，，是△的三个内角，向量，，，，且（）求；（）若，求的值()()()2313.3,0,0,3,cos sin .222sin sin 211.1tan A B C AC BC AC BC ππθθθθθθθ⎛⎫∈ ⎪⎝⎭-=⋅=-+ 在直角坐标系中，已知，，其中，（）若，求；若，求的值)()c cos =bcos .8m=cos 21cos n=1m n tan 54B C A A A π-⎛⎫⎛⎫+⊥+ ⎪ ⎪⎝⎭⎝⎭ 14.已知钝角△ABC 中，有（1）求B ；（2）设向量，，，-，且，求的值。

数学周测试一（三角函数和向量）一选择题：（每题5分共40分） 1．设四边形ABCD 中，有=21，且||=||，则这个四边形是（ ） A.平行四边形 B. 等腰梯形 C. 矩形 D.菱形2．某扇形的面积为12cm ，它的周长为4cm ，那么该扇形圆心角的度数为 （ ）A ．2°B ．2C ．4°D ．43.有下列四种变换方式:①向左平移4π,再将横坐标变为原来的21; ②横坐标变为原来的21,再向左平移8π;③横坐标变为原来的21,再向左平移4π; ④向左平移8π,再将横坐标变为原来的21;其中能将正弦曲线x y sin =的图像变为)42sin(π+=x y 的图像的是（ ）A.①和②B. ①和③C. ②和③D. ②和④4．若2sin 1log x θ=-，则x 的取值范围是 （ ）A ．[1,4]B ．1[,1]4C ．[2,4]D ． 1[,4]45．下列函数中，最小正周期为π，且图象关于直线3x π=成轴对称图形的是 （ ）A ．sin 23y x π⎛⎫=-⎪⎝⎭ B ．sin 26y x π⎛⎫=+ ⎪⎝⎭C ．sin 26y x π⎛⎫=- ⎪⎝⎭D ．1sin 26y x π⎛⎫=+ ⎪⎝⎭6、函数)23sin(x y -=π的单调递减区间是（ ）)(A ;32,6Z k k k ∈⎥⎦⎤⎢⎣⎡+-+-ππππ )(B ;1252,122Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ )(C ;3,6Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ )(D ;125,12Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ7．平面直角坐标系中，已知两点A （3,1），B （－1,3），若点C 满足βα1R ＝＋，且、其中βαβα∈，则点C 的轨迹方程是（ ） A ．3x+2y －11=0; B ．(x －1)2+(y －2)2=5;C ．2x －y=0;D ．x+2y －5=0; 8、函数f(x)=Asin(ωx+ψ)(A>O ，ω>0)的部分图象如图所示，则f(1)+f (2)+…+ f(2008)的值等于（ ）A B 2 C 、0 D 、不能确定二、填空题：（每题5分共20分） 9．cos()417cos(523ππ－）与－,其大小为 10．已知点)2,1(),1,0(),1,2(),0,1(--D C B A ，则AB 与CD 的夹角大小为._______________ 11、函数x x y sin 4cos 2-=的值域是______________ 12. 已知34παβ+=，则(1tan )(1tan )αβ--的值是________． 三、解答题:（每题8分共40分） 13． 已知tan()4x π-，求2sin 22cos 22cos 3sin 21x xx x +--的值14（1）．已知61)(2)3(23,||4,=+∙==－, 求∙的值； （2）设两个非零向量1e 和2e 不共线.如果=1e +2e ，=128e + 2e ，=133e - 2e，求证：A 、B 、D 三点共线15 . 3123<<<cos sin sin 224135ππβααβαβα-=+=-已知，（），（），求的值 16．已知)(,2sin 3cos 2)(2R a a x x x f ∈++=（1）若R x ∈，求f(x)的单调增区间； （2）若]2,0[π∈x 时，f(x)的最大值为4，求a 的值；（3）在（2）的条件下，求满足f(x)=1且],[ππ-∈x 的x 的集合。

三角函数、平面向量、解三角形一、选择题(每小题5分，共50分)1.化简cos15cos45cos75sin45︒︒-︒︒的值为（ ） A. 12-C.12D. -2.设向量,a b 满足:1||=a , 2||=b , ()0a a b ⋅+=, 则a 与b 的夹角是（ ）A ． 30B ． 60C ． 90D ． 120 3.已知角α的终边经过点)60cos 6,8(0--m P ，且54cos -=α，则m 的值为（ ） A 21 B 21- C 23- D 23 4.设函数22()cos ()sin (),44f x x x x R ππ=+-+∈，则函数()f x 是（ ） A ．最小正周期为π的奇函数 B ．最小正周期为π的偶函数C ．最小正周期为2π的奇函数D ．最小正周期为2π的偶函数 5.已知平面向量(1,2)a =，(2,)b m =-，且a //b ，则23a b +＝（ ）A ．(5,10)--B ．(4,8)--C ．(3,6)--D ．(2,4)-- 6.已知4cos 5α=-,且(,)2παπ∈,则tan()4πα-等于（ ） A.17- B.7- C.71 D.7 7.函数2tan2tan 12xy x =-的最小正周期为（ ） A ．π B ．2π C ．4π D ．2π 8.在ABC ∆中，M 是BC 的中点，1AM =，点P 在AM 上且满足2A P P M =，则()PA PB PC ⋅+等于 （A ）49- （B ）43- （C ）43 (D) 49（ ） 9.要得到函数sin2cos2y x x =-的图象，只要将函数sin2cos2y x x =+的图象沿x 轴（ ）A.向右平移4π个单位B.向左平移4π个单位C.向右平移2π个单位D.向左平移2π个单位 10.已知α为锐角，且4cos(),65πα+=则cos α的值为. （ ）A.410-B.410+C.310D.310二、填空题(每小题5分，共25分)11.在平行四边形ABCD 中，AC 为一条对角线，(2,4),(1,3),AB AC BD ===则12.设(2,4),(1,1)a b ==，若()b a m b ⊥+⋅，则实数m =13.已知点1),(cos ,sin )A B θθ-，其中[]0,θπ∈，则AB 的最大值为________.14.若函数())cos()(0)f x x x φφφπ=+-+<<为奇函数，则φ=________15.在斜三角形ABC 中，角C B A ,,所对的边分别为c b a ,,，若1tan tan tan tan =+BC A C ， 则=+222c b a ． 三、解答题(共75分)16.53()42ππθ<<17. 已知函数22()cos cos sin 2222x x x x f x ⎛⎫=-- ⎪⎝⎭．18. 如图2，渔船甲位于岛屿A 的南偏西60方向的B 处，且与岛屿A 相距12海里，渔船乙以10海里/小时的速度从岛屿A 出发沿正北方向航行，若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙，刚好用2小时追上．（1）求渔船甲的速度；（2）求sin α的值．19.已知向量1(sin ,1),(3cos ,)2=-=-a x b x ,函数()()2f x a b a =+⋅-.(Ⅰ)求函数()f x 的最小正周期T ;(Ⅱ)已知a 、b 、c 分别为ABC ∆内角A 、B 、C 的对边, 其中A 为锐角,4a c ==,且()1f A =,求,A b 和ABC ∆的面积S20.已知函数3cos 22sin 3)(2++=x x x f （1）当)2,0(π∈x 时，求函数)(x f 的值域； （2）若528)(=x f ，且)125,6(ππ∈x ，求sin(4)3x π+的值．21. 在ABC ∆中，sin sin sin sin()sin sin A B A C A B A B --=++. (Ⅰ)求角B ；(Ⅱ)若3sin 5A =，求cos C 的值.。

最新经典试题系列----三角函数与向量1、在ABC ∆中，，．5cos 13A =-4sin 5B =（Ⅰ）求sinC 的值；（Ⅱ）设5BC =，求ABC ∆的面积．2、设函数f(x)=q p ⋅，其中向量)sin cos ,cos 2()sin cos ,(sin x x x q x x x p -=+= ，,R x ∈.(1) 求f(3π)的值及f(x)的最大值。

(2) 求函数f(x)的单调递增区间3、已知a 、b 、c 分别是△ABC 中角A 、B 、C 的对边，且．222a c b ac +-=（Ⅰ）求角的大小； （Ⅱ）若，求的值． B 3c a =tan A 4、已知函数2π()2sin 24f x x x ⎛⎫=+ ⎪⎝⎭，ππ42x ⎡⎤∈⎢⎥⎣⎦，．（I ）求()f x 的最大值和最小值；（II ）若不等式()2f x m -<在ππ42x ⎡⎤∈⎢⎥⎣⎦，上恒成立，求实数m 的取值范围 5、在△ABC 中，设内角A 、B 、C 的对边分别为a 、b 、c ，23)4tan(-=-C π（1）求角C 的大小； （2）若ABC 的面积。

∆=+=求且,5,7b a c 6、已知函数()212cos ,2f x x x x =--∈R.（I ）求函数的最小值和最小正周期；()f x （II ）设的内角的对边分别为，且，若向量ABC ∆A B C 、、a b c、、()0c f C ==与向量共线，求的值.()1,sin A =m ()2,sin B =n ,a b 7、在中,分别为内角所对的边，且满足.ABC ∆,,a b c ,,A BC sin 2A A =(Ⅰ) 求的大小；A (Ⅱ) 现给出三个条件：①； ②；③.2a =45B =︒c =试从中选出两个可以确定的条件，写出你的选择并以此为依据求的面积.(只需写出一ABC ∆ABC ∆个选定方案即可,选多种方案以第一种方案记分)8、已知函数.2()sin cos 222x x x f x =+（1）将()f x 写成)sin(φω+x A 的形式，并求其图象对称中心的横坐标；（2）如果△ABC 的三边、、满足，且边所对的角为x ，试求角x 的范围及此时函数a b c 2b ac =b ()f x 的值域.9、设函数f(x)=2)0(sin sin cos 2cos sin 2πϕϕϕ<<-+x x x 在π=x 处取最小值.（1）求ϕ.的值;（2）在∆ABC 中,c b a ,,分别是角A,B,C 的对边,已知,2,1==b a 23)(=A f ,求角C.10、在ABC ∆中，c b a 、、分别为角A B C 、、的对边．已知)2sin ,2(cosC C = ，)2sin ,2(cos C C n -=，且12m n ⋅= .(1) 求角C ； (2) 若27=c ，ABC ∆的面积233=S ，求b a +的值.11、已知向量，其中．()11,,2,cos 2sin sin a b x x x ⎛⎫=-= ⎪⎝⎭⎥⎦⎤ ⎝⎛∈2,0πx （1）试判断向量与能否平行，并说明理由？ （2）求函数的最小值．a b ()f x =A a b 12、已知向量3(sin ,),(cos ,1).2a x b x ==- （1）当时，求的值； （2）（文科）求的值域； //a b 22cos sin 2x x -b b a x f ⋅+=)()(（3）（理科）求在上的值域．b b a x f ⋅+=)()(,02π⎡⎤-⎢⎥⎣⎦13、在1113cos ,cos 1414ABC A B ∆==中，（I ）求cos C 的值；（Ⅱ）若||||CA CB AB += 求14、设a 、b 、c 分别为△ABC 的内角A 、B 、C 的对边，向量，，,sin )m A B =(cos )n B A = 若.1cos()m n A B ⋅=++ （1）求角C 的大小； （2）若，ABC 的面积.4a b +=c =15、已知向量，且与向量所成角为，其中A ，B ，C 是△ABC 的内角。