向量和三角函数综合试题(卷)

高三数学三角函数试题答案及解析1.设角的终边在第一象限，函数的定义域为，且，当时，有，则使等式成立的的集合为．【答案】【解析】令得：，令得：，由得：，又角的终边在第一象限，所以因而的集合为.【考点】抽象函数赋值法2.“θ≠”是“cos θ≠”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】B【解析】因为“cos θ＝”是“θ＝”的必要不充分条件，所以“θ≠”是“cos θ≠”的必要不充分条件，选B.3.已知函数，则一定在函数图象上的点是（）A．B．C．D．【答案】C．【解析】根据的解析式，求出，判断函数的奇偶性，由函数的奇偶性去判断四个选项是否在图象上．．为奇函数，在图象上．故选C．【考点】函数的奇偶性．4.函数y=的定义域是.【答案】{x|kπ-<x≤kπ+,k∈Z}【解析】由1-tanx≥0,即tanx≤1,结合正切函数图象可得,kπ-<x≤kπ+,k∈Z,故函数的定义域是{x|kπ-<x≤kπ+,k∈Z}.5.若方程有实根，则实数的取值范围为【答案】【解析】由方程得，，即，因为，所以，若方程有实根，则，解得．【考点】方程的根．6.已知的三个内角所对的边分别为，且，则角的大小为 .【答案】【解析】根据正弦定理：，，即：，，【考点】1、正弦定理；2、两角和与差的三角函数公式.7.已知函数上有两个零点,则的值为（）A．B．C．D．【答案】D【解析】，由于，故，由于函数在区间上有两个零点，所以，所以，所以，故选D.【考点】1.三角函数的图象；2.三角函数的对称性8.已知函数d的最大值为2，是集合中的任意两个元素，且的最小值为.（1）求函数的解析式及其对称轴；（2）若，求的值.【答案】（1），；（2）.【解析】本题主要考查两角和与差的正弦公式、二倍角的余弦公式、诱导公式、三角函数的最小正周期、单调性等基础知识，考查运算能力.第一问，利用倍角公式化简表达式，先利用周期求出，再求最值，通过解方程求出，确定了解析式后求正弦函数的对称轴；第二问，通过角之间的关系转化角，考查诱导公式和倍角公式.试题解析：（1），由题意知：的周期为，由，知 2分由最大值为2，故，又， 4分∴ 5分令，解得的对称轴为 7分（2）由知，即， 8分∴ 10分12分【考点】1.倍角公式；2.两角和与差的三角函数；3.函数的周期；4.函数的对称轴.9.已知函数时有极大值，且为奇函数，则的一组可能值依次为( )A．B．C．D．【答案】D【解析】，因为当时有极大值，所以=0，解得当k=0时,；因为=为奇函数，所以,当k=0时,,故选D.【考点】1.求函数的导数及其导数的性质；2.三角函数的性质.10.已知函数的最大值为4，最小值为0，最小正周期为，直线是其图像的一条对称轴，则下列各式中符合条件的解析式是（）A．B．C．D．【答案】D【解析】由题意可得，则据此可知答案选D.【考点】函数的图像与性质.11.中，角所对的边分别为且．（Ⅰ）求角的大小；（Ⅱ）若向量，向量，，，求的值．【答案】（Ⅰ）；（Ⅱ）；【解析】（Ⅰ）主要利用三角形中内角和定理、三角恒等变换来求；（Ⅱ）通过余弦定理、解方程组可求；试题解析：（Ⅰ）∵∴，∴，∴或∴（II）∵∴，即①又，∴，即②由①②可得，∴又∴，∴【考点】解三角形中内角和定理以及余弦定理的使用、三角恒等变换等知识点，考查学生的计算能力.12.在中，角的对边分别为向量，,且．（１）求的值；（２）若,,求角的大小及向量在方向上的投影．【答案】（1）；（2），向量在方向上的投影．【解析】（1）由向量数量积坐标形式列式，可求得的值，再利用平方关系可求得的值；（2）先利用正弦定理可求得的值，再利用大边对大角可求得角的大小．由投影的定义可求得向量在方向上的投影．试题解析：(１)由,得, 1分, 2分.. ３分．４分(２)由正弦定理，有, ５分．６分，, ７分． 8分由余弦定理，有， 9分或（舍去）． 10分故向量在方向上的投影为 11分． 12分【考点】1、向量数量积、投影；2、三角恒等变换；3、解三角形．13.已知函数若方程有三个不同的实根，且从小到大依次成等比数列，则m的值为 .【答案】【解析】设三个根由小到大依次为，结合余弦函数图像可知关于直线对称，关于直线对称，代入计算得【考点】三角函数图像及性质点评：题目中主要结合三角函数图像的轴对称性找到三根之间的联系14.函数的最小正周期为．【答案】【解析】根据题意，由于即为其周期，故答案为【考点】三角函数的性质点评：主要是考查了三角函数的性质的运用，属于基础题。

专题03 三角函数与平面向量综合问题（答题指导）【题型解读】题型特点命题趋势▶▶题型一：三角函数的图象和性质1．注意对基本三角函数y ＝sin x ，y ＝cos x 的图象与性质的理解与记忆，有关三角函数的五点作图、图象的平移、由图象求解析式、周期、单调区间、最值和奇偶性等问题的求解，通常先将给出的函数转化为y ＝A sin(ωx ＋φ)的形式，然后利用整体代换的方法求解． 2．解决三角函数图象与性质综合问题的步骤 (1)将f (x )化为a sin x ＋b cos x 的形式． (2)构造f (x )＝a 2＋b 2⎝⎛⎭⎪⎫a a 2＋b 2·sin x ＋b a 2＋b 2·cos x . (3)和角公式逆用，得f (x )＝a 2＋b 2sin(x ＋φ)(其中φ为辅助角)． (4)利用f (x )＝a 2＋b 2sin(x ＋φ)研究三角函数的性质． (5)反思回顾，查看关键点、易错点和答题规范．【例1】 (2017·山东卷)设函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx －π6＋sin ⎝ ⎛⎭⎪⎫ωx －π2，其中0＜ω＜3.已知f ⎝ ⎛⎭⎪⎫π6＝0.(1)求ω；(2)将函数y ＝f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变)，再将得到的图象向左平移π4个单位，得到函数y ＝g (x )的图象，求g (x )在⎣⎢⎡⎦⎥⎤－π4，3π4上的最小值．【答案】见解析【解析】(1)因为f (x )＝sin ⎝ ⎛⎭⎪⎫ωx －π6＋sin ⎝⎛⎭⎪⎫ωx －π2，所以f (x )＝32sin ωx －12cos ωx －cos ωx ＝32sinωx －32cos ωx ＝3⎝ ⎛⎭⎪⎫12sin ωx －32cos ωx ＝3sin ⎝ ⎛⎭⎪⎫ωx －π3.因为f ⎝ ⎛⎭⎪⎫π6＝0，所以ωπ6－π3＝k π，k ∈Z .故ω＝6k ＋2，k ∈Z .又0＜ω＜3，所以ω＝2.(2)由(1)得f (x )＝3sin ⎝ ⎛⎭⎪⎫2x －π3，所以g (x )＝3sin ⎝ ⎛⎭⎪⎫x ＋π4－π3＝3sin ⎝ ⎛⎭⎪⎫x －π12.因为x ∈⎣⎢⎡⎦⎥⎤－π4，3π4，所以x －π12∈⎣⎢⎡⎦⎥⎤－π3，2π3，当x －π12＝－π3，即x ＝－π4时，g (x )取得最小值－32.【素养解读】本题中图象的变换考查了数学直观的核心素养，将复杂的三角函数通过变形整理得到正弦型函数，从而便于对性质的研究，考查数学建模的核心素养．【突破训练1】 设函数f (x )＝32－3sin 2ωx －sin ωx cos ωx (ω>0)，且y ＝f (x )的图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值；(2)求f (x )在区间⎣⎢⎡⎦⎥⎤π，3π2上的最大值和最小值． 【答案】见解析 【解析】(1)f (x )＝32－3·1－cos2ωx 2－12sin2ωx ＝32cos2ωx －12sin2ωx ＝ －sin ⎝ ⎛⎭⎪⎫2ωx －π3.因为y ＝f (x )的图象的一个对称中心到最近的对称轴的距离为π4，故该函数的周期T ＝4×π4＝π.又ω>0，所以2π2ω＝π，因此ω＝1.(2)由(1)知f (x )＝－sin ⎝ ⎛⎭⎪⎫2x －π3.当π≤x ≤3π2时，5π3≤2x －π3≤8π3，所以－32＝sin 5π3≤sin ⎝ ⎛⎭⎪⎫2x －π3≤sin 5π2＝1，所以－1≤f (x )≤32，即f (x )在区间⎣⎢⎡⎦⎥⎤π，3π2上的最大值和最小值分别为32，－1.▶▶题型二 解三角形1．高考对解三角形的考查，以正弦定理、余弦定理的综合运用为主．其命题规律可以从以下两方面看：(1)从内容上看，主要考查正弦定理、余弦定理以及三角函数公式，一般是以三角形或其他平面图形为背景，结合三角形的边角关系考查学生利用三角函数公式处理问题的能力；(2)从命题角度看，主要是在三角恒等变换的基础上融合正弦定理、余弦定理，在知识的交汇处命题． 2．用正、余弦定理求解三角形的步骤第一步：找条件，寻找三角形中已知的边和角，确定转化方向．第二步：定工具，根据已知条件和转化方向，选择使用的定理和公式，实施边角之间的转化． 第三步：求结果，根据前两步分析，代入求值得出结果．第四步：再反思，转化过程中要注意转化的方向，审视结果的合理性．【例2】 在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，且cos(C ＋B)cos(C －B)＝cos2A －sin Csin B ． (1)求A ；(2)若a ＝3，求b ＋2c 的最大值． 【答案】见解析【解析】(1)cos(C ＋B)cos(C －B)＝cos2A －sinCsinB ＝cos2(C ＋B)－sinCsinB ，则cos(C ＋B)[cos(C －B)－cos(C ＋B)]＝－sinCsinB ，则－cosA·2sinCsinB＝－sinCsinB ，可得cosA ＝12，因为0＜A ＜π，所以A＝60°.(2)由a sinA ＝b sinB ＝csinC ＝23，得b ＋2c ＝23(sinB ＋2sinC)＝23[sinB ＋2sin(120°－B)]＝23(2sinB＋3cosB)＝221sin(B ＋φ)，其中tanφ＝32，φ∈⎝ ⎛⎭⎪⎫0，π2.由B ∈⎝ ⎛⎭⎪⎫0，2π3得B ＋φ∈⎝⎛⎭⎪⎫0，7π6，所以sin(B ＋φ)的最大值为1，所以b ＋2c 的最大值为221.【素养解读】试题把设定的方程与三角形内含的方程(三角形的正弦定理、三角形内角和定理等)建立联系，从而求得三角形的部分度量关系，体现了逻辑推理、数学运算的核心素养．【突破训练2】 (2017·天津卷)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知a >b ，a ＝5，c ＝6，sin B ＝35.(1)求b 和sin A 的值； (2)求sin ⎝ ⎛⎭⎪⎫2A ＋π4的值．【答案】见解析【解析】(1)在△ABC 中，因为a >b ，故由sin B ＝35，可得cos B ＝45.由已知和余弦定理，有b 2＝a 2＋c 2－2ac cos B＝13，所以b ＝13.由正弦定理得sin A ＝a sin B b ＝31313. (2)由(1)及a <c ，得cos A ＝21313，所以sin2A ＝2sin A cos A ＝1213，cos2A ＝1－2sin 2A ＝－513.故sin ⎝⎛⎭⎪⎫2A ＋π4＝sin2A cos π4＋cos 2A ·sin π4＝7226.▶▶题型三 三角函数与平面向量的综合1．三角函数、解三角形与平面向量的综合主要体现在以下两个方面：(1)以三角函数式作为向量的坐标，由两个向量共线、垂直、求模或求数量积获得三角函数解析式；(2)根据平面向量加法、减法的几何意义构造三角形，然后利用正、余弦定理解决问题．2．(1)向量是一种解决问题的工具，是一个载体，通常是用向量的数量积运算或性质转化成三角函数问题．(2)三角形中的三角函数要结合正弦定理、余弦定理进行转化，注意角的范围对变形过程的影响． 【例3】 (2019·佛山调考)已知函数f (x )＝a ·b ，其中a ＝(2cos x ，－3sin2x )，b ＝(cos x,1)，x ∈R .(1)求函数y ＝f (x )的单调递减区间；(2)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，f (A )＝－1，a ＝7，且向量m ＝(3，sin B )与n ＝(2，sin C )共线，求边长b 和c 的值． 【答案】见解析【解析】(1)f (x )＝a ·b ＝2cos 2x －3sin2x ＝1＋cos2x －3sin2x ＝1＋2cos ⎝ ⎛⎭⎪⎫2x ＋π3，由2k π≤2x ＋π3≤2k π＋π(k ∈Z )，解得k π－π6≤x ≤k π＋π3(k ∈Z )，所以f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π－π6，k π＋π3(k ∈Z )．(2)因为f (A )＝1＋2cos ⎝ ⎛⎭⎪⎫2A ＋π3＝－1，所以cos ⎝ ⎛⎭⎪⎫2A ＋π3＝－1.因为0＜A ＜π，所以π3＜2A ＋π3＜7π3，所以2A ＋π3＝π，即A ＝π3.因为a ＝7，由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝(b ＋c )2－3bc ＝7.①因为向量m ＝(3，sin B )与n ＝(2，sin C )共线，所以2sin B ＝3sinC ． 由正弦定理得2b ＝3c ，② 由①②可得b ＝3，c ＝2.【突破训练3】(2019·湖北八校联考) 已知△ABC 的面积为S ，且32AB →·AC →＝S ，|AC →－AB →|＝3.(1)若f (x )＝2cos(ωx ＋B )(ω＞0)的图象与直线y ＝2相邻两个交点间的最短距离为2，且f ⎝ ⎛⎭⎪⎫16＝1，求△ABC 的面积S ；(2)求S ＋3 3 cos B cos C 的最大值． 【答案】见解析【解析】设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ， 因为32AB →·AC →＝S ，所以32bc cos A ＝12bc sin A ， 解得tan A ＝3，所以A ＝π3.由|AC →－AB →|＝3得|BC →|＝a ＝3.(1)因为f (x )＝2cos(ωx ＋B )(ω>0)的图象与直线y ＝2相邻两个交点间的最短距离T ＝2，即2πω＝2，解得ω＝π，故f (x )＝2cos(πx ＋B )．又f ⎝ ⎛⎭⎪⎫16＝2cos ⎝⎛⎭⎪⎫π6＋B ＝1，即cos ⎝ ⎛⎭⎪⎫π6＋B ＝12.因为B 是△ABC 的内角，所以B ＝π6，从而△ABC 是直角三角形，所以b ＝3，所以S △ABC ＝12ab ＝332.(2)由题意知A ＝π3，a ＝3，设△ABC 的外接圆半径为R ，则2R ＝a sin A ＝ 332＝23，解得R ＝3，所以S＋33cos B cos C ＝12bc sin A ＋33cos B cos C ＝34bc ＋33cos B cos C ＝33sin B sin C ＋33cos B cos C ＝33cos(B －C )，故S ＋33cos B cos C 的最大值为3 3.。

高三数学三角函数综合试题答案及解析1.已知函数，则的值为 .【答案】.【解析】∵，两边求导，∴，令，得，∴，∴，即.【考点】导数的运用.2.已知函数.（1）求的最小正周期和最小值；（2）若，且，求的值.【答案】（1），；（2）.【解析】(1)首先根据二倍角公式进行化简，并将函数的解析式化为的形式，然后利用最小正周期公式,最小值为,可得结果；(2)将代入,化简，利用得到三角函数值，根据，得到的值.此题考察三角函数的化简求值，属于基础题.试题解析：（1）解：， 4分，，所以的最小正周期为，最小值为. 8分（2）解：，所以， 11分因为，，所以，因此的值为. 13分【考点】1.三角函数的化简；2.三角函数的求值.3.函数的值域为．【答案】【解析】令，则.【考点】1、三角函数；2、二次函数；3、换元法.4.已知，，则x= .（结果用反三角函数表示）【答案】【解析】本题关键是注意反三角函数值的取值范围，适当利用诱导公式，，，而，故，即．【考点】反正弦函数．5.已知函数.（Ⅰ）求的单调减区间；（Ⅱ）求在区间上最大值和最小值.【答案】（Ⅰ）函数的单调减区间是：；（Ⅱ）.【解析】（Ⅰ）将降次化一，化为的形式，然后利用正弦函数的单调区间，即可求得其单调递增区间.（Ⅱ）由（Ⅰ）可得，又的范围为，由此可得的范围，进而求得的范围.试题解析：.函数的单调减区间是：.的范围为，所以，所以即：【考点】1、三角恒等变换；2、三角函数的单调区间及范围.6.如图，两座建筑物的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是9和15，从建筑物的顶部看建筑物的视角.⑴求的长度；⑵在线段上取一点点与点不重合），从点看这两座建筑物的视角分别为问点在何处时，最小？【答案】⑴;⑵当为时，取得最小值．【解析】⑴根据题中图形和条件不难想到作，垂足为，则可题中所有条件集中到两个直角三角形中，由，而在中，再由两角和的正切公式即可求出的值，又，可求出的值;⑵由题意易得在两直角三角形中，可得，再由两角和的正切公式可求出的表达式，由函数的特征，可通过导数求出函数的单调性和最值，进而求出的最小值，即可确定出的最小值．试题解析：⑴作，垂足为，则，，设，则 2分，化简得，解之得，或（舍）答：的长度为． 6分⑵设，则，． 8分设，，令，因为，得，当时，，是减函数；当时，，是增函数，所以，当时，取得最小值，即取得最小值， 12分因为恒成立，所以，所以，，因为在上是增函数，所以当时，取得最小值．答：当为时，取得最小值． 14分【考点】1.两角和差的正切公式;2.直角三角形中正切的表示;3.导数在函数中的运用7.已知以角为钝角的的三角形内角的对边分别为、、，，且与垂直．（1）求角的大小；（2）求的取值范围【答案】（1）；（2）．【解析】（1）观察要求的结论，易知要列出的边角之间的关系，题中只有与垂直提供的等量关系是，即，这正是我们需要的边角关系．因为要求角，故把等式中的边化为角，我们用正弦定理，，，代入上述等式得，得出，从而可求出角；（2）要求的范围，式子中有两个角不太好计算，可以先把两个角化为一个角，由（1），从而，再所其化为一个三角函数（这是解三角函数问题常用方法），下面只要注意这个范围即可．试题解析：1）∵垂直，∴（2分）由正弦定理得（4分）∵，∴，（6分）又∵∠B是钝角，∴∠B（7分）（2）（3分）由（1）知A∈（0，），, （4分），（6分）∴的取值范围是（7分）【考点】（1）向量的垂直，正弦定理；（2）三角函数的值域．8.已知向量，，(Ⅰ)若，求的值；(Ⅱ)在中，角的对边分别是，且满足，求函数的取值范围．【答案】（1）；（2）.【解析】本题主要考查两角和与差的正弦公式、二倍角公式、余弦定理、三角函数的值域等基础知识，考查运用三角公式进行三角变换的能力和基本的运算能力.第一问，利用向量的数量积将坐标代入得表达式，利用倍角公式、两角和的正弦公式化简表达式，因为，所以得到，而所求中的角是的2倍，利用二倍角公式计算；第二问，利用余弦定理将已知转化，得到，得到，得到角的范围，代入到中求值域.试题解析：（Ⅰ）∵，而，∴，∴，（Ⅱ）∵，∴，即，∴，又∵，∴，又∵，∴，∴.【考点】1.向量的数量积；2.倍角公式；3.两角和与差的正弦公式；4.余弦公式；5.三角函数的值域.9.若，且，则 ( )A．B．C．D．【答案】B．【解析】，故选B．【考点】1．三角函数诱导公式；2．三角函数平方关系．10.在△ABC中，角均为锐角，且，则△ABC的形状是（）A．锐角三角形B．直角三角形C．等腰三角形D．钝角三角形【答案】D．【解析】又角均为锐角，则且中，，故选D．【考点】1．诱导公式；2．正弦函数的单调性．11.已知函数为常数）．（Ⅰ）求函数的最小正周期；（Ⅱ）若时，的最小值为，求a的值．【答案】（Ⅰ）的最小正周期；（Ⅱ）．【解析】（Ⅰ）求函数的最小正周期，由函数为常数），通过三角恒等变化，把它转化为一个角的一个三角函数，从而可求函数的最小正周期；（Ⅱ）利用三角函数的图像，及，可求出的最小值，让最小值等于，可求出a的值．试题解析：（Ⅰ）∴的最小正周期（Ⅱ）时，时，取得最小值【考点】三角函数的性质．12.已知函数.(1)求函数的最小正周期；(2)求函数在区间上的函数值的取值范围.【答案】（1）；（2）.【解析】（1）函数.通过二倍角的逆运算将单角升为二倍角，再化为一个三角函数的形式，从而求出函数的周期.（2）x的范围是所以正弦函数在是递增的.所以f（x）的范围是本题考查三角函数的单调性，最值，三角函数的化一公式，涉及二倍角的逆运算等.三角函数的问题要关注角度的变化，角度统一，二次式化为一次的，三角函数名称相互转化.切化弦，弦化切等数学思想.试题解析：(1) 4分6分故的最小正周期为 8分(2)当时, 10分故所求的值域为 12分【考点】1.三角函数的化一公式.2.二倍角公式.3.函数的单调性最值问题.13.下列命题中：函数的最小值是；②在中，若，则是等腰或直角三角形；③如果正实数满足，则；④如果是可导函数，则是函数在处取到极值的必要不充分条件．其中正确的命题是_____________.【答案】②③④．【解析】当，等号成立时当且仅当“即”，显然不成立，则命题①不正确；在中，若，则或，则是等腰或直角三角形，故②正确；由，因为正实数，满足，所以，故③正确；如果是可导函数，若函数在处取到极值，则，当，，但函数在处无极值，则是函数在处取到极值的必要不充分条件，故④正确.【考点】基本不等式、三角函数性质、不等式及导数的性质.14.已知向量,函数．（1）求函数的最小正周期;（2）已知分别为内角、、的对边, 其中为锐角,且,求和的面积．【答案】（1）；（2）.【解析】（1）根据题意，再利用二倍角公式及辅助角公式将化简为；（2）将代入，得，因为，所以，再利用余弦定理，解出，最后根据三角形面积公式求出. 试题解析：（1）由题意所以.由（1），因为,所以，解得.又余弦定理，所以，解得，所以.【考点】1.三角函数恒等变形；2.三角函数周期；3.余弦定理及三角形面积公式.15.已知，，其中，若函数，且函数的图象与直线y=2两相邻公共点间的距离为．(l)求的值；(2)在△ABC中，以a，b，c(分别是角A，B，C的对边，且，求△ABC周长的取值范围．【答案】(1)；(2).【解析】(1)先根据，结合二倍角公式以及和角公式化简，求得，函数最大值是，那么函数的图像与直线两相邻公共点间的距离正好是一个周期，然后根据求解的值；(2)先将代入函数的解析式得到：，由已知条件以及，结合三角函数的图像与性质可以解得，所以，由正弦定理得，那么的周长可以表示为：，由差角公式以及和角公式将此式化简整理得，，结合角的取值以及三角函数的图像与性质可得.试题解析：（1）， 3分∵，∴函数的周期，∵函数的图象与直线两相邻公共点间的距离为.∴，解得. 4分（2）由（Ⅰ）可知，，∵，∴，即，又∵，∴，∴，解得. 7分由正弦定理得：，所以周长为：， 10分，所以三角形周长的取值范围是. 12分【考点】1.和角公式；2.差角公式；3.二倍角公式；4.三角函数的图像与性质；5.正弦定理16.已知向量，（Ⅰ）当时，求的值；（Ⅱ）求函数在上的值域.【答案】（Ⅰ）；（Ⅱ）.【解析】（Ⅰ）本小题主要利用向量平行的坐标运算得到，然后解出，再利用二倍角正切公式可得；（Ⅱ）本小题首先化简函数解析式，然后根据三角函数的图像与性质，得到三角函数的取值范围，进而求值域；试题解析：（Ⅰ），， 2分即，， 4分6分（Ⅱ）=10分，12分，即 14分【考点】1.平行向量；2.三角函数的图像与性质.17.已知 .【答案】【解析】.【考点】1.两角差的正切公式；2.三角函数的拆角方法.18.已知∈（,），sin=,则tan（）等于（）A．－7B．－C．7D．【答案】A．【解析】由题意，则．【考点】三角函数运算．19.在中，的对边分别为且成等差数列．（1）求B的值；（2）求的范围．【答案】(1)；（2）【解析】（1）对于三角形问题中的边角混合的式子，可以利用正弦定理和余弦定理边角转化，或边化角转化为三角函数问题，或角化边转化为代数问题来处理，该题由等差中项列式，再利用正弦定理边化角为，，又根据三角形内角的关系，得，进而求；(2)由（1）得，可得，代入所求式中，化为自变量为的函数解析式，再化为，然后根据的范围，确定的范围，进而结合的图象确定的范围，进而求的范围.试题解析：（1）成等差数列，∴，由正弦定理得，，代入得，，即：，，又在中，，∵，∴；（2）∵，∴，∴===，∵，∴，∴，∴的取值范围是.【考点】1、等差中项；2、正弦定理；3、型函数的值域.20.取得最小值a时，此时x的值为b，则取得最大值时，的值等于________。

第二讲 三角函数的图象与性质1．(2019·豫南九校联考)将函数y ＝sin ⎝⎛⎭⎪⎫x －π4的图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，再向右平移π6个单位，则所得函数图象的解析式为( )A ．y ＝sin ⎝ ⎛⎭⎪⎫x 2－5π24B ．y ＝sin ⎝ ⎛⎭⎪⎫x 2－π3C ．y ＝sin ⎝ ⎛⎭⎪⎫x 2－5π12 D.y ＝sin ⎝⎛⎭⎪⎫2x －7π12 解析：函数y ＝sin ⎝ ⎛⎭⎪⎫x －π4经伸长变换得y ＝sin ⎝ ⎛⎭⎪⎫x 2－π4，再作平移变换得y ＝sin ⎣⎢⎡⎦⎥⎤12⎝⎛⎭⎪⎫x －π6－π4＝sin ⎝ ⎛⎭⎪⎫x 2－π3.答案：B2．(2019·某某亳州一中月考)函数y ＝tan ⎝ ⎛⎭⎪⎫12x －π3在一个周期内的图象是( )解析：由题意得函数的周期为T ＝2π，故可排除B ，D.对于C ，图象过点⎝ ⎛⎭⎪⎫π3，0，代入解析式，不成立，故选A. 答案：A3．(2019·某某某某十校期末测试)要得到函数y ＝cos ⎝ ⎛⎭⎪⎫2x ＋π3的图象，只需将函数y ＝cos 2x的图象( )A ．向左平移π3个单位长度B ．向左平移π6个单位长度C ．向右平移π6个单位长度D ．向右平移π3个单位长度解析：∵y ＝cos ⎝ ⎛⎭⎪⎫2x ＋π3＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π6，∴要得到函数y ＝cos ⎝ ⎛⎭⎪⎫2x ＋π3的图象，只需将函数y ＝cos 2x 的图象向左平移π6个单位长度．答案：B4．(2019·东北三省三校一模)已知函数f (x )＝3sin ωx ＋cos ωx (ω>0)的图象的相邻两条对称轴之间的距离是π2，则该函数的一个单调增区间为( )A.⎣⎢⎡⎦⎥⎤－π3，π6 B.⎣⎢⎡⎦⎥⎤－5π12，π12 C.⎣⎢⎡⎦⎥⎤π6，2π3D.⎣⎢⎡⎦⎥⎤－π3，2π3解析：由题意得2πω＝2×π2，解得ω＝2，所以f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6.令－π2＋2k π≤2x ＋π6≤π2＋2k π(k ∈Z)，解得－π3＋k π≤x ≤π6＋k π.当k ＝0时，有x ∈⎣⎢⎡⎦⎥⎤－π3，π6.故选A.答案：A5．(2019·高考全国卷Ⅱ)若x 1＝π4，x 2＝3π4是函数f (x )＝sin ωx (ω>0)两个相邻的极值点，则ω＝( ) A ．2B.32 C ．1D.12解析：由题意及函数y ＝sin ωx 的图象与性质可知， 12T ＝3π4－π4，∴T ＝π，∴2πω＝π，∴ω＝2. 故选A. 答案：A6．(2019·某某某某一模)已知函数f (x )＝2sin ⎝ ⎛⎭⎪⎫ωx ＋π3的图象的一个对称中心为⎝ ⎛⎭⎪⎫π3，0，其中ω为常数，且ω∈(1,3)．若对任意的实数x ，总有f (x 1)≤f (x )≤f (x 2)，则|x 1－x 2|的最小值是( ) A ．1 B.π2C ．2D.π解析：∵函数f (x )＝2sin ⎝ ⎛⎭⎪⎫ωx ＋π3的图象的一个对称中心为⎝ ⎛⎭⎪⎫π3，0，∴π3ω＋π3＝k π，k ∈Z ，∴ω＝3k －1，k ∈Z ，由ω∈(1,3)，得ω＝2.由题意得|x 1－x 2|的最小值为函数的半个周期，即T 2＝πω＝π2.答案：B7．(2019·某某平遥中学调研)已知函数f (x )＝2sin(ωx ＋φ)(ω>0，|φ|<π)的部分图象如图所示，已知点A (0，3)，B ⎝ ⎛⎭⎪⎫π6，0，若将它的图象向右平移π6个单位长度，得到函数g (x )的图象，则函数g (x )图象的一条对称轴方程为( ) A ．x ＝π12B.x ＝π4C ．x ＝π3D.x ＝2π3解析：由题意知图象过A (0，3)，B ⎝ ⎛⎭⎪⎫π6，0， 即f (0)＝2sin φ＝3，f ⎝ ⎛⎭⎪⎫π6＝2sin ⎝ ⎛⎭⎪⎫π6·ω＋φ＝0，又ω>0，|φ|<π，并结合图象知φ＝2π3，π6·ω＋φ＝π＋2k π(k ∈Z)，得ω＝2，所以f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋2π3， 移动后g (x )＝2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x －π6＋2π3＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3，所以对称轴满足2x ＋π3＝π2＋k π(k ∈Z)，解得x ＝π12＋k π2(k ∈Z)，所以满足条件的一条对称轴方程是x ＝π12，故选A.答案：A8．(2019·某某某某适应性统考)已知A ，B ，C ，D ，E 是函数y ＝sin(ωx ＋φ)⎝⎛⎭⎪⎫ω>0，0<φ<π2一个周期内的图象上的五个点，如图所示，A ⎝ ⎛⎭⎪⎫－π6，0，B 为y 轴上的点，C 为图象上的最低点，E 为该函数图象的一个对称中心，B 与D 关于点E 对称，CD →在x 轴上的投影为π12，则ω，φ的值为( )A ．ω＝2，φ＝π3B.ω＝2，φ＝π6C ．ω＝12，φ＝π3D.ω＝12，φ＝π12解析：由题意知T ＝4×⎝⎛⎭⎪⎫π12＋π6＝π，所以ω＝2.因为A ⎝ ⎛⎭⎪⎫－π6，0，所以0＝sin ⎝ ⎛⎭⎪⎫－π3＋φ. 又0<φ<π2，所以φ＝π3.答案：A9．(2019·某某某某3月模拟)已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx －π6(ω>0)，f (0)＝－f ⎝ ⎛⎭⎪⎫π2，若f (x )在⎝⎛⎭⎪⎫0，π2上有且仅有三个零点，则ω的可能取值为( )A.23 B.2 C.143D.263解析：∵函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx －π6(ω>0)，f (0)＝－f ⎝ ⎛⎭⎪⎫π2， ∴sin ⎝ ⎛⎭⎪⎫－π6＝－sin ⎝ ⎛⎭⎪⎫π2ω－π6＝－12，∴π2ω－π6＝2k π＋π6或π2ω－π6＝2k π＋5π6，k ∈Z ，∴ω＝4k ＋23或ω＝4k ＋2，k ∈Z.∵函数f (x )在⎝⎛⎭⎪⎫0，π2上有且仅有三个零点，∴ωx －π6∈⎝ ⎛⎭⎪⎫－π6，ωπ2－π6，∴2π<ωπ2－π6≤3π，∴133<ω≤193，∴ω＝143或ω＝6.故选C.答案：C10．(2019·贺州一模)已知函数f (x )＝sin(2x ＋φ)(φ∈R)，若f ⎝ ⎛⎭⎪⎫π3－x ＝f (x )，且f (π)>f ⎝ ⎛⎭⎪⎫π2，则函数f (x )取得最大值时x 的可能值为( )A.π6B.π5C.π3D.π2解析：因为f ⎝ ⎛⎭⎪⎫π3－x ＝f (x )， 即y ＝f (x )的图象关于直线x ＝π6对称，即函数f (x )在x ＝π6时取得最值，①当函数f (x )在x ＝π6时取得最大值时，又因为函数f (x )的周期为π，所以f ⎝ ⎛⎭⎪⎫π2<f ⎝ ⎛⎭⎪⎫π3＝f (π)，满足题意， ②当函数f (x )在x ＝π6时取得最小值时，又因为函数f (x )的周期为π，所以f ⎝ ⎛⎭⎪⎫π2>f ⎝ ⎛⎭⎪⎫π3＝f (π)，不满足题意， 综合①②得：函数f (x )取得最大值时x 的可能值为π6.故选A. 答案：A11．(2019·某某一模)若函数f (x )＝sinωx2·sin ⎝⎛⎭⎪⎫ωx 2＋π2(ω>0)在⎣⎢⎡⎦⎥⎤－π3，π2内有且仅有一个最大值，则ω的取值X 围是( ) A ．(0,5)B.[1,5)C.⎝ ⎛⎭⎪⎫0，92 D.⎣⎢⎡⎭⎪⎫1，92 解析：f (x )＝sinωx2sin ⎝⎛⎭⎪⎫ωx 2＋π2＝12sin ωx ，当ωx ＝2k π＋π2，即x ＝2k π＋π2ω(k ∈Z)时函数取最大值，又函数f (x )在⎣⎢⎡⎦⎥⎤－π3，π2内有且仅有一个最大值，即有两种情况，一是区间⎣⎢⎡⎦⎥⎤－π3，π2内只有一个极值点，二是函数f (x )在区间⎣⎢⎡⎦⎥⎤－π3，π2内单调递增，所以有⎩⎪⎨⎪⎧π2≤ωπ2<5π2，－3π2<－ωπ3或⎩⎪⎨⎪⎧π2≥ωπ2，－π2≤－ωπ3，解得ω∈⎣⎢⎡⎭⎪⎫1，92或ω∈(－∞，1]，又∵ω>0，所以ω∈⎝ ⎛⎭⎪⎫0，92，故选C. 答案：C12．(2019·某某一模)函数f (x )＝sin(2x ＋θ)＋cos 2x ，若f (x )最大值为G (θ)，最小值为g (θ)，则( )A ．∃θ0∈R ，使G (θ0)＋g (θ0)＝πB ．∃θ0∈R ，使G (θ0)－g (θ0)＝πC ．∃θ0∈R ，使|G (θ0)·g (θ0)|＝πD ．∃θ0∈R ，使⎪⎪⎪⎪⎪⎪G (θ0)g (θ0)＝π解析：f (x )＝sin(2x ＋θ)＋cos 2x ＝cos θ·sin 2x ＋⎝ ⎛⎭⎪⎫sin θ＋12·cos 2x ＋12＝54＋sin θsin(2x ＋φ)＋12，所以G (θ)＝54＋sin θ＋12，g (θ)＝－54＋sin θ＋12， ①对于选项A ，G (θ0)＋g (θ0)＝54＋sin θ＋12－54＋sin θ＋12＝1，显然不满足题意，即A 错误，②对于选项B ，G (θ0)－g (θ0)＝54＋sin θ＋12＋54＋sin θ－12＝254＋sin θ∈[1,3]，显然不满足题意，即B 错误， ③对于选项C ，G (θ0)·g (θ0)＝⎝ ⎛⎭⎪⎫54＋sin θ＋12·⎝ ⎛⎭⎪⎫54＋sin θ－12＝1＋sin θ∈[0,2]，显然不满足题意，即C 错误，④对于选项D ，⎪⎪⎪⎪⎪⎪G (θ)g (θ)＝⎪⎪⎪⎪⎪⎪⎪⎪154＋sin θ－12＋1∈[2，＋∞)，即∃θ0∈R ，使⎪⎪⎪⎪⎪⎪G (θ0)g (θ0)＝π，故D 正确， 故选D. 答案：D13．(2019·某某模拟)函数f (x )＝4cos x sin ⎝⎛⎭⎪⎫x ＋π6－1(x ∈R)的最大值为________．解析：∵f (x )＝4cos x sin ⎝ ⎛⎭⎪⎫x ＋π6－1＝4cos x ⎝ ⎛⎭⎪⎫32sin x ＋12cos x －1＝23sin x cos x ＋2cos 2x －1＝3sin 2x ＋cos 2x ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6，∴f (x )max ＝2. 答案：214．设函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0)．若函数f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，且f ⎝ ⎛⎭⎪⎫π2＝f ⎝ ⎛⎭⎪⎫2π3＝－f ⎝ ⎛⎭⎪⎫π6，则函数f (x )的最小正周期为________． 解析：∵f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，且f ⎝ ⎛⎭⎪⎫π2＝f ⎝ ⎛⎭⎪⎫2π3， ∴x ＝π2和x ＝2π3均不是f (x )的极值点，其极值应该在x ＝π2＋2π32＝7π12处取得，∵f ⎝ ⎛⎭⎪⎫π2＝－f ⎝ ⎛⎭⎪⎫π6，∴x ＝π6也不是函数f (x )的极值点，又f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性， ∴x ＝π6－⎝⎛⎭⎪⎫7π12－π2＝π12为f (x )的另一个相邻的极值点，故函数f (x )的最小正周期T ＝2×⎝⎛⎭⎪⎫7π12－π12＝π.答案：π15．(2019·某某某某武邑中学模拟)将f (x )＝2sin ⎝⎛⎭⎪⎫ωx ＋π4(ω>0)的图象向右平移π4ω个单位，得到y ＝g (x )的图象，若y ＝g (x )在⎣⎢⎡⎦⎥⎤－π6，π4上为增函数，则ω的最大值为________．解析：将f (x )＝2sin ⎝ ⎛⎭⎪⎫ωx ＋π4(ω>0)的图象向右平移π4ω个单位，得到y ＝g (x )＝2sin ⎣⎢⎡⎦⎥⎤ω⎝ ⎛⎭⎪⎫x －π4ω＋π4＝2sin ωx 的图象，若y ＝g (x )在⎣⎢⎡⎦⎥⎤－π6，π4上为增函数，则满足T 4≥π4，即T ≥π，即2πω≥π，所以0<ω≤2，即ω的最大值为2.答案：216．已知函数f (x )＝2a sin(πωx ＋φ)⎝ ⎛⎭⎪⎫a ≠0，ω>0，|φ|≤π2，直线y ＝a 与f (x )的图象的相邻两个距离最近的交点的横坐标分别是2和4，现有如下命题： ①该函数在[2,4]上的值域是[a ，2a ]；②在[2,4]上，当且仅当x ＝3时函数取得最大值； ③f (x )的图象可能过原点． 其中真命题的个数为________．解析：对于①，∵直线y ＝a 与函数f (x )＝2a sin(πωx ＋φ)的图象的相邻两个距离最近的交点的横坐标分别为2和4，∴结合图象可以看出，当a >0时，f (x )在[2,4]上的值域为[a ，2a ]，当a <0时，f (x )在[2,4]上的值域为[2a ，a ]，①错误；对于②，根据三角函数图象的对称性，显然x ＝2和x ＝4的中点是x ＝3，即当a >0时，f (x )在x ＝3处有最大值f (3)＝2a ，当a <0时，f (x )在x ＝3处有最小值f (3)＝2a ，②错误； 对于③，f (0)＝2a sin φ，令f (0)＝0，得φ＝0，此时f (x )＝2a sin πωx ，由2a sin πωx ＝a 得sin πωx ＝22，则πωx ＝2k π＋π4(k ∈Z)或πωx ＝2k π＋3π4(k ∈Z)，∴x ＝2k ＋14ω(k ∈Z)或x ＝2k ＋34ω(k ∈Z)，∵直线y ＝a 与函数f (x )＝2a sin(πωx ＋φ)的图象的相邻两个距离最近的交点的横坐标分别为2和4，∴令⎩⎪⎨⎪⎧2k ＋14ω＝2，2k ＋34ω＝4，解得k ＝18∉Z ，即不存在这样的k 符合题意，③错误． 综上，没有真命题． 答案：0。

高三数学三角函数综合试题1.已知函数，则的值为 .【答案】.【解析】∵，两边求导，∴，令，得，∴，∴，即.【考点】导数的运用.2.设函数满足当时，，则（）A．B．C．0D．【答案】A【解析】由题意，，故选A.【考点】1.函数的求值.3.已知tan,是关于x的方程x2-kx+k2-3=0的两个实根，且3π＜＜,则cos+sin= ( )A．B．C．-D．-【答案】C【解析】∵tan·=k2-3=1∴k=±2,而3π＜＜,∴tan>0,即tan+=k=2，解之得tanα=1，所以sin=cos=∴cos+sin=-4.设函数f(x)=Asin(ωx+)(其中A>0,ω>0,-π<≤π)在x=处取得最大值2,其图象与x轴的相邻两个交点的距离为.(1)求f(x)的解析式;(2)求函数g(x)=的值域.【答案】(1) f(x)=2sin(2x+) (2) [1, ]∪(,]【解析】解:(1)由题设条件知f(x)的周期T=π,即=π,解得ω=2.因为f(x)在x=处取得最大值2,所以A=2,从而sin(2×+)=1,所以2×+=+2kπ,k∈Z.又由-π<≤π,得=.故f(x)的解析式为f(x)=2sin(2x+).(2)g(x)====cos2x+1(cos2x≠).因为cos2x∈[0,1],且cos2x≠,故g(x)的值域为[1,]∪(,].5.已知函数f(x)=-asin cos(π-)的最大值为2,则常数a的值为()A．B．-C．±D．±【答案】C【解析】【思路点拨】先利用公式进行三角恒等变形,把f(x)化成f(x)=Asin(ωx+φ)的形式,再利用最大值求得a.解:因为f(x)=+asinx=(cosx+asinx)=cos(x-φ)(其中tanφ=a),所以=2,解得a=±.6.已知向量a=(sin(α+),1),b=(4,4cosα-),若a⊥b,则sin(α+)=()A．-B．-C．D．【答案】B【解析】∵a⊥b,∴a·b=4sin(α+)+4cosα-=0,即sin(α+)+cosα=,即sinαcos+cosαsin+cosα=,即sinα+cosα=,故sinα+cosα=,故sin(α+)=,又sin(α+)=-sin(α+)=-.故选B.7.设向量a＝(sin x，sin x)，b＝(cos x，sin x)，x∈.(1)若|a|＝|b|，求x的值；(2)设函数f(x)＝a·b，求f(x)的最大值．【答案】（1）x＝（2）【解析】(1)由|a|2＝(sin x)2＋(sin x)2＝4sin2x，|b|2＝(cos x)2＋(sin x)2＝1，及|a|＝|b|，得4sin2x＝1.又x∈，从而sin x＝，所以x＝.(2)f(x)＝a·b＝sin x·cos x＋sin2x＝sin 2x－cos 2x＋＝sin＋，当x∈时，－≤2x－≤π，∴当2x－＝时，即x＝时，sin取最大值1.所以f(x)的最大值为.8.在△ABC中，内角A，B，C所对边长分别为，，，.（1）求的最大值及的取值范围；（2）求函数的最大值和最小值.【答案】（Ⅰ）的最大值为１６，及的取值范围0＜；（Ⅱ）最大值为３，最小值为２.【解析】（Ⅰ）求的最大值及的取值范围，由向量的数量积，即，由此可想到利用余弦定理求出，通过基本不等式，可求得b•c的最大值，再结合，可求出的取值范围；（Ⅱ）求函数的最大值和最小值，可利用二倍角的正弦函数化简函数，这样化为一个角的一个三角函数的形式，通过角的范围0＜，利用正弦函数的最值，从而求出函数的最大值和最小值．试题解析：（Ⅰ）即又所以，即的最大值为16即所以，又0＜＜所以0＜（Ⅱ）因0＜，所以＜，当即时，当即时，【考点】正弦函数的图象；平面向量数量积的运算．9.已知函数在一个周期上的系列对应值如下表：（1）求的表达式；（2）若锐角的三个内角、、所对的边分别为、、，且满足，，，求边长的值.【答案】（1）；（2）.【解析】（1）根据已知条件中表格给出的对应点，通过“五点作图法”，建立方程组，求出参数和的值，从而得到函数的解析式；（2）通过条件，并利用第（1）问的解析式可求出角的大小，进而利用正弦定理，变形求出的值，再求边长的值，解题过程体现方程思想的运用.试题解析：（1）由题设条件给出的点可知，，解得，，，将点代入得，求得，于是函数.（2）由得，即，设，则，，即，解得，.【考点】利用三角函数图像上的点求解析式，正弦定理.10.等于（）A．B．C．D．【答案】D【解析】【考点】三角函数的诱导公式及三角函数值.11.已知向量与，其中(Ⅰ)若，求和的值；(Ⅱ)若，求的值域.【答案】(Ⅰ)，；(Ⅱ)的值域为．【解析】(Ⅰ)由已知条件，得，由此可求得的值，由于为特殊值，从而可求得的值，进而求得和的值（也可利用平方关系求得和的值）；(Ⅱ)首先列出函数的表达式，利用三角函数的平方关系及三角函数辅助角公式，将其化为一个复合角的三角函数式：，最后利用整体思想来求函数的值域．试题解析：(Ⅰ)，， 2分求得. 3分又，， 5分，. 6分(Ⅱ) 8分又，，， 10分，即函数的值域为. 12分【考点】1．向量共线的充要条件；2．三角函数求值；3．三角函数的值域．12.已知函数则函数在[-1,1]上的单调增区间为（）A．B．C．D．【答案】A【解析】∵∵，∴.【考点】1.倍角公式；2.两角和的正弦公式；3.三角函数的单调区间.13.在中,若,则的形状一定是（）A．等边三角形B．直角三角形C．钝角三角形D．不含角的等腰三角形【答案】B【解析】∵，∴，∴，∴，∴，∴，∴三角形为直角三角形.【考点】1.两角差的正弦公式；2.两角和与差的余弦公式；3.特殊角的三角函数值.14.已知函数（）.（1）求函数的最小正周期；（2）求函数在区间上的值域.【答案】（1）；（2）.【解析】（1）利用三角函数公式化简为一个角的三角函数式，易得周期；（2）把x的取值范围代入（1）所求函数的解析式中，可得值域（注意函数的单调性）.试题解析：(1)(4分)的最小正周期为； (6分)(2)由(1)知,在区间上单调递增,在区间上单调递减; (10分); (12分)又,;所以函数在区间上的值域是 (15分)【考点】1、和差化积公式及二倍角公式；2三角函数的单调性及值域.15.设函数,且的图象的一个对称中心到最近的对称轴的距离为,(Ⅰ)求的值(Ⅱ)求在区间上的最大值和最小值.【答案】(Ⅰ)1；(Ⅱ).【解析】(Ⅰ)根据三角恒等变形化简，得，而的图象的一个对称中心到最近的对称轴的距离为，则，从而根据，解得；(Ⅱ)由(Ⅰ)知，当时，将当做一个整体，则，所以，所以，则在区间上的最大值和最小值分别为. 试题解析：(Ⅰ),的图象的一个对称中心到最近的对称轴的距离为,且，所以，解得.(Ⅱ)由(Ⅰ)知，当时，，所以，所以，在区间上的最大值和最小值分别为.【考点】1.三角恒等变形；2.三角函数的最值求解.16.已知函数.（Ⅰ）求函数的最小正周期；（Ⅱ）求函数在区间上的值域．【答案】（Ⅰ）；（Ⅱ）的值域为.【解析】（Ⅰ）先由三角恒等变换得，从而得；（Ⅱ）先由得得，再由正弦函数的单调性得，从而得的值域为.试题解析：(I)4分所以，周期． 6分（II）∵，∴ 8分，∴的值域为 12分【考点】1.三角恒等变换；2.三角函数的单调性；3.三角函数的值域17.已知向量，，函数的图象与直线的相邻两个交点之间的距离为．（Ⅰ）求的值；（Ⅱ）求函数在上的单调递增区间．【答案】（Ⅰ）；（Ⅱ）的单调增区间为和.【解析】（Ⅰ）先由向量数量积坐标运算得，再由图象与直线的相邻两个交点之间的距离为得，从而求得；（Ⅱ）由得，再由余弦函数的单调性可得的单调增区间为和.试题解析：（Ⅰ） 1分5分由题意，， 6分（Ⅱ），时，故或时，单调递增 9分即的单调增区间为和 12分【考点】1.向量的数量积；2.三角恒等变换；3.三角函数的单调性18.已知函数f（x）＝－ax（a∈R）既有最大值又有最小值，则f（x）值域为_______．【答案】【解析】若，则的值域为，会使无最大最小值，故，所以,令，则，即，故，解得，所以f（x）值域为.【考点】三角函数性质、函数值域的求法.19.已知α，β为锐角，且sinα＝，tan（α－β）＝－．求cosβ的值．【答案】.【解析】先由tan（α－β）＝－计算出和，再构造角，利用两角差的余弦公式解答.试题解析：2分4分5分6分10分【考点】角的构造、两角差的余弦公式、切割化弦.20.已知∈（,），sin=,则tan（）等于（）A．－7B．－C．7D．【答案】A．【解析】由题意，则．【考点】三角函数运算．21.在中，的对边分别为且成等差数列．（1）求B的值；（2）求的范围．【答案】(1)；（2）【解析】（1）对于三角形问题中的边角混合的式子，可以利用正弦定理和余弦定理边角转化，或边化角转化为三角函数问题，或角化边转化为代数问题来处理，该题由等差中项列式，再利用正弦定理边化角为，，又根据三角形内角的关系，得，进而求；(2)由（1）得，可得，代入所求式中，化为自变量为的函数解析式，再化为，然后根据的范围，确定的范围，进而结合的图象确定的范围，进而求的范围.试题解析：（1）成等差数列，∴，由正弦定理得，，代入得，，即：，，又在中，，∵，∴；（2）∵，∴，∴===，∵，∴，∴，∴的取值范围是.【考点】1、等差中项；2、正弦定理；3、型函数的值域.22.函数的最小正周期是（）A．B．C．2πD．4π【答案】B【解析】，所以周期.【考点】三角变换及三角函数的周期.23.已知函数（＞0）.在内有7个最值点，则的范围是______.【答案】【解析】∵函数f（x）=sin（ωx）在内有7个最值点，设其周期为，则，即，解得，∴ω的取值范围是．【考点】三角函数的周期性及其求法．24.已知函数（1）求的单调减区间；（2）在锐角三角形ABC 中，A、B、C的对边且满足,求的取值范围.【答案】（1）；（2）【解析】（1）求函数的单调区间需将已知化为的形式，然后利用复合函数的单调性处理，先逆用正弦的二倍角公式和降幂公式，然后利用辅助角公式即可求；（2）三角形问题中，如果有边角混合的式子，可考虑边角转化，或变为关于角的三角关系式，或变为关于边的代数式处理，该题先利用正弦定理把边化角，得三角关系式，从中解，然后结合已知条件得的范围（注意是锐角三角形这个条件），然后确定的范围，再结合的图象求的范围，从而可求出的取值范围.试题解析：（1）由得=，∴，解得，故的单调减区间为；（2）因为，由正弦定理得，化简为，所以=,∴=,又因为，所以，由是锐角三角形，所以，，，∴，∴的取值范围.为.【考点】1、三角函数的单调区间；2、正弦定理；3、三角函数的值域.25.已知向量，，，点A、B为函数的相邻两个零点，AB=π.（1）求的值；（2）若，，求的值；（3）求在区间上的单调递减区间.【答案】（1）；（2）；（3），.【解析】（1）由向量的数量积可得：.这个函数相邻两个零点间的距离等于半个周期，再利用求周期的公式可得的值.（2）由（1）得，则.这里不能展开来求，而应考虑凑角：，这样再利用差角的正弦公式就可以求出的值；（3）,这是一个三角函数与一个一次函数的差构成的函数，故可通过导数来求它的单调区间.试题解析：（1）, 3分由，得，则. 4分（2）由（1）得，则.由，得， 6分. 8分（3）,,∴, 10分∴（）,即（）,又,∴在区间上的单调递减区间为， 12分【考点】1、向量的数量积；2、三角函数的周期；3、三角变换；4、导数的应用.26.已知函数.（1）求的最小正周期和最大值；（2）若为锐角，且，求的值.【答案】（1）函数的最小正周期为，最大值为；（2）.【解析】（1）先将函数解析式化简为，然后根据相应公式求出函数的最小正周期与最大值；（2）先利用求出的值，然后利用已知条件确定的取值范围，进而确定的正负，并利用平方关系求出的值，最终求出的值.试题解析：（1），，即函数的最小正周期为，，即函数的最大值为；（2），，为锐角，所以，故，因此，，.【考点】1.三角函数的周期性与最值；2.同角三角函数的基本关系27.设函数，其中，角的顶点与坐标原点重合，始边与轴非负半轴重合，终边经过点，且.（1）若点的坐标为（-），求的值；（2）若点为平面区域上的一个动点，试确定角的取值范围，并求函数的值域.【答案】（1）；（2）.【解析】(1)由三角函数的定义求解与，进而求的值；（2）由平面区域的可行域可得角的范围，再求解的值域，本题将三角化简求值与线性规划知识联系在一起,具有新颖性.试题解析：（1）由三角函数的定义，得故 4分（2）作出平面区域（即三角形区域ABC）如图所示，其中于是 7分又且故当，即时，取得最小值，且最小值为1.当，即时，取得最大值，且最大值为.故函数的值域为. 12分【考点】1.三角化简求值；2.三角函数的值域；3.线性规划可行域.28.已知角的始边与轴的非负半轴重合，终边过点，则可以是（）A．B．C．D．【答案】B【解析】由三角函数的定义得，在选项中只有B选项的的正弦值为，故选B.【考点】三角函数定义、三角函数求值.29.已知函数的最大值为，且，是相邻的两对称轴方程.（1）求函数在上的值域;（2）中,，角所对的边分别是，且，，求的面积.【答案】（1）函数在上的值域为；（2）的面积为.【解析】（1）先根据函数的最大值为列式解出的值，并将函数的解析式化为的形式，根据三角函数两条相邻对称轴之间的距离与周期的关系，求出函数的最小正周期，进而求出的值，然后再由，确定出的取值范围，然后结合函数的图象确定函数的值域；（2）先利用正弦定理求出的外接圆的半径，然后利用正弦定理中的边角互化的思想并结合题中的等式将与所满足的等式确定下来，再利用余弦定理求出的值求出来，最后再利用三角形的面积公式即可算出的面积.试题解析：（1）由题意,的最大值为,所以.而,于是,. ∵是相邻的两对称轴方程.∴T=2π=, ∴ω=1,∵∴的值域为.（2）设△ABC的外接圆半径为,由题意,得.化简,得.由正弦定理,得,. ①由余弦定理,得,即. ②将①式代入②,得.解得,或(舍去). .【考点】1.三角函数的最值；2.三角函数的周期；3.正弦定理；4.余弦定理；5.三角形的面积公式30.已知，其中向量，，.在中，角A、B、C的对边分别为，，.(1)如果三边，，依次成等比数列，试求角的取值范围及此时函数的值域；(2) 在中，若，边，，依次成等差数列，且，求的值.【答案】（1），；（2）.【解析】（1）先根据向量的数量积的坐标运算和三角函数的积化和差公式，化简，然后根据三边关系结合余弦定理求得角的取值范围，再将代入化简后的，得到，根据三角函数在定区间上的值域求得函数的值域；（2）根据题中所给信息解得角的大小，由，得到，由已知条件得边，，依次成等差数列，结合余弦定理，得到两个等量关系，解得的值.试题解析：（1），2分由已知，所以，所以，，则，故函数f(B)的值域为； 6分（2）由已知得，所以， 8分所以或，解得或（舍去）， 10分由，得，解得，由三边，，依次成等差数列得，则，由余弦定理得, 解得. 12分【考点】1、平面向量的数量积的运算；2、余弦定理；3、解三角形；4、等差数列的性质及应用；5、特殊角的三角函数值.31.函数 ()的值域是_______________。

三角，向量及复数综三角合测试题一， 选择题1，复数,1,21i z i z +==那么复数21z z ⋅在复平面上的对应点所在象限是 ( ) A 第一象限 B 第二象限 C 第三象限 D 第四象限2，平面向量a 与b 的夹角为 ︒60，且,1,2==b a 则b a3-= ( )A5 B 7 C 19 D 53，△ABC 的外接圆的圆心为1，若,0=++C O B A A O 且,B A A O =则=⋅B C A C ( )A23B 3C 3D 324，在边长为1的菱形ABCD 中，∠BAD=E ,60︒是BC 的中点，则=⋅E A C A( )A333+ B 29 C3 D495，△ABC 中，,3222bc a c b +=+则=--)sin(cos sin 2C B C B （ ）A 33B 23C 22D 216，若满足条件AB=3，C=3π,的三角形ABC 有两个，则边长BC 的取值范围 ( )A ()2,1B ()3,2 C()2,3 D ()2,27,设函数())0(sin )3sin(>++=w wx wx x f π相邻两条对称轴间的距离为2，则()1f = ( )A23 B 23- C 23 D 23- 8，若,542sin ,532cos-==αα则角θ的终边所在的直线为 ( ) A 0247=+y x B 0247=-y x C 0724=+y x D 0724=-y x9,已知函数=+=y x x y ,cos sin ,cos sin 22x x 则下列结论正确的是 ( )A 两个函数的图像均关于点()0,4π-成中心对称 B 两个函数的图像均关于直线4π-=x 成轴对称C 两个函数在区间()4,4ππ-上都是单调递增函数D 两个函数的最小正周期相同10，函数()ϕπ+=x y sin 的部分图像如图所示，设p 是图像的最高点，A,B 是图像与x 轴的交点，则tan ∠=APB （ ）A 8B 81C 78D 87二，填空题11，若复数,,sin cos ,342121R z z i z i z ∈⋅+=+=θθ则=θtan _____________12，在△ABC 中，,21,2,1===ABC S AC AB 则=BC _______________ 13，已知正方形ABCD 的边长为1，则=-D B B A2______________14，若θθ,53sin =为第二象限角，则=θ2tan _______________ 15，已知函数()x f 满足下面关系:),2()2(ππ-=+x f x f 当(]π,0∈x 时，(),cos x x f -=给出下列命题:① 函数()x f 为周期函数 ② 函数()x f 是奇函数 ③ 函数()x f 的图像关于y 轴对称 ④ 方程()x x f lg =的解的个数是3， 其中正确命题的序号是_______________三，解答题16，(本题12分) 在△ABC 中，已知c B b aconB =-sin ()1 若,6π=B 求A ()2 求B A sin sin +的取值范围17，(本题12分) 已知向量)3,1()),2cos(),2(sin(=++=b x x aθθ，函数()b a x f ⋅=为偶函数，且[]πθ,0∈，()1 求函数()x f 的解析式；()2 设()1),2,0(=∈x f x π，求x 的值18，(本题12分) 已知函数(),233cos 33cos 3sin2-+=x x x x f ()1 求()x f 的最小正周期及对称中心；()2 若()π,0,21cos ∈≥x x ，试求x 的范围及此时函数()x f 3的值域；19，（本题13分） 在△ABC 中,若,1=⋅=⋅C B A B C A B A()1 求证:B A = ()2 求边长c的值，()3 若6=+C A B A,求△ABC 的面积；20，（本题13分） 已知向量(),)(),23,(cos ),1,(sin m n m x f x n x m⋅+==-= ()1当⎥⎦⎤⎢⎣⎡∈2,0πx 时，求函数()x f y =的值域 ()2 锐角三角形ABC ,若,10232,27,245=⎪⎭⎫ ⎝⎛==B f b c a 求边c a ,；21，（本题13分） 某地有三个村庄，分别位于等腰直角三角形ABC 的三个顶点处，已知,6km AC AB ==现计划在BC 边上的高AO 上一点P 处建造一个变电站，记P 点到三个村庄的距离之和为y ；()1 若∠,α=PBO 把y 表示成α的函数关系式；()2变电站建于何处时，它到三个村庄的距离之和最小?2。

高一数学三角函数试题1.已知向量．（1）若，且，求角的值；（2）若，且，求的值．【答案】（1）；（2）【解析】（1）根据向量垂直其数量积为0，可得到的关系式，从而得出的值，再根据角的范围得角的大小。

（2）根据数量积公式可得的关系式，用两角和差公式的逆用即化一公式将其化简为再根据角的范围找整体角的范围，从而可计算出的值。

用凑角的方法将写成的形式，用正弦的两角和公式展开计算即可。

（1）∵ , ∴ , 即 3分∴，又∴∴． 6分（2） 8分∴,又∵ , ∴, ∴ 10分∴． 12分【考点】1数量积公式；2两角和差公式。

2.如图，在中，已知,是上一点，,则【答案】【解析】由余弦定理得：，在三角形中，再由正弦定理得：【考点】正余弦定理综合3.已知，函数.（1）设，将函数表示为关于的函数，求的解析式和定义域；（2）对任意，不等式都成立，求实数的取值范围.【答案】（1），定义域为；（2）实数的取值范围是.【解析】（1）由恒等变换公式可求得，并可以表示出定义域；（2）由求出的取值范围，化简成形式，用函数单调性即可求出实数的取值范围.试题解析：（1）∴2分由可得4分∴6分定义域为 8分（2）∵∴10分∵恒成立∴恒成立化简得又∵∴ 12分令得∴在上为减函数14分∴∴ 16分【考点】恒等变换公式、恒成立问题.4.已知函数（1）用五点法画出它在一个周期内的闭区间上的图象；（2）求函数的单调增区间；（3）若，求的最大值和最小值.【答案】（1）（2）（3），【解析】（1）列表、作图 .4分6303（2）由得所以所以函数的单调增区间为 8分（3）因为所以，所以，所以当即时，当即时， -12分【考点】三角函数的性质点评：主要是考查了三角函数的图象与性质的求解运用，属于基础题。

5.已知函数(1)写出函数的单调递减区间；(2)设，的最小值是，最大值是，求实数的值．【答案】（1）（2）【解析】（1）为所求（2）【考点】三角函数的性质点评：主要是考查了三角函数的性质的运用，属于基础题。

约稿：三角函数与平面向量综合测试题广东省珠海市斗门区第一中学 于发智 519100 jianghua20011628@一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，恰有．．一项．．是符合题目要求的。

1．下列函数中，周期为2π的是（ ） A ．sin2x y = B ．sin 2y x = C ．cos 4xy = D ．cos 4y x = 2．已知命题:p x ∀∈R ，sin 1x ≤，则（ ） Ａ．:p x ⌝∃∈R ，sin 1x ≥ Ｂ．:p x ⌝∀∈R ，sin 1x ≥ Ｃ．:p x ⌝∃∈R ，sin 1x >Ｄ．:p x ⌝∀∈R ，sin 1x >3. 条件甲a =+θsin 1，条件乙a =+2cos2sin θθ，那么 （ ）A ．甲是乙的充分不必要条件B ．甲是乙的充要条件C ．甲是乙的必要不充分条件D ．甲是乙的既不充分也不必要条件4．已知O 是ABC △所在平面内一点，D 为BC 边中点，且2OA OB OC ++=0，那么（ ）Ａ．AO OD =Ｂ．2AO OD =Ｃ．3AO OD =Ｄ．2AO OD =5. 若函数f (x )=3sin21x , x ∈[0, 3π], 则函数f (x )的最大值是 ( ) A.21 B.32 C.22 D.23 6. (1+tan25°)(1+tan20°)的值是 ( ) A.-2 B.2 C.1 D.-1 7.α、β为锐角a =sin(βα+)，b =ααcos sin +，则a 、b 之间关系为 （ ）A ．a ＞bB ．b ＞aC ．a =bD ．不确定8. 下面有五个命题：①函数y =sin 4x -cos 4x 的最小正周期是π. ②终边在y 轴上的角的集合是{a |a =Z k k ∈π,2|.B ACD③在同一坐标系中，函数y =sin x 的图象和函数y =x 的图象有三个公共点. ④把函数.2sin 3632sin(3的图象得到的图象向右平移x y x y =ππ+= ⑤函数.0)2sin(〕上是减函数，在〔ππ-=x y 其中真命题的序号是 ① ④ （（写出所有真命题的编号））9. )sin()(ϕω+=x A x f （A ＞0，ω＞0）在x =1处取最大值，则 （ ） A ．)1(-x f 一定是奇函数 B ．)1(-x f 一定是偶函数 C ．)1(+x f 一定是奇函数D ．)1(+x f 一定是偶函数10. 使x y ωsin =（ω＞0）在区间[0，1]至少出现2次最大值，则ω的最小值为（ ） A ．π25B ．π45 C ．πD ．π2311、在直角坐标系xOy 中，,i j分别是与x 轴，y 轴平行的单位向量，若直角三角形ABC中，2AB i j =+ ，3AC i k j =+，则k 的可能值有 ( ) A 、1个 B 、2个 C 、3个 D 、4个12. 如图，l 1、l 2、l 3是同一平面内的三条平行直线，l 1与l 2间的距离是1， l 2与l 3间的距离是2，正三角形ABC 的三顶点分别在l 1、l 2、l 3上，则△ABC 的边长是 （ ）（A ）32 （B ）364（C ）4173 （D ）3212二、填空题：本大题共4小题，每小题4分，共16分。

2023北京重点校高一（上）期末汇编 向量的数量积与三角恒等变换章节综合|2|AB AD +=（ D ．①④（秋北京高一北京师大附中校考期末）已知平面向量a ，b 是非零向量，2a =，()2a a b ⊥+，则向量b 在向量a 方向上的投影为（1−BD ．22023秋·北京·高一北京师大附中校考期末）已知2a b ==，2a b ⋅=，则a b −=（ ） 1B D ．3或2二、填空题 2023秋·北京昌平·高一统考期末）已知向量,a b 在正方形网格中的位置如图所示.若网格纸上小正方形43a b −=__________.6．（2023秋·北京房山·高一统考期末）已知向量()1,1a =，非零向量b 满足a b a b +=−，请写出b 的一个坐标________．7．（2023秋·北京通州·高一统考期末）计算：2log sinlog 12π+=______．三、解答题 8．（2023秋·北京·高一北京师大附中校考期末）在ABC 中，D E ､为边BC AC ､上的点，且满足,BD CE m n BCEA==.(1)若ABC 为边长为，求AD BE ⋅；(2)若11,,32m n DE xAB yAC ===+，求x (3)若π,2,1,3A AB AC m n ∠====，求AD BE ⋅的最大值； 若将“D E ､为边BC AC ､上的点”改为“D E ､在ABC 的内部（包含边界），则AD BE ⋅是否为定值？若是，则写出该定值；若不是，则写出取值范围高一北京师大附中校考期末）已知函数(1)求函数()f x 的解析式；(2)将函数()f x 的图象向右平移()()()F x f x g x =+.当130,24x ⎡∈⎢⎣tan15tan15；πtan 5m(1)若矩形ABCD 为正方形，求正方形(2)求矩形ABCD 面积的最大值．15．（2023秋·北京通州17．（2023秋·北京东城·高一统考期末）如图，单位圆被点1212,,,A A A 分为12等份，其中1(1,0)A .角α的始,,A中选择，写出所有满足要求的点）2122222|2|(2)441AB AD AB AD AB AB AD AD +=+=+⋅+=+25AB AD ∴+=故选：D. 2．D【分析】利用辅助角公式化简函数解析式，结合正弦函数性质判断命题①，结合平方关系，正弦函数性质化简不等式求方程的解，判断命题②，根据奇函数的定义及正弦函数和余弦函数性质判断命题③，根据三角恒等变换及余弦型函数的周期公式判断命题④，由此可得正确选项【分析】首先通过条件()2a a b ⊥+求得·2a b =−，然后根据数量积的运算公式求出·b cos θ，进而求解b 在a 方向上投影【详解】平面向量ab 、是非零向量，()22a a a b =⊥+，，()2·2?2?||2?42?a a b a a a b a a b a b ∴+=+=+=+0=，则·2a b =−.设a 与b 夹角为θ，···2a b a b cos θ==−，则2·1b cos aθ−==−， b ∴在a 方向上投影为1−.故选：A ．C【分析】根据数量积的运算律，即可求出. 【详解】因为()22222a b a b a b a b −=−=+−⋅2222=+2a b −=. C.【分析】由图知||1,||2,,45a b a b ==<>=︒，应用向量数量积的运算律求得24310a b −=，即可得结果【详解】由图知：||1,||2,,45a b a b ==<>=︒，则12cos45a b ⋅=⨯⨯︒222431624916241810a b b b a a ⋅−=−=−++=，则4310a b −=. 故答案为：10 1,1(答案不唯一)【分析】设出向量b 的坐标，根据题意可得0a b ⋅=，进而即得. 【详解】设向量(),b x y =，220x y +≠，a b a b +=−，可得222222a a b b a a b b +⋅+=−⋅+，0a b ∴⋅=，又()1,1a =，所以0x y +=，1x =，可得()1,1b =−， 所以向量b 的坐标可为1,1. 故答案为：1,1. 【分析】根据给定条件利用对数运算法则，二倍角的正弦公式、特殊角的三角函数值计算作答2log sin log 12π+的中点，､AB AC 的夹角为60，()12AD AB AC =+，()122=−+BE AB AC ，计算AD BE ⋅即可；（2）若11,32m n ==，则距离是B 近的三等分点，E 近的AC 三等分点，则由2133=+=+DE DC CE BC AC 可得,x ，从而求出x +）11+==+CE AC n EAEA，()1=−+AD m AB mAC ，11=−++BE AB AC n ，且m ，由AD BE ⋅)1171++−+m m ，[]11,2+∈m ，令()[]13,1,2=+∈f x x x x ，由函数的单调性定义可得)13x x x=+在]1,2上单调递增，可求出AD BE ⋅的最大值；）以CB 的中点F 为原点，CB 所在的直线为x 轴，BC 的垂直平分线为y 轴建立平面直角坐标系，，设)(),E m n D 在以B 为圆心，半径为，点E 在三角形ABC 特殊位置可得答案.）若ABC 为边长为BC AC 、的中点，､AB AC 的夹角为60，()12AD AB AC =+，()()()1112222=+=−+−=−+BE BA BC AB AC AB AB AC ， 所以()()124⋅=+⋅−+AD BE AB AC AB AC ()221113282244422⎛⎫=−−⋅+=⨯−−⨯⨯+=− ⎪⎝⎭AB AB AC AC ；,DE xAB yAC =+，则()212112333333=+=−=−−=−DE DC CE BC AC AC AB AC AC AB ， 所以12,33==−x y ，121333+=−=−x y ；3）=CE n EA，所以11++===+CE CE EA AC n EAEAEA()()1=+=+=+−=−+AD AB BD AB mBC AB m AC AB m AB mAC ，11=+=−++BE BA AE AB AC n ， 因为m n =，所以11=−++BE AB AC m ，且[]0,1m ∈， 所以()()111⎛⎫⋅=−+⋅−+⎪+⎝⎭AD BE m AB mAC AB AC m ()221113111−⎛⎫=−+−⋅+=+ ⎪+++⎝⎭m m m AB m AB AC AC m m m m )1171++−+m m ，[]11,2+∈m ， ()[]13,1,2=+∈x x x x，设1212x x ≤<≤，)()()31133⎛⎫−=+−+=− ⎪x f x x x x x时AD BE ⋅有最大值为)1,12==BDCE BC EA，()223+−=+n n 310+=n ，为圆心，半径为1的三角形ABC 都为所在边的中点，点E 在三角形点重合时，12⎛==− ⎝AD AH ，0=BE ， 所以0⋅=AD BE ，,112m n ==时，由（）32⋅=−AD BE ，故AD BE ⋅不是定值.210,30，，，⎡==∈∠=⎣AB BD BE ABE ，所以向量AB 与BE 的夹角为150，设DBE θ∠=，则030，θ⎡⎤∈⎣⎦，3cos 12，θ⎡⎤∈⎢⎥⎣⎦，则()⋅=+⋅=⋅+⋅AD BE AB BD BE AB BE BD BE3cos 2θ=−⋅+⋅AB BE BD BE ()3cos 3cos θθ−+=−+BE BE BE ，所以()33cos ,132θ⎡⎤−+∈−−⎢⎥⎣⎦，而0,3⎡⎤∈⎣⎦BE ()33cos ,02θ⎡⎤−+∈−⎢⎥⎣⎦BE ，所以32⎡⎤⋅∈−⎢⎣AD BE9．(1)()π3sin 23f x x ⎛⎫=+ ⎪⎝⎭；(2)61,612⎡⎤−++⎢⎥⎣⎦. 【分析】（1）由图象可得()f xtan153tan15=25α=tan15tan45+tan15tan151tan45tan15=−⋅，根据两角和的正切公式逆用，即可得出；，根据两角差的正余弦公式以及诱导公式可得tan15tan45+tan15tan151tan45tan15=−⋅()tan 45+15tan 603===； cos 0α≠.π2，所以3ππcos sin 105=，3ππsin cos 105=.()()0x f x ，cos 2)cos()ln(1x x θ−+++2ln(1cos 2)cos cos x x θ−+−化简得，ln(1cos 2)cos x x −+ππ42x ≤<时，π22x ≤AD BC =，QOP ∠=OA AD ∴=AB OB ∴=矩形ABCD 为正方形，AB ∴即cos θ−，2sin θ∴2sin cos θ+，2sin θ∴+04πθ<<∴正方形ABCD （2）设矩形sin cos θ=15．(1)75；(2)72 cos410πα⎛⎫+=⎪⎝⎭，【详解】2ππ126=，所以终边经过π1112,Z 6i i i α的始边与x 轴的非负半轴重合，若的终边经过点5A ，则2π3α=， 2πcos 3α=ππsin sin cos sin 33ααα⎛=+⋅ ⎝，即1sin sin 2αα=⋅+4π3α=即ππ1112,Z 336i i i i 或4ππ1112,Z 936i i i i 经过点39,A A故答案为：12−；39,A A。

三角函数练习题及答案一、填空题1．如图，点C 为某沿海城市的高速公路出入口，直线BD 为海岸线，512BAC π∠=，BD AB ⊥，BC 是以A 为圆心，半径为1km 的圆弧型小路．该市拟修建一条从C 通往海岸的观光专线CP PQ -（新建道路PQ ，对道路CP 进行翻新），其中P 为BC 上异于B C ，的一点，PQ 与AB 平行，设012PAB θθ5π⎛⎫∠=<<⎪⎝⎭，新建道路PQ 的单位成本是翻新道路CP 的单位成本的2倍．要使观光专线CP PQ -的修建总成本最低，则θ的值为____________．2．已知()()()cos sin 3cos 0f x x x x ωωωω=+>，如果存在实数0x ，使得对任意的实数x ，都有()()()002016f x f x f x π≤≤+成立，则ω的最小值为___________.3．已知函数()2sin()f x x ωφ=+(0>ω，||φπ<)的部分图象如图所示，()f x 的图象与y 轴的交点的坐标是(0,1)，且关于点(,0)6π-对称，若()f x 在区间14(,)333ππ上单调，则ω的最大值是___________.4．给出下列命题：①若函数()f x 的定义域为[]0,2，则函数(2)f x 的定义域为[]0,4； ②函数()tan f x x =在定义域内单调递增；③若定义在R 上的函数()f x 满足(1)()f x f x +=-，则()f x 是以2为周期的函数；④设常数a ∈R ，函数2log ,04()10,41x x f x x x ⎧<≤⎪=⎨>⎪-⎩若方程()f x a =有三个不相等的实数根1x ，2x ，3x ，且123x x x <<，则312(1)x x x +的值域为[64,)+∞．其中正确命题的序号为_____．5．通信卫星与经济、军事等密切关联，它在地球静止轨道上运行，地球静止轨道位于地球赤道所在平面，轨道高度为km h （轨道高度是指卫星到地球表面的距离）．将地球看作是一个球（球心为O ，半径为km r ），地球上一点A 的纬度是指OA 与赤道平面所成角的度数，点A 处的水平面是指过点A 且与OA 垂直的平面，在点A 处放置一个仰角为θ的地面接收天线（仰角是天线对准卫星时，天线与水平面的夹角），若点A 的纬度为北纬30，则tan 3θ-=________．6．在ABC 中，设a ，b ，c 分别为角A ，B ，C 对应的边，记ABC 的面积为S ，且sin 2sin 4sin b B c C a A +=，则2Sa 的最大值为________. 7．已知ABC 为等边三角形，点G 是ABC 的重心．过点G 的直线l 与线段AB 交于点D ，与线段AC 交于点E ．设AD AB λ=，AE AC μ=，则11λμ+=__________；ADE 与ABC 周长之比的取值范围为__________．8．已知函数()cos()(0,0,0)f x A x A ωϕωϕπ=->><<的部分图像如图所示，设函数()266g x f x f x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭，则()g x 的值域为___________.9．已知a ，b ，c 分别为ABC 三个内角A ，B ，C 的对边，且222a c b ac +-=，则sin cos A C 的最大值为______．10．已知1OB →=，,A C 是以O 为圆心，220BA BC →→⋅=，设平面向量OA →与OB →的夹角为θ(π04θ≤≤)，则平面向量OA →在BC →方向上的投影的取值范围是_____.二、单选题11．已知函数()21ln e 1xf x x -⎛⎫=+ ⎪+⎝⎭，a ，b ，c 分别为ABC 的内角A ，B ，C 所对的边，且222446,a b c ab +-=则下列不等式一定成立的是（ ） A ．()()sin cos f A f B ≤ B ．f (cos A )≤f (cos B ) C ．f (sin A )≥f (sin B ) D ．f (sin A )≥f (cos B ) 12．若方程x 2 +2x +m 2 +3m = m cos(x +1) + 7有且仅有1个实数根，则实数m 的值为（ ） A ．2B ．-2C ．4D ．-413．已知函数()|sin |(0)f x x ωω=>在区间,53ππ⎡⎤⎢⎥⎣⎦上单调递减，则实数ω的取值范围为（ ） A ．5,32⎡⎤⎢⎥⎣⎦B ．30,2⎛⎤ ⎥⎝⎦C ．8,33⎡⎤⎢⎥⎣⎦D ．50,4⎛⎤ ⎥⎝⎦14．已知O 是三角形ABC 的外心，若()22AC ABAB AO AC AO m AO AB AC⋅+⋅=，且sin sin B C +=，则实数m 的最大值为（ ）A ．3B ．35C ．75D ．3215．已知点1F ，2F 分别为椭圆()2222:10x yC a b a b+=>>的左、右焦点，点M 在直线:l x a =-上运动，若12F MF ∠的最大值为60︒，则椭圆C 的离心率是（ ）A ．13B ．12C D 16．设函数()211f x x =-，()122x f e x --=，()31sin 23f x x π=，99i ia =，0i =、1、2、、99.记()()()()()()10219998k k k k k k k I f a f a f a f a f a f a =-+-++-，1k =、2、3，则（ ） A ．123I I I << B ．321I I I << C ．132I I I <<D ．213I I I <<17．在ABC 中，,E F 分别是,AC AB 的中点，且32AB AC =，若BEt CF <恒成立，则t 的最小值为（ ） A ．34B ．78C ．1D ．5418．已知双曲线22221(,0)x y a b a b-=>的两条渐近线分别与抛物线24y x ＝交于第一、四象限的A ，B 两点，设抛物线焦点为F ，若7cos 9AFB ∠＝﹣，则双曲线的离心率为（ ）AB ．3CD ．19．()sin()(0)f x x ωφφ=+>的部分图象如图所示，设P 是图象的最高点，A ，B 是图象与x 轴的交点，若tan 2APB ∠=-，则ω的值为（ ）A ．4π B ．3π C ．2π D ．π20．已知1sin ,sin ,sin ,222a x x b x ωωω⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，其中0>ω，若函数1()2f x a b =⋅-在区间(,2)ππ内有零点，则实数ω的取值可能是（ ）A ．18B ．14C ．12D ．34三、解答题21．如图，一幅壁画的最高点A 处离地面4米，最低点B 处离地面2米.正对壁画的是一条坡度为1:2的甬道（坡度指斜坡与水平面所成角α的正切值），若从离斜坡地面1.5米的C 处观赏它.（1）若C 对墙的投影（即过C 作AB 的垂线垂足为投影）恰在线段AB （包括端点）上，求点C 离墙的水平距离的范围；（2）在（1）的条件下，当点C 离墙的水平距离为多少时，视角θ（ACB ∠）最大？ 22．如图，甲、乙两个企业的用电负荷量y 关于投产持续时间t （单位：小时）的关系()y f t =均近似地满足函数()sin()(0,0,0)f t A t b A ωϕωϕπ=++>><<.（1）根据图象，求函数()f t 的解析式；（2）为使任意时刻两企业用电负荷量之和不超过9，现采用错峰用电的方式，让企业乙比企业甲推迟(0)m m >小时投产，求m 的最小值.23．已知ABC ∆的三个内角、、A B C 的对边分别为a b c 、、，且22b c ac =+， （1）求证：2B C =；（2）若ABC ∆是锐角三角形，求ac的取值范围.24．已知函数()()sin 0,2f x t x t πωϕϕ⎛⎫=+>< ⎪⎝⎭，()f x 的部分图像如图所示，点()0,3N ，,02M π⎛⎫- ⎪⎝⎭，,4P t π⎛⎫⎪⎝⎭都在()f x 的图象上.（1）求()f x 的解析式；（2）当,2x ππ⎡⎤∈-⎢⎥⎣⎦时，()33f x m --≤恒成立，求m 的取值范围.25．已知函数22()sin 22sin 26144f x x t x t t ππ⎛⎫⎛⎫=---+-+ ⎪ ⎪⎝⎭⎝⎭，,242x ππ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭，最小值为()g t .（1）求当1t =时，求8f π⎛⎫⎪⎝⎭的值；（2）求()g t 的表达式； （3）当112t -≤≤时，要使关于t 的方程2()9g t k t =-有一个实数根，求实数k 的取值范围. 26．在ABC ∆中，内角,,A B C 所对的边分别是,,a b c ，已知sin tan 1cos BC B=-．（Ⅰ）求证：ABC ∆为等腰三角形；（Ⅱ）若ABC ∆是钝角三角形，且面积为24a ，求2b ac的值．27．已知向量()cos sin ,sin a m x m x x ωωω=-，()cos sin ,2cos b x x n x ωωω=--，设函数()()2n f x a b x R =⋅+∈的图象关于点,112π⎛⎫⎪⎝⎭对称，且()1,2ω∈ （I ）若1m =，求函数()f x 的最小值；（II ）若()4f x f π⎛⎫≤ ⎪⎝⎭对一切实数恒成立，求()y f x =的单调递增区间．28．已知函数())2cos cos 1f x xx x =+-．（1）求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值；（2）若()85f x =-，2,3x ππ⎡⎤∈⎢⎥⎣⎦，求cos2x 的值；（3）若函数()()0y f x ωω=>在区间,62ππ⎡⎤⎢⎥⎣⎦上是单调递增函数，求正数ω的取值范围．29．设向量a =（2sin 2x cos 2xx ），b =（cos x ，sin x ），x ∈[-6π，3π]，函数f （x ）=2a •b ．（1）若|a b |，求x 的值；（2）若f （x ）-m m 的取值范围．30．函数()sin()16f x A x πω=-+（0,0A ω>>）的最大值为3， 其图象相邻两条对称轴之间的距离为2π， （1）求函数()f x 的解析式；（2）设π(0,)2α∈，则()22f α=，求α的值【参考答案】一、填空题1．6π2．140323．114．③④5．2rr h-+67． 3 21,32⎡⎢⎣⎦8．9[,4]4-9．12+10．⎡⎢⎣⎦二、单选题 11．D 12．A 13．A 14．D 15．C 16．D 17．B 18．B 19．C 20．D 三、解答题21．（1）点C 离墙的水平距离的范围为：1~5m m ；（2）当点C 离墙的水平距离为1m 时，视角θ（ACB ∠）最大. 【解析】 【分析】（1）如图所示：设(02),BF x x CF y =≤≤=，利用平行线成比例定理，结合锐角三角函数正切的定义进行求解即可；（2）利用两角和的正切公式、结合正切的定义，求出tan θ的表达式，利用换元法、基本不等式进行求解即可. 【详解】（1）如图所示：设(02),BF x x CF y =≤≤=，显然有1tan tan 2FGD α∠==，因此有 2(2)tan DFFG x FGD==+∠，由//GE DF ,可得： 1.52(2)22(2)CE CG x y DF GF x x +-=⇒=++，化简得：21y x =+，因为02x ≤≤，所以15y ≤≤，即点C 离墙的水平距离的范围为： 1~5m m ；（2）222tan tan 2tan tan()21tan tan 21x x BCF ACF y y yBCF ACF x x BCF ACF y x x y yθ-+∠+∠=∠+∠===--∠⋅∠-+-⋅,因为21y x =+，所以有12y x -=，代入上式化简得： 2222228tan 11522()5622y y y y y x x y y yθ===---+-⋅++-， 因为15y ≤≤，所以有55562564y y y y+-≥⋅=（当且仅当55y y =时取等号，即1y =时，取等号），因此有0tan 2θ<≤，因此当点C 离墙的水平距离为1m 时，视角θ（ACB ∠）最大. 【点睛】本题考查两角和的正切公式的应用，考查了基本不等式的应用，考查了平行线成比例定理，考查了数学建模能力，考查了数学运算能力.22．（1）()sin 462f t t ππ⎛⎫=++ ⎪⎝⎭；（2）4【解析】 【分析】 （1）由212T πω==，得ω，由53A b b A +=⎧⎨-=⎩，得A ，b ，代入(0,5)，求得ϕ，从而即可得到本题答案；（2）由题，得()()cos ()cos 8966f t m f t t m t ππ⎡⎤⎛⎫++=+++≤ ⎪⎢⎥⎣⎦⎝⎭恒成立，等价于cos ()cos 166t m t ππ⎡⎤⎛⎫++≤ ⎪⎢⎥⎣⎦⎝⎭恒成立，然后利用和差公式展开，结合辅助角公式，逐步转化，即可得到本题答案. 【详解】（1）解：由图知212T πω==，6πω∴=又53A b b A +=⎧⎨-=⎩，可得41b A =⎧⎨=⎩()sin 46f t t πϕ⎛⎫∴=++ ⎪⎝⎭，代入(0,5)，得22k πϕπ=+，又0ϕπ<<，2πϕ∴=所求为()sin 462f t t ππ⎛⎫=++ ⎪⎝⎭（2）设乙投产持续时间为t 小时，则甲的投产持续时间为()t m +小时，由诱导公式，企业乙用电负荷量随持续时间t 变化的关系式为：()sin 4cos 4626f t t t πππ⎛⎫=++=+ ⎪⎝⎭同理，企业甲用电负荷量变化关系式为：()cos ()46f t m t m π⎡⎤+=++⎢⎥⎣⎦两企业用电负荷量之和()()cos ()cos 866f t m f t t m t ππ⎡⎤⎛⎫++=+++ ⎪⎢⎥⎣⎦⎝⎭，0t ≥依题意，有()()cos ()cos 8966f t m f t t m t ππ⎡⎤⎛⎫++=+++≤ ⎪⎢⎥⎣⎦⎝⎭恒成立即cos ()cos 166t m t ππ⎡⎤⎛⎫++≤⎪⎢⎥⎣⎦⎝⎭恒成立 展开有cos 1cos sin sin 16666m t m t ππππ⎡⎤⎛⎫⎛⎫⎛⎫+-≤ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦恒成立cos 1cos sin sin cos 66666m t m t A t πππππϕ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+-=+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦其中，A =cos 16cos m Aπϕ⎛⎫+ ⎪⎝⎭=，sin 6sin m A πϕ=1A ∴=≤整理得：1cos 62m π⎛⎫≤- ⎪⎝⎭解得2422363k m k πππππ⎛⎫+≤≤+ ⎪⎝⎭即124128k m +≤≤+ 取0k =得：48m ≤≤ m ∴的最小值为4. 【点睛】本题主要考查根据三角函数的图象求出其解析式，以及三角函数的实际应用，主要考查学生的分析问题和解决问题的能力，以及计算能力，难度较大. 23．（1）证明见解析；（2）(1,2) 【解析】 【分析】（1）由22b c ac =+，联立2222cos b a c ac B =+-⋅，得2cos a c c B =+⋅，然后边角转化，利用和差公式化简，即可得到本题答案； （2）利用正弦定理和2B C =，得2cos 21aC c=+，再确定角C 的范围，即可得到本题答案. 【详解】解：（1）锐角ABC ∆中，22b c ac =+，故由余弦定理可得：2222cos b a c ac B =+-⋅，2222cos c ac a c ac B ∴+=+-⋅，22cos a ac ac B ∴=+⋅，即2cos a c c B =+⋅，∴利用正弦定理可得：sin sin 2sin cos A C C B =+， 即sin()sin cos sin cos sin 2sin cos B C B C C B C C B +=+=+，sin cos sin sin cos B C C C B ∴=+，可得：sin()sin B C C -=，∴可得：B C C -=，或B C C π-+=（舍去），2B C ∴=.（2）2sin sin()sin(2)2cos cos22cos21sin sin sin a A B C C C C C C c C C C++====+=+A B C π++=，,,A B C 均为锐角，由于：3C A π+=，022C π∴<<，04C π<<.再根据32C π<，可得6C π<，64C ππ∴<<，(1,2)ac∴∈ 【点睛】本题主要考查正余弦定理的综合应用，其中涉及到利用三角函数求取值范围的问题.24．（1）()22sin 33x f x π⎛⎫=+ ⎪⎝⎭；（2）[]1,0-【解析】 【分析】（1）由三角函数图像，求出,,t ωϕ即可；（2）求出函数()f x m -的值域，再列不等式组32m m +≥⎧⎪⎨≤⎪⎩.【详解】解：（1）由()f x 的图象可知34424T πππ⎛⎫=--= ⎪⎝⎭，则3T π=， 因为23T ππω==，0>ω，所以23ω=，故()2sin 3t x f x ϕ⎛⎫=+ ⎪⎝⎭. 因为,02M π⎛⎫- ⎪⎝⎭在函数()f x 的图象上，所以sin 023f t ππϕ⎛⎫⎛⎫-=-+= ⎪ ⎪⎝⎭⎝⎭， 所以()3k k Z πϕπ-+=∈，即()3k k Z πϕπ=+∈，因为2πϕ<，所以3πϕ=.因为点(N 在函数()f x 的图象上，所以()0sin 3f t π==解得2t =，故()22sin 33x f x π⎛⎫=+ ⎪⎝⎭.（2）因为,2x ππ⎡⎤∈-⎢⎥⎣⎦，所以22,3333x πππ⎡⎤+∈-⎢⎥⎣⎦，所以2sin 33x π⎡⎤⎛⎫+∈⎢⎥ ⎪⎝⎭⎣⎦，则()2f x ≤. 因为()33f x m -≤-≤，所以()3m f x m ≤+，所以32m m +≥⎧⎪⎨⎪⎩10m -≤≤.故m 的取值范围为[]1,0-. 【点睛】本题考查了利用三角函数图像求解析式，重点考查了三角函数值域的求法，属中档题.25．（1）4-（2）22515421()611282(1)t t t g t t t t t t ⎧⎛⎫-+<- ⎪⎪⎝⎭⎪⎪⎛⎫=-+-≤≤⎨ ⎪⎝⎭⎪⎪-+>⎪⎩（3）--22∞⋃+∞（，）（，） 【解析】 【分析】（1）直接代入计算得解；（2）先求出1sin(2)[,1]42x π-∈-，再对t 分三种情况讨论，结合二次函数求出()g t 的表达式；（3）令2()()9h t g t k t =-+，即2()(6)t 10h t k =-++有一个实数根，利用一次函数性质分析得解. 【详解】（1）当1t =时，2()sin 22sin 2444f x x t x ππ⎛⎫⎛⎫=---- ⎪ ⎪⎝⎭⎝⎭，所以48f π⎛⎫=- ⎪⎝⎭.（2）因为[,]242x ∈ππ，所以32[,]464x πππ-∈-，所以1sin(2)[,1]42x π-∈- 2()[sin(2)]614f x x t t π=---+（[,]242x ∈ππ）当12t <-时，则当1sin(2)42x π-=-时，2min 5[()]54f x t t =-+当112t -≤≤时，则当sin(2)4x t π-=时，min [()]61f x t =-+ 当1t >时，则当sin(2)14x π-=时，2min [()]82f x t t =-+故22515421()611282(1)t t t g t t t t t t ⎧⎛⎫-+<- ⎪⎪⎝⎭⎪⎪⎛⎫=-+-≤≤⎨ ⎪⎝⎭⎪⎪-+>⎪⎩ （3）当112t -≤≤时，()61g t t =-+，令2()()9h t g t k t =-+即2()(6)t 10h t k =-++ 欲使2()9g t kt =-有一个实根，则只需1()02(1)0h h ⎧-≤⎪⎨⎪≥⎩或1()02(1)0h h ⎧-≥⎪⎨⎪≤⎩ 解得-2k ≤或2k ≥.所以k 的范围：--22∞⋃+∞（，）（，）. 【点睛】本题主要考查三角函数的范围的计算，考查二次函数的最值的求法和方程的零点问题，意在考查学生对这些知识的理解掌握水平和分析推理能力，属于中档题. 26．（Ⅰ）证明见解析；（Ⅱ）2【解析】 【分析】（Ⅰ）将正切化弦，结合两角和差正弦公式可求得()sin sin C B C =+，根据三角形内角和可整理为sin sin C A =，则由正弦定理可得到结论；（Ⅱ）利用三角形面积公式可求得1sin 2B =；根据三角形为钝角三角形且（Ⅰ）中的c a =，可知B 为钝角，求得cos B ；利用余弦定理可构造方程求得,a b 之间关系，从而得到所求结果. 【详解】 （Ⅰ）由sin tan 1cos B C B =-得：sin sin cos 1cos C BC B=-则：()sin sin cos cos sin sin C B C B C B C =+=+A B C π++= ()()sin sin sin B C A A π∴+=-= sin sin C A ∴=由正弦定理可知：c a =ABC ∆∴为等腰三角形（Ⅱ）由题意得：2211sin sin 224a S ac B a B ===，解得：1sin 2B =ABC ∆为钝角三角形，且a c = B ∴为钝角 cos B ∴=由余弦定理得：(2222222cos 22b a c ac B a a =+-==+2222b b ac a ∴==【点睛】本题考查三角形形状的求解、利用余弦定理、三角形面积公式求解三角形边之间的关系问题，涉及到两角和差正弦公式、三角形内角和、诱导公式、同角三角函数值的求解等知识.27．（Ⅰ）1()22,31234k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 【解析】 【分析】化简()f x 解析式可得()()22n f x x ωϕ=-+；根据图象关于,112π⎛⎫ ⎪⎝⎭可求得n ；（Ⅰ）若1m =，则()()21f x x ωϕ=-+，从而可得函数最小值；（Ⅱ）利用4x π=为对称轴，,112π⎛⎫ ⎪⎝⎭为对称中心可得()*642T T k k N π=+⋅∈，根据周期和ω的范围可求得ω；将,112π⎛⎫ ⎪⎝⎭代入解析式可求得()314f x x π⎛⎫=-+ ⎪⎝⎭，将34x π-整体放入正弦函数的单调递增区间中，解出x 的范围即可. 【详解】由题意得：()()22cos sin 2sin cos 2n f x m x x n x x ωωωω=--++()sin 2cos 2222n n n x m x x ωωωϕ=-+=-+ 其中cos ϕ=sin ϕ=图象关于点,112π⎛⎫⎪⎝⎭对称 12n ∴=，解得：2n =()()21f x x ωϕ∴=-+（Ⅰ）若1m =，则()()21f x x ωϕ=-+()min 1f x ∴=（Ⅱ）()4f x f π⎛⎪≤⎫ ⎝⎭对一切实数恒成立 ()max 4f x f π⎛⎫∴= ⎪⎝⎭()*412642T T k k N πππ∴-==+⋅∈，即：()()*223212T k N k ππω==∈+()3212k ω∴=+，又()1,2ω∈ 32ω∴=()2sin3cos31f x x m x ∴=-+，又图象关于点,112π⎛⎫⎪⎝⎭对称2sin cos 111244f m πππ⎛⎫∴=-+= ⎪⎝⎭，解得：2m =()2sin 32cos31314f x x x x π⎛⎫∴=-+=-+ ⎪⎝⎭令232242k x k πππππ-+≤-≤+，k Z ∈，解得：2212343k k x ππππ-+≤≤+，k Z ∈ ()f x ∴的单调递增区间为：()22,31234k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 【点睛】本题考查三角函数图象与性质的综合应用问题，涉及到根据三角函数的性质求解函数解析式的求解、三角函数最值的求解、单调区间的求解问题.28．（I ）1-；（II ；（III ）10,3⎛⎤ ⎥⎝⎦【解析】 【分析】将()f x 整理为2sin 26x π⎛⎫+ ⎪⎝⎭；（I ）利用x 的范围求得26x π+的范围，结合sin x 的图象可求得最值；（II ）利用()85f x =-可求得sin 26x ；结合角的范围和同角三角函数关系可求得cos 26x π⎛⎫+ ⎪⎝⎭；根据cos 2cos 266x x ππ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦，利用两角和差余弦公式可求得结果；（III ）利用x 的范围求得26x πω+的范围，从而根据sin x 单调递增区间构造出关于ω的不等式组，解不等式组再结合0>ω即可得到结果. 【详解】()2cos 2cos 12cos 22sin 26f x x x x x x x π⎛⎫=+-=+=+ ⎪⎝⎭（I ）0,2x π⎡⎤∈⎢⎥⎣⎦ 72,666x πππ⎡⎤∴+∈⎢⎥⎣⎦[]2sin 21,26x π⎛⎫∴+∈- ⎪⎝⎭()f x ∴在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为：1-（II ）由题意得：82sin 265x π⎛⎫+=- ⎪⎝⎭ 4sin 265x π⎛⎫∴+=- ⎪⎝⎭2,3x ππ⎡⎤∈⎢⎥⎣⎦ 3132,626x πππ⎡⎤∴+∈⎢⎥⎣⎦ 3cos 265x π⎛⎫∴+= ⎪⎝⎭cos 2cos 2cos 2cos sin 2sin 666666x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫∴=+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦341552=⨯（III ）()2sin 26f x x πωω⎛⎫=+ ⎪⎝⎭,62x ππ⎡⎤∈⎢⎥⎣⎦时，2,6366x πωπππωωπ⎡⎤+∈++⎢⎥⎣⎦2622362k k ππωππωππππ⎧+≤+⎪⎪∴⎨⎪+≥-⎪⎩，k Z ∈，解得：12362k k ωω⎧≤+⎪⎨⎪≥-⎩，k Z ∈ 0ω>，可知当0k =时满足题意，即103ω<≤ω∴的取值范围为：10,3⎛⎤ ⎥⎝⎦【点睛】本题考查正弦型函数的值域求解、单调性应用、三角恒等变换公式应用、同角三角函数关系等问题.关键是能够利用二倍角公式和辅助角公式将函数化为()sin A x ωϕ+的形式，从而通过整体对应的方式来研究函数的值域和性质.29．（1）π4x =；（2）2⎤⎦.【解析】 【分析】（1）根据|a|=b |，利用化简函数化简解得x 的值； （2根据f （x ）＝2a •b ．结合向量的坐标运算，根据x ∈[6π-，3π]，求解范围，）﹣f （x ）﹣m ≤m 的取值范围． 【详解】解：（1）由|ab |， 可得222a b =； 即4sin 2x =2（cos 2x +sin 2x ） 即sin 2x =12； ∴sin x= ∵x ∈[-6π，3π]， ∴x =4π （2）由函数f （x ）=2a •b =2sin2x2x=sin2x +1122-cos2x ）=sin2x x （2x -3π）∵x ∈[-6π，3π]， ∴2x -3π∈[-23π，3π]，2≤2sin （2x -3π）要使f （x ）-m则2m m ⎧-≤⎪⎨≥⎪⎩2m ≤故得m 的取值范围是2]． 【点睛】本题考查三角函数的化简能力和向量的运算，考查转化思想以及计算能力．30．（1）()2sin(2) 1.6f x x π=-+；（2）3π.【解析】 【详解】（1）由三角函数性质得,最大值为A+1=3,∴A=2， 周期2222πππωω⨯==⇒=，∴f （x ）=2sin （2x-6π）+1 （2）π(0,)2α∈，f （2α）=2∴2sin （22α⨯-6π）+1=2,得sin （α-6π）=12，α=3π。

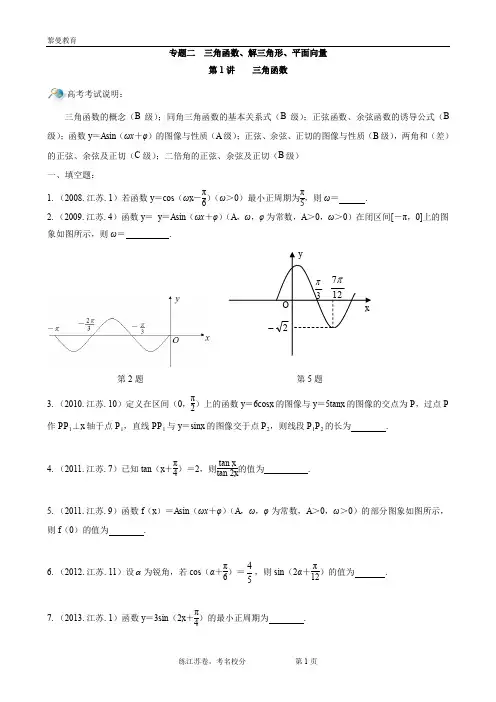
专题二 三角函数、解三角形、平面向量第1讲 三角函数高考考试说明：三角函数的概念（B 级）；同角三角函数的基本关系式（B 级）；正弦函数、余弦函数的诱导公式（B 级）；函数y ＝A sin （ωx ＋φ）的图像与性质（A 级）；正弦、余弦、正切的图像与性质（B 级），两角和（差）的正弦、余弦及正切（C 级）；二倍角的正弦、余弦及正切（B 级） 一、填空题：1.（2008.江苏.1）若函数y ＝cos （ωx －π6）（ω＞0）最小正周期为π5，则ω＝ .2.（2009.江苏.4）函数y ＝ y ＝A sin （ωx ＋φ）（A ，ω，φ为常数，A ＞0，ω＞0）在闭区间[－π，0]上的图象如图所示，则ω＝ .第2题 第5题3.（2010.江苏.10）定义在区间（0，π2）上的函数y ＝6cos x 的图像与y ＝5tan x 的图像的交点为P ，过点P作PP 1⊥x 轴于点P 1，直线PP 1与y ＝sin x 的图像交于点P 2，则线段P 1P 2的长为 .4.（2011.江苏.7）已知tan （x ＋π4）＝2，则tan xtan 2x 的值为 .5.（2011.江苏.9）函数f （x ）＝A sin （ωx ＋φ）（A ，ω，φ为常数，A ＞0，ω＞0）的部分图象如图所示，则f （0）的值为 .6.（2012.江苏.11）设α为锐角，若cos （α＋π6）＝45，则sin （2α＋π12）的值为 .7.（2013.江苏.1）函数y ＝3sin （2x ＋π4）的最小正周期为 .8.（2014江苏5）已知函数y ＝cos x 与y ＝sin （2x ＋φ）（0≤φ＜π），它们的图象有一个横坐标为π3的交点，则φ的值是 .9.（2015.江苏.8）已知tan α＝－2，tan （α＋β）＝17，则tan β的值为_______.10.（2015.江苏.14）设向量a k ＝（cos k π6，sin k π6＋cos k π6）（k ＝0，1，2，...，12），则11k =∑（a k →˙a k ＋１→）的值为 .11.（2016.江苏.9）定义在区间 [0，3π] 上的函数y ＝sin 2x 的图象与y ＝cos x 的图象的交点个数是________.12.（2017.江苏.5）若tan （α－π4）＝16，则 tan α＝ .13.（2018.江苏.7）已知函数f （x ）＝sin （2x ＋φ）（－π2＜φ＜π2）的图象关于直线x ＝π3对称，则φ的值是 .14.（2019.江苏.13）已知tan 2π3tan()4αα=-+，则sin （π24α+）值是_____. 二、解答题：1.（2008.江苏.15）如图，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别交单位圆于A ，B 两点.已知A ，B 两点的横坐标分别是210，255. （1）求tan （α＋β）的值； （2）求α＋2β的值.2.（2014.江苏.15）已知α∈（π2，π），sin α＝55.（1）求sin （π4＋α）的值；（2）求cos （5π6－2α）的值.3.（2017.江苏.16）已知向量a ＝（cos x ，sin x ），b ＝（3，－3），x ∈[0，π]. （1）若a ∥b ，求x 的值；（2）记f （x ）＝a ∙b ，求f （x ）的最大值和最小值以及对应的x 的值.4.（2018.江苏.16）已知α，β为锐角，tan α＝43，cos （α＋β）＝－55.（1）求cos2α的值； （2）求tan （α－β）的值.5.（2018.江苏.17）某农场有一块农田，如图所示，它的边界由圆O 的一段圆弧MPN （P 为此圆弧的中点）和线段MN 构成.已知圆O 的半径为40米，点P 到MN 的距离为50米.先规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD ，大棚 Ⅱ 内的地块形状为△CDP ，要求A ，B 均在线段MN 上，C ，D 均在圆弧上.设OC 与MN 所成的角为θ.（1）用θ分别表示矩形ABCD 和△CDP 的面积，并确定sin θ的取值范围；（2）若大棚 Ⅰ 内种植甲种蔬菜，大棚 Ⅱ 内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4：3.求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大.第2讲 解三角形高考考试说明：三角函数的概念（B 级）；同角三角函数的基本关系式（B 级）；正弦函数、余弦函数的诱导公式（B 级）；函数()ϕω+=x A y sin 的图像与性质（A 级）.正弦、余弦、正切的图像与性质（B 级），两角和（差）的正弦、余弦及正切（C 级）；二倍角的正弦、余弦及正切（B 级），正弦定理、余弦定理及其应用（B 级） 一、填空题：1.（2008.江苏.13）满足条件AB ＝2，AC ＝2BC 的三角形ABC 的面积的最大值是 .2.（2010.江苏.13）在锐角三角形ABC 中，A 、B 、C 的对边分别为a 、b 、c ，b a ＋a b ＝6cos C ，则 tan C tan A ＋tan C tan B ＝ .3.（2014.江苏.14）若△ABC 的内角满足sin A ＋2sin B ＝2sin C ，则cos C 的最小值是 .4.（2016.江苏.14）在锐角三角形ABC 中，若sin A ＝2sin B sin C ，则tan A tan B tan C 的最小值是________.5.（江苏.2018.13）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，∠ABC ＝120°，∠ABC 的平分线交AC 与点D ，且BD ＝1，则4a ＋c 的最小值为 . 二、解答题：1.（2011.江苏.15）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c . （1）若sin （A ＋π6）＝2cos A ，求A 的值；（2）若cos A ＝13，b ＝3c ，求sin C 的值.2.（2012.江苏.15）在△ABC 中，已知AB →·AC →＝3BA →·BC →. （1）求证：tan B ＝3tan A ； （2）若cos C ＝55，求A 的值.3.（2013.江苏.18）如图，游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ，另一种是先从A 沿索道乘缆车到B ，然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山，甲沿AC 匀速步行，速度为50m /min .在甲出发2min 后，乙从A 乘缆车到B ，在B 处停留1min 后，再以匀速步行到C .假设缆车匀速直线运动的速度为130m /min ，山路AC 长为1260m ，经测量，cos A ＝1213，cos C ＝35. （1）求索道AB 的长；（2）问乙出发多少分钟后，乙在缆车上与甲的距离最短？（3）为使两位游客在C 处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？4.（2015.江苏.15）在△ABC 中，已知AB ＝2，AC ＝3，A ＝60°. （1）求BC 的长； （2）求sin2C 的值.5.（2016.江苏.15）在△ABC 中，AC ＝6，cos B ＝45，C ＝π4.（1）求AB 的长； （2）cos （A －π6）的值.6.（2019.江苏.15）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .（1）若a ＝3c ，b ，cos B ＝23，求c 的值； （2）若sin cos 2A B a b =，求sin()2B π+的值.第3讲 平面向量高考考试说明：平面向量的概念（B 级），平面向量的加法、减法及数乘运算（B 级），平面向量的坐标表示（B 级），平面向量的概平行与垂直（B 级），平面向量的数量积（C 级），平面向量的应用（A 级） 一、填空题：1.（2008.江苏.5）已知向量a 和b 的夹角为120°，|a |＝1，|b |＝3，则 |5a －b |＝ .2.（2009.江苏.2）已知向量a 和向量b 的夹角为30°，|a |＝2，|b |＝3，则向量a 和b 的数量积a·b ＝ .3.（2011.江苏.10）已知e 1，e 2是夹角为2π3的两个单位向量，a ＝e 1－2e 2，b ＝k e 1＋e 2，若a·b ＝0，则实数k 的值为 .4.（2012.江苏.9）如图，在矩形ABCD 中，AB ＝2，BC ＝2，点E 为BC 的中点，点F 在边CD 上，若AB →·AF →＝2，则 AE →·BF → 的值是 .第4题5.（2013.江苏.10）设D ，E 分别是△ABC 的边AB ，BC 上的点，AD ＝12AB ，BE ＝23BC ，若DE →＝λ1AB →＋λ2AC→（λ1，λ2为实数），则λ1＋λ2的值为 .6.（2014.江苏.12）如图，在平行四边形ABCD 中，已知AB ＝8，AD ＝5，CP →＝3PD →，AP →·BP →＝2，则AB →·AD →的值是 .7.（2015.江苏.6）已知向量a ＝（2，1），b ＝（1，－2），若m a ＋n b ＝（9，－8）（m ，n R ），m －n 的的值为______.P（第6题）8.（2015.江苏.14.）（见第1讲第10题）设向量a k ＝（cos k π6，sin k π6＋cos k π6）（k ＝0，1，2，...，12），则11k =∑（a k →˙a k ＋１→）的值为 .9.（2016.江苏.13）如图，在△ABC 中，D 是BC 的中点，E ，F 是AD 上的两个三等分点，BA →·CA →＝4，BF →·CF →＝－1，则BE →·CE →的值是________.第9题 第10题10.（2017.江苏. 12）如图，在同一个平面内，向量OA →，OB →，OC →的模分别为1，1，2，OA →与OC →的夹角为α，且tan α＝7，OB →与OC →的夹角为45°.若OC →＝mOA →＋nOB →（m ，n ∈R ），则m ＋n ＝ .11.（江苏.2017.13）在平面直角坐标系xOy 中，A （－12，0），B （0，6），点P 在圆O ：x 2＋y 2＝50上，若P A →·PB →≤20则点P 的横坐标的取值范围是 .12.（江苏.2018.12）在平面直角坐标系xOy 中，A 为直线l ：y ＝2x 上在第一象限内的点，B （5，0），以AB 为直径的圆C 与直线l 交于另一点D .若AB →·CD →＝0，则点A 的横坐标为 .13.（江苏.2019.12）如图，在△ABC 中，D 是BC 的中点，E 在边AB 上，BE ＝2EA ，AD 与CE 交于点O .若6AB AC AO EC ⋅=⋅，则ABAC的值是_____.二、解答题：1.（2009.江苏.15）设向量a ＝（4cos α，sin α），b ＝（sin β，4cos β），c ＝（cos β，4sin β-）. （1）若a 与b －2c 垂直，求tan()αβ+的值； （2）求 |b ＋c | 的最大值；（3）若tan tan 16αβ=，求证：a ∥b .2.（2010.江苏.15）在平面直角坐标系xOy 中，点A （－1，－2），B （2，3），C （－2，－1）. （1）求以线段AB 、AC 为邻边的平行四边形两条对角线的长； （2）设实数t 满足（AB →－t OC →）·OC →＝0，求t 的值.3.（2012.江苏.15）在△ABC 中，已知AB →·AC →＝3BA →·BC →. （1）求证：tan B ＝3tan A ； （2）若cos C ＝55，求A 的值.A黎曼教育4.（2013.江苏.15）已知向量a＝（cos α，sin α），b＝（cos β，sin β），0＜β＜α＜π. （1）若| a－b | ＝2，求证：a⊥b；（2）设c＝（0，1），若a＋b＝c，求α，β的值.5.（2017.江苏.16）已知向量a＝（cos x，sin x），b＝（3，－3），x∈[0，π].（1）若a∥b，求x的值；（2）记f（x）＝a∙b，求f（x）的最大值和最小值以及对应的x的值.练江苏卷，考名校分第11页。

高一数学三角函数综合试题答案及解析1.已知cosα=﹣，，则sin（α﹣）= ．【答案】.【解析】，；则.【考点】两角和的正弦公式.2.，其中、是常数，且满足，是否存在这样的、，使是与无关的定值.若存在，求出的值；若不存在，说明理由.【答案】【解析】假设存在，由于函数的值与无关，故取的多个值函数值相同，为了能够尽可能的寻找的关系，这里取.试题解析：假设存在这样的，使是与无关的定值，可取的值分别为，则:且由此可解得 6分因为，所以所以解得， 10分此时，所以当时，是与无关的定值 14分【考点】存在性问题，任意性问题（特值法）.3.曲线和直线在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…，则|P2P4|等于______________。

【答案】π【解析】可以利用两角和与差的三角函数化简，然后求出曲线与y=的y轴右侧的交点按横坐标，即可求出|P2P4 |．【考点】三角函数化简.4.函数,的最小正周期为（）A．B．C．D．【答案】C【解析】这是三角函数图像与性质中的最小正周期问题，只要熟悉三角函数的最小正周期的计算公式即可求出，如的最小正周期为，而的最小正周期为，故函数的最小正周期为，故选C.【考点】三角函数的图像与性质.5.已知.（1）求的最小值及取最小值时的集合；（2）求在时的值域；（3）求在时的单调递减区间.【答案】（1）当，；（2）；（3）.【解析】先根据平方差公式、同角三角函数的基本关系式、二倍角公式化简所给的函数.（1）将看成整体，然后由正弦函数的最值可确定函数的最小值，并明确此时的值的集合；（2）先求出的范围为，从而，然后可求出时，函数的值域；（3）将当成整体，由正弦函数的单调减区间中解出的取值范围，然后对附值，取满足的区间即可.试题解析：化简4分（1）当时，取得最小值，此时即，故此时的集合为 6分（2）当时，所以，所以，从而即 9分（3）由解得当时，，而，此时应取当时，，而，此时应取故在的单调减区间为 14分.【考点】1.三角恒等变换；2.三角函数的图像与性质.6.（1）已知f(x)＝sinx＋2sin(＋)cos(＋)．(1)若f(α)＝，α∈(－，0)，求α的值；（2）若sin＝，x∈(，π)，求f(x)的值．【答案】(1);(2).【解析】(1)首先根据三角函数公式对函数进行化简,即,从而,则,再由,又,从而求出的值.(2)由,则,根据同角平方关系,由,得,再由倍角公式,可得,,从而求出函数的值.试题解析：(1)f(x)＝sin x＋2sin(＋)cos(＋)＝sin x＋sin(x＋)＝sin x＋cos x＝sin(x＋)，由f(α)＝，得sin(α＋)＝.∴sin(α＋)＝.∵α∈(－，0)，∴α＋∈(－，)．∴α＋＝.∴α＝－.(2)∵x∈(，π)，∴∈(，)．又sin＝，∴cos＝.∴sin x＝2sin cos＝，cos x＝－＝－.∴f(x)＝sin x＋cos x＝－＝.【考点】三角函数的公式及化简求值.7.若的值为（）A．2B．3C．4D．6【答案】D【解析】因为，所以答案选D．【考点】1．三角函数式的变形、化简、求值．8.求函数y=2-sinx+cos2x的值域。

专题：三角函数与向量的交汇题型分析及解题策略主要考点如下：1.考查三角式化简、求值、证明及求角问题.2.考查三角函数的性质与图像，特别是y=Asin(cox+(p)的性质和图像及其图像变换.3.考查平面向量的基本概念，向量的加减运算及几何意义，此类题一般难度不大，主要用以解决有关长度、夹角、垂直、平行问题等.4.考查向量的坐标表示，向量的线性运算，并能正确地进行运算.5.考查平面向量的数量积及运算律(包括坐标形式及非坐标形式)，两向量平行与垂直的充要条件等问题.6.考查利用正弦定理、余弦定理解三角形问题.题型一解斜三角形与向量的综合【例1】已知角A、B、C为^ABC的三个内角，其对边分别为a、b、c,京=(—cos成，sin*^"), / = (cos*^", sin*^"), a = 2^3? J E L= 2^*(I )若ZiABC的面积S=,,求b + c的值.(II )求b+c的取值范围.题型二三角函数与平面向量平行(共线)的综合【例2】已知A、B、C为三个锐角，且A+B +C=TI.若向量8 = (2sinA — 2, cosA + sinA)与向量2 =C — 3B(cosA—sinA, 1+sinA)是共线向量.(I )求角A； (II )求函数y=2sin2B+cos—-—的最大值.题型三三角函数与平面向量垂直的综合【例3】已知向量甘= (3sina,cosa), 3 = (2sina, 5sina—4cosa), aG(宇,2n),且甘_L言.Ct jr(I )求tana 的值； (II)求cos(y+~)的值.题型四三角函数与平面向量的模的综合此类题型主要是利用向量模的性质ltl2=t2,如果涉及到向量的坐标解答时可利用两种方法：(1)先进行向量运算，再代入向量的坐标进行求解；(2)先将向量的坐标代入向量的坐标，再利用向量的坐标运算进行求解.【例4】已知向量盲= (cosa,sina),言= (cosB,sir)B), |2 —言|=|>姑.TT TT 5(I )求cos(a—P)的值；(II )^—^<P<O<a<p 且sinP = ——,求sina 的值.题型五三角函数与平面向量数量积的综合此类题型主要表现为两种综合方式：(1)三角函数与向量的积直接联系；⑵利用三角函数与向量的夹角交汇，达到与数量积的综合.解答时也主要是利用向量首先进行转化，再利用三角函数知识求解.【例5】1.设函数f(x) = 4.含.其中向量冷= (m, cosx),言= (l+sinx, 1), x《R,且f(亨) = 2.(I )求实数m的值；(II)求函数f(x)的最小值.(3)求f(x)的对称中心和对称轴2.(山东)已知向量扁= (smx,l)〃(品cosx*s2W>0),函数/'(x) = M的最大值为6.JT(I)求刀；(II)将函数y = /(x)的图象向左平移g个单位，再将所得图象上各点的横坐标缩短为原来的5倍，纵坐标不变，得到函数V = g(x)的图象.(1)求g(x)在［0,芸］上的值域.(2)五点法做出g(x)在一个周期上的图像。

高三数学三角函数试题答案及解析1.若点在函数的图象上，则的值为 .【答案】.【解析】由题意知，解得，所以.【考点】1.幂函数；2.三角函数求值2.设，将函数在区间内的全部极值点按从小到大的顺序排成数列.(1)求数列的通项公式；(2)设，数列的前项和为，求.【答案】（1）；（2）.【解析】（1）先根据三角函数的恒等变换化简，得，再根据三角函数的性质找到极值点，利用等差数列的性质写出数列的通项公式；（2）先根据（1）中的结果写出的通项公式，然后写出的解析式，在构造出，利用错位相减法求，计算量比较大，要细心.试题解析：（1），其极值点为， 2分它在内的全部极值点构成以为首项，为公差的等差数列， 4分所以； 6分（2）， 8分所以，，相减，得，所以. 12分【考点】1、三角函数的恒等变换及化简；2、三角函数的性质的应用；3、等差数列的通项公式；4、错位相减法求数列的前项和；5、等比数列的前项和.3.若函数的一个对称中心是，则的最小值为（）A．B．C．D．【答案】B【解析】由于正切函数的对称中心坐标为，且函数的一个对称中心是，所以，因此有，因为，所以当时，取最小值，故选B.【考点】三角函数的对称性4.在锐角中，，，则的值等于；的取值范围为 .【答案】；【解析】，所以，由正弦定理得，即，所以，为锐角三角形，则，且，即，则有，且有，所以，故有，，所以，即，故的取值范围为.【考点】1.正弦定理；2.三角函数的取值范围5.已知是第二象限角,，则（）A．B．C．D．【答案】B【解析】已知是第二象限角,，所以，故选B.【考点】同角三角函数基本关系式.6.在中，角的对边分别为向量，,且．（１）求的值；（２）若,,求角的大小及向量在方向上的投影．【答案】（1）；（2），向量在方向上的投影．【解析】（1）由向量数量积坐标形式列式，可求得的值，再利用平方关系可求得的值；（2）先利用正弦定理可求得的值，再利用大边对大角可求得角的大小．由投影的定义可求得向量在方向上的投影．试题解析：(１)由,得, 1分, 2分.. ３分．４分(２)由正弦定理，有, ５分．６分，, ７分． 8分由余弦定理，有， 9分或（舍去）． 10分故向量在方向上的投影为 11分． 12分【考点】1、向量数量积、投影；2、三角恒等变换；3、解三角形．7.在中产生区间上均匀随机数的函数为“( )”,在用计算机模拟估计函数的图像、直线和轴在区间上部分围成的图形面积时，随机点与该区域内的点的坐标变换公式为( )A．B．C．D．【答案】D【解析】由于，，而，，所以坐标变换公式为，. 故选D.【考点】均匀随机数的意义与简单应用.8.已知函数，则下列结论正确的是（）A．函数的图象关于直线对称B．函数的最大值为C．函数在区间上是增函数D．函数的最小正周期为【答案】C【解析】令得错误；函数的最大值为，故错误；函数的最小正周期为，故错误；当时，，故函数在区间上是增函数，所以选．【考点】考查三角函数的图像及其性质．9.函数，，在上的部分图象如图所示，则的值为．【答案】【解析】根据题意，由于函数，，在上的部分图象可知周期为12，由此可知，A=5，将（5,0）代入可知，5sin(+)=0，可知=，故可知==，故答案为【考点】三角函数的解析式点评：主要是考查了三角函数的解析式的求解和运用，属于基础题。

高一数学试题（必修4）（特别适合按14523顺序的省份）必修4 第一章三角函数(1)一、选择题：1.已知A={第一象限角}，B={锐角}，C={小于90°的角}，那么A、B、C关系是（）A．B=A∩C B．B∪C=C C．AC D．A=B=C2 等于（）A B C D3.已知的值为（）A．－2 B．2 C．D．－4．下列函数中，最小正周期为π的偶函数是（）A.y=sin2xB.y=cos C .sin2x+cos2x D. y=5 若角的终边上有一点，则的值是（）A B C D6．要得到函数y=cos()的图象，只需将y=sin的图象（）A．向左平移个单位 B.同右平移个单位C．向左平移个单位 D.向右平移个单位7．若函数y=f(x)的图象上每一点的纵坐标保持不变，横坐标伸长到原来的2倍，再将整个图象沿x轴向左平移个单位，沿y轴向下平移1个单位，得到函数y=sinx的图象则y=f(x)是（）A．y= B.y=C.y=D.8. 函数y=sin(2x+)的图像的一条对轴方程是（）A.x=-B. x=- C .x=D.x=9．若，则下列结论中一定成立的是（）A. B． C． D．10.函数的图象（）A．关于原点对称 B．关于点（－，0）对称 C．关于y轴对称 D．关于直线x=对称11.函数是（）A．上是增函数 B．上是减函数C．上是减函数D．上是减函数12.函数的定义域是（）A．B．C． D．二、填空题：13. 函数的最小值是 .14 与终边相同的最小正角是_______________15. 已知则 .16 若集合，，则=_______________________________________三、解答题：17．已知，且．a)求sinx、cosx、tanx的值．b)求sin3x – cos3x的值．18 已知，（1）求的值（2）求的值19. 已知α是第三角限的角，化简20．已知曲线上最高点为（2，），由此最高点到相邻的最低点间曲线与x轴交于一点（6，0），求函数解析式，并求函数取最小值x的值及单调区间必修4 第一章三角函数(2)一、选择题：1．已知，则化简的结果为（）A． B. C． D. 以上都不对2．若角的终边过点(-3，-2)，则( )A．sin tan＞0 B．cos tan＞0C．sin cos＞0 D．sin cot＞03 已知，，那么的值是（）A B C D4．函数的图象的一条对称轴方程是（）A． B. C. D.5．已知，,则tan2x= ( ) A． B. C. D.6．已知，则的值为（）A． B. 1 C. D. 2 7．函数的最小正周期为（）A．1 B. C. D.8．函数的单调递增区间是（）A． B.C． D.9．函数，的最大值为（）A．1 B. 2 C. D.10．要得到的图象只需将y=3sin2x的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位 D．向右平移个单位11．已知sin(+α)=，则sin(-α)值为（）A. B. — C. D. —12．若，则（）A. B. C. D.二、填空题13．函数的定义域是14．的振幅为初相为15．求值：=_______________16．把函数先向右平移个单位，然后向下平移2个单位后所得的函数解析式为________________________________三、解答题17 已知是关于的方程的两个实根，且，求的值18．已知函数，求：（1）函数y的最大值，最小值及最小正周期；（2）函数y的单调递增区间19．已知是方程的两根，且，求的值20．如下图为函数图像的一部分（1）求此函数的周期及最大值和最小值（2）求与这个函数图像关于直线对称的函数解析式必修4 第三章三角恒等变换(1)一、选择题:1.的值为 ( ）A 0BC D2.，，，是第三象限角，则（）A B C D3.设则的值是( )A B C D4. 已知，则的值为（）A B C D5.都是锐角，且，，则的值是（）A B C D6. 且则cos2x的值是（）A B C D7.在中，的取值域范围是 ( )A B C D8. 已知等腰三角形顶角的余弦值等于,则这个三角形底角的正弦值为（）A B C D9.要得到函数的图像，只需将的图像（）A、向右平移个单位B、向右平移个单位C、向左平移个单位D、向左平移个单位10. 函数的图像的一条对称轴方程是（）A、 B、 C、 D、11.若是一个三角形的最小内角，则函数的值域是( )A B C D12.在中，，则等于 ( )A B C D二、填空题:13.若是方程的两根，且则等于14. .在中，已知tanA ,tanB是方程的两个实根，则15. 已知，则的值为16. 关于函数，下列命题：①若存在，有时，成立；②在区间上是单调递增；③函数的图像关于点成中心对称图像；④将函数的图像向左平移个单位后将与的图像重合．其中正确的命题序号（注：把你认为正确的序号都填上）三、解答题：17. 化简18. 求的值．19. 已知α为第二象限角，且sinα=求的值.20.已知函数，求（1）函数的最小值及此时的的集合。

高一数学三角函数综合试题答案及解析1.如图，已知角α的终边在第二象限，且与单位圆交于点P（m，）．（Ⅰ）求实数m的值；（Ⅱ）求的值．【答案】（Ⅰ） m=﹣；（Ⅱ）.【解析】（Ⅰ）由于该圆是单位圆，=1，又角α的终边在第二象限，所以m＜0，联立，可得到结果m=﹣；（Ⅱ）由m=﹣得sinα=，cosα=﹣，对式子化简，=得将数值代入，化简可得到答案.试题解析：（Ⅰ）根据题意得：=1，且m＜0，解得：m=﹣；（5分）（Ⅱ）∵sinα=，cosα=﹣，∴原式= === ．（10分）【考点】三角函数化简.2.（本小题满分12分）已知．(1)若,求的取值构成的集合．(2)若,求的值．【答案】(1) ;(2)【解析】(1) 先化简函数f(x),再解即可．(2) 由，即，然后代入即可．(1)由已知可得 (3分)因为,即,有 (5分)．所以取值的集合为 (6分)(2)因为, (9分)所以 (12分)【考点】解三角方程；诱导公式，三角函数式的化简．3.已知，（1）若，且∥（），求x的值；（2）若,求实数的取值范围.【答案】(1) (2) .【解析】(1)先将向量化为代数式，即,；（2）由已知先写出，的坐标，再由则有：当时等式不成立；将写成关于的函数，即，再求函数的值域即是的取值范围为（或解）用表示，即，又因为，可解得的取值范围为.试题解析：（1），，,（2），若则有：当时等式不成立；解得：的取值范围为【考点】本题考查向量的坐标运算；向量共线的；利用三角函数的有界性求参数.4.函数y=++的值域是（）A．{1}B．{1，3}C．{-1}D．{-1，3}【答案】D【解析】由题意知角X的终边不在坐标轴上。

当X为第一象限角时，当X为第二象限角时，当X为第三象限角时，当X为第四象限角时。

所以或【考点】三角函数正负符号问题5.已知向量m＝(sinA，cosA)，n＝(，－1)，m·n＝1，且A为锐角．(1)求角A的大小；(2)求函数f(x)＝cos2x＋4cosAsinx(x∈R)的值域．【答案】(1)A＝.(2)函数f(x)的值域是.【解析】(1)由题意得m·n＝sinA－cosA＝1，2sin＝1，sin＝，由A为锐角得，A－＝，∴A＝.(2)由(1)知cosA＝，所以f(x)＝cos2x＋2sinx＝1－2sin2x＋2sinx＝－22＋.因为x∈R，所以sinx∈[－1,1]，因此，当sinx＝时，f(x)有最大值，当sinx＝－1时，f(x)有最小值－3，所以所求函数f(x)的值域是.【考点】平面向量的坐标运算，和差倍半的三角函数，三角函数的图象和性质，二次函数的图象和性质。

高中数学三角函数专项练习(含答案)一、填空题1．如图，在棱长均为23的正四面体ABCD 中，M 为AC 中点，E 为AB 中点，P 是DM 上的动点，Q 是平面ECD 上的动点，则AP PQ +的最小值是______.2．在ABC 中，7AB =，23BC =，1cos 7BAC ∠=，动点D 在ABC 所在平面内且2π3BDC ∠=．给出下列三个结论：①BCD △的面积有最大值，且最大值为3；②线段AD 的长度只有最小值，无最大值，且最小值为1；③动点D 的轨迹的长度为8π3．其中正确结论的序号为______．3．如图，某城市准备在由ABC 和以C 为直角顶点的等腰直角三角形ACD 区域内修建公园，其中BD 是一条观赏道路，已知1AB =，3BC =，则观赏道路BD 长度的最大值为______．4．已知函数23tan ,,,2332()63233,,33x x f x x ππππππ⎧⎛⎤⎛⎫∈-⋃ ⎪⎪⎥⎝⎦⎝⎭⎪=⎨⎛⎤⎪+∈ ⎥⎪⎝⎦⎩若()f x 在区间D 上的最大值存在，记该最大值为{}K D ，则满足等式{[0,)}3{[,2]}K a K a a =⋅的实数a 的取值集合是___________. 5．在长方体1111ABCD A B C D -中，13AB =，5AD =，112AA =，过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内，则在平面α变化的过程中，这两个球的半径之和的最大值为___________.6．在直角坐标系中，ABC 的顶点()cos ,sin A αα，()cos ,sin B ββ，C ⎝，且ABC 的重心G 的坐标为⎝，()cos αβ-=__________. 7．在锐角△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ,若2cos b a a C -=，则ac的取值范围是______．8．在ABC 中，sin 2sin B C =，2BC =.则CA CB ⋅的取值范围为___________.（结果用区间表示）9．在ABC 中，设a ，b ，c 分别为角A ，B ，C 对应的边，记ABC 的面积为S ，且sin 2sin 4sin b B c C a A +=，则2Sa 的最大值为________. 10．已知ABC 为等边三角形，点G 是ABC 的重心．过点G 的直线l 与线段AB 交于点D ，与线段AC 交于点E ．设AD AB λ=，AE AC μ=，则11λμ+=__________；ADE 与ABC 周长之比的取值范围为__________．二、单选题11．在△ABC 中，24CA CB ==，F 为△ABC 的外心，则CF AB ⋅=（ ） A ．-6B ．-8C ．-9D ．-1212．已知函数()()sin cos sin cos 0f x x x x x ωωωωω=++->，则下列结论错误的是（ ）①1ω=时，函数()f x 图象关于π4x =对称；②函数()f x 的最小值为-2；③若函数()f x 在π,04⎡⎤-⎢⎥⎣⎦上单调递增，则(]03ω∈，；④1x ，2x 为两个不相等的实数，若()()124f x f x +=且12x x -的最小值为π，则2ω=. A ．②③B ．②④C ．①③④D ．②③④13．已知点P 是曲线y =α为曲线在点P 处的切线的倾斜角，则α的取值范围是（ ） A ．0,6π⎛⎤ ⎥⎝⎦B ．,62ππ⎡⎫⎪⎢⎣⎭C ．,63ππ⎡⎤⎢⎥⎣⎦D ．0,3π⎛⎤ ⎥⎝⎦14．已知,a b Z ∈，满足)sin 50a b ︒=，则a b +的值为（ ）A ．1B ．2C ．3D ．415．已知点1F ，2F 分别为椭圆()2222:10x yC a b a b+=>>的左、右焦点，点M 在直线:l x a =-上运动，若12F MF ∠的最大值为60︒，则椭圆C 的离心率是（ ）A ．13B ．12C ．32D ．3316．在三棱锥A BCD -中，5,2,2AC AD AB CD BC BD ======，则这个三棱锥的外接球的半径为（ ） A ．2105B ．2103C ．253D ．2517．已知函数()sin os 0(c f x x a x a ωω=+>且0>ω），周期2T π<，()33f π=，且()f x 在6x π=处取得最大值，则ω的最小值为（ ）A ．11B ．12C ．13D ．1418．如图是某市夏季某一天从6时到14时的温度变化曲线，若该曲线近似地满足函数()sin y A x B ωϕ=++，则该市这一天中午12时天气的温度大约是（ ）A ．25C ︒B ．26C ︒ C ．27C ︒D ．28C ︒19．已知函数2()sin f x x x =⋅各项均不相等的数列{}n x 满足||(1,2,3,,)2i x i n π≤=.令*1212()([()()()())]n n F n x x x f x f x f x n N =+++⋅+++∈.给出下列三个命题：（1）存在不少于3项的数列{},n x 使得()0F n =；（2）若数列{}n x 的通项公式为*1()()2n n x n N =-∈，则(2)0F k >对k *∈N 恒成立；（3）若数列{}n x 是等差数列，则()0F n ≥对n *∈N 恒成立，其中真命题的序号是（ ）A ．（1）（2）B ．（1）（3）C ．（2）（3）D ．（1）（2）（3）20．设锐角ABC ∆的三个内角,,A B C 的对边分别为,,a b c 且1c =，2A C =，则ABC ∆周长的取值范围为（ ） A ．(0,22)+B ．(0,33)C ．(22,33)+D ．(22,33]三、解答题21．已知向量()()()3cos ,cos ,sin ,cos 0a x x b x x ωωωωω=-=>，若函数()12f x a b =⋅+的最小正周期为π. （1）求()f x 的解析式；（2）若关于x 的方程22cos 22cos 23301212a f x x f x x a ππ⎡⎤⎡⎤⎛⎫⎛⎫++-+--+= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦在04π⎡⎤⎢⎥⎣⎦，有实数解，求实数a 的取值范围.22．在海岸A 处，发现北偏东45︒方向，距离A 为31-海里的B 处有一艘走私船，在A 处北偏西75︒方向，距离A 为2海里的C 处有一艘缉私艇奉命以103海里/时的速度追截走私船，此时，走私船正以10海里/时的速度从B 处向北偏东30方向逃窜.（1）问C 船与B 船相距多少海里？C 船在B 船的什么方向？ （2）问缉私艇沿什么方向行驶才能最快追上走私船？并求出所需时间. 23．已知函数()cos f x x x =，()sin g x x =，0,2x π⎡⎤∈⎢⎥⎣⎦.（1）求证:()()f x g x ≤；（2）若()ax g x bx <<在0,2π⎛⎫⎪⎝⎭上恒成立，求a 的最大值与b 的最小值.24．已知函数2211()cos sin cos sin 22f x x x x x =+-.（1）求()f x 的单调递增区间；（2）求()f x 在区间,82ππ⎡⎤-⎢⎥⎣⎦的最大值和最小值.25．已知函数2()232sin cos ()f x x x x a a R =-++∈，且(0)3f = （1）求a 的值；（2）若()f x ω在[0,]π上有且只有一个零点，0>ω，求ω的取值范围. 26．设函数()f x a b =⋅，其中向量(2cos ,1)a x =，(cos 32)=+b x x m ； 求：（1）函数的最小正周期和单调递增区间；（2）当0,2x π⎡⎤∈⎢⎥⎣⎦时，求实数m 的值，使函数()f x 的值域恰为17,22⎡⎤⎢⎥⎣⎦.27．已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的最大值是2，函数()f x 的图象的一条对称轴是3x π=，且与该对称轴相邻的一个对称中心是7,012π⎛⎫⎪⎝⎭. （1）求()f x 的解析式；（2）已知DBC △是锐角三角形，向量,,,2124233B B m f f n f f B ππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+=++ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，且3,sin 5m n C ⊥=，求cos D . 28．已知函数()2sin cos cos2x x x x f =+. （1）求()f x 的最小正周期及单调递减区间； （2）求()f x 在区间0,4π⎡⎤⎢⎥⎣⎦上的最大值和最小值.29．已知ABC ∆的外接圆．．．，内角A ，B ，C 的对边分别为a ，b ，c ，又向量()sin sin ,m A C b a =--，sin sin n A C B ⎛⎫=+ ⎪ ⎪⎝⎭，且m n ⊥. （1）求角C ；（2）求三角形ABC 的面积S 的最大值并求此时ABC ∆的周长.30．已知两个不共线的向量a ，b 满足a =，(cos ,sin )b =θθ，R θ∈． （1）若//a b ，求角θ的值；（2）若2a b -与7a b -垂直，求||a b ＋的值；（3）当0,2π⎡⎤θ∈⎢⎥⎣⎦时，存在两个不同的θ使得||||a ma =成立，求正数m 的取值范围.【参考答案】一、填空题12．①③31 4．47,912ππ⎧⎫⎨⎬⎩⎭5．165386．237．⎝⎭8．8,83⎛⎫ ⎪⎝⎭910． 3 21,32⎡⎢⎣⎦二、单选题 11．A 12．B 13．A 14．B 15．C 16．A 17．C 18．C 19．D 20．C 三、解答题21．（1）()sin(2)6f x x π=-；（2）1a 或732a +-.【解析】（1）根据向量数量积的坐标运算及三角公式，化简可得()f x 的解析式； （2）先化简()sin 212f x x π+=，利用换元法，设sin 2cos2t x x =-，把目标方程转化为关于t 的方程，分离参数后进行求解.【详解】 （1）因为()()()3cos ,cos ,sin ,cos 0a x x b x x ωωωωω=-=>，所以()2111cos 213sin cos 22222x f x a b x x x x ωωωωω+=⋅+=-+=-+ sin(2)6x πω=-.因为()f x 的最小正周期为π，所以22ππω=，即1ω=，所以()sin(2)6f x x π=-. （2）由（1）可知()sin 212f x x π+=.因为2(sin 2cos 2)x x +22sin 22sin 2cos 2cos 2x x x x =++12sin 2cos2x x =+， 222(sin 2cos 2)sin 22sin 2cos 2cos 2x x x x x x -=-+12sin 2cos2x x =-，所以22(sin 2cos2)12sin 2cos211(sin 2cos2)x x x x x x ⎡⎤+=+=+--⎣⎦.令sin 2cos2t x x =-，则22(sin 2cos 2)2x x t +=-，则方程22cos 22cos 23301212a fx x f x x a ππ⎡⎤⎡⎤⎛⎫⎛⎫++-+--+= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦可化为()2222330a t t a ---+=，即22230at t a +--=.因为0,4x π⎡⎤∈⎢⎥⎣⎦，所以2,444x πππ⎡⎤-∈-⎢⎥⎣⎦，所以sin 2cos 22[1,1]4t x x x π⎛⎫=-=-∈- ⎪⎝⎭.所以由题意可知，方程22230at t a +--=在[1,1]t ∈-时有解； 令2()223g t at t a =+--，当0a =时，()23g t t =-，由()0g t =得32t =（舍）；当0a ≠时，则22230at t a +--=可化为212132t a t-=-，令22132t y t-=-，[1,1]t ∈-，设32u t =-，则1(3),[1,5]2t u u =-∈，2212(3)11(3)222u u y u u⎡⎤--⎢⎥--⎣⎦==⨯1762u u ⎛⎫=+- ⎪⎝⎭，因为7u u+≥u = 当1u =时，7u u+取到最大值8，所以3,1]y ∈，所以13,1]a ∈，解得1a 或732a +-. 所以实数a 的取值范围是1a 或732a +- 【点睛】本题主要考查三角函数的性质，利用向量的坐标运算及三角公式把目标函数化简为最简形式，是这类问题常用求解方向，方程有解问题通常利用分离参数法来解决，侧重考查数学运算的核心素养.22．（1）=BC C 船在B 船的正西方向；（2）缉私艇沿东偏北30才能最快追上走私船． 【解析】（1）在ABC 中根据余弦定理计算BC ，再利用正弦定理计算ABC ∠即可得出方位； （2）在BCD △中，利用正弦定理计算BCD ∠，再计算BD 得出追击时间． 【详解】解：（1）由题意可知1=AB ，2AC =，120BAC ∠=︒， 在ABC 中，由余弦定理得：2222cos1206BC AB AC AB AC =+-︒=， BC ∴，由正弦定理得：sin sin AC BCABC BAC=∠∠，即2sin ABC∠解得：sin ABC ∠=， 45ABC ∴∠=︒，C ∴船在B 船的正西方向．（2）由（1）知=BC 120DBC ∠=︒， 设t 小时后缉私艇在D 处追上走私船，则10BD t =，CD =，在BCD △10sin tBCD∠， 解得：1sin 2BCD ∠=， 30BCD ∴∠=︒，BCD ∴△是等腰三角形，10t ∴=，即t =∴缉私艇沿东偏北30【点睛】本题考查了正余弦定理解三角形，以及解三角形的实际应用，考查转化能力和运算能力，属于中档题．23．（1）答案见解析；（2）a 最大值为2π,b 的最小值为1. 【解析】 【分析】（1）构建函数()cos sin h x x x x =-，通过导数研究函数()h x 在0,2π⎡⎤⎢⎥⎣⎦单调性并计算最值，可得结果.（2）构造函数()sin M x x cx =-，通过分类讨论的方法，0c ≤，1c ≥和01c <<，利用导数判断函数()M x 的单调性，并计算最值比较，可得结果. 【详解】（1）由()()()cos sin h x f x g x x x x =-=- 所以()'cos sin cos sin h x x x x x x x =--=-. 又0,2x π⎡⎤∈⎢⎥⎣⎦，()'sin 0h x x x =-≤,所以()h x 在区间上0,2π⎡⎤⎢⎥⎣⎦单调递减.从而()()00h x h ≤=,()()f x g x ≤. （2）当0x >时,“()ax g x <”等价于“sin 0x ax ->” “()g x bx <”等价于“sin 0x bx -<”.令()sin M x x cx =-,则()'cos M x x c =-,当0c ≤时,()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.当1c ≥时,因为对任意0,2x π⎛⎫∈ ⎪⎝⎭,()'cos 0M x x c =-<,所以()M x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减.从而()()00M x M <=对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.当01c <<时,存在唯一的00,2x π⎛⎫∈ ⎪⎝⎭，使得()'cos 0M x x c =-=.()M x 与()'M x 在区间0,2π⎛⎫⎪⎝⎭上的情况如下:因为M x 在区间00,x 上是增函数, 所以()()000M x M >=.进一步,“()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立”当且仅当1022M c ππ⎛⎫=-≥ ⎪⎝⎭,即20c π<≤,综上所述： 当且仅当2c π≤时,()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立; 当且仅当1c ≥时,()0M x <对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.所以，若()ax g x bx <<对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立,则a 最大值为2π,b 的最小值为1. 【点睛】本题考查导数的综合应用，关键在于构建函数，化繁为简，同时掌握分类讨论的思想，考验分析问题的能力以及计算能力，属中档题.24．（1）3,88k k ππππ⎡⎤-++⎢⎥⎣⎦，()k Z ∈；（2）()max f x =，()min 12f x =- 【解析】 【分析】（1）直接利用三角函数的恒等变换，把三角函数变形成正弦型函数．进一步求出函数的单调区间．（2）直接利用三角函数的定义域求出函数的最值． 【详解】 解：（1）2211()cos sin cos sin 22f x x x x x =+-11()cos 2sin 222f x x x ∴=+()24f x x π⎛⎫∴=+ ⎪⎝⎭ 令222242k x k πππππ-+≤+≤+，()k Z ∈解得388k x k ππππ-+≤≤+，()k Z ∈ 即函数的单调递增区间为3,88k k ππππ⎡⎤-++⎢⎥⎣⎦，()k Z ∈（2）由（1）知n ()224f x x π⎛⎫=+ ⎪⎝⎭ ,82x ππ⎡⎤∈-⎢⎥⎣⎦ 520,44x ππ⎡⎤∴+∈⎢⎥⎣⎦所以当242x ππ+=，即8x π=时，()max f x =当5244x ππ+=，即2x π=时，()min 12f x =- 【点睛】本题考查的知识要点：三角函数关系式的恒等变换，正弦型函数的单调性的应用，利用函数的定义域求三角函数的值域．属于基础型．25．（1）a =（2）15,36⎡⎫⎪⎢⎣⎭【解析】【分析】（1）利用降次公式、辅助角公式化简()f x 表达式，利用(0)f =a 的值.（2）令()0f x ω=，结合x 的取值范围以及三角函数的零点列不等式，解不等式求得ω的取值范围.【详解】（1）2()2sin cos f x x x x a =-++sin 2x x a =+2sin 23x a π⎛⎫=++- ⎪⎝⎭(0)f =(0)2sin 3f a π∴=+=即a =（2）令()0f x ω=，则sin 203x πω⎛⎫+= ⎪⎝⎭， [0,]x π∈，2,2333πππωπω⎡⎤∴+∈+⎢⎥⎣⎦， ()f x 在[0,]π上有且只有一个零点， 223πππωπ∴+<，1536ω∴<， ω∴的取值范围为15,36⎡⎫⎪⎢⎣⎭. 【点睛】本小题主要考查三角恒等变换，考查三角函数零点问题，考查化归与转化的数学思想方法，属于基础题. 26．（1）T π=，,36k k ππππ⎡⎤-+⎢⎥⎣⎦()k z ∈；（2）12. 【解析】【分析】（1）由数量积的坐标运算可得2()2cos 2f x x x m =+，然后将其化为基本型，即可求出周期和单调递增区间（2）由02x π≤≤，可得()3m f x m ≤≤+，和题目条件对应即可求出m【详解】（1）∵2()2cos 2f x a b x x m =⋅=+1cos22x x m =++2sin 216x m π⎛⎫=+++ ⎪⎝⎭， ∴函数()f x 的最小正周期T π=， 可知，当222262k x k πππππ-≤+≤+，k Z ∈时，函数单调递增， 解得：36k x k ππππ-≤≤+， 故函数的单调递增区间为,36k k ππππ⎡⎤-+⎢⎥⎣⎦()k z ∈. （2）∵02x π≤≤， ∴72666x πππ≤+≤， ∴1sin 2126x π⎛⎫-≤+≤ ⎪⎝⎭， ∴()3m f x m ≤≤+， 又17()22f x ≤≤， 故12m =. 【点睛】本题考查的是三角函数的图象及其性质，解决这类问题时首先应把函数化成三角函数基本型.27．（1）()2sin 26f x x π⎛⎫=- ⎪⎝⎭；（2 【解析】（1）根据函数的最值、周期、对称轴待定系数即可求解；（2）由（1）所求，可化简向量坐标，根据向量垂直得到角B ，再利用()cos cosD A B =-+求解.【详解】（1）设()f x 的最小正周期为T ， 依题意得71234T ππ-=，∴T π=，∴22πωπ==. ∵()f x 图象的一条对称轴是3x π=，∴2,32k k Z ππϕπ+=+∈， ∴,6k k Z πϕπ=-+∈.∵||2ϕπ<，∴6πϕ=-. 又∵()f x 的最大值是2，∴2A =， 从而()2sin 26f x x π⎛⎫=- ⎪⎝⎭. （2）∵()(),2sin ,3,2cos ,2cos 2m n m B n B B ⊥==，∴4sin cos 22sin 22m n B B B B B ⋅=⋅+=+4sin 203B π⎛⎫=+= ⎪⎝⎭ ∴2,3B k k Z ππ+=∈，∴:,62k B k Z ππ=-+∈， 又∵B 是锐角，∴3B π=. ∵3sin 5C =，∴4cos 5C =，∴cos cos()(cos cos sin sin )D B C B C B C =-+=--=.即cosD =. 【点睛】 本题考查三角函数解析式的求解，涉及向量垂直的转换，余弦函数的和角公式.属综合基础题.28．（1）最小正周期π；单调递减区间是5,88k k ππππ⎡⎤++⎢⎥⎣⎦，k Z ∈（2）最大值和最小值和1.【解析】（1）利用二倍角的正弦公式的逆用公式以及两角和的正弦公式的逆用公式化简得()24f x x π⎛⎫+ ⎪⎝⎭，再根据周期公式可得周期，利用正弦函数的递减区间可得()f x 的递减区间；（2）利用正弦函数的性质可求得结果.【详解】（1）因为()sin 2cos 224x f x x x π⎛⎫=+=+ ⎪⎝⎭. 所以()f x 的最小正周期22T ππ==. 由3222242k x k πππππ+≤+≤+，得588k x k ππππ+≤≤+， 所以()f x 的单调递减区间是5,88k k ππππ⎡⎤++⎢⎥⎣⎦，k Z ∈. （2）因为0,4x π⎡⎤∈⎢⎥⎣⎦，所以32,444x πππ⎡⎤+∈⎢⎥⎣⎦.所以当242x ππ+=，即8x π= 当244x ππ+=或34π，即0x =或4x π=时，函数取得最小值1.所以()f x 在区间0,4⎡⎤⎢⎥⎣⎦π和1.【点睛】本题考查了二倍角的正弦公式，考查了两角和的正弦公式，考查了正弦型函数的周期公式，考查了求三角函数的单调区间和最值，属于基础题.29．(1) 3C π=. (2) max S = 【解析】【分析】（1）由0m n m n ⊥⇒⋅=，利用坐标表示化简，结合余弦定理求角C （2）利用（1）中222c a b ab =+-，应用正弦定理和基本不等式，即可求出面积的最大值，此时三角形为正三角即可求周长.【详解】（1）∵0m n m n ⊥⇒⋅=，∴()())sin sin sin sin sin 0A C A C b a B -+-=，且2R =()2202242a c b b a R R R ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭， 化简得：222c a b ab =+-.由余弦定理：2222cos c a b ab C =+-，∴12cos 1cos 2C C =⇒=， ∵0C π<<，∴3C π=.（2）∵()22222sin 6a b ab c R C +-===，∴2262a b ab ab ab ab =+-≥-=（当且仅当a b =时取“=”）1sin 2S ab C ==≤所以，max S =ABC ∆为正三角形，此时三角形的周长为 【点睛】本题主要考查了利用数量积判断两个平面向量的垂直关系，正弦定理，余弦定理，基本不等式，属于中档题.30．（1）,3k k Z πθθπ⎧⎫=+∈⎨⎬⎩⎭｜（23）⎣⎭【解析】【分析】（1）由题得tan θ=2）先求出1a b ⋅=，再利用向量的模的公式求出||7a b +=；（3）等价于2476m πθ⎛⎫+=- ⎪⎝⎭在0,2π⎡⎤θ∈⎢⎥⎣⎦有两解，结合三角函数分析得解.【详解】（1）由题得sin 0,tan θθθ=∴=所以角θ的集合为,3k k Z πθθπ⎧⎫=+∈⎨⎬⎩⎭｜ . （2）由条件知2a =， 1b =，又2a b -与7a b -垂直，所以()()2781570a b a b a b -⋅-=-⋅+=，所以1a b ⋅=.所以222||||2||4217a b a a b b +=+⋅+=++=，故||7a b +=.（3）由3a b ma +=，得223a b ma +=， 即2222233a a b b m a +⋅+=，即2434b m +⋅+=，)27cos 4m θθ+=，所以2476m πθ⎛⎫+=- ⎪⎝⎭. 由0,2π⎡⎤θ∈⎢⎥⎣⎦得2,663πππθ⎡⎤+∈⎢⎥⎣⎦，又θ要有两解，结合三角函数图象可得，2647m ≤-<2134m ≤<又因为0m >m ≤<即m 的范围⎣⎭. 【点睛】本题主要考查向量平行垂直的坐标表示，考查向量的模的计算，考查三角函数图像和性质的综合应用，意在考查学生对这些知识的理解掌握水平和分析推理能力，属于中档题.。

新高考数学创新好题1情境创新之知识综合新高考数学创新好题主题一情境创新之知识综合学科知识综合1.[平面向量与三角函数综合]已知单位向量a,b满足a·b=0,若向量c=a+b,则sin=()A.B.C.D.2.[三角函数与数列综合]已知数列{an}的通项公式是an=f(),其中f(x)=sin(ωx+φ)(ω>0,|φ|.-1B.-C.1D.3.[逻辑联结词与二项式、正态分布综合]已知命题p:(x2-)n的展开式中,仅有第7项的二项式系数最大,则展开式中的常数项为495.命题q:随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.7,则P(0给出四个命题:①p∧q,②p∨q,③p∧(?q),④(?p)∨q,其中真命题是()A.①③B.①④C.②③D.②④4.[数列与平面向量综合]设{an}是首项为-10,公差为2的等差数列,{bn}是首项为-,公差为的等差数列.O为原点,向量=(-1,1),=(1,1),点Pn满足=an+bn(n∈N).若存在点Pk(k∈N)位于第一象限,则k=()A.5或6B.6C.7D.6或75.[导数与三角函数综合]已知函数f(x)的定义域为R,f()=-,对任意的x∈R,满足f''(x)>4x.当α∈[0,2π]时,不等式f(sinα)+cos2α>0的解集为()A.(,)B.(,)C.(,)D.(,)6.[函数与数列综合]定义在[0,+∞)上的函数f(x)满足:当0≤x<2时,f(x)=2x-x2;当x≥2时,f(x)=3f(x-2).若函数f(x)的极大值点从小到大依次记为a1,a2,…,an,…,并记相应的极大值为b1,b2,…,bn,…,则a1b1+a2b2+…+a20b20的值为()A.19×320+1B.19×319+1C.20×319+1D.20×320+17.[椭圆与平面向量综合]已知椭圆C:=1,F1,F2分别是其左、右焦点,若对椭圆C上的任意一点P,·>0恒成立,则实数m的取值范围为()A.(-3,0)∪(0,3)B.[-3,0)∪(0,3]C.(-∞,-3)∪(3,+∞)D.(-∞,-3]∪[3,+∞)8.[抛物线与平面向量综合]已知抛物线C:y2=4x的焦点为F,准线为l,P是l上一点,直线PF与抛物线C交于M,N两点,若=4,则|MN|=()A.B.3C.D.9图1-29.[立体几何与函数综合]如图1-2所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为3的正方形,侧棱AA1=t,P为矩形CDD1C1上及内部的动点,M为BC 的中点,∠APD=∠CPM,三棱锥A1-PCD的体积的最大值记为V(t),则下列关于函数V(t)的结论正确的是()A.V(t)为奇函数B.V(t)在(0,+∞)上单调递增C.V(2)=3D.V(3)=10.[双曲线与解三角形综合]已知双曲线E:=1(a>0,b>0)的左、右顶点分别为A,B,M是E上一点,且△ABM为等腰三角形,其外接圆的半径为a,则双曲线E的离心率为()A.B.+1C.D.+111.[解三角形与平面向量、基本不等式综合] 已知锐角△ABC的内角A,B,C的对边分别为a,b,c.若向量m=(a-b,sinC),n=(c-b,sinA+sinB),m=λn(λ≠0),则tanC的最小值为()A.B.2C.D.12.[直线斜率与三角恒等变换综合]若正方形一条对角线所在直线的斜率为2,则该正方形的两条邻边所在直线的斜率分别为,.?13.[数列与双曲线综合]已知一族双曲线En:x2-y2=(n∈N,n≤2019),设直线x=2与En在第一象限内的交点为An,点An在En的两条渐近线上的射影分别为Bn,Cn,记△AnBnCn的面积为an,则a1+a2+a3+…+a2019=.?跨学科知识综合14.[数学与化学综合]溶液的酸碱度是通过pH来刻画的,已知某溶液的pH等于-lg[H+],其中[H+]表示该溶液中氢离子的浓度,且该溶液中氢离子的浓度为10-6mol/L,则该溶液的pH为()A.4B.5C.6D.715.[数学与物理综合]长江流域内某地南北两岸平行,如图1-3所示,已知游船在静水中的航行速度v1的大小|v1|=10km/h,水流的速度v2的大小|v2|=4km/h,设v1和v2所成的角为θ(0行到正北方向上位于北岸的码头B处,则cosθ等于()图1-3A.-B.-C.-D.-16.[数学与物理综合]体育锻炼是青少年学习生活中非常重要的组成部分.某学生做引体向上运动,处于图1-4所示的平衡状态时,两只胳膊的夹角为,每只胳膊的拉力大小均为400 N,则该学生的体重(单位:kg)约为()图1-4(参考数据:重力加速度大小取g=10m/s2,≈1.732)A.63kgB.69kgC.75kgD.81kg17.[2020山东,4,5分][数学与地理综合]日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A 处的水平面所成角为()A.20°B.40°C.50°D.90°图1-518.[数学与体育综合]台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从反射定律.如图1-5,有一张长方形球台ABCD,AB=2AD,现从角落A沿角α的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则tanα的值为()A.B.C.或D.19.[2020全国卷Ⅱ,12,5分][理][数学与通信技术综合]0-1周期序列在通信技术中有着重要应用.若序列a1a2…an…满足ai∈{0,1}(i=1,2,…),且存在正整数m,使得ai+m=ai(i=1,2,…)成立,则称其为0-1周期序列,并称满足ai+m=ai(i=1,2,…)的最小正整数m为这个序列的周期.对于周期为m的0-1序列a1a2…an…,C(k)=aiai+k(k=1,2,…,m-1)是描述其性质的重要指标.下列周期为5的0-1序列中,满足C(k)≤(k=1,2,3,4)的序列是()A.11010…B.11011…C.10001…D.11001…20.[数学与化学综合]稠环芳烃类化合物中有不少致癌物质,比如学生钟爱的快餐油炸食品中会产生苯并芘,它可看作是由一个苯环和一个芘分子结合而成的稠环芳烃类化合物,长期食用会致癌.下面是一组稠环芳烃的结构简式和分子式:名称萘蒽并四苯…并n苯结构简式……分子式C10H8C14H10C18H12……由此推断并十苯的分子式为.?答案主题一情境创新之知识综合1.B解法一由已知知|a|=|b|=1,|c|=|a+b|==3,则cos=,因为∈(0,π),所以sin=.解法二由题可设a=(1,0),b=(0,1),则c=(,),cos=,因为∈(0,π),所以sin=,故选B.2.B由题图可得(T为f(x)的最小正周期),则T=π,ω==2.将(,-1)代入f(x)=sin(2x+φ)中,可得+φ=2kπ+,k∈Z,则φ=2kπ+,k∈Z.又|φ|n=f()=sin,则{an}为周期为6的数列,因为a1=,a2=0,a3=-,a4=-,a5=0,a6=,所以S2020=336S6+(a1+a2+a3+a4)=0-=-.故选B.3.C对于命题p,(x2-)n的展开式中,仅有第7项的二项式系数最大,即最大,所以n=12.展开式的通项公式为Tr+1=··=(-1)r··x24-3r,令24-3r=0,得r=8,故展开式中的常数项为(-1)8·=495,所以p为真命题.对于命题q,根据正态分布的对称性可知P(0假命题.所以p∧q,(?p)∨q为假命题,p∨q,p∧(?q)为真命题,即②③为真命题.故选C.4.D由已知得an=2n-12,bn=-1.因为=an+bn=(2n-12)·(-1,1)+(-1)·(1,1)=(11-,-13),所以点Pn的坐标为(11-,-13),可得Pk(11-,-13).若存在点Pk(k∈N)位于第一象限,则解得造函数g(x)=f(x)-2x2+1,则g''(x)=f''(x)-4x>0,所以函数g(x)在R上为增函数.因为f()=-,所以g()=f()-2×()2+1=0.又f(sinα)+cos2α>0,所以g(sinα)=f(sinα)-2sin2α+1=f(sinα)+cos2α>0=g(),所以sinα>.因为0≤α≤2π,所以α>0的解集为(,).故选D.6.A当0≤x<2时,f(x)=2x-x2=1-(x-1)2,可得f(x)的极大值点a1=1,极大值b1=1,当2≤x<4,即0≤x-2<2时,可得f(x)=3f(x-2)=3[1-(x-3)2],可得a2=3,b2=3,当4≤x<6,即0≤x-4<2时,可得f(x)=9f(x-4)=9[1-(x-5)2],可得a3=5,b3=9,…,即有a20=39,b20=319.记S20=a1b1+a2b2+…+a20b20,则S20=1×1+3×3+5×9+…+39×319①,3S20=1×3+3×9+5×27+…+39×320②,①-②得-2S20=1+2×(3+9+27+…+319)-39×320=1+2×-39×320,化简可得S20=19×320+1,故选A.7.C当点P为短轴上的顶点时,∠F1PF2最大,要使·>0恒成立,则∠F1PF2为锐角,即∠F1PO<45°(O为坐标原点),即tan∠F1PO=<1,所以c29,所以93或m,M(xM,yM),N(xN,yN),因为=4,所以(2,-t)=4(1-xM,-yM),所以解得因为MN为过抛物线焦点的弦,由焦点弦的常用结论(详见主书P215【规律总结】)可得xM·xN==1,所以xN=2,所以xM+xN=.由抛物线的定义,得|MN|=xM+xN+p=+2=,故选C.解法二设准线l与x轴交于点E,点N在第一象限,如图D1-1所示,作MM''⊥l于点M'',NN''⊥l于点N'',则由抛物线的定义知,|MM''|=|MF|,|NN''|=|NF|.因为=4,所以|PF|∶|PM|=4∶3.因为△PFE∽△PMM'',所以,即,解得|MF|=,所以|PF|=6.又△PFE∽△PNN'',所以,即,解得|NF|=3,所以|MN|=|MF|+|NF|=+3=,故选 C.9.D由题意知,AD⊥PD,MC⊥PC.因为∠APD=∠CPM,所以Rt△PDA∽Rt△PCM.又M为BC的中点,所以=2,即PD=2PC,即PD2=4PC2.在平面DCC1D1中,以DC的中点为坐标原点,以DC所在直线为x轴,DC的垂直平分线为y轴,以的方向为x轴的正方向,的方向为y轴的正方向建立平面直角坐标系,则D(-,0),C(,0).设P(x'',y'')(-≤x''≤,0≤y''≤t),则(x''+)2+(y'')2=4(x''-)2+4(y'')2,整理得(y'')2=-(x'')2+5x''-,易知当x''=时,y''取得最大值.若0,则(S△PCD)max=.又A1到平面PCD的距离为3,所以V(t)=所以V(t)为非奇非偶函数,故A错误;函数V(t)在(0,+∞)上不是单调函数,故B错误;V(2)=,故C错误;V(3)=,故D正确.故选D.10.C解法一不妨设M在第一象限,M(x0,y0),因为△ABM是等腰三角形,所以结合图形可知,只能|AB|=|BM|=2a.令∠MAB=θ,则∠AMB=θ,∠ABM=π-2θ,∠MBx=2θ,在△MAB中,由正弦定理可得=2×a,所以sinθ=,则cos2θ=1-2sin2θ=,sin2θ=,则x0=a+2acos2θ=,y0=2asin2θ=,即M(,).又点M在双曲线上,所以·=1,解得=2,则e2=1+=3,则e=,故选C.解法二不妨设M在第一象限,因为△ABM是等腰三角形,所以结合图形可知,只能|AB|=|BM|=2a.令∠MAB=θ,则∠AMB=θ,∠ABM=π-2θ,∠MBx=2θ,由正弦定理可得=2×a,所以sinθ=,则cosθ=,tanθ=,即kMA=,cos2θ=1-2sin2θ=,则sin2θ=,tan2θ==2,即kMB=2,根据kMA·kMB=2=,得e2=1+=3,则e=,故选C.11.C∵m=λn(λ≠0),∴m∥n,∴(a-b)(sinA+sinB)=sinC(c-b),由正弦定理得(a-b)(a+b)=c(c-b),整理得a2=b2+c2-bc,由余弦定理得cosA=.∵A∈(0,),∴A=,又C∈(0,),∴,∴tanC=tanC.∵△ABC是锐角三角形,且A=,∴解得,∴tanC=tanC≥+2,当且仅当tanC,即tanC=2时等号成立,故tanC的最小值为,选C.图D1-212.-3如图D1-2,以A为原点建系,AC的斜率为2,设AB的倾斜角为θ,则AC的倾斜角为θ+,则tan(θ+)=2.kAB=tanθ=tan(θ+)=,则kAD=-=-3.所以正方形的两条邻边所在直线的斜率分别为和-3.13.设An(x0,y0),可得.双曲线En:x2-y2=(n∈N,n≤2019)的渐近线方程为x-y=0,x+y=0.已知点An在En的两条渐近线上的射影分别为Bn,Cn,不妨设Bn在第一象限内,可得|AnBn|=,|AnCn|=,易知双曲线En的两条渐近线互相垂直,可得AnBn⊥AnCn,则△AnBnCn的面积an=|AnBn|·|AnCn|=··,则a1+a2+a3+…+a2019=×2019×2020=.14.C由题意可得,该溶液的pH为-lg10-6=6.故选C.15.B设游船的实际速度为v,v1与河流南岸上游的夹角为α,v1=,v2=.以AD,AC为邻边作平行四边形如图D1-3所示,要使得游船正好航行到B处,则|v1|cosα=|v2|,即cosα=.又θ=π-α,所以cosθ=cos(π-α)=-cosα=-,故选B.16.B作出示意图,如图D1-4所示,设图中重力为G,两只胳膊的拉力分别为F1,F2,F1与F2的合力为F'',则|G|=|F''|.由余弦定理得|F''|2=4002+4002-2×400×400×cos=3×4002(N2),解得|F''|=400N.所以|G|=400N.所以该学生的体重约为≈69(kg).故选B.图D1-517.B过球心O,点A以及晷针的轴截面如图D1-5所示,其中CD为晷面,GF为晷针所在直线,EF为点A处的水平面,GF⊥CD,CD∥OB,∠AOB=40°,∠OAE=∠OAF=90°,所以∠GFA=∠CAO=∠AOB=40°.故选B.18.C由题意知,可分为两种,且仅有两种情况.第一种情况,球碰撞CD与AB边内沿后进入角落C的球袋中,如图D1-6所示.根据台球碰撞障碍物后也遵从反射定律知,AE=EF=FC,于是根据图形的对称性知E,F分别为CD与AB的三等分点,则DE=DC=AD,所以tanα=tan∠AED=.第二种情况,球碰撞BC与AD边内沿后进入角落C的球袋中,如图D1-7所示.同理,由第一种情况的解法知M,N分别为BC,AD的三等分点,所以BM=BC=AB=AB,所以tanα=.综上可知,选C.图D1-6图D1-719.C对于A,因为C(1)=,C(2)=,不满足C(k)≤,故A不正确;对于B,因为C(1)=,不满足C(k)≤,故B不正确;对于C,因为C(1)=,C(2)==0,C(3)==0,C(4)=,满足C(k)≤,故C正确;对于D,因为C(1)=,不满足C(k)≤,故D不正确.综上所述,故选C.20.C42H24因为表格中所给的稠环芳烃的分子式中C的下标分别是10,14,18,…,H的下标分别是8,10,12,…,所以表格中所给的稠环芳烃的分子式中C的下标构成等差数列,设为{am},则首项a1=10,公差为4,所以其通项公式为am=10+(m-1)·4=4m+6,表格中所给的稠环芳烃的分子式中H的下标构成等差数列,设为{bm},首项b1=8,公差为2,所以其通项公式为bm=8+(m-1)·2=2m+6.易知m=n-1,所以并n苯的分子式为C4n+2H2n+4(n≥4,n∈N),所以并十苯的分子式为C42H24.第8页共8页。