直线平面简单几何体9.12

第九章直线平面简单几何体教材分析一、教学内容与课时安排本章11小节，教学时间约需36课时，具体分配如下（仅供参考）：9．1平面的基本性质约3课时9．2空间直线约5课时9．3直线与平面平行的判定与性质约3课时9．4直线和平面垂直的判定与性质约4课时9．5两个平面平行的判定与性质约3课时9．6两个平面垂直的判定与性质约3课时9．7棱柱约4课时9．8棱锥约2课时研究性课题：多面体欧拉定理的发现约2课时9．9球约4课时小结与复习约3课时二、教学内容考试内容：平面及其基本性质.平面图形直观图的画法.平行直线.对应边分别平行的角.异面直线所成的角.异面直线的公垂线.异面直线的距离.直线和平面平行的判定与性质.直线和平面垂直的判定与性质.点到平面的距离.斜线在平面上的射影.直线和平面所成的角.三垂线定理及其逆定理.平行平面的判定与性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定与性质.多面体.正多面体.棱柱.棱锥.球.三、考试要求：(1)掌握平面的基本性质，会用斜二测的画法画水平放置的平面图形的直观图.能够画出空间两条直线、直线和平面的各种位置关系的图形.能够根据图形想像它们的位置关系.(2)掌握两条直线平行与垂直的判定定理和性质定理.掌握两条直线所成的角和距离的概念，对于异面直线的距离，只要求会计算已给出公垂线时的距离.(3)掌握直线和平面平行的判定定理和性质定理.掌握直线和平面垂直的判定定理和性质定理.掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念.掌握三垂线定理及其逆定理.(4)掌握两个平面平行的判定定理和性质定理.掌握二面角、二面角的平面角、两个平行平面间的距离的概念.掌握两个平面垂直的判定定理和性质定理.(5)会用反证法证明简单的问题.(6)了解多面体、凸多面体的概念，了解正多面体的概念.(7)了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图.(8)了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图.(9)了解球的概念，掌握球的性质，掌握球的表面积、体积公式.四、立体几何内容和结构的特征一、增添了富有创新意义的新内容教材吸取了以往课程、教材内容改革中一贯采用的“精简、增加、渗透”等成功经验，本着“基础性、全面性、文化性、发掘性、主体性、开放性和实践性”等基本思想，融入了体现现代教学意识的新的教学观和学习观，更新了教材的许多内容。

第九章（A）“直线、平面、简单几何体”简介《全日制普通高级中学教科书（试验修订本·必修）数学》第二册（下）的第九章（A）为《直线、平面、简单几何体》。

这一章是根据《全日制普通高级中学数学教学大纲（实验修订版）》中的“9（A）直线、平面、简单几何体”部分所规定的教学内容和教学目标而编写的。

它在原《立体几何》（必修本）的基础上作了较大的修改，精简了教学内容，减少了教学时间，在体系安排和内容的具体处理方法上也有所改革。

本章教学时间约需39课时，具体分配如下（仅供参考）：一、空间直线和平面9．1平面约3课时9．2空间直线约5课时9．3直线与平面平行的判定和性质约3课时9．4直线与平面垂直的判定和性质约4课时9．5两个平面平行的判定和性质约3课时9．6两个平面垂直的判定和性质约3课时二、简单几何体9．7棱柱约4课时9．8棱锥约4课时9．9研究性课题：多面体欧拉公式的发现约3课时9．10球约4课时小结与复习约3课时一、内容与要求（一）本章主要内容是立体几何的基础知识和解决立体几何问题的基本思想方法本章的具体知识点主要包括：平面及其基本性质，平行直线，对应边分别平行的角，异面直线所成的角，异面直线的公垂线，异面直线的距离，直线和平面平行的判定与性质，直线和平面垂直的判定与性质，点到平面的距离，斜线在平面上的射影，直线和平面所成的角，三垂线定理及其逆定理，两个平面平行的判定与性质，平行平面间的距离，二面角及其平面角，两个平面垂直的判定与性质，棱柱，棱锥，平面图形与简单立体图形直观图的画法，多面体和正多面体，球。

（二）本章在体系编排上分为两大节：第一大节是“空间直线和平面”，第二大节是“简单几何体”1．直线和平面是最基本的几何元素，空间直线和平面的位置关系是立体几何的基础知识。

学好这一部分内容，对于学生在已有的平面图形知识基础上，建立空间观念，实现从平面图形到立体图形的认识飞跃，是非常重要的。

第一大节包括6小节，依次按照平面、空间直线、直线和平面平行、直线和平面垂直、两个平面平行、两个平面垂直的顺序编排。

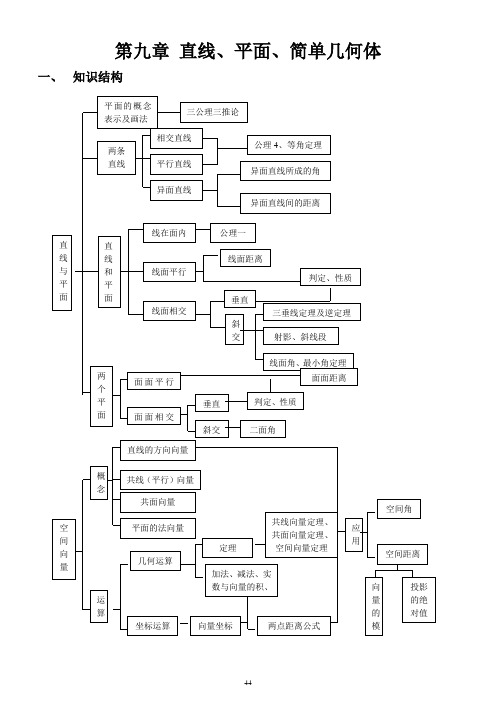
第九章直线、平面、简单几何体一、知识结构二、知识内容1、平面（1）概念（2）平面的表示（3）平面的画法2、平面的基本性质公理一：公理二：公理三：推论1：推论2：推论3：3、水平放置的平面的斜二测画法：4 、两条直线的位置关系（1）异面直线（2）异面直线的画法（3）异面直线的判定（4）两条直线的位置关系：5、直线和平面的位置关系（1）位置关系：（2）平面的垂线、斜线、斜线段的射影6、两个平面的位置关系7、平行的判定8、垂直的判定10、空间的距离七种距离的概念：（1）点点距离（2）点线距离（3）点面距离：（4）平行直线间距离（5）异面直线间的距离：（6）直线和平面间的距离：（7）平行平面间的距离：两种距离的计算11、最小角定理12、向量和基本概念（1）向量（2）向量的表示（3）共线（平行）向量（4）相等向量（5）共面向量13、向量基本定理（1）共线向量定理及推论（2）共面向量定理及推论（3）空间向量基本定理14、空间直角坐标系15、向量的坐标17、多面体、简单多面体、欧拉定理19、球（1）球面、球（2）球的性质（3）球面距离（4）球的表面积、体积（5）纬度、纬线圈（6）经度、经线圈三、基本题型1、证明共面例、下列命题中正确命题的个数是（ A ）⑵ 若点P 不在平面α内，A 、B 、C 三点都在平面α内，则P 、A 、B 、C 四点不在 同一平面内 ⑶ 两两相交的三条直线在同一平面内 ⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2D.32、 证明共点共线例、如图所示，一空间四边形ABCD ，E 、G 分别为BC 、AB 的中点，F 在CD 上，H 在AD 上，且有DF ∶FC =2∶3，DH ∶HA =2∶3，求证：EF 、GH 、BD 交于一点.3、 斜二测画法（1） 画水平放置的平面图形：常见的三角形、四边形、五边形、六边形的水平放置的图形要心中有数 （2） 还原水平放置的平面图形例、按照斜二测画法作水平放置的平面图形的直观图，可能改变的是 （ D ） A ．两线段的平行性 B ．平行于x 轴的线段的长度 C ．同方向上两线段的比 D ．角的大小 4、 证明两直线是异面直线及相关问题已知m 、n 为异面直线，⊂m 平面α，⊂n 平面β，l =⋂βα，则l （ B ） A.与m 、n 都相交 B.与m 、n 中至少一条相交 C.与m 、n 都不相交 D.至多与m 、n 中的一条相交 5、 判定直线与平面、平面与平面的基本位置关系 6、 平行的转化证明（1）用线线平行证明线面平行：需要寻找过．已知直线的一平面．．．与已知平面的交线．．（2）用面面平行证明线面平行：先直观寻找过已知直线的平行平面，再寻找相应的直线与已知平面平行 7、 垂直的转化证明线线平行面面平行线线垂直↔线面垂直↔面面垂直例、如图：在四面体ABCD 中，BCD AB 平面⊥，BC=CD ，︒=∠90BCD ，︒=∠30ADB ，E 、F 分别是AC 、AD 的中点。

九.直线、平面、简单几何体1.从一点O 出发的三条射线OA 、OB 、OC .若AOB AOC ∠=∠,则点A 在平面BOC 上的射影在B OC ∠的平分线上；2.立平斜三角余弦公式：(图略)AB 和平面所成的角是1θ,AC 在平面内,AC 和AB 的射影1AB 成2θ,设3BAC θ∠=,则123cos cos cos θθθ=；3.异面直线所成角的求法：⑴平移法：在异面直线中的一条直线中选择一特殊点,作另一条的平行线.⑵补形法：把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系；4.直线与平面所成角：过斜线上某个特殊点作出平面的垂线段,是产生线面角的关键.5.二面角的求法：⑴定义法；⑵三垂线法；⑶垂面法；⑷射影法：利用面积射影公式cos S S θ=射斜其中θ为平面角的大小，此方法不必在图形中画出平面角； 6.空间距离的求法：⑴两异面直线间的距离，高考要求是给出公垂线,所以一般先利用垂直作出公垂线,然后再进行计算.⑵求点到直线的距离,一般用三垂线定理作出垂线再求解.⑶求点到平面的距离,一是用垂面法,借助面面垂直的性质来作.因此,确定已知面的垂面是关键；二是不作出公垂线,转化为求三棱锥的高,利用等体积法列方程求解.7.用向量方法求空间角和距离：⑴求异面直线所成的角：设a 、b分别为异面直线a 、b 的方向向量,则两异面直线所成的角||||||arccos a b a b α⋅⋅=.⑵求线面角：设l 是斜线l 的方向向量,n 是平面α的法向量,则斜线l 与平面α所成的角||||||arcsin l n l n α⋅⋅=. ⑶求二面角(法一)在α内a l ⊥,在β内b l ⊥ ,其方向如图(略),则二面角l αβ--的平面角||||arccos a ba b α⋅⋅=.(法二)设1n ,2n 是二面角l αβ--的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧,则二面角l αβ--的平面角1212||||arccos n n n n α⋅⋅=.（4)求点面距离：设n 是平面α的法向量,在α内取一点B ,则A 到α的距离|||||cos |||AB n d AB n θ⋅==(即AB 在n 方向上投影的绝对值). 8.正棱锥的各侧面与底面所成的角相等,记为θ,则cos S S θ=侧底. 9.正四面体(设棱长为a )的性质： ①全面积23S a =；②体积3212V a =；③对棱间的距离22d a =；④相邻面所成二面角13arccos α=；⑤外接球半径64R a =；⑥内切球半径612r a =；⑦正四面体内任一点到各面距离之和为定值63h a =.10.直角四面体的性质：(直角四面体—三条侧棱两两垂直的四面体).在直角四面体O ABC - 中,,,OA OB OC 两两垂直,令,,OA a OB b OC c ===,则⑴底面三角形ABC 为锐角三角形；⑵直角顶点O 在底面的射影H 为三角形ABC 的垂心；⑶2BOC BHC ABC S S S ∆∆∆=； ⑷2222AOB BOC COA ABC S S S S ∆∆∆∆++=；⑸22221111OHabc=++；⑹外接球半径R=22212a b c R ++=.11.已知长方体的体对角线与过同一顶点的三条棱所成的角分别为,,αβγ因此有22cos cos αβ+2c o s 1γ+=或222sin sin sin 2αβγ++=；若长方体的体对角线与过同一顶点的三侧面所成的角分别为,,αβγ,则有222sin sin sin 1αβγ++=或222cos cos cos 2αβγ++=. 12.正方体和长方体的外接球的直径等与其体对角线长；13.球的体积公式343V R π=,表面积公式24S R π=；掌握球面上两点A 、B 间的距离求法：⑴计算线段AB 的长；⑵计算球心角AOB ∠的弧度数；⑶用弧长公式计算劣弧AB 的长.。

九章 直线、平面、简单的几何体9.1～9.2 平面的基本性质以及平行直线和异面直线一、教学重点和难点：1.认真体会平面是无限延展的，它无大小之分，仅有位置上的区别；2.三个公理及三个推论在运用上的各自分工；3.正确理解异面直线的概念，并能够利用平移法作出异面直线所成的角；4.难点是养成良好的空间作图习惯和思维方法，特别是集合符号的合理利用。

二、知识精讲： 1.平面的概念：(1)平面是一个只描述不定义的基本概念。

具体的例如：桌面、黑板面、平静的水面，我们可 以认识到“平面”是绝对平坦，没有厚度，没有边界无限延展的一个理想的几何图形。

(2)记为：r αβ、、，平面ABCD 或平面AC 。

(3)画多个平面时，一个平面被另一个平面遮住的线段要画成虚线或不画。

(4)图形语言为：2. (1)公理1：图形语言 符号语言：A l B l l A B ααα∈∈⎫⇒⊂⎬∈∈⎭(2)公理2：图形语言 符号语言：p l p l αβαβ∈⇒=∈ 且(3) 公理3：图形语言 符号语言：A 、B 、C 不共线 ⇒存在唯一平面α使得A B C ααα∈⎧⎪∈⎨⎪∈⎩3.推论：（推论2：经过两条相交直线有且只有一个平面） 已知：直线a 、b 且a b P = ． 求证：过a 、b 有且只有一个平面． 证法一：①存在性在直线a 、b 上分别取不同于点P 的点A 、B ，则点A 、B 、P 是不共线的三点（否则与a 、b 是两条相交直线矛盾）． 根据公理3，过A 、B 、P 三点有一个平面α． ,,A a p a AP a ∈∈⊂∴ ，即αα⊂．同理b a ⊂，因此过直线a 、b 有平面α．②唯一性∵经过直线a 、b 的平面一定经过点A 、B 、P ，根据公理3，经过不共线的三点A 、B 、P 的平面只有一个，∴经过a 、b 的平面只有一个． 由①、②，可知经过两条相交直线有且只有一个平面． 推论3：经过两条平行直线有且只有一个平面． 已知：直线a 、b 且a//b ．求证：经过a 、b 有且只有一个平面． 证明：①存在性∵a//b ，由平行线的定义，a 、b 在同一平面内， ∴过直线a 、b 有一个平面α． ②唯一性在直线b 上任取一点B ，则B a ∉（否则与a//b 矛盾），且B 、a 在过a 、b 的平面α内． 又由推论1，过点B 和直线a 的平面只有一个， ∴过直线a 、b 的平面只有一个．由①、②，可知经过两条平行直线的平面有且只有一个． 4.空间两直线的位置关系：(2)两条异面直线所成的角(0,]2πθ∈．5.集合符号的利用：点A 在平面a 内，记作A a ∈，否则A a ∉ 点A 在直线l 上，记作A l ∈，否则A l ∉ 直线l 在平面a 内，记作l α⊂，否则l α⊂ 直线l 1与l 2相交于A 点，记作12l l A = 三、典型范例 1.平面的概念：例1.判断下列说法是否正确？并说明理由：(1)平等四边形是一个平面． (2)任何一个平面图形都是一个平面． (3)在空间图形中，原图中的线都要画成实线，后补画的线都画成虚线． (4)用平行四边形表示的平面，以四边为边界．解：(1)不正确，平面是无限延展的，而平行四边形是有限的，它只是平面的一部分．(2)不正确，平面图形和平面是完全不同的概念，平面图形有的（如角）也可以无限延展，但 不可能向四周无限延展．(3)不正确，空间图形中把被平面遮住的线段画成虚线（无论原先有的还是后来画的辅助线）． (4)不正确，平面是没有边界的． 2.共点、共线、共面问题：例2.四条直线两两相交且任何三条都不交于一点，则这四条直线共面．分析：说明四条直线共面，必须先找到一个平面，再想办法说明这四条直线都在这个平面内． 已知：如图a 、b 、c 、d 两两相交且任何三条不交于一点， 求证：a 、b 、c 、d 共面．证法一：a b A = ，,a b ∴确定一个平面α（推论2）．,C aB b ∈∈ ， ,C B αα∈∈∴CB α⊂∴，即c α⊂（公理1）．同理d α⊂．a b cd ∴、、、共面．点拨：证明直线（或点）共面，一般先由其中的一部分或点确定一个平面，再由公理1，公理3及其推论证明其余的直线或点也在这个平面内．例3.已知:四边形ABCD ，AB//CD ，直线AB 、BC 、CD 、DA 交平面α于E 、G 、F 、H ，求证：E 、F 、G 、H 四点共线．证明：如图9－1－6．∵AB//CD ，∴AB 、CD 确定平面β．∵E 、F 、G 、H 分别在直线AB 、CD 、BC 、AD 上，∴E 、F 、G 、H 都在β内．又∵E 、F 、G 、H 都在α内，αβ、不是同一个平面且有交点，αβ∴、有且只有一条交线l ，即l αβ= ．∴E 、F 、G 、H l ∈，即E 、F 、G 、H 共线．点拨：公里2中两个平面的交线是由这两个平面中所有公共点组成的集合，因此公理2往往用来证明多点共线问题，也常常用来证明像下例中的多线共点问题．例4.如图9－1－7，E 、F 、G 、H 分别是空间四边形ABCD 的边AB 、AD 、BC 、CD 上的点，且直线EF 和GH 交于一点，求证：EF 、BD 、GH 交于一点． 证明：设EF ，GH 交于一点P ，p ∈ 直线EF ，则p ∈平面ABD ． p ∈ 直线GH ，则p ∈平面CBD ．p ∈∴平面ABD 平面CBD=直线BD ．∴EF 、GH 、BD 三线共点P ．例5.如图9－1－8，在棱长为α的正方体1111ABCD A BC D -中，M 、N 分别为111AA D C 、的中点， 过D 、M 、N 的平面a 与正方体的下底面相交于直线l ． (1)画出直线l ；(2)画出a 与正方体的各面的交线； (3)设11l A B P = ，求1PB 的长．解：(1)a 与平面11ADD A 的交线为DM ，DM 与11A D 的交点为Q ，11Q A D ∈则Q ∈平面1111A B C D ，连结QN ，则QN 即为l ．(2)设11l A B P = ，连结MP ，再连结DN ．a 与正方体的四个面相交，交线为 DM 、MP 、PN 、ND ．(3)由M 是1AA 中点得1A 是1QD 中点．图9－1－6图9－1－7图9－1－83.两条异面直线的证明，所成角的问题：例6.已知,a b αββ=⊂ 且,b a A c α=⊂ 且c//a ，求证：b 、c 是异面直线．分析：b 与c 的位置关系只有三种，假设b 、c 不是异面直线即是相交的或平行的，势必会推出已知或事实相矛盾的结果．从而可证明b 、c 是异面的． 证明：假设b 、c 不异面即b//c 或b c B = ．(1)若b//c ，又因为c//a ，∴a//b 与b a A = 矛盾．(2)若b c B = ，又因为,b c βα⊂⊂．B a a β∈=∴ 则a 与c 相交与c//a 矛盾．综上得b 、c 是异面直线．点拨：证明两条直线是异面直线的常用方法有(1)直接法：根据异面直线的定义或根据教材P 14例3的结论来证明；(2)反证法：更为常用，因为书写简明，条理性强．例7.如图9－2－5，在正方体1111ABCD A BC D -中，E 、F 分别是棱1111,A B B C 的中点，求EF与1AD 所成角的大小．分析：把EF 平移到11AC ，再平移到AC ，则所求角与1DAC ∠有关，求出角1D AC ∠，即可得EF 与1AD 所成角． 解：连结11AC 和AC ． 111//,//E F A C A C A C，//EF AC ∴由定义所求角与1D AC ∠有关．连结1CD 得正三角形1ACD ，即160D AC ∠=︒． ∴EF 与AD 1所成角为60°．点拨：求两条异面直线所成角的一般步骤为“作（或找）角求角”，具体为①用平移法找或作出角. ②认定此角（或其补角）即为所要求的角．③解三角形求角．例8.已知空间四边形ABCD 中，各边长均为a ，且对角线AD ＝BC=a ，如图9－2－6，E 、F 分别为AD 、BC 的中点，连结AF 、CE ．求异面直线AF 与CE 所成角． 解：连结FD ，取FD 的中点O ，连结EO ，OC ，图9－2－5∵E 、O 分别为AD 、FD 的中点，∴EO//AF ，则CEO ∠或其补角即为所求的角． 在△CEO中，CE =，12EO AF ==，4CO ===，222222)))2cos 23CE EO CO CEO CE CO+-+-∠===⋅∴ ∴AF 与CE 所成角为2arccos3． 点拨：由于作角的关键是平移直线，而移法可能不同，有时移一条，有时要移两条，因此作出的角的位置也不尽相同，有时所求角是作出的角的补角，因此求异面直线所成角的具体做法较多．四、课后巩固训练： <一>选择题：1.一条直线和两条异面直线中的一条平行，则它与另一条直线的位置关系是（ ）A.平行或异面B.平行或相交C.相交或异面D.互相垂直2.异面直线a 、b 分别在平面α和β内，且c αβ= ，那么直线c 一定（ ） A.与a 、b 都相交 B.只能与a 、b 中的一条相交 C.至少与a 、b 中的一条相交 D.与a 、b 都不相交3.下面有四个命题①若两条直线没有公共点，则这两条直线互相平行；②若两条直线都和另一条 直线相交且垂直，则这两条直线互相平行；③若两条直线都和另一条直线没有公共点，则这两 条直线平行；④若两条直线和另一条直线相交所成的角相等，则这两条直线互相平行，其中正 确的命题的个数为（ ）A. 0B. 1C. 2D. 3 4.在正方体1111ABCD A BC D -中与1A B 成45°角的棱有A.2条B.3条C.6条D.8条 5.“1111//,//OA O A OB O B ”是“111AOB AO B ∠=∠”的图9－2－6A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件 6.分别和两条异面直线都相交的两条直线一定是（ ） A.异面直线 B.相交直线 C.不相交直线 D.不平行直线7.对于已知直线a ，如果直线b 同时满足下列三个条件：(1)与a 是异面直线；(2)与a 所成的角为定值θ；(3)与a 的距离为定值d ，那么这样的直线b 有（ ） A.1条 B.2条 C.3条 D.无数条 8.如图9－2－19，在棱长为2的正方体1111ABCD A BC D -中， O 是底面ABCD 的中心，E 、F 分别是CC 1、AD 的中点， 那么异面直线OE 和FD 1所成角的余弦值等于（ ）A.5B.5C.45D.23<二>填空题：9.已知异面直线a 、b 所成的角是80°，P 为空间一定点，则过P 且与a 、b 所成角都是50°的直线有______________条．10.在空间四边形ABCD 中，对角线AC ＝BD ＝2a ，M 、N 分别是边AB 、CD 的中点，若MN ，则AC 与BD 所成角为_________，MN 与AC 所成角为_____________．11.在空间四边形ABCD 中，AB ＝CD ＝8，M 、N 分别是边BD 、AC 的中点，若异面直线AB 与CD 成角为60°，则MN 的长为______________．12.下列四个命题：①垂直于同一条直线的两条直线平行；②一条直线垂直于两条平行线中的一条，也垂直于另一条；③经过直线外一点，有无数条直线与这条直线垂直；④已知111AOB AO B ∠=∠，若1//OA OA ，则11//OB O B ．其中正确命题的序号为___________．<三>解答题：13.如图9－2－21，空间四边形ABCD 中，四条边AB 、BC 、CD 、DA 及对角线AC 、BD 均相等，E 为AD 的中点，求AB 与CE 所成的角．图9－2－19图9－2－2114.如图9－2－23的长方体中，AB=BC=2a ，AA 1=a ，E 、F 分别为A 1B 1和BB 1的中点．求： (1)EF 和AD 1所成的角； (2)A 1D 1和B 1C 1间距离； (3)AC 1与B 1C 所成的角．15.如图9－2－24在空间四边形ABCD 中，AB=BD=AD=2，3,2BC CD AC ===，延长BC 到E 使CE=BC ，F 为BD 中点，求：异面直线AF 与DE 的距离和所成角．图9－2－23图9－2－24参 考 答 案<一>选择题：1.C2.C3.A4.D5.D6.D7.D8.B<二>填空题：9. 3 10. 90°，45° 11. 4或 12.②③<三>解答题：13.简解：取BD 中点F ，连EF 、CF ，求得FEC ∠=14.(1)连结D 1C ，AC ，则D 1C//EF ．在△AD 1C 中，222111112cos AC AD DC AD DC ADC =+-⋅∠解得11cos 5AD C ∠=．故所求角为1arccos 5． (2)A 1D 1与B 1C 1距离为2a ．(3)延长BC 至M ，使BC=CM ，连结C 1M ，AM ，在△AC 1M 中．11,3,AM AC a C M ===．由余弦定理得1cos AC M ∠=故所求角为1AC M ∠的补角，值为15.连结FC ，则FC//DE ，,1,BC CD BF === FC ===∴.2,A B B D A D A ===∴在△AFC 中，222,90AC FC AF ACF +=∠=︒∴ ．又1cos 2FC AFC AF ∠==，60AFC ∠=︒∴，//FC DE ，∴AF 与DE 的成角为60°．,DF AF DF DE ⊥⊥ ，∴DF 是AF 与DE 公垂线段．∴AF 与DE 距离为1．。

第二章 直线 平面 简单几何体一、平面1. 点A 在直线上,记作A a ∈；点A 在平面α内,记作A α∈；直线a 在平面α内,记作a α⊂.2. 平面基本性质即三条公理的“文字语言”、“符号语言”、“图形语言”列表如下：公理1 公理2 公理3图形语言文字语言如果一条直线上的两点在一个平面内，那么这条直线在此平面内. 过不在一条直线上的三点，有且只有一个平面.如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.符号语言 ,,A l B l l A B ααα∈∈⎫⇒⊂⎬∈∈⎭ ,,,,A B C A B C α⇒不共线确定平面 ,lP P P l αβαβ=⎧∈∈⇒⎨∈⎩3.公理2的三条推论：推论1 经过一条直线和这条直线外的一点，有且只有一个平面； 推论2 经过两条相交直线，有且只有一个平面； 推论3 经过两条平行直线，有且只有一个平面. 例题讲解：例1、空间四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 上的点，已知EF 和GH交于P 点，求证：EF 、GH 、AC 三线共点.例2、求证：两两相交且不过同一个点的三条直线必在同一平面内.例3、在正方体1111ABCD A B C D -中，（1）1AA 与1CC 是否在同一平面内？（2）点1,,B C D 是否在同一平面内？ （3）画出平面1AC 与平面1BC D 的交线，平面1ACD 与平面1BDC 的交线.二、空间中直线与直线之间的位置关系1.空间两条直线的位置关系：⎧⎧⎪⎨⎨⎩⎪⎩相交直线：同一平面内，有且只有一个公共点；共面直线平行直线：同一平面内，没有公共点；异面直线：不同在任何一个平面内，没有公共点.2. 已知两条异面直线,a b ，经过空间任一点O 作直线//,//a a b b ''，把,a b ''所成的锐角（或直角）叫异面直线,a b 所成的角（或夹角）. ,a b ''所成的角的大小与点O 的选择无关，为了简便，点O 通常取在异面直线的一条上；异面直线所成的角的范围为(0,90]︒，如果两条异面直线所成的角是直角，则叫两条异面直线垂直，记作a b ⊥. 求两条异面直线所成角的步骤可以归纳为四步：选点→平移→定角→计算.αCBA例题讲解：例1、已知异面直线a 和b 所成的角为50°，P 为空间一定点，则过点P 且与a 、b 所成角都是 30°的直线有且仅有（ ）.A. 1条B. 2条C. 3条D. 4条例2、如图正方体1111ABCD A B C D -中，E 、F 分别为D 1C 1和B 1C 1的中点，P 、Q 分别为AC 与BD 、A 1C 1与EF 的交点. （1）求证：D 、B 、F 、E 四点共面；（2）若A 1C 与面DBFE 交于点R ，求证：P 、Q 、R 三点共线.例3、已知直线a //b //c ，直线d 与a 、b 、c 分别相交于A 、B 、C ，求证：a 、b 、c 、d 四线共面.例4、如图中，正方体ABCD —A 1B 1C 1D 1，E 、F 分别是AD 、AA 1的中点.（1）求直线AB 1和CC 1所成的角的大小；（2）求直线AB 1和EF 所成的角的大小.三、直线与平面、平面与平面位置关系1. 直线与平面的位置关系：（1）直线在平面内（有无数个公共点）；（2）直线与平面相交（有且只有一个公共点）；（3）直线与平面平行（没有公共点）. 分别记作：l α⊂；l P α=；//l α.2. 两平面的位置关系：平行（没有公共点）；相交（有一条公共直线）.分别记作//αβ；l αβ=.例题讲解：例1、已知空间边边形ABCD 各边长与对角线都相等，求异面直线AB 和CD 所成的角的大小.PQ FE D 1C 1B 1A 1DC BAc'ba dc αC B AAB CDE F G MO例2、在空间四边形ABCD 中，E 、H 分别是AB 、AD 的中点，F 、G 分别是CB 、CD 的中点，若AC + BD = a ，AC ⋅BD =b ，求22EG FH +.例3、已知空间四边形ABCD 中，E 、H 分别是AB 、AD 的中点，F 、G 分别是BC 、CD 上的点，且23CF CG CB CD ==.求证：（1）E 、F 、G 、H 四点共面；（2）三条直线EF 、GH 、AC 交于一点.四、直线与平面平行的判定1. 定义：直线和平面没有公共点，则直线和平面平行.2. 判定定理：平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行. 符号表示为：,,////a b a b a ααα⊄⊂⇒.3. 定理：如果一条直线和一个平面平行，经过这条只限定平面和这个平面相交，那么这条直线和交线平行例题讲解例1、已知P 是平行四边形ABCD 所在平面外一点，E 、F 分别为AB 、PD 的中点，求证：AF ∥平面PEC例2、在正方体ABCD -A 1B 1C 1D 1中，E 、F 分别为棱BC 、C 1D 1的中点. 求证：EF ∥平面BB 1D 1D.例3、如图，已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点，求证：AM ∥平面EFG .ABCDEHFGA BCDE FGH例4、如图，已知P 是平行四边形ABCD 所在平面外一点，M 、N 分别是AB 、PC 的中点（1）求证：MN //平面P AD ；（2）若4MN BC ==，43PA =，求异面直线P A 与MN 所成的角的大小.五、 平面与平面平行的判定面面平行判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．用符号表示为：,,////,//a b ab P a b βββααα⊂⊂=⎫⇒⎬⎭推论：如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线那么这两个平面 平行。

9．直线、平面、简单几何体「平面」平面是一个只描述而不定义的最基本的概念。

可以从下述几方面加深认识：①平面的最本质的一个属性就是具有无限延展性。

应注意把立体几何中的平面与日常接触到的平面严格加以区分，不能混为一谈。

作为立体几何概念的平面，已经不再具有平面形象物体的属性，它不计厚薄，不计质量，没有任何物理的或化学的属性。

②可以将平面几何中直线的无限延展性与立体几何中平面的无限延展性加以类比，从而加深对平面的认识：直线可以看成是一点沿一定方向运动以后形成的；平面可以看成是一条直线沿一定方向运动以后形成的。

一条直线把它所在平面分成两部分；一个平面把空间分成两部分。

「平面的画法及其表示法」用图形表示直线只有一种方法，而用图形表示平面的方法却不是惟一的。

它可以用常见的图形，如三角形、平行四边形、矩形、正方形、平面多边形和圆等表示。

总之，可以用任意封闭的平面图形表示平面。

值得注意的是，虽然是用有限的封闭图形表示具有无限延展性的平面，但不能动摇对平面无限延展性的认识。

立体几何中，通常用平行四边形表示平面，画表示水平平面的平行四边形时，通常把它的锐角画成45°，横边画成邻边的2倍，如图（1）所示，画非水平平面时，只要画成适当的平行四边形即可，如图（2）所示；画直立的平面时，应把一组对边用铅垂线表示，如图（3）所示。

一个平面通常用一个字母表示，如平面M，平在α，也可以用表示平面的平行四边形的顶点上的字母表示，如平面ABCD或平面AC。

「用集合符号表示点、直线和平面之间的基本关系」①点和平面的位置关系：点A在平面α内，记作A∈平面α；点B不在平面α内，记作B∉平面α。

②直线和平面的位置关系：直线l在平面M内，记作直线l⊂平面M，在不发生误会的前提下，可⊂；直线l不在平在M内，记作直线l⊂平面M。

以记作l M③平面和平面的位置关系：平面α和平面β相交于直线l，记作平面αI平面β=直线l。

「平面的基本性质」公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内。

专题八直线、平面、简单几何体【考点聚焦】考点1：空间两条直线的位置关系.考点2：直线与平面平行与垂直.考点3：两平面平行与垂直.考点4：空间角与距离.考点5：棱柱的概念与性质.考点6：棱锥的概念，正棱锥的性质.考点7：球的概念、性质.考点8：异面直线间的距离、多面体的欧拉公式、简单几何体的面积和体积.【自我检测】1、平面的基本性质：公理1：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.公理2：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.公理3：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.推论1：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.推论2：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.推论3：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.2、＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿叫做异面直线.判断异面直线的方法有＿＿＿＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.3、平行与垂直的判断（叙述定理的内容）：4、空间中的角角2、范围：3、求法：2、范围：3、求法：2、范围：3、求法：5、空间中的距离空间中的八种距离：两点间距离、点到直线距离、点到平面距离、平行直线间的距离、异面直线间距离、直线到平面距离、两平行平面间的距离、球面上两点间距离.【重点•难点•热点】问题1：位置关系的判断根据概念、性质和定理进行判断，认定是正确的，要能证明；认定上不正确的，只需举反例.注意作图辅助说明.例1．设α、β、γ为两两不重合的平面，l、m、n为两两不重合的直线．给出下列四个命题：①若α⊥γ，β⊥γ，则α∥β；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；③若α∥β，l⊂α，则l∥β；④若α∩β=l，β∩γ=m，γ∩α=n，l∥γ，则m∥n．其中真命题个数是（）A．1 B．2 C．3 D．4思路分析：根据面面平行的判定和性质定理来判断.解：①显然不对；②要保证m、n相交才有α∥β，此选项不对；③由面面平行性质定理可知对；④∵l∥γ，β∩γ=m，l⊂β，∴l∥m，又m ⊂α，∴l ∥α，又α∩β=l 且l β，∴l ∥n ．从而l ∥m ∥n ，故④对．最后应选B ．点评：本题主要考查空间想象能力，判定定理、性质定理的理解与掌握及简单的推理论证能力．演变1：已知m 、n 是两条不重合的直线，α、β、γ是三个两两不重合的平面．给出下列的四个命题：①若α⊥m ，β⊥m ，则βα//；②若γα⊥，γβ⊥，则βα//； ③若α⊂m ，β⊂n ，n m //，则βα//；④若m 、n 是异面直线，α⊂m ，β//m ，β⊂n ，α//n ，则βα//， 其中真命题是Ａ.①和②Ｂ.①和③Ｃ.③和④Ｄ.①和④点拨与提示：解立几推断题应联系具体图形以及相关定理解决． 问题2：证明空间线面平行与垂直由已知想性质，由求证想判定，即分析法与综合法相结合寻找证明思路.例1：如图, 在直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AA 1＝4，点D 是AB 的中点， （I ）求证：AC ⊥BC 1； （II ）求证：AC 1//平面CDB 1；思路分析：（1）证明线线垂直方法有两类：一是通过三垂线定理或逆定理证明，二是通过线面垂直来证明线线垂直；（2）证明线面平行也有两类：一是通过线线平行得到线面平行，二是通过面面平行得到线面平行.解法一：（I ）直三棱柱ABC －A 1B 1C 1，底面三边长AC =3，BC =4AB =5，∴ AC ⊥BC ，且BC 1在平面ABC 内的射影为BC ，∴ AC ⊥BC 1； （II ）设CB 1与C 1B 的交点为E ，连结DE ，∵ D 是AB 的中点，E 是BC 1的中点，∴ DE//AC 1，∵ DE ⊂平面C D B 1，AC 1⊄平面C D B 1，∴ AC 1//平面C D B 1；解法二：∵直三棱柱ABC －A 1B 1C 1底面三边长AC ＝3，BC ＝4，AB ＝5，∴AC 、BC 、C 1C 两两垂直，如图，以C 为坐标原点，直线CA 、CB 、C 1C 分别为x 轴、y 轴、z 轴，建立空间直角坐标系，则C （0,0，0），A （3,0，0），C 1（0,0，4），B （0,4，0），B 1（0,4，4），D （23，2,0）（1）∵AC ＝（－3,0，0），1BC ＝（0，－4,0），∴AC •1BC ＝0，∴AC ⊥BC 1. （2）设CB 1与C 1B 的交战为E ，则E （0,2，2）.∵DE ＝（－23，0,2），1AC ＝（－3,0，4），∴121AC DE =，∴DE ∥AC 1. 点评：2．平行问题的转化： 面面平行线面平行线线平行； AB CABCExyz主要依据是有关定义及判定定理和性质定理．演变2：如图，在斜三棱柱111C B A ABC -中，a B A A A AC AB AC A AB A ===∠=∠1111,,，侧面11BCC B 与底面ABC 所成的二面角为ο120，E 、F 分别是棱A A CB 111、的中点（Ⅰ）求A A 1与底面ABC 所成的角；（Ⅱ）证明E A 1∥平面FC B 1 点拨与提示：例2在斜三棱柱A 1B 1C 1—ABC 中，底面是等腰三角形，AB =AC ，侧面BB 1C 1C ⊥底面ABC(1)若D 是BC 的中点，求证 AD ⊥CC 1；(2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ，若AM =MA 1，求证 截面MBC 1⊥侧面BB 1C 1C ；思路分析：（1）线面垂直⇒线线垂直；（2）利用面面垂直的判断定理证明面面垂直.证明 (1) ∵AB =AC ，D 是BC 的中点，∴AD ⊥BC∵底面ABC ⊥平面BB 1C 1C ，∴AD ⊥侧面BB 1C 1C ，∴AD ⊥CC 1(2) 延长B 1A 1与BM 交于N ，连结C 1N ，∵AM =MA 1，∴NA 1=A 1B 1，∵A 1B 1=A 1C 1，C 1B 1ABC D EMA 1D 1C 1B 1BCD A 1∴A1C1=A1N=A1B1，∴C1N⊥C1B1，∵底面NB1C1⊥侧面BB1C1C，∴C1N⊥侧面BB1C1C∴截面C1NB⊥侧面BB1C1C，∴截面MBC1⊥侧面BB1C1C 点评：（1）本题属于知识组合题类，关键在于对题目中条件的思考与分析，掌握做此类题目的一般技巧与方法，以及如何巧妙作辅助线（2）垂直问题的转化：面面垂直线面垂直线线垂直；演变3：已知斜三棱柱ABC—A1B1C1中，A1C1=B1C1=2，D、D1分别是AB、A1B1的中点，平面A1ABB1⊥平面A1B1C1，异面直线AB1和C1B互相垂直(1)求证AB1⊥C1D1；(2)求证AB1⊥面A1CD；问题3：求空间图形中的角与距离根据定义找出或作出所求的角与距离，然后通过解三角形等方法求值，注意“作、证、算”的有机统一.解题时注意各种角的范围：异面直线所成角的范围是0°＜θ≤90°，其方法是平移法和补形法；直线与平面所成角的范围是0°≤θ≤90°，其解法是作垂线、找射影；二面角0°≤θ≤180°，其方法是：①定义法；②三垂线定理及其逆定理；③垂面法另也可借助空间向量求这三种角的大小.例4：在棱长为a的正方体ABCD—A′B′C′D′中，E、F分别是BC、A′D′的中点F D'C'A'(1)求直线A ′C 与DE 所成的角； (2)求直线AD 与平面B ′EDF 所成的角； (3)求面B ′EDF 与面ABCD 所成的角思路分析：求线面角关键是作垂线，找射影，求异面直线所成的角采用平移法 求二面角的大小也可应用面积射影法(1)解 如图所示，在平面ABCD 内，过C 作CP ∥DE ，交直线AD 于P ，则∠A ′CP (或补角)为异面直线A ′C 与DE 所成的角在△A ′CP 中，易得A ′C =3a ，CP =DE =25a ,A ′P =213a 由余弦定理得cos A ′CP =1515 故A ′C 与DE 所成角为(2)解 ∵∠ADE =∠ADF ,∴AD 在平面B ′EDF 内的射影在∠EDF 的平分线上（如图）又可证明四边形B ′EDF 为菱形（证明略），∴DB ′为∠EDF 的平分线，故直线AD 与平面B ′EDF 所成的角为∠ADB ′，在Rt △B ′AD 中，AD =2a ，AB ′=2a ,B ′D =2a ， 则cos ADB ′=33，故AD 与平面B ′EDF 所成的角是arccos 33(3)解 如图，连结EF 、B ′D ，交于O 点，显然O 为B ′D 的中点，从而O 为正方形ABCD —A ′B ′C ′D 的中心，作OH ⊥平面ABCD ，则H 为正方形ABCD 的中心，再作HM ⊥DE ，垂足为M ，连结OM ，则OM ⊥DE ，故∠OMH 为二面角B ′—DE ′—A 的平面角在Rt △DOE 中，OE =22a ,OD =23a ,斜边DE =25a , 则由面积关系得OM =1030=⋅DE OE OD a 在Rt △OHM 中，sin OMH =630=OM OH 故面B ′EDF 与面ABCD 所成的角为方法二（向量法）（1） 如图建立坐标系，则(0,0,),(,,0),(0,,0),(,,0)2a A a C a a D a E a '(,,),(,,0)2a A C a a a DE a '⇒=-=-u u u u r u uu rcos ,15||||A C DE A C DE A C DE ''⇒<>=='u u u u r u u u ru u u u r u u u r g u u u ur u u u r 故A ′C 与DE 所成角为（2）∵∠ADE =∠ADF ,∴AD 在平面B ′EDF 内的射影在∠EDF 的平分线上 如下图所示 又∵B ′EDF 为菱形，∴DB ′为∠EDF 的平分线，故直线AD 与平面B ′EDF 所成的角为∠ADB ′，如图建立坐标系，则(0,0,0),(,0,),(0,,0)A B a a D a '(0,,0),(,,)DA a DB a a a '⇒=-=-u u u r u u u u r33||||,cos !!!=>=<⇒DB DA DB DA ， 故AD 与平面B ′EDF 所成的角是arccos33(3) 由(1)知(0,0,0),(0,0,),(,0,),(0,,0),(,,0)2a A A a B a a D a E a ''，所以面ABCD 的法向量为 (0,0,),m AA a '==u u u rr 下面求面B ′EDF 的法向量n r设(1,,)n y z =r，由(,,0),(0,,),22a a ED a EB a '=-=-u u u r u u u r ⎪⎩⎪⎨⎧=+-=+-⇒⎪⎩⎪⎨⎧⊥⊥02021az y a y a ax EBn ED n 取z=1，得(1,2,1)n =r∴66||||,cos =>=<m n m n m n . 故面B ′EDF 与面ABCD 所成的角为6arccos6点评：本题主要考查异面直线所成的角、线面角及二面角的一般求法，综合性较强 用平移法求异面直线所成的角，利用三垂线定理求作二面角的平面角，是常用的方法.演变4：已知四棱锥P-ABC D 的底面为直角梯形，AB ∥D C ，⊥=∠PA DAB ,90ο底面ABC D ，且P A =A D=D C =21AB =1，M 是P B 的中点. （Ⅰ）证明：面P A D ⊥面P C D ； （Ⅱ）求AC 与P B 所成的角；（Ⅲ）求面A M C 与面B M C 所成二面角的大小.例5：在长方体ABC D —A 1B 1C 1D 1，中，A D=AA 1=1，AB =2，点E 在棱AB 上移动.（1）证明：D 1E ⊥A 1D ；（2）当E 为AB 的中点时，求点E 到面AC D 1的距离；（3）A E 等于何值时，二面角D 1—E C —D 的大小为4π. 思路分析：本题涉及立体几何线面关系的有关知识, 本题实质上求解角度和距离,在求此类问题中，要将这些量处于三角形中,最好是直角三角形,这样有利于问题的解决，此外用向量也是一种比较好的方法.解法一：（1）证明：∵A E ⊥平面AA 1DD 1，A 1D ⊥A D 1，∴A 1D ⊥D 1E. （2）设点E 到面AC D 1的距离为h ，在△AC D 1中，AC =C D 1=5，A D 1=2， 故.2121,232152211=⋅⋅==-⋅⋅=∆∆BC AE S S ACE C AD 而 .31,23121,3131111=∴⨯=⨯∴⋅=⋅=∴∆∆-h h h S DD S V C AD AEC AEC D（3）过D 作DH ⊥C E 于H ，连D 1H 、DE ，则D 1H ⊥C E ， ∴∠DHD 1为二面角D 1—E C —D 的平面角. 设A E=x ，则B E=2－x,,,1,.1,4,211x EH DHE Rt x DE ADE Rt DH DHD DH D Rt =∆∴+=∆=∴=∠∆中在中在中在ΘΘπ.4,32.32543.54,3122π的大小为二面角时中在中在D EC D AE x x x x x x CE CBE Rt CH DHC Rt ---=∴-=⇒+-=+∴+-=∆=∆解法（二）：以D 为坐标原点，直线D A ，D C ，DD 1分别为x,y,z 轴，建立空间直角坐标系，设A E=x ，则A 1（1，0，1），D 1（0，0，1），E （1，x ，0），A （1，0，0）C （0，2，0）（1）.,0)1,,1()1,0,1(1111D DA x D DA ⊥=-⋅=⋅所以因为（2）因为E 为AB 的中点，则E （1，1，0），从而)0,2,1(),1,1,1(1-=-=AC E D ，)1,0,1(1-=AD ，设平面AC D 1的法向量为),,(c b a =，则⎪⎩⎪⎨⎧=⋅=⋅,0,01AD AC n 也即⎩⎨⎧=+-=+-002c a b a ，得⎩⎨⎧==ca ba 2，从而)2,1,2(=，所以点E 到平面A D 1C的距离为.313212||1=-+==n h 点评：立体几何的内容就是空间的判断、推理、证明、角度和距离、面积与体积的计算，这是立体几何的重点内容,本题实质上求解角度和距离,在求此类问题中,尽量要将这些量处于三角形中,最好是直角三角形,这样计算起来,比较简单,此外用向量也是一种比较好的方法,不过建系一定要恰当,这样坐标才比较好写出来.演变5：如图所示的多面体是由底面为ABC D 的长方体被截面A E C 1F 所截面而得到的，其中AB =4，BC =2，CC 1=3，B E=1.（Ⅰ）求B F 的长；（Ⅱ）求点C 到平面A E C 1F 的距离. 问题4：与几何体的侧面积和体积有关的计算问题根据基本概念和公式来计算，要重视方程的思想和割补法、等积转换法的运用.例6：如图，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且BCF ADE ∆∆、均为正三角形，EF ∥AB ，EF =2，则该多面体的体积为（ ）（A ）32 （B ）33（C ）34 （D ）23思路分析：将该几何体分割成一个柱体和两个锥体，然后再利用柱体和锥体的体积公式求它的体积.解：过A 、B 两点分别作AM 、BN 垂直于EF ，垂足分别为M 、N ，连结DM 、CN ，可证得DM ⊥EF 、CN ⊥EF ，多面体ABCDEF 分为三部分，多面体的体积V 为+=-BNC AMD ABCDEF V VBNC F AMD E V V --+，∵21=NF ，1=BF ，∴23=BN ，作NH 垂直于点H ，则H 为BC 的中点，则22=NH ，∴4221=⋅⋅=∆NH BC S BNC ，∴EFABCDM NH24231=⋅⋅=∆-NF S V BNC BNC F ，242==--BNC F AMD E V V ， 42=⋅=∆-MN S V BNC BNC AMD ，∴32=ABCDEF V ，故选A ．点评：将不规则的多面体分割或补全为规则的几何体进行计算．演变6：如图，在体积为1的三棱锥A —BC D 侧棱AB 、AC 、A D 上分别取点E 、F 、G ， 使A E : E B =A F : F C =A G : GD=2 : 1，记O 为三平面BC G 、C DE 、D B F 的交点，则三棱锥O —BC D 的体积等于 （ ）A ．91B ．81C ． 71D ．41 问题5：翻折与展开要对照翻折（或展开）前后两个图形，分清哪些元素的位置（或数量）关系改变了，哪些没有改变. 例7：如图1，已知ABC D 是上．下底边长分别为2和6，高为3的等腰梯形，将它沿对称轴OO 1折成直二面角，如图2.（Ⅰ）证明：AC ⊥B O 1；（Ⅱ）求二面角O －AC －O 1的大小.思路分析：（1）由题知可证得A O ⊥平面O BC O 1 ，O C 为AC 在平面O BC O 1内的射影，只要证明B O 1⊥O C 即可；（2）由（1）结论可证明B O 1⊥平面A O C ，由三垂线定理找出二面角的平面角即可.解：（I ）证明 由题设知O A ⊥OO 1，O B ⊥OO 1， 所以∠A O B 是所折成的直二面角的平面角，即O A ⊥O B . 从而A O ⊥平面O BC O 1， O C 是AC 在面O BC O 1内的射影.因为3tan 11==∠OO OBB OO 33tan 111==∠OOC O OC O ，所以∠OO 1B =60°，∠O 1O C =30°，从而O C ⊥B O 1，由三垂线定理得AC ⊥B O 1.（II ）解 由（I ）AC ⊥B O 1，O C ⊥B O 1， 知B O 1⊥平面A O C .设O C ∩O 1B =E ，过点E 作EF ⊥AC 于F ，连结O 1F （如图3），则EF 是O 1F 在平面A O C 内的射影，由三垂线定理得O 1F ⊥AC .所以∠O 1FE 是二面角O —AC —O 1的平面角.由题设知O A =3，OO 1=3，O 1C =1，所以13,3221212121=+==+=C O A O AC OO OA A O ，从而1332111=⋅=AC C O A O F O ， 又O 1E=OO 1·sin30°=23，所以.413sin 111==∠F O E O FE O 即二面角O —AC —O 1的大小是图3ABO CO 1DF.43arcsin点评：平面图形的翻折与空间图形的展开近两年的高考中都出现了，通过对图形的翻折与展开，很好地考查了学生的空间想象能力，体现了解决立体几何问题的基本思想：空间问题平面化.演变7：设M 、N 是直角梯形ABCD 两腰的中点，DE ⊥AB 于E (如图)．现将△ADE 沿DE 折起，使二面角A －DE －B 为45°，此时点A 在平面BCDE 内的射影恰为点B ，则M 、N 的连线与AE 所成角的大小等于_________． 专题小结1、位置关系的判断，根据概念、性质和定理进行判断，认定是正确的，要能证明；认定上不正确的，只需举反例.注意作图辅助说明.2、证明空间线面平行与垂直，是必考题型，解题时要由已知想性质，由求证想判定，即分析法与综合法相结合寻找证明思路.3、空间图形中的角与距离，先根据定义找出或作出所求的角与距离，然后通过解三角形等方法求值，注意“作、证、算”的有机统一.解题时注意各种角的范围.异面直线所成角的范围是0°＜θ≤90°，其方法是平移法和补形法；直线与平面所成角的范围是0°≤θ≤90°，其解法是ABC DE MN作垂线、找射影；二面角0°≤θ≤180°，其方法是：①定义法；②三垂线定理及其逆定理；③垂面法 另也可借助空间向量求这三种角的大小.4、与几何体的侧面积和体积有关的计算问题，根据基本概念和公式来计算，要重视方程的思想和割补法、等积转换法的运用5、平面图形的翻折与空间图形的展开问题，要对照翻折（或展开）前后两个图形，分清哪些元素的位置（或数量）关系改变了，哪些没有改变.【临阵磨枪】一．选择题1 在长方体ABCD —A 1B 1C 1D 1中，底面是边长为2的正方形，高为4，则点A 1到截面AB 1D 1的距离是( )A 38B 83C 34D 432 在直二面角α—l —β中，直线a ⊂α,直线b ⊂β,a 、b 与l 斜交，则( )A a 不和b 垂直，但可能a ∥bB a 可能和b 垂直，也可能a∥bC a 不和b 垂直，a 也不和b 平行D a 不和b 平行，但可能a ⊥b3 在正方体ABCD —A 1B 1C 1D 1中，M 为DD 1的中点，O 为底面ABCD 的中心，P 为棱A 1B 1上任意一点，则直线OP 与直线AM 所成的角是( )A 6πB 4πC 3πD2π 4 正方形ABCD 边长为2，E 、F 分别是AB 和CD 的中点，将正方形沿EF 折成直二面角(如图)，M 为矩形AEFD 内一点，如果∠MBE =∠MBC ，MB 和平面BCF 所成角的正切值为21，那么点M 到直线EF 的距离为( )AB 1 CD 125 三棱柱ABC —A 1B 1C 1中，AA 1=1，AB =4，BC =3，∠ABC =90°,设平面A 1BC 1与平面ABC 的交线为l ，则A 1C 1与l 的距离为( )A 10B 11C 2.6D 2.46．△ABC 的顶点B 在平面a 内，A 、C 在a 的同一侧，AB 、BC 与a 所成的角分别是30°和45°,若AB =3,BC =24 ,AC =5,则AC 与a 所成的角为(A )60° (B )45° (C )30° (D)15° 7．已知a 、b 、c 是直线，β是平面，给出下列命题：①若c a c b b a //,,则⊥⊥；②若c a c b b a ⊥⊥则,,//；③若b a b a //,,//则ββ⊂；④若a 与b 异面，且ββ与则b a ,//相交；⑤若a 与b 异面，则至多有一条直线与a ，b 都垂直. 其中真命题的个数是F（ ）A ．1B ．2C ．3D ．48、如图，正方体ABC D －A 1B 1C 1D 1的棱长为1，O 是底面A 1B 1C 1D 1的中心，则O 到平面AB C 1D 1的距离为 （B ）A 、21 B 、42 C 、22D 、239．设地球的半径为R ，若甲地位于北纬45︒东经120︒，乙地位于南纬75︒东经120︒，则甲、乙两地的球面距离为（ ） （A（B ）6R π（C ）56R π （D ）23R π10．矩形ABC D 中，AB =4，BC =3，沿AC 将矩形ABC D 折成一个直二面角B －AC －D ，则四面体ABC D 的外接球的体积为 （ ）A ．π12125B ．π9125C ．π6125D ．π3125二、填空题11 设X 、Y 、Z 是空间不同的直线或平面，对下面四种情形，使“X⊥Z 且Y ⊥Z ⇒X ∥Y ”为真命题的是_________(填序号)①X 、Y 、Z 是直线；②X 、Y 是直线，Z 是平面；③Z 是直线，X 、Y 是平面；④X 、Y 、Z 是平面.12 已知∠AOB =90°,过O 点引∠AOB 所在平面的斜线OC ，与OA 、OB分别成45°、60°，则以OC 为棱的二面角A —OC —B 的余弦值等于______13 正三棱锥的一个侧面的面积与底面积之比为2∶3,则这个三棱锥的侧面和底面所成二面角的度数为_________14．空间四点A 、B 、C 、D 中，每两点所连线段的长都等于a ，动点P 在线段AB 上，动点Q 在线段CD 上，则P 与Q 的最短距离为_________三、解答题15 如图，在四棱锥P —ABCD 中，底面ABCD 是矩形，侧棱PA 垂直于底面，E 、F 分别是AB 、PC 的中点(1)求证 CD ⊥PD ;(2)求证 EF ∥平面PAD ;(3)当平面PCD 与平面ABCD 成多大角时，直线EF ⊥平面PCD ？ 16 如图，正三棱柱ABC —A 1B 1C 1的各棱长都相等，D 、E 分别是CC 1和AB 1的中点，点F 在BC 上且满足BF ∶FC =1∶3(1)若M 为AB 中点，求证 BB 1∥平面EFM ；(2)求证 EF ⊥BC ；(3)求二面角A 1—B 1D —C 1的大小17 如图，已知平行六面体ABCD —A 1B 1C 1D 1的底面是菱形且∠C 1CB =∠C 1CD =∠BCD =60°,(1)证明 C 1C ⊥BD ；(2)假定CD =2，CC 1=23，记面C 1BD 为α,1A11面CBD 为β,求二面角α—BD —β的平面角的余弦值；(3)当1CC CD的值为多少时，可使A 1C ⊥面C 1BD ？18 设△ABC 和△DBC 所在的两个平面互相垂直，且AB =BC =BD ，∠ABC =∠DBC =120°，求(1)直线AD 与平面BCD 所成角的大小； (2)异面直线AD 与BC 所成的角； (3)二面角A —BD —C 的大小19 如图，在梯形ABCD 中，AD ∥BC ，∠ABC =2π,AB = 31AD =a ,∠ADC =arccos552,PA ⊥面ABCD 且PA =a (1)求异面直线AD 与PC 间的距离；(2)在线段AD 上是否存在一点F ，使点A 到平面PCF 的距离为36参考答案1 C 解析 设A 1C 1∩B 1D 1=O 1，∵B 1D 1⊥A 1O 1，B 1D 1⊥AA 1，∴B 1D 1⊥平面AA 1O 1，故平面AA 1O 1⊥AB 1D 1，交线为AO 1，在面AA 1O 1内过A 1作A 1H ⊥AO 1于H ，则易知A 1H 长即是点A 1到平面AB 1D 1的距离，在Rt △A 1O 1A 中，A 1O 1=2，AO 1=32，由A 1O 1·A 1A =h ·AO 1,可得A 1H =34答案 C2 C 解析 如图，在l 上任取一点P ，过P 分别在α、β内作a ′βαP a'b b'a CBAABCACD P∥a ,b ′∥b ,在a ′上任取一点A ，过A 作AC ⊥l ，垂足为C ，则AC ⊥β,过C 作CB ⊥b ′交b ′于B ，连AB ，由三垂线定理知AB ⊥b ′，∴△APB 为直角三角形,故∠APB 为锐角3 D 解析 (特殊位置法）将P 点取为A 1，作OE ⊥AD 于E ，连结A 1E ，则A 1E 为OA 1的射影，又AM ⊥A 1E ，∴AM ⊥OA 1，即AM 与OP 成90°角 答案 D4．A 解析 过点M 作MM ′⊥EF ,则MM ′⊥平面BCF ，∵∠MBE =∠MBC ，∴BM ′为∠EBC 为角平分线，∴∠EBM ′=45°,BM ′=2,从而MN =225 C 解析 交线l 过B 与AC 平行，作CD ⊥l 于D ，连C 1D ，则C 1D 为A 1C 1与l 的距离，而CD 等于AC 上的高，即CD =512,Rt △C 1CD 中易求得C 1D =513=2.6.答案 C6、C 解：如图，A E ⊥平面α于E,C D ⊥平面α于D,EF ∥AC ,EF 交C D 于F,则∠AB E=300,∠CB D=450,由此得C D=4,A E=1.5,∴EF=2.5,而EF=AC =5 ∴∠FED=300,即AC 与平面α所成的角为300,∴选(C ) 7、A 解：①③④⑤是假命题,②是真命题,选(A )8．B 解：取B 1C 1的中点M ，连B 1C 交BC 1于O '，取O 'C 1的中点N ，连MN ，则MN 1BC ⊥又在正方体ABC D-A 1B 1C 1D 1中OM 平行于平面ABC 1D 1. 则O 到平面ABC 1D 1距离转化为M 到平面ABC 1D 1的距离，即MN=42，故选B A BCEDF9．D10．C 解析：连接矩形ABC D 的对角线AC 、B D 交于O ，则A O ＝B O ＝C O＝DO ，则O 为四面体ABC D 的外接球的圆心，因此四面体ABC D 的外接球的半径为52，体积为345125()326ππ=.选C . 11 ②③ 解析 ①是假命题，直线X 、Y 、Z 位于正方体的三条共点棱时为反例，②③是真命题，④是假命题，平面X 、Y 、Z 位于正方体的三个共点侧面时为反例12 －33解析 在OC 上取一点C ，使OC =1，过C 分别作CA ⊥OC 交OA 于A ，CB ⊥OC 交OB 于B ，则AC =1，，OA =2，BC =3，OB =2，Rt △AOB中，AB 2=6，△ABC 中，由余弦定理，得cos ACB =－答案 －3313 60° 解析 设一个侧面面积为S 1，底面面积为S ，则这个侧面在底面上射影的面积为3S，由题设得321=S S ，设侧面与底面所成二面角为θ,则cos θ=2133111==S S S S,∴θ=60° 答案 60°1422a 解析 以A 、B 、C 、D 为顶点的四边形为空间四边形，且为正四面体，取P 、Q 分别为AB 、CD 的中点，因为AQ =BQ =22a ,∴PQ ⊥AB , 同理可得PQ ⊥CD ，故线段PQ 的长为P 、Q 两点间的最短距离，在Rt △APQ 中，PQ =22)2()23(2222=-=-a a AP AQ a.答案22a 15 证明 (1)∵PA ⊥底面ABCD ，∴AD 是PD 在平面ABCD 内的射影，∵CD⊂平面ABCD且CD⊥AD，∴CD⊥PD(2)取CD中点G，连EG、FG，∵E、F分别是AB、PC的中点，∴EG∥AD，FG∥PD∴平面EFG∥平面PAD，故EF∥平面PAD(3）解当平面PCD与平面ABCD成45°角时，直线EF⊥面PCD证明G为CD中点，则EG⊥CD,由(1)知FG⊥CD，故∠EGF为平面PCD 与平面ABCD所成二面角的平面角即∠EGF=45°，从而得∠ADP=45°，AD=AP由Rt△PAE≌Rt△CBE,得PE=CE又F是PC的中点，∴EF⊥PC，由CD⊥EG，CD⊥FG，得CD⊥平面EFG，CD⊥EF即EF⊥CD，故EF⊥平面PCD16 (1)证明连结EM、MF，∵M、E分别是正三棱柱的棱AB和AB1的中点，∴BB1∥ME，又BB1⊄平面EFM，∴BB1∥平面EFM(2)证明取BC的中点N，连结AN由正三棱柱得AN⊥BC，又BF∶FC=1∶3，∴F是BN的中点，故MF∥AN，∴MF⊥BC，而BC⊥BB1，BB1∥ME∴ME⊥BC，由于MF∩ME=M，∴BC⊥平面EFM，又EF⊂平面EFM，∴BC⊥EF(3)解取B1C1的中点O，连结A1O知，A1O⊥面BCC1B1，由点O作B1D的垂线OQ ，垂足为Q ，连结A 1Q ，由三垂线定理，A 1Q ⊥B 1D ，故∠A 1QD 为二面角A 1—B 1D —C 的平面角，易得∠A 1QO17 (1)证明 连结A 1C 1、AC ，AC 和BD 交于点O ，连结C 1O ，∵四边形ABCD 是菱形，∴AC ⊥BD ，BC =CD又∵∠BCC 1=∠DCC 1，C 1C 是公共边，∴△C 1BC ≌△C 1DC ，∴C 1B =C 1D ∵DO =OB ，∴C 1O ⊥BD ，但AC ⊥BD ，AC ∩C 1O =O ∴BD ⊥平面AC 1，又C 1C ⊂平面AC 1，∴C 1C ⊥BD(2)解 由(1)知AC ⊥BD ，C 1O ⊥BD ，∴∠C 1OC 是二面角α—BD —β的平面角在△C 1BC 中，BC =2，C 1C =23，∠BCC 1=60°，∴C 1B 2=22+(23)2－2×2×23×cos60°=413∵∠OCB =30°,∴OB =21,BC =1,C 1O =23,即C 1O =C 1C作C 1H ⊥OC ，垂足为H ，则H 是OC 中点且OH =23，∴cos C 1OC =33 (3)解 由(1)知BD ⊥平面AC 1，∵A 1O ⊂平面AC 1，∴BD ⊥A 1C ，当1CC CD=1时，平行六面体的六个面是全等的菱形，同理可证BC 1⊥A 1C ，又∵BD ∩BC 1=B ，∴A 1C ⊥平面C 1BD18 解 (1)如图，在平面ABC 内，过A 作AH ⊥BC ，垂足为H ，则AH ⊥平面DBC ，∴∠ADH 即为直线AD 与平面BCD 所成的角 由题设知△AHB ≌△AHD ，则DH ⊥BH ，AH =DH ，∴∠ADH =45°(2)∵BC ⊥DH ，且DH 为AD 在平面BCD 上的射影， ∴BC ⊥AD ，故AD 与BC 所成的角为90°(3)过H 作HR ⊥BD ，垂足为R ，连结AR ，则由三垂线定理知，AR ⊥BD ，故∠ARH 为二面角A —BD —C 的平面角的补角 设BC =a ,则由题设知，AH =DH =2,23a BH a =,在△HDB 中，HR =43a ，∴tan ARH =HRAH =2故二面角A —BD —C 大小为π－arctan219 解 (1)∵BC ∥AD ,BC ⊂面PBC ,∴AD ∥面PBC从而AD 与PC 间的距离就是直线AD 与平面PBC 间的距离过A 作AE ⊥PB ，又AE ⊥BC ∴AE ⊥平面PBC ，AE 为所求在等腰直角三角形PAB 中，PA =AB =a ∴AE =22a (2)作CM ∥AB ，由已知cos ADC =552 ∴tan ADC =21,即CM =21DM∴ABCM 为正方形，AC =2a ,PC =3a 过A 作AH ⊥PC ,在Rt △PAC 中，得AH =36 下面在AD 上找一点F ，使PC ⊥CF取MD 中点F ，△ACM 、△FCM 均为等腰直角三角形 ∴∠ACM +∠FCM =45°+45°=90°∴FC ⊥AC ,即FC ⊥PC ∴在AD 上存在满足条件的点F【挑战自我】如图，已知PD ⊥平面ABC D ，A D ⊥D C ，A D ∥BC ，PD ∶D C ∶BC ＝1∶1∶2.（1）求二面角D －P B －C 的正切值；（2）当A D ∶BC 的值是多少时，能使平面P AB ⊥平面P BC ？证明你的结论.解：（1）如图，取P C 中点E ，连DE.∵PD ＝D C ，∴DE ⊥P C .又∵BC ⊥D C ，BC ⊥PD ， ∴BC ⊥平面PD C ，则面B P C ⊥面PD C ，∴DE ⊥面P BC .过E 作EF ⊥P B于F ，连DF ，则由三垂线定理有DF ⊥P B .∴∠DFE ＝θ为二面角D －P B －C 的平面角.设PD ＝D C ＝1，则BC ＝2，DE ＝22，P C ＝2.又∵在Rt △DEF 中，tan θ=2=EFDE∴二面角D －P B －C 的正切值为2（2）A D ∶BC ＝1∶2时，平面P AB ⊥平面P BC . 设PD ＝1，x BCAD=时，平面P AB ⊥平面P BC ，则D C ＝1，BC ＝P C ＝2，A D ＝2x.P A BCDP ABCD GEθ F过A 作A G ⊥P B 于G 点，∵平面P AB ⊥平面P BC ，∴A G ⊥面P BC ，又∵DE ⊥面P BC （已证），∴A G ∥DE ，而A D ∥BC ，∴A D ∥面P BC ，故A D ∥GE ，进而有GE ∥BC ，又E 为P C 中点，∴G 为P B 中点，故GE ＝2221=BC . 即 21222=⇒=x x . ∴当平面P AB ⊥平面P BC 时，21=BC AD 【答案及点拨】演变1：因为垂直于同一条直线的两平面互相平行，所以①正确；因为垂直于同一平面的两平面不一定平行，所以②错误；因为当α与β相交时，若m 、n 平行于两平面的交线，则n m //，所以③错误；因为若m 、n 是异面直线，α⊂m ，β//m ，β⊂n ，α//n ，当且仅当βα//，所以④正确． 演变2：（Ⅰ）过1A 作⊥H A 1平面ABC ，垂足为H ．连结AH ，并延长交BC 于G ，于是AH A 1∠为A A 1与底面ABC 所成的角． ∵AC A AB A 11∠=∠，∴AG 为BAC ∠的平分线．又∵AC AB =，∴BC AG ⊥，且G 为BC 的中点．因此，由三垂线定理BC A A ⊥1．∵B B A A 11//，且B B EG 1//，∴BC EG ⊥．于是AGE ∠为二面角E BC A --的平面角，即ο120=∠AGE ． 由于四边形AGE A 1为平行四边形，得ο601=∠AG A ．（Ⅱ）证明：设EG 与C B 1的交点为P ，则点P 为EG 的中点．连结PF ． 在平行四边形1AGEA 中，因F 为A A 1的中点，故FP E A //1． 而⊂FP 平面FC B 1，⊄E A 1平面FC B 1，所以//1E A 平面FC B 1．演变3： (1)证明 ∵A 1C 1=B 1C 1，D 1是A 1B 1的中点，∴C 1D 1⊥A 1B 1于D 1，又∵平面A 1ABB 1⊥平面A 1B 1C 1，∴C 1D 1⊥平面A 1B 1BA ， 而AB 1⊂平面A 1ABB 1，∴AB 1⊥C 1D 1(2)证明 连结D 1D ，∵D 是AB 中点，∴DD 1CC 1，∴C 1D 1∥CD ，由(1)得CD ⊥AB 1，又∵C 1D 1⊥平面A 1ABB 1，C 1B ⊥AB 1， 由三垂线定理得BD 1⊥AB 1，又∵A 1D ∥D 1B ，∴AB 1⊥A 1D 而CD ∩A 1D =D ，∴AB 1⊥平面A 1CD演变4：（Ⅰ）证明：∵P A ⊥面ABC D ，C D ⊥A D ， ∴由三垂线定理得：C D ⊥PD.因而，C D 与面P A D 内两条相交直线A D ，PD 都垂直， ∴C D ⊥面P A D.又C D ⊂面P C D ，∴面P A D ⊥面P C D. （Ⅱ）解：过点B 作B E//CA ，且B E=CA ， 则∠P B E 是AC 与P B 所成的角.连结A E ，可知AC =CB =B E=A E=2，又AB =2，所以四边形ACB E 为正方形. 由P A ⊥面ABC D 得∠PE B =90° 在Rt △PE B 中B E=2，P B =5， .510cos ==∠∴PB BE PBE .510arccos所成的角为与PB AC ∴ （Ⅲ）解：作A N ⊥C M ，垂足为N ，连结B N.在Rt △P AB 中，A M=M B ，又AC =CB ，∴△A M C ≌△B M C , ∴B N ⊥C M ，故∠A N B 为所求二面角的平面角. ∵CB ⊥AC ，由三垂线定理，得CB ⊥P C ， 在Rt △P CB 中，C M=M B ，所以C M=A M. 在等腰三角形A M C 中，A N ·M C =AC AC CM ⋅-22)2(， 5625223=⨯=∴AN . ∴AB =2，322cos 222-=⨯⨯-+=∠∴BN AN AB BN AN ANB 故所求的二面角为).32arccos(-演变5：（Ⅰ）过E 作EH//BC 交CC 1于H ，则C H=B E=1，EH//A D ，且EH=A D. 又∵A F ∥E C 1，∴∠F A D=∠C 1EH.∴Rt △A DF ≌Rt △EH C 1. ∴DF=C 1H=2..6222=+=∴DF BD BF（Ⅱ）延长C 1E 与CB 交于G ，连A G ，则平面A E C 1F 与平面ABC D 相交于A G. 过C 作C M ⊥A G ，垂足为M ，连C 1M ，由三垂线定理可知A G ⊥C 1M.由于A G ⊥面C 1M C ，且A G ⊂面A E C 1F ，所以平面A E C 1F ⊥面C 1M C .在Rt △C 1C M 中，作C Q ⊥M C 1，垂足为Q ，则C Q 的长即为C 到平面A E C 1F 的距离..113341712317123,17121743cos 3cos 3,.17,1,2211221=+⨯=⨯=∴=⨯===∠=∠=+===MC CC CM CQ GAB MCG CM MCG GAB BG AB AG BG CGBGCC EB 知由从而可得由演变6：如图,B M 是平面BC G 与平面B DF 的交线,C L 是平面BC G 与平面C DE 的交线,则B M 子C L 的交点即为O.作EG ⊥平面BC D,LN ⊥平面BC D,OQ ⊥平面BC D,设A 到平面BC D 的高为h,由题意可知EK=13h ,LN=33115535EK h h =⋅=,∵32CM BL MG LG ==,∴75CL CQ =∴OQ=55117757LN h h =⋅=, ∴11137173BCDO BCD A BCDBCD hS V V hS --⋅==V V ,选(C ).演变7：如左图,在平面A ED 内作MQ ∥A E 交ED 于Q,则MQ ⊥ED,且Q为ED 的中点,连结QN,则NQ ⊥ED 且QN ∥E B ,QN=E B ,∠MQN 为二面角A －DE －B 的平面角,∴∠MQN=45°，∵AB ⊥平面BC DE,又∠A E B =∠MQN=45°,MQ=12A B ,在平面MQN 内作MP ⊥B Q,得QP=MP=12E B ,故P B =QP=12E B ,故QMN 是以∠QMN 为直角的等腰三角形,即MN ⊥QM,也即MN 子A E 所成角大小等于90°希望以上资料对你有所帮助，附励志名言3条：1、生命对某些人来说是美丽的，这些人的一生都为某个目标而奋斗。

平面的基本性质〖知识点分布〗1、平面；2、平面的基本性质；3、平面图形的直观图的画法。

〖考纲要求〗1、掌握平面的基本性质；2、会用斜二测画法画水平放置的直观图；3、熟悉各种符号及其应用。

〖复习要求〗掌握平面的基本性质，主要是三个公理、三个推论及其应用.会用斜二测画法画水平放置的直观图；会证明共面、共点、共线问题；掌握反证法的应用；知道什么叫“空间四边形”.〖双基回顾〗公理1：________________________________ ____.用符号表示为：_____________________. 公理2：_________________________________ _________.用符号表示为：_____________________.公理3：_____________________._______________________________________________________ 推论1：_________________________________________________.推论2：_________________________________________________.推论3：___________________________________________________.公理1是证明____________________________________的依据；公理2是证明___________________的依据；公理3及其三个推论是证明__________________________________________.的依据。

2、斜二测画法的规则：①________________ _____,②______________________________,③___________________ ___,④_____________________________. 〖课前练习〗1、下面几个命题：⑴两两相交的三条直线共面；⑵如果两个平面有公共点，则公共点有无数个；⑶一条直线与两条平行直线都相交，那么这三条直线共面；⑷有三个内角是直角的空间四边形一定是矩形；⑸顺次连接空间四边形各边中点所得的四边形是平行四边形。

第九章直线、平面简单的几何体编写：王建宏【网络图】1.空间的线线关系是:相交、平行、异面(不同在任何一个平面内). 空间的线面关系是:直线在平面内（平面过直线）,直线和平面相交,直线和平面平行(统称“外”). 空间的面面关系是:平行、相交.2.证明直线与直线平行的思考途径(1)转化为判定共面两直线无交点；(2)转化为两条直线同时与第三条直线平行；(3)转化为线面平行；（4）转化为线面垂直；（5）转化为面面平行. 证明直线与平面平行的思考途径(1)转化为直线与平面无公共点；(2)转化为线线平行；(3)转化为面面平行.证明平面与平面平行的思考途径(1)转化为判定两平面无公共点；（2）转化为线面平行（3）转化为线面垂直.证明直线与直线的垂直的思考途径(1)转化为相交垂直；(2)转化为线面垂直；（3）转化为该线与另一线的射影垂直；（4）转化为该线与形成射影的斜线垂直.证明直线与平面垂直的思考途径(1)转化为该直线与平面内任一直线垂直；（2）转化为该直线与平面内相交二直线垂直；（3）转化为该直线与平面的一条垂线平行；（4）转化为该直线垂直于另一个平行平面；（5）转化为该直线与两个垂直平面的交线垂直.证明平面与平面的垂直的思考途径(1)转化为判断二面角是直二面角；（2）转化为线面垂直. 3.异面直线所成角的求法：(1)平移法（2）补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系. 4.直线与平面所成角:斜线和平面所成的是一个直角三角形的锐角，它的三条边分别是平面的垂线段、斜线段及斜线段在平面上的射影.通常通过斜线上某个特殊点作出平面的垂线段，垂足和斜足的连线，是产生线面角的关键；或三余弦公式(最小角定理)；或选用等积求点到平面的距离,后虚拟直角三角形求解.注:从一点O 出发的三条射线OA 、OB 、OC ，若∠AOB=∠AOC(或A 到OB 、OC 等距离)，则点A 在平面BOC 上的射影是在∠BOC 的平分线上.5.二面角的求法（1）定义法：用定义法时，要认真观察图形的特性.（2）三垂线法：利用三垂线定理找二面角的平面角的作法：1、找一垂是关键（通常在其中一个半平面内取一特殊点，作两个互相垂直平面交线的垂线） 2、作二垂（过一垂的垂足作要求二面角棱的垂线）3、连三垂（连结特殊点与二垂的垂足，根据三垂线定理可迅速得到二面角的平面角，即为二垂与三垂的夹角）.（3）垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个半平面的交线所成的角即为平面角，由此可知，二面角的平面角所在的平面与棱垂直；（4）射影法：利用面积射影公式S 射＝S 原cos θ,其中θ为平面角的大小，此方法不必在图形中画出平面角；特别地:对于一类没有给出棱的二面角，应先延伸两个半平面，使之相交出现棱，然后再选用上述方法（尤其要考虑射影法）.6.空间距离的求法:（1）两异面直线间的距离，高考要求是给出公垂线(可转化为平行线面、面面的距离)；注：两条异面直线的公垂线有且仅有一条.（2）求点到直线的距离，一般用三垂线定理作出垂线再求解；（3）求点到平面的距离，一是用垂面法，借助面面垂直的性质来作，因此，确定已知面的垂面是关键；二是不作出公垂线，转化为求三棱锥的高，利用等体积法列方程求解.7.柱体、锥体的体积:V Sh =柱体（S 是柱体的底面积、h 是柱体的高）.13V Sh =锥体（S 是锥体的底面积、h 是锥体的高）.两个常用的结论：（1）锥体被平行于底面的平面所截，截面与底面相似，其面积之比等于截去小锥体的高与原锥体高比的平方.截去小锥体的体积(侧面积)与原锥体体积(侧面积)之比等于截去小锥体的高与原锥体高比的立方（此处应明确相似比的含义）．(2)长方体对角线性质:长度为l 的线段在三条两两互相垂直的直线上的射影长分别为123l l l 、、，夹角分别为123θθθ、、,则2222123l l l l =++222123cos cos cos 1θθθ⇔++=222123sin sin sin 2θθθ⇔++=. 棱锥的各侧面与底面所成的角相等，记为θ，则S 侧cos θ=S 底.8.球的半径是R ，则其体积343V R π=,其表面积24S R π=.球的载面性质(球的载面往往以不共线三点确定的平面而呈现，往往化归为研究三棱锥的问题),球面距离l =R α,（α为球心角，通常利用等腰三角形求α大小.）纬度圆的半径r ＝Rcos θ（θ为纬度的大小）．球的组合体(1)球与长方体的组合体: 长方体的外接球的直径是长方体的体对角线长.(2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长,(3)球与正四面体的组合体: 棱长为a ,外接.3.【网络导读】1.解决关于向量问题时，一要善于运用向量的平移、伸缩、合成、分解等变换，正确地进行向量的各种运算，加深对向量的本质的认识.二是向量的坐标运算体现了数与形互相转化和密切结合的思想.2.向量的数量积常用于有关向量相等，两向量垂直、射影、夹角等问题中.常用向量的直角坐标运算来证明向量的垂直和平行问题；利用向量的夹角公式和距离公式求解空间两条直线的夹角和两点间距离的问题.3.用空间向量解决立体几何问题一般可按以下过程进行思考：(1)要解决的问题可用什么向量知识来解决？需要用到哪些向量？(2)所需要的向量是否已知？若未知，是否可用已知条件转化成的向量直接表示？(3)所需要的向量若不能直接用已知条件转化成的向量表示，则它们分别最易用哪个未知向量表示？这些未知向量与由已知条件转化的向量有何关系？(4)怎样对已经表示出来的所需向量进行运算，才能得到需要的结论？【易错指导】易错点1：立体图形的截面作图不准确,空间位置关系把握不到位. 不会判断过空间一点与两异面直线成相等角的直线的条数.易错点2：有关线面平行的证明问题中,对定理的理解不准确,往往忽视三个条件中的某一个.对于两个平面平行及垂直的判断定理时,易把条件放宽,使证明过程跨步太大.求异面直线所成的角,若所成角为90度,容易忽视用证明垂直的方法来求夹角大小这一重要方法.易错点3：在求异面直线所成的角,直线与平面所成的角以及二面角时,易忽视各自所成的角的范围.对于经度和纬度两个概念,经度是二面角,纬度是线面角,二者容易找不到位.向量知识在立体几何中的应用不能顺利由平面类比至空间.易错点4：常见几何体的体积计算公式,特别是棱锥、球的体积公式,容易忽视公式系数,导致出错.求点到平面的距离的方法有直接法、等体积法等,对方法的选择上不到位而延时. 二面角平面角的求法,主要有定义法、三垂线法、垂面法等,此类方法不能灵活选择.例题1给出以下四个命题①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;③如果两条直线都平行于一个平面,那么这两条直线互相平行;④如果一个平面经过另一个平面的一条重线,那么些两个平面互相垂直.其中真命题的个数是A.4B.3C.2D.1【解析】命题①为直线与平面平行的性质定理; 命题②为直线与平面垂直的判定定理; 命题④为平面与平面垂直的判定定理; 命题③是错误的,如果两直线均平行于一个平面,则这两条直线的位置关系可以平行,也可以异面或相交. 即真命题的个数为3个,故应选B.【点评】本题考查了空间直线与平面、平面与平面平行及垂直判定与性质的相关理论,考生对逻辑命题正确率不太高.例题2两相同的正四棱锥组成如图1所示的几何体，可放棱长 为1的正方体内，使正四棱锥的底面ABCD 与正方体的某一 个平面平行，且各顶点．．．均在正方体的面上，则这样的几何体 体积的可能值有（A ）1个 （B ）2个 （C ）3个 （D ）无穷多个【解法一】八面体上下两项点间距离即两正四棱锥 高之和为定值1,则本题可以转化为一个正方形可以 有多少个内接正方形，显然有无穷多个.其面积变化 何积显然变化.应选D.【解法二】如图所示,在正方体的俯视图中,可得正 八面体中截面四边形正方形ABCD 的内接于另一个 正方形,此正方形ABCD 的面积的范围为1[,1)2S ∈ ∴八面体的体积1111[,363V S =⨯∈, 即其体积的 可能值有穷多个.故应选D.【点评】本题考查了正方体内接几何体的空间模型建构考查通过截面图来化归分析几何问题的策略.该题渗透了新课标中三视图的解法,应引起足够的重视.考生对此类体积向面积的化归转化问题往往浮于表面.例题3如图，在长方体1111ABCD A BC D -中，,E P 分别是11,BC A D 的 中点，,M N 分别是1,AE CD 的中点，1,2AD AA a AB a === （Ⅰ）求证：//MN 面11ADD A ； （Ⅱ）求二面角P AE D --的大小。