一次函数与三角形存在性问题

特殊三角形存在性知识点睛1.存在性问题：通常是在变化的过程中，根据已知条件，探索某种状态是否存在的题目，主要考查运动的结果．2.存在性问题处理框架：①研究背景图形．②分析不变特征，确定分类标准．③分析特殊状态的形成因素，画出符合题意的图形并求解．④结果验证．3.不变特征举例：①等腰三角形以定线段作为底边或者腰确定分类标准，利用两圆一线确定点的位置．②等腰直角三角形根据直角顶点确定分类标准，然后借助两腰相等或者45°角确定点的位置．精讲精练1.如图，在平面直角坐标系中，已知点A的坐标为(-3，4)，P是x轴上的一个动点，则当△AOP是等腰三角形时，点P的坐标为____________．2.如图，在平面直角坐标系中，一次函数y x =+与x 轴交于点A ，与y 轴交于点B ．将△AOB 沿过点B 的直线折叠，使点O 落在AB 上的点D 处，折痕交x 轴于点E ． （1）求点D 的坐标．（2）x 轴上是否存在点P ，使得△PAD 是等腰三角形？若存在，求出点P 的坐标；若不存在，请说明理由．3. 直线y =kx -4与x 轴、y 轴分别交于点A ，B ，且43OB OA =．点C 在第一象限，是直线y =kx -4上的一个动点，当△AOC 的面积为6时，x 轴上是否存在点P ，使△ACP 是等腰三角形？若存在，求出点P 的坐标；若不存在，请说明理由．4.如图，直线334y x=-+与x轴、y轴分别交于点A，B，在第一象限内是否存在点P，使以A，B，P为顶点的三角形是等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．5.如图，直线y=x轴、y轴分别交于点A，B，点C在点A左侧，是x轴上一点，且满足AC=OA，过点C作x轴的垂线交直线AB于点D，在第二象限内是否存在点P，使得△PAD是等腰直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．6.如图，在平面直角坐标系中，点A的坐标为(2，0)，Q是直线x=3上的一个动点，y轴正半轴上是否存在点P，使△APQ为等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．【参考答案】 知识点睛1.运动的结果2.坐标或表达式 精讲精练1.(5,0)，(-5,0)，(-6，0)，(256-，0)2.（1）(-3（2）存在 (，0)，(-6-0)， (0，0)，(-4，0)3.存在(8，0)，(-2，0)，(9，0)，(436，0)4.存在(7，4)，(3，7)，(72，72)5.存在3，3)，6，3+)，6.存在(0，1)，(0，3)，(0，4)。

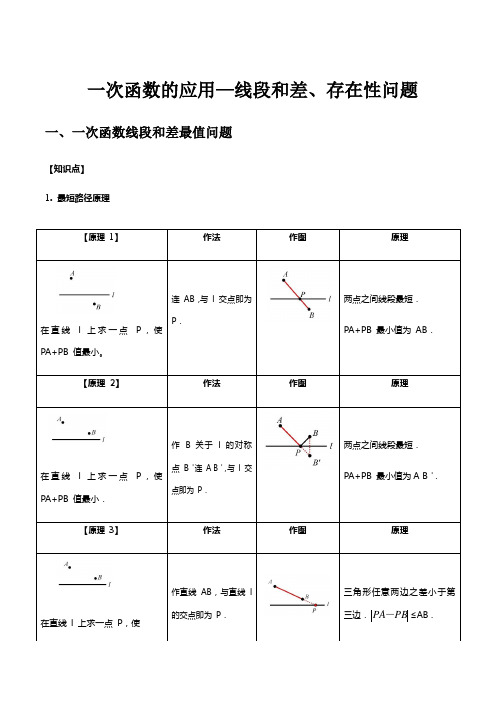
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。

连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式； （2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。

3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy 中，y 轴上有一点P ，它到点(4,3)A ，(3,1)B 的距离之和最小，则点P 的坐标是( ) A ．(0,0)B ．4(0,)7C ．5(0,)7D ．4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ，使的值最大 .作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点即为 P ．三角形任意两边之差小于第三边．≤A B ＇ .PB PA －PB PA －PB PA －【解析】解：作A 关于y 轴的对称点C ，连接BC 交y 轴于P ，则此时AP PB +最小，即此时点P 到点A 和点B 的距离之和最小，(4,3)A ，(4,3)C ∴-，设直线CB 的解析式是y kx b =+，把C 、B 的坐标代入得：3413k bk b =-+⎧⎨-=+⎩，解得：47k =-，57b =，4577y x ∴=-+，把0x =代入得：57y =， 即P 的坐标是5(0,)7，故选：C ．【备注】本题考查了轴对称-最短路线问题，一次函数的解析式，坐标与图形性质等知识点，关键是能画出P 的位置，题目比较典型，是一道比较好的题目．★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)A ，点(2,1)B -，在x 轴上存在点P 到A ，B 两点的距离之和最小，则P 点的坐标是 ．【答案】(1,0)-【解析】解：作A 关于x 轴的对称点C ，连接BC 交x 轴于P ，则此时AP BP +最小，A 点的坐标为(2,3)，B 点的坐标为(2,1)-，(2,3)C ∴-，设直线BC 的解析式是：y kx b =+，把B 、C 的坐标代入得：2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩．即直线BC 的解析式是1y x =--，当0y =时，10x --=，解得：1x =-，P ∴点的坐标是(1,0)-．故答案为：(1,0)-．【备注】本题考查了一次函数图象上点的坐标特征，用待定系数法求一次函数的解析式，轴对称-最短路线问题的应用，关键是能找出P 点，题目具有一定的代表性，难度适中．★★☆练习2．如图，直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，以线段AB 为边在第一象限内作正方形ABCD ．若点P 为x 轴上的一个动点，求当PC PD +的长最小时点P 的坐标．【答案】详见解析【解析】解：直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，则点A 、B 的坐标分别为：(0,3)，(4,0)，如图所示，过点C 作CH x ⊥轴交于点H ，90ABO BAO ∠+∠=︒，90ABO CBH ∠+∠=︒，CBH BAO ∴∠=∠，又90AOB CHB ∠=∠=︒，AB BC =，()AOB BHC AAS ∴∆≅∆，4CH OB ∴==，3HB OA ==，故点(7,4)C ，同理可得点(3,7)D ，确定点C 关于x 轴的对称点(7,4)C '-，连接C D '交x 轴于点P ，则此时PC PD +的长最小，将点C '、D 的坐标代入一次函数表达式并解得： 直线CD 的表达式为：116144y x =-+， 当0y =时，6111x =，故点61P，0)．(11【备注】本题考查的是一次函数上坐标点的特征，涉及到点的对称性、正方形性质等，本题的难点在于：通过证明三角形全等，确定点C、D的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3OB=，D为边OB的中点，若E为x轴上的一个动点，当CDE∆的周长最小时，求点E OA=，4的坐标()A．(3,0)-B．(1,0)C．(0,0)D．(3,0)【答案】B【解析】解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE．若在边OA上任取点E'与点E不重合，连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+，可知CDE∆的周长最小．OB=，D为边OB的中点，42∴=，OD∴，(0,2)D在矩形OACB 中，3OA =，4OB =，D 为OB 的中点，3BC ∴=，2D O DO '==，6D B '=，//OE BC ，Rt ∴△D OE Rt '∽△D BC '，∴OE D OBC D B '=' 即236OE = 1OE =，∴点E 的坐标为(1,0)故选：B ．【备注】此题主要考查轴对称--最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．【答案】3【解析】解：如图，作点A 关于y 轴的对称点A '，连接A B '交y 轴于点C '，此时ABC ∆'的周长最小，设直线A B ' 的解析式为y kx b =+，(1,4)A '-，(3,0)B ，∴430k b k b -+=⎧⎨+=⎩，1k ∴=-，3b =，∴直线A B ' 的解析式为3y x =-+，当0x =时，3y =，(0,3)C ∴'，ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=．所以ABC ∆'的面积为3．故答案为：3．【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积，解决本题的关键是掌握轴对称的性质．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．【答案】详见解析【解析】解： （1）对于直线122y x =+， 令0x =，得到2y =；令0y =，得到4x =-，(4,0)A ∴-，(0,2)B ，即4OA =，2OB =， 则224225AB =+=；（2）过D 作DE x ⊥轴，过C 作CF y ⊥轴，四边形ABCD 为正方形，AB BC AD ∴==，90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒，90FBC ABO ∠+∠=︒，90ABO BAO ∠+∠=︒，90DAE BAO ∠+∠=︒，FBC OAB EDA ∴∠=∠=∠，()DEA AOB BFC AAS ∴∆≅∆≅∆，2AE OB CF ∴===，4DE OA FB ===，即426OE OA AE =+=+=，246OF OB BF =+=+=，则(6,4)D -，(2,6)C -；（3）如图所示，连接BD ，找出B 关于y 轴的对称点B '，连接DB '，交x 轴于点M ，此时BM MD DM MB DB +=+'='最小，即BDM ∆周长最小，(0,2)B ，(0,2)B ∴'-，设直线DB '解析式为y kx b =+，把(6,4)D -，(0,2)B '-代入得：642k b b -+=⎧⎨=-⎩，解得：1k =-，2b =-，∴直线DB '解析式为2y x =--，令0y =，得到2x =-，则M 坐标为(2,0)-， 此时MDB ∆的周长为21062+．【备注】本题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾 股定理，全等三角形的判定与性质，正方形的性质，对称性质，以及一次函数与坐标轴的交点，熟练掌握 性质及定理是解本题的关键（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A ，(2,3)B -，点P 为x 轴上一点，当||PA PB -最大时，点P的坐标为( )A ．1(,0)2B ．5(,0)4C ．1(,0)2-D ．(1,0)【答案】A【解析】解：作A 关于x 轴对称点C ，连接BC 并延长交x 轴于点P ， (1,1)A ，C ∴的坐标为(1,1)-，连接BC ，设直线BC 的解析式为：y kx b =+，∴123k b k b +=-⎧⎨+=-⎩， 解得：21k b =-⎧⎨=⎩， ∴直线BC 的解析式为：21y x =-+， 当0y =时，12x =， ∴点P 的坐标为：1(2，0)，当B ，C ，P 不共线时，根据三角形三边的关系可得：||||PA PB PC PB BC -=-<，∴此时||||PA PB PC PB BC -=-=取得最大值．故选：A ．【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系．此题难度较大，解题的关键是找到P 点，注意数形结合思想与方程思想的应用．★★☆练习1．平面直角坐标系中，已知(4,3)A 、(2,1)B ，x 轴上有一点P ，要使PA PB -最大，则P 点坐 标为【答案】(1,0)【解析】解：(4,3)A 、(2,1)B ，x 轴上有一点P ，||PA PB AB ∴-，∴当A ，B ，P 三点共线时，PA PB -最大值等于AB 长，此时，设直线AB 的解析式为y kx b =+，把(4,3)A 、(2,1)B 代入，可得3412k b k b =+⎧⎨=+⎩， 解得11k b =⎧⎨=-⎩， ∴直线AB 的解析式为1y x =-，令0y =，则1x =，P ∴点坐标为(1,0)，故答案为：(1,0)． 【备注】本题主要考查了坐标与图形性质，利用待定系数法求得直线AB 的解析式是解决问题的关键． ★★☆练习2．如图，在平面直角坐标系中，点A 的坐标为(0,4)，点B 的坐标为(6,0)，点P 在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【答案】C【解析】解：如图，作点A 关于直线1322y x =+的对称点K ，连接AK 交直线于H ，连接PK ．AK PH ⊥，(0,4)A ，∴直线AK 的解析式为24y x =-+，由132224y x y x ⎧=+⎪⎨⎪=-+⎩，解得12x y =⎧⎨=⎩， (1H ∴，20，AH KH =，(2,0)K ∴．PB PA PB PK KB ∴-=-，∴当点P 在BK 的延长线上时，P B P K BK '-'=的值最大，最大值为624-=，故选：C ．【备注】本题考查一次函数图象上的点的特征、轴对称等知识，解题的关键是学会利用对称解决最值问题 属于中考常考题型．【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。

一次函数之等腰直角三角形的存在性(讲义及答案).1. 在正方形网格中，网格线交点称为格点。

已知A、B是两个格点，若点C也是格点且使△ABC为等腰直角三角形，则符合条件的点C只有一个。

2. 做讲义第一题时，先看知识点，再用铅笔计算并将演算保留在讲义上。

如果思路受阻（例如某个点做了2-3分钟），重复上述动作。

如果仍无法解决，重点听课堂讲解。

知识点：1. 解决存在性问题的处理思路①分析不变特征：分析所求图形中的定点、定线、定角等不变特征。

②分类、画图：结合所求图形的形成因素，依据其判定、定义等确定分类，并画出符合题意的图形。

通常先尝试画出其中一种情形，分析解决后，再类比解决其他情形。

③求解、验证：围绕不变特征、画图依据来设计方案进行求解。

验证时，要回归点的运动范围，画图或推理，判断是否符合题意。

注：复杂背景下的存在性问题往往需要研究背景图形，几何背景往往研究点、线、角；函数背景研究点坐标、表达式等。

2. 等腰直角三角形存在性的特征分析及操作要点：三角形的三个顶点分别为直角顶点进行分类，在直角的基础上，再考虑等腰。

通常借助构造弦图模型进行求解。

精讲精练：1. 如图，直线y=-2x+6与x轴、y轴分别交于点A、B。

点P是第一象限内的一个动点，若以A、B、P为顶点的三角形为等腰直角三角形，则点P的坐标为。

2. 如图，直线y=-x+b与x轴、y轴分别交于点A、B。

点C在直线y=-x+b上，且其纵坐标为1。

△___的面积为。

（1）求直线y=-x+b的表达式及点C的坐标。

（2）点P是第二象限内的一个动点，若△ACP是等腰直角三角形，则点P的坐标为。

3. 如图，在平面直角坐标系中，点A的坐标为(2，0)。

点P是y轴正半轴上的一个动点，Q是直线x=3上的一个动点。

若△APQ为等腰直角三角形，则点P的坐标为。

4. 如图，直线y=3x+4与y轴交于点A，点P是直线x=6上的一个动点，点Q是直线y=3x+4上的一个动点，且点Q在第一象限。

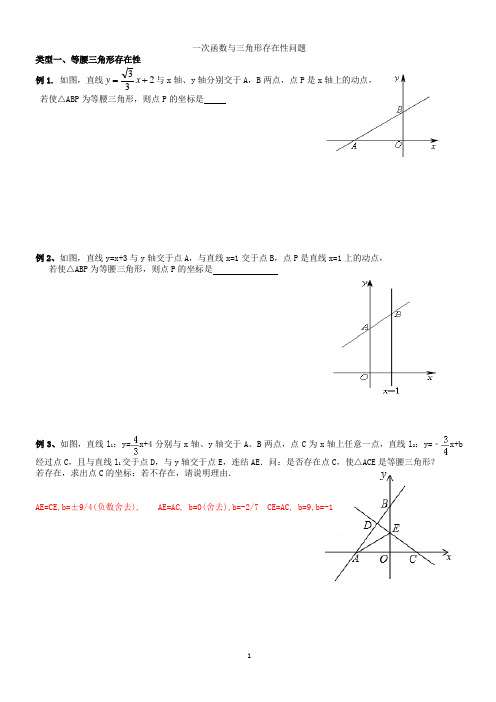
一次函数与三角形存在性问题类型一、等腰三角形存在性例1. 如图，直线233+=x y 与x 轴、y 轴分别交于A ，B 两点，点P 是x 轴上的动点， 若使△ABP 为等腰三角形，则点P 的坐标是例2、如图，直线y=x+3与y 轴交于点A ，与直线x=1交于点B ，点P 是直线x=1上的动点，若使△ABP 为等腰三角形，则点P 的坐标是例3、如图，直线l 1：y=x+4分别与x 轴、y 轴交于A 、B 两点，点C 为x 轴上任意一点，直线l 2：y=﹣x+b 经过点C ，且与直线l 1交于点D ，与y 轴交于点E ，连结AE ．问：是否存在点C ，使△ACE 是等腰三角形？ 若存在，求出点C 的坐标；若不存在，请说明理由．AE=CE,b=±9/4(负数舍去), AE=AC, b=0(舍去),b=-2/7 CE=AC, b=9,b=-1类型二、等腰直角三角形存在性例4、如图3，矩形ABCO，O为坐标原点，B的坐标为（8，6），A，C分别在坐标轴上，P是线段BC上动点，设PC=m，已知点D在第一象限，且是直线y=2x﹣6上的一点，若△APD是不以A为直角顶点的等腰直角三角形，请直接写出点D的坐标．当点D位于直线y=2x-6上时，分三种情况：①点A为直角顶点，结合图形可知，此种情况显然不合题意；②点D为直角顶点，分两种情况：1、点D在矩形AOCB的内部时，设D（x，2x-6）；则OE=2x-6，AE=6-（2x-6）=12-2x，DF=EF-DE=8-x；过D作x轴的平行线EF，交直线OA于E，交直线BC于F；则△ADE≌△DPF，得DF=AE，即：12-2x=8-x，x=4；∴D（4，2）；2、点D在矩形AOCB的外部时，设D（x，2x-6）；则OE=2x-6，AE=OE-OA=2x-6-6=2x-12，DF=EF-DE=8-x；同1可知：△ADE≌△DPF⇒AE=DF，即：2x-12=8-x，x=；∴D（，）；③点P为直角顶点，显然此时点D位于矩形AOCB的外部；设点D（x，2x-6），则CF=2x-6，BF=2x-6-6=2x-12；易证得△APB≌△PDF，得：AB=PF=8，PB=DF=x-8；故BF=PF-PB=8-（x-8）=16-x；联立两个表示BF的式子可得：2x-12=16-x，即x=；∴D（，）；综合上面六种情况可得：存在符合条件的等腰直角三角形；且D点的坐标为：（4，2），（4，14），（，），（，）．例5、如图，点M是直线y=2x+3在第二象限上的动点，过点M作MN垂直x轴于点N，在y轴的正半轴上求点P，使△MNP为等腰直角三角形，请写出符合条件的点P的坐标．如图1，当M运动到（-1，1）时，ON=1，MN=1，∵MN⊥x轴，所以由ON=MN可知，△MNP为等腰直角三角形；如图2，当M运动到第三象限时，要MN=MP，且PM⊥MN，设点M（x，2x+3），则有：-x=-（2x+3），解得：x=-3，所以点M坐标为（-3，-3）．若MN为斜边时，则∠ONP=45°，所以ON=OP，设点M（x，2x+3），则有-x=-1/2（2x+3），化简得-2x=-2x-3，这方程无解，所以这时不存在符合条件的M点；如图2，∵当点M′在第二象限，M′N′为斜边时，这时N′P=M′P，∠M′N′P=45°，设点M′（x，2x+3），则OP=ON′，而OP=1/2M′N′，∴有-x=1/2（2x+3），解得：x=-3/4，∴M′（-3/4，3/2），综上，符合条件的点M坐标是（-3，-3），（-1，1），（-3/4，3/2）练习：1、如图，直线343-+=x y 与x 轴、y 轴分别交于A ，B 两点，点P 是线段AB 上的动点， 若使△OAP 为等腰三角形，求点P 的坐标P 点的坐标是（-28/25，46/25）、（2，3/2）或（36/5，-12/5）．2、如图，在平面直角坐标系中，过点A 的两条直线分别交y 轴于B （0，3）、C （0，﹣1）两点，且∠ABC=30°，AC ⊥AB 于A ．（1）求线段AO 的长，及直线AC 的解析式；（2）若点D 在直线AC 上，且DB=DC ，求点D 的坐标；（3）在（2）的条件下，直线BD 上是否存在点P ，使以A 、B 、P 三点为顶点的三角形是等腰三角形？若存在，请求出P 点的坐标；若不存在，请说明理由．3、直线131+=x y 与x 轴，y 轴分别交于A,B 两点，C 是第二象限点，则求使△ABC 是等腰直角三角形的C 点坐标4、如图1，在平面直角坐标系中，点O 为坐标原点，点A （5，5）为第一象限内一点，点B 在x 轴正半轴上，且∠AOB=45°，OA=OB ．（1）求点B 的坐标；（2）动点P 以每秒2个单位长度的速度，从点O 出发，沿x 轴正半轴匀速运动，设点P 的运动时间为t 秒，△ABP 的面积为S ，请用含有t 的式子表示S （S ≠0），并直接写出t 的取值范围；（3）如图2，在（2）的条件下，点D 坐标为（2，0），连接AD ，AK ⊥AD ，过点B 作x 轴的垂线交AK 于点K ，过点A 作x 轴的平行线a ，在点P 的运动过程中，直线a 上是否存在一点R ，使△PKR 是以PR 为腰的等腰直角三角形？若存在，求出点R 坐标；若不存在，请说明理由．。

专题二：一次函数中等腰直角三角形存在性问题方法总结类型二、等腰直角三角形以(,)A A A x y 、(,)c c C x y 为三角形的边，在平面内找一点B 使得△ABC为等腰直角三角形（二定一动）一.找法：画圆和作垂直平分线①以A 直角顶点，即有23B B 、点；②以C 直角顶点，即有14B B 、点；③以AC 为斜边，即有56B B 、点；二、算法：利用三垂直模型进行计算(,)A A A x y 、(,)B B B x y 、(,)C C C x y 、(,)M M M x y 、(,)M M C x y由MBC ≌NCA可得：MB CN MC AN ==可推出B M C N M C A Nx x y y y y x x -=-⎧⎨-=-⎩例题1、如图，已知直线AB 与x 轴，y 轴分别交于点A （-3,0）、点B （0,2），以点A 为直角顶点，AB 为直角边作等腰直角△ADB ，线段AD 所在直线交y 轴于点P.（1）求直线AB 的解析式；（2）求△BDP 得面积；（3）点C 在x 轴上，D 在x 轴下方时，且△BOC 也是等腰直角三角形，动点M 在y 轴上，若使MC MD -取最大值，求出这个最大值及此时点M 的坐标.【答案】（1）AB 解析式：2+23y x = （2）①1(1,3)D -- 算法：利用1AOB AID ≅ 设1(,)D m n 20(3)0(3)0m n -=--⎧⎨--=-⎩解得13m n =-⎧⎨=-⎩ 则1(1,3)D -- 同理2(5,3)D -（3）根据题意，如图：12(2,0)(2,0)C C -、（两种情况答案一样，自行分类分析）当11,,C D M 三点共线时，MC MD -取最大值，最大值为11C D 11C D 解析式：36y x =--则M （0，-6）11max 10MC MD C D -==练习：1.已知直线1:l y x b =-+与x 轴交于点A ，直线2416:33l y x =-与x 轴交于点B ，直线12l l 、交于点C ，且C 点的横坐标为1．（1）求直线1l 的解析式和点A 的坐标．（2）直线1l 与y 轴交于点D ，将1l 向上平移9个单位得3l ，3l 与x 轴、y 轴分别交于点E 、F ，点P 为3l 上一动点，连接AP 、BP ，当△ABP 的周长最小时，求△ABP 的周长和点P 的坐标．（3）将1l 绕点C 逆时针旋转，使旋转后的直线4l 过点G （-2,0），过点C 作5l 平行于x 轴，点M 、N 分别为直线4l 、5l 上两个动点，是否存在点M 、点N ，使△BMN 是以点M 为直角顶点的等腰直角三角形，若存在，求出点M 的坐标，若不存在，请说明理由．【答案】解：（1）将1x =代入直线41633y x =-，得4161433y =⨯-=-， 故点C 的坐标为(1,4)-，将C 的坐标(1,4)-代入直线y x b =-+得，41b -=-+， 解得3b =-，∴直线1:3l y x =--，令0y =，则30x --=，解得3x =-，故点A 的坐标为(3,0)-，（2）直线3l 为1l 向上平移9个单位所得，故直线3l 的解析式为：6y x =-+，令0x =，得6y =，令0y =，得6x =，故点E ，点F 的坐标分别为(6,0)，(0,6)， 直线2416:33l y x =-与x 轴交于点B ， 令0y =，得4x =，故B 点的坐标为(4,0)，取点B 关于3l 的对称点Q ，设点Q 的坐标为(,)a b ，则线段BQ 的中点坐标为(2a b +，)2b 在直线3l ， ∴622b a b +=-+，（1） 且(1)14b a ⋅-=--即14b a =-，（2） 联立（1）（2）得622b a b b +⎧=-+⎪⎪⎨⎪，解得：62a b =⎧⎨=⎩， (6,2)Q ∴，直线AQ 的解析式：2293y x =+， 当ABP ∆的周长最小时，即AP BP +最小， 连接AQ ，交直线3l 于点P ，此时AP BP +最小，最小值为22(63)(20)85AQ =++-=，7AB =，此时ABP ∆的周长为785+，由22936y x y x ⎧=+⎪⎨⎪=-+⎩解得48111811x y ⎧=⎪⎪⎨⎪=⎪⎩， P ∴点坐标为48(11，18)11， （3）设4l 的解析式：y mx n =+，将(1,4)C -，(2,0)G -，代入y mx n =+得，024m n m n =-+⎧⎨-=+⎩，解得4383m n ⎧=-⎪⎪⎨⎪=-⎪⎩， 4l ∴的解析式为：4833y x =--， 1︒当点M 在直线4l 的上方时，设点(,4)N n -，点48(,)33M s s --， 过点N ，B 分别作y 轴的平行线，过点M 作x 轴的平行线，三条直线分别交于R ，S 两点，如图则R ，S 的坐标分别为48(,)33n s --，48(4,)33s --， RM s n ∴=-，48433RN s =--，4MS s =-，4833SB s =--， 90NMB ∠=︒，90NMR SMB ∴∠+∠=︒，90BMS MBS ∠+∠=︒，90S R ∠=∠=︒，MB MN =，()MNR MBS AAS ∴∆≅∆，RM SB ∴=，RN SM =， 即4833s n s -=--，484433s s --=-， 解得8s =-，16n =-，∴点M 的坐标为(8,8)-，2︒当点M 在直线4l 的下方时，设点(,4)N n -，点48(,)33M s s --， 过点N ，B 分别作y 轴的平行线，过点M 作x 轴的平行线，三条直线分别交于R ，S 两点，如图则R ，S 的坐标分别为48(,)33n s --，48(4,)33s --， RM n s ∴=-，48433RN s =+-，4MS s =-，4833SB s =+， 90NMB ∠=︒，90NMR SMB ∴∠+∠=︒，90BMS MBS ∠+∠=︒，NMR MBS ∴∠=∠，90S R ∠=∠=︒，MB MN =，()MNR MBS AAS ∴∆≅∆，RM SB ∴=，RN SM =，即4833n s s -=+，484433s s +-=-， 解得407s =，16n =， ∴点M 的坐标为40(7，72)7-， 综上点M 的坐标为(8,8)-或40(7，72)7-，练习2：7．（2020春•官渡区期末）如图，在平面直角坐标系中，直线13:4l y x =与直线2:(0)l y kx b k =+≠相交于点(,3)A a ，直线2l 与y 轴交于点(0,5)B -． （1）求直线2l 的函数解析式；（2）将OAB ∆沿直线2l 翻折得到CAB ∆，使点O 与点C 重合，AC 与x 轴交于点D ．求证：四边形AOBC 是菱形；（3）在直线BC 下方是否存在点P ，使BCP ∆为等腰直角三角形？若存在，直接写出点P 坐标；若不存在，请说明理由．【答案】解：（1）直线3?:4l y x =与直线?:l y kx b =+相交于点(,3)A a ， (4,3)A ∴， 直线交?l 交y 轴于点(0,5)B -，5y kx ∴=-，把(4,3)A 代入得，345k =-，2k ∴=，∴直线2l 的解析式为25y x =-；（2）22345OA =+=，OA OB ∴=，将OAB ∆沿直线?l 翻折得到CAB ∆，OB OC ∴=，OA AC =，OA OB BC AC ∴===，∴四边形AOBC 是菱形；（3）如图，过C 作CM OB ⊥于M ，则4CM OD ==，5BC OB ==，3BM ∴=，(4,2)C ∴-， 过1P 作1PN y ⊥轴于N ， BCP ∆是等腰直角三角形， 190CBP ∴∠=︒，1MCB NBP ∴∠=∠， 1BC BP =，BCM ∴∆≅△1()PBN AAS ， 4BN CM ∴==， 1(3,9)P ∴-；同理可得，2(7,6)P -，37(2P ，11)2-． 综上所述，点P 的坐标是(3,9)-或(7,6)-或7(2P ，11)2-．。

2021年第02期总第495期数理化解题研究一次函数背景下的存在性问题王帅兵(河南省郑州市孜文教育信息咨询有限公司450000)摘 要：一次函数是八年级数学的学习内容，在平面直角坐标系中，研究点和直线的动态特征，以及在动 态情境下产生的几何图形存在性问题，是考察学生思维能力的有效载体，已成为考试的重难点.本文将结合具 体题目，从不同方面探讨存在性问题的解法.关键词：一次函数;存在性；对称；两圆一线；弦图中图分类号:G632 文献标识码：A 文章编号：1008 -0333(2021)02 -0017 -02一、两定一动型，注意好“一上一下”两定一动型,是指在给定两个点的情况下,另一点在一条线上运动所产生的面积问题,解决这类问题，要做好 题目分析,有一边与坐标轴平行时直接求解;没有边与坐 标轴平行时，用好“铅锤法”(或“割补法”)，同时注意好 “ 一一上 —下”.例1如图1所示,一次 函数y 二2% +4的图像与坐标 轴分别交于点A 、B ,在一次函数的图象上是否存在一点P , 使得A AOP 的面积为3？思路分析由题设条件，易求出点A 和点0坐标分别为(-2,0)和(0,0),点P 为直 图1线上一动点，不妨设其坐标为(%,y ),当点P 位于%轴上方时,S △A0P 二2 ； y 二3 ,解得y 二3,代入表达式y 二2% + 4 可得点P 坐标为(-1 /2,3).由于坐标系中的对称性，点 P 也可以位于%轴下方，此时可求出点P 的坐标为 (-7/2,-3).综上，点 P 坐标为(-1/2,3)或者(-7/2, -3).一例2如图2所示，直线y 二1 /2%与直线y 二-% + 3 相交于点A ,点B 是直线y 二1 /2%上的一个点，且横坐标 为4.如果点P 是直线y 二-% +3上的一个动点，且满足 △ABP 的面积为9,那么点P 的坐标为 .思路分析 如图2,易求出点A 和点B 坐标分别为(2,1) 和(4,2).如图3,过点P 向%轴做垂线交直线AB 于点F ,设点P ( a , - a +3),那么点F 坐标为(a , ； a )，则A ABP 的面积为："F x ( %B 一 ％a)(3 -a - 2 a )(4 -2)-----------「 - 9.解得 a 二-4,点P 的坐标为(-4,7).同理，如图4时,可得点P 的坐标 为(8,-5).综上，点P 的坐标为(-4,7)或(8,-5).二、等腰三角形，用好“两圆一线”在一次函数的背景下,等腰三角形的存在性问题可 以借助图形的基本性质来解,利用同端点、等长度作圆和 线段垂直平分线.例 3 如图 5 所示, 直线 y - % + 4 与坐标轴交于点 A 和点B ，在%轴上是否存在点P ,使得A ABP 为等腰三角 形？若存在，求出所有满足条件的点P 的坐标.图5 图6思路分析如图6所示,分别以点A 和点B 为圆心 作圆，同时作出线段AB 的垂直平分线，可得与%轴的4个 交点：P ］、戶2、P 3和P 4.分别求解,可得其坐标分别为P 1( -4-4 2 ,0)、P 2(0,0)、P s (4 2 -4,0)心4,0).三、直角三角形，利用顶点来分类对于直角三角形的存在性,可以利用顶点来分类，然 后结合具体条件求解.例4如图7所示,在平面直角坐标系％oy 中，三角收稿日期：2020 -10 -15作者简介：王帅兵(1988. 7 -)，男，河南省鲁山人，本科，从事数学教学研究.17数理化解题研究2021年第02期总第495期板的直角顶点P的坐标为(2,2),一条直角边与兀轴的正半轴交于点A,另一直角边与y轴交于点B,三角板绕点P在坐标平面内转动的过程中，当MA为直角三角形时，请求出所有满足条件的点B的坐标.思路分析分析题设条件可得，乙POA二45°,不可能为直角，'FOA的另两个角可以是直角.如图8,当OA丄AP时，可求出点B的坐标为(0,2);如图9,当OP丄PA时，点B和点O重合，点B坐标为(0,0).综上所述，点B的坐标为(0,2)或(0,0).图7图8图9四、等腰直角三角形，借助弦图轻松解等腰直角三角形的分类问题，可以在构造基本直角的情况下，借助弦图求解.例5如图10所示，直线y二-2兀+4与坐标轴交于点A和点B,在第一象限内是否存在点P,使得A ABP为等腰直角三角形？思路分析由题设条件易得,A(2,0)、B(0,4),OA二2,OB二4.利用心A AOB作弦图，如图11所示,其中P】、P2、戶3是满足条件的点.利用弦图中的全等三角形的性质,以及线段长与坐标的相互转化,可得三点的坐标分别为:P1(4,6)、P2(6,2)、P3(3,3).五、全等三角形，对应后综合求解全等三角形的存在性问题,要注意好顶点的对应，然后借助多种基本方法解题.例6如图12所示，在平面直角坐标系中作矩形OABC,点B坐标为(4,8),将A ABC对折,使点A与点C 重合,折痕交AB于点D,坐标系内是否存在点P(除点B 外),使A APC与A ABC全等？若存在，直接写出符合条件的点P的坐标;若不存在,请说明理由.思路分析由题设条件易得点A与点C的坐标分别为(4,0)、(0,8),直线AC表达式为:y二-2%+8.由矩形性质可得A AOC=△CBA,此时点P与点O重合,坐标为(0,0).由翻折性质可得△ADB'^A CDB',此时,如图13, 18可以延长CP，过点A作CP丄AP于点P,利用等面积法可得点P坐标为(；，?)•如图14,作A ABC关于直线AC 的对称图形，此时，过点P作PQ丄y轴于点Q,利用等面积法可得点P坐标为(-12,24).六、等距离轨迹问题,借助坐标轴三角形构造相似在一次函数背景下的等距离轨迹问题，可以借助一次函数图像与坐标轴的交点,构造相似图形,求出点的坐标，进而找到点所在直线的表达式.例7如图15所示，直线y二2%+6与坐标轴分别交于点A和点B，在平面直角坐标系中是否存在一点,使得点P到直线AB的距离等于25，若存在，请求出点P所在轨迹的表达式;若不存在，请说明理由.思路分析到直线AB距离等于25的点的集合是与直线AB平行的两条直线.由题设条件易得，点A和点B 的坐标分别为(-3,0)和(0,6).如图16,过点B作直线AB的垂线-，在直线-上分别截取BP】二BP?二25,再分别过点P1和点P2作垂直于直线z1的直线z2和z3,直线12和人即为点P的轨迹.因为直线J和厶与直线AB平行,要求其表达式，只要求出点P1和点P2的坐标即可,此时,过点P1作P1Q1丄y轴于点Q1，则△P1Q1B^△BOA,可得P1Q1二4,BQ1二2,可得点P1坐标为(4,4),可求出心:y二2%-4.同理可求出厶：y二2%+16.综上,解决一次函数的存在性问题，一定要研究好背景图形，调用基本技巧和方法,构图确定位置，画图解答.参考文献：[1]王玉新.学好一次函数，善于梳理总结是关键[J].数学学习与研究，2019(19)：135.[2]王淑艳.一次函数解初中几何动点问题[J].理科爱好者，2019(4)：147.[责任编辑:李璟]。

一次函数之存在性（直角三角形）（人教版）一、单选题(共3道，每道33分)1.如图，直线y=2x+4与坐标轴交于A，B两点，P为直线x=1上一动点，连接AP，BP．当△ABP是以点A，B为直角顶点的直角三角形时，点P的坐标为( )A. B.C. D.答案：D解题思路：1．解题要点①首先研究基本图形，对信息进行标注；②研究目标△ABP，A，B为定点，P为动点，若△ABP是直角三角形，需要根据直角顶点进行分类，根据题目信息，分别以B，A作为直角顶点；③对于直角，需要结合题目背景灵活处理，如以点B，点A为直角顶点时，可以借助坐标系背景用函数解析式来求点坐标．2．解题过程由题意得，A（-2，0），B（0，4）．①当时，如图所示，．∵点的横坐标为1，∴．②当时，如图所示，，∴．综上得，点P的坐标为．试题难度：三颗星知识点：直角三角形的存在性2.如图，直线交y轴于点A，且经过点B（4,1）．若P是y轴上的一动点，当△ABP是以点A，B为直角顶点的直角三角形时，点P的坐标为( )A. B.C. D.答案：A解题思路：1．解题要点①首先研究基本图形，对信息进行标注；②研究目标△ABP，A，B为定点，P为动点，若△ABP是直角三角形，需要根据直角顶点进行分类，根据题意信息，点A，B轮流作为直角顶点；③对于直角，需要结合题目背景灵活处理，如以点B为直角顶点时，可以借助坐标系背景用函数解析式来求点坐标；④审题需要注意，点P是y轴上的一动点，需要弄清目标．2．解题过程①若点Ａ充当直角顶点，即时，显然不成立；②若点Ｂ充当直角顶点，即时，过点B作⊥AB，交y轴于点，如图所示，则，∴．综上所述，符合题意的点P的坐标为．试题难度：三颗星知识点：直角三角形的存在性3.如图，将△ABC放在平面直角坐标系中，三个顶点的坐标分别为A（-1，0），B（3，0），C （0，2），P是线段AC上的一个动点（不与点A，C重合），过点P作平行于x轴的直线，交BC于点Q，若在x轴上存在点R，使得△PQR是等腰直角三角形，则点R的坐标为( )A. B.C. D.答案：C解题思路：1．解题要点①观察题目特征，确定为等腰直角三角形存在性问题．②分析定点、动点、不变特征．从直角入手，分类讨论．③画图，表达线段长，借助等腰直角三角形性质建等式．2．解题过程由题意，得A（-1，0），B（3，0），C（0，2），则，．设，则，PQ=-2m+4．①如图，当点Q为直角顶点时，PQ=RQ．，，由-2m+4=m，得，∴．②如图，当点P为直角顶点时，PQ=PR．，，由-2m+4=m，得，∴．③如图，当点R为直角顶点时，RP=RQ．过点R作RD⊥于点D，则，由，得m=1，∴．综上得，点R的坐标为．试题难度：三颗星知识点：等腰直角三角形存在性。

一次函数视角下的特殊三角形存在性问题解题策略探究【摘要】一次函数视角下的特殊三角形存在问题的探究，借助几何画板画图操作活动，正确分析问题、转化化归，模型意识反思，对数形结合思想、方程思想、分类讨论思想的感悟，利用几何法和代数法求解问题。

【关键词】运算意识；几何作图；模型意识；一次函数；特殊三角形一次函数视角下的特殊三角形存在性问题是在变化的过程中，研究背景图形，根据条件探索某种状态是否存在，把函数信息坐标或表达式转化为几何信息。

分析不变特征，确定分类标准，探寻特殊状态运动的结果，画出符合题意的图形求解。

知识储备：用待定系数法求解一次函数的解析式，联立方程组求解两个一次函数图象的交点，求解三个顶点为定点的三角形的面积，用铅锤法求解有顶点是动点的三角形的面积。

解题困惑：对一次函数视角下的特殊三角形存在性问题，如直角三角形、等腰三角形、等腰直角三角形、全等三角形等的存在性问题，学生解题过程存在一些困难，无法画图，进行正确的分类讨论，易出现漏解、错解。

策略探究：假设特殊三角形存在→推理论证→得出相应结论。

类型：两定一动及一定两动，思路：代数法→算理意识，几何法→构图识图，函数法→待定系数法。

一、直角三角形的构造→直角顶点的分类讨论方法策略：分别对三角形三个顶点为直角顶点的情況进行分类讨论，需要同时利用全等、勾股定理等相关知识计算，从而求出对应的点坐标。

【数学活动1】一次函数图象与坐标轴交于点A、B，在坐标轴上找一点C，使得△ABC为直角三角形，求符合条件的C点坐标。

思路探析：找点→两条垂线一个圆，求点→解析式法、距离公式与勾股定理、斜率法（圆上的点），增（舍）点→斜率不存在或等于零，需结合图形检查是否遗漏。

画图探寻：满足条件的坐标轴上的 C 点共有 3 个，如图所示：两垂线→→①若∠BAC=90°，则AB⊥AC，所以以A为垂足作线段AB的垂线，交x轴于C1，则△C1AB是以AB为直角边的直角三角形。

每日一题 079一次函数与等腰三角形武穴市百汇学校徐国纲解题技巧如果△ABC是等腰三角形，那么存在①AB＝AC，②BA＝BC，③CA＝CB三种情况．已知腰长画等腰三角形用圆规画圆，已知底边画等腰三角形用刻度尺画垂直平分线．如图，已知线段AB作等腰三角形，则符合要求的点都在以A、B为圆心，AB长为半径的圆和AB的垂直平分线上，这就是传说中的“两圆一线”.解等腰三角形的存在性问题，有几何法和代数法，把几何法和代数法相结合，可以使得解题又好又快．几何法一般分三步：分类、画图、计算．代数法一般也分三步：表示三边长，分类列方程，解方程并检验．例题解析例❶ 如图1-1，在平面直角坐标系xOy中，已知点D的坐标为(3, 4)，点P是x轴正半轴上的一个动点，如果△DOP是等腰三角形，求点P的坐标．图1-1【解析】分三种情况讨论等腰三角形△DOP：①DO＝DP，②OD＝OP，③PO＝PD．①当DO＝DP时，以D为圆心、DO为半径画圆，与x轴的正半轴交于点P，此时点D 在OP的垂直平分线上，所以点P的坐标为(6, 0)（如图1-2）．②当OD＝OP＝5时，以O为圆心、OD为半径画圆，与x轴的正半轴交于点P(5, 0) （如图1-3）．③当PO＝PD时，画OD的垂直平分线与x轴的正半轴交于点P，设垂足为E（如图1-4）．可求325:48PEl y x=-+，∴25(,0)6P．图1-2 图1-3 图1-4上面是几何法的解题过程，我们可以看到，画图可以帮助我们快速找到目标P ，其中①和②画好图就知道答案了，只需要对③进行计算．代数法先设点P 的坐标为(x , 0)，其中x ＞0，然后表达△DOP 的三边长（的平方）． DO 2＝52，OP 2＝x 2，PD 2＝(x －3)2+42．①当DO ＝DP 时，52＝(x －3)2+42．解得x ＝6，或x ＝0．当x ＝0时既不符合点P 在x 轴的正半轴上，也不存在△DOP ．②当OD ＝OP 时，52＝x 2．解得x ＝±5．当x ＝－5时等腰三角形DOP 是存在的，但是点P 此时不在x 轴的正半轴上（如图1-5）．③当PO ＝PD 时，x 2＝(x －3)2+42．这是一个一元一次方程，有唯一解，它的几何意义是两条直线（x 轴和OD 的垂直平分线）有且只有一个交点．代数法不需要画三种情况的示意图，但是计算量比较大，而且要进行检验．图1-5例❷ 如图2-1，直线3y x =+与y 、x 轴相交于点A 、C ，动点P 以1个单位/秒的速度从点A 出发，沿AC 向点C 移动，同时动点Q 以1个单位/秒的速度从点C 出发，沿CO 向点O 移动，当P 、Q 两点中其中一点到达终点时则停止运动．在P 、Q 两点移动的过程中，当△PCQ 为等腰三角形时，求t 的值．图2-1【解析】在P 、Q 两点移动的过程中，△PCQ 的6个元素（3个角和3条边）中，唯一不变的就是∠PCQ 的大小，夹∠PCQ 的两条边CQ ＝t ，CP ＝6－t .因此△PQC 符合“边角边”的解题条件，我们只需要在∠PCQ 的边上取点P 或Q 画圆．图2-2 图2-3 图2-4①如图2-2，当CP ＝CQ 时，t ＝6－t ，解得3t =(秒).②如图2-3，当QP ＝QC 时，过点Q 作QM ⊥AC 于M ，则CM 1622t PC -==. 在Rt △QMC 中，∵30PCQ =︒∠，∴2CQ =，62tt -=，解得3t =-(秒). ③如图2-4，当PQ ＝PC 时，过点P 作PN ⊥BC 于N ，则1122CN CQ t ==. 在Rt △PNC 中，∵30PCQ =︒∠，∴2CP =，62tt -=，解得9t =-秒).例❸ 如图3-1，已知正方形OABC 的边长为2，顶点A 、C 分别在x 、y 轴的正半轴上，M 是BC 的中点．P(0, m)是线段OC 上一动点（C 点除外），直线PM 交AB 的延长线于点D ．当△APD 是等腰三角形时，求m 的值．图3-1【解析】点P(0, m)在运动的过程中，△APD 的三个角都在变化，因此不符合几何法“边角边”的解题条件，我们用代数法来解．因为PC//DB ，M 是BC 的中点，所以BD ＝CP ＝2－m ．所以D(2, 4－m)．于是我们可以表达出△APD 的三边长（的平方）：22(4)AD m =-，224AP m =+，2222(42)PD m =+-．①当AP ＝AD 时，22(4)4m m -=+．解得32m =（如图3-2）． ②当P A ＝PD 时，22242(42)m m +=+-． 解得43m =（如图3-3）或4m =（不合题意，舍去）． ③当DA ＝DP 时，222(4)2(42)m m -=+-．解得23m=（如图3-4）或2m=（不合题意，舍去）．综上所述，当△APD为等腰三角形时，m的值为32，43或23．图3-2 图3-3 图3-4其实①、②两种情况，可以用几何说理的方法，计算更简单：①如图3-2，当AP＝AD时，AM垂直平分PD，那么△PCM∽△MBA．所以12PC MBCM BA==．因此12PC=，32m=．②如图3-3，当P A＝PD时，P在AD的垂直平分线上．所以DA＝2PO．因此42m m-=．解得43m=．小结：1、等腰三角形的存在性问题，又可以细分为两个定点一个动点，或一个定点一个定角，或只有一个定点，甚至三个点都是动点等几种类型；2、当条件中有定线段时，可以利用“两圆一线”来画图，再计算；在有定角时，可以借助特殊三角形三边比的特征或相似来建立方程；对于既无定线又无定角的问题，可以用代数法来解，即先表达三边，再分类列方程求解，要注意根据题目条件进行检验.对于不同类型的等腰三角形，我们可以灵活选用几何法或代数法，有时候将两种方法结合起来使用，可以使得解题又快又好；3、在进行有关等腰三角形的计算时，常用到勾股定理、三线合一、特殊角的三角函数、相似、一元二次方程等知识；在这个过程中，贯穿了分类讨论、数形结合、方程等数学思想方法.。