下载文档原格式
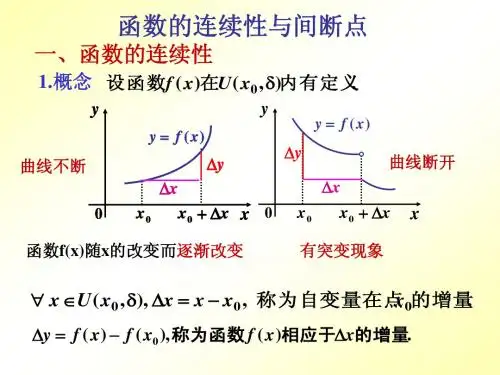
函数的连续性一、函数连续的定义如果函数f(x)在点x0的邻域内有定义，如果limx→x0f(x)=f(x0)，那么称函数f(x)在点x0连续。
如果函数f(x)在点x0的邻域内有定义，如果limx→x0−f(x)=f(x0)，那么称函数f(x)在点x0左连续。
如果函数f(x)在点x0的邻域内有定义，如果limx→x0+f(x)=f(x0)，那么称函数f(x)在点x0右连续。
如果limx→x0+f(x)=limx→x0−f(x)=f(x0)，则函数f(x)在点x0连续。
如果函数f(x)在点x0连续，则limx→x0+f(x)=limx→x0−f(x)=f(x0)。
二、函数的间断点：函数f(x)在点x0的某去心邻域内有定义，如果函数f(x)有下列三种情形之一，则称x0是函数f(x)的间断点。
（1）.在x0处无定义；（2）.在x0处有定义，但limx→x0f(x)在x0处的极限不存在；（3）.在x0处有定义，而且limx→x0f(x)在x0处的极限也存在，但limx→x0f(x)≠f(x0)；间断点可分为两类，即第一类间断点和第二类间断点。
如果函数的左极限和右极限都存在，则称为第一类间断点。
如果左右极限至少有一个不存在，则称为第二类间断点。
如果左右极限都存在且相等，则该间断点称为可去间断点，可去间断点很显然是第一类间断点。
如果函数在x0处的极限值为∞，则点x0称为无穷间断点。
至于震荡间断点和跳跃间断点，可以很容易根据函数图像的特征加以判别。
历年真题1、函数f (x )=|x |x −1x (x+1)ln |x |的可去间断点的个数为(A )0 (B )1 (C )2 (D )3(2013，数三，4分)【解析】函数f (x )=|x |x −1x (x+1)ln |x |在x =−1,0,1处没定义，lim x→−1f (x )=lim x→−1|x |x −1x (x +1)ln |x |=lim x→−1e xln |x |−1x (x +1)ln |x |=lim x→−1xln |x |x (x +1)ln |x |=limx→−11(x +1)=∞lim x→0f (x )=lim x→0|x |x −1x (x +1)ln |x |=lim x→0e xln |x |−1x (x +1)ln |x |=lim x→0xln |x |x (x +1)ln |x |=limx→01(x +1)=1lim x→1f (x )=lim x→1|x |x −1x (x +1)ln |x |=lim x→1e xln |x |−1x (x +1)ln |x |=lim x→1xln |x |x (x +1)ln |x |=limx→11(x +1)=12所以x =0和x =1为可去间断点。
函数的连续性与间断点分析函数的连续性是数学中的重要概念，它描述了函数在某个区间上的平滑性和无间断性。
本文将探讨函数的连续性以及间断点的分类与分析。
一、函数的连续性函数的连续性是指函数在其定义域上的无间断性。
具体而言，对于定义域内的任意两个数a和b，如果函数f在区间[a, b]上的值无论多么接近于f(a)，都能使函数在该区间上连续，那么函数f就被称为在该区间上连续。
函数的连续性可以用极限的概念进行描述。
如果对于函数f的每一个定义域内的点x0，都有lim(x→x₀) f(x) = f(x₀)，那么函数f在点x₀处连续。
换句话说，函数在某一点的函数值等于该点的极限值，这就是函数在该点的连续性。
函数的连续性在实际问题中具有广泛的应用。
例如，在物理学中，我们可以通过函数的连续性分析质体的运动轨迹；在经济学中，连续函数被用于分析经济增长模型等。
函数的连续性是数学建模中常见的假设之一。
二、间断点的分类与分析间断点是指函数在某些点处不满足连续性的现象。
根据函数在间断点的性质，可以将间断点分为三类，即可去除间断点、跳跃间断点和无穷间断点。
1. 可去除间断点可去除间断点是指函数在某点x₀处的极限存在，但函数在x₀处的函数值与该极限值不相等。
通常情况下，通过修正函数在间断点的定义，可以消除可去除间断点。
例如，考虑函数f(x) = (x - 1)/(x - 1)，在x=1处有可去除间断点，但若将f(1)的定义修改为1，则可将间断点去除。
2. 跳跃间断点跳跃间断点是指函数在某点x₀处的左右极限存在且有限，但两侧极限值不相等。
这种间断点的存在导致函数在该点处存在一个突变或跳跃。
例如，考虑函数f(x) = 1/x，在x=0处有跳跃间断点，因为lim(x→0⁺) f(x) = +∞，而lim(x→0⁻) f(x) = -∞。
3. 无穷间断点无穷间断点是指函数在某点x₀处的一侧或两侧的极限为无穷大。
例如，考虑函数f(x) = 1/x，在x=0处有无穷间断点，因为lim(x→0⁺) f(x) = +∞，而lim(x→0⁻) f(x) = -∞。
函数的连续点与间断点在数学中，连续性是描述函数的一种性质。
一个函数在某个点连续意味着在该点附近可以通过函数图像的一条连续曲线来表示。
换句话说，函数在该点的值与该点的极限值相等。
在函数的定义域上，我们可以将连续点分为两类：间断点和连续点。
一个函数的间断点是指在函数定义域上的某个点，该点的函数值与该点的极限值不相等。
可以将间断点进一步细分为可去间断点、跳跃间断点和无穷间断点。
1. 可去间断点：在这种情况下，函数在该点的极限存在，但函数的值与极限值不相等。
这种情况发生在该点存在一个孤立点，也就是说，通过改变函数在该点的定义，可以使其在该点处连续。
例如，函数$f(某) = \frac{某^2 - 1}{某-1}$在$某 = 1$处有一个可去间断点。
2. 跳跃间断点：在这种情况下，函数在该点的左右极限都存在，但极限值不相等。
这种情况下，函数图像会出现一个间断或跳跃。
例如，函数$g(某) = \begin{cases} 1, & 某 < 0 \\ 0, & 某 \geq 0\end{cases}$在$某 = 0$处有一个跳跃间断点。
3. 无穷间断点：在这种情况下，函数在该点的左右极限至少有一个为无穷大。
例如，函数$h(某) = \frac{1}{某}$在$某 = 0$处有一个无穷间断点，在该点的左右极限分别是负无穷和正无穷。
连续点是指在函数定义域上的点，其函数值与该点的极限值相等。
换句话说，函数图像在该点处没有间断或跳跃。
对于一个函数$f(某)$，如果$f(某)$在其定义域上的每一个点都连续，那么该函数被称为在其定义域上连续的函数。
连续性在数学中具有很多重要的性质和应用。
例如，连续函数具有介值定理，即如果$f(a)<y<f(b)$，那么在闭区间$[a,b]$上存在一个$某$使得$f(某)=y$。
这个定理可以应用于实际生活中的许多问题，例如求根问题、优化问题等。
在微积分中，连续性是很重要的。
1.8函数的连续性与间断点一、函数的连续性变量的增量设变量u从它的一个初值u1变到终值u2终值与初值的差u2−u1就叫做变量u的增量记作Δu即Δu=u2−u1设函数y=f(x)在点x0的某一个邻域内是有定义的当自变量x在这邻域内从x0变到x0+Δx时函数y相应地从f(x0)变到f(x0+Δx) 因此函数y的对应增量为Δy= f(x0+Δx)− f(x0)函数连续的定义设函数y=f(x)在点x0的某一个邻域内有定义如果当自变量的增量Δx=x −x0趋于零时对应的函数的增量Δy= f(x0+Δx)− f(x0)也趋于零即或那么就称函数y=f(x)在点x0处连续注①②设x=x0+Δx则当Δx0时xx0因此函数连续的等价定义2设函数y=f(x)在点x0的某一个邻域内有定义如果对于任意给定义的正数ε总存在着正数δ使得对于适合不等式|x−x0|<δ的一切x对应的函数值f(x)都满足不等式|f(x)−f(x0)|<ε那么就称函数y=f(x)在点x0处连续左右连续性如果则称y=f(x)在点处左连续如果则称y=f(x)在点处右连续左右连续与连续的关系函数y=f(x)在点x0处连续函数y=f(x)在点x0处左连续且右连续函数在区间上的连续性在区间上每一点都连续的函数叫做在该区间上的连续函数或者说函数在该区间上连续如果区间包括端点那么函数在右端点连续是指左连续在左端点连续是指右连续连续函数举例1 如果f(x)是多项式函数则函数f(x)在区间(−+)内是连续的这是因为f(x)在(−+)内任意一点x0处有定义且.2 函数在区间[0 +)内是连续的3 函数y=sin x在区间(−+)内是连续的证明设x为区间(−+)内任意一点则有Δy sin(xΔx)sin x因为当D x0时 D y是无穷小与有界函数的乘积所以这就证明了函数y=sin x在区间(-+)内任意一点x都是连续的．4 函数y=cos x在区间(−+)内是连续的二、函数的间断点间断定义设函数f(x)在点x0的某去心邻域内有定义在此前提下如果函数f(x)有下列三种情形之一(1)在x0没有定义(2)虽然在x0有定义但f(x)不存在(3)虽然在x0有定义且f(x)存在但f(x)f(x0)则函数f(x)在点x0为不连续而点x0称为函数f(x)的不连续点或间断点例1正切函数y=tan x在处没有定义所以点是函数tan x的间断点因为故称为函数tan x的无穷间断点例2 函数在点x=0没有定义所以点x=0是函数的间断点当x0时函数值在−1与+1之间变动无限多次所以点x=0称为函数的振荡间断点例3函数在x=1没有定义所以点x=1是函数的间断点因为如果补充定义令x=1时y=2 则所给函数在x=1成为连续所以x=1称为该函数的可去间断点例4 设函数因为所以x=1是函数f(x)的间断点如果改变函数f(x)在x=1处的定义令f(1)=1 则函数f(x)在x=1 成为连续所以x=1也称为该函数的可去间断点例5 设函数因为,所以极限不存在x0是函数f(x)的间断点因函数f(x)的图形在x=0处产生跳跃现象我们称x=0为函数f(x)的跳跃间断点间断点的分类:通常把间断点分成两类如果x0是函数f(x)的间断点但左极限f(x0−0)及右极限f(x0+0)都存在那么x0称为函数f(x)的第一类间断点不是第一类间断点的任何间断点称为第二类间断点在第一类间断点中左、右极限相等者称为可去间断点不相等者称为跳跃间断点无穷间断点和振荡间断点显然是第二间断点。
函数连续性与间断点例题和知识点总结在数学分析中，函数的连续性与间断点是一个非常重要的概念。
理解它们对于解决各种数学问题，特别是涉及到函数的性质和极限的问题，具有关键作用。
下面我们将通过一些例题来深入探讨函数的连续性与间断点，并对相关知识点进行总结。
一、函数连续性的定义设函数＄f(x)＄在点＄x_0$ 的某一邻域内有定义，如果当自变量的增量＄＼Delta x$ 趋近于零时，函数对应的增量＄＼Delta y ＝ f(x_0 ＋＼Delta x) f(x_0)＄也趋近于零，那么就称函数＄f(x)＄在点＄x_0$ 处连续。
用数学语言表示为：＄＼lim_{＼Delta x ＼to 0} ＼Delta y ＝＼lim_{＼Delta x ＼to 0}f(x_0 ＋＼Delta x) f(x_0) ＝ 0$或者＄＼lim_{x ＼to x_0} f(x) ＝ f(x_0)＄二、函数连续性的条件1、函数＄f(x)＄在点＄x_0$ 处有定义。
2、＄＼lim_{x ＼to x_0} f(x)＄存在。
3、＄＼lim_{x ＼to x_0} f(x) ＝ f(x_0)＄三、间断点的定义如果函数＄f(x)＄在点＄x_0$ 处不满足上述连续性的条件，那么就称点＄x_0$ 为函数＄f(x)＄的间断点。
四、间断点的类型1、可去间断点函数在该点处的左极限、右极限都存在且相等，但不等于该点的函数值，或者函数在该点无定义。
例如，函数＄f(x) ＝＼frac{x^2 1}｛x 1}＄在＄x ＝ 1$ 处无定义，但＄＼lim_{x ＼to 1} ＼frac{x^2 1}｛x 1} ＝ 2$ ，所以＄x ＝ 1$ 是可去间断点。
2、跳跃间断点函数在该点处的左极限、右极限都存在，但不相等。
比如，函数＄f(x) ＝＼begin{cases} x ＋ 1, ＆ x ＜ 0 ＼＼ x 1, ＆ x＼geq 0 ＼end{cases}＄在＄x ＝ 0$ 处，左极限为＄1$ ，右极限为＄－1$ ，所以＄x ＝ 0$ 是跳跃间断点。
第 6 次课 2 学时
§1.9 函数的连续性与间断点
一、函数的连续性
连续性是函数的重要性态之一，在实际问题中普遍存在连续性问题，如气温的变化，物体速度的变化，动植物的生长等。
这些现象在函数上的反映，就是函数的连续性问题。
1．函数的增量
一个变量u 由初值1u 变到终值2u ，终值与初值之差称为u 的增量( 或改变量)，记作 1,u u ∆∆-2即 u=u
对于函数()y f x =，设它在0x 及0x 的某个邻域内有定义，在0x 处给自变量 x 一个增量x ∆，则函数有相应的增量00((y y f x f x ∆∆=∆， +x)- )
（几何解释）
21()2 1.f x x =-∆∆例设分别求：
(1) x 由１变到1.2时，
（2) x 由１变到0.8时，
的增量x 和y .
解：（略）
2．函数的连续性
如果自变量 x 的增量 x ∆很小时，函数y 的增量y ∆ 也很小，则说明函数是随着自变量的渐变而渐变的，这时称函数是连续的。
定义 1：设)(x f y =在0x 的某邻域内有定义，如果当自变量x 在0x 的增量0x ∆→时，相应函数的增量00()()0y f x x f x ∆=+∆-→，就称函数)(x f y =在0x 点处连续。
注 ：)(x f 在0x 点连续0lim 0x y ∆→⇔∆=。
例2 ：证明函数2
()21f x x =-在x=1 处连续。
证明：函数的定义域为(),-∞+∞，在x=1 的邻域内有定义。
()()()()2222002:1112*1142lim lim 420()211x x x x x x y x x f x x x ∆→∆→→+∆→∆⎡⎤∆∆∆---=∆+∆⎣⎦
⎡⎤∆=∆+∆=⎣
⎦=-= ， f(x): f(1)f(1+x)
y=f(1+x)-f(1)=21+x 故 在 处连续 ．
（类似可证该函数在其定义域内的任意一点处都连续。
）
[]0
00000000()()
lim lim ()()0lim ()()x x x x x x x x x x x y f x f x f x f x f x f x ∆→→→=+∆∆→→∆=-∆-== ，则当时， ，这时根据定义１ ， y=0 可以写作 ，即 .
定义2：设)(x f y =在0x 的某邻域内有定义，如果0x x → 时f(x)的极限存在，且等于它在0x 的函数值,即0
0lim ()()x x f x f x →= ，则称 f(x) 在点0x 连续。
左（右）连续：若)()0()(lim 00x f x f x f x x =-=-←→，就称)(x f 在0x 点左连续。
若)()0()(lim 00x f x f x f x x =+=+
→，就称)(x f 在0x 点右连续。
如果)(x f 在区间I 上的每一点处都连续，就称)(x f 在I 上连续；并称)(x f 为I 上的连续函数；若I 包含端点，那么)(x f 在左端点连续是指右连续，在右端点连续是
指左连续。
连续函数的图像是一条不断开的曲线。
定义1ˊ：设)(x f y =在0x 的某邻域内有定义，若对0,0>∃>∀δε，当δ<-0x x 时，有ε<-)()(0x f x f ，就称)(x f 在0x 点连续。
定理：)(x f 在0x 点连续)(x f ⇔在0x 点既左连续，又右连续。
【例3】多项式函数在),(+∞-∞上是连续的；所以)()(lim 00
x f x f x x =→，有理函数在分母不等于零的点处是连续的，即在定义域内是连续的。
以上由§1.6【例2】的推论1、推论2即得。
【例4】不难证明x y x y cos ,sin ==在),(+∞-∞上是连续的。
【例5】证明x x f =)(在0=x 点连续。
证明：0lim lim ,0)(lim lim 0
00000===-=+→+→-→-→x x x x x x x x ，又0)0(=f ，所以由定理 ⇒ x x f =)(在0=x 点连续；
或由前§1.4习题5知)0(0lim 0
f x x ==→，所以 ⇒ x x f =)(在0=x 点连续。
【例6】讨论函数⎩⎨⎧<-≥+=02
02x x x x y 在0=x 的连续性。
解：220)2(lim lim ,220)2(lim lim 0
0000000=+=+=-=-=-=+→+→-→-→x y x y x x x x ，因为22≠-，所以该函数在0=x 点不连续，又因为2)0(=f ，所以为右连续函数。
二、函数的间断点
通俗地说，若)(x f 在0x 点不连续，就称0x 为)(x f 的间断点，或不连续点，为方
便起见，在此要求0x 的任一邻域均含有)(x f 的定义域中非0x 的点。
间断点有下列三种情况：
（1）)(x f 在0x x =没有定义；
（2）)(lim 0
x f x x →不存在； （3）虽然)(lim 0x f x x →存在，()f x 在0x 点也有定义，但)()(lim 00
x f x f x ≠→。
几种常见的间断点类型：
【例7】设21)(x x f =
，当∞→→)(,0x f x ，即极限不存在，所以0=x 为)(x f 的间断点。
因为∞=→2
01lim x x ，所以0=x 为无穷间断点。
【例8】x
y 1sin =在0=x 点无定义，且当0→x 时，函数值在1-与1+之间无限次地振荡，而不超于某一定数，见书上图，这种间断点称为振荡间断点。
1.⎩⎨⎧∉∈=Q x Q x x f 1
)( x ∀均为振荡间断点。
2、⎪⎩⎪⎨⎧===或无理数1,00
1
)(x q p x q x f Q x ∈不连续，Q x ∉连续。
【例9】 x x y sin =在0=x 点无定义，所以0=x 为其间断点，又1sin lim 0=→x x x ，所以若补充定义1)0(=f ，那么函数在0=x 点就连续了。
故这种间断点称为可去间断点。
【例10】 [例6]的函数在0=x 点不连续，但左、右极限均存在，且有不等于)0(f 的，这种间断点称为跳跃间断点。
例如x y sgn =在0=x 处即为跳跃间断点。
归纳：(1)∞=→)(lim 0
x f x x ，0x 为无穷间断点； (2))(lim 0
x f x x →震荡不存在，0x 为震荡间断点； (3))()(lim 00
x f A x f x x ≠=→，0x 为可去间断点； (4))(lim )(lim 0
000x f x f x x x x +→-→≠，0x 为跳跃间断点。
如果)(x f 在间断点0x 处的左右极限都存在，就称0x 为)(x f 的第一类间断点，显然它包含(3)、(4)两种情况；否则就称为第二类间断点。
