当前位置：文档之家 › 连续性间断点,连续函数的运算

连续性间断点,连续函数的运算

  • 格式：pdf
  • 大小：868.55 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

函数连续性定义和间断点.

函数连续性定义和间断点.
性质1:（局部有界性）若函数 y f ( x) 在 x0点连续 则存在 x0的一个邻域 U ( x0 , ) 及定值 M ，当 x U ( x0 , ) 时，有 f ( x) M 。 性质2:（局部保号性）若函数 y f ( x) 在 x0点连续
f ( x0 ) 0(或f ( x0 ) 0)，则存在 x0的一个邻域 U ( x0 , ) ，
x x0
lim f ( x) f ( x0 ) , 则称函数 f ( x) 在 x0 连续.
在点 x0 连续必须具备下列条件: 有定义 , 即 存在 ;
可见 , 函数 (1) (2) 极限 (3)
在点
存在 ;
例1:讨论函数
在点
处的连续性
注意: (1)若 f ( x) 在 x0 点连续, 则极限运算和函数运
1
1
1
x
x2 例3：设,讨论在x=0处的连续性 x0
2
解: lim f ( x) lim x 0 , f (0) 1
lim f ( x) f (0)
x 0
x 0为函数的可去间断点.
注意：可去间断点只要改变或者补充间断处函数的
算 f 可以交换顺序。即：
x x0
lim f ( x) f ( x0 ) f ( lim x)
x x0
(2)函数 f ( x) 在 x0 连续.
x x0
lim f ( x) 存在
2.函数 f ( x)在 x0 点连续的等价定义 定义：设函数 f ( x)自变量由 x0变到 x ,则 x x x0
连续函数的图形是一条连续而不间断的曲线. 及 由例2知函数 内是连续的 在其定义域区间
二、 函数的间断点

《高等数学》函数的连续性与连续函数的计算

《高等数学》函数的连续性与连续函数的计算

,)0),,
都lim有
x x0
Pli(mx)R(Px)(
x x0
x0R) (
x0c)ontinue
机动 目录 上页 下页 返回 结束
对自变量的增量
有函数的增量
函数 在点 连续有下列等价命题:
lim
x x0
f
(x)
f
(x0 )
lim y 0
x0
lim
x0
f
( x0
x)
f (x0 )
y y f (x)
第七节（2-1）
第一章
函数的连续性与
连续函数的运算
一、函数的连续性
二、函数的间断点 三、小结、思考题
机动 目录 上页 下页 返回 结束
一、 函数连续性的定义
定义: 设函数
在 的某邻域内有定义 , 且
则称函数 f (x)在 x0 连续.
可见 , 函数
在点 x0 连续必须具备下列条件:
(1)
在点 有定义 , 即
间断点分类:
第一类间断点: 及
均存在 ,
若 若 第二类间断点:
称 x0为可去间断点 . 称 x0 为跳跃间断点 .
及
中至少一个不存在 ,
若其中有一个为 , 称 x0 为无穷间断点 .
若其中有一个为振荡 , 称 x0 为振荡间断点 .
机动 目录 上页 下页 返回 结束
例4
讨论函数
f
(
x)
x, 1 x,
2
(k
0,1,2,).
2
x, x 1
四 、 f ( x) 0, x 0 x 1 和 x 1 为 第 一 类 间 断 点 .
x, x 1
五、(1)a 0, b 1;

03.函数的连续性

03.函数的连续性
并且, lim sin x = sin x0
x → s x = cos x0
x→x0
所以, 多项式及正, 余弦函数在任何点x0处连续.
一、函数的连续点与间断点
x, 当x ≥ 0时, 在x = 0处连续. 例1. 证明f ( x) =| x |= − x, 当x < 0时,
0
x→ x0
间断点有2类： 跳跃间断点：f ( x0 + 0), f ( x0 − 0)存在但不相等； 第一类间断点： 可去间断点： f ( x)存在但 lim f ( x) ≠ f ( x ).或f ( x )无定义 lim 0 0 x → x0 x → x0 第二类间断点：f ( x0 + 0), f ( x0 − 0)中至少有一不存在.
第 二 类 间 断 点
0
x0
y
y
x
0
x 振荡型
无穷型
一、函数的连续点与间断点
lim f ( x) ≠ f ( x0 )或f ( x0 )无定义
+ 0 − 0
间 断 点
可去间断点
x → x0
跳跃间断点 xlim f ( x ) ≠ xlim f ( x ) →x →x 无穷间断点
f ( x ) 在 x 0点 左 右 极 限 至 少 有 一 个 为 无 穷 大
x →0
故, f (x)在x=0间断. 图形为
y 1 o –1
y=f (x)
x
一、函数的连续点与间断点
若f (x)在(a, b)内每一点连续, 则称f (x)在 开区间(a, b)内连续.
若f (x)在(a, b)内连续, 且f (x)在x=a右连续. 在x=b左连续. 则称f (x)在闭区间[a, b]上连续.

间断点的分类及连续函数的性质

间断点的分类及连续函数的性质
间断点的分类及连 续函数的性质
目 录
• 连续函数的基本性质 • 间断点的分类 • 连续函数的应用 • 连续函数与离散函数的关系 • 连续函数与极限的关系
01
CATALOGUE
连续函数的基本性质
定义与性质
定义
如果对于任意给定的正数ε，都存在一个正数δ，使得当|x'-x|<δ时，|f(x')-f(x)|<ε，则称函数f在点x处 连续。
连续函数的运算性质
线性性质
若函数f和g在某点连续，则f+g、f-g、fg和f/g（g≠0） 也在该点连续。
01
指数性质
若函数f在某点连续，则对于任意实数a ，函数f^a和e^f在在该点也连续。
02
03
幂性质
若函数f和g在某点连续，则f^g在在该 点也连续。
02
CATALOGUE
间断点的分类
第一类间断点（可去间断点和跳跃间断点）
VS
区别
离散函数和连续函数在定义域和值域上存 在本质的区别。离散函数的定义域和值域 都是离散的数集，而连续函数的定义域和 值域都是实数集。此外，离散函数和连续 函数的性质也存在较大的差异，如连续函 数具有可微性、可积性等性质，而离散函 数则没有这些性质。
离散函数在实际问题中的应用
• 离散函数在实际问题中有着广泛的应用， 如计算机科学、统计学、物理学等领域。 在计算机科学中，离散函数被广泛应用于 算法设计和数据结构中，如排序算法、图 算法等。在统计学中，离散函数被用来描 述概率分布和概率密度函数。在物理学中 ，离散函数被用来描述离散系统的状态和 行为，如量子力学中的波函数、分子动力 学中的粒子位置等。
可去间断点
在这一点，函数值存在，但导数不存 在。

函数的间断点及其分类

函数的间断点及其分类

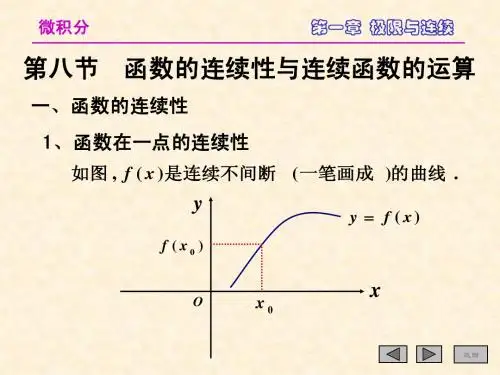
第一章第八节函数的连续性定义1.10.)()(00内有定义的某邻域在点设x U x x f 1.函数在一点连续的定义存在；)(lim )1(0x f x x →若)()(lim )2(00x f x f x x =→则称函数.)(0处连续在点x x f 注1°函数在一点连续的等价定义之一设有函数y = f (x ). 当自变量x 从增量概念:0x 变到,0x x ∆+x ∆则称为自变量的增量(或改变量).若相应地函数y 从)(0x f ),(0x x f ∆+变到则称)()(00x f x x f y −∆+=∆为函数的增量(或改变量).定义1.9（函数在一点连续的增量定义）,00→∆→x x x 就是.0)()(0→∆→y x f x f 就是.0lim 0=→y x ∆∆.)()(00内有定义的某邻域在点设x U x x f ⇔处连续在点0)(x x f定理处连续点在函数0)(x x f 处既左连续又右连续点在0)(x x f ⇔).()()(000x f x f x f ==⇔+−例2解⎪⎪⎩⎪⎪⎨⎧≤<−=<≤=.21,2,1,2,10,)(2x x x x x x f 讨论函数在点x = 1处的连续性.由于=−→)(lim 1x f x 21lim x x −→,1==+→)(lim 1x f x )2(lim 1x x −+→,1=1)(lim 1=→x f x ,2)1(=f 所以f (x ) 在点x = 1 处不连续.≠在区间上每一点都连续的函数, 叫做在该区间上连续的函数, 或者说函数在该区间上连续.,),(内连续如果函数在开区间b a 连续函数的图形是一条连续而不间断的曲线.3. 函数在区间上的连续性.],[)(b a C x f ∈记作, 处右连续端点并且在左a x =,处左连续在右端点b x =.],[)(上连续在闭区间则称函数b a x f如果上述三个条件中有一个不满足，则称f (x )在二、函数的间断点及其分类:)(00条件连续必须满足以下三个处在点函数的去心邻域内有定义的在点x x f x ;)()1(0有定义在点x x f ;)(lim )2(0存在x f x x →).()(lim )3(00x f x f x x =→内有定义，的某去心邻域在点设)()(00x U x x f o1. 定义(或间断点).点x 0 处不连续(或间断)，并称点x 0为f (x )的不连续点lim lim 1=+∞=>−∞→+∞→xx xx a a a 时，当lim lim 1=+∞=>−∞→+∞→xx xx a a a 时，当，x x cot ,tan x csc ,sec 结论：三角函数在其定义域内连续.利用极限的四则运算法则可以证明：推论(连续函数的线性运算法则))( )(x g x f 和α和β是常数,)()(x g x f βα+若函数此运算法则对有限个函数成立.在点0x 连续,则函数)( )(x g x f 和的线性组合在点0 x 连续.结论：反三角函数在其定义域内连续.结论：指数函数，对数函数在其定义域内皆连续.1. 函数记号f 与极限记号可以交换次序;意义:变量代换x=.2的理论依据uϕ(.))(特别地，若定理1.17是定理1.16 的特殊情形例9.),0()(内连续在为常数证明：+∞=µµxy 证xx y ln e µµ==内连续，在),0(ln )(+∞==x x u µϕQ 内连续在而),(e )(+∞−∞==uu f y .),0()(内连续在为常数+∞=∴µµx y 可以证明：µx y =对于μ取任何实数,均在其定义域内连续.结论：幂函数在其定义域内连续.结论：一切初等函数在其定义区间内连续.是指包含在定义域内的区间.）端点为单侧连续=])([x f ϕ1,2≤x x 1,2>−−x x.0,0,2,0,2)(连续性处的在讨论函数=⎩⎨⎧<−≥+=x x x x x x f 解)2(lim )(lim 0+=++→→x x f x x 2=)2(lim )(lim 0−=−−→→x x f x x 2−=.0)(处不连续在点故函数=x x f 备用题例2-1)0()0(+−≠f f =+)0(f =−)0(f ∵∴不存在)(lim 0x f x→例2-3解⎪⎩⎪⎨⎧≥+<=,0,,0,)(x x a x e x f x 设函数应当怎样选择a,使得f (x ) 在x =0 处连续.=−)0(f xx e−→0lim ,1==+)0(f )(lim 0x a x ++→,a =,)0(a f =由连续的充要条件)0()0()0(f f f ==+−得a =1.所以当a =1时，f (x )在x =0处连续.。

4函数的连续性与间断点+总结

4函数的连续性与间断点+总结
第一章
§1.1 映射与函数
函数与极限
§1.2 §1.3 §1.4 §1.6 §1.7 §1.8 §1.9 §1.10
数列的极限 函数的极限 无穷小与无穷大 §1.5极限运算法则 极限存在准则 两个重要极限 无穷小的比较 函数的连续性与间断点 连续函数运算与初等函数连续性 闭区间上连续函数的性质
极限概念, 无穷小与极限的关系, 极限运算法则, 两个重要极限, 连续概念, 初等函数的连续性, 间断点及其分类。
设 在点 的某去心邻域内有定义 , 则有下列情 形之一： 函数f(x)在点x0处连续必须满足以下三个条件: 无 定义; (1) f(x)在点x0处 有
( 2) 函数 lim f ( x )存在 (2) 在 ; 虽有定义 , 但
( 3) 函数 lim f ( x ) (3) 在f ( x虽有定义 ,且 0 ).
2
例1：求 lim
x 3
x 3 2 x 9
P66 例3
ln(1 x ) . 例2：求 lim x 0 x
x a 例3：求 lim 1. x 0 x
解 原式 lim ln(1 x ) ln[lim(1 x ) ] ln e 1. x 0 x 0 P68 例7
三角函数的和差化积公式
sin sin 2 sin

2 2
2
cos cos

2
sin sin 2 sin


2

2
cos cos 2 cos

cos
cos cos 2 sin

2
sin

2
二、函数的间断点
o
x
称x 0为函数的跳跃间断点 . ∴

第二讲 函数的连续性讨论

机动 目录 上页 下页 返回 结束
例2 1. 讨论函数 间断点的类型.
答案: x = 1 是第一类可去间断点 , x = 2 是第二类无穷间断点 . 2. 设 时 为
连续函数.
提示:
机动
目录
上页
下页
返回
结束
例3
证明函数
sin x 1. 证 因为 lim x 0 x
sin x , x 0, f ( x) x 在 x = 0 处是第一类间断点. 0 ,x0 y

故 x 1 为跳跃间断点.
在 x 0 , 1处 , f ( x) 连续.
机动 目录 上页 下页 返回 结束
二、连续函数的运算与初等函数的连续性
1、连续函数的运算法则 2、初等函数的连续性
机动
目录
上页
下页
返回
结束
1、连续函数的运算法则
定理1. 在某点连续的有限个函数经有限次和,差,积 , 商(分母不为 0) 运算,结果仍是一个在该点连续的函数 . 例如, 在其定义域内连续 定理2. 连续单调递增 (递减)函数的反函数 也连续单调 递增(递减). (证明略) 例如, y sin x 在 上连续单调递增，
二分法


1 2
0
1 x
3 4
则 ( 1 , 3 ) 内必有方程的根 ; 可用此法求近似根. 2 4
机动 目录 上页 下页 返回 结束
故复合函数
机动 目录 上页 下页 返回 结束
例如,
是由连续函数链
x R*
复合而成 , 因此
x R * 上连续 . 在
y
1 y sin x
o
x
机动

东南大学考研课件-极限,连续,间断

若 f ( x ) 为 偶 函 数 , 则 F ( x ) 也 为 偶 函 数
东南大学
例.高阶导数问题
贺传富
东南大学
3.
贺传富
东南大学
贺传富
例 4 (1)求 f(x)ln i m 1 1 x x 2n
(2 )求 f(x ) lim (s in t)s in t x s in x t xs in x
(3 )求 f(x ) tl im x 2 e e tt (( x x 1 1 )) 1 a x
一.基本内容:
1.导数 导数与左右导数以及它们的关系 导数的几何意义 可导与连续的关系
18个基本导数公式
贺传富
东南大学
2.求导法则 四则运算求导法则;
贺传富
复合函数求导法则;
反函数求导法则; 隐函数求导法则;
由参数方程确定的函数的求导法则;
对数求导法则;
东南大学
3. 变限函数的导数:
贺传富
东南大学
2.
贺传富
东南大学
贺传富
例. 变限所定义的函数的导数:
1. 设 f(x)=xlntdt(x0),
11t 求f (x) f ( 1 )
x
2 . 设 f ( x ) 在 ( , ) 上 连 续 ,
F ( x ) = x ( x 2 t)f( t) d t( x 0 ) ,证 明 : 0
东南大学
贺传富
2)常用极限


limarctanx , limarctanx
x
2 x
2
limarccotx0, limarccotx
x
x
lim ex 0,
limex

1-8函数的连续性与连续函数的运算


x 1 可去间断点 .
(2)
x , y f ( x) 1 2,
x 1 x 1
x 1
可去间断点 .
返回
微积分
第一章 极限与连续
x 1 , (3) y f ( x) 0 , x 1 ,
x0 x0 x0
x0
跳跃间断点 .
1 / x , x 0 (4) y f ( x) x, x0
O
: 令 f (1 ) 2 ,
y
2
y f (x)

1
x
返回
微积分
第一章 极限与连续
注意：
可去间断点的特点是 或修改定义
x x0
lim f ( x ) 存在 ， 通过补充定义
x x0
, 令 f ( x 0 ) lim f ( x ), 可使 f ( x ) 在 x 0 连续 .

结论：
f ( x ) 在 x 0 连续 f ( x ) 在 x 0 既左连续又右连续 f ( x ) f ( x ) f ( x0 )
0 0
返回
微积分
第一章 极限与连续
x 2 1, x 0 例 3 . 已知 f ( x ) 在 x 0 处连续 , 求 b . 2 x b, x 0
x 0 x 0 .
返回
微积分
第一章 极限与连续
x 1 (2) f ( x ) 0
x1 x1
x 1 x 1
在 x 1 处有定义 ,
但 lim f ( x ) lim ( x 1 ) 2 f ( 1 ). 故 f ( x ) 在 x 1间断 .修改定义 则 f ( x ) 在 x 1 连续 . 称 x 1为 f ( x )的 可去间断点 .

函数的连续性与连续函数的运算

连续，由此得到函数 x , x 的连续性.
y
x0 处
y max{ f ( x), g ( x)}
y f x y g x
y min{ f ( x), g ( x)}
O
x
2.复合函数的连续性 定理2 若函数 y f (u ) 在点 u
u u ( x) 在点 x x0 处连续, 则复合函数 y f u( x)
1 f ( x) g ( x) f ( x) g ( x) , 2
( x) min{ f ( x), g ( x)}
1 f ( x) g ( x) f ( x) g ( x) , 2
再注意到：若 f ( x)在点 x0 处连续，则 f ( x) 在点
g x
f x
g ( x0 ) 0
都在点 x0 处连续.
例
设函数 f ( x), g ( x) 在点 x0 处连续，则函数
( x) max{ f ( x), g ( x)}, ( x) min{ f ( x), g ( x)},
在点 证
x0 处连续. 因 ( x) max{ f ( x), g ( x)}
y
1

1
之间变动，则把点 x0 称为函数 f ( x)的振荡间断点. 可去间断点与跳跃间断点的特征是,
若当 x x0 时，函数值 f ( x) 无限次地在两个不同的数
函数在这一点的左右极限均存在. 通常把这一类间断点
称为第一类间断点.
除此之外的间断点称为第二类间断点.
x 2 1 x 1 例 讨论函数 f ( x) 0 1 x 1 的连续性. x x 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

无穷间断点 左右极限至少有一 第二类间断点 振荡间断点 个不存在
思考与练习
讨论函数
f
(x)
x2
x2 1 3x
2
间断点的类型.
答案: x = 1 是第一类可去间断点 ,
x = 2 是第二类无穷间断点 .
备用题 确定函数 f (x)
1 间断点的类型. x
1 e1x
解: 间断点 x 0, x 1
证: x ( , )
y sin(x x) sin x
2
sin
x 2
cos(
x
x 2
)
y
2
sin
x
2
cos(
x
x
2
)
2
x
2
1
x
x 0
0
即 lim y 0
x0
这说明 y sin x 在 ( , )内连续 .
同样可证: 函数 y cos x 在( , )内连续 .
二、 函数的间断点
y
y f (x)
y x
0 x0 x0 x x
y
y f (x)
y
x
0 x0 x0 x x
2. 连续的定义
定义 1：设 f (x) 在U (x0 , )内有定义，若
lim y
x0
lim [
x0
f
( x0
x)
f
(x0 )]
0,
则称 f (x) 在 x0 点连续，x0 称为 f (x)的连续点.
设 x x x0 ,
y
y f (x)
y f ( x) f ( x0 ),
y
x 0 就是 x x0,
x
0 x0 x0 x x
y 0 就是 f ( x) f ( x0 ).
定义2: 设函数 y f (x) 在 x0 的某邻域内有定义 , 且
lim
x x0
f (x)
f (x0 ),
f (x0 ) 及 f (x0 ) 中至少一个不存在 ,
若其中有一个为 ,称 x0 为无穷间断点 .
若其中有一个为振荡, 称 x0 为振荡间断点 .
例如:
(1) y tan x
x
π 2
为其无穷间断点
.
(2) y sin 1 x
x 0 为其振荡间断点 .
y y tan x
O
x
2
y y sin 1 x
(3)
lim
x x0
f (x)
f (x0 ).
若 f (x) 在某区间上每一点都连续 , 则称它在该区间上 连续 , 或称它为该区间上的连续函数 .
在闭区间 [a , b] 上的连续函数的集合记作 C [ a , b ].
例如, P(x) a0 a1x an xn ( 有理整函数 ) 在 ( , ) 上连续 .
一、连续函数的运算法则
定理1. 在某点连续的有限个函数经有限次和 , 差 , 积 ,
商(分母不为 0) 运算, 结果仍是一个在该点连续的函数 .
( 利用极限的四则运算法则证明)
例如, sin x , cos x 连续 tan x , cot x 在其定义域内连续
若 f ( x )在 [ x0 , b )内 有 定 义 ， 且 f ( x0 ) f ( x0 )， 则 称 f (x)在 x0 处 右 连 续.
定理：f (x)在 x0 处连续
f (x)在 x0 处既左连续又右连续，即，f (x0 ) f (x0 ) f (x0 ).
9
例. 证明函数 y sin x 在( , )内连续 .
lim f (x) , x 0为无穷间断点;
x0
当 x 1 时,
x 1
x
,
f (x) 0
当 x 1 时,
x , 1 x
f (x) 1
故 x 1 为跳跃间断点.
在 x 0, 1处, f (x) 连续.
第九节
第一章
连续函数的运算与
初等函数的连续性
一、连续函数的运算法则 二、初等函数的连续性
O
x
(3) y x2 1
y
x 1
x 1 为可去间断点 . O 1 x
x , x 1
(4)
y
f
(x)
1 2
,
x 1
y
1
1
显然 lim f (x) 1 f (1)
2
x1
O
x 1 为其可去间断点 .
(5)
y
f
(x)
x
0
1
, ,
x0 x0
x 1 , x 0
f (0 ) 1,
f (0 ) 1
x 0 为其跳跃间断点 .
1x
y
1
O
x
1
内容小结
1. f (x) 在点 x0 连续的等价形式
lim
x x0
பைடு நூலகம்
f
(x)
f
(x0 )
lim [
x0
f
( x0
x)
f
(x0 )]
0
f (x0 ) f (x0 ) f (x0 )
左连续 右连续
2. f (x) 在点 x0 间断的类型
可去间断点 第一类间断点 跳跃间断点 左右极限都存在
设 f (x) 在点 x0 的某去心邻域内有定义 , 则下列情形 之一, 函数 f (x) 在点 x0不连续 :
(1) 函数 f (x) 在 x0 无定义 ;
(2) 函数
f (x)
在
x0
虽有定义
,
但
lim
x x0
f (x) 不存在;
(3) 函数 f (x)在 x0 虽有定义 , 且 lim f (x) 存在 , 但
lim
x x0
f (x)
f (x0 )
x x0
这样的点 x0 称为间断点 .
间断点分类:
第一类间断点:
f (x0 ) 及 f (x0 ) 均存在 ,
若 f (x0 ) f (x0 ) , 称 x0 为可去间断点 . 若 f (x0 ) f (x0 ) , 称 x0 为跳跃间断点 .
第二类间断点:
第八节
第一章
函数的连续性与间断点
一、 函数连续性的定义 二、 函数的间断点
引例：
一、函数的连续性
1. 函数的增量
设 f (x)在U (x0 , )内有定义， x U (x0 , ),
x x x0，称为自变量 x 在点 x0 的增量.
y f (x) f (x0 )，称为 f (x)相应于x的增量.
则称函数
f (x) 在 x0 连续.
0, 0, 当 x x0 x
f (x) f (x0 ) y
可见 , 函数 f (x) 在点 x0 连续必须具备下列条件:
(1) f (x) 在点 x0 有定义 , 即 f (x0 ) 存在 ;
(2) 极限 lim f (x) 存在 ;
x x0
又如, 有理分式函数 R(x) P(x) Q(x)
在其定义域内连续.
只x要0 Q((x0
,)0),
,
都lim有
x x0
Pli(mx)
x x0
R(
Px)(
x0R) (
x0
c)ontinue
3. 左右连续 若 f ( x)在(a, x0 ]内 有 定 义 ， 且 f ( x0 ) f ( x0 )， 则称 f (x) 在 x0 处左连续;