当前位置：文档之家 › 高中数学(人教版)函数的连续性与间断点课件

高中数学(人教版)函数的连续性与间断点课件

  • 格式：ppt
  • 大小：1.43 MB
  • 文档页数：44

下载文档原格式

  / 44

合集下载

高数高等数学1.8函数的连续性与间断点

高数高等数学1.8函数的连续性与间断点
sin sin 2sin

2
cos

2
x x y 2 sin cos( x ) 2 2
x 0, sin x x
x
x 0
0
即函数 y sin x在(, )内连续 .
同理可证 y cos x在(, )内连续 .
x 2 , x 0, 例3 讨论函数 f ( x ) 在 x 0处的 x 2, x 0, 连续性.
下列情形之一，y f ( x)在 x0不连续：
(1) f ( x)在 x0无定义；
(2) f ( x )在 x0有定义，但 lim f ( x )不存在；
x x0
(3) f ( x )在 x0有定义，且 lim f ( x )存在，但是
x x0
x x0
lim f ( x ) f ( x0 )
lim f ( x0 x ) f ( x0 )
yy f ( x) Nhomakorabealim y 0

y
f ( x0 ) f ( x0 ) f ( x0 )
左连续 右连续
x
o
x0
x
x
0 , 0, 当 x x0 x 时，有
f ( x ) f ( x0 ) y .
x U ( x0 ),
y f ( x) f ( x0 ) ---函数的增量
y
y f ( x)
y
y
x
0
x
0
x0
x 0 x x
x0
x 0 x
x
2. 函数连续的定义 定义 设函数y f ( x )在 x0的某邻域内有定义，如果

高数：函数的连续性与间断点

高数：函数的连续性与间断点

二、 函数的间断点
一、 函数连续性的定义
第八节
函数的连续性与间断点
第一章
可见 , 函数
在点
一、 函数连续性的定义
定义:
在
的某邻域内有定义 ,
则称函数
(1)
在点
即
(2) 极限
(3)
设函数
连续必须具备下列条件:
存在 ;
且
有定义 ,
存在 ;
continue
若
在某区间上每一点都连续 ,
同样可证: 函数
在
内连续 .
在
在
二、 函数的间断点
(1) 函数
(2) 函数
不存在;
(3) 函数
存在 ,
但
不பைடு நூலகம்续 :
设
在点
的某去心邻域内有定义 ,
则下列情形
这样的点
之一函数 f (x) 在点
虽有定义 , 但
虽有定义 , 且
称为间断点 .
在
无定义 ;
间断点分类:
第一类间断点:
及
均存在 ,
若
称
若
称
第二类间断点:
及
中至少一个不存在 ,
称
若其中有一个为振荡 ,
称
若其中有一个为
为可去间断点 .
为跳跃间断点 .
为无穷间断点 .
为振荡间断点 .
为其无穷间断点 .
为其振荡间断点 .
为可去间断点 .
例如:
显然
为其可去间断点 .
(4)
(5)
为其跳跃间断点 .
内容小结
左连续
右连续
第一类间断点
可去间断点

3-1 函数的连续性与间断点

3-1 函数的连续性与间断点

y
x
x1 x1 x
x
∆y=y2 -y1
或∆y=f(x1+∆x)-f(x1)

§3-1 函数的连续性与间断点
1.自变量与函数的增量
自变量的改变量或增量，记为 ∆x=x2 -x1 函数的改变量或增量，记为
∆y=y2 -y1 或∆y=f(x1+∆x)-f(x1)
第三章 函数的连续性
引言： 客观世界的许多现象都是连续变化 的，比如,时间的变化是连续的。所谓连续就 是不间断，但是在数学上要用数学的语言来 描述着这种现象。
§3-1 函数的连续性与间断点
一、函数连续性的概念 二、函数的间断点及其分类 三、连续函数求极限的简便法则

x2 2 lim f ( x ) lim x 4 f (2), x 2
左连续但不右连续 ,
故函数 f ( x )在点 x 0处不连续.

§3-1 函数的连续性与间断点
一、函数连续性的概念
x0 x 1， 例4 讨论函数 f ( x) 2 在定义域内连续性 . x ， x 0
即 lim f ( x) f ( x0 ) ,则称函数y=f(x)在点x0处连续， 称x0为函数f(x)的连续点。 由定义可知，函数f(x)在点x0处连续， x0必属于函数f(x)的定义域。
x x0

§3-1 函数的连续性与间断点
一、函数连续性的概念
2.函数的点连续的概念 例如： 讨论函数 y x 2 ，在 x 2 处的连续性.
函数 f ( x )在x 0处连续.

§3-1 函数的连续性与间断点
例2 证明函数 y sin x在区间( ,)内连续. 证

§1.8 函数的连续性与间断点 35页PPT文档

§1.8 函数的连续性与间断点 35页PPT文档
5
注
由上述定义可知, f(x)在x0点的连续性 是描述 f(x)在x0点邻域的性态的. 即它是对 某一邻域而言. 因此在孤立点处无连续可言.
一般讲,证明的命题用函数连续的定 义1方便; 判断函数在某点是否连续, 尤其 是判断分段函数在分界点处是否连续用 定义2方便.
6
l i my 0
x0
f(x)xln i m 1 1 x x22n n x
若 |x|1则 f(x)xln i m 1 1 x x22n n
( 1 )2n
x

lim
n
(
x 1
)2
n

1 1
x
若 |x|1则 f(x)0 x
lim(x)0 lim(1x)1
1
x0
x0
f(00)f(00),
O
x
故x0为f (x)的第一类 间断点.且是跳跃间断点.
f(x00)及 f(x00)均存在, 则点x0为
f (x)的第一类间断点. 但 f(x 0 0 )f(x 0 0 ),
则点x0为函数 f(x) 的 跳跃型间断点(Jump discontinuity).
§1.8 函数的连续性 与间断点
函数的连续(continuity) 函数的间断点 (discontinuous point) 小结 思考题 作业
1
在自然界中,许多事物的变化是连续的, 如气温变化很小时,单摆摆长变化也很小.时 间变化很小时,生物生长的也很少. 这种现象 在函数关系上的反映就是函数的连续性.
x1
O 1x
lim f (x)lim(x1)2 f(1),
x1
x1
所以 f(x)在x1左连续,在x 1右不连续.

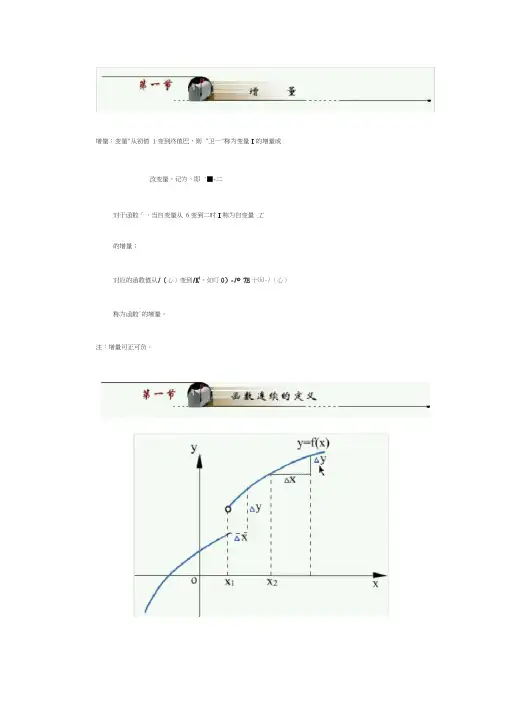
函数的连续性连续性与间断点

函数的连续性连续性与间断点

增量：变量"从初值 1变到终值巴，则“卫一"称为变量I的增量或改变量，记为，即'■-二对于函数「，当自变量从 6变到二时I称为自变量工的增量；对应的函数值从/（心）变到/K1，如叮0）-/© 7E十㈤-/（心）称为函数°的增量。

注：增量可正可负。

图3-1定义设函数」-■■在点门的某一邻域内有定义,如果当自变量的增量-一 --趋于零时，对应函数的增量I 一」「:匚:也趋于零lim ]/国 +&) -/E)]・Q那么就称函数」■■在点 r连续，i 称为函数J \的连续点。

如“㉛=lim[/(x0十㈤-/(r0)] = 0 r「寺血I/W - /(勺)]=0 丄」- -■- 可与^成:_极限所以此定义也可改写为如果！］丁—定义设函数」在点"的某一邻域内有定义,那么就称函数•- L在点'连续。

由定义可知，函数在点连续，必满足三个条件(1) '在点&有定义Im; /(A)(2)-」存在(左、右极限存在且相等)to/W=/(x0)如果三条中有一条不满足，则■■' '■'■■■在厂点就不连续。

(3)1< 2解 在〔处图 3-2SF ~* 0—Hrn /W ir-rti-t-WO-/w例1设尹十4解丿「丿是一分段函数,所以'；L '''不存在，故在 「「=〔处不连续。

例2讨论函数在卞=：，二=［及=-处的连续性。

liin =lim (x-t =-l T TT (T 4旷:亠二二、」讨论-‘ ‘在工=〔的连续性。

x >lim/(A )片不存在，所以不连续。

在K =］处:= lim_2x = 2, lun / (x) = lim (f +1) = 2,jf-^rr-j-l"x-4rFT ■广在x = 2处:bm 丁(£ = bm.C?十 1) = 5, Inn /迂)=lim +(lx 十 4) = 5r JCT ST r ->2 KT Z*富—^2，2/⑵7所以连续。

《连续性与间断点》课件

《连续性与间断点》课件

连续函数与无穷间断点
定义
无穷间断点是指函数在该点的极 限为无穷大。
举例
$f(x) = frac{1}{x}$在x=0处存在无 穷间断点，因为lim(x->0)f(x)=∞ 。
性质
无穷间断点会破坏函数的连续性， 因为该点的极限为无穷大。
PART 04
连续性与间断点的应用
利用连续性判断函数性质
总结词
连续函数与跳跃间断点
定义
性质
跳跃间断点是指函数在该点的左右极 限不相等，即函数在该点处发生“跳 跃”。
跳跃间断点会破坏函数的连续性，因 为该点的左右极限不相等。
举例
$f(x) = begin{cases} x, & x leq 0 2x, & x > 0 end{cases}$在x=0处存 在跳跃间断点，因为lim(x>0+)f(x)=0!=lim(x->0-)f(x)=0。
在某一点左侧和右侧的函数值相 等，即$f(x_{0} - 0) = f(x_{0} + 0)$，则称$x_{0}$为函数$f(x)$的 可去间断点。
描述
可去间断点是间断点中最容易处 理的一种，可以通过补充定义使 得函数在该点连续。
第二类间断点（跳跃间断点、无穷间断点）
定义
在某一点左侧和右侧的函数值不相等，即$f(x_{0} - 0) neq f(x_{0} + 0)$，则称 $x_{0}$为函数$f(x)$的跳跃间断点。如果函数值在某一点趋于无穷，则称该点为 无穷间断点。
详细描述
在物理学、工程学、经济学等领域中，许多实际问题 需要用到连续性与间断点的概念。例如，在物理学中 的速度、加速度、力的变化规律分析中，可以利用连 续性来描述平滑的变化过程；在经济学中的供需关系 、价格形成机制中，可以利用间断点来描述市场价格 的突变和调整。此外，在信号处理、图像处理等领域 中，连续性与间断点的概念也具有重要应用价值。

《连续性和间断点》课件

深入研究连续性和间断点可以提高对函数行为的理解。
连续性和间断点在实际问题中的应用
连续性和间断点在实际问题中具有广泛的应用价值。
3
第一类间断点
在此点处函数的极限存在，但函数本身在此 点处不连续。
可去间断点
在此点处函数有间断，但可以通过修补来使 函数连续。
连续性和间断点的判定方法
1 函数的分段定义
可以通过分段定义来描述函数的连续性。
2 左右极限的存在性
函数在间断点两侧的极限是否存在能够判定连续性。
3 极限的大小关系
极限的大小关系可以提供连续性的信息。
连续性和间断点
# 连续性和间断点 PPT课件 大纲
连续性的定义
连续性的概念
连续性是函数在一个区间上无 间断的特性。
连续Байду номын сангаас数的定义
连续函数是定义域上处处连续 的函数。
闭区间上的连续函数
在闭区间上连续的函数在区间 的两个端点都有定义。
间断点的分类
1
第二类间断点
2
在此点处函数的极限不存在，函数也不连续。
应用实例
连续函数的应用
连续函数在科学、工程、经济等领 域中有广泛的应用。
间断点的应用
间断点在物理、计算机等领域中有 各种实际应用。
数学建模中的连续性和间断 点问题
连续性和间断点问题在数学建模中 具有重要实际意义。
总结
连续性和间断点的意义
连续性和间断点是研究函数特性的重要概念。
连续性和间断点的深入研究

高等数学教学课件 第八节 函数的连续性与间断点


例6 讨论函 f(x) 数 1 x, x0,在 x f(0)0, f(0),
x1为函数的第二类间. 断点 o x
这种情况称为 无穷间 断点.
16/18
例7 讨论f(函 x)s数 i1 n在 x0处的连 . 续 x
解 在x0处没有,定义
且limsin1不存.在 x0 x
例4
讨论f(函 x) 1 数 x x ,,
x0,在 x0处的.连 x0,
解 f(0)0, f(0)1, y
即f(0)f(0),
x0为函数的跳跃间.断点 o
x
12/18
2.可去间断点如果 f(x)在点 x0处的极限 , 存
但lx ixm 0 f(x)Af(x0),或f(x)在点 x0处无定 义则称 x0为 点函f数 (x)的可去间 . 断点
2、指 出 y x 2 x 在 x 0 是 第 ________ 类 间 x ( x 2 1)
断点；在 x 1 是第______类间断点；在 x 1
是第_____类间断点 .
x, x 1
二、研究函数 f (x)
的连续性，并画出函数
1, x 1
的图形 .
24/18
三、指出下列函数在指定范围内的间断点，并说明这些
间断点的类型，如果是可去间断点，则补充或改变
函数的定义使它连续 .
1、
f
(x
)
x
3
1, x x, x
1在 1
x R
上
.
2、 f (x) x ,在 x R 上 . tan x
四 、 讨 论 函 数 f ( x ) lim 1 x 2 n 的 连 续 性 ， 若 有 间 断 n 1 x 2n
定理 函数 f(x)在x0处连 续 是函f(数 x)在x0 处既左连续 . 又右连续
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（一）概念 （二）分类 （三）举例
可去间断点 f ( x 0 ) f ( x0 )
第一类间断点 f ( x0 )和 f ( x0 )
间断点
都存在
跳跃间断点 f ( x 0 ) f ( x0 )
无穷间断点 第二类间断点 f ( x0 )和 f ( x0 ) 至少一个不存在
1．定义1
2．定义2
3．定义3
4．左连续与右连续 5．性质
（一）函数在一点处连续的概念
1．定义1
2．定义2
3．定义3
4．左连续与右连续 5．性质
y
o
x
y
o
x
y
o
y
x
o
x
y
o
y
x
o
x
y
o
y
x
o
x
增量
u u2 u1
u 0 u2 u1 u 0 u2 u1 u 0 u2 u1
显然
y
1 2
1
lim f ( x ) 1 f (1)
x 1
x 1为其可去间断点
.
o
y
1
1
x
x 1 , x 0 (5) y f ( x ) 0 , x 0 x 1 , x 0
o
f (0 ) 1 ,

f (0 ) 1
.

1
x
x 0 为其跳跃间断点
[a , b ]上连续.
函数的连续性与间断点
一、函数的连续性
二、函数的间断点
函数的连续性与间断点
一、函数的连续性
二、函数的间断点
二、函数的间断点
（一）概念 （二）分类 （三）举例
二、函数的间断点
（x ) 在点x0 的某去心邻域内有定义, 若函数 y f ( x ) 在点x0 不连续, 则称函数 y f ( x ) 在点 x0间断，而点 x0称为 y f ( x ) 的不连续点或间断点. 函数 y f ( x )在 x0 处间断的情形 (1) 在 x x0 没有定义;
那么称函数f (x)在点x0连续. 注 函数f (x)在点x0连续的要点：
函数f (x)在点x0的某一邻域内有定义 lim f ( x )存在
x x0 x x0
lim f ( x ) f ( x0 )
（一）函数在一点处连续的概念
1．定义1
2．定义2
3．定义3
4．左连续与右连续 5．性质
lim y lim f ( x0 x ) f ( x0 ) 0
x 0
那么就称函数f (x)在点x0连续. 注 在定义式中,Δx为变量,x0要视为常量. 例1 证明 y sin x 在 x 0 ( x 0 R ) 处连续.
（一）函数在一点处连续的概念
1．定义1
那么称函数f (x)在点x0连续. 注 函数f (x)在点x0连续的要点：
函数f (x)在点x0的某一邻域内有定义
x 0
lim y lim f ( x0 x ) f ( x0 ) 0
x 0
x 0
x x0
lim f ( x0 x ) f ( x0 ) 令 x0 x x x 0 lim f ( x) f ( x0 )
(2) 虽在 x x0 有定义,但 lim f ( x ) 不存在;
(3) 虽在 x x0 有定义,且 lim f ( x ) 存在,但 lim f ( x ) f ( x0 )
x x0 x x0
x x0
二、函数的间断点 （一）概念 （二）分类 （三）举例
二、函数的间断点
振荡间断点
二、函数的间断点
（一）概念 （二）分类 （三）举例
二、函数的间断点
（一）概念 （二）分类 （三）举例
y
y tan x

2
x 为其无穷间断点. 2
o
x
y
y sin
1 x
x 0为其振荡间断点.
y
0
x
x 1为可去间断点.
o 1
x
x , x 1 (4) y f ( x ) 1 2 , x 1
x 0
x 0
x x0
lim f ( x0 x ) f ( x0 ) 令 x0 x x x 0 lim f ( x) f ( x0 )
x x0
定义2 设函数f (x)在点x0的某一邻域内有定义，如果
x x0
lim f ( x )
f (x )
0
x0 .
（一）函数在一点处连续的概念
1．定义1
2．定义2
3．定义3
4．左连续与右连续 5．性质
（一）函数在一点处连续的概念
1．定义1
2．定义2
3．定义3
4．左连续与右连续 5．性质
定义 设函数y=f(x)在点x0的某右邻域内有定义，如果
x x0
lim f ( x ) f ( x0 )
(2) u 是一个整体记号
y
f ( x 0 x ) f ( x0 )
f ( x)
注 (1) u 可正可负
o
x0
x 0 x
x
u
2
u
2
y f ( x 0 x ) f ( x 0 )
定义1 设函数f (x)在点x0的某一邻域内有定义，如果
x 0
一、函数的连续性
（一）函数在一点处连续的概念
（二）函数在区间上连续的概念
定义
若函数 y f ( x ) 在 ( a , b )内的每一点处连续， 则称函数
y f ( x ) 在 ( a , b )内连续.
定义 若函数 y f ( x )在 ( a , b )内的每一点处连续， 在x a 处右连续, 在 x b 处左连续， 则称函数 y f ( x ) 在
那么称函数f(x)在点x0右连续. 类似可得左连续的定义 定理 函数y=f(x)在点x0连续 例2
y=f(x)在点x0既左连续又右连续
x 2 讨论函数 f ( x ) x 2
x0 x0
在 x 0 处的连续性.
（一）函数在一点处连续的概念
1．定义1
2．定义2
3．定义3
x x0
定义2 设函数f (x)在点x0的某一邻域内有定义，如果
x x0
lim f ( x )
f (x )
0
那么称函数f (x)在点x0连续. 注 函数f (x)在点x0连续的要点：
函数f (x)在点x0的某一邻域内有定义 lim f ( x )存在
x x0
x 0
lim y lim f ( x0 x ) f ( x0 ) 0
第八讲 函数的连续性与间断点
函数的连续性与间断点
一、函数的连续性
二、函数的间断点
函数的连续性与间断点
一、函数的连续性
二、函数的间断点
一、函数的连续性
（一）函数在一点处连续的概念
（二）函数在区间上连续的概念
一、函数的连续性
（一）函数在一点处连续的概念
（二）函数在区间上连续的概念
（一）函数在一点处连续的概念
思 考
1．处处有定义，但处处不连续的函数
2．处处有定义，仅在一点连续的函数
x0 , x0 内有界.
定理 函数 y f ( x )在 x0处连续,且 f ( x 0 ) 0, 则 0 使y=f (x)在 x 0 , x0 内恒有 f ( x ) 0.
一、函数的连续性
（一）函数在一点处连续的概念
（二）函数在区间上连续的概念
x 0
x 0
x x0
lim f ( x0 x ) f ( x0 ) 令 x0 x x x 0 lim f ( x) f ( x0 )
x x0
定义2 设函数f (x)在点x0的某一邻域内有定义，如果
x x0
lim f ( x )
f (x )
0
4．左连续与右连续 5．性质
（一）函数在一点处连续的概念
1．定义1
2．定义2
3．定义3
4．左连续与右连续 5．性质
定理
函数 y f ( x ) 在 x0 处连续的充要条件是： 组成的数列 f ( x n )的极限都存在,且都等于 f ( x0 ). 定理 函数 y f ( x ) 在 x0 处连续， 则 0, 使y=f (x)在 对于任意一个以 x0为极限的数列 x n , 对应的函数值
x x0
定义2 设函数f (x)在点x0的某一邻域内有定义，如果
x x0
lim f ( x )
f (x )
0
那么称函数f (x)在点x0连续. 注 函数f (x)在点x0连续的要点：
x 0
lim y lim f ( x0 x ) f ( x0 ) 0
2．定义2
3．定义3
4．左连续与右连续 5．性质
（一）函数在一点处连续的概念
1．定义1
2．定义2
3．定义3
4．左连续与右连续 5．性质
x 0
lim y lim f ( x0 x ) f ( x0 ) 0
x 0
x 0
x x0
lim f ( x0 x ) f ( x0 ) 令 x0 x x x 0 lim f ( x) f ( x0 )
（一）函数在一点处连续的概念
1．定义1
2．定义2
3．定义3