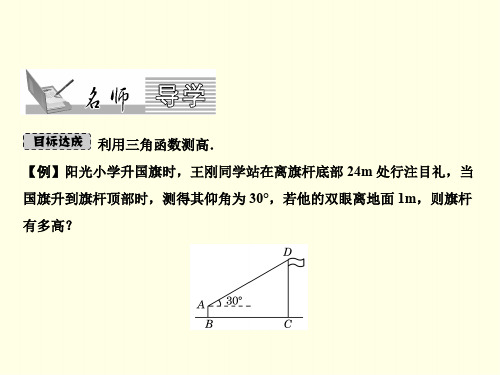
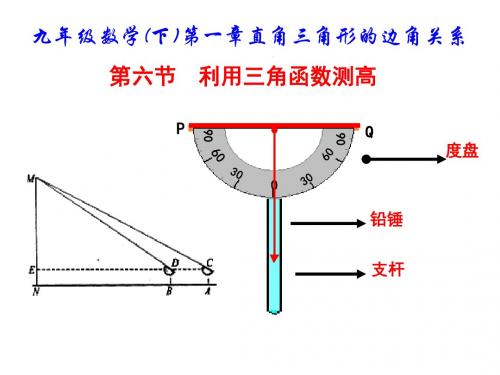
九年级数学下册知识点---利用三角函数测高
- 格式:pdf
- 大小:463.19 KB
- 文档页数:20



第03讲三角函数的应用及利用三角函数测高1.会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题.2.理解用三角函数解决实际问题的有关概念;3.理解并解决实际问题中转化为三角函数模型解决实际问题。
知识点01锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;(2)平方关系:;(3)倒数关系:或;(4)商数关系:.要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.【知识拓展1】利用同角三角函数关系求值计算:(1)2tan452sin30cos30-+;(2)22tan1tan89sin1sin89⋅++.【即学即练1】已知∠A为锐角且sinA=12,则4sin2A-4sinAcosA+cos2A的值是多少。
知识精讲目标导航【即学即练2】.如图,在ABCD 中,E ,F 是对角线BD 上的两点(点E 在点F 左侧),且90AEB CFD ∠=∠=︒.(1)求证:四边形AECF 是平行四边形.(2)当5AB =,3tan 4ABE ∠=,CBE EAF ∠=∠时,求BD 的长.【即学即练3】求值:(1)260453456cos sin tan tan +-⋅; ()2已知2tanA =,求245sinA cosAsinA cosA-+的值.【知识拓展2】求证同角三角函数关系式已知:1sin15cos15sin302⋅=,1sin20cos20sin402⋅=,1sin30cos30sin602⋅=,请你根据上式写出你发现的规律________.【即学即练1】已知:实常数a b c d 、、、同时满足下列两个等式:⑴sin cos 0a b c θθ+-=;⑵cos sin 0a b d θθ-+=(其中θ为任意锐角),则a b c d 、、、之间的关系式是:___________ 【即学即练2】.①sin 2A+cos 2A=________,②tanA•cotA=________. 【知识拓展3】互余两角的三角函数的关系在Rt △ABC 中,已知∠C =90°,sin A =35,求cos A 、tan A 以及∠B 的三个三角函数值.【即学即练1】在Rt △ABC 中,∠C =90°,sin B =35,求cos A 的值.【即学即练2】在Rt △ABC 中,∠C=90°,sinA=34,求cosA ,sinB ,cosB ,tanA ,tanB 的值.【知识拓展4】三角函数综合如图,在△ABC中,∠ACB=90°,sin A=45,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.(1)求线段CD的长;(2)求cos ∠ABE的值.【即学即练1】如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.【即学即练2】.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.(1)若∠A=60°,求BC 的长; (2)若sinA=45,求AD 的长.(注意:本题中的计算过程和结果均保留根号)【即学即练3】.如图,在Rt ABC ∆中,0090,30,23B A AC ∠=∠==.(1)利用尺规作线段AC 的垂直平分线DE ,垂足为E ,交AB 于点D ;(保留作图痕迹,不写作法)(2)若ADE ∆的周长为a ,先化简()()211T a a a =+--,再求T 的值.知识点02 利用三角函数测高解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是:(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.拓展:在用直角三角形知识解决实际问题时,经常会用到以下概念:(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成=∶的形式.(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.特别说明:1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.【知识拓展5】直接求三角形的高数学课外学习小组利用矩形建筑物ABED测量广场灯塔CF的高,如图所示,在点B处测得灯塔顶端C的仰角为28°,在点D处测得灯塔顶端C的仰角为45°,已知AB=10m,AD=30m.求灯塔CF的高(结果保留整数).(参考数据:tan28°≈0.53,cos28°≈0.88,sin28°≈0.47,2≈1.41)【即学即练1】.如图,为测量建筑物CD 的高度,在点A 测得建筑物顶部D 点的仰角是22︒,再向建筑物CD 前进30米到达B 点,测得建筑物顶部D 点的仰角为58︒(A ,B ,C 在同一直线上),求建筑物CD 的高度.(结果保留整数.参考数据:sin 220.37cos 220.93tan 220.40sin580.85cos580.53tan58 1.60︒︒︒︒︒︒≈≈≈≈≈≈,,,,,)【即学即练2】.如图,某数学兴趣小组的同学利用标杆测量旗杆(AB )的高度:将一根5米高的标杆(CD )竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(EF )1.6米,求旗杆的高度AB .【即学即练3】. “永定楼”是门头沟区的地标性建筑,某中学九年级数学兴趣小组进行了测量它高度的社会实践活动.如图,他们在A 点测得顶端D 的仰角∠DAC=30°,向前走了46米到达B 点后,在B 点测得顶端D 的仰角∠DBC=45°.求永定楼的高度CD .(结果保留根号)【知识拓展6】由两个直角三角形求高在一次课外综合实践活动中,甲、乙两位同学测量校园内的一棵大树的高度,他们分别在A ,B 两处用高度为1.5m 的测角仪(AE 和BD )测得大树顶部C 的仰角分别为30°,45°,两人间的水平距离()AB 为20m ,已知点A ,E ,F ,C ,B ,D 在同一竖直平面内,且FC AB ⊥,求大树的高度CF .(结果保留根号)【即学即练1】.如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C的仰角∠ADC=45°,从点E处看点B的仰角∠AEB=53°,且DE=2.4米.(1)求点C到墙壁AM的距离;(2)求匾额悬挂的高度AB的长.(参考数据:sin37°≈35,cos37°≈45,tan37°≈34)【即学即练2】.数学实践课上,同学们分组测量教学楼前国旗杆的高度.小明同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°.室外测量组测得BF的长度为5米,求旗杆AB的高度.【即学即练3】.如图,在坡角为20°的山坡上有一铁塔AB、其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD=10米,落在广告牌上的影子CD=5米,已知AB,CD均与水平面垂直,请根据相关测量信息,求铁塔AB的高.(sin20°≈0.34,c os20°≈0.94,tan20°≈0.36)【知识拓展7】由多个直角三角形求高小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面旋转的标杆在地面上的影长为2米,求树的高度为多少米?【即学即练1】.如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为30°,沿坡面向下走到坡脚C处,然后在地面上沿CB向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为60°.已知坡面CD=10米,山坡的坡度i=1:3(坡度是指坡面的铅直高度与水平宽度的比).求楼房AB高度.(结果保留根式)【即学即练2】..如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度1:3,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈43,cos53°≈0.60)【即学即练3】.如图,某风景区内有一瀑布,AB表示瀑布的垂直高度,在与瀑布底端同一水平位置的点D处测得瀑布顶端A的仰角β为45°,沿坡度i=1:3的斜坡向上走100米,到达观景台C,在C处测得瀑布顶端A的仰角α为37°,若点B、D、E在同一水平线上.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,2≈1.41,10≈3.16)(1)观景台的高度CE为米(结果保留准确值);(2)求瀑布的落差AB(结果保留整数).【知识拓展8】其他运用2017年9月8日—10日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的A点出发(AB=1000米),沿俯角为30 的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为60 的方向降落到地面上的C点,求该选手飞行的水平距离BC.【即学即练1】.如图,从点A看一山坡上的电线杆PQ,观测杆顶端点P的仰角是45°,向前走6 m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ 的高度(精确到0.1 m).【即学即练2】.图1所示的是某景区的“关帝圣像”,它从2007年1月开始铸造,共用铜500吨,铁2000吨,甚是伟岸壮观.其侧面示意图如图2所示.在B 处测得圣像顶A 的仰角为52.8,在点E 处测得圣像顶A 的仰角为63.4︒.已知AC BC ⊥于点,C EG BC ⊥于点,//,30G EF BC BG =米,19FC =米,求圣像的高度AF . (结果保留整数.参考数据:52.80.80,52.80.60sin cos ≈︒≈,52.8 1.32,63.40.89tan sin ︒≈︒≈,63.40.45,63.4 2.00cos tan ≈︒≈)【即学即练3】.如图,在河流的右岸边有一高楼AB ,左岸边有一坡度1:2i =的山坡CF ,点C 与点B 在同一水平面上,CF 与AB 在同一平面内.某数学兴趣小组为了测量楼AB 的高度,在坡底C 处测得楼顶A 的仰角为45︒,然后沿坡面CF 上行了205(即205CD =︒≈,到达点D处,此时在D处测得楼顶A的仰角为26.7︒.(参考数据:sin26.70.45︒≈)︒≈,tan26.70.50cos26.70.89(1)求点C到点D的水平距离CE的长;(2)求楼AB的高度.能力拓展1.如图,有一个晾衣架放置在水平地面上,在其示意图中,支架OA、OB的长均为108cm,支架OA与水平晾衣杆OC的夹角∠AOC为59°,求支架两个着地点之间的距离AB.(结果精确到0.1cm)(参考数据:sin59°=0.86,cos59°=0.52,tan59°=1.66).2.如图,小明想用所学的知识来测量湖心岛上的迎宾槐与湖岸上凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一平面上),请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).(参考数据sin25°≈0.4226,cos25°≈0.9063,tan25°≈0.4663,sin65°≈0.5563,cos65°≈0.4226,tan65°≈2.1445)3.某校学生去春游,在风景区看到一棵汉柏树,不知这棵汉柏树有多高,下面是两位同学的一段对话:小明:我站在此处看树顶仰角为45。