2020中考数学 几何复习：平移与旋转变换(含详解版)

平移旋转对称三大变换1.（2020•安徽）在数学探究活动中，敏敏进行了如下操作：如图，将四边形纸片ABCD沿过点A的直线折叠，使得点B落在CD上的点Q处．折痕为AP；再将△PCQ，△ADQ分别沿PQ，AQ折叠，此时点C，D落在AP上的同一点R处．请完成下列探究：（1）∠PAQ的大小为30 °；（2）当四边形APCD是平行四边形时，的值为．【解答】解：（1）由折叠的性质可得：∠B＝∠AQP，∠DAQ＝∠QAP＝∠PAB，∠DQA＝∠AQR，∠CQP＝∠PQR，∠D＝∠ARQ，∠C＝∠QRP，∵∠QRA+∠QRP＝180°，∴∠D+∠C＝180°，∴AD∥BC，∴∠B+∠DAB＝180°，∵∠DQR+∠CQR＝180°，∴∠DQA+∠CQP＝90°，∴∠AQP＝90°，∴∠B＝∠AQP＝90°，∴∠DAB＝90°，∴∠DAQ＝∠QAP＝∠PAB＝30°，故答案为：30；（2）由折叠的性质可得：AD＝AR，CP＝PR，∵四边形APCD是平行四边形，∴AD＝PC，∴AR＝PR，又∵∠AQP＝90°，∴QR AP，∵∠PAB＝30°，∠B＝90°，∴AP＝2PB，AB PB，∴PB＝QR，∴，故答案为：．2.（2020•天水）如图，在边长为6的正方形ABCD内作∠EAF＝45°，AE交BC于点E，AF交CD于点F，连接EF，将△ADF绕点A顺时针旋转90°得到△ABG．若DF＝3，则BE的长为 2 ．【解答】解：法一：由题意可得，△ADF≌△ABG，∴DF＝BG，∠DAF＝∠BAG，∵∠DAB＝90°，∠EAF＝45°，∴∠DAF+∠EAB＝45°，∴∠BAG+∠EAB＝45°，∴∠EAF＝∠EAG，在△EAG和△EAF中，，∴△EAG≌△EAF（SAS），∴GE＝FE，设BE＝x，则GE＝BG+BE＝3+x，CE＝6﹣x，∴EF＝3+x，∵CD＝6，DF＝3，∴CF＝3，∵∠C＝90°，∴（6﹣x）2+32＝（3+x）2，解得，x＝2，即BE＝2，法二：设BE＝x，连接GF，如下图所示，∵四边形ABCD为正方形，∴∠ABE＝∠GCF＝90°，∵△ADF绕点A顺时针旋转90°得到△ABG，∴∠CAF＝90°，GA＝FA，∴△GAF为等腰直角三角形，∵∠EAF＝45°，∴AE垂直平分GF，∴∠AEB+∠CGF＝90°，∵在Rt△AEB中，∠AEB+∠BAE＝90°，∴∠BAE＝∠CGF，∴△BAE～△CGF，∴，∵CF＝CD﹣DF＝6﹣3＝3，GC＝BC+BG＝BC+DF＝6+3＝9，∴，∴x＝2，即BE＝2，故答案为：2．3.（2020•深圳）如图，矩形纸片ABCD中，AB＝6，BC＝12．将纸片折叠，使点B落在边AD的延长线上的点G处，折痕为EF，点E、F分别在边AD和边BC上．连接BG，交CD于点K，FG交CD于点H．给出以下结论：①EF⊥BG；②GE＝GF；③△GDK和△GKH的面积相等；④当点F与点C重合时，∠DEF＝75°，其中正确的结论共有（）A．1个B．2个C．3个D．4个【解答】解：如图，连接BE，设EF与BG交于点O，∵将纸片折叠，使点B落在边AD的延长线上的点G处，∴EF垂直平分BG，∴EF⊥BG，BO＝GO，BE＝EG，BF＝FG，故①正确，∵AD∥BC，∴∠EGO＝∠FBO，又∵∠EOG＝∠BOF，∴△BOF≌△GOE（ASA），∴BF＝EG，∴BF＝EG＝GF，故②正确，∵BE＝EG＝BF＝FG，∴四边形BEGF是菱形，∴∠BEF＝∠GEF，当点F与点C重合时，则BF＝BC＝BE＝12，∵sin∠AEB，∴∠AEB＝30°，∴∠DEF＝75°，故④正确，由题意无法证明△GDK和△GKH的面积相等，故③错误；故选：C．4.（2020•随州）如图，已知矩形ABCD中，AB＝3，BC＝4，点M，N分别在边AD，BC上，沿着MN折叠矩形ABCD，使点A，B分别落在E，F处，且点F在线段CD上（不与两端点重合），过点M作MH⊥BC于点H，连接BF，给出下列判断：①△MHN∽△BCF；②折痕MN的长度的取值范围为3＜MN；③当四边形CDMH为正方形时，N为HC的中点；④若DF DC，则折叠后重叠部分的面积为．其中正确的是①②③④．（写出所有正确判断的序号）【解答】解：①如图1，由折叠可知BF⊥MN，∴∠BOM＝90°，∵MH⊥BC，∴∠BHP＝90°＝∠BOM，∵∠BPH＝∠OPM，∴∠CBF＝∠NMH，∵∠MHN＝∠C＝90°，∴△MHN∽△BCF，故①正确；②当F与C重合时，MN＝3，此时MN最小，当F与D重合时，如图2，此时MN最大，由勾股定理得：BD＝5，∵OB＝OD，∵tan∠DBC，即，∴ON，∵AD∥BC，∴∠MDO＝∠OBN，在△MOD和△NOB中，∵，∴△DOM≌△BON（ASA），∴OM＝ON，∴MN＝2ON，∵点F在线段CD上（不与两端点重合），∴折痕MN的长度的取值范围为3＜MN；故②正确；③如图3，连接BM，FM，当四边形CDMH为正方形时，MH＝CH＝CD＝DM＝3，∵AD＝BC＝4，∴AM＝BH＝1，由勾股定理得：BM，∴FM，∴DF1，∴CF＝3﹣1＝2，设HN＝x，则BN＝FN＝x+1，在Rt△CNF中，CN2+CF2＝FN2，∴（3﹣x）2+22＝（x+1）2，解得：x，∴HN，∵CH＝3，∴CN＝HN，∴N为HC的中点；故③正确；④如图4，连接FM，∵DF DC，CD＝3，∴DF＝1，CF＝2，∴BF2，∴OF，设FN＝a，则BN＝a，CN＝4﹣a，由勾股定理得：FN2＝CN2+CF2，∴a2＝（4﹣a）2+22，∴a，∴BN＝FN，CN，∵∠NFE＝∠CFN+∠DFQ＝90°，∠CFN+∠CNF＝90°，∴∠DFQ＝∠CNF，∵∠D＝∠C＝90°，∴△QDF∽△FCN，∴，即，∴QD，∴FQ，∵tan∠HMN＝tan∠CBF，∴，∴HN，∴MN，∵CH＝MD＝HN+CN3，∴MQ＝3，∴折叠后重叠部分的面积为：S△MNF+S△MQF；故④正确；所以本题正确的结论有：①②③④；故答案为：①②③④．5.（2020•武汉）如图，折叠矩形纸片ABCD，使点D落在AB边的点M处，EF为折痕，AB＝1，AD＝2．设AM的长为t，用含有t的式子表示四边形CDEF的面积是．【解答】解：连接DM，过点E作EG⊥BC于点G，设DE＝x＝EM，则EA＝2﹣x，∵AE2+AM2＝EM2，∴（2﹣x）2+t2＝x2，解得x1，∴DE1，∵折叠矩形纸片ABCD，使点D落在AB边的点M处，∴EF⊥DM，∠ADM+∠DEF＝90°，∵EG⊥AD，∴∠DEF+∠FEG＝90°，∴∠ADM＝∠FEG，∴tan∠ADM，∴FG，∵CG＝DE1，∴CF1，∴S四边形CDEF（CF+DE）×1t+1．故答案为：t+1．6.（2020•咸宁）如图，在矩形ABCD中，AB＝2，BC＝2，E是BC的中点，将△ABE沿直线AE翻折，点B落在点F处，连结CF，则cos∠ECF的值为（）A．B．C．D．【解答】解：如图，∵四边形ABCD是矩形，∴∠B＝90°，∵E是BC的中点，BC＝2，∴BE＝CE BC，∴AE3，由翻折变换的性质得：△AFE≌△ABE，∴∠AEF＝∠AEB，EF＝BE，∴EF＝CE，∴∠EFC＝∠ECF，∵∠BEF＝∠EFC+∠ECF，∴∠AEB＝∠ECF，∴cos∠ECF＝cos∠AEB．故选：C．7.（2020•襄阳）如图，矩形ABCD中，E为边AB上一点，将△ADE沿DE折叠，使点A的对应点F恰好落在边BC上，连接AF交DE于点N，连接BN．若BF•AD＝15，tan∠BNF，则矩形ABCD的面积为15．【解答】解：∵将△ADE沿DE折叠，使点A的对应点F恰好落在边BC上，∴AF⊥DE，AE＝EF，∵矩形ABCD中，∠ABF＝90°，∴B，E，N，F四点共圆，∴∠BNF＝∠BEF，∴tan∠BEF，设BF x，BE＝2x，∴EF3x，∴AE＝3x，∴AB＝5x，∴AB BF．∴S矩形ABCD＝AB•AD BF•AD15＝15．故答案为：15．8.（2020•孝感）如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G．若BG＝3，CG＝2，则CE的长为（）A．B．C．4 D．【解答】解：如图所示，连接EG，由旋转可得，△ADE≌△ABF，∴AE＝AF，DE＝BF，又∵AG⊥EF，∴H为EF的中点，∴AG垂直平分EF，∴EG＝FG，设CE＝x，则DE＝5﹣x＝BF，FG＝8﹣x，∴EG＝8﹣x，∵∠C＝90°，∴Rt△CEG中，CE2+CG2＝EG2，即x2+22＝（8﹣x）2，解得x，∴CE的长为，故选：B．9.（2020•衡阳）如图1，在平面直角坐标系中，▱ABCD在第一象限，且BC∥x轴．直线y＝x从原点O出发沿x轴正方向平移，在平移过程中，直线被▱ABCD截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示．那么▱ABCD的面积为（）A．3 B．3C．6 D．6【解答】解：过B作BM⊥AD于点M，分别过B，D作直线y＝x的平行线，交AD于E，如图1所示，由图象和题意可得，AE＝6﹣4＝2，DE＝7﹣6＝1，BE＝2，∴AB＝2+1＝3，∵直线BE平行直线y＝x，∴BM＝EM，∴平行四边形ABCD的面积是：AD•BM＝33．故选：B．10.（2020•江西）矩形纸片ABCD，长AD＝8cm，宽AB＝4cm，折叠纸片，使折痕经过点B，交AD边于点E，点A落在点A'处，展平后得到折痕BE，同时得到线段BA'，EA'，不再添加其它线段．当图中存在30°角时，AE的长为厘米或4厘米或厘米．【解答】解：①当∠ABE＝30°时，AE＝AB×tan30°；②当∠AEB＝30°时，AE4；③∠ABE＝15°时，∠ABA′＝30°，延长BA′交AD于F，如下图所示，设AE＝x，则EA′＝x，EF，∵AF＝AE+EF＝AB tan30°，∴x，∴x＝8﹣4，∴AE＝8﹣4．故答案为：厘米或4厘米或8﹣4厘米．11.（2020•滨州）如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平后再次折叠，使点A落在EF上的点A′处，得到折痕BM，BM与EF相交于点N．若直线BA′交直线CD于点O，BC＝5，EN＝1，则OD的长为（）A．B．C．D．【解答】解：∵EN＝1，∴由中位线定理得AM＝2，由折叠的性质可得A′M＝2，∵AD∥EF，∴∠AMB＝∠A′NM，∵∠AMB＝∠A′MB，∴∠A′NM＝∠A′MB，∴A′N＝2，∴A′E＝3，A′F＝2过M点作MG⊥EF于G，∴NG＝EN＝1，∴A′G＝1，由勾股定理得MG，∴BE＝OF＝MG，∴OF：BE＝2：3，解得OF，∴OD．故选：B．12.（2020•德州）如图，在矩形ABCD中，AB2，AD．把AD沿AE折叠，使点D恰好落在AB边上的D′处，再将△AED′绕点E顺时针旋转α，得到△A'ED″，使得EA′恰好经过BD′的中点F．A′D″交AB于点G，连接AA′．有如下结论：①A′F的长度是2；②弧D'D″的长度是π；③△A′AF ≌△A′EG；④△AA′F∽△EGF．上述结论中，所有正确的序号是①②④．【解答】解：∵把AD沿AE折叠，使点D恰好落在AB边上的D′处，∴∠D＝∠AD'E＝90°＝∠DAD'，AD＝AD'，∴四边形ADED'是矩形，又∵AD＝AD'，∴四边形ADED'是正方形，∴AD＝AD'＝D'E＝DE，AE AD，∠EAD'＝∠AED'＝45°，∴D'B＝AB﹣AD'＝2，∵点F是BD'中点，∴D'F＝1，∴EF2，∵将△AED′绕点E顺时针旋转α，∴AE＝A'E，∠D'ED''＝α，∠EA'D''＝∠EAD'＝45°，∴A'F2，故①正确；∵tan∠FED'，∴∠FED'＝30°∴α＝30°+45°＝75°，∴弧D'D″的长度π，故②正确；∵AE＝A'E，∠AEA'＝75°，∴∠EAA'＝∠EA'A＝52.5°，∴∠A'AF＝7.5°，∵∠AA'F≠∠EA'G，∠AA'E≠∠EA'G，∠AFA'＝120°≠∠EA'G，∴△AA'F与△A'GE不全等，故③错误；∵D'E＝D''E，EG＝EG，∴Rt△ED'G≌Rt△ED''G（HL），∴∠D'GE＝∠D''GE，∵∠AGD''＝∠A'AG+∠AA'G＝105°，∴∠D'GE＝52.5°＝∠AA'F，又∵∠AFA'＝∠EFG，∴△AFA'∽△EFG，故④正确，故答案为：①②④．13.（2020•聊城）如图，在Rt△ABC中，AB＝2，∠C＝30°，将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，在B′C′上取点D，使B′D＝2，那么点D到BC的距离等于（）A．2（1）B． 1 C． 1 D． 1【解答】解：∵在Rt△ABC中，AB＝2，∠C＝30°，∴BC＝2，AC＝4，∵将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，∴AB′＝AB＝2，B′C′＝BC＝2，∴B′C＝2，延长C′B′交BC于F，∴∠CB′F＝∠AB′C′＝90°，∵∠C＝30°，∴∠CFB′＝60°，B′F B′C，∵B′D＝2，∴DF＝2，过D作DE⊥BC于E，∴DE DF（2）1，故选：D．14.（2020•杭州）如图是一张矩形纸片，点E在AB边上，把△BCE沿直线CE对折，使点B落在对角线AC上的点F处，连接DF．若点E，F，D在同一条直线上，AE＝2，则DF＝ 2 ，BE＝ 1 ．【解答】解：∵四边形ABCD是矩形，∴AD＝BC，∠ADC＝∠B＝∠DAE＝90°，∵把△BCE沿直线CE对折，使点B落在对角线AC上的点F处，∴CF＝BC，∠CFE＝∠B＝90°，EF＝BE，∴CF＝AD，∠CFD＝90°，∴∠ADE+∠CDF＝∠CDF+∠DCF＝90°，∴∠ADF＝∠DCF，∴△ADE≌△FCD（ASA），∴DF＝AE＝2；∵∠AFE＝∠CFD＝90°，∴∠AFE＝∠DAE＝90°，∵∠AEF＝∠DEA，∴△AEF∽△DEA，∴，∴，∴EF1（负值舍去），∴BE＝EF1，故答案为：2，1．15.（2020•嘉兴）如图，有一张矩形纸条ABCD，AB＝5cm，BC＝2cm，点M，N分别在边AB，CD上，CN＝1cm．现将四边形BCNM沿MN折叠，使点B，C分别落在点B'，C'上．当点B'恰好落在边CD上时，线段BM的长为cm；在点M从点A运动到点B的过程中，若边MB'与边CD交于点E，则点E相应运动的路径长为（）cm．【解答】解：如图1中，∵四边形ABCD是矩形，∴AB∥CD，∴∠1＝∠3，由翻折的性质可知：∠1＝∠2，BM＝MB′，∴∠2＝∠3，∴MB′＝NB′，∵NB′（cm），∴BM＝NB′（cm）．如图2中，当点M与A重合时，AE＝EN，设AE＝EN＝xcm，在Rt△ADE中，则有x2＝22+（4﹣x）2，解得x，∴DE＝4（cm），如图3中，当点M运动到MB′⊥AB时，DE′的值最大，DE′＝5﹣1﹣2＝2（cm），如图4中，当点M运动到点B′落在CD时，DB′（即DE″）＝5﹣1（4）（cm），∴点E的运动轨迹E→E′→E″，运动路径＝EE′+E′B′＝22﹣（4）＝（）（cm）．故答案为，（）．16.（2020•衢州）如图，把一张矩形纸片ABCD按所示方法进行两次折叠，得到等腰直角三角形BEF，若BC＝1，则AB的长度为（）A．B．C．D．【解答】解：由折叠补全图形如图所示，∵四边形ABCD是矩形，∴∠ADA'＝∠B＝∠C＝∠A＝90°，AD＝BC＝1，CD＝AB，由第一次折叠得：∠DAE＝∠A＝90°，∠ADE∠ADC＝45°，∴∠AED＝∠ADE＝45°，∴AE＝AD＝1，在Rt△ADE中，根据勾股定理得，DE AD，故选：A．。

第五章图形与变换本章思维导图考点精要解析考点一:平移变换1.平移是指图形按照一定的方向从一个位置平移到另一个位置,平移后所得图形与原图形的形状、大小都没有发生变化.2.平移变换的性质(1)平移后，对应线段平行(或在同一直线上)且相等，对应角相等.(2)平移后，对应点所连的线段平行(或在同一直线上)且相等.考点二:旋转变换1.旋转是指图形绕着某一个点按一定的旋转方向旋转一定的角度，旋转后所得图形与原来的图形的形状、大小都没有发生变化.中心对称变换是旋转180°的特殊旋转变换.2.旋转变换的基本性质①旋转变换的对应点到旋转中心的距离相等.②旋转前后两图形的对应线段和对应角分别相等.③对应边所夹的角等于旋转角.考点三:轴对称变换1.轴对称是指将一个图形沿着某条直线翻折180°与另一个图形完全重合，则这两个图形关于这条直线成轴对称，这条直线是对称轴.2.轴对称、轴对称图形的性质(1)关于某条直线对称的两个图形是全等形；(2)如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线；(3)对应边所在直线交于对称轴.注：成轴对称的两个图形一定全等，全等的图形不一定成轴对称.高频考点过关考点一:平移变换例题1.如下左图所示，将△ABC沿着XY方向平移一定的距离就得到△MNL，则下列结论中正确的有（）个.①AM∥BN；②AM=BN；③BC=ML；④∠ACB=∠MNLA.1B.2C.3D.4答案：B例题2.如下右图所示，线段AB=CD，AB与CD相交于点O，且∠AOC=60°，CE是由AB平移得到的，则AC+BD与AB的大小关系是 .答案：AC+BD AB提示：连接DE，可证四边形ACEB是平行四边形，△CED是等边三角形.在△EBD中，根据三边关系得证，当AC∥BD时，取“=”号.考点二:平移变换例题3.如右图所示，O是锐角三角形ABC内一点，∠AOB=∠BOC=∠COA=120°，P是△ABC 内不同于O的另一点；△A1BO1，△A1BP1分别由△AOB，△APB旋转而得，旋转角都为60°，则下列结论：①△O1BO为等边三角形，且A1，O1，O，C在一条直线上．②A1O1+O1O=AO+BO．③A1P1+PP1=PA+PB．④PA+PB+PC＞OA+OB+OC．其中正确的有（填序号）.答案：①②③④提示：连接O1O,P1P,此题通过旋转60°得到△OBO1,△P1PB是等边三角形，然后利用等边三角形的性质转化线段.考点三:轴对称变换例题4.如右图所示，AD是△ABC的中线，∠ADC=60°，BC=4，把△ADC沿直线AD折叠后，点C/落在的位置上，连接BC/，则BC/的长为（）A.1B.3C.2D.23答案：C例题5.如右图所示，在平面直角坐标系中，A,B两点的坐标分别为A(2,-3),B(4,-1).(1)若P(p,0)是x轴上的一个动点，则当p= 时，△PAB的周长最短；(2)若C(a,0),D(a+3,0)是x轴上的两个动点，则当a= 时，四边形ABCD的周长最短；(3)设M,N分别为x轴和y轴上的动点，请问：是否存在这样的点M(m,0),N(0,n),使四边形ABMN的周长最短？若存在，请求出m= ，n= (不必写解答过程)；若不存在，请说明理由.答案：（1）72；［提示］作点B关于x轴的对称点B/,连接AB/交x轴于点P，则点P即为所求，易求直线AB/的解析式为y=2x－7，所以点P的坐标为(72,0).(2)54；［提示］将点A向右平移3个单位得到点A1，其坐标为(5,-3).作点A1关于x轴的对称点A2，其坐标为(5,3)，连接A2B交x轴于点D，将点D 向左平移3个单位得到点C .易求直线A 2B 的解析式为y =4x －17，所以点D 的坐标为(174,0)，则点C 的坐标为(54,0). (3)存在使四边形ABMN 周长最短的点M 、N ,m =52，n =53-. 中考真题链接真题1.(鄂州中考) 如下左图所示，已知直线a ∥b ，且a 与b 之间的距离为4，点A 到直线a 的距离为2，点B 到直线b 的距离为3，AB =230.试在直线a 上找一点M ，在直线b 上找一点N ，满足MN ⊥a 且AM +MN +NB 的长度和最短，则此时AM +NB 的值为（ ）A ．6B ．8C ．10D ．12真题2.(济宁中考) 如下右图所示，在平面直角坐标系中，点A ，B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上一个动点，且A ，B ，C 三点不在同一条直线上，当△ABC 的周长最小时，点C 的坐标是（ ）A .(0，0)B .(0，1)C .(0，2)D .(0，3)真题3.(苏州中考) 如下左图所示，在平面直角坐标系中，Rt △OAB 的顶点A 在x 轴的正半轴上，顶点B 的坐标为（3，3），点C 的坐标为（12，0），点P 为斜边OB 上的一动点，则PA ＋PC 的最小值为（ ） A ．132 B ．312 C ．3192+ D ．27 真题4.(南京中考) 如下右图所示，在菱形ABCD 中，∠A =60°，将纸片折叠，点A ，D 分别落在点A ′、D ′处，且A ′D ′经过点B ，EF 为折叠，当D ′F ⊥CD 时，CF DF 的值为（ ） A ． B ． C ．D ．真题5.(葫芦岛中考)两个形状和大小完全一样的梯形纸片如图(a )摆放，将梯形纸片ABCD沿上底AD 方向向右平移得到图(b )．已知AD ＝4，BC ＝8，若阴影部分的面积是四边形A ′B ′CD 的面积的13，则图(b )中平移距离A ′A ＝________.xyOABC真题6.(南京中考)如下左图所示，将矩形ABCD绕点A顺时针旋转到矩形A’B’C’D’的位置，旋转角为α (0︒<α<90︒).若∠1=110︒，则α= .真题7.(烟台中考) 如下右图所示，在△ABC中，AB=AC,BAC=54°，∠BAC的平分线与AB 的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为度．真题8.(安徽中考) 如下图所示，已知A(-3，-3)，B(-2，-1)，C(-1，-2)是平面直角坐标系上三点.（1）请画出△ABC关于原点O对称的△A1B1C1.（2）请写出点B关于y轴对称点B2的坐标，若将点B2向上平移h个单位，使其落在△A1B1C1的内部，指出h的取值范围.真题9.(义乌中考)如图(a)所示，小明将一张矩形纸片沿对角线剪开，得到两种三角形纸片（如图（b）所示），量得它们的斜边长为10cm，较小锐角为30°，再将这两张三角纸片摆成如图（c）的形状，但点B，C，F，D在同一条直线上，且点C与点F重合（在图（c）至图（f）中统一用F表示）（a）（b）（c）小明在对这两张三角形纸片进行如下操作时遇到了三个问题，请你帮助解决.（1）将图（c）中的△ABF沿BD向右平移到图（d）的位置，使点B与点F重合，请你求出平移的距离；AB CDB’1C’D’（2）将图（c）中的△ABF绕点F顺时针方向旋转30°到图（e）的位置，A1F交DE 于点G，请你求出线段FG的长度；（3）将图（c）中的△ABF沿直线AF翻折到图（f）的位置，AB1交DE于点H，请证明：AH﹦DH.（d）（e）（f）真题10.(娄底中考)某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按图按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．（1）求证：AM=AN；（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．真题11. （潍坊中考）如图（a）所示，将一个边长为2的正方形ABCD和一个长为2，宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF，现将小长方形CEFD绕点C顺时针旋转至CE＇F＇D＇，旋转角为α.⑴当点D＇恰好落在EF边上时，求旋转角α的值；⑵如图（b）所示，G为BC的中点，且0°<α<90°，求证：G D＇= E＇D；⑶小长方形CEFD绕点C顺时针旋转一周的过程中，△DC D＇与△CB D＇能否全等？若能，直接写出旋转角α的值；若不能，说明理由.真题12. （北京中考）如右图所示，已知△ABC，⑴请你在BC边上分别取两点D、E（BC的中点除外），连接AD，AE，写出使此图中只存在两对面积相等的三角形的相应条件，并表示出面积相等的三角形；⑵请你根据使⑴成立的相应条件，证明AB+AC>AD+AE.真题13. （日照中考改编）如图（a ）所示，点A 、B 在直线l 的同侧，要在直线l 上找一点C ，使AC 与BC 的距离之和最小.我们可以作出点B 关于l 的对称点B ＇，连接AB ＇与直线l 交于点C ，则点C 即为所求.⑴实践运用如图（b ）所示，已知，⊙O 的直径CD 为4，点A 在⊙O 上，∠ACD=30°，点B为弧AD 的中点，P 为直径CD 上一动点，则BP+AP 的最小值为_________.⑵知识拓展如图（c ）所示，在Rt △ABC 中，AB=10，∠BAC=45°，∠BAC 的平分线交BC 与点D ，E 、F 分别是线段AD 和AB 上的动点，求BE+EF 的最小值，并写出解答过程. ⑶如图（d ）所示，点P 是四边形ABCD 内一点，分别在边AB 、BC 上作出点M 、N ，使PM+PN+MN 的值最小，保留作图痕迹，不写作法.创训练新思维创新 1. 将两块含30°角且大小相同的直角三角形如图（a ）所示.⑴将图（a ）中的△A 1B 1C 绕点C 顺时针旋转45°得到图（b ），点P 1是A 1 C 与AB的交点.求证：112CP AP . ⑵将图（b ）中的△A 1B 1C 绕点C 顺时针旋转15°得到△A 2B 2C ，如图（c ），点P 2是A 2C 与AB 的交点，直接写出直线A 1B 1与直线A 2B 2所夹的角的度数.⑶在⑵的条件下，写出线段CP 1与P 1P 2之间的数量关系，并证明你的结论.创新2. 在Rt△ABC中，∠ACB=90°，点P在△ABC的内部.⑴如图（a）所示，若∠BAC=30°，AP=4，点D、E分别在AB、AC边上，则△PDE 周长的最小值为______________；此时∠DPE=______________.⑵如图（b）所示，若∠BAC=45°，AP=4，点D、E分别在AB、AC边上，则△PDE 周长的最小值为______________；此时∠DPE=______________.⑶如图（c）所示，若∠BAC=α，AP=4，点D、E分别在AB、AC边上，求△PDE 周长的最小值及此时∠DPE的度数.⑷如图（d）所示，若PA=a，PB=b，PC=c，∠BAC=α，且c=bcosα=asinα，直接写出∠APB的度数.。

专题14 几何变换问题【考点1】平移变换问题【例1】（2019·山东中考真题）在平面直角坐标系中，将点A （1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是（ ）A ．（﹣1，1）B ．（﹣1，﹣2）C ．（﹣1，2）D ．（1，2）【答案】A【解析】试题分析：已知将点A （1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，根据向左平移横坐标减，向上平移纵坐标加可得点A′的横坐标为1﹣2=﹣1，纵坐标为﹣2+3=1，即A ′的坐标为（﹣1，1）．故选A ．考点：坐标与图形变化-平移．【变式1-1】（2019·甘肃中考真题）如图，在平面直角坐标系xOy 中，将四边形ABCD 向下平移，再向右平移得到四边形1111A B C D ，已知1(3,5),(4,3),(3,3)A B A --，则点1B 坐标为（ ）A ．(1,2)B ．(2,1)C ．(1,4)D ．(4,1)【答案】B【解析】【分析】 根据A 和A 1的坐标得出四边形ABCD 先向下平移2个单位，再向右平移6个单位得到四边形1111A B C D ，则B 的平移方法与A 点相同，即可得到答案．【详解】图形向下平移，纵坐标发生变化，图形向右平移，横坐标发生变化. A （－3，5）到A 1（3，3）得向右平移3－（－3）＝6个单位，向下平移5－3＝2个单位.所以B （－4，3）平移后B 1（2，1）.故选B.【点睛】此题考查图形的平移.，掌握平移的性质是解题关键【变式1-2】（2019·广西中考真题）如图，在平面直角坐标系中，已知ABC ∆的三个顶点坐标分别是2,1,1,()()2,3,3()A B C ---（1）将ABC ∆向上平移4个单位长度得到111A B C ∆，请画出111A B C ∆；（2）请画出与ABC ∆关于y 轴对称的222A B C ∆；（3）请写出12A A 、的坐标．【答案】（1）如图所示：111A B C ∆，即为所求；见解析；（2）如图所示：222A B C ∆，即为所求；见解析；（3）122,3,),1(()2A A --．【解析】【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）直接利用轴对称的性质得出对应点位置进而得出答案；（3）利用所画图象得出对应点坐标.【详解】（1）如图所示：111A B C ∆，即为所求；（2）如图所示：222A B C ∆，即为所求；（3）122,3,),1(()2A A --．【点睛】此题主要考查了轴对称变换以及平移变换，正确得出对应点位置是解题关键.【考点2】轴对称变换问题（含折叠变换）【例2】（2019·四川中考真题）如图，在菱形ABCD 中，4sin 5B =，点,E F 分别在边,AD BC 上，将四边形AEFB 沿EF 翻折，使AB 的对应线段MN 经过顶点C ，当MN BC ⊥时，AE AD 的值是_____．【答案】29. 【解析】【分析】延长CM 交AD 于点G ，进而利用翻折变换的性质得出AE ME =，A EMC ∠=∠，BF FN =，B N ∠=∠，AB MN =，再利用菱形的性质得出AB BC CD AD ===，B D ∠=∠，180A B ︒∠+∠=，设4CF x =，5FN x =，利用勾股定理得出9BC x AB CD AD ====，再根据三角函数进行计算即可解答【详解】延长CM 交AD 于点G ，∵将四边形AEFB 沿EF 翻折，∴AE ME =，A EMC ∠=∠，BF FN =，B N ∠=∠，AB MN =∵四边形ABCD 是菱形∴AB BC CD AD ===，B D ∠=∠，180A B ︒∠+∠=∵4sin sin 5CF B N FN===， ∴设4CF x =，5FN x =，∴223CN FN CF x =-=， ∴9BC x AB CD AD ====，∵4sin sin 5GC B D CD=== ∴365x GC = ∴()36x 6655GM GC MN CN x x =--=-= ∵180A B ︒∠+∠=，180EMC EMG ︒∠+∠=∴B EMG ∠=∠∴4sin sin 5EG B EMG EM=∠== ∴3cos 5GM EMG EM ∠== ∴=2EM x ，∴2AE x =，∴2299AE x AD x == 故答案为：29. 【点睛】此题考查翻折变换，菱形的性质，三角函数，解题关键在于利用折叠的性质进行解答【变式2-1】（2019·江苏中考真题）如图，将平行四边形纸片ABCD 沿一条直线折叠，使点A 与点C 重合，点D 落在点G 处，折痕为EF ．求证：（1）ECB FCG ∠=∠；（2）EBC FGC ∆≅∆．【答案】（1）见解析；（2）见解析.【解析】【分析】(1)依据平行四边形的性质，即可得到A BCD ∠=∠，由折叠可得，A ECG ∠=∠，即可得到ECB FCG ∠=∠；(2)依据平行四边形的性质，即可得出D B ∠=∠，AD BC =，由折叠可得，D G ∠=∠，AD CG =，即可得到B G ∠=∠，BC CG =，进而得出EBC FGC ∆≅∆．【详解】(1)Q 四边形ABCD 是平行四边形，A BCD ∴=∠，由折叠可得， A ECG ∠=∠，BCD ECG ∴∠=∠，BCD ECF ECG ECF ∴∠-∠=∠-∠，ECB FCG ∴∠=∠；(2)Q 四边形ABCD 是平行四边形，D B ∴∠=∠，AD BC =，由折叠可得，D G ∠=∠，AD CG =，B G ∴∠=∠，BC CG =，又ECB FCG ∠=∠Q ，()EBC FGC ASA ∴∆≅∆．【点睛】本题考查了平行四边形的性质，折叠的性质，全等三角形的判定，熟练掌握平行四边形的性质以及折叠的性质是解题的关键.【变式2-2】（2019·江苏中考真题）如图，已知等边△ABC 的边长为8，点P 是AB 边上的一个动点（与点A 、B 不重合），直线l 是经过点P 的一条直线，把△ABC 沿直线l 折叠，点B 的对应点是点B’. （1）如图1，当PB=4时，若点B’恰好在AC 边上，则AB’的长度为_____；（2）如图2，当PB=5时，若直线l //AC ，则BB’的长度为 ；（3）如图3，点P 在AB 边上运动过程中，若直线l 始终垂直于AC ，△ACB’的面积是否变化？若变化，说明理由；若不变化，求出面积；（4）当PB=6时，在直线l 变化过程中，求△ACB’面积的最大值.【答案】（1）4；（2）53；（3）面积不变，S△ACB’=163；（4）24+43【解析】【分析】(1)证明△APB′是等边三角形即可解决问题；(2)如图2中，设直线l交BC于点E，连接B B′交PE于O，证明△PEB是等边三角形，求出OB即可解决问题；(3)如图3中，结论：面积不变，证明B B′//AC即可；(4)如图4中，当PB′⊥AC时，△ACB′的面积最大，设直线PB′交AC于点E，求出B′E即可解决问题. 【详解】(1)如图1，∵△ABC为等边三角形，∴∠A=60°，AB=BC=CA=8，∵PB=4，∴PB′=PB=PA=4，∵∠A=60°，∴△APB′是等边三角形，∴AB′=AP=4，故答案为4；(2)如图2，设直线l交BC于点E，连接B B′交PE于O，∵PE∥AC，∴∠BPE=∠A=60°，∠BEP=∠C=60°，∴△PEB是等边三角形，∵PB=5，B、B′关于PE对称，∴BB′⊥PE，BB′=2OB，∴OB=PB·sin60°=53，∴BB′=53，故答案为53；(3)如图3，结论：面积不变.过点B作BE⊥AC于E，则有BE=AB·sin60°=3843=∴S△ABC=1184322AC BE=⨯⨯g3，∵B、B′关于直线l对称，∴BB′⊥直线l，∵直线l⊥AC，∴AC//BB′，∴S△ACB’=S△ABC=163；(4)如图4，当B′P⊥AC时，△ACB′的面积最大，设直线PB′交AC于E，在Rt△APE中，PA=2，∠PAE=60°，∴PE=PA·sin60°3，∴3∴S△ACB最大值=12×3)×3【点睛】本题是几何变换综合题，考查了等边三角形的判定与性质，轴对称变换，解直角三角形，平行线的判定与性质等知识，理解题意，熟练掌握和灵活运用相关知识是解题的关键.【考点3】旋转变换问题【例3】（2019·山东中考真题）(1)问题发现如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.填空:线段AD,BE之间的关系为.(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由. (3)解决问题如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.【答案】(1) AD=BE ，AD ⊥BE ．(2) AD=BE ，AD ⊥BE ．(3) 5-32≤PC≤5+32．【解析】【分析】（1）根据等腰三角形性质证△ACD ≌△BCE （SAS ），得AD=BE ，∠EBC=∠CAD ，延长BE 交AD 于点F ，由垂直定义得AD ⊥BE ．（2）根据等腰三角形性质证△ACD ≌△BCE （SAS ），AD=BE ，∠CAD=∠CBE ，由垂直定义得∠OHB=90°，AD ⊥BE ；（3）作AE ⊥AP ，使得AE=PA ，则易证△APE ≌△ACP ，PC=BE ，当P 、E 、B 共线时，BE 最小，最小值=PB-PE ；当P 、E 、B 共线时，BE 最大，最大值=PB+PE ，故5-32≤BE≤5+32.【详解】（1）结论：AD=BE ，AD ⊥BE ．理由：如图1中，∵△ACB 与△DCE 均为等腰直角三角形，∴AC=BC ，CE=CD ，∠ACB=∠ACD=90°，在Rt △ACD 和Rt △BCE 中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩＝＝＝∴△ACD ≌△BCE （SAS ），∴AD=BE ，∠EBC=∠CAD延长BE 交AD 于点F ，∵BC ⊥AD ，∴∠EBC+∠CEB=90°，∵∠CEB=AEF ，∴∠EAD+∠AEF=90°，∴∠AFE=90°，即AD ⊥BE ．∴AD=BE ，AD ⊥BE ．故答案为AD=BE ，AD ⊥BE ．（2）结论：AD=BE ，AD ⊥BE ．理由：如图2中，设AD 交BE 于H ，AD 交BC 于O ．∵△ACB 与△DCE 均为等腰直角三角形，∴AC=BC ，CE=CD ，∠ACB=∠ECD=90°，∴ACD=∠BCE ，在Rt △ACD 和Rt △BCE 中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ACD ≌△BCE （SAS ），∴AD=BE ，∠CAD=∠CBE ，∵∠CAO+∠AOC=90°，∠AOC=∠BOH ，∴∠BOH+∠OBH=90°，∴∠OHB=90°，∴AD⊥BE，∴AD=BE，AD⊥BE．（3）如图3中，作AE⊥AP，使得AE=PA，则易证△APE≌△ACP，∴PC=BE，图3-1中，当P、E、B共线时，BE最小，最小值=PB-PE=5-32，图3-2中，当P、E、B共线时，BE最大，最大值=PB+PE=5+32，∴5-32≤BE≤5+32，即5-32≤PC≤5+32．【点睛】本题是几何变换综合题，考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识，解题的关键是正确寻找三角形全等的条件，学会添加辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．【变式3-1】（2019·辽宁中考真题）如图，△ABC在平面直角坐标系中，顶点的坐标分别为A(-4，4)，B(-1，1)，C(-1，4)．(1)画出与△ABC关于y轴对称的△A1B1C1．(2)将△ABC绕点B逆时针旋转90°，得到△A2BC2，画两出△A2BC2．(3)求线段AB在旋转过程中扫过的图形面积．(结果保留π)【答案】(1)作图见解析；(2)作图见解析；(3)9 2π.【解析】【分析】(1)根据关于y轴对称的点的坐标特征写出A1、B1、C1的坐标，然后描点即可；(2)利用网格特点和旋转的性质画出A、C的对应点A2、C2即可；(3)线段AB在旋转过程中扫过的图形为扇形，然后根据扇形面积公式计算即可．【详解】解：(1)如图，△A l B1C1为所作.(2)如图，△A2BC2为所作；(3)AB=2233+=32，所以线段AB在旋转过程中扫过的图形面积=290π(32)360⋅⋅=92π．【点睛】本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了扇形面积公式．【变式3-2】（2019·江苏中考真题）如图①，在ABC∆中，3AB AC==，100BAC︒∠=，D是BC的中点．小明对图①进行了如下探究：在线段AD上任取一点P，连接PB．将线段PB绕点P按逆时针方向旋转80︒，点B的对应点是点E，连接BE，得到BPE∆．小明发现，随着点P在线段AD上位置的变化，点E的位置也在变化，点E可能在直线AD的左侧，也可能在直线AD上，还可能在直线AD的右侧．请你帮助小明继续探究，并解答下列问题：（1）当点E 在直线AD 上时，如图②所示．①BEP ∠= ；②连接CE ，直线CE 与直线AB 的位置关系是 ．（2）请在图③中画出BPE ∆，使点E 在直线AD 的右侧，连接CE ．试判断直线CE 与直线AB 的位置关系，并说明理由．（3）当点P 在线段AD 上运动时，求AE 的最小值．【答案】（1）①50︒；②EC AB ∥；（2）AB EC ∥；（3）AE 的最小值3．【解析】【分析】（1）①利用等腰三角形的性质即可解决问题．②证明40ABC ︒∠=，40ECB ︒∠=，推出ABC ECB ∠=∠即可．（2）如图③中，以P 为圆心，PB 为半径作⊙P ．利用圆周角定理证明1402BCE BPE ︒∠=∠=即可解决问题．（3）因为点E 在射线CE 上运动，点P 在线段AD 上运动，所以当点P 运动到与点A 重合时，AE 的值最小，此时AE 的最小值3AB ==．【详解】（1）①如图②中，∵80BPE ︒∠=，PB PE =，∴50PEB PBE ︒∠=∠=，②结论：AB EC ∥．理由：∵AB AC =，BD DC =，∴AD BC ⊥，∴90BDE ︒∠=，∴905040EBD ︒︒︒∠=-=，∵AE 垂直平分线段BC ，∴EB EC =，∴40ECB EBC ︒∠=∠=，∵AB AC =，100BAC ︒∠=，∴40ABC ACB ︒∠=∠=，∴ABC ECB ∠=∠，∴AB EC ∥．故答案为50，AB EC ∥．（2）如图③中，以P 为圆心，PB 为半径作⊙P ．∵AD 垂直平分线段BC ，∴PB PC =， ∴1402BCE BPE ︒∠=∠=， ∵40ABC ︒∠=，∴ AB EC ∥．（3）如图④中，作AH CE ⊥于H ，∵点E 在射线CE 上运动，点P 在线段AD 上运动，∴当点P 运动到与点A 重合时，AE 的值最小，此时AE 的最小值3AB ==．【点睛】本题属于几何变换综合题，考查了等腰三角形的性质，平行线的判定，圆周角定理等知识，解题的关键是熟练掌握基本知识，灵活运用所学知识解决问题，学会利用辅助圆解决问题，属于中考压轴题．【考点4】位似变换问题【例4】（2019·广西中考真题）如图，ABC ∆与'''A B C ∆是以坐标原点O 为位似中心的位似图形，若点()()2,2,3,4A B ，()6,1C ，()'6,8B 则'''A B C ∆的面积为__．【答案】18．【解析】【分析】根据()3,4B ，()'6,8B 的坐标得到位似比，继而得到A 、C 对应点的坐标，再用'''A B C ∆所在的矩形的面积减去顶点处的三角形面积即可求得答案.【详解】∵ABC ∆与'''A B C ∆是以坐标原点O 为位似中心的位似图形，若点()3,4B ，()'6,8B ，∴位似比为：31=62， ∵()2,2A ，()6,1C ，∴()()'4,4,'12,2A C ，∴'''A B C ∆的面积为：1116824662818222⨯-⨯⨯-⨯⨯-⨯⨯=， 故答案为：18．【点睛】本题考查了位似变换以及三角形面积求法，正确得出对应点位置是解题关键． 【变式4-1】（2019·山东中考真题）在平面直角坐标系中，ABO V 三个顶点的坐标分别为()()()2,4,4,0,0,0A B O --．以原点O 为位似中心，把这个三角形缩小为原来的12，得到CDO V ，则点A 的对应点C 的坐标是__________．【答案】()1,2-或()1,2-【解析】【分析】根据位似图形的中心和位似比例即可得到点A 的对应点C.【详解】解：以原点O 为位似中心，把这个三角形缩小为原来的12，点A 的坐标为()2,4-， ∴点C 的坐标为112,22(4)-⨯⨯或112,22(4)⨯-⨯，即()1,2-或()1,2-，故答案为：()1,2-或()1,2-．【点睛】本题主要考查位似图形的对应点，关键在于原点的位似图形，要注意方向. 【变式4-2】（2018·四川中考真题）如图，ABC ∆在方格纸中.（1）请在方格纸上建立平面直角坐标系，使(2,3)A ，(6,2)C ，并求出B 点坐标；（2）以原点O 为位似中心，相似比为2，在第一象限内将ABC ∆放大，画出放大后的图形'''A B C ∆； （3）计算'''A B C ∆的面积S .【答案】（1）作图见解析；(2,1)B .（2）作图见解析；（3）16.【解析】分析：（1）直接利用A ，C 点坐标得出原点位置进而得出答案；（2）利用位似图形的性质即可得出△A'B'C'；（3）直接利用（2）中图形求出三角形面积即可．详解：（1）如图所示，即为所求的直角坐标系；B （2，1）；（2）如图：△A'B'C'即为所求；（3）S △A'B'C '=12×4×8=16． 点睛：此题主要考查了位似变换以及三角形面积求法，正确得出对应点位置是解题的关键．画位似图形的一般步骤为：①确定位似中心；②分别连接并延长位似中心和关键点；③根据位似比，确定位似图形的关键点；④顺次连接上述各点，得到放大或缩小的图形．一、单选题1．（2019·浙江中考真题）在平面直角坐标系中，点(),2A m 与点()3,b n 关于y 轴对称，则（ ） A ．3m =，2n =B ．3m =-，2n =C ．2m =，3n =D ．2m =-，3n = 【答案】B【解析】【分析】根据点关于y 轴对称，其横坐标互为相反数，纵坐标相同即可得到答案.【详解】A ，B 关于y 轴对称，则横坐标互为相反数，纵坐标相同,故选B【点睛】本题考查点坐标的轴对称，解题的关键熟练掌握点坐标的轴对称.2．（2019·辽宁中考真题）如图，点P （8，6）在△ABC 的边AC 上，以原点O 为位似中心，在第一象限内将△ABC 缩小到原来的12，得到△A ′B ′C ′，点P 在A ′C ′上的对应点P ′的的坐标为（ ）A ．（4，3）B ．（3，4）C ．（5，3）D ．（4，4）【答案】A【解析】【分析】 直接利用在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或−k ，进而结合已知得出答案．【详解】∵点P （8，6）在△ABC 的边AC 上，以原点O 为位似中心，在第一象限内将△ABC 缩小到原来的12，得到△A′B′C′，∴点P 在A′C′上的对应点P′的的坐标为：（4，3）．故选：A ．【点睛】此题主要考查了位似变换，正确得出位似比是解题关键．3．（2019·湖南中考真题）如图，将OAB ∆绕点O 逆时针旋转70°到OCD ∆的位置，若40AOB ∠=o ，则AOD ∠=（ ）A ．45°B ．40°C ．35°D ．30°【答案】D【解析】【分析】 首先根据旋转角定义可以知道70BOD ∠=o ，而40AOB ∠=o ，然后根据图形即可求出AOD ∠．【详解】解：∵OAB ∆绕点O 逆时针旋转70°到OCD ∆的位置，∴70BOD ︒∠=，而40AOB ︒∠=，∴704030AOD ∠=-=o o o故选：D ．【点睛】此题主要考查了旋转的定义及性质，其中解题主要利用了旋转前后图形全等，对应角相等等知识． 4．（2019·广东中考真题）下列四个银行标志中，既是中心对称图形，又是轴对称图形的是( ) A ． B ． C ． D ．【答案】C【解析】【分析】根据轴对称图形和中心对称图形的概念逐一进行判断即可得.【详解】A、是轴对称图形，不是中心对称图形，故不符合题意；B、是轴对称图形，不是中心对称图形，故不符合题意；C、是轴对称图形，也是中心对称图形，故符合题意；D、是轴对称图形，不是中心对称图形，故不符合题意，故选C.【点睛】本题主要考查轴对称图形和中心对称图形，在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形；在平面内，如果把一个图形绕某个点旋转180°后，能与原图形重合，那么就说这个图形是中心对称图形.5．（2019·浙江中考真题）如图，在直角坐标系中，已知菱形OABC的顶点A(1,2)，B(3,3)．作菱形OABC 关于y轴的对称图形OA′B′C′，再作图形OA′B′C′关于点O的中心对称图形OA″B″C″，则点C的对应点C″的坐标是（）A．(2,-1) B．(1,-2) C．(-2,1) D．(-2,-1)【答案】A【解析】【分析】先找出对应点，再用线段顺次连接作出图形，根据图形解答即可.【详解】如图，()''21C -，.故选A.【点睛】本题考查了轴对称作图及中心对称作图，熟练掌握轴对称作图及中心对称的性质是解答本题的关键，中心对称的性质：①关于中心对称的两个图形能够完全重合；②关于中心对称的两个图形，对应点的连线都经过对称中心，并且被对称中心平分.6．（2019·四川中考真题）在平面直角坐标系中，将点()2,3-向右平移4个单位长度后得到的点的坐标为（ ）A ．()2,3B ．()6,3-C ．()2,7-D ．()2,1--【答案】A【解析】【分析】根据直角坐标系的坐标平移即可求解.【详解】一个点向右平移之后的点的坐标，纵坐标不变，横坐标加4，故选A【点睛】此题主要考查坐标的平移，解题的关键是熟知直角坐标系的特点.7．（2019·湖南中考真题）点(1,2)-关于原点的对称点坐标是（ ）A ．(1,2)--B ．(1,2)-C ．(1,2)D ．(2,1)- 【答案】B【解析】【分析】坐标系中任意一点(),P x y ，关于原点的对称点是(),x y --，即关于原点的对称点，横纵坐标都变成相反数．【详解】根据中心对称的性质，得点()1,2-关于原点的对称点的坐标为()1,2-．故选B ．【点睛】本题考查了关于原点对称的点的坐标，关于原点的对称点，横纵坐标都变成相反数．8．（2019·湖南中考真题）如图，以点O 为位似中心，把ABC V 放大为原图形的2倍得到A'B'C'V ，以下说法中错误的是（ ）A ．ABC A'B'C'V V ∽B ．点C 、点O 、点C′三点在同一直线上 C ．AO:AA'1:2=D ．AB A'B'P【答案】C【解析】【分析】 直接利用位似图形的性质进而分别分析得出答案．【详解】∵以点O 为位似中心，把ABC V 放大为原图形的2倍得到A'B'C'V ，∴ABC A'B'C'V V ∽，点C 、点O 、点C′三点在同一直线上，AB A'B'P ，AO:AA'1:3=，∴C 选项错误，符合题意．故选C ．【点睛】此题主要考查了位似变换，正确把握位似图形的性质是解题关键．9．（2018·湖南中考真题）如图所示，在平面直角坐标系中，已知点A （2，4），过点A 作AB ⊥x 轴于点B ．将△AOB 以坐标原点O 为位似中心缩小为原图形的12，得到△COD ，则CD 的长度是（ ）A ．2B ．1C ．4D ．25【答案】A【解析】 【分析】直接利用位似图形的性质结合A 点坐标可直接得出点C 的坐标，即可得出答案．【详解】∵点A （2，4），过点A 作AB ⊥x 轴于点B ，将△AOB 以坐标原点O 为位似中心缩小为原图形的12，得到△COD ， ∴C （1，2），则CD 的长度是2，故选A ．【点睛】本题主要考查了位似变换以及坐标与图形的性质，正确把握位似图形的性质是解题关键．10．（2019·山东中考真题）如图，点A 的坐标是(-2,0)，点B 的坐标是(0,6)，C 为OB 的中点，将△ABC 绕点B 逆时针旋转90°后得到A B C '''∆．若反比例函数k y x=的图象恰好经过A B '的中点D ，则k 的值是（ ）A ．9B ．12C ．15D ．18【答案】C【解析】【分析】 作'A H y ⊥轴于.H 证明AOB V ≌()'BHA AAS V ，推出OA BH =，'OB A H =，求出点'A 坐标，再利用中点坐标公式求出点D 坐标即可解决问题．【详解】解：作A H y '⊥轴于H ．∵90AOB A HB ABA ∠=∠'=∠'=︒，∴90ABO A BH ∠+∠'=︒，90ABO BAO ∠+∠=︒，∴BAO A BH ∠=∠'，∵BA BA ='，∴()AOB BHA AAS 'V V ≌，∴OA BH =，OB A H ='，∵点A 的坐标是()2,0-，点B 的坐标是()0,6，∴2OA =，6OB =，∴2BH OA ==，6A H OB '==，∴4OH =，∴()6,4A '，∵BD A D ='，∴()3,5D ，∵反比例函数k y x=的图象经过点D ， ∴15k =．故选：C ．【点睛】本题考查反比例函数图形上的点的坐标特征，坐标与图形的变化-旋转等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题．11．（2019·浙江中考真题）在数学拓展课上，小明发现：若一条直线经过平行四边形对角线的交点，则这条直线平分该平行四边形的面积. 如图是由5个边长为1的小正方形拼成的图形，P 是其中4个小正方形的公共顶点，小强在小明的启发下，将该图形沿着过点P 的某条直线剪一刀，把它剪成了面积相等的两部分，则剪痕的长度是（ ）A ．22B ．5C ．35D ．10【答案】D【解析】【分析】 根据中心对称的性质即可作出剪痕，根据三角形全等的性质即可证得EM=DN ，利用勾股定理即可求得．【详解】如图，EF 为剪痕，过点F 作FG EM ⊥于G .∵EF 将该图形分成了面积相等的两部分，∴EF 经过正方形ABCD 对角线的交点，∴,AF CN BF DN ==.易证PME PDN ∆∆≌，∴EM DN =，而AF MG =，∴1EG EM MG DN AF DN CN DC =+=+=+==.在Rt FGE ∆中， 22223110FG EG EF +=+=故选：D.【点睛】本题考查了图形的剪拼，中心对称的性质，勾股定理的应用，熟练掌握中心对称的性质是解题的关键． 12．（2019·湖北中考真题）如图，矩形ABCD 中，AC 与BD 相交于点E ，:3AD AB =，将ABD △沿BD 折叠，点A 的对应点为F ，连接AF 交BC 于点G ，且2BG =，在AD 边上有一点H ，使得BH EH +的值最小，此时BH CF=（ ）A 3B ．233C ．62D ．32【答案】B【解析】【分析】设BD 与AF 交于点M ．设AB=a ，3a ，根据矩形的性质可得△ABE 、△CDE 都是等边三角形，利用折叠的性质得到BM 垂直平分AF ，BF=AB=a ，3a ．解直角△BGM ，求出BM ，再表示DM ，由△ADM ∽△GBM ，求出33B 点关于AD 的对称点B′，连接B′E ，设B′E 与AD 交于点H ，则此时BH+EH=B′E ，值最小．建立平面直角坐标系，得出B （3，3，B′（3，3，E （03，利用待定系数法求出直线B′E 的解析式，得到H （1，0），然后利用两点间的距离公式求出BH=4，进而求出23BH CF =23． 【详解】 如图，设BD 与AF 交于点M ．设AB=a ，3a ，∵四边形ABCD是矩形，∴∠DAB=90°，tan∠ABD=31 ADAB=，∴22AB AD+，∠ABD=60°，∴△ABE、△CDE都是等边三角形，∴BE=DE=AE=CE=AB=CD=a，∵将△ABD沿BD折叠，点A的对应点为F，∴BM垂直平分AF，BF=AB=a，3a，在△BGM中，∵∠BMG=90°，∠GBM=30°，BG=2，∴GM=12BG=1，33∴3∵矩形ABCD中，BC∥AD，∴△ADM∽△GBM，∴AD DMBG BM=，即3323a=，∴3，∴3AD=BC=6，3，易证∠BAF=∠FAC=∠CAD=∠ADB=∠BDF=∠CDF=30°，∴△ADF是等边三角形，∵AC平分∠DAF，∴AC 垂直平分DF ，∴CF=CD=23，作B 点关于AD 的对称点B′，连接B′E ，设B′E 与AD 交于点H ，则此时BH+EH=B′E ，值最小． 如图，建立平面直角坐标系，则A （3，0），B （3，3，B′（3，3，E （03，易求直线B′E 的解析式为33∴H （1，0），∴22(31)(230)-+-，∴23BH CF ==233． 故选：B ．【点睛】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了矩形的性质，解直角三角形，等边三角形、垂直平分线、相似三角形的判定与性质，待定系数法求直线的解析式，轴对称-最短路线问题，两点间的距离公式等知识．综合性较强，有一定难度．分别求出BH 、CF 的长是解题的关键．13．（2019·湖南中考真题）如图，在平面直角坐标系中，将边长为1的正方形OABC 绕点O 顺时针旋转45︒后得到正方形111OA B C ，依此方式，绕点O 连续旋转2019次得到正方形201920192019OA B C ，那么点2019A 的坐标是( )A ．22⎝⎭B ．(1,0)C ．22⎛ ⎝⎭D ．(0,1)- 【答案】A【解析】【分析】 根据旋转的性质分别求出点A 1、A 2、A 3、…的坐标，继而发现8次为一个循环，用2019除以8，看余数即可求得答案.【详解】Q 四边形OABC 是正方形，且OA 1=，()A 0,1∴，Q 将正方形OABC 绕点O 逆时针旋转45︒后得到正方形111OA B C ，∴点A 1的横坐标为12sin 452⨯︒=，点A 1的纵坐标为12cos 452⨯︒=， 122A ∴⎝⎭，继续旋转则()2A 1,0，322A 22⎛⎫- ⎪ ⎪⎝⎭，A 4(0，-1)，A 52222⎛⎫-- ⎪ ⎪⎝⎭，A 6(-1，0)，A 722,22⎛⎫- ⎪ ⎪⎝⎭，A 8(0，1)，A 922⎝⎭，……，发现是8次一循环，所以20198252÷= (3)∴点2019A 的坐标为22,22⎛- ⎝⎭，故选A ．【点睛】本题考查了旋转的性质，规律题——点的坐标的变化规律，通过分析正确得出坐标的变化规律是解题的关键.14．（2019·江苏中考真题）如图，△ABC 中，AB=AC=2，∠B=30°，△ABC 绕点A 逆时针旋转α(0<α<120°)得到AB C ''∆，''B C 与BC ，AC 分别交于点D ，E.设CD DE x +=，AEC ∆'的面积为y ，则y 与x 的函数图象大致为( )A ．B ．C ．D ．【答案】B【解析】【分析】连接B′C ，作AH ⊥B′C′，垂足为H ，由已知以及旋转的性质可得AB′=AB=AC=AC′=2，∠AB′C′=∠C′=30°，继而可求出AH 长，B′C′的长，由等腰三角形的性质可得∠AB′C=∠ACB′，再根据∠AB′D=∠ACD=30°，可得∠DB′C=∠DCB′，从而可得B′D=CD ，进而可得 B′E=x ，由此可得3，再根据三角形面积公式即可求得y 与x 的关系式，由此即可得到答案.【详解】连接B′C ，作AH ⊥B′C′，垂足为H ，∵AB=AC，∠B=30°，∴∠C=∠B=30°，∵△ABC绕点A逆时针旋转α(0<α<120°)得到AB C''∆，∴AB′=AB=AC=AC′=2，∠AB′C′=∠C′=30°，∴AH=12AC′=1，∴C′H=223AC AH'-=，∴B′C′=2C′H=23，∵AB′=AC，∴∠AB′C=∠ACB′，∵∠A B′D=∠ACD=30°，∴∠AB′C-∠AB′D=∠ACB′-∠ACD，即∠DB′C=∠DCB′，∴B′D=CD，∵CD+DE=x，∴B′D+DE=x，即B′E=x，∴C′E=B′C′-B′E=23-x，∴y=12C E AH'g=12×(23-x)×1=132x-+，观察只有B选项的图象符合题意，故选B.【点睛】本题考查的是几何综合题，涉及了旋转的性质，等腰三角形的判定与性质，勾股定理，一次函数的应用等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.15．（2019·辽宁中考真题）如图，在平面直角坐标系中，将△ABO沿x轴向右滚动到△AB1C1的位置，再到△A1B1C2的位置……依次进行下去，若已知点A(4，0)，B(0，3)，则点C100的坐标为( )A．121200,5⎛⎫⎪⎝⎭B．()600,0C．12600,5⎛⎫⎪⎝⎭D．()1200,0【答案】B【解析】【分析】根据三角形的滚动，可得出：每滚动3次为一个周期，点C1，C3，C5，…在第一象限，点C2，C4，C6，…在x轴上，由点A，B的坐标利用勾股定理可求出AB的长，进而可得出点C2的横坐标，同理可得出点C4，C6的横坐标，根据点的横坐标的变化可找出变化规律“点C2n的横坐标为2n×6(n为正整数)”，再代入2n=100即可求出结论．【详解】解：根据题意，可知：每滚动3次为一个周期，点C1，C3，C5，...在第一象限，点C2，C4，C6， (x)上．∵A(4，0)，B(0，3)，∴OA=4，OB=3，∴22OA OB+，∴点C2的横坐标为4+5+3=12=2×6，同理，可得出：点C4的横坐标为4×6，点C6的横坐标为6×6，…，∴点C2n的横坐标为2n×6(n为正整数)，∴点C100的横坐标为100×6=600，∴点C100的坐标为(600，0)．故选：B．【点睛】本题考查了规律型：点的坐标，根据点的坐标的变化找出变化规律是解题的关键．二、填空题16．（2019·湖南中考真题）在如图所示的方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC 绕点O 按顺时针方向旋转得到△A'B'C'，使各顶点仍在格点上，则其旋转角的度数是____________．．【答案】90°【解析】【分析】根据旋转角的概念找到∠BOB′是旋转角，从图形中可求出其度数即可．【详解】根据旋转角的概念：对应点与旋转中心连线的夹角，可知∠BOB′是旋转角，且∠BOB′＝90°，故答案为：90°．【点睛】本题主要考查了旋转角的概念，解题的关键是根据旋转角的概念找到旋转角．17．（2019·山东中考真题）如图，在正方形网格中，格点ABC ∆绕某点顺时针旋转角()0180αα<<︒得到格点111A B C ∆，点A 与点1A ，点B 与点1B ，点C 与点1C 是对应点，则α=_____度．【答案】90【解析】【分析】先连接1CC ，1AA ，作1CC ，1AA 的垂直平分线交于点E ，连接AE ，1A E ，再由题意得到旋转中心，由旋转的性质即可得到答案.【详解】如图，连接1CC ，1AA ，作1CC ，1AA 的垂直平分线交于点E ，连接AE ，1A E ，∵1CC ，1AA 的垂直平分线交于点E ，∴点E 是旋转中心，∵190AEA ∠=︒，∴旋转角90α=︒.故答案为：90.【点睛】本题考查旋转，解题的关键是掌握旋转的性质.18．（2019·海南中考真题）如图，将Rt ABC ∆的斜边AB 绕点A 顺时针旋转()090αα︒︒<<得到AE ，直角边AC 绕点A 逆时针旋转()090ββ︒︒<<得到AF ，连结EF ．若=3AB ，=2AC ，且B αβ+=∠，则=EF _____．13【解析】【分析】由旋转的性质可得3AE AB ==，2AC AF ==，由勾股定理可求EF 的长．【详解】解：由旋转的性质可得3AE AB ==，2AC AF ==，90B BAC ︒∠+∠=Q ，且B αβ+=∠，90BAC αβ︒∴∠++=90EAF ︒∴∠=2213EF AE AF ∴=+=故答案为：13【点睛】本题考查了旋转的性质，勾股定理，灵活运用旋转的性质是本题的关键．19．（2019·山东中考真题）在平面直角坐标系中，点()4,2P 关于直线1x =的对称点的坐标是_____．【答案】()2,2-【解析】【分析】先求出点P 到直线1x =的距离，再根据对称性求出对称点P'到直线1x =的距离，从而得到点P'的横坐标，即可得解．【详解】∵点()4,2P ，∴点P 到直线1x =的距离为413-=，∴点P 关于直线1x =的对称点P'到直线1x =的距离为3， ∴点P'的横坐标为132-=-，∴对称点P'的坐标为()2,2-.故答案为：()2,2-．【点睛】本题考查了坐标与图形变化﹣对称，根据轴对称性求出对称点到直线1x =的距离，从而得到横坐标是解题的关键，作出图形更形象直观．20．（2019·山东中考真题）如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，ABO V 与A B O '''V 是以点P 为位似中心的位似图形，它们的顶点均在格点（网格线的交点）上，则点P 的坐标为_____。

2020中考数学几何专题：平移和旋转（含答案）例题1.如图，△ ABC绕点A顺时针旋转45°得到△ A' B' C',若/BAC=90° AB=AC^2，则图中阴影部分的面积等于3例题2.如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3 ,点Q为对角线AC上的动点，则△ BEQ周长的最小值为 .例题3. 如图，在△ ABC中，AB=2, AC=4，将△ ABC绕点C按逆时针方向旋转得到^ A' B' C,使CB' // AB,分别延长AB, CA '相交于点D ,贝U线段BD的长为.例题4.如图，把△ ABC绕点C按顺时针方向旋转35° ,得到△ A' B' C, A' B'交AC 于点D.若/ A' DC=90。

，贝U Z A=.巩固练习-旋转1.如图，在^ ABC中，NCAB =70。

在同一平面内，将^ ABC绕点A旋转到△ AB/C/的位置，使得CC / // AB ,则NBAB/ =()A. 30：B. 35：C. 40：D. 50：B2.如图，APQR是AABC经过某种变换后得到的图形.如果AABC中任意一点M的坐标为3.如图，在Rt△ ABC 中，Z ACB=90o, Z BAC= 60o, AB=6. RtAAB' C'可以看作是由RtA ABC绕A点逆时针方向旋转60o得到的，则线段B' C的长为4.如图，£AOB=90°, NB=30°, △ A’OB’可以看作是由△ AOB绕点。

顺时针旋转"角度得到的.若点A '在AB上，则旋转角的大小可以是( )A、30°B、450C、600D、90°5.如图，若将AABC绕点C,顺时针旋转90。

后得到MBC，贝U A点的对应点6.下列图形中，中心对称图形有（）. ® OA,1个2个C. 3个D. 4个中7.下列几何图形中，即是中心对称图形又是轴对称图形的是（）A .正三角形 B.等腰直角三角形C.等腰梯形8.如图，点A, B, C的坐标分别为（2, 4） , （5, 2） , （3, — 1）.若以点D为顶点的四边形既是轴对称图形，又是中心对称图形，则点D的坐标为A'的坐标D.正方形A, B, C,9.如图，在平面直角坐标系中，△ ABC的三个顶点的坐标分别为 A (0,1) , B (-1,1),C (-1,3)。

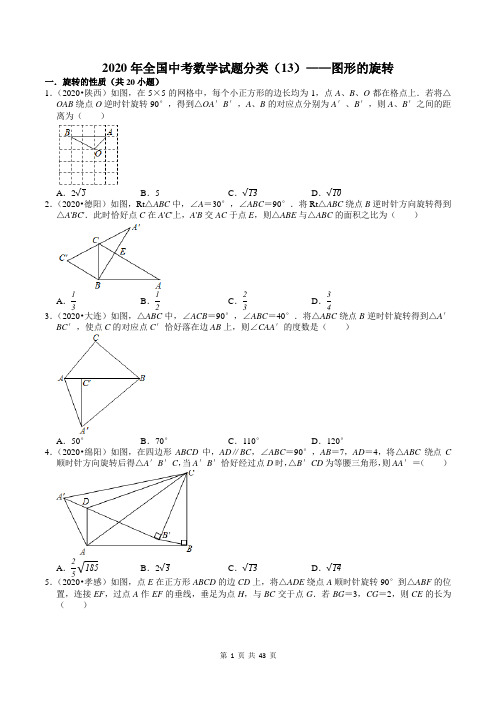
2020年全国中考数学试题分类（13）——图形的旋转一．旋转的性质（共20小题）1．（2020•陕西）如图，在5×5的网格中，每个小正方形的边长均为1，点A 、B 、O 都在格点上．若将△OAB 绕点O 逆时针旋转90°，得到△OA ′B ′，A 、B 的对应点分别为A ′、B ′，则A 、B ′之间的距离为（ ）A ．2√5B ．5C ．√13D ．√102．（2020•德阳）如图，Rt △ABC 中，∠A ＝30°，∠ABC ＝90°．将Rt △ABC 绕点B 逆时针方向旋转得到△A 'BC '．此时恰好点C 在A 'C '上，A 'B 交AC 于点E ，则△ABE 与△ABC 的面积之比为（ ）A ．13B ．12C ．23D ．34 3．（2020•大连）如图，△ABC 中，∠ACB ＝90°，∠ABC ＝40°．将△ABC 绕点B 逆时针旋转得到△A ′BC ′，使点C 的对应点C ′恰好落在边AB 上，则∠CAA ′的度数是（ ）A ．50°B ．70°C ．110°D ．120°4．（2020•绵阳）如图，在四边形ABCD 中，AD ∥BC ，∠ABC ＝90°，AB ＝7，AD ＝4，将△ABC 绕点C 顺时针方向旋转后得△A ′B ′C ，当A ′B ′恰好经过点D 时，△B ′CD 为等腰三角形，则AA ′＝（ ）A ．25√185B ．2√3C ．√13D ．√145．（2020•孝感）如图，点E 在正方形ABCD 的边CD 上，将△ADE 绕点A 顺时针旋转90°到△ABF 的位置，连接EF ，过点A 作EF 的垂线，垂足为点H ，与BC 交于点G ．若BG ＝3，CG ＝2，则CE 的长为（ ）A ．54B ．154C ．4D ．92 6．（2020•河北）如图，将△ABC 绕边AC 的中点O 顺时针旋转180°．嘉淇发现，旋转后的△CDA 与△ABC 构成平行四边形，并推理如下：小明为保证嘉淇的推理更严谨，想在方框中“∵CB ＝AD ，”和“∴四边形…”之间作补充，下列正确的是（ ）A ．嘉淇推理严谨，不必补充B ．应补充：且AB ＝CDC ．应补充：且AB ∥CDD ．应补充：且OA ＝OC7．（2020•天津）如图，在△ABC 中，∠ACB ＝90°，将△ABC 绕点C 顺时针旋转得到△DEC ，使点B 的对应点E 恰好落在边AC 上，点A 的对应点为D ，延长DE 交AB 于点F ，则下列结论一定正确的是（ ）A ．AC ＝DEB ．BC ＝EF C ．∠AEF ＝∠D D ．AB ⊥DF8．（2020•齐齐哈尔）有两个直角三角形纸板，一个含45°角，另一个含30°角，如图①所示叠放，先将含30°角的纸板固定不动，再将含45°角的纸板绕顶点A 顺时针旋转，使BC ∥DE ，如图②所示，则旋转角∠BAD 的度数为（ ）A ．15°B ．30°C ．45°D ．60°9．（2020•苏州）如图，在△ABC 中，∠BAC ＝108°，将△ABC 绕点A 按逆时针方向旋转得到△AB 'C '．若点B '恰好落在BC 边上，且AB '＝CB '，则∠C '的度数为（ ）A ．18°B ．20°C ．24°D ．28°10．（2020•聊城）如图，在Rt △ABC 中，AB ＝2，∠C ＝30°，将Rt △ABC 绕点A 旋转得到Rt △AB ′C ′，使点B 的对应点B ′落在AC 上，在B ′C ′上取点D ，使B ′D ＝2，那么点D 到BC 的距离等于（ ）A ．2（√33+1） B ．√33+1 C ．√3−1 D ．√3+111．（2020•绍兴）如图，等腰直角三角形ABC 中，∠ABC ＝90°，BA ＝BC ，将BC 绕点B 顺时针旋转θ（0°＜θ＜90°），得到BP ，连结CP ，过点A 作AH ⊥CP 交CP 的延长线于点H ，连结AP ，则∠P AH 的度数（ ）A ．随着θ的增大而增大B ．随着θ的增大而减小C ．不变D ．随着θ的增大，先增大后减小12．（2020•海南）如图，在Rt △ABC 中，∠C ＝90°，∠ABC ＝30°，AC ＝1cm ，将Rt △ABC 绕点A 逆时针旋转得到Rt △AB 'C '，使点C '落在AB 边上，连接BB '，则BB '的长度是（ ）A ．1cmB ．2cmC ．√3cmD ．2√3cm13．（2020•菏泽）如图，将△ABC 绕点A 顺时针旋转角α，得到△ADE ，若点E 恰好在CB 的延长线上，则∠BED 等于（ ）A ．α2B ．23αC ．αD ．180°﹣α14．（2020•阜新）如图，在△ABC 中，∠ABC ＝90°，AB ＝BC ＝2．将△ABC 绕点B 逆时针旋转60°，得到△A 1BC 1，则AC 边的中点D 与其对应点D 1的距离是 ．15．（2020•眉山）如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝2．将△ABC 绕点A 按顺时针方向旋转至△AB 1C 1的位置，点B 1恰好落在边BC 的中点处，则CC 1的长为 ．16．（2020•天水）如图，在边长为6的正方形ABCD 内作∠EAF ＝45°，AE 交BC 于点E ，AF 交CD 于点F ，连接EF ，将△ADF 绕点A 顺时针旋转90°得到△ABG ．若DF ＝3，则BE 的长为 ．17．（2020•滨州）如图，点P 是正方形ABCD 内一点，且点P 到点A 、B 、C 的距离分别为2√3、√2、4，则正方形ABCD 的面积为 ．18．（2020•金华）图1是一个闭合时的夹子，图2是该夹子的主视示意图，夹子两边为AC，BD（点A与点B重合），点O是夹子转轴位置，OE⊥AC于点E，OF⊥BD于点F，OE＝OF＝1cm，AC＝BD＝6cm，CE＝DF，CE：AE＝2：3．按图示方式用手指按夹子，夹子两边绕点O转动．（1）当E，F两点的距离最大时，以点A，B，C，D为顶点的四边形的周长是cm．（2）当夹子的开口最大（即点C与点D重合）时，A，B两点的距离为cm．19．（2020•广州）如图，正方形ABCD中，△ABC绕点A逆时针旋转到△AB'C'，AB'，AC'分别交对角线BD 于点E，F，若AE＝4，则EF•ED的值为．20．（2020•玉林）如图，四边形ABCD中，对角线AC与BD交于点O，且OA＝OB＝OC＝OD=√22AB．（1）求证：四边形ABCD是正方形；（2）若H是边AB上一点（H与A，B不重合），连接DH，将线段DH绕点H顺时针旋转90°，得到线段HE，过点E分别作BC及AB延长线的垂线，垂足分别为F，G．设四边形BGEF的面积为s1，以HB，BC为邻边的矩形的面积为s2，且s1＝s2．当AB＝2时，求AH的长．二．旋转对称图形（共1小题）21．（2020•镇江）点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）．这个图案绕点O至少旋转°后能与原来的图案互相重合．三．中心对称（共3小题）22．（2020•绍兴）如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B 停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（）A．平行四边形→正方形→平行四边形→矩形B．平行四边形→菱形→平行四边形→矩形C．平行四边形→正方形→菱形→矩形D．平行四边形→菱形→正方形→矩形23．（2020•泰安）如图，将正方形网格放置在平面直角坐标系中，其中，每个小正方形的边长均为1，点A，B，C的坐标分别为A（0，3），B（﹣1，1），C（3，1）．△A'B'C′是△ABC关于x轴的对称图形，将△A'B'C'绕点B'逆时针旋转180°，点A'的对应点为M，则点M的坐标为．24．（2020•台州）用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为b，依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD 的面积为．（用含a，b的代数式表示）四．中心对称图形（共3小题）25．（2020•黄石）下列图形中，既是中心对称又是轴对称图形的是（）A．B．C．D．26．（2020•天水）下列图形中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．27．（2020•呼伦贝尔）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．五．关于原点对称的点的坐标（共1小题）28．（2020•淮安）在平面直角坐标系中，点（3，2）关于原点对称的点的坐标是（）A．（2，3）B．（﹣3，2）C．（﹣3，﹣2）D．（﹣2，﹣3）六．坐标与图形变化-旋转（共6小题）29．（2020•青岛）如图，将△ABC先向上平移1个单位，再绕点P按逆时针方向旋转90°，得到△A′B′C′，则点A的对应点A′的坐标是（）A．（0，4）B．（2，﹣2）C．（3，﹣2）D．（﹣1，4）30．（2020•枣庄）如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2．将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是（）A．（−√3，3）B．（﹣3，√3）C．（−√3，2+√3）D．（﹣1，2+√3）31．（2020•黄石）在平面直角坐标系中，点G的坐标是（﹣2，1），连接OG，将线段OG绕原点O旋转180°，得到对应线段OG'，则点G'的坐标为（）A．（2，﹣1）B．（2，1）C．（1，﹣2）D．（﹣2，﹣1）32．（2020•恩施州）如图，在平面直角坐标系中，△ABC的顶点坐标分别为：A（﹣2，0），B（1，2），C （1，﹣2）．已知N（﹣1，0），作点N关于点A的对称点N1，点N1关于点B的对称点N2，点N2关于点C 的对称点N3，点N3关于点A的对称点N4，点N4关于点B的对称点N5，…，依此类推，则点N2020的坐标为．33．（2020•烟台）如图，已知点A （2，0），B （0，4），C （2，4），D （6，6），连接AB ，CD ，将线段AB绕着某一点旋转一定角度，使其与线段CD 重合（点A 与点C 重合，点B 与点D 重合），则这个旋转中心的坐标为 ．34．（2020•衡阳）如图，在平面直角坐标系中，点P 1的坐标为（√22，√22），将线段OP 1绕点O 按顺时针方向旋转45°，再将其长度伸长为OP 1的2倍，得到线段OP 2；又将线段OP 2绕点O 按顺时针方向旋转45°，长度伸长为OP 2的2倍，得到线段OP 3；如此下去，得到线段OP 4，OP 5，…，OP n （n 为正整数），则点P 2020的坐标是 ．七．作图-旋转变换（共6小题）35．（2020•广西）如图，在平面直角坐标系中，△ABC 的三个顶点分别是A （1，1），B （4，1），C （5，3）．（1）将△ABC 向左平移6个单位长度得到△A 1B 1C 1，请画出△A 1B 1C 1，并写出点A 1，C 1的坐标．（2）请画出△ABC 关于原点O 成中心对称的△A 2B 2C 2．36．（2020•巴中）如图所示，△ABC在边长为1cm的小正方形组成的网格中．（1）将△ABC沿y轴正方向向上平移5个单位长度后，得到△A1B1C1，请作出△A1B1C1，并求出A1B1的长度；（2）再将△A1B1C1绕坐标原点O顺时针旋转180°，得到△A2B2C2，请作出△A2B2C2，并直接写出点B2的坐标；（3）在（1）（2）的条件下，求线段AB在变换过程中扫过图形的面积和．37．（2020•贵港）如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（1，4），B（4，1），C（4，3）．（1）画出将△ABC向左平移5个单位得到的△A1B1C1；（2）画出将△ABC绕原点O顺时针旋转90°得到的△A2B2C2．38．（2020•阜新）如图，△ABC在平面直角坐标系中，顶点的坐标分别为A（4，4），B（1，1），C（4，1）．（1）画出与△ABC关于y轴对称的△A1B1C1；（2）将△ABC绕点O1顺时针旋转90°得到△A2B2C2，弧AA2是点A所经过的路径，则旋转中心O1的坐标为；（3）求图中阴影部分的面积（结果保留π）．39．（2020•桂林）如图，在平面直角坐标系中，△ABC的三个顶点分别是A（1，3），B（4，4），C（2，1）．（1）把△ABC向左平移4个单位后得到对应的△A1B1C1，请画出平移后的△A1B1C1；（2）把△ABC绕原点O旋转180°后得到对应的△A2B2C2，请画出旋转后的△A2B2C2；（3）观察图形可知，△A1B1C1与△A2B2C2关于点（，）中心对称．40．（2020•常州）如图1，点B在线段CE上，Rt△ABC≌Rt△CEF，∠ABC＝∠CEF＝90°，∠BAC＝30°，BC＝1．（1）点F到直线CA的距离是；（2）固定△ABC，将△CEF绕点C按顺时针方向旋转30°，使得CF与CA重合，并停止旋转．①请你在图1中用直尺和圆规画出线段EF经旋转运动所形成的平面图形（用阴影表示，保留画图痕迹，不要求写画法）．该图形的面积为；②如图2，在旋转过程中，线段CF与AB交于点O，当OE＝OB时，求OF的长．八．利用旋转设计图案（共1小题）41．（2020•枣庄）如图的四个三角形中，不能由△ABC 经过旋转或平移得到的是（ ）A ．B ．C ．D ．九．几何变换综合题（共9小题） 42．（2020•锦州）已知△AOB 和△MON 都是等腰直角三角形（√22OA ＜OM ＝ON ），∠AOB ＝∠MON ＝90°．（1）如图1：连AM ，BN ，求证：△AOM ≌△BON ；（2）若将△MON 绕点O 顺时针旋转，①如图2，当点N 恰好在AB 边上时，求证：BN 2+AN 2＝2ON 2；②当点A ，M ，N 在同一条直线上时，若OB ＝4，ON ＝3，请直接写出线段BN 的长．43．（2020•葫芦岛）在等腰△ADC 和等腰△BEC 中，∠ADC ＝∠BEC ＝90°，BC ＜CD ，将△BEC 绕点C 逆时针旋转，连接AB ，点O 为线段AB 的中点，连接DO ，EO ．（1）如图1，当点B 旋转到CD 边上时，请直接写出线段DO 与EO 的位置关系和数量关系；（2）如图2，当点B 旋转到AC 边上时，（1）中的结论是否成立？若成立，请写出证明过程，若不成立，请说明理由；（3）若BC ＝4，CD ＝2√6，在△BEC 绕点C 逆时针旋转的过程中，当∠ACB ＝60°时，请直接写出线段OD 的长．44．（2020•沈阳）在△ABC 中，AB ＝AC ，∠BAC ＝α，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接DB ，DC ．（1）如图1，当α＝60°时，①求证：P A ＝DC ；②求∠DCP的度数；（2）如图2，当α＝120°时，请直接写出P A和DC的数量关系．（3）当α＝120°时，若AB＝6，BP=√31，请直接写出点D到CP的距离为．45．（2020•长春）如图①，在△ABC中，∠ABC＝90°，AB＝4，BC＝3．点P从点A出发，沿折线AB﹣BC以每秒5个单位长度的速度向点C运动，同时点D从点C出发，沿CA以每秒2个单位长度的速度向点A运动，点P到达点C时，点P、D同时停止运动．当点P不与点A、C重合时，作点P关于直线AC的对称点Q，连结PQ交AC于点E，连结DP、DQ．设点P的运动时间为t秒．（1）当点P与点B重合时，求t的值．（2）用含t的代数式表示线段CE的长．（3）当△PDQ为锐角三角形时，求t的取值范围．（4）如图②，取PD的中点M，连结QM．当直线QM与△ABC的一条直角边平行时，直接写出t的值．46．（2020•鄂尔多斯）（1）【操作发现】如图1，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．①请按要求画图：将△ABC绕点A顺时针方向旋转90°，点B的对应点为点B′，点C的对应点为点C′．连接BB′；②在①中所画图形中，∠AB′B＝°．（2）【问题解决】如图2，在Rt△ABC中，BC＝1，∠C＝90°，延长CA到D，使CD＝1，将斜边AB绕点A顺时针旋转90°到AE，连接DE，求∠ADE的度数．（3）【拓展延伸】如图3，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝1，CD＝3，AD＝kAB（k 为常数），求BD的长（用含k的式子表示）．47．（2020•十堰）如图1，已知△ABC≌△EBD，∠ACB＝∠EDB＝90°，点D在AB上，连接CD并延长交AE于点F．（1）猜想：线段AF与EF的数量关系为；（2）探究：若将图1的△EBD绕点B顺时针方向旋转，当∠CBE小于180°时，得到图2，连接CD并延长交AE 于点F ，则（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由；（3）拓展：图1中，过点E 作EG ⊥CB ，垂足为点G ．当∠ABC 的大小发生变化，其它条件不变时，若∠EBG ＝∠BAE ，BC ＝6，直接写出AB 的长．48．（2020•包头）如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝4，BC ＝2，Rt △ABC 绕点C 按顺时针方向旋转得到Rt △A ′B ′C ，A ′C 与AB 交于点D ．（1）如图1，当A ′B ′∥AC 时，过点B 作BE ⊥A ′C ，垂足为E ，连接AE ．①求证：AD ＝BD ；②求α△αααα△ααα的值； （2）如图2，当A ′C ⊥AB 时，过点D 作DM ∥A ′B ′，交B ′C 于点N ，交AC 的延长线于点M ，求αααα的值．49．（2020•东营）如图1，在等腰三角形ABC 中，∠A ＝120°，AB ＝AC ，点D 、E 分别在边AB 、AC 上，AD ＝AE ，连接BE ，点M 、N 、P 分别为DE 、BE 、BC 的中点．（1）观察猜想．图1中，线段NM 、NP 的数量关系是 ，∠MNP 的大小为 ．（2）探究证明把△ADE 绕点A 顺时针方向旋转到如图2所示的位置，连接MP 、BD 、CE ，判断△MNP 的形状，并说明理由；（3）拓展延伸把△ADE 绕点A 在平面内自由旋转，若AD ＝1，AB ＝3，请求出△MNP 面积的最大值．50．（2020•威海）发现规律（1）如图①，△ABC 与△ADE 都是等边三角形，直线BD ，CE 交于点F ．直线BD ，AC 交于点H ．求∠BFC 的度数．（2）已知：△ABC与△ADE的位置如图②所示，直线BD，CE交于点F．直线BD，AC交于点H．若∠ABC＝∠ADE＝α，∠ACB＝∠AED＝β，求∠BFC的度数．应用结论（3）如图③，在平面直角坐标系中，点O的坐标为（0，0），点M的坐标为（3，0），N为y轴上一动点，连接MN．将线段MN绕点M逆时针旋转60°得到线段MK，连接NK，OK．求线段OK长度的最小值．2020年全国中考数学试题分类（13）——图形的旋转参考答案与试题解析一．旋转的性质（共20小题）1．【解答】解：如图，由旋转的性质作出△A 'OB '，连接AB '，∵每个小正方形的边长均为1，∴AB '=√22+32=√13，故选：C ．2．【解答】解：∵∠A ＝30°，∠ABC ＝90°，∴∠ACB ＝60°，∵将Rt △ABC 绕点B 逆时针方向旋转得到△A 'BC '，∴BC ＝BC '，∠ACB ＝∠A 'C 'B ＝60°，∴△BCC '是等边三角形，∴∠CBC '＝60°，∴∠ABA '＝60°，∴∠BEA ＝90°，设CE ＝a ，则BE =√3a ，AE ＝3a ，∴αααα=13， ∴αααα=34， ∴△ABE 与△ABC 的面积之比为34．故选：D ．3．【解答】解：∵∠ACB ＝90°，∠ABC ＝40°，∴∠CAB ＝90°﹣∠ABC ＝90°﹣40°＝50°，∵将△ABC 绕点B 逆时针旋转得到△A ′BC ′，使点C 的对应点C ′恰好落在边AB 上，∴∠A ′BA ＝∠ABC ＝40°，A ′B ＝AB ，∴∠BAA ′＝∠BA ′A =12（180°﹣40°）＝70°，∴∠CAA '＝∠CAB +∠BAA ′＝50°+70°＝120°．故选：D ．4．【解答】解：过D 作DE ⊥BC 于E ，则BE ＝AD ＝4，DE ＝7，设B ′C ＝BC ＝x ，则DC =√2x ，∴DC 2＝DE 2+EC 2，即2x 2＝49+（x ﹣4）2，解得：x ＝5（负值舍去），∴BC ＝5，AC =√74，在AB 上取一点F ，使得BF ＝BC ＝5，连接DF ，则△DFC ∽△CB ′B ，且相似比为√2：1，∴AF ＝7﹣5＝2，∵AD ＝4，∴DF ＝2√5，∴BB ′=√2=√10， ∵将△ABC 绕点C 顺时针方向旋转后得△A ′B ′C ，∴∠DB ′C ＝∠ABC ＝90°，B ′C ＝BC ，A ′C ＝AC ，∠A ′CA ＝∠B ′CB ，∴△A ′CA ∽△B ′CB ，∴α′αα′α=αααα，∴AA ′=√745×√10=25√185， 故选：A ．5．【解答】解：如图所示，连接EG ，由旋转可得，△ADE ≌△ABF ，∴AE ＝AF ，DE ＝BF ，又∵AG ⊥EF ，∴H 为EF 的中点，∴AG 垂直平分EF ，∴EG ＝FG ，设CE ＝x ，则DE ＝5﹣x ＝BF ，FG ＝8﹣x ，∴EG ＝8﹣x ，∵∠C ＝90°，∴Rt △CEG 中，CE 2+CG 2＝EG 2，即x 2+22＝（8﹣x ）2，解得x =154， ∴CE 的长为154，故选：B ．6．【解答】解：∵CB ＝AD ，AB ＝CD ，∴四边形ABCD 是平行四边形，故应补充“AB ＝CD ”，故选：B ．7．【解答】解：由旋转可得，△ABC ≌△DEC ，∴AC ＝DC ，故A 选项错误，BC ＝EC ，故B 选项错误，∠AEF ＝∠DEC ＝∠B ，故C 选项错误，∠A ＝∠D ，又∵∠ACB ＝90°，∴∠A +∠B ＝90°，∴∠D +∠B ＝90°，∴∠BFD ＝90°，即DF ⊥AB ，故D 选项正确，故选：D ．8．【解答】解：如图，设AD与BC交于点F，∵BC∥DE，∴∠CF A＝∠D＝90°，∵∠CF A＝∠B+∠BAD＝60°+∠BAD，∴∠BAD＝30°故选：B．9．【解答】解：∵AB'＝CB'，∴∠C＝∠CAB'，∴∠AB'B＝∠C+∠CAB'＝2∠C，∵将△ABC绕点A按逆时针方向旋转得到△AB'C'，∴∠C＝∠C'，AB＝AB'，∴∠B＝∠AB'B＝2∠C，∵∠B+∠C+∠CAB＝180°，∴3∠C＝180°﹣108°，∴∠C＝24°，∴∠C'＝∠C＝24°，故选：C．10．【解答】解：方法一：∵在Rt△ABC中，AB＝2，∠C＝30°，∴BC＝2√3，AC＝4，∵将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，∴AB′＝AB＝2，B′C′＝BC＝2√3，∴B′C＝2，延长C′B′交BC于F，∴∠CB′F＝∠AB′C′＝90°，∵∠C＝30°，∴∠CFB′＝60°，B′F=√33B′C=2√33，∵B′D＝2，∴DF＝2+2√3 3，过D作DE⊥BC于E，∴DE=√32DF=√32×（2+2√33）=√3+1，方法二：过B′作B′F⊥BC于F，B′H⊥DE于H，则B′F＝HE，B′H＝EF，在Rt△ABC中，AB＝2，∠C＝30°，∴BC＝2√3，AC＝4，∵将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，∴AB′＝AB＝2，B′C′＝BC＝2√3，∴B′C＝2，∴B′F=12AB＝1，∴HE＝1，∵∠B′HD＝∠HEC＝90°，∴∠HB′C＝∠C＝30°，∴∠DB′H＝60°，∴∠B′DH＝30°，∴B′H＝1，DH=√3，∴DE=√3+1，故选：D．11．【解答】解：∵将BC绕点B顺时针旋转θ（0°＜θ＜90°），得到BP，∴BC＝BP＝BA，∴∠BCP＝∠BPC，∠BP A＝∠BAP，∵∠CBP+∠BCP+∠BPC＝180°，∠ABP+∠BAP+∠BP A＝180°，∠ABP+∠CBP＝90°，∴∠BPC+∠BP A＝135°＝∠CP A，∵∠CP A＝∠AHC+∠P AH＝135°，∴∠P AH＝135°﹣90°＝45°，∴∠P AH的度数是定值，故选：C．12．【解答】解：∵在Rt△ABC中，∠C＝90°，∠ABC＝30°，AC＝1cm，∴AC=12AB，则AB＝2AC＝2cm．又由旋转的性质知，AC′＝AC=12AB，B′C′⊥AB，∴B′C′是△ABB′的中垂线，∴AB′＝BB′．根据旋转的性质知AB ＝AB ′＝BB ′＝2cm ．故选：B ．13．【解答】解：∵∠ABC ＝∠ADE ，∠ABC +∠ABE ＝180°，∴∠ABE +∠ADE ＝180°，∴∠BAD +∠BED ＝180°，∵∠BAD ＝α，∴∠BED ＝180°﹣α．故选：D ．14．【解答】解：连接BD 、BD 1，如图，∵∠ABC ＝90°，AB ＝BC ＝2，∴AC =√22+22=2√2，∵D 点为AC 的中点，∴BD =12AC =√2，∵△ABC 绕点B 逆时针旋转60°，得到△A 1BC 1，∴BD 1＝BD ，∠DBD 1＝60°，∴△BDD 1为等边三角形，∴DD 1＝BD =√2．故答案为√2．15．【解答】解：∵在Rt △ABC 中，∠BAC ＝90°，将该三角形绕点A 按顺时针方向旋转到△AB 1C 1的位置，点B 1恰好落在边BC 的中点处，∴AB 1=12BC ，BB 1＝B 1C ，AB ＝AB 1，∴BB 1＝AB ＝AB 1，∴△ABB 1是等边三角形，∴∠BAB 1＝∠B ＝60°，∴∠CAC 1＝60°，∵将△ABC 绕点A 按顺时针方向旋转至△AB 1C 1的位置，∴CA ＝C 1A ，∴△AC 1C 是等边三角形，∴CC 1＝CA ，∵AB ＝2，∴CA ＝2√3，∴CC 1＝2√3．故答案为：2√3．16．【解答】解：法一：由题意可得，△ADF ≌△ABG ，∴DF ＝BG ，∠DAF ＝∠BAG ，∵∠DAB ＝90°，∠EAF ＝45°，∴∠DAF +∠EAB ＝45°，∴∠BAG +∠EAB ＝45°，∴∠EAF ＝∠EAG ，在△EAG 和△EAF 中，{αα=αααααα=αααααα=αα，∴△EAG ≌△EAF （SAS ），∴GE ＝FE ，设BE ＝x ，则GE ＝BG +BE ＝3+x ，CE ＝6﹣x ，∴EF ＝3+x ，∵CD ＝6，DF ＝3，∴CF ＝3，∵∠C ＝90°，∴（6﹣x ）2+32＝（3+x ）2，解得，x ＝2，即BE ＝2，法二：设BE ＝x ，连接GF ，如下图所示，∵四边形ABCD 为正方形，∴∠ABE ＝∠GCF ＝90°，∵△ADF 绕点A 顺时针旋转90°得到△ABG ，∴∠CAF ＝90°，GA ＝F A ，∴△GAF 为等腰直角三角形，∵∠EAF ＝45°，∴AE 垂直平分GF ，∴∠AEB +∠CGF ＝90°，∵在Rt △AEB 中，∠AEB +∠BAE ＝90°，∴∠BAE ＝∠CGF ，∴△BAE ∽△CGF ，∴αααα=αααα， ∵CF ＝CD ﹣DF ＝6﹣3＝3，GC ＝BC +BG ＝BC +DF ＝6+3＝9， ∴α3=69，∴x ＝2，即BE ＝2，故答案为：2．17．【解答】解：如图，将△ABP 绕点B 顺时针旋转90°得到△CBM ，连接PM ，过点B 作BH ⊥PM 于H ．∵BP ＝BM =√2，∠PBM ＝90°，∴PM =√2PB ＝2，∵PC ＝4，P A ＝CM ＝2√3，∴PC 2＝CM 2+PM 2，∴∠PMC ＝90°，∵∠BPM ＝∠BMP ＝45°，∴∠CMB ＝∠APB ＝135°，∴∠APB +∠BPM ＝180°，∴A ，P ，M 共线，∵BH ⊥PM ，∴PH ＝HM ，∴BH ＝PH ＝HM ＝1，∴AH ＝2√3+1，∴AB 2＝AH 2+BH 2＝（2√3+1）2+12＝14+4√3，∴正方形ABCD 的面积为14+4√3．解法二：连接AC ，利用勾股定理求出AC 即可．故答案为14+4√3．18．【解答】解：（1）当E ，F 两点的距离最大时，E ，O ，F 共线，此时四边形ABCD 是矩形， ∵OE ＝OF ＝1cm ，∴EF ＝2cm ，∴AB ＝CD ＝2cm ，∴此时四边形ABCD 的周长为2+2+6+6＝16（cm ），故答案为16．（2）如图3中，连接EF 交OC 于H ．由题意CE ＝CF =25×6=125（cm ）， ∵OE ＝OF ＝1cm ，∴CO 垂直平分线段EF ，∵OC =√αα2+αα2=√(125)2+12=135（cm ）， ∵12•OE •EC =12•CO •EH ， ∴EH =1×125135=1213（cm ），∴EF ＝2EH =2413（cm ）∵EF ∥AB ，∴αααα=αααα=25， ∴AB =52×2413=6013（cm ）．故答案为6013． 19．【解答】解：∵四边形ABCD 是正方形，∴∠BAC ＝∠ADB ＝45°，∵把△ABC 绕点A 逆时针旋转到△AB 'C '，∴∠EAF ＝∠BAC ＝45°，∵∠AEF ＝∠DEA ，∴△AEF ∽△DEA ，∴αααα=αααα，∴EF •ED ＝AE 2，∵AE ＝4，∴EF •ED 的值为16，故答案为：16．20．【解答】（1）证明：∵OA ＝OB ＝OC ＝OD ，∴四边形ABCD 是平行四边形，∴AC ＝BD ，∴平行四边形ABCD 是矩形，∵OA ＝OB ＝OC ＝OD =√22AB ，∴OA 2+OB 2＝AB 2，∴∠AOB ＝90°，即AC ⊥BD ，∴四边形ABCD 是正方形；（2）解：∵EF ⊥BC ，EG ⊥AG ，∴∠G ＝∠EFB ＝∠FBG ＝90°，∴四边形BGEF 是矩形，∵将线段DH 绕点H 顺时针旋转90°，得到线段HE ，∴∠DHE ＝90°，DH ＝HE ，∴∠ADH +∠AHD ＝∠AHD +∠EHG ＝90°，∴∠ADH ＝∠EHG ，∵∠DAH ＝∠G ＝90°，∴△ADH ≌△GHE （AAS ），∴AD ＝HG ，AH ＝EG ，∵AB ＝AD ，∴AB ＝HG ，∴AH ＝BG ，∴BG ＝EG ，∴矩形BGEF 是正方形，设AH ＝x ，则BG ＝EG ＝x ，∵s 1＝s 2．∴x 2＝2（2﹣x ），解得：x =√5−1（负值舍去），∴AH =√5−1．二．旋转对称图形（共1小题）21．【解答】解：连接OA ，OE ，则这个图形至少旋转∠AOE 才能与原图象重合，∠AOE =360°5=72°．故答案为：72．三．中心对称（共3小题）22．【解答】解：观察图形可知，四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形．故选：B．23．【解答】解：将△A'B'C'绕点B'逆时针旋转180°，如图所示：所以点M的坐标为（﹣2，1），故答案为：（﹣2，1）．24．【解答】解：如图，连接DK，DN，∵∠KDN＝∠MDT＝90°，∴∠KDM＝∠NDT，∵DK＝DN，∠DKM＝∠DNT＝45°，∴△DKM≌△DNT（ASA），∴S△DKM＝S△DNT，∴S四边形DMNT＝S△DKN=14a，∴正方形ABCD的面积＝4×14a+b＝a+b．故答案为（a+b）．四．中心对称图形（共3小题）25．【解答】解：A、既不是中心对称图形，又不是轴对称图形，故本选项不符合题意；B、是中心对称图形，但不是轴对称图形，故本选项不符合题意；C、不是中心对称图形，是轴对称图形，故本选项不符合题意；D、既是中心对称图形，又是轴对称图形，故本选项符合题意；故选：D．26．【解答】解：A、是轴对称图形，不是中心对称图形，故本选项不合题意；B、既是轴对称图形，又是中心对称图形，故本选项不合题意；C、是中心对称图形但不是轴对称图形，故本选项符合题意；D、是轴对称图形，不是中心对称图形，故本选项不合题意．故选：C．27．【解答】解：A、不是轴对称图形，是中心对称图形，故此选项错误；B、是轴对称图形，不是中心对称图形，故此选项错误；C、既是轴对称图形，也是中心对称图形，故此选项正确；D、是轴对称图形，不是中心对称图形，故此选项错误；故选：C．五．关于原点对称的点的坐标（共1小题）28．【解答】解：点（3，2）关于原点对称的点的坐标是：（﹣3，﹣2）．故选：C．六．坐标与图形变化-旋转（共6小题）29．【解答】解：如图，△A′B′C′即为所求，则点A的对应点A′的坐标是（﹣1，4）．故选：D．30．【解答】解：如图，过点B′作B′H⊥y轴于H．在Rt△A′B′H中，∵A′B′＝2，∠B′A′H＝60°，∴A′H＝A′B′cos60°＝1，B′H＝A′B′sin60°=√3，∴OH＝2+1＝3，∴B′（−√3，3），故选：A．31．【解答】解：由题意G与G′关于原点对称，∵G（﹣2，1），∴G′（2，﹣1），故选：A．32．【解答】解：由题意得，作出如下图形：N 点坐标为（﹣1，0），N 点关于A 点对称的N 1点的坐标为（﹣3，0），N 1点关于B 点对称的N 2点的坐标为（5，4），N 2点关于C 点对称的N 3点的坐标为（﹣3，﹣8），N 3点关于A 点对称的N 4点的坐标为（﹣1，8），N 4点关于B 点对称的N 5点的坐标为（3，﹣4），N 5点关于C 点对称的N 6点的坐标为（﹣1，0），此时刚好回到最开始的点N 处，∴其每6个点循环一次，∴2020÷6＝336……4，即循环了336次后余下4，故N 2020的坐标与N 4点的坐标相同，其坐标为（﹣1，8）．故答案为：（﹣1，8）．33．【解答】解：平面直角坐标系如图所示，旋转中心是P 点，P （4，2）．故答案为（4，2）．34．【解答】解：∵点P 1的坐标为（√22，√22），将线段OP 1绕点O 按逆时针方向旋转45°，再将其长度伸长为OP 1的2倍，得到线段OP 2；∴OP 1＝1，OP 2＝2，∴OP 3＝4，如此下去，得到线段OP 4＝23，OP 5＝24…，∴OP n ＝2n ﹣1，由题意可得出线段每旋转8次旋转一周，∵2020÷8＝252…4，∴点P2020的坐标与点P4的坐标在同一直线上，正好在y轴的负半轴上，∴点P2020的坐标是（0，﹣22019）．故答案为：（0，﹣22019）．七．作图-旋转变换（共6小题）35．【解答】解：（1）如图，△A1B1C1即为所求，∴A1（﹣5，1）C1（﹣1，3）；（2）如图，△A2B2C2即为所求．36．【解答】解：（1）如图所示，△A1B1C1即为所求，α1α1=3√2αα；（2）如图，△A2B2C2即为所求，B2（4，﹣4）；（3）在（1）（2）的条件下，线段AB在变换过程中扫过图形的面积和为：5×3+12π×（4√2）2−12π×（√2）2＝（15+15π）cm2．37．【解答】解：（1）如图所示，△A1B1C1即为所求．（2）如图所示，△A2B2C2即为所求．38．【解答】解：（1）如图，△A1B1C1为所作；（2）旋转中心O1的坐标为（2，0），故答案为（2，0）；（3）设旋转半径为r，则r2＝22+42＝20，∴阴影部分的图形面积为：α阴影=14⋅αα2−12×2×4−12×2×2+12×1×1=5π−112．39．【解答】解：（1）如图所示，△A1B1C1即为所求；（2）如图所示，△A2B2C2即为所求；（3）由图可得，△A1B1C1与△A2B2C2关于点（﹣2，0）中心对称．故答案为：﹣2，0．40．【解答】解：（1）如图1中，作FD⊥AC于D，∵Rt △ABC ≌Rt △CEF ，∠ABC ＝∠CEF ＝90°，∠BAC ＝30°，BC ＝1．∴∠ACB ＝60°，∠FCE ＝∠BAC ＝30°，AC ＝CF ，∴∠ACF ＝30°，∴∠BAC ＝∠FCD ，在△ABC 和△CDF 中，{∠ααα=∠ααααααα=αααααα=αα，∴△ABC ≌△CDF （AAS ），∴FD ＝BC ＝1，法二：∵∠ECF ＝∠FCD ＝30°，FD ⊥CD ，FE ⊥CE ，∴DF ＝EF ，∵EF ＝BC ＝1，∴DF ＝1．故答案为1；（2）线段EF 经旋转运动所形成的平面图形如图所示，此时点E 落在CF 上的点H 处．S 阴＝S △EFC +S 扇形ACF ﹣S 扇形CEH ﹣S △AHC ＝S 扇形ACF ﹣S 扇形ECH =30⋅α⋅22360−30⋅α⋅(√3)2360=α12． 故答案为α12．（3）如图2中，过点E 作EH ⊥CF 于H ．设OB ＝OE ＝x ．在Rt △ECF 中，∵EF ＝1，∠ECF ＝30°，EH ⊥CF ，∴EC =√3EF =√3，EH =√32，CH =√3EH =32， 在Rt △BOC 中，OC =√αα2+αα2=√1+α2， ∴OH ＝CH ﹣OC =32−√1+α2，在Rt △EOH 中，则有x 2＝（√32）2+（32−√1+α2）2，解得x =√73或−√73（不合题意舍弃），∴OC =1+(√73)2=43， ∵CF ＝2EF ＝2，∴OF ＝CF ﹣OC ＝2−43=23． 八．利用旋转设计图案（共1小题）41．【解答】解：由题意，选项A ，C ，D 可以通过平移，旋转得到，选项B 可以通过翻折得到． 故选：B ．九．几何变换综合题（共9小题）42．【解答】（1）证明：如图1中，∵∠AOB ＝∠MON ＝90°，∴∠AOM ＝∠BON ，∵AO ＝BO ，OM ＝ON ，∴△AOM ≌△BON （SAS ）．（2）①证明：如图2中，连接AM ．同法可证△AOM≌△BON，∴AM＝BN，∠OAM＝∠B＝45°，∵∠OAB＝∠B＝45°，∴∠MAN＝∠OAM+∠OAB＝90°，∴MN2＝AN2+AM2，∵△MON是等腰直角三角形，∴MN2＝2ON2，∴NB2+AN2＝2ON2．②如图3﹣1中，设OA交BN于J，过点O作OH⊥MN于H．∵△AOM≌△BON，∴AM＝BN，∠OAM＝∠OBN，∵∠AJN＝∠BJO，∴∠ANJ＝∠JOB＝90°，∵OM＝ON＝3，∠MON＝90°，OH⊥MN，∴MN＝3√2，MH＝HN═OH=3√2 2，∴AH=√αα2−αα2=42−(3√22)2=√462，∴BN＝AM＝MH+AH=√46+3√22．如图3﹣2中，同法可证AM＝BN=√46−3√22．43．【解答】解：（1）DO⊥EO，DO＝EO；理由：当点B旋转到CD边上时，点E必在边AC上，∴∠AEB＝∠CEB＝90°，在Rt△ABE中，点O是AB的中点，∴OE＝OA=12AB，∴∠BOE＝2∠BAE，在Rt△ABD中，点O是AB的中点，∴OD＝OA=12AB，∴∠DOE＝2∠BAD，∴OD＝OE，∵等腰△ADC，且∠ADC＝90°，∴∠DAC＝45°，∴∠DOE＝∠BOE+∠DOE＝2∠BAE+2∠BAD＝2（∠BAE+∠DAE）＝2∠DAC＝90°，∴OD⊥OE；（2）仍然成立，理由：如图2，延长EO到点M，使得OM＝OE，连接AM，DM，DE，∵O是AB的中点，∴OA＝OB，∵∠AOM＝∠BOE，∴△AOM≌△BOE（SAS），∴∠MAO＝∠EBO，MA＝EB，∵△ACD和△CBE是等腰三角形，∠ADC＝∠CEB＝90°，∴∠CAD＝∠ACD＝∠EBC＝∠BCE＝45°，∵∠OBE＝180°﹣∠EBC＝135°，∴∠MAO＝135°，∴∠MAD＝∠MAO﹣∠DAC＝90°，∵∠DCE＝∠DCA+∠BCE＝90°，∴∠MAD＝∠DCE，∵MA＝EB，EB＝EC，∴MA＝EC，∵AD＝DC，∴△MAD≌△ECD，∴MD＝ED，∠ADM＝∠CDE，∵∠CDE+∠ADE＝90°，∴∠ADM+∠ADE＝90°，∴∠MDE＝90°，∵MO＝EO，MD＝DE，∴αα=12αα，OD⊥ME，∵αα=12αα，∴OD＝OE，OD⊥OE；（3）①当点B在AC左侧时，如图3，延长EO到点M，使得OM＝OE，连接AM，DM，DE，同（2）的方法得，△OBE≌△OAM（SAS），∴∠OBE＝∠OAM，OM＝OE，BE＝AM，∵BE＝CE，∴AM＝CE，在四边形ABECD中，∠ADC+∠DCE+∠BEC+∠OBE+∠BAD＝540°，∵∠ADC＝∠BEC＝90°，∴∠DCE＝540°﹣90°﹣90°﹣∠OBE﹣∠BAD＝360°﹣∠OBE＝360°﹣∠OAM﹣∠BAD，∵∠DAM+∠OAM+∠BAD＝360°，∴∠DAM＝360°﹣∠OAM﹣∠BAD，∴∠DAM＝∠DCE，∵AD＝CD，∴△DAM≌△DCE（SAS），∴DM＝DE，∠ADM＝∠CDE，∴∠EDM＝∠ADM+∠ADE＝∠CDE+∠ADE＝∠ADC＝90°，∵OM＝OE，∴OD＝OE=12ME，∠DOE＝90°，在Rt△BCE中，CE=√22BC＝2√2，过点E作EH⊥DC交DC的延长线于H，在Rt△CHE中，∠ECH＝180°﹣∠ACD﹣∠ACB﹣∠BCE＝180°﹣45°﹣60°﹣45°＝30°，∴EH=12CE=√2，根据勾股定理得，CH=√3EH=√6，∴DH＝CD+CH＝3√6，在Rt△DHE中，根据勾股定理得，DE=√αα2+αα2=2√14，∴OD=√22DE＝2√7，②当点B在AC右侧时，如图4，同①的方法得，OD＝OE，∠DOE＝90°，连接DE，过点E作EH⊥CD于H，在Rt△EHC中，∠ECH＝30°∴EH=12CE=√2，根据勾股定理得，CH=√6，∴DH＝CD﹣CH=√6，在Rt△DHE中，根据勾股定理得，DE＝2√2，∴OD=√22DE＝2，即：线段OD的长为2或2√7．44．【解答】（1）①证明：如图1中，∵将线段PB绕点P逆时针旋转，旋转角为α，得到线段PD，∴PB＝PD，∵AB＝AC，PB＝PD，∠BAC＝∠BPD＝60°，∴△ABC，△PBD是等边三角形，∴∠ABC＝∠PBD＝60°，∴∠PBA＝∠DBC，∵BP＝BD，BA＝BC，∴△PBA≌△DBC（SAS），∴P A＝DC．②解：如图1中，设BD交PC于点O．∵△PBA≌△DBC，∴∠BP A＝∠BDC，∵∠BOP＝∠COD，∴∠OBP＝∠OCD＝60°，即∠DCP＝60°．（2）解：结论：CD=√3P A．理由：如图2中，∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝120°，∴BC ＝2•AB •cos30°=√3BA ，BD ═2BP •cos30°=√3BP ，∴αααα=αααα=√3，∵∠ABC ＝∠PBD ＝30°，∴∠ABP ＝∠CBD ，∴△CBD ∽△ABP ，∴αααα=αααα=√3，∴CD =√3P A ．（3）过点D 作DM ⊥PC 于M ，过点B 作BN ⊥CP 交CP 的延长线于N ． 如图3﹣1中，当△PBA 是钝角三角形时，在Rt △ABN 中，∵∠N ＝90°，AB ＝6，∠BAN ＝60°，∴AN ＝AB •cos60°＝3，BN ＝AB •sin60°＝3√3，∵PN =√αα2−αα2=√31−27=2，∴P A ＝3﹣2＝1，由（2）可知，CD =√3P A =√3，∵∠BP A ＝∠BDC ，∴∠DCA ＝∠PBD ＝30°，∵DM ⊥PC ，∴DM =12CD =√32如图3﹣2中，当△ABP 是锐角三角形时，同法可得P A ＝2+3＝5，CD ＝5√3，DM =12CD =5√32，综上所述，满足条件的DM 的值为√32或5√32． 故答案为√32或5√32．45．【解答】解：（1）当点P 与B 重合时，5t ＝4，解得t =45．（2）在Rt △ABC 中，∵∠B ＝90°，AB ＝4，BC ＝3，∴AC =√αα2+αα2=√42+32=5，∴sin A =35，cos A =45， 如图①中，当点P 在线段AB 上时，在Rt △APE 中，AE ＝AP •cos A ＝4t ，∴EC ＝5﹣4t ．如图③中，当点P 在线段BC 上时，在Rt △PEC 中，PC ＝7﹣5t ，cos C =35， ∴EC ＝PC •cos C =35（7﹣5t ）=215−3t ． （3）当△PDQ 是等腰直角三角形时，则PE ＝DE ，如图④中，当点P 在线段AB 上时，在Rt △APE 中，PE ＝P A •sin A ＝3t ，∵DE ＝AC ﹣AE ﹣CD ＝5﹣4t ﹣2t ＝5﹣6t ，∵PE ＝DE ，∴3t ＝5﹣6t ，∴t =59．如图⑤中，当点P 在线段BC 上时， 在Rt △PCE 中，PE ＝PC •sin C =45（7﹣5t ）=285−4t ，∵DE ＝CD ﹣CE ＝2t −35（7﹣5t ）＝5t −215，∴285−4t ＝5t −215， 解得t =4945．∵△PDQ 是锐角三角形，∴观察图象可知满足条件的t 的值为0＜t ＜59或4945＜t ＜75．（4）如图⑥中，当点P 在线段AB 上，QM ∥AB 时，过点Q 作QG ⊥AB 于G ，延长QM 交BC 于N ，过点D 作DH ⊥BC 于H ．∵PB ∥MN ∥DH ，PM ＝DM ，∴BN ＝NH ，在Rt △PQG 中，PQ ＝2PE ＝6t ，∴QG =45PQ =245t ，在Rt △DCH 中，HC =35DC =65t ，∵BC ＝BH +CH =245t +245t +65t ＝3，解得t =518．如图⑦中，当点P 在线段BC 上，QM ∥BC 时，过点D 作DH ⊥BC 于H ，过点P 作PK ⊥QM 于K ．∵QM ∥BC ，DM ＝PM ，∴DH ＝2PK ，在Rt △PQK 中，PQ ＝2PE =85（7﹣5t ），∴PK =35PQ =2425（7﹣5t ），在Rt △DCH 中，DH =45DC =85t ，∵DH ＝2PK ，∴85t ＝2×2425（7﹣5t ）， 解得t =65， 综上所述，满足条件的t 的值为518或65．46．【解答】解：（1）①如图1中，△AB ′C ′即为所求．②由作图可知，△ABB ′是等腰直角三角形，∴∠AB ′B ＝45°，故答案为45．（2）如图2中，过点E 作EH ⊥CD 交CD 的延长线于H ．∵∠C ＝∠BAE ＝∠H ＝90°，∴∠B+∠CAB＝90°，∠CAB+∠EAH＝90°，∴∠B＝∠EAH，∵AB＝AE，∴△ABC≌△EAH（AAS），∴BC＝AH，EH＝AC，∵BC＝CD，∴CD＝AH，∴DH＝AC＝EH，∴∠EDH＝45°，∴∠ADE＝135°．（3）如图3中，连接AC，∵AE⊥BC，BE＝EC，∴AB＝AC，将△ABD绕点A逆时针旋转得到△ACG，连接DG．则BD＝CG，∵∠BAD＝∠CAG，∴∠BAC＝∠DAG，∵AB＝AC，AD＝AG，∴∠ABC＝∠ACB＝∠ADG＝∠AGD，∴△ABC∽△ADG，∵AD＝kAB，∴DG＝kBC＝2k，∵∠BAE+∠ABC＝90°，∠BAE＝∠ADC，∴∠ADG+∠ADC＝90°，∴∠GDC＝90°，∴CG=√αα2+αα2=√4α2+9．∴BD＝CG=√4α2+9．47．【解答】解：（1）延长DF到K点，并使FK＝DC，连接KE，如图1所示，∵△ABC≌△EBD，∴DE＝AC，BD＝BC，∴∠CDB＝∠DCB，且∠CDB＝∠ADF，∴∠ADF＝∠DCB，∵∠ACB＝90°，∴∠ACD+∠DCB＝90°，∵∠EDB＝90°，∴∠ADF+∠FDE＝90°，∴∠ACD＝∠FDE，∵FK+DF＝DC+DF，∴DK＝CF，在△ACF 和△EDK 中，{αα=αααααα=αααααα=αα，∴△ACF ≌△EDK （SAS ），∴KE ＝AF ，∠K ＝∠AFC ，又∠AFC ＝∠KFE ，∴∠K ＝∠KFE∴KE ＝EF∴AF ＝EF ，故AF 与EF 的数量关系为：AF ＝EF ．故答案为：AF ＝EF ；（2）仍然成立，理由如下：延长DF 到K 点，并使FK ＝DC ，连接KE ，如图2所示，设BD 延长线DM 交AE 于M 点，∵△ABC ≌△EBD ，∴DE ＝AC ，BD ＝BC ，∴∠CDB ＝∠DCB ，且∠CDB ＝∠MDF ，∴∠MDF ＝∠DCB ，∵∠ACB ＝90°，∴∠ACD +∠DCB ＝90°，∵∠EDB ＝90°，∴∠MDF +∠FDE ＝90°，∴∠ACD ＝∠FDE ，∵FK +DF ＝DC +DF ，∴DK ＝CF ，在△ACF 和△EDK 中，{αα=αααααα=αααααα=αα，∴△ACF ≌△EDK （SAS ），∴KE ＝AF ，∠K ＝∠AFC ，又∠AFC ＝∠KFE ，∴∠K ＝∠KFE ，∴KE ＝EF ，∴AF ＝EF ，故AF 与EF 的数量关系为：AF ＝EF ．（3）当点G 在点B 右侧时，如图3所示，过点E 作EG ⊥BC 交CB 的延长线于G ， ∵BA ＝BE ，∴∠BAE ＝∠BEA ，∵∠BAE ＝∠EBG ，∴∠BEA ＝∠EBG ，∴AE ∥CG ，∴∠AEG +∠G ＝180°，∴∠AEG ＝90°，∴∠ACG ＝∠G ＝∠AEG ＝90°，∴四边形AEGC 为矩形，∴AC ＝EG ，且AB ＝BE ，∴Rt △ACB ≌Rt △EGB （HL ），∴BG ＝BC ＝6，∠ABC ＝∠EBG ，又∵ED ＝AC ＝EG ，且EB ＝EB ，∴Rt △EDB ≌Rt △EGB （HL ），∴DB＝GB＝6，∠EBG＝∠ABE，∴∠ABC＝∠ABE＝∠EBG＝60°，∴∠BAC＝30°，在Rt△ABC中，由30°所对的直角边等于斜边的一半可知：AB＝2BC＝12．当点G在点B左侧时，如图4所示，由旋转知，∠ABC＝∠ABE，AB＝BE，∴∠BAE＝∠BEA，∵∠BAE＝∠EBG＝2∠ABC＝2∠ABE，∴∠BAE＝∠AEB＝2∠ABE，∵∠AEB+∠BAE+∠ABE＝180°，∴2∠ABE+2∠ABE+∠ABE＝180°，∴∠BAE＝36°，∴∠ABC＝36°，在Rt△ABC中，cos36°=αααα，∴AB=ααααα36°=6ααα36°，即满足条件的AB＝12或6ααα36°．48．【解答】解：（1）①∵A ′B ′∥AC ，∴∠B ′A ′C ＝∠A ′CA ，∵∠B ′A ′C ＝∠BAC ，∴∠A ′CA ＝∠BAC ，∴AD ＝CD ，∵∠ACB ＝90°，∴∠BCD ＝90°﹣∠ACD ，∵∠ABC ＝90°﹣∠BAC ，∴∠CBD ＝∠BCD ，∴BD ＝CD ，∴AD ＝BD ；②∵∠ACB ＝90°，BC ＝2，AC ＝4，∴AB =√22+42=2√5，∵BE ⊥CD ，∴∠BEC ＝∠ACB ＝90°，∵∠BCE ＝∠ABC ，∴△BEC ∽△ACB ，∴αααα=αααα，即αα2=2√5， ∴CE =25√5，∵∠ACB ＝90°，AD ＝BD ， ∴CD =12AB =√5， ∴CE =25CD ，∴S △ACE =23S △ADE ，∵AD ＝BD ，∴S △ABE ＝2S △ADE ，∴α△αααα△ααα=13；（2）∵CD ⊥AB ，∴∠ADC ＝90°＝∠A ′CB ′，∴AB ∥CN ，∴△MCN ∽△MAD ，∴αααα=αααα，∵α△ααα=12αα⋅αα=12αα⋅αα，∴αα=αα⋅αααα=4×22√5=45√5，∴AD =√αα2−αα2=85√5，∵DM ∥A ′B ′，。

专题32 中考几何平移类问题专题知识点概述1.平移的定义：平面图形的每个点沿着某一方向移动相同的距离，这样的图形运动称为平移.平移是由移动的方向和移动的距离所决定.平移后得到的新图形中每一点，都是由原图形中的某一点移动后得到的，这样的两个点叫做对应点。

2.平移的特点：经平移运动后的图形图形的位置发生变化, 形状和大小不变.3.理解并掌握平移的三个特征：（1）对应线段平行（或在一条直线上）且相等；对应角相等.（2）对应点所连的线段平行（或在一条直线上）且相等.（3）图形在平移后形状和大小都不变.4.图形平移的画法：（1）确定点；（2）定方向；（3）定距离。

例题解析与对点练习【例题1】（2020•广东）在平面直角坐标系中，点（3，2）关于x轴对称的点的坐标为（）A．（﹣3，2）B．（﹣2，3）C．（2，﹣3）D．（3，﹣2）【答案】D【解析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答即可．点（3，2）关于x轴对称的点的坐标为（3，﹣2）．【对点练习】（2019湖南邵阳）一次函数y1=k1x+b1的图象l1如图所示，将直线l1向下平移若干个单位后得直线l2，l2的函数表达式为y2=k2x+b2．下列说法中错误的是（）A．k1=k2 B．b1＜b2C．b1＞b2 D．当x=5时，y1＞y2【答案】B【解析】根据两函数图象平行k相同，以及向下平移减即可判断．∵将直线l1向下平移若干个单位后得直线l2，∴直线l1∥直线l2，∴k1＝k2，∵直线l1向下平移若干个单位后得直线l2，∴b1＞b2，∴当x＝5时，y1＞y2【点拨】本题考查图形的平移变换和函数解析式之间的关系，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标左移加，右移减；纵坐标上移加，下移减．平移后解析式有这样一个规律“左加右减，上加下减”．关键是要搞清楚平移前后的解析式有什么关系．【例题2】（2019桂林）如图，在平面直角坐标系中，反比例y＝（k＞0）的图象和△ABC都在第一象限内，AB＝AC＝，BC∥x轴，且BC＝4，点A的坐标为（3，5）．若将△ABC向下平移m个单位长度，A，C两点同时落在反比例函数图象上，则m的值为．【答案】；【解析】∵AB＝AC＝，BC＝4，点A（3，5）．∴B（1，），C（5，），将△ABC向下平移m个单位长度，∴A（3，5﹣m），C（5，﹣m），∵A，C两点同时落在反比例函数图象上，∴3（5﹣m）＝5（﹣m），∴m＝【对点练习】（2020枣庄模拟）已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B （3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是；（3）△A2B2C2的面积是平方单位．【答案】见解析。

平移旋转对称三大变换1.（2020•安徽）在数学探究活动中，敏敏进行了如下操作：如图，将四边形纸片ABCD沿过点A的直线折叠，使得点B落在CD上的点Q处．折痕为AP；再将△PCQ，△ADQ分别沿PQ，AQ折叠，此时点C，D落在AP上的同一点R处．请完成下列探究：（1）∠PAQ的大小为30 °；（2）当四边形APCD是平行四边形时，的值为．【解答】解：（1）由折叠的性质可得：∠B＝∠AQP，∠DAQ＝∠QAP＝∠PAB，∠DQA＝∠AQR，∠CQP＝∠PQR，∠D＝∠ARQ，∠C＝∠QRP，∵∠QRA+∠QRP＝180°，∴∠D+∠C＝180°，∴AD∥BC，∴∠B+∠DAB＝180°，∵∠DQR+∠CQR＝180°，∴∠DQA+∠CQP＝90°，∴∠AQP＝90°，∴∠B＝∠AQP＝90°，∴∠DAB＝90°，∴∠DAQ＝∠QAP＝∠PAB＝30°，故答案为：30；（2）由折叠的性质可得：AD＝AR，CP＝PR，∵四边形APCD是平行四边形，∴AD＝PC，∴AR＝PR，又∵∠AQP＝90°，∴QR AP，∵∠PAB＝30°，∠B＝90°，∴AP＝2PB，AB PB，∴PB＝QR，∴，故答案为：．2.（2020•天水）如图，在边长为6的正方形ABCD内作∠EAF＝45°，AE交BC于点E，AF交CD于点F，连接EF，将△ADF绕点A顺时针旋转90°得到△ABG．若DF＝3，则BE的长为 2 ．【解答】解：法一：由题意可得，△ADF≌△ABG，∴DF＝BG，∠DAF＝∠BAG，∵∠DAB＝90°，∠EAF＝45°，∴∠DAF+∠EAB＝45°，∴∠BAG+∠EAB＝45°，∴∠EAF＝∠EAG，在△EAG和△EAF中，，∴△EAG≌△EAF（SAS），∴GE＝FE，设BE＝x，则GE＝BG+BE＝3+x，CE＝6﹣x，∴EF＝3+x，∵CD＝6，DF＝3，∴CF＝3，∵∠C＝90°，∴（6﹣x）2+32＝（3+x）2，解得，x＝2，即BE＝2，法二：设BE＝x，连接GF，如下图所示，∵四边形ABCD为正方形，∴∠ABE＝∠GCF＝90°，∵△ADF绕点A顺时针旋转90°得到△ABG，∴∠CAF＝90°，GA＝FA，∴△GAF为等腰直角三角形，∵∠EAF＝45°，∴AE垂直平分GF，∴∠AEB+∠CGF＝90°，∵在Rt△AEB中，∠AEB+∠BAE＝90°，∴∠BAE＝∠CGF，∴△BAE～△CGF，∴，∵CF＝CD﹣DF＝6﹣3＝3，GC＝BC+BG＝BC+DF＝6+3＝9，∴，∴x＝2，即BE＝2，故答案为：2．3.（2020•深圳）如图，矩形纸片ABCD中，AB＝6，BC＝12．将纸片折叠，使点B落在边AD的延长线上的点G处，折痕为EF，点E、F分别在边AD和边BC上．连接BG，交CD于点K，FG交CD于点H．给出以下结论：①EF⊥BG；②GE＝GF；③△GDK和△GKH的面积相等；④当点F与点C重合时，∠DEF＝75°，其中正确的结论共有（）A．1个B．2个C．3个D．4个【解答】解：如图，连接BE，设EF与BG交于点O，∵将纸片折叠，使点B落在边AD的延长线上的点G处，∴EF垂直平分BG，∴EF⊥BG，BO＝GO，BE＝EG，BF＝FG，故①正确，∵AD∥BC，∴∠EGO＝∠FBO，又∵∠EOG＝∠BOF，∴△BOF≌△GOE（ASA），∴BF＝EG，∴BF＝EG＝GF，故②正确，∵BE＝EG＝BF＝FG，∴四边形BEGF是菱形，∴∠BEF＝∠GEF，当点F与点C重合时，则BF＝BC＝BE＝12，∵sin∠AEB，∴∠AEB＝30°，∴∠DEF＝75°，故④正确，由题意无法证明△GDK和△GKH的面积相等，故③错误；故选：C．4.（2020•随州）如图，已知矩形ABCD中，AB＝3，BC＝4，点M，N分别在边AD，BC上，沿着MN折叠矩形ABCD，使点A，B分别落在E，F处，且点F在线段CD上（不与两端点重合），过点M作MH⊥BC于点H，连接BF，给出下列判断：①△MHN∽△BCF；②折痕MN的长度的取值范围为3＜MN；③当四边形CDMH为正方形时，N为HC的中点；④若DF DC，则折叠后重叠部分的面积为．其中正确的是①②③④．（写出所有正确判断的序号）【解答】解：①如图1，由折叠可知BF⊥MN，∴∠BOM＝90°，∵MH⊥BC，∴∠BHP＝90°＝∠BOM，∵∠BPH＝∠OPM，∴∠CBF＝∠NMH，∵∠MHN＝∠C＝90°，∴△MHN∽△BCF，故①正确；②当F与C重合时，MN＝3，此时MN最小，当F与D重合时，如图2，此时MN最大，由勾股定理得：BD＝5，∵OB＝OD，∵tan∠DBC，即，∴ON，∵AD∥BC，∴∠MDO＝∠OBN，在△MOD和△NOB中，∵，∴△DOM≌△BON（ASA），∴OM＝ON，∴MN＝2ON，∵点F在线段CD上（不与两端点重合），∴折痕MN的长度的取值范围为3＜MN；故②正确；③如图3，连接BM，FM，当四边形CDMH为正方形时，MH＝CH＝CD＝DM＝3，∵AD＝BC＝4，∴AM＝BH＝1，由勾股定理得：BM，∴FM，∴DF1，∴CF＝3﹣1＝2，设HN＝x，则BN＝FN＝x+1，在Rt△CNF中，CN2+CF2＝FN2，∴（3﹣x）2+22＝（x+1）2，解得：x，∴HN，∵CH＝3，∴CN＝HN，∴N为HC的中点；故③正确；④如图4，连接FM，∵DF DC，CD＝3，∴DF＝1，CF＝2，∴BF2，∴OF，设FN＝a，则BN＝a，CN＝4﹣a，由勾股定理得：FN2＝CN2+CF2，∴a2＝（4﹣a）2+22，∴a，∴BN＝FN，CN，∵∠NFE＝∠CFN+∠DFQ＝90°，∠CFN+∠CNF＝90°，∴∠DFQ＝∠CNF，∵∠D＝∠C＝90°，∴△QDF∽△FCN，∴，即，∴QD，∴FQ，∵tan∠HMN＝tan∠CBF，∴，∴HN，∴MN，∵CH＝MD＝HN+CN3，∴MQ＝3，∴折叠后重叠部分的面积为：S△MNF+S△MQF；故④正确；所以本题正确的结论有：①②③④；故答案为：①②③④．5.（2020•武汉）如图，折叠矩形纸片ABCD，使点D落在AB边的点M处，EF为折痕，AB＝1，AD＝2．设AM的长为t，用含有t的式子表示四边形CDEF的面积是．【解答】解：连接DM，过点E作EG⊥BC于点G，设DE＝x＝EM，则EA＝2﹣x，∵AE2+AM2＝EM2，∴（2﹣x）2+t2＝x2，解得x1，∴DE1，∵折叠矩形纸片ABCD，使点D落在AB边的点M处，∴EF⊥DM，∠ADM+∠DEF＝90°，∵EG⊥AD，∴∠DEF+∠FEG＝90°，∴∠ADM＝∠FEG，∴tan∠ADM，∴FG，∵CG＝DE1，∴CF1，∴S四边形CDEF（CF+DE）×1t+1．故答案为：t+1．6.（2020•咸宁）如图，在矩形ABCD中，AB＝2，BC＝2，E是BC的中点，将△ABE沿直线AE翻折，点B落在点F处，连结CF，则cos∠ECF的值为（）A．B．C．D．【解答】解：如图，∵四边形ABCD是矩形，∴∠B＝90°，∵E是BC的中点，BC＝2，∴BE＝CE BC，∴AE3，由翻折变换的性质得：△AFE≌△ABE，∴∠AEF＝∠AEB，EF＝BE，∴EF＝CE，∴∠EFC＝∠ECF，∵∠BEF＝∠EFC+∠ECF，∴∠AEB＝∠ECF，∴cos∠ECF＝cos∠AEB．故选：C．7.（2020•襄阳）如图，矩形ABCD中，E为边AB上一点，将△ADE沿DE折叠，使点A的对应点F恰好落在边BC上，连接AF交DE于点N，连接BN．若BF•AD＝15，tan∠BNF，则矩形ABCD的面积为15．【解答】解：∵将△ADE沿DE折叠，使点A的对应点F恰好落在边BC上，∴AF⊥DE，AE＝EF，∵矩形ABCD中，∠ABF＝90°，∴B，E，N，F四点共圆，∴∠BNF＝∠BEF，∴tan∠BEF，设BF x，BE＝2x，∴EF3x，∴AE＝3x，∴AB＝5x，∴AB BF．∴S矩形ABCD＝AB•AD BF•AD15＝15．故答案为：15．8.（2020•孝感）如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G．若BG＝3，CG＝2，则CE的长为（）A．B．C．4 D．【解答】解：如图所示，连接EG，由旋转可得，△ADE≌△ABF，∴AE＝AF，DE＝BF，又∵AG⊥EF，∴H为EF的中点，∴AG垂直平分EF，∴EG＝FG，设CE＝x，则DE＝5﹣x＝BF，FG＝8﹣x，∴EG＝8﹣x，∵∠C＝90°，∴Rt△CEG中，CE2+CG2＝EG2，即x2+22＝（8﹣x）2，解得x，∴CE的长为，故选：B．9.（2020•衡阳）如图1，在平面直角坐标系中，▱ABCD在第一象限，且BC∥x轴．直线y＝x从原点O出发沿x轴正方向平移，在平移过程中，直线被▱ABCD截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示．那么▱ABCD的面积为（）A．3 B．3C．6 D．6【解答】解：过B作BM⊥AD于点M，分别过B，D作直线y＝x的平行线，交AD于E，如图1所示，由图象和题意可得，AE＝6﹣4＝2，DE＝7﹣6＝1，BE＝2，∴AB＝2+1＝3，∵直线BE平行直线y＝x，∴BM＝EM，∴平行四边形ABCD的面积是：AD•BM＝33．故选：B．10.（2020•江西）矩形纸片ABCD，长AD＝8cm，宽AB＝4cm，折叠纸片，使折痕经过点B，交AD边于点E，点A落在点A'处，展平后得到折痕BE，同时得到线段BA'，EA'，不再添加其它线段．当图中存在30°角时，AE的长为厘米或4厘米或厘米．【解答】解：①当∠ABE＝30°时，AE＝AB×tan30°；②当∠AEB＝30°时，AE4；③∠ABE＝15°时，∠ABA′＝30°，延长BA′交AD于F，如下图所示，设AE＝x，则EA′＝x，EF，∵AF＝AE+EF＝AB tan30°，∴x，∴x＝8﹣4，∴AE＝8﹣4．故答案为：厘米或4厘米或8﹣4厘米．11.（2020•滨州）如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平后再次折叠，使点A落在EF上的点A′处，得到折痕BM，BM与EF相交于点N．若直线BA′交直线CD于点O，BC＝5，EN＝1，则OD的长为（）A．B．C．D．【解答】解：∵EN＝1，∴由中位线定理得AM＝2，由折叠的性质可得A′M＝2，∵AD∥EF，∴∠AMB＝∠A′NM，∵∠AMB＝∠A′MB，∴∠A′NM＝∠A′MB，∴A′N＝2，∴A′E＝3，A′F＝2过M点作MG⊥EF于G，∴NG＝EN＝1，∴A′G＝1，由勾股定理得MG，∴BE＝OF＝MG，∴OF：BE＝2：3，解得OF，∴OD．故选：B．12.（2020•德州）如图，在矩形ABCD中，AB2，AD．把AD沿AE折叠，使点D恰好落在AB边上的D′处，再将△AED′绕点E顺时针旋转α，得到△A'ED″，使得EA′恰好经过BD′的中点F．A′D″交AB于点G，连接AA′．有如下结论：①A′F的长度是2；②弧D'D″的长度是π；③△A′AF ≌△A′EG；④△AA′F∽△EGF．上述结论中，所有正确的序号是①②④．【解答】解：∵把AD沿AE折叠，使点D恰好落在AB边上的D′处，∴∠D＝∠AD'E＝90°＝∠DAD'，AD＝AD'，∴四边形ADED'是矩形，又∵AD＝AD'，∴四边形ADED'是正方形，∴AD＝AD'＝D'E＝DE，AE AD，∠EAD'＝∠AED'＝45°，∴D'B＝AB﹣AD'＝2，∵点F是BD'中点，∴D'F＝1，∴EF2，∵将△AED′绕点E顺时针旋转α，∴AE＝A'E，∠D'ED''＝α，∠EA'D''＝∠EAD'＝45°，∴A'F2，故①正确；∵tan∠FED'，∴∠FED'＝30°∴α＝30°+45°＝75°，∴弧D'D″的长度π，故②正确；∵AE＝A'E，∠AEA'＝75°，∴∠EAA'＝∠EA'A＝52.5°，∴∠A'AF＝7.5°，∵∠AA'F≠∠EA'G，∠AA'E≠∠EA'G，∠AFA'＝120°≠∠EA'G，∴△AA'F与△A'GE不全等，故③错误；∵D'E＝D''E，EG＝EG，∴Rt△ED'G≌Rt△ED''G（HL），∴∠D'GE＝∠D''GE，∵∠AGD''＝∠A'AG+∠AA'G＝105°，∴∠D'GE＝52.5°＝∠AA'F，又∵∠AFA'＝∠EFG，∴△AFA'∽△EFG，故④正确，故答案为：①②④．13.（2020•聊城）如图，在Rt△ABC中，AB＝2，∠C＝30°，将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，在B′C′上取点D，使B′D＝2，那么点D到BC的距离等于（）A．2（1）B． 1 C． 1 D． 1【解答】解：∵在Rt△ABC中，AB＝2，∠C＝30°，∴BC＝2，AC＝4，∵将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，∴AB′＝AB＝2，B′C′＝BC＝2，∴B′C＝2，延长C′B′交BC于F，∴∠CB′F＝∠AB′C′＝90°，∵∠C＝30°，∴∠CFB′＝60°，B′F B′C，∵B′D＝2，∴DF＝2，过D作DE⊥BC于E，∴DE DF（2）1，故选：D．14.（2020•杭州）如图是一张矩形纸片，点E在AB边上，把△BCE沿直线CE对折，使点B落在对角线AC上的点F处，连接DF．若点E，F，D在同一条直线上，AE＝2，则DF＝ 2 ，BE＝ 1 ．【解答】解：∵四边形ABCD是矩形，∴AD＝BC，∠ADC＝∠B＝∠DAE＝90°，∵把△BCE沿直线CE对折，使点B落在对角线AC上的点F处，∴CF＝BC，∠CFE＝∠B＝90°，EF＝BE，∴CF＝AD，∠CFD＝90°，∴∠ADE+∠CDF＝∠CDF+∠DCF＝90°，∴∠ADF＝∠DCF，∴△ADE≌△FCD（ASA），∴DF＝AE＝2；∵∠AFE＝∠CFD＝90°，∴∠AFE＝∠DAE＝90°，∵∠AEF＝∠DEA，∴△AEF∽△DEA，∴，∴，∴EF1（负值舍去），∴BE＝EF1，故答案为：2，1．15.（2020•嘉兴）如图，有一张矩形纸条ABCD，AB＝5cm，BC＝2cm，点M，N分别在边AB，CD上，CN＝1cm．现将四边形BCNM沿MN折叠，使点B，C分别落在点B'，C'上．当点B'恰好落在边CD上时，线段BM的长为cm；在点M从点A运动到点B的过程中，若边MB'与边CD交于点E，则点E相应运动的路径长为（）cm．【解答】解：如图1中，∵四边形ABCD是矩形，∴AB∥CD，∴∠1＝∠3，由翻折的性质可知：∠1＝∠2，BM＝MB′，∴∠2＝∠3，∴MB′＝NB′，∵NB′（cm），∴BM＝NB′（cm）．如图2中，当点M与A重合时，AE＝EN，设AE＝EN＝xcm，在Rt△ADE中，则有x2＝22+（4﹣x）2，解得x，∴DE＝4（cm），如图3中，当点M运动到MB′⊥AB时，DE′的值最大，DE′＝5﹣1﹣2＝2（cm），如图4中，当点M运动到点B′落在CD时，DB′（即DE″）＝5﹣1（4）（cm），∴点E的运动轨迹E→E′→E″，运动路径＝EE′+E′B′＝22﹣（4）＝（）（cm）．故答案为，（）．16.（2020•衢州）如图，把一张矩形纸片ABCD按所示方法进行两次折叠，得到等腰直角三角形BEF，若BC＝1，则AB的长度为（）A．B．C．D．【解答】解：由折叠补全图形如图所示，∵四边形ABCD是矩形，∴∠ADA'＝∠B＝∠C＝∠A＝90°，AD＝BC＝1，CD＝AB，由第一次折叠得：∠DAE＝∠A＝90°，∠ADE∠ADC＝45°，∴∠AED＝∠ADE＝45°，∴AE＝AD＝1，在Rt△ADE中，根据勾股定理得，DE AD，故选：A．。

第27讲图形的平移与旋转1．图形的平移(1)定义：在平面内，将某一图形沿着某个方向移动一定的距离，这种图形运动称为平移；平移不改变图形的大小和形状．(2)平移的要素：平移方向、平移距离．(2)性质：①平移后的图形与原来的图形全等；②对应线段平行且相等，对应角相等；③对应点所连的线段平行且相等．2．图形的旋转(1)定义：把一个图形绕着某一个点O转动一定角度的图形变换叫做旋转，如果图形上的点P经过旋转变为点P′，那么这两个点叫做这个旋转的对应点；(2)要素：确定一个旋转运动的条件是要确定旋转中心、旋转方向和旋转角度；(3)性质：①对应点到旋转中心的距离相等；②对应点与旋转中心所连线段的夹角等于旋转角；③旋转前、后的图形全等.考点1：关于平移问题【例题1】在6×6方格中，将图①中的图形N平移后位置如图②所示，则图形N的平移方法中，正确的是() A．向下移动1格 B．向上移动1格C．向上移动2格 D．向下移动2格解析：结合图形按平移的定义判断．【同步练】在由相同的小正方形组成的3×4的网格中，有3个小正方形已经涂黑，请你再涂黑一个小正方形，使涂黑的四个小正方形中，其中两个可以由另外两个平移得到，则还需要涂黑的小正方形序号是(D)A．①或②B．③或④C．⑤或⑥D．①或⑨【解析】：根据题意可涂黑①和⑨，涂黑①时，可将左上和左下两个黑色正方形向右平移1个单位即可得；涂黑⑨时，可将左上和左下两个黑色正方形向右平移2个单位、再向下平移1个单位可得；故选：D．归纳：1．平移前后图形的形状、大小都不变，平移得到的对应线段与原线段平行且相等，对应角相等．2．判断时选择某一特殊点，验证其平移情况即可．考点2：关于旋转问题【例题2】(2016·娄底改编)如图，将等腰△ABC绕顶点B逆时针方向旋转角为α旋转到△A1BC1的位置，AB与A1C1相交于点D，AC与A1C1、BC1分别相交于点E、F.(1)试判断A1D和CF的数量关系；(2)当∠C＝α时，判定四边形A1BCE的形状并说明理由．【分析】(1)根据等腰三角形的性质得到AB＝BC，∠A＝∠C，由旋转的性质得到A1B＝AB＝BC，∠A＝∠A1＝∠C，∠A1BD＝∠CBC1，根据全等三角形的判定及性质即可求解；(2)由旋转的性质得到∠A1＝∠A，根据平角的定义得到∠DEC ＝180°－α，在四边形A 1BCE 中，根据四边形的内角和得到∠A 1BC ＝360°－∠A 1－∠C －∠A 1EC ＝180°－α，进而证得四边形A 1BCE 是平行四边形，由A 1B ＝BC 即邻边相等的平行四边形是菱形即可证明．【解析】：(1)∵△ABC 是等腰三角形，∴AB ＝BC ，∠A ＝∠C，∵将等腰△ABC 绕顶点B 逆时针方向旋转α度到△A 1BC 1的位置，∴A 1B ＝AB ＝BC ，∠A ＝∠A 1＝∠C，∠A 1BD ＝∠CBC 1，在△BCF 与△BA 1D 中，⎩⎪⎨⎪⎧∠A 1＝∠C，A 1B ＝BC ∠A 1BD ＝∠CBF ，∴△BCF ≌△BA 1D(ASA )，∴A 1D ＝CF ；(2)四边形A 1BCE 是菱形，∵将等腰△ABC 绕顶点B 逆时针方向旋转到△A 1BC 1的位置， ∴∠A 1＝∠A，∵∠ADE ＝∠A 1DB ，∴∠AED ＝∠A 1BD ＝α，∴∠DEC ＝180°－α，∵∠C ＝α，∴∠A 1＝α，在四边形A 1BCE 中，∠A 1BC ＝360°－∠A 1－∠C－∠A 1EC ＝180°－α， ∴∠A 1＝∠C，∠A 1BC ＝∠A 1EC ， ∴四边形A 1BCE 是平行四边形， ∴A 1B ＝BC ，∴四边形A 1BCE 是菱形归纳：图形的旋转为背景的探究问题，常涉及的设问有：探究两条线段的数量关系、特殊四边形形状的判定，解决此类问题，需掌握如下方法：1．探究两条线段的数量关系一般指的是两条线段的倍数关系，常考虑利用特殊三角形、全等三角形、特殊四边形的性质或根据题中对应角的关系得到相似三角形，再根据相似三角形对应边成比例进行求解．2．探究特殊四边形的形状，通常先判定该四边形是否是平行四边形，再结合旋转的性质，根据其边或角的之间的等量关系进一步判定其为哪种特殊的平行四边形． 考点3：关于旋转的综合探究问题【例题3】（2018·湖北江汉·10分）问题：如图①，在Rt△ABC 中，AB=AC ，D 为BC 边上一点（不与点B ，C 重合），将线段AD 绕点A 逆时针旋转90°得到AE ，连接EC ，则线段BC ，DC ，EC 之间满足的等量关系式为 BC=DC+EC ； 探索：如图②，在Rt△ABC 与Rt△ADE 中，AB=AC ，AD=AE ，将△ADE 绕点A 旋转，使点D 落在BC 边上，试探索线段AD ，BD ，CD 之间满足的等量关系，并证明你的结论；应用：如图③，在四边形ABCD 中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD 的长．【分析】（1）证明△BAD≌△CAE，根据全等三角形的性质解答；（2）连接CE，根据全等三角形的性质得到BD=CE，∠ACE=∠B，得到∠DCE=90°，根据勾股定理计算即可；（3）作AE⊥AD，使AE=AD，连接CE，DE，证明△BAD≌△CAE，得到BD=CE=9，根据勾股定理计算即可．【解答】解：（1）BC=DC+EC，理由如下：∵∠BAC=∠DAE=90°，∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE，∴BD=CE，∴BC=BD+CD=EC+CD，故答案为：BC=DC+EC；（2）BD2+CD2=2AD2，理由如下：连接CE，由（1）得，△BAD≌△CAE，∴BD=CE，∠ACE=∠B，∴∠DCE=90°，∴CE2+CD2=ED2，在Rt△ADE中，AD2+AE2=ED2，又AD=AE，∴BD2+CD2=2AD2；（3）作AE⊥AD，使AE=AD，连接CE，DE，∵∠BAC+∠CAD=∠DAE+∠CAD，即∠BAD=∠CAD′，在△BAD与△CAE中，，∴△BAD≌△CAE（SAS），∴BD=CE=9，∵∠ADC=45°，∠EDA=45°，∴∠ED C=90°，∴DE==6，∵∠DAE=90°，∴AD=AE=DE=6．一、选择题：1. （2017山东泰安）如图，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与A 对应，则角α的大小为（）A．30° B．60° C．90° D．120°【答案】C【解答】解：如图：显然，旋转角为90°，故选C．2. （2018·辽宁省抚顺市）（3.00分）已知点A的坐标为（1，3），点B的坐标为（2，1）．将线段AB沿某一方向平移后，点A的对应点的坐标为（﹣2，1）．则点B的对应点的坐标为（）A．（5，3）B．（﹣1，﹣2）C．（﹣1，﹣1）D．（0，﹣1）【答案】C【解答】解：∵A（1，3）的对应点的坐标为（﹣2，1），∴平移规律为横坐标减3，纵坐标减2，∵点B（2，1）的对应点的坐标为（﹣1，﹣1）．故选：C．3. （2018·广西贺州·3分）如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接BB'，若∠A′B′B=20°，则∠A的度数是．A．60° B．65° C．70° D．80°【答案】B【解答】解：∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C，∴BC=B′C，∴△BCB′是等腰直角三角形，∴∠CBB′=45°，∴∠B′A′C=∠A′B′B+∠CBB′=20°+45°=65°，由旋转的性质得∠A=∠B′A′C=65°．故答案为：65°．4. （2018·辽宁大连·3分）如图，将△ABC绕点B逆时针旋转α，得到△EBD，若点A恰好在ED的延长线上，则∠CAD的度数为（）A．90°﹣αB．αC．180°﹣αD．2α【答案】C【解析】解：由题意可得：∠CBD=α，∠ACB=∠EDB．∵∠EDB+∠ADB=180°，∴∠ADB+∠ACB=180°．∵∠ADB+∠DBC+∠BCA+∠CAD=360°，∠CBD=α，∴∠CAD=180°﹣α．故选C．5. 如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（）A．5 B．4 C．D．【答案】D【解答】解：如图，在等腰直角三角形△DEF中，∠EDF=90°，DE=DF，∠1=∠2=∠3，∵∠1+∠QEF=∠3+∠DFQ=45°，∴∠QEF=∠DFQ，∵∠2=∠3，∴△DQF∽△FQE，∴===，∵DQ=1，∴FQ=，EQ=2，∴EQ+FQ=2+，故选D二、填空题：6. (2019•湖南常德•3分)如图，已知△ABC是等腰三角形，AB＝AC，∠BAC＝45°，点D在AC边上，将△ABD绕点A 逆时针旋转45°得到△ACD′，且点D′、D、B三点在同一条直线上，则∠A BD的度数是．【答案】22.5°．【解答】解：∵将△ABD绕点A逆时针旋转45°得到△ACD′，∴∠BAC＝∠CAD'＝45°，AD＝AD'，∴∠AD'D＝67.5°，∠D'AB＝90°，∴∠ABD＝22.5°．故答案为22.5°．7. （2019湖北宜昌3分）如图，平面直角坐标系中，点B 在第一象限，点A 在x 轴的正半轴上，∠AOB ＝∠B ＝30°，OA ＝2，将△AOB 绕点O 逆时针旋转90°，点B 的对应点B'的坐标是 .【答案】，3），【解答】解：如图，作B′H⊥y 轴于H ．由题意：OA′＝A′B′＝2，∠B′A′H＝60°，∴AH′＝A′B′＝1， ∴OH＝3，3），8. (2019，山西，3分）如图，在△ABC 中，∠BAC=90°，AB=AC=10cm ，点D 为△ABC 内一点，∠BAD=15°，AD=6cm ，连接BD ，将△ABD 绕点A 逆时针方向旋转，使AB 与AC 重合，点D 的对应点E ，连接DE ，DE 交AC 于点F ，则CF 的长为 cm.【答案】6210-【解析】过点A 作AG⊥DE 于点G ，由旋转可知：AD=AE ，∠DAE=90°，∠CAE=∠BAD=15° ∴∠AED=45°；在△AEF 中：∠AFD=∠AED+∠CAE=60° 在Rt△ADG 中：AG=DG=232=AD在Rt△AFG 中：2GF AF FG ====∴10CF AC AF =-=- 故答案为：6210-三、解答题：9. 如图所示，在正方形ABCD 中，G 是CD 上一点，延长BC 到E ，使CE ＝CG ，连接BG 并延长交DE 于F ，将△DCE 绕点D 顺时针旋转90°得到△DAE′.(1)判断四边形E′BGD 是什么特殊四边形，并说明理由；(2)由△BCG 经过怎样的变换可得到△DAE′？请说出具体的变换过程．解：(1)四边形E′BGD 是平行四边形．理由：∵四边形ABCD 是矩形，∴AB ∥CD ，AB ＝CD ，∵将△DCE 绕点D 顺时针旋转90°得到△DAE′，∴CE ＝AE′， ∵CE ＝CG ，∴AE ′＝CG ，∴BE ′＝DG ， ∴四边形E′BGD 是平行四边形；(2)∵四边形ABCD 是正方形，∴BC ＝CD ，∠BCD ＝90°.∵∠BCD ＋∠DCE＝180°，∴∠BCD ＝∠DCE＝90°.在△BCG 和△DCE，⎩⎪⎨⎪⎧∠BCG＝∠DCE BC ＝DC ∠CBG＝∠CD E ，∴△BCG ≌△DCE(ASA )；∴由△BCG 绕点C 顺时针旋转90°可得到△DCE，再绕点D 顺时针旋转90°得到△DAE′10. （2018·浙江宁波·10分）如图，在△ABC 中，∠ACB=90°，AC=BC ，D 是AB 边上一点（点D 与A ，B 不重合），连结CD ，将线段CD 绕点C 按逆时针方向旋转90°得到线段CE ，连结DE 交BC 于点F ，连接BE ．（1）求证：△ACD≌△BCE；（2）当AD=BF时，求∠BEF的度数．【考点】旋转的性质、全等三角形的判定与性质【分析】（1）由题意可知：CD=CE，∠DCE=90°，由于∠ACB=90°，所以∠ACD=∠ACB﹣∠DCB，∠BCE=∠DCE﹣∠DCB，所以∠ACD=∠BCE，从而可证明△ACD≌△BCE（SAS）（2）由△ACD≌△BCE（SAS）可知：∠A=∠CBE=45°，BE=BF，从而可求出∠BEF的度数．【解答】解：（1）由题意可知：CD=CE，∠DCE=90°，∵∠ACB=90°，∴∠ACD=∠ACB﹣∠D CB，∠BCE=∠DCE﹣∠DCB，∴∠ACD=∠BCE，在△ACD与△BCE中，∴△ACD≌△BCE（SAS）（2）∵∠ACB=90°，AC=BC，∴∠A=45°，由（1）可知：∠A=∠CBE=45°，∵AD=BF，∴BE=BF，∴∠BEF=67.5°11. （2018·浙江临安·3分）如图直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=3，将腰CD以D为中心逆时针旋转90°至ED，连AE、CE，则△ADE的面积是（）A．1 B．2 C．3 D．不能确定【考点】梯形的性质和旋转的性质【分析】如图作辅助线，利用旋转和三角形全等证明△DCG与△DEF全等，再根据全等三角形对应边相等可得EF的长，即△ADE的高，然后得出三角形的面积．【解答】解：如图所示，作EF⊥AD交AD延长线于F，作DG⊥BC，∵CD以D为中心逆时针旋转90°至ED，∴∠EDF+∠CDF=90°，DE=CD，又∵∠CDF+∠CDG=90°，∴∠CDG=∠EDF，在△DCG与△DEF中，，∴△DCG≌△DEF（AAS），∴EF=CG，∵AD=2，BC=3，∴CG=BC﹣AD=3﹣2=1，∴EF=1，∴△ADE的面积是：×AD×EF=×2×1=1．故选：A．12. (2019•江苏苏州•8分)如图，ABC=，将线段AC绕点A旋转到AF的位置，使△中，点E在BC边上，AE AB得CAF BAE∠=∠，连接EF，EF与AC交于点G（1）求证：EF BC=；（2）若65∠=︒，求FGC∠的度数.ACB∠=︒，28ABC（1）CAF BAE∠=∠∴∠=∠BAC EAFAE AB AC AF==又，()BAC EAF SAS∴△≌△EF BC∴=（2）65AB AE ABC=∠=︒，18065250BAE∴∠=︒-︒⨯=︒50FAG∴∠=︒BAC EAF又△≌△28F C∴∠=∠=︒502878FGC∴∠=︒+︒=︒13. （2019•湖北十堰•10分）如图1，△ABC中，CA＝CB，∠ACB＝α，D为△ABC内一点，将△CAD绕点C按逆时针方向旋转角α得到△CBE，点A，D的对应点分别为点B，E，且A，D，E三点在同一直线上．（1）填空：∠CDE＝2（用含α的代数式表示）；（2）如图2，若α＝60°，请补全图形，再过点C作CF⊥AE于点F，然后探究线段CF，AE，BE之间的数量关系，并证明你的结论；（3）若α＝90°，AC＝，且点G满足∠AGB＝90°，BG＝6，直接写出点C到AG的距离．【分析】（1）由旋转的性质可得CD＝CE，∠DCE＝α，即可求解；（2）由旋转的性质可得AD＝BE，CD＝CE，∠DCE＝60°，可证△CDE是等边三角形，由等边三角形的性质可得DF＝EF，即可求解；（3）分点G在AB的上方和AB的下方两种情况讨论，利用勾股定理可求解．【解答】解：（1）∵将△CAD绕点C按逆时针方向旋转角α得到△CBE∴△ACD≌△BCE，∠DCE＝α∴CD＝CE∴∠CDE＝1802α-故答案为：1802α-（2）AE＝理由如下：如图，∵将△CAD绕点C按逆时针方向旋转角60°得到△CBE∴△ACD≌△BCE∴AD＝BE，CD＝CE，∠DCE＝60°∴△CDE是等边三角形，且CF⊥DE∴DF＝EF∵AE＝AD+DF+EF∴AE＝CF（3）如图，当点G在AB上方时，过点C作CE⊥AG于点E，∵∠ACB＝90°，AC＝BC＝，∴∠CAB＝∠ABC＝45°，AB＝10∵∠ACB＝90°＝∠AGB∴点C，点G，点B，点A四点共圆∴∠AGC＝∠ABC＝45°，且CE⊥AG∴∠AGC＝∠ECG＝45°∴CE＝GE∵AB＝10，GB＝6，∠AGB＝90°∴AG＝8∵AC2＝AE2+CE2，∴（）2＝（8﹣CE）2+CE2，∴CE＝7（不合题意舍去），CE＝1若点G在AB的下方，过点C作CF⊥AG，同理可得：CF＝7∴点C到AG的距离为1或7．。