图论论文

课程名称图论入门论文题目图论在物流物配送上的应用指导教师刘颖学院管理学院姓名郭凤午学号2011030284图论在物流货物配送中的应用摘要：最短路径问题对于节约人们的时间成本具有重要意义。

最短路问题是图论理论的一个经典问题。

寻找最短路径就是在指定网络中两结点间找一条距离最小的路。

最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。

它可被用来解决厂区布局、管路铺设、线路安装等实际问题。

本文介绍了图论的起源和发展、最短路径问题及其算法，并应用图论最短路径问题的分析方法解决物流货物配送中问题。

1 引言数学是一门古老的学科，它已经有了几千年的历史。

然而，图论作为数学的一个分支，却只有200多年的历史，但是其发展十分迅速。

图论是以图为研究对象，图形中我们用点表示对象，两点之间的连线表示对象之间的某种特定的关系。

事实上，任何一个包含了某种二元关系的系统都可以用图形来模拟，而且它具有形象直观的特点，在图中点的位置和线的长短曲直无关紧要[1]。

图论的发展大力地推进了科学文明的进步，解决了很多实际应用问题。

图论是数学领域中发展最快的分支之一，它以图为研究对象。

图论中的图是有若干给定的点及连接两点的线所构成的图形，这种图形常用来描述某些事物之间的某种特定关系，用来代表事物，用连接两点的线表示相应两个事物间具有这种关系。

图论本身是应用数学的一部分，因此，历史上图论曾经被好多位数学家各自独立的建立过。

关于图论的文字记载最早出现在欧拉1736年的论文中，他所考虑的原始问题有很强的实际背景。

数学史上著名的七桥问题欧拉只用了一步就证明了不重复地通过7座桥的路线是根本不存在的!这是拓扑学研究的先声。

图的染色问题一直是图论研究的焦点问题。

数学家赫伍德成功地运用肯普的方法证明了五色定理，即一张地图能够用五种或者更少的颜色染色。

美国伊利诺斯大学的黑肯和阿佩尔，经过四年的艰苦工作．终于完成了四色猜想的证明。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==图论的论文篇一：图论论文课程论文课程名称题目最短路径在最优截断切割问题中的应用姓名学号学院专业摘要本文是把长方体切割的最小代价问题，转化成一个我们所熟悉的图论问题，把其抽象成为一个图论之中求路径的最短路的问题，并采用了图论中的Dijkstra 算法，以求其的最短路，最终得到了对长方体切割问题的求解，最后我们通过了一个长方体切割实例，说明了我们的算法是可靠，有效的。

关键字：最短路径Dijkstra算法最优截断切割1. 预备知识1.1图的基本概念有序三元组G =(V,E,)称为一个图，其中:(1)V是有穷非空集，称为顶点集，其元素叫做图的顶点；(2)E称为边集,其元素叫做图的边；(3)是从边集E到顶点集的有序或者无序对集合的映射，称为关联函数。

1.2 权如果图G中任意一条边上都附有一个数，则称这样的图G为加权图。

若边e标记数为k，称边e的权为k。

定义１在无向图G=(V,E,?)中：（1）顶点与边相互交错且?(ei)?vi?1vi (i=1,2,…k)的有限非空序列w?(v0e1v1e2?vk?1ekvk)称为一条从v0到vk的通路，记为Wv0vk（2）边不重复但顶点可重复的通路称为道路，记为Tvv0k（3）边与顶点均不重复的通路称为路径，记为Pv右图中，我们可以根据定义得到：通路Wvv?v1e4v4e5v2e1v1e4v414vk道路Tvv?v1e1v2e5v4e6v2e2v3e3v414路径Pvv?v1e1v2e5v414定义２（1）任意两点均有路径的图称为连通图．（2）起点与终点重合的路径称为圈．（3）连通而无圈的图称为树．定义３（1）设P(u,v)是赋权图G中从u到v的路径，则称w(P)??w(e)为路径P的权．e?E(P)（2）在赋权图G中，从顶点u到顶点v的具有最小权的路 P*(u,v)，称为u到v的最短路．1.3 固定起点的最短路最短路是一条路径，且最短路的任一段也是最短路．假设在u0-v0的最短路中只取一条，则从u0到其余顶点的最短路将构成一棵以u0为根的树．因此, 可采用树生长的过程来求指定顶点到其余顶点的最短路．Dijkstra算法：求G中从顶点u0到其余顶点的最短路，如图1所示:设G为赋权有向图或无向图，G边上的权均非负．对每个顶点，定义两个标记（l(v)，z(v)），其中:l(v)：表从顶点u0到v的一条路的权．z(v)：v的父亲点，用以确定最短路的路线算法的过程就是在每一步改进这两个标记，使最终l(v)为从顶点u0到v的最短路的权。

图论毕业论文图论是数学的一个分支，主要研究图的性质和结构。

它对于解决各种实际问题具有重要的意义，如交通网络优化、电子芯片设计等。

本文将就图论的概念、基本性质以及其在实际问题中的应用等方面进行论述。

首先，图论是研究图的性质和结构的数学学科。

图是由节点和边组成的数学结构，可以用来描述各种实际问题，如交通网络、社交关系等。

图由节点和边构成，节点表示图中的元素或对象，边表示节点之间的关系。

图可以分为有向图和无向图，有向图中的边有方向性，无向图中的边没有方向性。

图的回路是指从一个节点出发，沿着边走过一系列节点之后再回到起始节点的路径。

图的连通性是指图中的任意两个节点之间存在一条路径。

其次，图论具有一些基本性质。

首先是图的度数。

图的度数是指图中一个节点与其相邻节点的边的个数。

度数为奇数的节点称为奇节点，度数为偶数的节点称为偶节点。

其次是图的邻接矩阵和关联矩阵。

邻接矩阵是一个n×n的矩阵，其中n是图的节点数，矩阵元素a_ij表示节点i与节点j之间是否存在边。

关联矩阵是一个n×m的矩阵，其中n是图的节点数，m是图的边数，矩阵元素b_ij表示节点i是否与边j相关联。

最后是图的连通性。

图的连通性决定了图中是否存在从一个节点到达另一个节点的路径。

如果图中的任意两个节点之间都存在路径，则图是连通的；否则，图是非连通的。

最后，图论在实际问题中有广泛的应用。

首先是交通网络优化。

图论可以用来优化交通网络中的路径规划和交通流量分析等问题，从而提高交通的效率和安全性。

其次是电子芯片设计。

图论可以用来分析电子芯片中各个元件之间的连接关系，从而提高芯片的性能和可靠性。

此外，图论还可以用来解决诸如社交网络分析、物流规划等实际问题。

综上所述，图论是数学的一个分支，主要研究图的性质和结构。

它对于解决各种实际问题具有重要的意义。

未来，随着科学技术的不断发展，图论在实际问题中的应用将会越来越广泛。

因此，对图论的进一步研究和应用具有重要的意义。

课程名称图论入门论文题目图论在物流物配送上的应用指导教师刘颖学院管理学院姓名郭凤午学号2011030284图论在物流货物配送中的应用摘要：最短路径问题对于节约人们的时间成本具有重要意义。

最短路问题是图论理论的一个经典问题。

寻找最短路径就是在指定网络中两结点间找一条距离最小的路。

最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。

它可被用来解决厂区布局、管路铺设、线路安装等实际问题。

本文介绍了图论的起源和发展、最短路径问题及其算法，并应用图论最短路径问题的分析方法解决物流货物配送中问题。

1 引言数学是一门古老的学科，它已经有了几千年的历史。

然而，图论作为数学的一个分支，却只有200多年的历史，但是其发展十分迅速。

图论是以图为研究对象，图形中我们用点表示对象，两点之间的连线表示对象之间的某种特定的关系。

事实上，任何一个包含了某种二元关系的系统都可以用图形来模拟，而且它具有形象直观的特点，在图中点的位置和线的长短曲直无关紧要[1]。

图论的发展大力地推进了科学文明的进步，解决了很多实际应用问题。

图论是数学领域中发展最快的分支之一，它以图为研究对象。

图论中的图是有若干给定的点及连接两点的线所构成的图形，这种图形常用来描述某些事物之间的某种特定关系，用来代表事物，用连接两点的线表示相应两个事物间具有这种关系。

图论本身是应用数学的一部分，因此，历史上图论曾经被好多位数学家各自独立的建立过。

关于图论的文字记载最早出现在欧拉1736年的论文中，他所考虑的原始问题有很强的实际背景。

数学史上著名的七桥问题欧拉只用了一步就证明了不重复地通过7座桥的路线是根本不存在的!这是拓扑学研究的先声。

图的染色问题一直是图论研究的焦点问题。

数学家赫伍德成功地运用肯普的方法证明了五色定理，即一张地图能够用五种或者更少的颜色染色。

美国伊利诺斯大学的黑肯和阿佩尔，经过四年的艰苦工作．终于完成了四色猜想的证明。

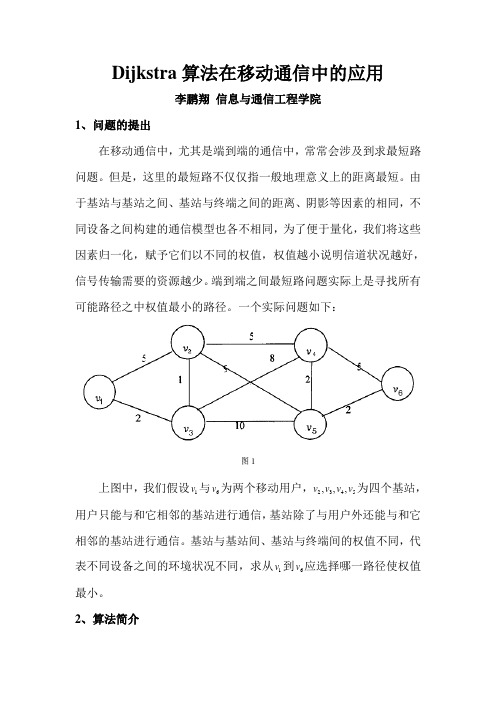
Dijkstra 算法在移动通信中的应用李鹏翔 信息与通信工程学院1、问题的提出在移动通信中，尤其是端到端的通信中，常常会涉及到求最短路问题。

但是，这里的最短路不仅仅指一般地理意义上的距离最短。

由于基站与基站之间、基站与终端之间的距离、阴影等因素的相同，不同设备之间构建的通信模型也各不相同，为了便于量化，我们将这些因素归一化，赋予它们以不同的权值，权值越小说明信道状况越好，信号传输需要的资源越少。

端到端之间最短路问题实际上是寻找所有可能路径之中权值最小的路径。

一个实际问题如下：上图中，我们假设1v 与6v 为两个移动用户，2345,,,v v v v 为四个基站，用户只能与和它相邻的基站进行通信，基站除了与用户外还能与和它相邻的基站进行通信。

基站与基站间、基站与终端间的权值不同，代表不同设备之间的环境状况不同，求从1v 到6v 应选择哪一路径使权值最小。

2、算法简介Dijkstra 算法是图论中确定最短路的基本方法，也是其它算法的基础。

Dijkstra 算法基本步骤： 令：{}{}_23,1,,,,i n s v i s v v v === 并令：{()()10,j j W v T v v s-==∞∈（1）、对j v s -∈，求()(){}()min ,j i ij j T v W v w T v +=。

（2）、求(){}min j j v sT v ∈得()k T v ，使()k T v =(){}min j j v sT v ∈令()()k k W v T v =（3）、若k n v v =则已找到1v 到n v 的最短路距离()k W v ，否则令i k =从s -中删去i v 转（1）。

这样经过有限次迭代则可以求出1v 到n v 的最短路线，可以用一个流程图来表示：第一步：先取()10W v =意即1v 到1v 的距离为0，而()j T v 是对()j T v 所赋的初值。

第二步：利用()1W v 已知，根据()(){}min ,j i ij T v W v w +对()j T v 进行修正。

1.引言图论是数学的一个分支，并且是组合数学和应用数学的一部分。

它以图做为研究对象，而图是由若干节点和节点之间的边所构成的图型。

在图论中，图往往是某个具体现实生活中问题的数学抽象，可以说，图中的节点代表着生活中的某些特定事物，而节点之间的边则代表着节点之间的特定联系。

图论这门学科需要解决的就是如何利用数学知识去解决它们之间的关系。

图论最早起源于1736年著名的柯尼斯堡七桥问题[1]。

这个问题的内容是：在柯尼斯堡的普莱格尔河上有七座桥将河中的岛屿与河岸连接起来。

问题是要从这四块陆地中任何一块开始，通过每一座桥正好一次，最后再回到起始点。

然而人们无数次的尝试解决却都没有成功。

直到1736年，欧拉解决了这个问题。

他用抽像分析法将这个问题化为世界上第一个图论问题：即把每一块陆地用一个点来代替，将每一座桥用联接相应的两个点的一条边来代替，从而得到了一个“图”。

最终，欧拉成功证明了这个问题是无解的，并且推广了这个问题的意义，给出了对于一个给定的图可以某种方式走遍的判定法则。

这就是后来的欧拉通路、欧拉回路以及欧拉图问题。

于是，欧拉成为了图论学的创始人。

从那以后开始的几百年间，图论开始了飞速的发展。

虽然图论研究的是点和边之间所构成图的问题，但其应用领域还是十分广阔的。

图论的应用不仅仅局限于数学问题和计算机领域，它同时还涵盖了交通管理、通信领域、社会学等诸多其他研究领域。

而最短路径问题是图论应用中的基本问题。

最短路径顾名思义就是在所有的路径中找出一条距离最短的有效路径。

实际上，这里所指的“距离”不仅仅是指地理意义上的距离，还可以引申到时间、费用、等其他度量单位上面。

本文中，以重庆地铁为研究对象，利用图论知识解决在搭乘重庆地铁时的最短路径问题。

可以说，最短路径问题再交通网络结构的分析以及交通路线的选择中都有重要的应用价值。

此外，最短路径问题一直是计算机科学、地理信息学、交通管理学等学科中一个研究的热点问题。

图的着色是指对图的每个节点指定一种颜色，使得相邻的节点的颜色不相同。

基于图论的世界贸易网络的方差研究【摘要】世界贸易网络是一个复杂的自组织系统，本文基于图的熵的最可几估计，不同于其他研究——独立的考虑各国进口额和出口额，这里将两国有相互贸易的情形引入世界贸易网络，形成一组无参数模型，运用这些模型计算分析其拓扑性质的方差。

【关键词】自组织；图；拓扑；期望；方差1.引言如果一个系统不靠外部指令而形成组织，系统在内在机制的驱动下，系统内要素各尽其责而又协调地自动地形成有序结构，就是自组织系统；在一定条件下，系统自动地由无序走向有序，由低级有序走向高级有序[1]。

世界经济就是一个复杂的自组织系统，实际情况表明世界经济系统中，各国从事行业多种多样，规模差距很大，赢利能力千差万别，成长性迥异（有每年成倍增长的，也有大幅萎缩的），国家与国家之间以贸易联系起来，从而形成一个复杂网络，而这个复杂网络自行从简单向复杂、从粗糙向精细方向发展，不断地提高自身的复杂度和精细度。

研究表明，世界贸易网络的拓扑性质依赖于世界各国的国民生产总值，国民生产总值又依赖于国际贸易，而国际贸易又促进世界经济，这样世界贸易网络是一个连续的反馈，其动力学性质和其拓扑性质在该网络中共同进化[2]。

一般来说，理解自组织网络在科学上是个大挑战，这类网络的模型只有极少数是解析的。

不过，世界贸易网络的拓扑可以由包含度序列的无参数模型产生，该做法使得研究复杂世界贸易网络成为可能[3]。

本文，在介绍离散化方法后，运用该法去研究相互关联的发生，即研究有向图。

图论算法中，度是一个非常重要的概念，所谓顶点的度，就是指和该顶点相关联的边数。

“入度”是指有向图中某点作为图中边的终点的次数之和；以某顶点为起点，起始于该顶点的边的数目称为该顶点的“出度”[4]。

这里我们引入一个新的概念——互惠度，即两个独立国家之间有相互的贸易往来，在有向图中a是起点有指向b的边，同时b是起点有指向a的边，此联系称为a的一个互惠度。

与其它研究不同的是，一般研究结果仅通过点的入度或仅通过点的出度得到，这里我们考虑每个点的互惠度和非互惠度，则局部信息被强化，图的随机方差很小。

最小生成树——Prim算法1、算法问题的提出首先介绍生成树的概念连通图G=(V,E)是无向带权图，若一个子图G’是一棵包含G的所有顶点的树，则该子图G’称为G的生成树。

生成树是连通图的极小连通子图。

所谓极小是指：若在树中任意增加一条边，则将出现一个回路；若去掉一条边，将会使之变成非连通图。

生成树各边的权值总和称为生成树的权。

本次设计是求在图G中所有生成树中权值总和（费用/代价）最小的生成树，即最小生成树。

用两个例子进行实例演示。

2、Prim算法思想用哲学的观点来说，每个事物都有自己特有的性质，那么图的最小生成树也是不例外的。

按照生成树的定义，n 个顶点的连通网络的生成树有n 个顶点、n-1 条边。

（1）从树中某一个顶点V0开始，将V0到其他顶点的所有边当作候选边。

（2）重复以下步骤n-1次，使得其他n-1个顶点被并入到生成树中。

○1从候选边挑出权值最小的边输出，并将与该边另一端的相接的顶点V并入生成树中。

○2考察所有剩余顶点V i，如果(V,V i)的权值比lowcost[V i]小，则用（V,V i）的权值更新lowcost[V i]。

其中的vset[i]的值记录顶点V[i]顶点是否被选入最小生成树中，V[i]=0,表示为被选入，V[i]=1，表示已被选入。

用到辅助数组pre[]，记录当前所选入顶点的前驱结点，当并入前一个顶点时，剩下顶点到生成树的权值发生了改变时，就需要及时修改剩下顶点V[i]的前驱结点。

3、程序设计（1）所用数据结构，图的存储结构模块（nodetype.h）#define MAXSIZE 7#define INF 100typedef struct{int no;}VertexType; //顶点类型定义typedef struct{int edges[MAXSIZE][MAXSIZE]; //存入边的权值int n; //顶点数int e; //总的边数VertexType vex[MAXSIZE];}MGraph; //图的存储结构MGraph g;（2）主模块（main.cpp）#include#include"nodetype.h"#include"initiate.h"#include"prim.h"void prim(MGraph g,int v0,int &sum);int main(){int sum=0;int v0;initiate(g); //图的初始化printf("请输入起点编号：\n");scanf("%d",&v0);//输入起始节点prim(g,v0,sum); //调用prim算法，构成最小生成树printf("最小生成树的总代价为%d\n",sum);return 0;}（3）读取数据模块,图的初始化（initiate.h）void initiate(MGraph &g){int i,j,v0=0;printf("Please input the Sumnum of MGraph:\n");scanf("%d",&g.n);printf("依次输入各边权值（不相临接的边权值为100）!\n\n"); for(i=1;i<=g.n;i++){g.vex[i].no=i; //节点编号for(j=1;j<=g.n;j++){printf("边[%d][%d]的权值为：",i,j);//各边的权值scanf("%d",&g.edges[i][j]);printf("\n");}}}(4）运用贪心策略——Prim算法构造最小生成树（prim.h）void prim(MGraph g,int v0,int &sum){int lowcost[MAXSIZE],vset[MAXSIZE];int v,pre[MAXSIZE]; //pre[]存入前驱结点数组int i,j,k,min;v=v0; //初始起点for(i=1;i<=g.n;i++){lowcost[i]=g.edges[v0][i]; //lowcost[]的数组pre[i]=v0;vset[i]=0;}vset[v0]=1;sum=0;for(i=1;imin=INF;for(j=1;j<=g.n;j++){if(vset[j]==0&&lowcost[j]min=lowcost[j];k=j;}}vset[k]=1; //将此结点并入到所够造的生成树中v=k;if(min!=INF){printf("边的起点为：%d 终点为：%d 权值为%d\n",pre[v],v,min);sum+=min;}else{break;}for(j=1;j<=g.n;j++){//并入新结点后修改剩下的结点到生成树的权值if(vset[j]==0&&g.edges[v][j]lowcost[j]=g.edges[v][j];pre[j]=v; //并记其下全趋结点}}}}4、算法分析Prim算法的时间复杂度主要是在双重循环构造最小生成树的过程中，设图的顶点数为n，则双重循环的时间复杂度为O(n2)，在生成最小生成树的过程中，增加了两个数组，vset[]和lowcost[]数组，同时增加了一个前驱数组prey[]，用来记录所选顶点的全趋结点，故空间复杂度为O(3n)。

图论本科毕业论文近年来，随着社会的发展和科技的进步，图论在各个领域中得到了广泛应用，尤其是网络科学、计算机科学和数学领域。

图论的基础理论和应用研究，也受到越来越多的关注。

本文主要介绍了图论的基础理论和应用研究，以及本人在此领域中的研究工作。

一、图论的基础理论图论是一门基础数学学科，它主要研究图的结构、性质和算法等方面的问题。

在图论中，图是由节点和边组成的集合，它可以用来描述各种实际问题，例如社交网络、电子电路、物流运输等。

图可以分为有向图和无向图两种类型。

有向图是由有向边连接节点而成的图，可以描述各种节点之间的方向关系。

而无向图则是由无向边连接节点而成的图，不考虑节点之间的方向关系，可以表示各种关系网络。

图论中的一些基本概念包括节点、边、路径、回路和连通性等。

节点是图中的基本元素，边是节点之间的连接线，路径指的是由一系列连续的边连接的节点序列，回路是一个首尾相接的路径。

而连通性则是描述图中各个节点之间的相互可达性的层次结构。

图论的另外一个重要的概念是图的度数。

节点的度数指与此节点相邻的边的数目，而图的度数则是所有节点度数之和。

在研究图的性质和结构时，度数是一个非常重要的指标，它可以用来刻画图的稠密或稀疏程度。

二、图论的应用研究图论在实际中的应用非常广泛。

例如，图论可以用于描述社交网络中各个节点之间的关系网络。

在这个网络中，节点代表人或组织，边则代表人和组织之间的关系。

通过研究这个网络的结构和性质，可以分析社交网络中的信息传播和节点的影响力等问题。

图论也广泛应用于计算机科学领域中。

例如，在计算机网络中，图论可以用来描述网络拓扑结构，并通过研究图的各种性质和算法，来优化网络的性能和安全性。

图论还可以用于描述物流和运输网络中的各种问题。

例如，在交通运输中，可以通过赋予各个节点和边合适的权重来刻画交通拥堵程度，从而优化交通运输的效率。

三、本人在图论领域的研究工作在本人的毕业论文中，我主要研究了图论中的连通性问题。

最短路算法的比较与应用[摘要]本文较详尽地介绍了最短路算法相关的基本概念，给出了Dijkstra 算法、Floyd 算法、SPFA 算法等常用算法及其核心思想，并对各种最短算法做了多角度的比较，阐述了各种算法的应用范围，并对其在运输网络、舰船通道路线设计、工业生产中的应用做出了举例说明，侧重于模型的建立、思考和证明的过程，最后作出总结。

关键词：最短路算法 Dijkstra 算法 Floyd 算法 SPFA 算法1 引言最短路算法是图论中的核心问题之一，他是许多更深层次算法的基础，同时，该问题有着大量的生产实际的背景.很多问题从表面上看与最短问题没有什么关系，却也可以归结为最短路问题，本文通过收集整理关于最短路径的普遍算法，为研究最短路径问题在一些出行问题，工程问题，及实际生活问题中的应用，为企业和个人提供方便的选择方法。

2 最短路2.1 最短路的定义对最短路问题的研究早在上个世纪60年代以前就卓有成效了,其中对赋权)0(≥ij w 的有效算法是由荷兰著名计算机专家E.W.Dijkstra 在1959年首次提出的,该算法能够解决两指定点间的最短路,也可以求解图G 中一特定点到其它各顶点的最短路。

后来海斯在Dijkstra 算法的基础之上提出了海斯算法.但这两种算法都不能解决含有负权的图的最短路问题.因此由Ford 提出了Ford 算法,它能有效地解决含有负权的最短路问题.但在现实生活中,我们所遇到的问题大都不含负权,所以我们在)0(≥ij w 的情况下选择Dijkstra 算法。

定义1 若图),(E V G G =中各边e 都赋有一个实数)(e W ,称为边e 的权,则称这种图为赋权图,记为),,(W E V G G =。

定义2 若图),(E V G G =是赋权图且)(,0)(G E e e W ∈≥,若u 是i v 到jv 的路)(u W 的权,则称)(u W 为u 的长,长最小的i V 到j V 的路)(u W 称为最短路.若要找出从i v 到n v 的通路u ,使全长最短,即()()min ij e uW u W e ∈=∑。