最新2019年高中数学单元测试试题-推理与证明专题完整考题库(含参考答案)

2019年高中数学单元测试试题 推理与证明专题（含答案）学校：__________第I 卷（选择题）请点击修改第I 卷的文字说明 一、选择题1． 有一段演绎推理是这样的：“直线平行于平面,则平行于平面内所有直线；已知直线b ⊆/平面α，直线a ≠⊂平面α，直线b ∥平面α，则直线b ∥直线a ”的结论显然是错误的，这是因为A.大前提错误B.小前提错误C.推理形式错误D.非以上错误2．下面使用类比推理正确的是 A.“若33a b ⋅=⋅,则a b =”类推出“若00a b ⋅=⋅,则a b =” B.“若()a b c ac bc +=+”类推出“()a b c ac bc ⋅=⋅”C.“若()a b c ac bc +=+” 类推出“a b a bc c c+=+ （c ≠0）” D.“n n a a b =n （b ）” 类推出“n n a a b +=+n（b ）”第II 卷（非选择题）请点击修改第II 卷的文字说明 二、填空题3．已知结论：“在三边长都相等的ABC ∆中，若D 是BC 的中点，G 是ABC ∆外接圆的圆心，则2AGGD=”．若把该结论推广到空间，则有结论：“在六条棱长都相等的四面体ABCD 中，若M 是BCD ∆的三边中线的交点，O 为四面体ABCD 外接球的球心，则AOOM = ”． (2011年3月苏、锡、常、镇四市高三数学教学情况调查一) 34． 对大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”:3325⎧⎨⎩ 373911⎧⎪⎨⎪⎩ 3131541719⎧⎪⎪⎨⎪⎪⎩ …. 仿此,若3m 的“分裂数”中有一个是59,则m 的值为 .5．已知P 为抛物线x y 42=的焦点,过P 的直线l 与抛物线交与A,B 两点，若Q 在直线l 上,且满足||||||||AP QB AQ PB =，则点Q 总在定直线1x =-上．试猜测如果P 为椭圆221259x y +=的左焦点，过P 的直线l 与椭圆交与A,B 两点，若Q 在直线l 上,且满足||||||||AP QB AQ PB =，则点Q 总在定直线 上．6．已知命题：△ABC 的顶点A(−P ，0)，C(P ，0)，顶点B 在椭圆x 2m 2 + y 2n 2 = 1(m >n >0，P = m 2−n 2)上，椭圆的离心率为e ，则sinA+sinC sinB = 1e 。

2019年高中数学单元测试试题 推理与证明专题（含答案）学校：__________第I 卷（选择题）请点击修改第I 卷的文字说明 一、选择题1．下面使用类比推理正确的是 A.“若33a b ⋅=⋅,则a b =”类推出“若00a b ⋅=⋅,则a b =” B.“若()a b c ac bc +=+”类推出“()a b c ac bc ⋅=⋅”C.“若()a b c ac bc +=+” 类推出“a b a bc c c+=+ （c ≠0）” D.“n n a a b =n （b ）” 类推出“n n a a b +=+n（b ）”2． [文科]若nn n a n 212111+⋅⋅⋅++++=（n 是正整数），则+=+n n a a 1（ ）.(A))1(21+n (B)11221+-+n n (C) 11221121+-+++n n n (D) 221121+++n n [理科] 观察下列式子： ,474131211,3531211,23211222222<+++<++<+，可以猜想结论为( ) . (A)2221112n 1123n n++++⋅⋅⋅+< (n N*)∈ (B) 2221112n 1123(n 1)n-+++⋅⋅⋅+<+(n N*)∈ (C) 2221112n 1123(n 1)n 1++++⋅⋅⋅+<++(n N*)∈ (D) 2221112n 1123n n 1++++⋅⋅⋅+<+(n N*)∈3．下列推理正确的是----------------------------------------------------------（ ）(A) 把()a b c + 与 log ()a x y + 类比，则有：log ()log log a a a x y x y +=+ ． (B) 把()a b c + 与 sin()x y + 类比，则有：sin()sin sin x y x y +=+．(C) 把()n ab 与 ()na b + 类比，则有：nnn()x y x y +=+．(D) 把()a b c ++ 与 ()xy z 类比，则有：()()xy z x yz =．第II 卷（非选择题）请点击修改第II 卷的文字说明 二、填空题4．用反证法证明命题：“如果x y <，那么1155x y >”时，假设的内容应该是 ▲5．在计算“1223(1)n n ⨯+⨯+⋅⋅⋅++”时，某同学学到了如下一种方法： 先改写第k 项：1(1)[(1)(2)(1)(1)],3k k k k k k k k +=++--+由此得112(123012),3⨯=⨯⨯-⨯⨯123(234123),3⨯=⨯⨯-⨯⨯…1(1)[(1)(2)(1)(1)].3n n n n n n n n +=++--+相加，得11223(1)(1)(2).3n n n n n ⨯+⨯+⋅⋅⋅++=++类比上述方法，请你计算“123234(1)(2)n n n ⨯⨯+⨯⨯+⋅⋅⋅+++”，其结果为 ▲ .6．已知P 为抛物线x y 42=的焦点,过P 的直线l 与抛物线交与A,B 两点，若Q 在直线l 上,且满足||||||||AP QB AQ PB =，则点Q 总在定直线1x =-上．试猜测如果P 为椭圆221259x y +=的左焦点，过P 的直线l 与椭圆交与A,B 两点，若Q 在直线l 上,且满足||||||||AP QB AQ PB =，则点Q 总在定直线 上．7．观察下列各图，并阅读下面的文字，像这样，10条直线相交，交点的个数最多是____________；2条直线相交， 3条直线相交， 4条直线相交， 最多有1个交点 最多有3个交点 最多6个交点8．设面积为S 的平面四边形的第i 条边的边长记为a i （i =1，2，3，4），P 是该四边形内任意一点，P 点到第i 条边的距离记为h i ，若31241234a a a a k ====, 则412()i i S ih k ==∑.类比上述结论，体积为V 的三棱锥的第i 个面的面积记为S i （i =1，2，3，4），Q 是该三棱锥内的任意一点，Q 点到第i 个面的距离记为H i ，则相应的正确命题是：若31241234S S S S k ====,则 ．9．在平面上有n 条直线，任何两条都不平行，并且任何三条都不交于同一点，问这些直线把平面分成几部分？______________10．观察x x 2)(2='，344)(x x ='，x x sin )(cos -='，由归纳推理可得：若定义在R 上的函数)(x f 满足)()(x f x f =-，记()g x 为)(x f 的导函数，则)(x g -与()g x 的关系是 ▲ ．11．====试推测___,___a b ==12．记123k k k k k S n =+++⋅⋅⋅+, 当123k =⋅⋅⋅, , , 时，观察下列等式：211122S n n =+， 322111326S n n n =++，4323111424S n n n =++， 5434111152330S n n n n =++-，6542515212S An n n Bn =+++， ⋅⋅⋅可以推测，A B -= ▲ ．13．用数学归纳法证明“当n 为正奇数时，nn y x +能被y x +整除”的第二步是__________.14．已知一个关于正整数n 的命题P （n ）满足“若n=k （k ∈N *）时命题P （n ）成立，则n=k+1时命题P （n ）也成立”．有下列判断：（1）当n=2013时命题P （n ）不成立，则n ≥2013时命题P （n ）不成立； （2）当n=2013时命题P （n ）不成立，则n=1时命题P （n ）不成立； （3）当n=2013时命题P （n ）成立，则n ≥2013时命题P （n ）成立； （4）当n=2013时命题P （n ）成立，则n=1时命题P （n ）成立．其中正确判断的序号是 （2）（3） ．（写出所有正确判断的序号）（5分）15．已知结论：“在等边ABC ∆中，若D 是边BC 的中点， G 是ABC ∆外接圆的圆心，则2AGGD=”。

2019年高中数学单元测试试题推理与证明专题（含答案）学校：__________第I卷（选择题）请点击修改第I卷的文字说明一、选择题1．已知2()(1),(1)1()2f xf x ff x+==+*x N∈（），猜想(f x）的表达式为A.4()22xf x=+B.2()1f xx=+C.1()1f xx=+D.2()21f xx=+2．右边所示的三角形数组是我国古代数学家杨辉发现的，称为杨辉三角形，根据图中的数构成的规律，a所表示的数是-------------------------------（）(A)2 (B) 4 (C) 6 (D) 8第II卷（非选择题）请点击修改第II卷的文字说明二、填空题11 2 1 1 3 3 1 1 4 a 4 11 5 10 10 5 13．将全体正整数排成一个三角形数阵：按照以上排列的规律，第n 行()4n ≥从左向右的第4个数为 ▲ ．4．在平面直角坐标平面内,不难得到“对于双曲线xy k =（0k >）上任意一点P ,若点P 在x 轴、y 轴上的射影分别为M 、N ，则PM PN ⋅必为定值k ”.类比于此，对于双曲线22221x y a b-=（0a >,0b >）上任意一点P ,类似的命题为:____ ____.5．设等差数列{}n a 的前n 项和为n S ，则4S ，84S S -，128S S -，1612S S -成等差数列．类比以上结论有：设等比数列{}n b 的前n 项积为n T ，则4T ， ， ，1612T T 成等比数列．6．请阅读下列材料：若两个正实数12,a a 满足22121a a +=，那么12a a +≤．证明：构造函数2221212()()()22()1f x x a x a x a a x =-+-=-++，因为对一切实数x ，恒有()0f x ≥，所以0∆≤，从而得2124()80a a +-≤，所以12a a +≤．根据上述证明方法，若n 个正实数满足222121n a a a ++⋅⋅⋅+=时，你能得到的结论为▲ .（不必证明）7．用数学归纳法证明等式：aa aa a n n --=++++++111212（1≠a ，*N n ∈），验证1=n 时，等式左边= .8． 已知整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…则第30个数对是 .1 2 3 4 5 6 7 8 9 10 11 12 13 14 15第16题9．二维空间中，圆的一维测度(周长)l ＝2πr ，二维测度(面积)S ＝πr 2；三维空间中，球的二维测度(表面积)S ＝4πr 2，三维测度(体积)V ＝43πr 3.应用合情推理，若四维空间中，“超球”的三维测度V ＝8πr 3，则其四维测度W ＝ ▲ .10．已知下列结论：① 1x 、2x 都是正数⇔⎩⎨⎧>>+002121x x x x ，② 1x 、2x 、3x 都是正数⇔⎪⎩⎪⎨⎧>>++>++000321133221321x x x x x x x x x x x x ，则由①②猜想：1x 、2x 、3x 、4x 都是正数⇔11． 观察下列各式：①2/33)(x x =；②x x cos )(sin /=；③x x xx --+=-22)22(/；④x x x x x sin cos )cos (/-=根据其中函数)(x f 及其导函数)(/x f 的奇偶性，运用归纳推理可得到的一个命题是： ．12． 如图所示：有三根针和套在一根针上的n 个金属片，按下列规则，把金属片从一根针上全部移到另一根针上． （1）每次只能移动一个金属片；（2）在每次移动过程中，每根针上较大的金属片不能放在较小的金属片上面．将n 个金属片从1号针移到3号针最少需要移动的次数记为()f n ；则：（1）(3)f = (2) ()f n = .13．在直角三角形ABC 中，∠C 为直角，两直角边长分别为a ，b ，求其外接圆半径时，可采取如下方法：将三角形ABC 补成以其两直角边为邻边的矩形，则矩形的对角线为三角04321>+++x x x x434232413121>+++++x x x x x x x x x x x x12340.x x x x >▲形外接圆的直径，可得三角形外接圆半径为；按此方法，在三棱锥S ﹣ABC 中，三条侧棱两两互相垂直，且长度分别为a ，b ，c ，通过类比可得三棱锥S ﹣ABC 外接球的半径为．（3分）14．观察下列式子：474131211,3531211,2321122222<+++<++<+…则可归纳出第(1,)n n n N *≥∈个不等式是 ▲ ．15．边长为a 的等边三角形内一点到三边的距离之和为定值，这个定值为a 23，推广到空间，棱长为a 的正四面体内任一点到各个面距离之和为 ▲16． 若将推理“四边形的内角和为360，所以平行四边形的内角和为360”改为三段论的形式，则它的小前提是 ▲ .17．用数学归纳法证明“当n 为正奇数时，nn y x +能被y x +整除”的第二步是__________.18．观察下列一组等式根据下面的规律写出第13行等式 。

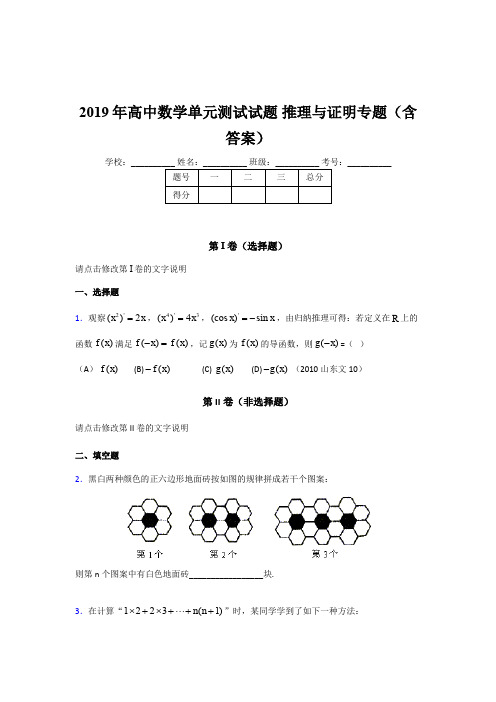
2019年高中数学单元测试试题 推理与证明专题（含答案）学校：__________第I 卷（选择题）请点击修改第I 卷的文字说明 一、选择题1．观察2'()2x x =，4'3()4x x =，'(cos )sin x x =-，由归纳推理可得：若定义在R 上的函数()f x 满足()()f x f x -=，记()g x 为()f x 的导函数，则()g x -=（ ） （A ）()f x (B)()f x - (C) ()g x (D)()g x - （2010山东文10）第II 卷（非选择题）请点击修改第II 卷的文字说明 二、填空题2．黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：则第n 个图案中有白色地面砖_________________块.3．在计算“1223(1)n n ⨯+⨯+⋅⋅⋅++”时，某同学学到了如下一种方法：先改写第k 项：1(1)[(1)(2)(1)(1)],3k k k k k k k k +=++--+由此得112(123012),3⨯=⨯⨯-⨯⨯123(234123),3⨯=⨯⨯-⨯⨯…1(1)[(1)(2)(1)(1)].3n n n n n n n n +=++--+相加，得11223(1)(1)(2).3n n n n n ⨯+⨯+⋅⋅⋅++=++类比上述方法，请你计算“123234(1)(2)n n n ⨯⨯+⨯⨯+⋅⋅⋅+++”，其结果为 ▲ .4．已知各项为正数的等比数列}{n b ，若m b a =，n b b =，)(n m >， 则m m n b +=，类比上述性质，得出在等差数列{}n a 中的相关性质，若s a m =，t a n =，)(n m >，则 .5．古希腊数学家把数1,3,6,10,15,21,…，叫做三角数，它有一定的规律性，则第30个三角数减去第28个三角数的值为 ．6．若ABC 的三边长分别为a, b, c ，其内切圆半径为r ，则S △ABC =12 （a+b+c ）·r ，类比这一结论到空间，写出三棱锥中的一个正确结论为7．观察x x 2)(2='，344)(x x ='，x x sin )(cos -='，由归纳推理可得：若定义在R 上的函数)(x f 满足)()(x f x f =-，记()g x 为)(x f 的导函数，则)(x g -与()g x 的关系是 ▲ ．8．已知下列结论： ① 1x 、2x 都是正数⇔⎩⎨⎧>>+02121x x x x ，② 1x 、2x 、3x 都是正数⇔⎪⎩⎪⎨⎧>>++>++000321133221321x x x x x x x x x x x x ，则由①②猜想：1x 、2x 、3x 、4x 都是正数⇔9．下列不等式：121⋅≥2111⋅，⎪⎭⎫ ⎝⎛+⋅31131≥⎪⎭⎫⎝⎛+⋅412121 ，⎪⎭⎫ ⎝⎛++⋅5131141≥⎪⎭⎫⎝⎛++⋅61412131，…，由此猜测第1+n 个不等式为 ▲ （*n N ∈） 10．用反证法证明结论“a ，b ，c 至少有一个是正数”时，应假设 ▲ ．11．二维空间中，圆的一维测度(周长)l ＝2πr ，二维测度(面积)S ＝πr 2；三维空间中，球的二维测度(表面积)S ＝4πr 2，三维测度(体积)V ＝43πr 3.应用合情推理，若四维空间中，“超球”的三维测度V ＝8πr 3，则其四维测度W ＝ ▲ .12．观察下列等式：=（﹣）×，=（﹣）×，=（﹣）×，=（﹣）×，…可推测当n ≥3，n ∈N *时，= （﹣）×．（3分）13．如图，将全体奇数排成一个三角形数阵，根据以上排列规律，数阵中第(4)n n ≥行的从左到右的第4个数是 ▲ ．14．用反证法证明命题“三角形的内角中至少有一个角不大于60”时应假设 ▲ . 15．整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…则第61个数对是 ▲ ．04321>+++x x x x434232413121>+++++x x x x x x x x x x x x12340.x x x x >▲13 5 7 9 11 13 15 17 19 ………………16．用数学归纳法证明“当n 为正奇数时，nn y x +能被y x +整除”的第二步是__________.17．若三角形内切圆半径为ｒ，三边长分别为ａ，ｂ，ｃ,则三角形面积Ｓ＝21ｒ（ａ＋ｂ＋ｃ），根据类比推理方法，若一个四面体的内切球半径为Ｒ，四个面的面积分别为4321,,,S S S S ，则四面体的体积Ｖ＝__________三、解答题18．（本小题满分10分）如图，圆周上有n 个固定点，分别为A 1，A 2，…，A n （n *∈N ，n ≥2），在每一个点上分别标上1，2，3中的某一个数字，但相邻的两个数字不相同，记所有的标法总数为a n ． （1）写出a 2，a 3，a 4的值；（2）写出a n 的表达式，并用数学归纳法证明．19．已知n x x f )2()(+=, 其中*N n ∈．（1）若展开式中含3x 项的系数为14, 求n 的值；（2）当3=x 时, 求证：)(x f*)s N ∈的形式. （本小题满分15分）20．试用两种方法证明： （1）；（2）．（15分）21．设n ∈*N 且2n ≥，证明：()22221212n n a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232n a a a a ⎡+++⋅⋅⋅+⎣()234n a a a a +++⋅⋅⋅++⋅⋅⋅]1n n a a -+．A A证明：（1）当2n =时，有()2221212122a a a a a a +=++，命题成立． ………2分 （2）假设当(2)n k k =≥时，命题成立，即()22221212k k a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232k a a a a ⎡+++⋅⋅⋅+⎣()234k a a a a +++⋅⋅⋅+ +⋅⋅⋅]1k k a a -+成立， ………4分 那么，当1n k =+时，有()2121k k a a a a +++⋅⋅⋅++ ()()221212112k k k k a a a a a a a a ++=++⋅⋅⋅++++⋅⋅⋅++22212k a a a =++⋅⋅⋅+()1232k a a a a ⎡+++⋅⋅⋅+⎣()234k a a a a +++⋅⋅⋅++⋅⋅⋅]1k k a a -+ (12a +2a ++⋅⋅⋅)211k k k a a a ++++．2222121k k a a a a +=++⋅⋅⋅++()12312k k a a a a a +⎡+++⋅⋅⋅++⎣+(234a a a ++⋅⋅⋅k a +)1k a ++ +⋅⋅⋅ ]1k k a a ++．所以当1n k =+时，命题也成立． ………8分根据（1）和（2），可知结论对任意的n ∈*N 且2n ≥都成立． ………10分22．在数列{}n a 中，1112(2)2()n n n n a a a n λλλ+*+==++-∈N ，，其中0λ>．（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）求数列{}n a 的前n 项和n S ； （Ⅲ）证明存在k *∈N ，使得11n k n ka aa a ++≤对任意n *∈N 均成立． 本小题以数列的递推关系式为载体，主要考查等比数列的前n 项和公式、数列求和、不等式的证明等基础知识与基本方法，考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力．满分14分．（Ⅰ）解法一：22222(2)22a λλλλ=++-=+，2232333(2)(2)222a λλλλλ=+++-=+， 3343444(22)(2)232a λλλλλ=+++-=+．由此可猜想出数列{}n a 的通项公式为(1)2n nn a n λ=-+．以下用数学归纳法证明．（1）当1n =时，12a =，等式成立．（2）假设当n k =时等式成立，即(1)2k kk a k λ=-+，那么111(2)2k k k a a λλλ++=++-11(1)222k k k k kk λλλλλ++=-+++-11[(1)1]2k k k λ++=+-+．这就是说，当1n k =+时等式也成立．根据（1）和（2）可知，等式(1)2n nn a n λ=-+对任何n *∈N 都成立．解法二：由11(2)2()n n n n a a n λλλ+*+=++-∈N ，0λ>，可得111221n nn nn n a a λλλλ+++⎛⎫⎛⎫-=-+ ⎪⎪⎝⎭⎝⎭， 所以2nn n a λλ⎧⎫⎪⎪⎛⎫-⎨⎬ ⎪⎝⎭⎪⎪⎩⎭为等差数列，其公差为1，首项为0，故21n n n a n λλ⎛⎫-=- ⎪⎝⎭，所以数列{}n a 的通项公式为(1)2n n n a n λ=-+．（Ⅱ）23．已知等比数列{}n a 的首项12a =，公比3q =，n S 是它的前n 项和.求证：131n n S n S n++≤.(江苏省南京市2011届高三第一次模拟考试) 24．观察下面运算结果：22393941641624,24,3,3,441122223333+=⨯=+=⨯=+=⨯=，，525525554444+=⨯=，，…，根据这些运算结果，归纳出一个关于正整数n 的等式，这个等式为________________25．已知,m n 是正数，证明：33m n n m+≥22m n +．26． 已知各项均为整数的等比数列{}n a ，公比q>1，且满足a 2a 4=64，a 3+2是a 2,a 4的等差中项。

2019年高中数学单元测试试题推理与证明专题（含答案）学校：__________第I卷（选择题）请点击修改第I卷的文字说明一、选择题1．把下面在平面内成立的结论类比地推广到空间，结论还正确的是-----------------------------------（）(A) 如果一条直线与两条平行线中的一条相交，则比与另一条相交．(B) 如果一条直线与两条平行线中的一条垂直，则比与另一条垂直．(C) 如果两条直线同时与第三条直线相交，则这两条直线相交．(D) 如果两条直线同时与第三条直线垂直，则这两条直线平行．第II卷（非选择题）请点击修改第II卷的文字说明二、填空题2．由“若直角三角形两直角边长分别为a、b，则其外接圆半径r ”类比可得“若三棱锥三条侧棱两两垂直，侧棱长分别为a、b、c，则其外接球半径r =_____________” .3．平面内的1条直线把平面分成两部分，2条相交直线把平面分成4部分，3条相交但不共点的直线把平面分成7部分，则15条彼此相交而无3条直线共点的直线把平面分成▲部分．4．用数学归纳法证明:(31)(1)(2)()2n nn n n n+++++++=*()n N∈的第二步中,当1n k =+时等式左边与n k =时的等式左边的差等于 ▲ .5．观察下列一组等式根据下面的规律写出第13行等式 。

6．半径为r 的圆的面积()2S r r π=，周长()2C r r π=，若将r 看作()0,+∞上的变量，则()22rr ππ'=，① ①式可用语言叙述为：圆的面积函数的导数等于圆的周长函数。

对于半径为R 的球，若将R 看作()0,+∞上的变量，请你写出类似于①的式子: (注：球体积公式为343V R R π=为球体半径)7．有下列各式：11111131111 ,1 1 ,1... ,1 (222323722315)>++>++++>++++>，……则按此规律可猜想此类不等式的一般形式为： ．8．设等边ABC ∆的边长为a ,P 是ABC ∆内任意一点,且P 到三边AB 、BC 、CA 的距离分别为1d 、2d 、3d ,则有321d d d ++为定值a 23;由以上平面图形的特性类比到空间图形:设正四面体ABCD 的棱长为a ,P 是正四面体ABCD 内任意一点,且P 到平面ABC 、平面ABD 、平面ACD 、平面BCD 的距离分别为1h 、2h 、3h 、h 4，则有321h h h +++h 4为定值______▲______.9．观察x x 2)(2='，344)(x x ='，x x sin )(cos -='，由归纳推理可得：若定义在R 上的函数)(x f 满足)()(x f x f =-，记()g x 为)(x f 的导函数，则)(x g -与()g x 的关系是 ▲ ．1=1 3+5=87+9+11=2713+15+17+19=64 21+23+25+27+29=12510．若ABC 的三边长分别为a, b, c ，其内切圆半径为r ，则S △ABC =12 （a+b+c ）·r ，类比这一结论到空间，写出三棱锥中的一个正确结论为11．用反证法证明命题“),(*∈⋅Z b a b a 是偶数，那么a ，b 中至少有一个是偶数．”那么 反设的内容是 ；12．设等差数列{}n a 的前n 项和为n S ，则4S ，84S S -，128S S -，1612S S -成等差数列．类比以上结论有：设等比数列{}n b 的前n 项积为n T ，则4T ， ， ，1612T T 成等比数列．13．随着科学技术的不断发展，人类通过计算机已找到了630万位的最大质数。

2019年高中数学单元测试试题 推理与证明专题（含答案）学校：__________考号：__________一、填空题1．将全体正整数排成一个三角形数阵：按照以上排列的规律，第n 行()4n ≥从左向右的第4个数为 ▲ ．2．在计算“1223(1)n n ⨯+⨯+⋅⋅⋅++”时，某同学学到了如下一种方法：先改写第k 项：1(1)[(1)(2)(1)(1)],3k k k k k k k k +=++--+由此得 112(123012),3⨯=⨯⨯-⨯⨯ 123(234123),3⨯=⨯⨯-⨯⨯ …1(1)[(1)(2)(1)(1)].3n n n n n n n n +=++--+ 相加，得11223(1)(1)(2).3n n n n n ⨯+⨯+⋅⋅⋅++=++ 类比上述方法，请你计算“123234(1)(2)n n n ⨯⨯+⨯⨯+⋅⋅⋅+++”，其结果为 ▲ .3．已知P 为抛物线x y 42=的焦点,过P 的直线l 与抛物线交与A,B 两点，若Q 在直线l 上,1 2 3 4 5 6 7 8 9 10 11 12 13 14 15且满足||||||||AP QB AQ PB =，则点Q 总在定直线1x =-上．试猜测如果P 为椭圆221259x y +=的左焦点，过P 的直线l 与椭圆交与A,B 两点，若Q 在直线l 上,且满足||||||||AP QB AQ PB =，则点Q 总在定直线 上．4．若从点O 所作的两条射线OM 、ON 上分别有点1M 、2M 与点1N 、2N ，则三角形面积之比为：21212211ON ON OM OM S S N OM N OM ⋅=∆∆. 若从点O 所作的不在同一个平面内的三条射线OP 、OQ 和OR 上分别有点1P 、2P 与点1Q 、2Q 和1R 、2R ，则类似的结论为：__5．用数学归纳法证明等式：aa a a a n n --=++++++111212 （1≠a ，*N n ∈），验证1=n 时，等式左边= .6．设M 1(0，0)，M 2(1，0)，以M 1为圆心，| M 1 M 2 | 为半径作圆交x 轴于点M 3 (不同于M 2)，记作⊙M 1；以M 2为圆心，| M 2 M 3 | 为半径作圆交x 轴于点M 4 (不同于M 3)，记作⊙M 2；……；以M n 为圆心，| M n M n +1 | 为半径作圆交x 轴于点M n +2 (不同于M n +1)，记作⊙M n ；…… 当n ∈N*时，过原点作倾斜角为30°的直线与⊙M n 交于A n ，B n ．考察下列论断：当n ＝1时，| A 1B 1 |＝2；当n ＝2时，| A 2B 2 |当n ＝3时，| A 3B 3 |3当n ＝4时，| A 4B 4 |3…… 由以上论断推测一个一般的结论：对于n ∈N*，| A n B n |＝ ▲7．三段论：“①船准时启航就能准时到达目的港，②这艘船准时到达了目的港，③这艘船是准时启航的”中，“小前提”是 ．8．半径为r 的圆的面积2()S r r π=，周长()2C r r π=，若将r 看作(0,)+∞上的变量，则2()'2r r ππ=，即圆的面积关于半径的函数的导数等于圆的周长关于半径的函数。

2019年高中数学单元测试试题 推理与证明专题（含答案）学校：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．已知()f x 是定义域为正整数集的函数，对于定义域内任意的k ，若 ()2f k k ≥成立，则()()211f k k +≥+成立，下列命题成立的是A ．若()39f ≥成立，则对于任意1k ≥，均有()2f k k ≥成立；B ．若()416f ≥成立，则对于任意的4k ≥，均有()2f k k <成立； C ．若()749f ≥成立，则对于任意的7k <，均有()2f k k <成立； D ．若()425f =成立，则对于任意的4k ≥，均有()2f k k ≥成立。

（2007上海文理15）2．有这样一段演绎推理是这样的“有些有理数是真分数，整数是有理数，则整数是真分数”结论显然是错误的，是因为A.大前提错误B.小前提错误C.推理形式错误D.非以上错误3． [文科]若n n n a n 212111+⋅⋅⋅++++=（n 是正整数），则+=+n n a a 1（ ）. (A))1(21+n (B)11221+-+n n (C) 11221121+-+++n n n (D) 221121+++n n第16题[理科] 观察下列式子： ,474131211,3531211,23211222222<+++<++<+，可以猜想结论为( ) . (A)2221112n 1123n n ++++⋅⋅⋅+< (n N*)∈ (B) 2221112n 1123(n 1)n -+++⋅⋅⋅+<+(n N*)∈ (C) 2221112n 1123(n 1)n 1++++⋅⋅⋅+<++(n N*)∈ (D) 2221112n 1123n n 1++++⋅⋅⋅+<+(n N*)∈第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题4． 如图所示：有三根针和套在一根针上的n 个金属片，按下列规则，把金属片从一根针上全部移到另一根针上．（1）每次只能移动一个金属片；（2）在每次移动过程中，每根针上较大的金属片不能放在较小的金属片上面．将n 个金属片从1号针移到3号针最少需要移动的次数记为()f n ； 则：（1）(3)f = (2) ()f n = .5． 平面内的1条直线把平面分成两部分，2条相交直线把平面分成4部分，3条相交但不共点的直线把平面分成7部分，则15条彼此相交而无3条直线共点的直线把平面分成 ▲ 部分．6．用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设是 ▲7．在直角三角形ABC 中，∠C 为直角，两直角边长分别为a ，b ，求其外接圆半径时，可采取如下方法：将三角形ABC 补成以其两直角边为邻边的矩形，则矩形的对角线为三角形外接圆的直径，可得三角形外接圆半径为；按此方法，在三棱锥S ﹣ABC 中，三条侧棱两两互相垂直，且长度分别为a ，b ，c ，通过类比可得三棱锥S ﹣ABC 外接球的半径为．（3分）8．观察下列等式：1＝12，2＋3＋4＝32，3＋4＋5＋6＋7＝52，4＋5＋6＋7＋8＋9＋10＝72，…从中可归纳得出第n 个等式是 ．9．在平面几何里，可以得出正确结论：“正三角形的内切圆半径等于这正三角形的高的13”.拓展到空间，类比平面几何的上述结论，则正四面体的内切球半径等于这个正四面体的高的 .10．观察下列等式：11,358,791127,1315171964,2123252729125,=+=++=+++=++++= 由此猜测第n 个等式为 ▲ ．11．已知x x x f cos sin )(1+=,且21()()f x f x '=,32()()f x f x '=,…,1()()n n f x f x -'=,… *(,2)n n ∈N ≥,则122012()()()444f f f πππ+++= ▲ ． 12．对大于或等于2的自然数m 的3次方幂有如下分解方式：23=3+5,最小数是3, 33=7+9+11,最小数是7, 43=13+15+17+19,最小数是13。

2019年高中数学单元测试试题推理与证明专题（含答案）学校：__________第I卷（选择题）请点击修改第I卷的文字说明一、选择题1．观察下列事实|x|+|y|=1的不同整数解(x,y)的个数为 4 , |x|+|y|=2的不同整数解(x,y)的个数为8, |x|+|y|=3的不同整数解(x,y)的个数为12 .则|x|+|y|=20的不同整数解(x,y)的个数为（）A．76 B．80 C．86 D．92（2012江西文）2．如图，第n个图形是由正n+2边形“扩展”而来，(n=1、2、3、…)则在第n个图形中共有（）个顶点. （）A．(n+1)(n+2) B． (n+2)(n+3) C．2n D．n3．把下面在平面内成立的结论类比地推广到空间，结论还正确的是-----------------------------------（）(A) 如果一条直线与两条平行线中的一条相交，则比与另一条相交．(B) 如果一条直线与两条平行线中的一条垂直，则比与另一条垂直．(C) 如果两条直线同时与第三条直线相交，则这两条直线相交．(D) 如果两条直线同时与第三条直线垂直，则这两条直线平行．第II 卷（非选择题）请点击修改第II 卷的文字说明 二、填空题4．下列不等式：121⋅≥2111⋅，⎪⎭⎫ ⎝⎛+⋅31131≥⎪⎭⎫⎝⎛+⋅412121 ，⎪⎭⎫ ⎝⎛++⋅5131141≥⎪⎭⎫⎝⎛++⋅61412131，…，由此猜测第1+n 个不等式为 ▲ （*n N ∈） 5．随着科学技术的不断发展，人类通过计算机已找到了630万位的最大质数。

陈成在学习中发现由41，43，47，53，61，71，83，97组成的数列中每一个数都是质数，他根据这列数的一个通项公式，得出了数列的后几项，发现它们也是质数。

于是他断言：根据这个通项公式写出的数均为质数。

请你写出这个通项公式 ，从这个通项公式举出一个反例，说明陈成的说法是错误的： 。

2019年高中数学单元测试试题 推理与证明专题（含答案）学校：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．下列推理正确的是----------------------------------------------------------（ ）(A) 把()a b c + 与 log ()a x y + 类比，则有：log ()log log a a a x y x y +=+ ．(B) 把()a b c + 与 sin()x y + 类比，则有：sin()sin sin x y x y +=+．(C) 把()n ab 与 ()n a b + 类比，则有：n n n()x y x y +=+． (D) 把()a b c ++ 与 ()xy z 类比，则有：()()xy z x yz =．第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题2．已知 ,8173cos 72cos 7cos ,4152cos 5cos ,213cos ===ππππππ，根据这些结果，猜想出的一般结论是 ．3．在ABC ∆中，若,,AB AC AC b BC a ⊥==，则ABC ∆的外接圆半径r =，将此结论拓展到空间，可得出的正确结论是：在四面体S ABC -中，若SA SB SC 、、两两垂直，,,SA a SB b SC c ===，则四面体S ABC -的外接球半径R =____________．4． 对大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”:3325⎧⎨⎩ 373911⎧⎪⎨⎪⎩ 3131541719⎧⎪⎪⎨⎪⎪⎩ ….仿此,若3m 的“分裂数”中有一个是59,则m 的值为 .5．在小时候，我们就用手指练习过数数. 一个小朋友按如图所示的规则练习数数，数到2008时对应的指头是 ▲ .(填出指头的名称，各指头的名称依次为大拇指、食指、中指、无名指、小指).6．在等差数列{a n }中，若a 10＝0，则有等式a 1＋a 2＋……＋a n ＝a 1＋a 2＋……＋a 19－n (n ＜19，n ∈N)成立，类比上述性质，相应地，在等比数列{b n }中，若b 9＝1，则有等式___________________________________成立.7．用数学归纳法证明不等式11119123310n n n n +++⋅⋅⋅+>+++(,1)n N n *∈>且时，第一步:不等式的左边是 .8．已知下列结论：① 1x 、2x 都是正数⇔⎩⎨⎧>>+002121x x x x ，第16题② 1x 、2x 、3x 都是正数⇔⎪⎩⎪⎨⎧>>++>++000321133221321x x x x x x x x x x x x ，则由①②猜想：1x 、2x 、3x 、4x 都是正数⇔9．在平面几何中,有射影定理：“在ABC ∆中,AC AB ⊥，点A 在BC 边上的射影为D ，有BC BD AB ⋅=2.”类比平面几何定理，研究三棱锥的侧面面积与射影面积、底面面积的关系，可以得出的正确结论是：“在三棱锥BCD A -中,⊥AD 平面ABC ，点A 在底面BCD 上的射影为O ，则有 .”10． 如图所示：有三根针和套在一根针上的n 个金属片，按下列规则，把金属片从一根针上全部移到另一根针上．（1）每次只能移动一个金属片；（2）在每次移动过程中，每根针上较大的金属片不能放在较小的金属片上面．将n 个金属片从1号针移到3号针最少需要移动的次数记为()f n ； 则：（1）(3)f = (2) ()f n = .04321>+++x x x x0434232413121>+++++x x x x x x x x x x x x12340.x x x x >▲C BD AADC B O11．如图3都是由边长为1的正方体叠成的图形图3例如第（1）个图形的表面积为6个平方单位，第（2）个图形的表面积为18个平方单位，第（3）个图形的表面积是36个平方单位．依此规律，则第n 个图形的表面积是__________个平方单位．12．观察下列等式：1＝12，2＋3＋4＝32，3＋4＋5＋6＋7＝52，4＋5＋6＋7＋8＋9＋10＝72，…从中可归纳得出第n 个等式是 ．13．用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设是 ▲14．用反证法证明命题“若210x -=，则1x =-或1x =”时，假设命题的结论不成立的正确叙述是“ ▲ ”.15．用数学归纳法证明“(1)(2)()213(21)n n n n n n ++⋅⋅⋅+=⋅⋅⋅⋅⋅⋅⋅-”，从“k 到k +1”左端需增乘的代数式为 2（2k +1） .16．用数学归纳法证明: (31)(1)(2)()2n n n n n n +++++++=*()n N ∈的第二步中,当1n k =+时等式左边与n k =时的等式左边的差等于 ▲ .17．用数学归纳法证明等式：aa a a a n n --=++++++111212 （1≠a ，*N n ∈），验证1=n 时，等式左边= .三、解答题18．>本题满分14分）19．已知数列{a n }满足a 1=1，且4a n+1﹣a n a n+1+2a n =9（n ∈N *）．（1）求a 2，a 3，a 4的值，并猜想{a n }的通项公式；（2）用数学归纳法证明你的猜想．（10分）20．已知)(131211)(+∈+⋅⋅⋅+++=N n nn f ． 经计算得()232=f ，()244>f ，()258>f ，()2616>f ，()2732>f ，通过观察，我们可以得到一个一般性的结论．（1）试写出这个一般性的结论；（2）请用数学归纳法证明这个一般性的结论；（3）对任一给定的正整数a ，试问是否存在正整数m ，使得111123a m+++⋅⋅⋅+>？ 若存在，请给出符合条件的正整数m 的一个值；若不存在，请说明理由．（本小题共16分）21． 已知2012(1)(1)(1)(1),(*).n n n x a a x a x a x n N +=+-+-++-∈(1) 求0a 及1n n ii S a ==∑； (2) 试比较n S 与2(2)22n n n -+的大小，并说明理由.22．已知数列{n a }满足：112a =，*12 ()1n n n a a n a +=∈+N ． （1）求2a ，3a 的值；（2）证明：不等式10n n a a +<<对于任意*n ∈N 都成立．（本小题满分10分）23．已知数列{n a }和{n b }满足：对于任何*N ∈n ，有n n n b b a -=+1，λλλ()1(12n n n b b b -+=++为非零常数），且2121==b b ，．（1）求数列{n a }和{n b }的通项公式；（2）若3b 是6b 与9b 的等差中项，试求λ的值，并研究：对任意的*N ∈n ，n b 是否一定能是数列{n b }中某两项（不同于n b ）的等差中项，并证明你的结论．（满分20分）本题有2小题，第1小题12分，第2小题8分．24．用数学归纳法证明不等式：211111(1)12n N n n n n n*++++>∈>++且．25．在△ABC 中，C B C B A cos cos sin sin sin ++=，判断△ABC 的形状.26．设0 < a , b , c < 1，求证：(1 - a )b , (1 - b )c , (1 - c )a ,不可能同时大于4127．已知数列{}n a 满足11a =，*1112,)n nn a a n n N a --=+≥∈（.求证：1na <-28．在数列{a n }中，若a 1＝1，a n ＋1＝nn a a 21 ， (1)写出数列{a n }的前5项；(2)猜想出数列的一个通项公式．29．已知函数()2ln ,(1)0.b f x ax x f x =--= 若函数()f x 的图象在1=x 处的切线的斜率为0，且11()11n n n a f na a +'=-++，若13,:2n a a n +≥求证≥30．用数学归纳法证明：l 3+23+33+…+n 3=14n 2(n +1)2(n ∈N ﹡)．。

2019年高中数学单元测试试题 推理与证明专题（含答案）学校：__________第I 卷（选择题）请点击修改第I 卷的文字说明 一、选择题1．观察下列事实|x|+|y|=1的不同整数解(x,y)的个数为 4 , |x|+|y|=2的不同整数解(x,y)的个数为8, |x|+|y|=3的不同整数解(x,y)的个数为12 .则|x|+|y|=20的不同整数解(x,y)的个数为 （ ）A ．76B ．80C ．86D ．92（2012江西文）2．在十进制中01232004410010010210=⨯+⨯+⨯+⨯，那么在5进制中数码2004折合成十进制为 A.29 B. 254 C. 602 D. 20043．类比平面内正三角形的“三边相等，三内角相等”的性质，可推知正四体的下列的一些性质，①各棱长相等，同一顶点上的两条棱的夹角相等；②各个面都是全等的正三角形， 相邻两个面所成的二面角相等；③各个面都是全等的正三角形，同一顶点上的任何两条棱的夹角相等．你认为比较恰当的是 ．第II 卷（非选择题）请点击修改第II 卷的文字说明 二、填空题4．已知x x x f cos sin )(1+=,且21()()f x f x '=,32()()f x f x '=,…,1()()n n f x f x -'=,…*(,2)n n ∈N ≥,则122012()()()444f f f πππ+++= ▲ ．5．====试推测___,___a b ==6． 对大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”:3325⎧⎨⎩ 373911⎧⎪⎨⎪⎩ 3131541719⎧⎪⎪⎨⎪⎪⎩ …. 仿此,若3m 的“分裂数”中有一个是59,则m 的值为 .7．观察下列算式，猜测由此表提供的一般法则，用适当的数学式子表示它。

则这个式子为 。

8．在平面几何里，有勾股定理：“设ABC ∆的两边AB 、AC 互相垂直，则222BC AC AB =+。