2020学年九年级数学下册第三章圆3.9弧长及扇形的面积同步练习新版北师大版1

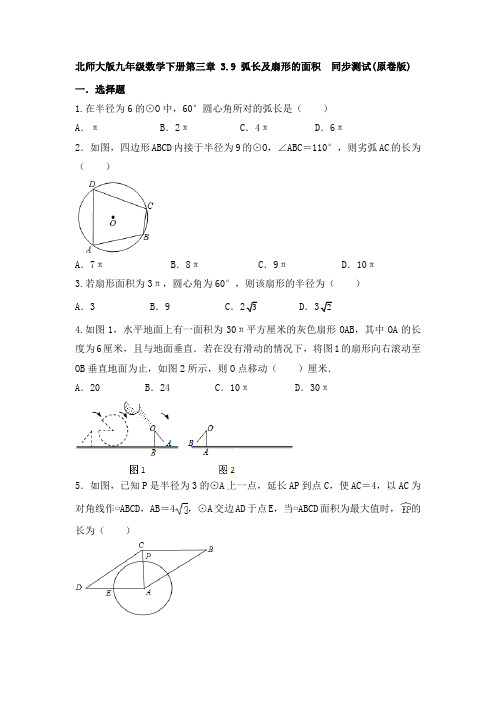
北师大版九年级数学下册第三章 3.9 弧长及扇形的面积同步测试(原卷版) 一．选择题1.在半径为6的⊙O中，60°圆心角所对的弧长是（）A．π B．2π C．4π D．6π2．如图，四边形ABCD内接于半径为9的⊙O，∠ABC＝110°，则劣弧AC的长为（）A．7πB．8πC．9πD．10π3.若扇形面积为3π，圆心角为60°，则该扇形的半径为（）A．3 B．9 C．．4.如图1，水平地面上有一面积为30π平方厘米的灰色扇形OAB，其中OA的长度为6厘米，且与地面垂直．若在没有滑动的情况下，将图1的扇形向右滚动至OB垂直地面为止，如图2所示，则O点移动（）厘米．A．20 B．24 C．10π D．30π5．如图，已知P是半径为3的⊙A上一点，延长AP到点C，使AC＝4，以AC为对角线作▱ABCD，AB＝4，⊙A交边AD于点E，当▱ABCD面积为最大值时，的长为（）A．πB．πC．πD．3π6．如图，将矩形ABCD绕点A逆时针旋转90°至矩形AEFG，点D的旋转路径为，若AB＝2，BC＝4，则阴影部分的面积为（）A．B．C．D．7.如图，△ABC是等边三角形，AC=6，以点A为圆心，AB长为半径画弧DE，若∠1=∠2，则弧DE的长为（）A．1π B．1.5π C．2π D．3π8．如图，5×3的网格图中，每个小正方形的边长均为1，设经过图中格点A，C，B三点的圆弧与AE交于H，则弧AH的弧长为（）A．πB．πC．πD．π9.如图，四边形OCBA是菱形，点A、B在以点O为圆心的圆弧DE上，若AO=3，∠COE=∠DOA，则扇形ODE的面积为（）A．23π B．2π C．2.5 π D．3π10．如图，矩形ABCD中，对角线AC、BD交于O，以B为圆心、BC长为半径画弧，交AB于点F，若点O恰好在圆弧上，且AB＝6，则阴影部分的面积为（）A．18﹣6πB．54﹣18πC．36﹣6πD．27﹣9π11．如图一个扇形纸片的圆心角为90°，半径为4，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，则图中阴影部分的面积为（）A．﹣4B．4﹣C．﹣8D．9﹣3π12．如图，在Rt△ABC中，∠C＝90°，AB＝6，AD是∠BAC的平分线，经过A，D两点的圆的圆心O恰好落在AB上，⊙O分别与AB、AC相交于点E、F．若圆半径为2．则阴影部分面积（）A．B．C．D．二．填空题13．一个扇形的半径为6，弧长为3π，则此扇形的圆心角为度．14．一个扇形的圆心角为60°，半径为3，则此扇形的弧长是．15.如图，正六边形ABCDEF内接于⊙O，⊙O的半径为1，则AB的长为16．如图，AB是半圆O的直径，AC＝，∠BAC＝30°，则的长为．17．如图，平行四边形ABCD中，∠A＝60°，CD＝4，以点A为圆心，AB的长为半径画弧交AD边于点E，以点B为圆心，BE的长为半径画弧交BC边于点F，则阴影部分的面积为．18．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，∠BCD＝30°，CD＝2，＝．则阴影部分面积S阴影19．如图，已知⊙O的半径是3，点A、B、C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为．20．如图，在扇形AOB中，∠AOB＝120°，半径OC交弦AB于点D，且OC⊥AO，若OA＝6，则阴影部分的面积为．三.解答题21.如图，一只狗用皮带系在10×10的正方形狗窝的一角上，皮带长为14，在狗窝外面狗能活动的范围面积是多少？22．如图，A、B、C三点在半径为1的⊙O上，四边形ABCO是菱形，求的长．23.如图，四边形ABCD内接于⊙O，BC是直径，∠BAD=120°，AB=AD．（1）求证：四边形ABCD是等腰梯形；（2）已知AC=6，求阴影部分的面积．24．如图，四边形ABCD是正方形，以边AB为直径作⊙O，点E在BC边上，连结AE交⊙O于点F，连结BF并延长交CD于点G．（1）求证：△ABE≌△BCG；（2）若∠AEB＝55°，OA＝3，求劣弧的长．（结果保留π）25．如图，已知Rt△ABC中，∠A＝90°，将斜边BC绕点B顺时针方向旋转至BD，使BD∥AC，过点D作DE⊥BC于点E．（1）求证：△ABC≌△EDB；（2）若CD＝BD，AC＝3，求在上述旋转过程中，线段BC扫过的面积．26．如图1，已知四边形ABCD内接于⊙O，AC为⊙O的直径，AD＝DB，AC与BD 交于点E，且AE＝BC．（1）求证：AB＝CB；（2）如图2，△ABC绕点C逆时针旋转35°得到△FGC，点A经过的路径为弧AF，若AC＝4，求图中阴影部分的面积．北师大版九年级数学下册第三章 3.9 弧长及扇形的面积 同步测试(解析版)一．选择题1.在半径为6的⊙O 中，60°圆心角所对的弧长是（ ）A ．πB ．2πC ．4πD ．6π 606180180n rl ππ=2π． 2．如图，四边形ABCD 内接于半径为9的⊙O ，∠ABC ＝110°，则劣弧AC 的长为（ ）A ．7πB ．8πC ．9πD ．10π解：连接OA 、OC ，∵四边形ABCD 内接于⊙O ，∴∠D+∠ABC ＝180°，∵∠ABC＝110°，∴∠D＝70°，∴由圆周角定理得：∠AOC＝2∠D＝140°，∴劣弧AC的长为＝7π，故选：A．3.若扇形面积为3π，圆心角为60°，则该扇形的半径为（）A．3 B．9 C．．解：扇形的面积=260360r =3π．解得：．故选D．4.如图1，水平地面上有一面积为30π平方厘米的灰色扇形OAB，其中OA的长度为6厘米，且与地面垂直．若在没有滑动的情况下，将图1的扇形向右滚动至OB垂直地面为止，如图2所示，则O点移动（）厘米．A．20 B．24 C．10π D．30π解：点O移动的距离为扇形的弧长，根据面积公式求出弧长，即30π=12×l×6，解得l=10π．故选C．5．如图，已知P是半径为3的⊙A上一点，延长AP到点C，使AC＝4，以AC为对角线作▱ABCD，AB＝4，⊙A交边AD于点E，当▱ABCD面积为最大值时，的长为（）A．πB．πC．πD．3π解：如图，作CF⊥AB于F．∵四边形ABCD是平行四边形，∴S＝AB•CF，平行四边形ABCD∵AB是定值，∴CF定值最大时，平行四边形ABCD的面积最大，∵CF≤AC，∴当AC⊥AB时，平行四边形ABCD的面积最大，此时tan∠ACB＝＝，∴∠ACB＝60°，∵BC∥AD，∴∠DAC＝∠ACB＝60°，∴的长＝＝π，故选：B．6．如图，将矩形ABCD绕点A逆时针旋转90°至矩形AEFG，点D的旋转路径为，若AB＝2，BC＝4，则阴影部分的面积为（）A．B．C．D．解：如图，设与EF交于H，连接AH，∵四边形ABCD是矩形，AB＝2，BC＝4，∴AH＝AD＝BC＝4，∴∠AHE＝∠GAH＝30°，∵AE＝AB＝2，∴HE＝2，∴阴影部分的面积＝S扇形AHG +S△AHE＝+×2×2＝+2，故选：D．7.如图，△ABC是等边三角形，AC=6，以点A为圆心，AB长为半径画弧DE，若∠1=∠2，则弧DE的长为（）A．1π B．1.5π C．2π D．3π解：∵△ABC是等边三角形，AC=6，∴AB=AC=6，∠CAB=60°．∵∠1=∠2，62180ππ， 8．如图，5×3的网格图中，每个小正方形的边长均为1，设经过图中格点A ，C ，B 三点的圆弧与AE 交于H ，则弧AH 的弧长为（ ）A ．πB ．πC ．πD ．π 解：连接EB ，BH ，AB ，∵BE ＝AB ＝＝，AE ＝＝，∴BE 2+AB 2＝AE 2，∴∠ABE ＝90°，∴△ABE 是等腰直角三角形，∵∠ACB ＝90°，∴AB 是圆的直径， ∴∠AHB ＝90°， ∴BH ⊥AH ，∴∠ABH ＝∠BAH ＝45°，∴弧AH 所对的圆心角为90°，∴的长＝＝．故选：B ．9.如图，四边形OCBA 是菱形，点A 、B 在以点O 为圆心的圆弧DE 上，若AO=3，∠COE=∠DOA ，则扇形ODE 的面积为（ ）A ．23π B ．2π C ．2.5 π D ．3π9360=3π．10．如图，矩形ABCD 中，对角线AC 、BD 交于O ，以B 为圆心、BC 长为半径画弧，交AB 于点F ，若点O 恰好在圆弧上，且AB ＝6，则阴影部分的面积为（ ）A．18﹣6πB．54﹣18πC．36﹣6πD．27﹣9π解：∵四边形ABCD是矩形，∴AB＝CD＝6，∠DCB＝90°，AC＝BD，OC＝AC，OB＝BD，∴OB＝OC，∵BC＝OB，∴△OBC是等边三角形，∴∠CBO＝60°，BC＝BO，即AC＝2BC，在Rt△ABC中，由勾股定理得：AB2+BC2＝AC2，（6）2+BC2＝（2BC）2，解得：BC＝6，∴阴影部分的面积＝S△BCD ﹣S扇形BOC＝﹣＝18﹣6π，故选：A．11．如图一个扇形纸片的圆心角为90°，半径为4，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，则图中阴影部分的面积为（）A．﹣4B．4﹣C．﹣8D．9﹣3π解：由折叠可知，S弓形AD ＝S弓形OD，DA＝DO，∵OA＝OD，∴AD＝OD＝OA，∴△AOD为等边三角形，∴∠AOD＝60°，∠DOB＝30°，∵AD＝OD＝OA＝4，∴CD＝2，∴S弓形AD ＝S扇形ADO﹣S△ADO＝﹣＝，∴S弓形OD＝，阴影部分的面积＝S扇形BDO ﹣S弓形OD＝﹣（）＝4﹣，故选：B．12．如图，在Rt△ABC中，∠C＝90°，AB＝6，AD是∠BAC的平分线，经过A，D两点的圆的圆心O恰好落在AB上，⊙O分别与AB、AC相交于点E、F．若圆半径为2．则阴影部分面积（）A．B．C．D．解：连接OD，OF．∵AD是∠BAC的平分线，∴∠DAB＝∠DAC，∵OD＝OA，∴∠ODA＝∠OAD，∴∠ODA＝∠DAC，∴OD∥AC，∴∠ODB＝∠C＝90°，∴S△AFD ＝S△OFA，∴S阴＝S扇形OFA，∵OD＝OA＝2，AB＝6，∴OB＝4，∴OB＝2OD，∴∠B＝30°，∴∠A＝60°，∵OF＝OA，∴△AOF是等边三角形，∴∠AOF＝60°，∴S阴＝S扇形OFA＝＝．故选：C．二．填空题13．一个扇形的半径为6，弧长为3π，则此扇形的圆心角为90 度．解：设这个扇形的圆心角为n°，则＝3π，解得，n＝90，故答案为：90．14．一个扇形的圆心角为60°，半径为3，则此扇形的弧长是π．解：∵一个扇形的圆心角为60°，半径为3，∴此扇形的弧长是＝π，故答案为：π．15.如图，正六边形ABCDEF内接于⊙O，⊙O的半径为1，则AB的长为解：∵ABCDEF 为正六边形，∴∠AOB=360°÷ 6 =60°，AB 的长为601803ππ．故答案为：3π．16．如图，AB 是半圆O 的直径，AC ＝，∠BAC ＝30°，则的长为 ．解：如图，连接BC ．∵AB 是直径，∴∠ACB ＝90°，∵∠A ＝30°，∴∠B ＝60°，∵OC ＝OB ，∴△OBC 是等边三角形，∵BC ＝AC •tan ∠BAC ＝1，∴OC ＝OB ＝1，∠BOC ＝60°，∴的长＝＝，故答案为．17．如图，平行四边形ABCD中，∠A＝60°，CD＝4，以点A为圆心，AB的长为半径画弧交AD边于点E，以点B为圆心，BE的长为半径画弧交BC边于点F，则阴影部分的面积为4．解：如图连接BE，EF．∵四边形ABCD是平行四边形，∴AD∥BC，∴∠A+∠ABC＝180°，∵∠A＝60°，∴∠ABC＝120°，∵AE＝AB，∴△ABE是等边三角形，∴∠ABE＝∠EBF＝60°，∵BE＝BF，∴△EBF是等边三角形，∵S阴＝S△BEF＝×42＝4，故答案为4．18．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，∠BCD＝30°，CD＝2，则阴影部分面积S阴影＝．解：连接OC．∵AB⊥CD，∴＝，CE＝DE＝，∴∠COB＝∠BOD，∵∠BOD＝2∠BCD＝60°，∴∠COB＝60°，∵OC＝OB＝OD，∴△OBC，△OBD都是等边三角形，∴OC＝BC＝BD＝OD，∴四边形OCBD是菱形，∴OC∥BD，∴S△BDC ＝S△BOD，∴S阴＝S扇形OBD，∵OD＝＝2，∴S阴＝＝，故答案为．19．如图，已知⊙O的半径是3，点A、B、C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为3π﹣．解：连接OB和AC交于点D，∵圆的半径为3，∴OB＝OA＝OC＝3，又四边形OABC是菱形，∴OB⊥AC，OD＝OB＝，在Rt△COD中利用勾股定理可知：CD＝＝，∴AC＝2CD＝3，∵sin∠COD＝，∴∠COD＝60°，∠AOC＝2∠COD＝120°，∴S菱形ABCO＝×3×3＝，S扇形AOC＝＝3π，则图中阴影部分面积为S扇形AOC ﹣S菱形ABCO＝3π﹣，故答案为：3π﹣．20．如图，在扇形AOB中，∠AOB＝120°，半径OC交弦AB于点D，且OC⊥AO，若OA＝6，则阴影部分的面积为．解：∵∠AOB＝120°，OA＝OB，∴∠A＝∠OBA＝30°，∵OC⊥AO，∴∠AOD＝90°，∴∠BOD＝30°，∴DO＝DB，在Rt△AOD中，OD＝OA＝，OD＝AD，∴BD＝AD，∵S△AOD＝×6×＝6，∴S△BOD ＝S△AOD＝3，∴阴影部分的面积＝S△AOD +S扇形BOC﹣S△BOD＝6+﹣3＝3+3π．故答案为3+3π．三.解答题21.如图，一只狗用皮带系在10×10的正方形狗窝的一角上，皮带长为14，在狗窝外面狗能活动的范围面积是多少？解：狗能活动的范围面积=34π×142+12π×42=147π+8π=155π．答：在狗窝外面狗能活动的范围面积是155π．22．如图，A、B、C三点在半径为1的⊙O上，四边形ABCO是菱形，求的长．解：连接OB．∵四边形OABC是菱形，∴OA＝AB＝OB＝OC＝BC，∴△AOB，△BOC都是等边三角形，∴∠AOB＝∠BOC＝60°，∴∠AOC＝120°，∴的长＝＝23.如图，四边形ABCD内接于⊙O，BC是直径，∠BAD=120°，AB=AD．（1）求证：四边形ABCD是等腰梯形；（2）已知AC=6，求阴影部分的面积．解：（1）证明：∵∠BAD=120°，AB=AD，∴∠ABD=∠ADB=30°，∴弧AB和弧AD的度数都等于60°，又∵BC是直径，∴弧CD的度数也是60°，∴AB=CD且∠CAD=∠ACB=30°，∴BC∥AD，∴四边形ABCD 是等腰梯形；（2）解：∵BC 是直径，∴∠BAC=90°∵∠ACB=30°，AC=6，∴BC=30°cos AC =4√3 ，故R=2√3 ， ∵弧AB 和弧AD 的度数都等于60°，∴∠BOD=120°，连接OA 交BD 于点E ，则OA ⊥BD ，在Rt △BOE 中：OE=OBsin30°= √3 ，BE=OB •cos30°=3，BD=2BE=6，故S 阴影=S 扇形BOD -S △BOD =21202313602()×6=4π 24．如图，四边形ABCD 是正方形，以边AB 为直径作⊙O ，点E 在BC 边上，连结AE 交⊙O 于点F ，连结BF 并延长交CD 于点G ．（1）求证：△ABE ≌△BCG ；（2）若∠AEB ＝55°，OA ＝3，求劣弧的长．（结果保留π）（1）证明：∵四边形ABCD 是正方形，AB 为⊙O 的直径，∴∠ABE ＝∠BCG ＝∠AFB ＝90°，∴∠BAF+∠ABF ＝90°，∠ABF+∠EBF ＝90°， ∴∠EBF ＝∠BAF ，在△ABE与△BCG中，，∴△ABE≌△BCG（ASA）；（2）解：连接OF，∵∠ABE＝∠AFB＝90°，∠AEB＝55°，∴∠BAE＝90°﹣55°＝35°，∴∠BOF＝2∠BAE＝70°，∵OA＝3，∴的长＝＝．25．如图，已知Rt△ABC中，∠A＝90°，将斜边BC绕点B顺时针方向旋转至BD，使BD∥AC，过点D作DE⊥BC于点E．（1）求证：△ABC≌△EDB；（2）若CD＝BD，AC＝3，求在上述旋转过程中，线段BC扫过的面积．解：（1）∵DE⊥BC，∴∠DEB＝90°，∵AC∥BD，∴∠A＝∠ABD＝∠DEB＝90°，∵∠ABC+∠CBD＝90°，∴∠CBD+∠BDE＝90°，∴∠ABC＝∠BDE，∵BC＝BD，∴△ABC≌△EDB（AAS）．（2）∵CD＝BD＝BC，∴△BCD为等边三角形，∴∠CBD＝60°，∠ABC＝90°﹣∠CBD＝30°，∵AC＝3，∴BC＝2AC＝6，∴线段BC扫过的面积＝6π．26．如图1，已知四边形ABCD内接于⊙O，AC为⊙O的直径，AD＝DB，AC与BD 交于点E，且AE＝BC．（1）求证：AB＝CB；（2）如图2，△ABC绕点C逆时针旋转35°得到△FGC，点A经过的路径为弧AF，若AC＝4，求图中阴影部分的面积．（1）证明：∵AD＝BD，∠DAE＝∠DBC，AE＝BC，∴△ADE≌△BDC（SAS），∴∠ADE＝∠BDC，∴＝．∴AB＝BC．（2）解：S阴＝S扇形CAF+S△CFG﹣S△ABC＝S扇形CAF＝＝．。

3.9 弧长及扇形的面积同步测试一、选择题1.如图，半径为1cm 、圆心角为90°的扇形OAB 中，分别以OA 、OB 为直径作半圆，则图中阴影部分的面积为( )A.πcm2B.32πcm2C.21cm2D.32cm22.一圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是（ ）A.．5π B ．4π C ．3π D ．2π3.如图，在△ABC 中，∠A=90°，AB=AC=2，以BC 的中点O 为圆心的圆弧分别与AB 、AC 相切于点D 、E ，则图中阴影部分的面积是（ ）A. B. C. D.4.如图，小方格都是边长为1的正方形，则以格点为圆心，半径为1和2的两种弧围成的“叶状”阴影图案的面积为( )A ．4π－2B ．2π－2C ．4π－4D ．2π－45.如图，直径AB 为6的半圆，绕A 点逆时针旋转60°，此时 点B 到了点B ’，则图中阴影部分的面积是（ ）A. B. C. D.6.如图，已知一块圆心角为270°的扇形铁皮，用它做一个圆锥形的烟囱帽(接缝忽略不计)，圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是（）A．40cm B．50cm C．60cm D．80cm7.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2．将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，点B，A，C′在同一条直线上，则线段BC扫过的区域面积为（）A. B. C. D.8.如图，Rt△ABC中，∠ACB=90°∠A=30°,BC=2,O、H分别为AB、AC的中点，将△ABC顺时针旋转120°到△A1BC1的位置，则整个旋转过程中线段OH所扫过的面积为（）A. B．C. D.9.如图所示，扇形AOB的圆心角120°，半径为2，则图中阴影部分的面积为（）A. B. C. D.10.如图,在Rt △ABC 中,∠ABC ＝90°,AB ＝＝2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D,则图中阴影部分的面积为( )2π 2π C.π- D.2π-二、填空题11.已知扇形的圆心角为60°，半径为1，则扇形的弧长为 ．12．一个扇形的半径为8cm ，弧长为 cm ，则扇形的圆心角为 ．13.如图，四边形ABCD 是⊙O 的内接四边形，⊙O 的半径为4，∠B=135°，则弧AC 的长为_________.14.)如图,在边长为4的正方形ABCD 中,以点B 为圆心,AB 为半径画弧,交对角线BD与点E,则图中阴影部分的面积是 (结果保留π)15.如图，在边长为4的正方形ABCD 中，先以点A 为圆心，AD 的长为半径画弧，再以AB 边的中点为圆心，AB 长的一半为半径画弧，则阴影部分面积是________(结果保留π)．16.如图，在△ABC 中，CA ＝CB ，∠ACB ＝90°，AB ＝2，点D 为AB 的中点，以点D 为圆心作圆心角为90°的扇形DEF ，点C 恰在弧EF 上，则图中阴影部分的面积为________．三、综合题17.如图，⊙O的半径为6cm，直线AB是⊙O的切线，切点为点B，弦BC∥AO.若∠A ＝30°，求劣弧BC的长。

北师大版九年级数学下册同步练习：3.9弧长及扇形的面积编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（北师大版九年级数学下册同步练习：3.9弧长及扇形的面积）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为北师大版九年级数学下册同步练习：3.9弧长及扇形的面积的全部内容。

3.9弧长及扇形的面积一、选择题1．在半径为12 cm 的圆中，150°的圆心角所对的弧长等于 （ )A ．34πcmB ．12πcmC ．10πcmD ．5π cm2．一个扇形的弧长为20π cm ，面积为240πcm 2，则这个扇形的圆心角是 ( ）A ．120°B ．150°C ．210°D ．240°3． (2014•辽宁本溪，第7题3分）底面半径为4，高为3的圆锥的侧面积是( ）A ． 12πB ． 15πC ． 20πD ．36π 4．（2014•内蒙古包头，第9题3分）如图，在正方形ABCD 中，对角线BD 的长为．若将BD 绕点B 旋转后，点D 落在BC 延长线上的点D′处，点D 经过的路径为，则图中阴影部分的面积是（ ）A ﹣1B ﹣2C ﹣1D π﹣25．如图3－147所示，图中有五个半圆,邻近的两半圆相切，两只小虫同时出发，以相同的速度爬行，甲虫沿，，,的路线爬行,乙虫沿的路线爬行，则下列结论正确的是 （ ）A ．甲虫先到B 点 B ．乙虫先到B 点C ．甲、乙两虫同时到B 点D ．无法确定6。

（2014•甘肃天水，第10题4分）如图，是某公园的一角，∠AOB=90°，的半径OA 长是6米,点C 是OA 的中点，点D 在上，CD∥OB，则图中草坪区（阴影1ADA 12A EA 23A FA 3A GB ACB部分）的面积是（）A ．（3π+）米B．（π+）米C．（3π+9）米D．（π﹣9）米二、填空题7．如图3－148所示,四边形OABC为菱形，点B，C在以点O为圆心的上．若OA＝3,∠OCB＝60°,∠1＝∠2，则扇形OEF的面积为．8．如图3－149所示，⊙A，⊙B,⊙C，⊙D，⊙E相互外离，它们的半径都为1，顺次连接五个圆心得到五边形ABCDE，则图中五个阴影部分的面积之和是． 9．一个扇形的圆心角为30°，半径为12 cm，则这个扇形的面积为．10．若一扇形的弧长是12π，圆心角是120°，则这个扇形的半径是．11．如图3－150所示，AB是半圆O的直径,以O为圆心,OE为半径的半圆交AB 于E，F两点,弦AC切小半圆于点D．已知AO＝4，EO＝2，那么阴影部分的面积是．E F。

课时作业(二十九)[第三章 9 弧长及扇形的面积]一、选择题1．2017·武汉期末如图K －29－1，等边三角形ABC 的边长为4，D ，E ，F 分别为边AB ，BC ，AC 的中点，分别以A ，B ，C 三点为圆心，以AD 长为半径作三条圆弧，则图中三条圆弧的弧长之和是( )图K －29－1A ．πB ．2πC ．4πD ．6π 2.2018·福州二模如图K －29－2，AD 是半圆O 的直径，AD ＝12，B ，C 是半圆O 上两点．若AB ︵＝BC ︵＝CD ︵，则图中阴影部分的面积是( )链接听课例3归纳总结图K －29－2A ．6πB ．12πC ．18πD ．24π 二、填空题3．2017·长春如图K －29－3，在△ABC 中，∠BAC ＝100°，AB ＝AC ＝4，以点B 为圆心，AB 长为半径作圆弧，交BC 于点D ，则AD ︵的长为________．(结果保留π)链接听课例2归纳总结图K －29－34．如图K －29－4，在边长为4的正方形ABCD 中，先以点A 为圆心，AD 长为半径画弧，再以AB 边的中点为圆心，AB 长的一半为半径画弧，则两弧之间的阴影部分的面积是________．(结果保留π)链接听课例4归纳总结图K －29－45．如图K －29－5，△ABC 是正三角形，曲线CDEF 叫正三角形的渐开线，其中CD ︵，DE ︵，EF ︵的圆心依次是A ，B ，C ，如果AB ＝1，那么曲线CDEF 的长是________．图K －29－56．如图K －29－6，在Rt △ABC 中，∠ACB ＝90°，AC ＝2 3，以点C 为圆心，CB 长为半径画弧，与AB 边交于点D ，将BD ︵绕点D 旋转180°后点B 与点A 恰好重合，则图中阴影部分的面积为________．图K －29－6三、解答题7．如图K －29－7，在扇形OAB 中，∠AOB ＝90°，半径OA ＝6.将扇形OAB 沿过点B 的直线折叠，点O 恰好落在扇形上的点D 处，折痕交OA 于点C ，求整个阴影部分的周长和面积．图K －29－78．2018·椒江区模拟如图K －29－8，AB 是⊙O 的直径，C 是圆上一点，连接CA ，CB ，过点O 作弦BC 的垂线，交BC ︵于点D ，连接AD .(1)求证：∠CAD ＝∠BAD ；(2)若⊙O 的半径为1，∠B ＝50°，求AC ︵的长．图K －29－89．2017·如东县一模如图K －29－9，在△ABC 中，∠ACB ＝130°，∠BAC ＝20°，BC ＝4，以点C 为圆心，BC 长为半径的圆交AB 于点D ，交AC 于点E .(1)求BD 的长；(2)求阴影部分的面积．图K －29－910．2017·贵阳如图K－29－10，C，D是半圆O上的三等分点，直径AB＝4，连接AD，AC，DE⊥AB，垂足为E，DE交AC于点F.(1)求∠AFE的度数；(3)求阴影部分的面积(结果保留π和根号).链接听课例4归纳总结图K－29－1011．如图K－29－11，把Rt△ABC的斜边AB放在直线l上，按顺时针方向将△ABC在l 上转动两次，使它转到△A″B″C″的位置，设BC＝1，AC＝3，则顶点A运动到点A″的位置时，(1)求点A所经过的路线长；(2)点A所经过的路线与l围成的图形的面积是多少？图K－29－11研究型在学习扇形的面积公式时，同学们推得S 扇形＝n πR 2360，并通过比较扇形面积公式与弧长公式l ＝n πR180，得出扇形面积的另一种计算方法S 扇形＝12lR .接着老师让同学们解决两个问题：问题 Ⅰ：求弧长为4π，圆心角为120°的扇形面积． 问题Ⅱ：某小区设计的花坛形状如图K －29－12中的阴影部分，已知弧AB 和弧CD 所在圆的圆心都是点O ，弧AB 的长为l 1，弧CD 的长为l 2，AC ＝BD ＝d ，求花坛的面积．(1)请你解答问题Ⅰ.(2)在解完问题 Ⅱ 后的全班交流中，有名同学发现扇形面积公式S扇形＝12lR 类似于三角形面积公式；类比梯形面积公式，他猜想花坛的面积S ＝12(l 1＋l 2)d .他的猜想正确吗？如果正确，写出推导过程；如果不正确，请说明理由．图K －29－12详解详析【课时作业】 [课堂达标]1．[解析] B 依题意知：图中三条圆弧的弧长之和＝60π×12×4180×3＝2π.故选B.2．[解析] A ∵AB ︵＝BC ︵＝CD ︵， ∴∠AOB ＝∠BOC ＝∠COD ＝60°，∴阴影部分的面积＝60π×62360＝6π.故选A.3．[答案] 8π9[解析] ∵在△ABC 中，∠BAC ＝100°，AB ＝AC ， ∴∠B ＝∠C ＝12(180°－100°)＝40°.∵AB ＝4，∴AD ︵的长为40π×4180＝8π9.4．[答案] 2π5．[答案] 4π[解析] CD ︵的长是120π×1180＝2π3，DE ︵的长是120π×2180＝4π3，EF ︵的长是120π×3180＝2π， 则曲线CDEF 的长是2π3＋4π3＋2π＝4π.故答案为4π. 6．[答案] 2 3－2π3[解析] 依题意，有AD ＝BD .又∠ACB ＝90°，所以CB ＝CD ＝BD ，即△BCD 为等边三角形，∴∠BCD ＝∠B ＝60°，∠A ＝∠ACD ＝30°.由AC ＝2 3，求得BC ＝2，AB ＝4，S 弓形BD ＝S 扇形BCD －S △BCD ＝60π×22360－3＝23π－3，故阴影部分的面积为S △ACD －S 弓形AD ＝3－(2π3－3)＝2 3－2π3.7．解：如图，连接OD .根据折叠的性质，得CD ＝CO ，BD ＝BO ，∠DBC ＝∠OBC ， ∴OB ＝OD ＝BD ，即△OBD 是等边三角形，∴∠DBO ＝60°，∴∠CBO ＝12∠DBO ＝30°.∵∠AOB ＝90°， ∴OC ＝OB ·tan∠CBO ＝6×33＝2 3， ∴S △BDC ＝S △OBC ＝12·OB ·OC ＝12×6×2 3＝6 3.∵S 扇形OAB ＝90360π×62＝9π，lAB ︵＝90180π×6＝3π，∴整个阴影部分的周长为AC ＋CD ＋BD ＋lAB ︵＝AC ＋OC ＋OB ＋lAB ︵＝OA ＋OB ＋lAB ︵＝6＋6＋3π＝12＋3π，整个阴影部分的面积为S 扇形OAB －S △BDC －S △OBC ＝9π－6 3－6 3＝9π－12 3. 8．解：(1)证明：∵点O 是圆心，OD ⊥BC ， ∴CD ︵＝BD ︵，∴∠CAD ＝∠BAD .(2)连接CO ，∵∠B ＝50°，OB ＝OC ， ∴∠OCB ＝∠B ＝50°， ∴∠AOC ＝100°， ∴AC ︵的长为100π×1180＝5π9.9．解：(1)如图，过点C 作CH ⊥AB 于点H .在△ABC 中，∠B ＝180°－∠A －∠ACB ＝180°－20°－130°＝30°. 在Rt △BCH 中，∵∠CHB ＝90°，∠B ＝30°，BC ＝4， ∴CH ＝12BC ＝2，BH ＝3CH ＝2 3.∵CH ⊥BD ，∴DH ＝BH ，∴BD ＝2BH ＝4 3. (2)连接CD .∵BC ＝DC ，∴∠CDB ＝∠B ＝30°，∴∠BCD ＝120°，∴阴影部分的面积＝扇形CBD 的面积－△CBD 的面积＝120π×42360－12×4 3×2＝163π－4 3.10．解：(1)连接OD ，OC ，∵C ，D 是半圆O 上的三等分点，∴AD ︵＝CD ︵＝BC ︵， ∴∠AOD ＝∠DOC ＝∠COB ＝60°，∴∠CAB ＝30°. ∵DE ⊥AB ，∴∠AEF ＝90°， ∴∠AFE ＝90°－30°＝60°. (2)由(1)知∠AOD ＝60°.又∵OA ＝OD ，∴△AOD 是等边三角形． ∵AB ＝4，∴OA ＝AD ＝2.∵DE ⊥AO ，∴DE ＝3，∴S 阴影＝S 扇形AOD －S △AOD ＝60·π×22360－12×2×3＝23π－ 3.11．解：(1)在Rt △ABC 中，BC ＝1，AC ＝3， ∴AB ＝2，∴cos ∠ABC ＝12，∴∠ABC ＝60°，则∠ABA ′＝120°，∠A ′C ″A ″＝90°，∴lAA ′︵＝120π×2180＝4π3，lA ′A ″︵＝90π×3180＝32π，∴点A 所经过的路线长为4π3＋32π.(2)S 扇形BAA ′＝12lAA ′︵·AB ＝12×4π3×2＝4π3，S 扇形C ″A ′A ″＝12lA ′A ″︵·C ″A ′＝12×3π2×3＝34π，S △A ′B ′C ′＝12×1×3＝32， ∴点A 所经过的路线与l 围成的图形的面积是43π＋34π＋32＝2512π＋32.[素养提升][解析] 根据扇形面积公式、弧长公式之间的关系，结合已知条件推出结果． 解：(1)根据弧长公式l ＝n πR180，弧长为4π，圆心角为120°，可得R ＝6，∴S 扇形＝12lR ＝12×4π×6＝12π. (2)他的猜想正确．设大扇形的半径为R ，小扇形的半径为r ，圆心角的度数为n °，则由l ＝n πR180，得R ＝180l 1n π，r ＝180l 2n π， ∴花坛的面积为 12l 1R －12l 2r ＝12·l 1·180l 1n π－12·l 2·180l 2n π ＝90n π()l 12－l 22 ＝90n π(l 1＋l 2)(l 1－l 2) ＝12·180n π(l 1＋l 2)(n π180R －n π180r ) ＝12(l 1＋l 2)(R －r )＝12(l 1＋l 2)d . 故他的猜想正确．。

2019-2020年九年级数学下册第3章圆3.9弧长及扇形的面积同步练习新版北师大版一、夯实基础1．一个扇形的弧长为20π cm，面积为240πcm2，则这个扇形的圆心角是 ( ) A．120° B．150° C．210° D．240°2．（2014•辽宁本溪，第7题3分）底面半径为4，高为3的圆锥的侧面积是（）A. 12πB.15πC.20πD.36π3．（2014•内蒙古包头，第9题3分）如图，在正方形ABCD中，对角线BD的长为．若将BD绕点B旋转后，点D落在BC延长线上的点D′处，点D经过的路径为，则图中阴影部分的面积是（）A ﹣1B ﹣2C ﹣1D π﹣24. （2014•湖北宜昌,第13题3分）如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则的长为（）A πB 6πC 3πD 1.5π5．如果圆锥的底面半径为4 cm，圆锥的高为3 cm，那么圆锥的侧面积为 ( ) A．15 cm2 B．45 cm2 C．20π cm2D．45π cm2 6．在△ABC中，AB＝3，AC＝4，∠A＝90°，把Rt△ABC绕直线AC旋转一周得到一个圆锥，其表面积为S1，把Rt△ABC绕直线AB旋转一周得到另一个圆锥，其表面积为S2，则S1∶S2等于 ( )A．2∶3 B．3∶4 C．4∶9 D．39∶56 7．一个形如圆锥的冰淇淋纸简(无底)，其底面直径为6 cm，母线长为5 cm，围成这样的冰淇淋纸筒所需纸片的面积为 ( )A．66πcm2 B．30π cm2 C．24π cm2 D．15π cm2二、能力提升8．如图所示，AB是半圆O的直径，以O为圆心，OE为半径的半圆交AB于E，F两点，弦AC切小半圆于点D．已知AO＝4，EO＝2，那么阴影部分的面积是．9. （2014•福建三明，第14题4分）如图，AB是⊙O的直径，分别以OA，OB为直径作半圆．若AB=4，则阴影部分的面积是．10. （2014•吉林，第14题3分）如图，将半径为3的圆形纸片，按下列顺序折叠．若和都经过圆心O，则阴影部分的面积是（结果保留π）11．若△ABC为等腰直角三角形，其中∠ABC＝90°，AB＝BC＝cm，求将等腰直角三角形绕直线AC旋转一周所得旋转体的表面积．三、课外拓展12．（2014•莆田，第20题8分）如图，点D是线段BC的中点，分别以点B，C为圆心，BC长为半径画弧，两弧相交于点A，连接AB，AC，AD，点E为AD上一点，连接BE，CE．（1）求证：BE=CE；（2）以点E为圆心，ED长为半径画弧，分别交BE，CE于点F，G．若BC=4，∠EBD=30°，求图中阴影部分（扇形）的面积．13.（2014•贵阳，第23题10分）如图，PA，PB分别与⊙O相切于点A，B，∠APB=60°，连接AO，BO．（1）所对的圆心角∠AOB= 120°；（2）求证：PA=PB；（3）若OA=3，求阴影部分的面积．四、中考链接1．（2016•桂林）如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt △AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是（）A．πB．C．3+πD．8﹣π2．（2016•内江）如图，点A 、B 、C 在⊙O 上，若∠BAC=45°，OB=2，则图中阴影部分的面积为（ ）A ．π﹣4B ．C ．π﹣2D ．3．（2016•资阳）在Rt △ABC 中，∠ACB=90°，AC=2，以点B 为圆心，BC 的长为半径作弧，交AB 于点D ，若点D 为AB 的中点，则阴影部分的面积是（ ）A ．2﹣π B ．4﹣π C ．2﹣π D ．π答案1．B[提示：先利用S ＝12lR ，求出R ＝24，再利用180n Rl π=，求出n 即可．] 2.C 3.C 4.D5．C[提示：12×(2×4π)=20π．] 6．A[提示：由题可知BC ＝5，则S 1＝12×2π×3×5＋π×32＝24π，S 2＝12×2π×4×5＋π×42＝36π，S 1∶S 2＝24π∶36π＝2∶3．]7．D[提示：S ＝12×5×π×6＝15π．]8．43π+[提示：连接DO ，OC ，OC 交DF 于点G ，易证∠OAD ＝30°，则∠DOC ＝∠AOD ＝∠COB ＝60°，通过面积分割，可求得S 阴影＝S △ODC ＋S 扇形OCB －2S 扇ODG ＝43π．]9.2π10.3π11．解：如图3－170所示，△ABC 绕直线AC 旋转一周所得的旋转体是由同底的两个圆锥组成的组合体．在Rt △ABC中，AC ＝=＝10．∵S △ABC ＝12AB ·BC ＝12BD ·AC ，∴AB ·BC＝BD ·AC ，∴BD ＝52AB BC AC =＝5，∴S ＝π·BD ·AB ＋π·BD ·BC＝π×5×π×5×(cm 2)．∴△ABC 绕直线AC 旋转一周所得旋转体的表面积为cm 2．12．（1）证明：∵点D 是线段BC 的中点， ∴BD=CD ， ∵AB=AC=BC ，∴△ABC 为等边三角形， ∴AD 为BC 的垂直平分线， ∴BE=CE ；（2）解：∵EB=EC ， ∴∠EBC=∠ECB=30°， ∴∠BEC=120°，在Rt △BDE 中，BD=BC=2，∠EBD=30°， ∴ED=BD=，∴阴影部分（扇形）的面积==π．10．解：如图3－172所示，作DH ⊥BC 于点H ，∴DH ＝AB ＝2，CH ＝BC －BH ＝BC －AD ＝7－3＝4．在Rt △CDH 中，CD ＝=S 表＝S 圆锥侧＋S 圆柱侧＋S 底＝π·DH ·CD ＋2π·AB ·AD＋π·(AB)2＝π×2×2π×2×3＋π×22＝16)π+．13.（1）解：∵PA ，PB 分别与⊙O 相切于点A ，B ， ∴∠OAP=∠OBP=90°，∴∠AOB=180°﹣90°﹣90°﹣60°=120°； （2）证明：连接OP ．在Rt△OAP和Rt△OBP中，，∴Rt△OAP≌Rt△OBP，∴PA=PB；（3）解：∵Rt△OAP≌Rt△OBP，∴∠OPA=OPB=∠APB=30°，在Rt△OAP中，OA=3，∴AP=3，∴S△OPA=×3×3=，∴S阴影=2×﹣=9﹣3π．中考链接：1．解：作DH⊥AE于H，∵∠AOB=90°，OA=3，OB=2，∴AB==，由旋转的性质可知，OE=OB=2，DE=EF=AB=，△DHE≌△BOA，∴DH=OB=2，阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF 的面积=×5×2+×2×3+﹣=8﹣π，故选：D．2．解：∵∠BAC=45°， ∴∠BOC=90°，∴△OBC 是等腰直角三角形， ∵OB=2，∴△OBC 的BC 边上的高为： OB=，∴BC=2∴S阴影=S扇形O B C﹣S △O B C =﹣×2×=π﹣2，故选C ．3．解：∵D 为AB 的中点，∴BC=BD=AB ，∴∠A=30°，∠B=60°．∵AC=2，∴BC=AC•tan30°=2•=2，∴S阴影=S △A B C ﹣S扇形C B D=×2×2﹣=2﹣π．故选A ．。

《弧长及扇形的面积》分层练习◆ 基础题1．已知圆O 的半径是3，A ，B ，C 三点在圆O 上，∠ACB =60°，则弧AB 的长是（ ）A ．2πB ．πC ．32π D ．12π2．如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于（ ）A ．3π B ．2πC ．πD ．2π 3．扇形的弧长为20πcm ，面积为240πcm 2，那么扇形的半径是（ ）A ．6cmB ．12cmC ．24cmD ．28cm4．扇形的圆心角为60°，面积为6π，则扇形的半径是（ ）A ．3B ．6C ．18D ．365．如图，半径为6的⊙O 的直径AB 与弦CD 垂直，且∠BAC =40°，则劣弧BD 的长是 （结果保留π）．6．如图，一块等边三角形的木板，边长为1，现将木板沿水平线翻滚，那么B 点从开始至结束所走过的路径长度为 ．7．如图，直径AB 为12的半圆，绕A 点逆时针旋转60°，此时点B 到了点B ′，则图中阴影部分的面积是 ．8．如图，直角△ABC中，∠A=90°，∠B=30°，AC=4，以A为圆心，AC长为半径画四分之一圆，则图中阴影部分的面积是（结果保留π）．9．如图，秋千拉绳长AB为3米，静止时踩板离地面0.5米，某小朋友荡该秋千时，秋千在最高处时踩板离地面2米（左右对称），请计算该秋千所荡过的圆弧长（精确到0.1米）？10．如图，半径为12的圆中，两圆心角∠AOB=60°、∠COD=120°，连接AB、CD，求图中阴影部分的面积．◆能力题1．如图，△ABC为等边三角形，保持各边的长度不变，将BC边向三角形外弯曲得到扇形ABC，设△ABC的面积为S1，扇形ABC的面积为S2，则S1与S2的大小关系为（）A．S1＜S2 B．S1=S2 C．S1＞S2 D．无法确定2．如图，正方形ABCD的面积为36cm2，点E在BC上，点G在AB的延长线上，四边形EFGB是正方形，以B为圆心，BC长为半径画弧AC，连结AF，CF，则图中阴影部分面积为（）cm2．A．6π B．8π C．9π D．12π3．一个扇形的半径等于一个圆的半径的2倍，且扇形面积是圆的面积的一半，则这个扇形的圆心角度数是（）A．45° B．60° C．90° D．75°4．如图所示，半圆O的直径AB=4，以点B为圆心，为半径作弧，交半圆O于点C，交直径AB于点D，则图中阴影部分的面积是．5．如图，正方形ABCD中，AB=2，将线段CD绕点C顺时针旋转90°得到线段CE，线段BD绕点B顺时针旋转90°得到线段BF，连接BF，则图中阴影部分的面积是．6．如图，将半径为2，圆心角为120°的扇形OAB绕点A逆时针旋转60°，点O，B的对应点分别为O′，B′，连接BB′，则图中阴影部分的面积是．7．多少年来人们一直误认为“在月球上能看到长城”，直到“神舟五号”载人飞船发射成功，我们的航空英雄杨利伟亲口说出：“在那个高度不能看到长城”之后才得以验证．（飞船距地面343千米，而月球距地球38.4万千米）科学研究显示，眼睛的分辨率是指眼睛能够分辨两个相邻的点或线的能力，通常以刚能被分开的两点或两线对眼睛瞳孔中心的张角来表示．人眼分辨率的张角为0.1°，而长城的宽为10米左右，那么，请同学们算一算，离开长城有多高它就会在我们的视野中细得成为一条线了呢？（13600圆周的弧长可大略的看成是一段线段，取π值为3）8．如图，在矩形ABCD中，点F在边BC上，且AF=AD，过点D作DE⊥AF，垂足为点E．（1）求证：DE=AB；（2）以D为圆心，DE为半径作圆弧交AD于点G，若BF=FC=1，试求EG的长．◆提升题1．如图，AB为半圆O的直径，C是半圆上一点，且∠COA=60°，设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3，则它们之间的关系是（）A．S1＜S2＜S3 B．S2＜S1＜S3 C．S1＜S3＜S2 D．S3＜S2＜S12．如图，一个等边三角形的边长与它的一边相外切的圆的周长相等，当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转，直至回到原出发位置时，则这个圆共转了（）A．4圈 B．3圈 C．5圈 D．3.5圈3．如图，在正方形ABCD中，AB=2，连接AC，以点C为圆心、AC长为半径画弧，与BC 的延长线交于点E，则图中AE的长为．4.如图，一个圆作滚动运动，它从A位置开始，滚过与它相同的其他六个圆的上部，到达B位置．则该圆共滚过圈．5．用一根长22cm 的铁丝：（1）能否围成面积是30cm 2的扇形？若能，求出扇形半径；若不能，请说明理由． （2）能否围成面积是32cm 2的扇形？并说明理由．6．如图所示，一只羊用一条长12米的绳子拴住，绳子的另一头被绑在一堵墙的大门外的点A 处，大门的边缘底下B ，C 两点恰好与点A 构成了等边三角形ABC 的顶点，如果墙的那一边是一片足够大的草场，△ABC 的边长为6米，那么这只羊最多可以吃到多少平方米的草（精确到0.1平方米）？答案和解析◆ 基础题1．【答案】A解：∵∠ACB =60°，∴∠AOB =2∠ACB =120°，∴l =180n rπ=2π． 2．【答案】C解：∵△ABC 为正三角形，∴∠A =∠B =∠C =60°，AB =AC =BC =1，∴AB =AC =BC =3π，根据题意可知凸轮的周长为三个弧长的和，即凸轮的周长=AB +AC +BC =3×3π=π． 3．【答案】C 解：∵S 扇形=12lr ，∴240π=12•20π•r ，∴r =24（cm ）． 4．【答案】B解：扇形的面积=260360r π=6π．解得：r =6．5．【答案】83π解：如图，连接OC 、OD ，∵∠BAC =40°，∴∠BOC =2∠BAC =80°．∵⊙O 的直径AB 与弦CD 垂直，∴BC =BD ，∴∠BOC =∠BOD =80°，∴劣弧BD 的长是83π．6．【答案】43π解：从图中发现：B 点从开始至结束所走过的路径长度为两段弧长，即第一段=1201180π⨯，第二段=1201180π⨯．故B 点从开始至结束所走过的路径长度=1201180π⨯+1201180π⨯=43π． 7．【答案】24π解：阴影部分的面积=以AB ′为直径的半圆的面积+扇形ABB ′的面积﹣以AB 为直径的半圆的面积=扇形ABB ′的面积．则阴影部分的面积是：26012360π⨯=24π．8．【答案】﹣43π解：连结AD ．∵直角△ABC 中，∠A =90°，∠B =30°，AC =4，∴∠C =60°，AB ∵AD =AC ，∴三角形ACD 是等边三角形，∴∠CAD =60°，∴∠DAE =30°，∴图中阴影部分的面积=4×2﹣4×2﹣2304360π⨯43π．9．解：由题意得，BE =2m ，AC =3m ，CD =0.5m ，作BG ⊥AC 于G ，则AG =AD ﹣GD =AC +CD ﹣BE =1.5m ，由于AB =3，所以在Rt △ABG 中，∠BAG =60°，根据对称性，知∠BAF =120°，故秋千所荡过的圆弧长是1203180π⨯=2π≈6.3（米）．10．解：S 扇形AOB =26012360π⨯=24π，S △AOB S 弓形AB =24π﹣，S扇形COD =212012360π⨯=48π，作OE ⊥CD 于点E ．则OE =12OD =6，CD =2DE =2×，S △COD=12OE •CD =12×6×，则S 弓形CD =48π﹣则S 阴影=S 弓形CD ﹣S 弓形AB =48π﹣24π﹣）=24π．◆ 能力题1．【答案】A解：设三角形的边长是a ，高是h ，则a ＞h ．∵S 1=12ah ，S 2=12•BC •a =12a 2，∴S 1＜S 2．2．【答案】C解：∵四边形ABCD 和四边形EFGB 是正方形，且正方形ABCD 的面积为36cm 2，∴∠G =∠ABC =∠CEF =90°，AB =BC =6，EF =BE =GF =BG ，设EF =BE =GF =BG =a ，则阴影部分的面积S =S 扇形BAC +S 正方形EFGB +S △CEF ﹣S △AGF =2906360π⨯+a 2+12•a •（6﹣a ）﹣12•（6+a ）a =9π． 3．【答案】A解：设圆的半径为r ，扇形圆心角为n °．则扇形的半径为2r ，利用面积公式可得：()22213602n r r ππ⨯=，解得n =45．4．【3π解：连接BC 、OC 、AC ．∵AB 是直径，∴∠ACB =90°，∵AB =4，BD =BC，∴AC =2，∴AC =OA =OC =2，∴AB =2AC ，∴∠ABC =30°，∴S 阴=S 扇形OAC +S △BOC ﹣S 扇形BDC =2602360π⨯+12×2﹣(230360π⨯﹣3π． 5．【答案】6﹣π 解：过F 作FM ⊥BE 于M ，则∠FME =∠FMB =90°，∵四边形ABCD 是正方形，AB =2，∴∠DCB =90°，DC =BC =AB =2，∠DCB =45°，由勾股定理得：BD，∵将线段CD 绕点C 顺时针旋转90°得到线段CE ，线段BD 绕点B 顺时针旋转90°得到线段BF ，∴∠DCE =90°，BF =BD，∠FBE =90°﹣45°=45°，∴BM =FM =2，ME =2，∴阴影部分的面积S =S △BCD +S △BFE +S扇形DCE﹣S扇形DBF =1222⨯⨯+1422⨯⨯+2902360π⨯﹣(290360π⨯=6﹣π．6．【答案】﹣23π解：连接OO ′，BO ′，∵将半径为2，圆心角为120°的扇形OAB 绕点A 逆时针旋转60°，∴∠OAO ′=60°，∴△OAO ′是等边三角形，∴∠AOO ′=60°，OO ′=OA ，∴当O ′中⊙O 上，∵∠AOB =120°，∴∠O ′OB =60°，∴△OO ′B 是等边三角形，∴∠AO ′B =120°，∵∠AO ′B ′=120°，∴∠B ′O ′B =120°，∴∠O ′B ′B =∠O ′BB ′=30°，∴图中阴影部分的面积=S△B ′O ′B ﹣（S 扇形O ′OB ﹣S △OO ′B ）=12×1×2602360π⨯﹣12×2﹣23π．7．解：根据题意得，10=0.1180Rπ⨯⨯，解得，R =6000（米），所以离开长城有6000米高它就会在我们的视野中细得成为一条线了．8．（1）证明：∵四边形ABCD 是矩形，∴∠B =∠C =90°，AB =DC ，BC =AD ，AD ∥BC ， ∴∠EAD =∠AFB ，∵DE ⊥AF ， ∴∠AED =90°，在△ADE 和△FAB 中，90AED B EAD AFB AD AF ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△ADE ≌△FAB （AAS ），∴DE =AB ；（2）连接DF ，如图所示：在△DCF 和△ABF 中，DC AB C B FC BF =⎧⎪∠=∠⎨⎪=⎩，∴△DCF ≌△ABF （SAS ），∴DF =AF ，∵AF =AD ，∴DF =AF =AD ，∴△ADF 是等边三角形，∴∠DAE =60°，∵DE ⊥AF ，∴∠AED =90°，∴∠ADE =30°，∵△ADE ≌△FAB ，∴AE =BF =1，∴DE，∴EG 的长==．◆ 提升题1．【答案】B解：作OD ⊥BC 交BC 与点D ，∵∠COA =60°，∴∠COB =120°，则∠COD =60°．∴S 扇形AOC =22603606R R ππ=；S 扇形BOC =221203603R R ππ=． 在三角形OCD 中，∠OCD =30°，∴OD =2R，CD，BCR ，∴S △OBCS 弓形=23Rπ(2412Rπ-，(2412Rπ-＞26Rπ，∴S2＜S1＜S3．2．【答案】A解：如图，设圆的周长是C，则圆所走的路程是圆心所走过的路程即等边三角形的周长+三条圆心角是120°的弧长=4C，则这个圆共转了4C÷C=4圈．3．解：∵四边形ABCD为正方形，∴CA，∠ACB=45°，∴∠ACE=135°，∴AE的长度=135180π⨯⨯=2．4.【答案】8 3解：观察图1中，当⊙A旋转到⊙A′位置时，∠COD=90°，这个圆已经旋转180°，即得出结论：⊙A旋转的度数是∠COD的两倍．第一段和最后一段圆心角为120度．中间一共是4段6圆心角0度的弧，120°×2+60°×4=480度，480°×2=960°，960°÷360°=8 3（圈）．5．解：（1）设扇形半径为xcm，依题意有x（22﹣2x）=30，x2﹣11y+15=0，解得x1=112，x2=112（舍去）．故扇形半径为112-cm；小初高资料学习小初高资料学习 （2）设扇形半径为ycm ，依题意有y （22﹣2y ）=32，y 2﹣11y +16=0，解得y 1=112，y 2（舍去）cm ． 6．解：羊可以吃到的草的最大面积由三部分组成：第一部分：以点A 为圆心，12米为半径．圆心角为60°的扇形的面积减去三角形ABC 的面积；第二部分：以点B 为圆心，6米为半径，圆心角为60°的扇形面积；第三部分与第二部分相等．因此，羊可以吃到的草的面积是：222601216066sin 60297.53602360ππ⨯⨯-⨯︒+⨯≈（平方米）．。

2022-2023学年北师大版九年级数学下册《3.9弧长及扇形面积》假期同步提升练习题（附答案）一．选择题1．半径为6，圆心角为60°的弧长为（）A．6B．3πC．2πD．4π2．如图，已知⊙O的半径为6，AB，BC是⊙O的弦，若∠ABC＝50°，则的长是（）A．B．10πC．D．12π3．如图，在△ABC中，AC＝2，将△ABC绕点A顺时针旋转90°后得到△ADE，则C点运行痕迹长为（）A．B．C．πD．2π4．一个扇形的弧长是10πcm，其圆心角是150°，此扇形的面积为（）A．30πcm2B．60πcm2C．120πcm2D．180πcm25．已知扇形的面积为12πcm2，圆心角为120°，则扇形的弧长为（）A．4 cm B．2cm C．4πcm D．2πcm6．已知一个圆锥的母线长为是30，底面半径为10，则这个圆锥的侧面展开图的圆心角等于（）A．90°B．100°C．120°D．150°7．圆锥的底面半径为3，侧面积为12π，则圆锥的母线长为（）A．4B．5C．5D．二．填空题8．已知扇形的弧长是π，圆心角120°，则这个扇形的半径是．9．如图，从一个腰长为60cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，则此扇形的弧长为cm．10．如图，已知⊙O的半径为2，AB是⊙O的弦．若AB＝2，则劣弧的长为．11．一扇形的圆心角是40°，弧长是2π，则此扇形的面积是．12．已知直角三角形ABC的一条直角边AB＝12cm，斜边AC＝13cm，则以AB为轴旋转一周，所得到的圆锥的侧面积是．13．若一个圆锥的母线长为5cm，它的半径为3cm，则这个圆锥的全面积为cm2．14．如图，若圆锥的母线长为6，底面半径为2，则其侧面展开图的圆心角为．三．解答题15．如图，已知扇形AOB的圆心角为120°，半径OA为6cm．求扇形AOB的弧长和面积．16．如图所示，扇形OAB的面积为4πcm2，∠AOB＝90°，用这个扇形围成一个圆锥的侧面．求这个圆锥的底面圆的半径．17．已知：如图，AB是⊙O的直径，弦CD⊥AB于点E，G是弧AC上一动点且不与点A，C重合，AG，DC的延长线交于点F，连结BC．CD＝4，BE＝2．（1）求半径长；（2）求扇形DOC的面积．18．如图所示，菱形ABCD，∠B＝120°，AD＝1，扇形BEF的半径为1，圆心角为60°，求图中阴影部分的面积．19．如图，⊙O的直径AB＝12，弦AC＝6，∠ACB的平分线交⊙O于D，过点D作DE∥AB交CA的延长线于点E，连接AD，BD．（1）由AB，BD，围成的阴影部分的面积是；（2）求线段DE的长．20．如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连接EO、FO，若DE＝4，∠DP A＝45°（1）求⊙O的半径．（2）若图中扇形OEF围成一个圆锥侧面，试求这个圆锥的底面圆的半径．参考答案一．选择题1．解：半径为6，圆心角为60°的弧长为＝2π，故选：C．2．解：如图，连接OA，OC，∵∠ABC＝50°，∴∠AOC＝2∠ABC＝100°，∴弧AC的长为：＝，故选：C．3．解：由题意得，AC＝AE＝2，∠CAE＝90°，由弧长的计算方法可得，的长为＝π，故选：C．4．解：根据题意可得，设扇形的半径为rcm，则l＝，即10π＝，解得：r＝12，∴S＝＝＝60π（cm2）．故选：B．5．解：令扇形的半径和弧长分别为R和l，则∵S＝＝12π，∴R＝6cm，∴l＝＝4πcm．∴扇形的弧长为4πcm．故选：C．6．解：设这个圆锥的侧面展开图的圆心角为n°，根据题意得2π×10＝，解得n＝120，即这个圆锥的侧面展开图的圆心角等于120°．故选：C．7．解：设圆锥的母线长为l，根据题意得×2π×3×l＝12π，解得l＝4，即圆锥的母线长为4．故选：A．二．填空题8．解：根据弧长的公式l＝，得到：π＝，解得r＝2，故答案为：2．9．解：过O作OE⊥AB于E，当扇形的半径为OE时扇形OCD最大，∵OA＝OB＝60cm，∠AOB＝120°，∴∠A＝∠B＝30°，∴OE＝OA＝30cm，∴弧CD的长＝＝20πcm，故答案为：20π．10．解：∵⊙O的半径为2，∴AO＝BO＝2，∵AB＝2，∴AO2+BO2＝22+22＝＝AB2，∴△AOB是等腰直角三角形，∴∠AOB＝90°，∴的长＝＝π．故答案为：π．11．解：设该扇形的半径为r，∵扇形的圆心角是40°，扇形的弧长是2π，∴2π＝，解得：r＝9，∴该扇形的面积为2π×9＝9π，故选：9π．12．解：∵直角三角形ABC的一条直角边AB＝12cm、斜边AC＝13cm，∴BC＝＝5cm，∴圆锥的侧面积＝•2π•13•5＝65π（cm2）．，故答案为：65πcm2．13．解：底面圆的半径为3cm，则底面周长＝6πcm，侧面面积＝×6π×5＝15π（cm2）；底面积为＝9π（cm2）；全面积为：15π+9π＝24π（cm2）．故答案为24π．14．解：设圆锥的侧面展开图的圆心角为n°，根据题意得2π×2＝，解得n＝120，所以侧面展开图的圆心角为120°．故答案为：120°．三．解答题15．解：扇形AOB的弧长＝＝4π（cm）；扇形AOB的扇形面积＝＝12π（cm2）．16．解：设扇形的半径为Rcm，根据题意得＝4π，解得R＝4（负值舍去），设这个圆锥的底面圆的半径为rcm，则×2πr×4＝4π，解得r＝1，所以这个圆锥的底面圆的半径为1cm．17．解：（1）连接OD．设OD＝OB＝r．∵AB是直径，AB⊥CD，∴DE＝EC＝2，在Rt△ODE中，则有r2＝（2）2+（r﹣2）2，∴r＝4，∴⊙O的半径为4；（2）连接OC．∵tan∠DOE＝＝＝，∴∠DOE＝60°，∵OD＝OC，OE⊥CD，∴∠COE＝∠DOE＝60°，∴∠DOC＝120°，∴扇形DOC的面积＝＝．18．解：如图，延长弧EF交半径BC于点C，连接BD，∠EBD+∠DBF＝60°，∠DBF+∠FBC＝60°，∴∠EBD＝∠FBC，∠DBC＝60°，∴原来阴影部分的面积等于弧DFC所对应部分的面积，S原来阴影部分的面积＝S扇形BDFC﹣S△BDC＝•1﹣•1•＝﹣．19．解：（1）连接OD，∵⊙O的直径AB＝12，弦AC＝6，∠ACB的平分线交⊙O于D，∴∠ADB＝90°，AD＝BD，∴∠OBD＝∠ODB＝45°，∴OB＝OD＝6，∴由AB，BD，围成的阴影部分的面积是：＝9π+18，故答案为：9π+18；（2）作AF⊥DE于点F，则AF＝OD＝6，∵AB∥DE，∠OAB＝45°，∴∠ADF＝∠OAB＝45°，∴DF＝AF＝6，∵∠ACB＝90°，AC＝6，AB＝12，∴∠CBA＝30°，∴∠CAB＝60°，∵AB∥DE，∴∠E＝∠CAB＝60°，∵AF＝6，∠AFE＝90°，2，∴EF＝3∴DE＝EF+DF＝2+6．20．解：（1）∵弦DE垂直平分半径OA，∴CE＝DC＝DE＝2，OC＝OE，∴∠OEC＝30°，∴OC＝＝2，∴OE＝2OC＝4，即⊙O的半径为4；（2）∵∠DP A＝45°，∴∠D＝45°，∴∠EOF＝2∠D＝90°，设这个圆锥的底面圆的半径为r，∴2πr＝，解得r＝1，即这个圆锥的底面圆的半径为1．。

2020年春北师大版九年级数学下册第三章圆3.9弧长及扇形的面积同步练习题一、选择题1. 一个扇形的弧长是10πcm，面积是60πcm2，则此扇形的圆心角的度数是（）A. 300°B. 150°C. 120°D. 75°2.已知一条弧长为，它所对圆心角的度数为，则这条弦所在圆的半径为（）A. B. C. D.3.若一个扇形的半径是18cm，且它的弧长是12π cm，则此扇形的圆心角等于（）A. 30°B. 60°C. 90°D. 120°4.如图，从一块直径是2的圆形硬纸片上剪出一个圆心角为90°扇形．则这个扇形的面积为（）A. πB. πC. πD. π5.如图，在△ABC中，∠A=90°，AB=AC=2，以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E，则图中阴影部分的面积是（）A. B. C. D.6.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2．将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，点B，A，C′在同一条直线上，则线段BC扫过的区域面积为（）A. B. C. D.7.如图，将一个半径为2的圆等分成四段弧，再将这四段弧围成星形，则该图形的面积与原来圆的面积之比为（）A. B. C. D.8.如图，直径AB为6的半圆，绕A点逆时针旋转60°，此时点B到了点B’，则图中阴影部分的面积是（）A. B. D.9.如图，在边长为2的正方形内部，以各边为直径画四个半圆，则图中阴影部分的面积是（）A. 2B.C.D. 110.如图所示，扇形AOB的圆心角120°，半径为2，则图中阴影部分的面积为（）A. B. C. D.二、填空题11.如果扇形的圆心角为120°，半径为3cm，那么扇形的面积是________ .12.已知扇形的圆心角为120°，弧长等于一个半径为5cm的圆的周长，则扇形的面积为________．13.如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，E为BC边上的一点，以A为圆心，AE为半径的圆弧交AB于点D，交AC的延长于点F，若图中两个阴影部分的面积相等，则AF2为________ ．14. 已知扇形的圆心角为120°，弧长为2π，则它的半径为________ ．15.如图，扇形OAB的圆心角为120°，半径为3cm，则该扇形的弧长为________ cm，面积为________ cm2．（结果保留π）16.如图，将一块三角板和半圆形量角器按图中方式叠放，三角板一边与量角器的零刻度线所在直线重合，重叠部分的量角器弧AB对应的圆心角（∠AOB）为120°，OC的长为2cm，则三角板和量角器重叠部分的面积为________.17.如图，已知点A、B、C、D均在以BC为直径的圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10，则图中阴影部分的面积为________．三、解答题18.一段圆弧形公路弯道，圆弧的半径为2km，弯道所对圆心角为10°，一辆汽车从此弯道上驶过，用时20 s，弯道有一块限速警示牌，限速为40km/h，问这辆汽车经过弯道时有没有超速？（π取3）19.如图，半径为2的⊙E交x轴于A、B，交y轴于点C、D，直线CF交x轴负半轴于点F，连接EB、EC．已知点E的坐标为(1，1)，∠OFC＝30°．(1)求证：直线CF是⊙E的切线；(2)求证：AB＝CD；(3)求图中阴影部分的面积．20.如图，在扇形纸片AOB中，OA=10，∠AOB=36°，OB在桌面内的直线l上．现将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA落在l上时，停止旋转．求点O所经过的路线长。

北师版数学九年级下册 第三章 圆9 弧长及扇形的面积1．120°的圆心角所对的弧长是6π，则此弧所在圆的半径是( C ) A ．3B ．4C ．9D ．182．如图，AB 为⊙O 的直径，点C 在⊙O 上，若∠OCA ＝50°，AB ＝4，则BC ︵的长为( B ) A.10π3B.10π9C.5π9D.5π18第2题图 第3题图3．如图，有一段弯道是圆弧形的，道长是12 m ，弧所对的圆心角是∠α，这段弧的半径R 为8.5 m ，则∠α的度数是__81°__.(结果保留整数)4．(2018·湖南永州中考)如图，在平面直角坐标系中，已知点A (1，1)，以点O 为旋转中心，将点A 逆时针旋转到点B 的位置，则AB ︵的长为__24π__.第4题图 第5题图5．(教材P102，习题3.11，T2改编)一个滑轮起重装置如图所示，滑轮的半径是10 cm ，当滑轮的一条半径OA 绕轴心O 按逆时针方向旋转的角度为120°时，重物上升__203π__cm(结果保留π)．6．(2019·广西南宁中考)如图，△ABC 是⊙O 的内接三角形，AB 为⊙O 的直径，AB ＝6，AD 平分∠BAC ，交BC 于点E ，交⊙O 于点D ，连接BD . (1)求证：∠BAD ＝∠CBD ；(2)若∠AEB ＝125°，求BD ︵的长(结果保留π)． 解：(1)证明：∵AD 平分∠BAC ，∴∠CAD ＝∠BAD . ∵∠CAD ＝∠CBD ，∴∠BAD ＝∠CBD . (2)如图，连接OD .∵∠AEB ＝125°，∴∠AEC ＝55°.∵AB 为⊙O 的直径，∴∠ACE ＝90°，∴∠CAE ＝35°，∴∠DAB ＝∠CAE ＝35°， ∴∠BOD ＝2∠DAB ＝70°， ∴BD ︵的长＝70π×3180＝76π.7．如图，点A ，B ，C 在⊙O 上，若∠BAC ＝45°，OB ＝2，则图中阴影部分的面积为( C ) A ．π－4 B.23π－1 C ．π－2 D.23π－2第7题图 第8题图8．如图，从一块直径为2 m 的圆形铁皮上剪出一个圆心角为90°的扇形，则此扇形的面积为( A )A.π2 m 2B.32π m 2 C ．π m 2D ．2π m 29．(2019·四川凉山州中考)如图，在△AOC 中，OA ＝3 cm ，OC ＝1 cm.将△AOC 绕点O 顺时针旋转90°后得到△BOD ，则AC 边在旋转过程中所扫过的图形的面积为( B ) A.π2 cm 2B ．2π cm 2 C.178π cm 2 D.198π cm 2第9题图 第11题图10．已知扇形的圆心角为240°，所对的弧长为16π3，则此扇形的面积是__323π__.11．(2019·广西梧州中考)如图，已知半径为1的⊙O 上有三点A ，B ，C ，OC 与AB 交于点D ，∠ADO ＝85°，∠CAB ＝20°，则阴影部分的扇形OAC 的面积是__5π36__.12．AB 是⊙O 的直径，点D ，E 是半圆的三等分点，AE ，BD 的延长线交于点C ，且CE ＝2，求图中阴影部分的面积． 解：如图，连接OE ，OD ，DE .∵点D ，E 是半圆的三等分点，AB 是⊙O 的直径，∴∠AOE ＝∠EOD ＝∠DOB ＝60°，∠AEB ＝90°.∵OA ＝OE ＝OD ＝OB ，∴△OAE ，△ODE ，△OBD 都是等边三角形，∴∠OAC ＝∠OBC ＝60°，∴△ABC 是等边三角形，∴AB ＝BC ＝AC ＝2CE ＝4，∴⊙O 的半径为2.∵△AOE ，△OED 是等边三角形，∴AB ∥DE ，∴S △ODE ＝S △BDE . ∴S 阴影＝S 扇形OAD －S △OAE ＝120π·22360－34×22＝4π3－ 3.13．如图，将矩形ABCD 绕其右下角的顶点按顺时针方向旋转90°至图①位置，继续绕其右下角的顶点按顺时针方向旋转90°至图②位置，依次类推，这样连续旋转2 019次．若AB ＝4，AD ＝3，则顶点A 在整个旋转过程中所经过的路径总长为( D )A ．2 019πB ．2 038πC ．3 024πD ．3 030π14．(2019·山东临沂中考)如图，⊙O 中，AB ︵＝AC ︵，∠ACB ＝75°，BC ＝2，则阴影部分的面积是( A )A ．2＋23πB ．2＋3＋23π C ．4＋23πD ．2＋43π15．如图，在Rt △ABC 中，∠BCA ＝90°，∠BAC ＝30°，BC ＝2，将Rt △ABC 绕A 点顺时针旋转90°得到Rt △ADE ，则BC 扫过区域(图中阴影部分)的面积为( D )A.π2B ．(2－3)π C.2－32πD ．π16．(2018·湖北恩施州中考)如图所示，在Rt △ABC 中，AB ＝1，∠A ＝60°，∠ABC ＝90°，将Rt △ABC 沿直线l 无滑动地滚动至Rt △DEF ，则点B 所经过的路径与直线l 所围成的封闭图形的面积为__1912π＋32__.(结果不取近似值)17．(2019·河南中考)如图，在扇形AOB 中，∠AOB ＝120°，半径OC 交弦AB 于点D ，且OC ⊥OA .若OA ＝23，则阴影部分的面积为__3＋π__.18．(2019·黑龙江齐齐哈尔中考)如图，以△ABC 的边BC 为直径作⊙O ，点A 在⊙O 上，点D 在线段BC 的延长线上，AD ＝AB ，∠D ＝30°. (1)求证：直线AD 是⊙O 的切线；(2)若直径BC ＝4，求图中阴影部分的面积．解：(1)证明：如图，连接OA ，则∠COA ＝2∠B .∵AD ＝AB ，∴∠B ＝∠D ＝30°，∴∠COA ＝60°，∴∠OAD ＝180°－60°－30°＝90°，∴OA ⊥AD ，即直线AD 是⊙O 的切线． (2)∵BC ＝4，∴OA ＝OC ＝2. 在Rt △OAD 中，OA ＝2，∠D ＝30°， ∴OD ＝2OA ＝4，AD ＝23， ∴S △OAD ＝12OA ·AD ＝12×2×23＝2 3. ∵∠COA ＝60°，∴S 扇形COA ＝60π·22360＝2π3， ∴S 阴影＝S △OAD －S 扇形COA ＝23－2π3.19．如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB .已知OA ＝6，取OA 的中点C ，过点C 作CD ⊥OA 交 AB ︵于点D .点F 是 AB ︵上一点，若将扇形BOD 沿OD 翻折，点B 恰好与点F 重合．用剪刀沿着线段BD ，DF ，F A 依次剪下，求剪下的纸片(形状同阴影图形)面积之和是多少．解：如图，过点D作DE⊥OB于点E，连接OF.由题意得∠AOB＝90°.∵CD⊥OA，∴∠DCO＝90°.∵OA＝OD＝OB＝6，OC＝12OA＝12OD，∴∠ODC＝30°.易知CD∥OE，∴∠BOD＝30°，则DE＝12OD＝3，∴S弓形BD＝S扇形BOD－S△BOD＝30×π×62360－12×6×3＝3π－9.由折叠的性质可得，∠DOF＝∠BOD＝30°，∴∠AOF＝30°，故剪下的纸片面积之和是12×(3π－9)＝36π－108.。