学案31
- 格式:doc
- 大小:339.50 KB
- 文档页数:10

离子浓度大小比较编号:31班级组别姓名.【学习目标】1、能够准确地判断离子浓度的大小。
2、小组合作探究守恒法判断离子浓度的方法。
3、以极度的热情全力以赴投入课堂,体验学习的快乐。
【使用说明】利用一节课完成导学案,收齐后及时批改。
下节课学生先自纠10分钟,然后针对不会的问题讨论10分钟,学生展示教师点拨20分钟,最后用5分钟搞好落实并进行当堂检测。
【基础自学】离子浓度大小比较1、单一溶质溶液:(离子浓度按由大到小的顺序排列)Na2CO3溶液_____________________________________________NaHCO3溶液_____________________________________________2、混合溶液:例1.物质的量浓度相同的CH3COOH与CH3COONa溶液等体积混合后,溶液中离子浓度关系错误的是( )A.c(Na+) + c(H+)=c(OH-) + c(CH3COO-)B.c(CH3COOH) + c(CH3COO-)=2c(Na+)C.c(CH3COO-)>c(Na+)>c(CH3COOH)>c(H+)>c(OH-)D.c(CH3COO-)>c(Na+)>c(H+)>c(CH3COOH)>c(OH-)练习1.将0.2mol/L HCN溶液和0.1mol/L的NaOH溶液等体积混合后,溶液中c(Na+)>c(CN-),下列关系式正确的是( )A.c(HCN)<c(CN-) B.c(H+)<c(OH-)C.c(HCN)-c(CN-)=c(OH-) D.c(HCN)+c(CN-)=0.2 mol/L【小结】混合溶液中离子浓度大小的比较方法:3、不同溶液中同一离子浓度大小比较:例2.等物质的量浓度的下列四种溶液中,NH4+浓度最大的是( )A.NH4Cl B.NH4 HCO3C.NH4HSO4D.NH4NO3【小结】不同溶液中同一离子浓度大小比较方法:4、溶液中的守恒关系:例3:在Na2CO3溶液中下列关系式错误的是( )A.c(Na+) + c(H+) =c(OH-) + c(CO32-)B.c(OH-) =c(H+) + c(HCO3-) + 2c(H2CO3)C.c(Na+) =2c(CO32-) + 2c(HCO3-) + 2c(H2CO3)D.c(Na+) + c(H+) =c(OH-) + 2c(CO32-) + c(HCO3-)【合作探究】★★1、某二元酸(化学式H2A表示)在水中的电离方程式为:H2A=H+ + HA-;HA-H+ + A2-请回答下列问题:⑴ Na2A 溶液显(填“酸性”“中性”或“碱性”),理由是(用离子方程式表示)__________⑵若0.1mol/LNaHA溶液的PH=2,则0.1mol/LH2A溶液中H+的物质的量浓度可能0.11mol/L(填“>” “<”或“=”),理由是⑶ 0.1mol/LNaHA溶液中各种离子浓度由大到小的顺序是______2、现有常温下的0.1mol/L纯碱溶液:⑴你认为该溶液呈碱性的原因是(用离子方程式表示):________________________。


高三化学一轮复习学案 31 常见气体的实验室制备【基础知识回顾】知识点1---(1(2知识点2---(1)设计原则 (2)常见气体制备的反应原理 氧气:2KClO 32KMnO 4H 2O 2Na 2O 2+ H 2O=氨气:2NH 4Cl+Ca(OH)2 NH 3·H 2O NH 3↑+H 2O (CaO 可换成 )氢气:Zn+H 2SO 4(稀)= 二氧化碳:CaCO 3 + HCl== 二氧化硫:Na 2SO 3+H 2SO 4(浓)= Cu+2H 2SO 4浓)二氧化氮; Cu +4HNO 3(浓)==氯气:MnO 2+4HCl(浓)=== 2KMnO 4+16HCl=2KCl+2MnCl 2+5Cl 2↑+8H 2O一氧化氮:3Cu +8HNO 3(稀) ═乙烯: 乙炔: CaC 2+2H 2O→O 2、NH 3、CH 4等 H 2、CO 2、SO 2、Cl 2、NO 、CH 2=CH 2等(1)可通过分液漏斗来控(1)加细瓷片。
(2)若用排水法收集气体,停止加热前,应先将导气管从水中取出。
改良装置:1、杂质产生原因:①反应过程中有挥发性物质,如用盐酸制取的气体中一般有HCl ;从溶液中冒出的气体中含有水气。
②副反应或杂质参加反应引起,如制乙烯时含SO2、CO 2等。
23、气体净化剂的选择一般情况下:①易溶于水的气体杂质可用水来吸收;②酸性杂质可用碱性物质吸收;③碱性杂质可用酸性物质吸收;④水分可用干燥剂来吸收;⑤能与杂质反应生成沉淀(或可溶物)的物质也可作为吸收剂。
4、气体干燥剂的类型及选择①酸性干燥剂,如浓硫酸、五氧化二磷、硅胶。
干燥显酸性或中性的气体,如 ②碱性干燥剂,如生石灰、碱石灰、固体NaOH 。
可以用来干燥NH 3或中性的气体,如 ③中性干燥剂,如无水氯化钙等,不能用CaCl 2来干燥NH 3(因生成 CaCl 2〃8NH 3), 不能用浓 H 2SO 4干燥 NH 3、H 2S 、HBr 、HI 等。
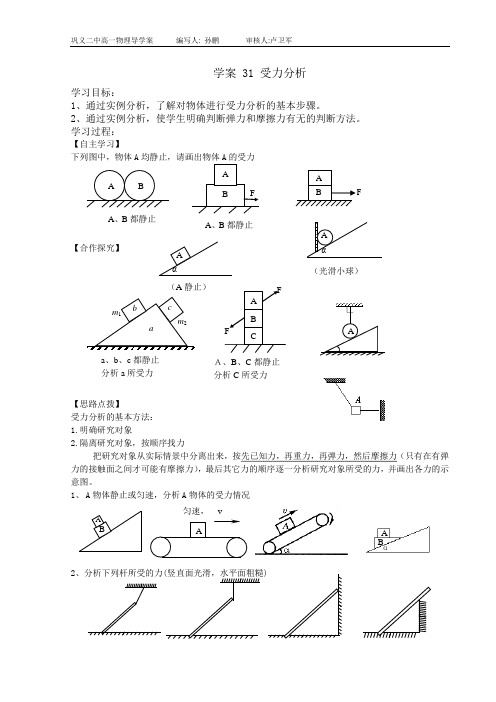
学案 31 受力分析
学习目标:
1、通过实例分析,了解对物体进行受力分析的基本步骤。
2、通过实例分析,使学生明确判断弹力和摩擦力有无的判断方法。
学习过程:
【自主学习】
下列图中,物体A 均静止,请画出物体A 的受力
【合作探究】
【思路点拨】
受力分析的基本方法: 1.明确研究对象
2.隔离研究对象,按顺序找力
把研究对象从实际情景中分离出来,按先已知力,再重力,再弹力,然后摩擦力(只有在有弹力的接触面之间才可能有摩擦力),最后其它力的顺序逐一分析研究对象所受的力,并画出各力的示意图。
1、 A 物体静止或匀速,分析A 物体的受力情况
2、分析下列杆所受的力
A B
A 、
B 都静止
A 、
B 都静止
(A 静止) (光滑小球)
a 、
b 、
c 都静止 分析a 所受力 A、B 、C 都静止 分析C 所受力 α B
A 匀速, v
3.分析A的受力
(A静止) (A匀速下滑)
A沿着墙匀速向上
A
沿着水平面匀速向右
A沿着斜面向上运动
A静止
C
(A、B一起匀速向右运动)
光滑小球。

第一单元第三课发现自己第一框认识自己自主学习主干梳理1.我们越来越关注自我的原因是什么?进入初中,随着的不断增强,我们越来越关注自我。
2.正确认识自己有什么重要的意义?(1)可以促进。
每个人都是独一无二的个体,认识到自己的禀赋和独特性,有助于我们增强对自己的信心,更好地发展自己的能力。
(2)可以促进与。
①有助于我们认识到自己离不开。
②更好地理解、他人,与他人积极互动。
3.我们可以从哪些方面来认识自己?(1)方面:从身体特征和生理状况来认识自己,如自己的身材、相貌、体能、性别等。
(2)方面:从个性心理特征来认识自己,如性格、气质等。
(3)方面:从在群体中的关系来认识自己,如自己在家庭或班级中的角色等。
4.认识目己的途径有哪些?这对正确认识目已有什么意义?5.怎样正确对待他人评价?(1)要他人的态度与评价,但也要客观冷静分析,既不能,也不能忽视。
(2)用面对他人的评价,是走向成熟的表现。
合作探究,热点剖析1.人贵自知【关键词】孙杨发现自己的不足在20XX年全国游泳冠军赛男子1500米自由泳决赛中,孙杨轻松夺冠,最终收获4枚个人项目金牌。
赛后孙杨表示:“通过比赛发现了我自己很多细节上的不足,这会令我更强大。
真正的较量还是在世锦赛上。
”孙杨对自己夺得世锦赛冠军非常有信心。
(1)孙杨对自己的认识是否正确?为什么?(2)你觉得这种认识会对孙杨产生怎样的影响?2.多把尺子量自己【关键词】了解自己认识自己在一次班会上,同学们围绕“了解自己,认识自己,融入新的集体”展开了一次讨论并积极发言。
同学甲:我做值日不太积极,有时还迟到。
我认识到我没有积极维护集体利益。
同学乙:我的同桌遇到难题经常请别的同学讲解,却不找我。
他认为我对他人缺乏热情。
同学丙:学校体育运动会上,我克服困难积极为班级争得荣誉,同学们对我称赞不已。
(1)上述这些同学通过哪些途径认识和评价自己?(2)这对他们的人生会起到什么作用?(3)你认为他们应如何面对同学们的评价?参考答案第一框认识自己真主学习主干梳理1.自我意识2.(1)自我发展(2)他人的交往①他人和社会②宽容和善待3.(1)生理(2)心理(3)社会4.自我②调节和控制他人①他人评价②客观完整清晰5.(1)重视盲从(2)理性的心态合作探究热点剖析1.点拨:(1)正确。

1第三章基因的本质第一节DNA 是主要的遗传物质(Ⅱ)[目标导读]1.结合教材P 44图3—4及相关内容,掌握噬菌体的结构及增殖的过程;2.阅读教材P 45第一段,理解并掌握标记噬菌体的方法及原因;3.结合教材图3—6及相关实验,分析噬菌体侵染细菌的过程,掌握放射性分布不同的原因以及得出的结论;4.阅读教材P 46相关内容,分析并掌握不同生物的遗传物质。
课前自主预习案[自主梳理]一、噬菌体侵染细菌的实验为了进一步研究生物的遗传物质,赫尔希和蔡斯以T 2噬菌体为实验材料,做了利用放射性同位素标记的噬菌体侵染细菌的实验,阅读教材,结合材料完成下面的思考。
1.实验材料——T 2噬菌体(1)①结构(如图1):由头部和尾部组成,头部和尾部的外壳都是由__________构成的,头部内含有________。
②特点:一种专门寄生在大肠杆菌体内的细菌病毒,在宿主细胞外_______(有、没有)独立代谢能力。
③生活史(如图2):T 2噬菌体侵染大肠杆菌后,会在__________的作用下,利用__________体内的物质来合成自身的组成成分,进行大量增殖。
当噬菌体增殖到一定数量后,大肠杆菌________,释放出子代噬菌体。
(2)大肠杆菌:单细胞___核生物。
2.实验方法:______________法,用____标记一部分噬菌体的蛋白质,用____标记另一部分噬菌体的DNA 。
3.实验过程和结果24.实验分析(1)实验中能否直接用含有放射性同位素的培养基来培养噬菌体呢?(2)实验中搅拌的目的是使________________________分离;离心的目的是让上清液中析出重量较轻的_________,离心管的沉淀物中留下____________。
(3)实验中需用___标记蛋白质,用___标记DNA ,不用其他元素的原因是蛋白质的组成元素是C 、H 、O 、N ,大部分含有___,DNA 的组成元素为____________,只有标记S 、P 两种元素才能够分别标记蛋白质和DNA 。
31化学元素与健康预习学案化学元素是构成物质的基本单位,对于维持人体健康起着重要的作用。
本预习学案将介绍与健康密切相关的31个化学元素,包括它们的特性、作用以及人体对它们的需求。
一、微量元素1.钴(Co):作为维生素B12的重要组成部分,参与细胞分裂和血红素合成,维持神经系统和脑功能。
2.铜(Cu):参与血液和胶原蛋白的合成,维持免疫系统和铁的吸收,促进骨骼发育和神经传导。
3.铁(Fe):是血红蛋白和肌红蛋白的组成部分,参与氧气运输和呼吸作用,维持健康的血液循环和免疫系统。
4.锰(Mn):是多种重要酶的辅助因子,参与氨基酸代谢和骨骼形成,维持神经系统和血糖稳定。
5.硒(Se):具有很强的抗氧化作用,参与甲状腺功能、免疫系统和基因表达的调节,预防心血管疾病和癌症。
6.锌(Zn):参与酶的活性和DNA合成,维持免疫系统和生长发育,促进伤口愈合和味觉感知。
7.钼(Mo):作为辅酶参与多种代谢反应,包括氨基酸和嘌呤的合成,维持神经系统和肝脏功能。
8.碘(I):是甲状腺素的组成部分,参与代谢和神经发育,维持正常的能量代谢和体温调节。
9.硼(B):可能与钙代谢和骨骼健康有关,参与维持细胞膜和细胞通透性。
二、主要元素10.氢(H):是构成水分子的主要元素,维持体内的水平衡和酸碱平衡。
11.氧(O):是呼吸和氧化作用的重要元素,为身体提供能量。
12.碳(C):是有机物的基础元素,构成脂肪、蛋白质和碳水化合物等营养物质。
13.氮(N):是构成蛋白质和核酸的基础元素,参与细胞生长和修复。
14.硫(S):构成蛋白质的硫氨酸和甲硫氨酸,维持骨骼和关节的健康。
15.钙(Ca):是骨骼和牙齿的基础元素,参与神经传导、酶的活性和血液凝固。
16.钠(Na)和17.钾(K):维持细胞内外的水平衡、神经传导和肌肉收缩。
18.磷(P):构成DNA和RNA的组成部分,参与能量代谢和骨骼健康。
19.氯(Cl):是体液和胃酸的主要组成成分,维持水平衡和酸碱平衡。
学案31 机械能【学习目标】1.理解机械能的基本组成;2.理解动能与重力势能的影响因素;3.能进行动能影响因素的实验探究。
【知识梳理】一.机械能的组成二.动能与重力势能的影响因素【典例分析】1.一个物体,我们就说它具有能量。
一个物体越多,表示这个物体的能量越大。
2.物体由于运动而具有的能叫做;物体由于被举高而具有的能叫做;物体由于发生弹性形变而具有的能叫做。
3.运动物体的越大,越大,具有的动能就越大。
4.物体被举得越高,质量越大,它具有的重力势能就。
5.判断下列情况下物体的动能、重力势能、机械能的变化情况。
(选填“增大”或“减小”“不变”)(l)在平直轨道上,列车从车站启动,动能,势能,机械能。
(2)站在匀速下降的电梯中的乘客,动能,势能,机械能。
6.人推开弹簧门的过程中,弹簧由于发生弹性形变而具有能;当弹簧门自动关闭的过程中,弹簧由于形变减小,其能减小,能转化为门的能。
7.骑自行车上坡前,往往要加紧蹬几下,这是为了增大能;下坡时不蹬,速度还会越来越大,这是因为能转化为能。
8.跳伞运动员跳出机舱后,在打开降落伞之前,他的动能将,重力势能将,机械能;打开降落伞后匀速下降时,他的动能将,重力势能将,机械能将。
(选填“变大”或“不变”“变小”)。
9.匀速行驶的洒水车,在洒水过程之中动能,机械能 .【课堂达标】1.下列说法正确的是( )A.做完功的物体一定具有能B.能够做功的物体一定具有能C.没有做功的物体不具有能D.具有能的物体一定在做功2.下列情况中,属于势能转化为动能的是()。
A.火箭发射升空 B.玩具弹簧枪将子弹水平射出C.单摆的摆球从最低点上升 D.足球在地上越滚越慢3.下列情况中,属于动能转化为势能的是()。
A.爆竹爆炸 B.上紧的钟表发条带动指针转动C.滚摆上升 D.雪橇从山坡上滑下.4飞机在高空水平方向上匀速飞行,同时空投救灾物品,在飞机空投救灾物品的前后,飞机的动能和重力势能变化的情况是()A.动能增加,重力势能减少B.动能减少,重力势能增加C.动能和重力势能都增加D.动能和重力势能都减少5、一个小朋友从滑梯上匀速滑下来的过程中,下列说法正确的是 ( )A、动能减小,重力势能减小,机械能减小B、动能减小,重力势能增大,机械能减小C、动能不变,重力势力减小,机械能减小D、动能不变,重力势能减小,机械能不变6、跳伞运动员跳出飞机舱门,打开降落伞前他下降的速度越来越大,这一过程运动员的A.动能增大,重力势能增大 B.动能增大,重力势能减小C.动能减小,重力势能增大 D.动能减小,重力势能减小7.说明下列物体具有哪种形式的机械..能.:⑴在水平轨道上行驶的火车具有____________________。
复习课题:第三单元明清帝国的繁盛与近代前夜的危机(2)学习目标:识记:明清科技文学成就;郑和下西洋概况;康乾盛世;近代因素的出现;理解:明清的外交政策;封建制度衰弱的趋势;近代繁荣下的危机;学习重点:明清的民族、外交政策及表现;闭关政策;学习难点:封建制度衰弱的趋势;近代繁荣下的危机;◆成功第一步:巩固基础、构建知识体系第2 1课大一统的气派与中华民族的象征一、明清皇宫1、北京建都史:把都城从南京迁到了。
清朝继续定都北京。
2、北京城布局:①由外向里依次为、和。
宫城旧称,现在称。
②紫禁城前方的左右两侧分布着气象庄严的和。
3、宫城:①象征政权中心的三大殿是、、。
②故宫是我国现存、的古建筑群。
二、明长城1、修建目的:防范。
2、规模:东起,西至,全长多千米,规模、质量都达到历史最高水平。
第22课科学技术与世俗文学1、明清科技、文化成就著作作者内容成就记载1879种药物,11000则药方,图文并茂描写了东汉及三国各统治集团政治、军事、外交的斗争;是我国第一部;反映了元末人民渴望统一;北宋末年宋江起义围绕“官逼民反”的主题,揭露了当时社会的黑暗,唐玄奘西天取经的故事反映人民要求挣脱束缚,追求自由的愿望。
贾宝玉和林黛玉的爱情悲剧为主线它是中国的巅峰;揭示了清王朝走向衰亡的命运。
明清科技特点:(1),注重运用数理方法,开始显露出近代科学研究的特点;(2)由于实行、。
总体上与西方科技水平的差距越拉越大。
2、明清文化趋势:明朝中后期,兴起。
明清小说出现条件:(1)工商业市镇的繁荣;(2)书坊、刊刻印刷业的迅速发展。
第23课从郑和下西洋到闭关锁国一、郑和下西洋1、时间:—年,明政府先后次派郑和下西洋。
2、目的:和3、概况:到达亚非三十多个国家,最远到达和一带。
4、★意义:③5、废止原因:①主要目的是和到西洋“取宝”,不计。
②明朝国力。
二、★闭关政策1、含义:清廷对对外贸易进行严格的,并非完全断绝往来。
2、影响:②启示:开放导致繁荣,闭关锁国导致衰落,在社会主义建设中,必须坚持对外开放的政策。
学案31 数列的通项与求和导学目标: 1.能利用等差、等比数列前n 项和公式及其性质求一些特殊数列的和.2.能在具体的问题情境中,识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.自主梳理1.求数列的通项(1)数列前n 项和S n 与通项a n 的关系:a n =⎩⎪⎨⎪⎧S 1, n =1,S n -S n -1, n ≥2.(2)当已知数列{a n }中,满足a n +1-a n =f (n ),且f (1)+f (2)+…+f (n )可求,则可用________求数列的通项a n ,常利用恒等式a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1).(3)当已知数列{a n }中,满足a n +1a n=f (n ),且f (1)·f (2)·…·f (n )可求,则可用__________求数列的通项a n ,常利用恒等式a n =a 1·a 2a 1·a 3a 2·…·a na n -1.(4)作新数列法:对由递推公式给出的数列,经过变形后化归成等差数列或等比数列来求通项.(5)归纳、猜想、证明法. 2.求数列的前n 项的和 (1)公式法①等差数列前n 项和S n =____________=________________,推导方法:____________;②等比数列前n 项和S n =⎩⎪⎨⎪⎧,q =1,= ,q ≠1.推导方法:乘公比,错位相减法. ③常见数列的前n 项和:a .1+2+3+…+n =__________;b .2+4+6+…+2n =__________;c .1+3+5+…+(2n -1)=______;d .12+22+32+…+n 2=__________;e .13+23+33+…+n 3=__________________.(2)分组求和:把一个数列分成几个可以直接求和的数列. (3)裂项(相消)法:有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和.常见的裂项公式有:①1n (n +1)=1n -1n +1; ②1(2n -1)(2n +1)=12⎝⎛⎭⎫12n -1-12n +1;③1n +n +1=n +1-n .(4)错位相减:适用于一个等差数列和一个等比数列对应项相乘构成的数列求和. (5)倒序相加:例如,等差数列前n 项和公式的推导. 自我检测 1.(原创题)已知数列{a n }的前n 项的乘积为T n =3n 2(n ∈N *),则数列{a n }的前n 项的( ) A.32(3n -1) B.92(3n -1)C.38(9n -1)D.98(9n -1) 2.(2011·邯郸月考)设{a n }是公比为q 的等比数列,S n 是其前n 项和,若{S n }是等差数列,则q 为 ( )A .-1B .1C .±1D .03.已知等比数列{a n }的公比为4,且a 1+a 2=20,设b n =log 2a n ,则b 2+b 4+b 6+…+b 2n 等于 ( )A .n 2+nB .2(n 2+n )C .2n 2+nD .4(n 2+n )4.(2010·天津高三十校联考)已知数列{a n }的通项公式a n =log 2n +1n +2(n ∈N *),设{a n }的前n 项的和为S n ,则使S n <-5成立的自然数n ( )A .有最大值63B .有最小值63C .有最大值31D .有最小值31 5.(2011·北京海淀区期末)设关于x 的不等式x 2-x <2nx (n ∈N *)的解集中整数的个数为a n ,数列{a n }的前n 项和为S n ,则S 100的值为________.6.数列1,412,714,1018,…前10项的和为________.探究点一 求通项公式例1 已知数列{a n }满足a n +1=2n +1·a na n +2n +1,a 1=2,求数列{a n }的通项公式.变式迁移1 设数列{a n }的前n 项和为S n ,已知a 1=1,S n +1=4a n +2. (1)设b n =a n +1-2a n ,证明数列{b n }是等比数列; (2)求数列{a n }的通项公式.探究点二 裂项相消法求和例2 已知数列{a n },S n 是其前n 项和,且a n =7S n -1+2(n ≥2),a 1=2. (1)求数列{a n }的通项公式;(2)设b n =1log 2a n ·log 2a n +1,T n 是数列{b n }的前n 项和,求使得T n <m20对所有n ∈N *都成立的最小正整数m .变式迁移2 求数列1,11+2,11+2+3,…,11+2+3+…+n,…的前n 项和.探究点三 错位相减法求和 例3 (2011·荆门月考)已知数列{a n }是首项、公比都为q (q >0且q ≠1)的等比数列,b n=a n log 4a n (n ∈N *).(1)当q =5时,求数列{b n }的前n 项和S n ;(2)当q =1415时,若b n <b n +1,求n 的最小值.变式迁移3 求和S n =1a +2a 2+3a 3+…+nan .分类讨论思想的应用例 (5分)二次函数f (x )=x 2+x ,当x ∈[n ,n +1](n ∈N *)时,f (x )的函数值中所有整数值的个数为g (n ),a n =2n 3+3n 2g (n )(n ∈N *),则S n =a 1-a 2+a 3-a 4+…+(-1)n -1a n =( )A .(-1)n -1n (n +1)2 B .(-1)n n (n +1)2C.n (n +1)2 D .-n (n +1)2【答题模板】 答案 A解析 本题考查二次函数的性质以及并项转化法求和.当x ∈[n ,n +1](n ∈N *)时,函数f (x )=x 2+x 的值随x 的增大而增大,则f (x )的值域为[n 2+n ,n 2+3n +2](n ∈N *),∴g (n )=2n +3(n ∈N *),于是a n =2n 3+3n 2g (n )=n 2.方法一 当n 为偶数时,S n =a 1-a 2+a 3-a 4+…+a n -1-a n =(12-22)+(32-42)+…+[(n -1)2-n 2]=-[3+7+…+(2n -1)]=-3+(2n -1)2·n 2=-n (n +1)2;当n 为奇数时,S n =(a 1-a 2)+(a 3-a 4)+…+(a n -2-a n -1)+a n=S n -1+a n =-n (n -1)2+n 2=n (n +1)2,∴S n =(-1)n -1n (n +1)2.方法二 a 1=1,a 2=4,S 1=a 1=1, S 2=a 1-a 2=-3,检验选择项,可确定A 正确. 【突破思维障碍】在利用并项转化求和时,由于数列的各项是正负交替的,所以一般需要对项数n 进行分类讨论,但最终的结果却往往可以用一个公式来表示.1.求数列的通项:(1)公式法:例如等差数列、等比数列的通项; (2)观察法:例如由数列的前几项来求通项;(3)可化归为使用累加法、累积法;(4)可化归为等差数列或等比数列,然后利用公式法; (5)求出数列的前几项,然后归纳、猜想、证明. 2.数列求和的方法:一般的数列求和,应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为与特殊数列有关或具备某种方法适用特点的形式,从而选择合适的方法求和.3.求和时应注意的问题:(1)直接用公式求和时,注意公式的应用范围和公式的推导过程.(2)注意观察数列的特点和规律,在分析数列通项的基础上或分解为基本数列求和,或转化为基本数列求和.(满分:75分)一、选择题(每小题5分,共25分) 1.(2010·广东)已知数列{a n }为等比数列,S n 是它的前n 项和,若a 2·a 3=2a 1且a 4与2a 7的等差中项为54,则S 5等于( )A .35B .33C .31D .292.(2011·黄冈调研)有两个等差数列{a n },{b n },其前n 项和分别为S n ,T n ,若S n T n =7n +2n +3,则a 5b 5=( )A.6512B.378C.7213D.943.如果数列{a n }满足a 1=2,a 2=1且a n -1-a n a n a n -1=a n -a n +1a n a n +1(n ≥2),则此数列的第10项( )A.1210B.129C.110D.154.数列{a n }的前n 项和为S n ,若a n =1n (n +1),则S 5等于 ( )A .1 B.56 C.16 D.1305.数列1,1+2,1+2+4,…,1+2+22+…+2n -1,…的前n 项和S n >1 020,那么n 的最小值是 ( )6.(2010·东北师大附中高三月考)数列{a n }的前n 项和为S n 且a 1=1,a n +1=3S n (n =1,2,3,…),则log 4S 10=__________.7.(原创题)已知数列{a n }满足a 1=1,a 2=-2,a n +2=-1a n,则该数列前26项的和为________.8.对于数列{a n },定义数列{a n +1-a n }为数列{a n }的“差数列”,若a 1=2,{a n }的“差数列”的通项为2n ,则数列{a n }的前n 项和S n =____________.三、解答题(共38分) 9.(12分)(2011·河源月考)已知函数f (x )=x 2-2(n +1)x +n 2+5n -7(n ∈N *).(1)若函数f (x )的图象的顶点的横坐标构成数列{a n },试证明数列{a n }是等差数列; (2)设函数f (x )的图象的顶点到x 轴的距离构成数列{b n },试求数列{b n }的前n 项和S n .10.(12分)(2011·三门峡月考)设等差数列{a n }的前n 项和为S n ,且S n =12na n +a n -c (c 是常数,n ∈N *),a 2=6.(1)求c 的值及数列{a n }的通项公式;(2)证明1a 1a 2+1a 2a 3+…+1a n a n +1<18.11.(14分)(2010·北京宣武高三期中)已知数列{a n }的前n 项和为S n =3n ,数列{b n }满足b 1=-1,b n +1=b n +(2n -1) (n ∈N *).(1)求数列{a n }的通项公式a n ; (2)求数列{b n }的通项公式b n ;(3)若c n =a n ·b nn,求数列{c n }的前n 项和T n .答案 自主梳理1.(2)累加法 (3)累积法 2.(1)①n (a 1+a n )2 na 1+n (n -1)2d 倒序相加法 ②na 1a 1(1-q n )1-q a 1-a n q 1-q③n (n +1)2 n 2+n n 2 n (n +1)(2n +1)6⎣⎡⎦⎤n (n +1)22自我检测1.C 2.B 3.B 4.B5.10 100 6.145511512课堂活动区例1 解题导引 已知递推关系求通项公式这类问题要求不高,主要掌握由a 1和递推关系先求出前几项,再归纳、猜想a n 的方法,以及累加:a n =(a n -a n -1)+(a n -1-a n -2)+…+(a 2-a 1)+a 1;累乘:a n =a n a n -1·a n -1a n -2·…·a 2a 1·a 1等方法.解 已知递推可化为 1a n +1-1a n =12n +1, ∴1a 2-1a 1=122,1a 3-1a 2=123,1a 4-1a 3=124,…,1a n -1a n -1=12n . 将以上(n -1)个式子相加得 1a n -1a 1=122+123+124+…+12n ,∴1a n =12⎝⎛⎭⎫1-12n 1-12=1-12n . ∴a n =2n2n -1.变式迁移1 (1)证明 由已知有 a 1+a 2=4a 1+2,解得a 2=3a 1+2=5,故b 1=a 2-2a 1=3. 又a n +2=S n +2-S n +1=4a n +1+2-(4a n +2) =4a n +1-4a n ;于是a n +2-2a n +1=2(a n +1-2a n ), 即b n +1=2b n .因此数列{b n }是首项为3,公比为2的等比数列. (2)解 由(1)知等比数列{b n }中,b 1=3,公比q =2,所以a n +1-2a n =3×2n -1,于是a n +12n +1-a n 2n =34,因此数列⎩⎨⎧⎭⎬⎫a n 2n 是首项为12,公差为34的等差数列,a n 2n =12+(n -1)×34=34n -14, 所以a n =(3n -1)·2n -2.例2 解题导引 1.利用裂项相消法求和时,应注意抵消后并不一定只剩下第一项和最后一项,也有可能前面剩两项,后面也剩两项.再就是将通项公式裂项后,有时候需要调整前面的系数,使裂开的两项之差和系数之积与原通项公式相等.2.一般情况如下,若{a n }是等差数列,则1a n a n +1=1d ⎝⎛⎭⎫1a n -1a n +1,1a n a n +2=12d ⎝⎛⎭⎫1a n -1a n +2. 此外根式在分母上时可考虑利用有理化因式相消求和. 解 (1)∵n ≥2时,a n =7S n -1+2,∴a n +1=7S n +2, 两式相减,得a n +1-a n =7a n ,∴a n +1=8a n (n ≥2). 又a 1=2,∴a 2=7a 1+2=16=8a 1, ∴a n +1=8a n (n ∈N *).∴{a n }是一个以2为首项,8为公比的等比数列,∴a n =2·8n -1=23n -2.(2)∵b n =1log 2a n ·log 2a n +1=1(3n -2)(3n +1)=13(13n -2-13n +1), ∴T n =13(1-14+14-17+…+13n -2-13n +1)=13(1-13n +1)<13. ∴m 20≥13,∴最小正整数m =7. 变式迁移2 解 a n =2n (n +1)=2⎝⎛⎭⎫1n -1n +1,∴S n =2·[⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫1n -1n +1]=2·⎝⎛⎭⎫1-1n +1=2n n +1. 例3 解题导引 1.一般地,如果数列{a n }是等差数列,{b n }是等比数列,求数列{a n ·b n }的前n 项和时,可采用错位相减法.2.用乘公比错位相减法求和时,应注意:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n -qS n ”的表达式.解 (1)由题意得a n =q n , ∴b n =a n ·log 4a n =q n ·log 4q n =n ·5n ·log 45,∴S n =(1×5+2×52+…+n ×5n )log 45, 设T n =1×5+2×52+…+n ×5n ,①则5T n =1×52+2×53+…+(n -1)×5n +n ×5n +1,②①-②得-4T n =5+52+53+…+5n -n ×5n +1 =5(5n -1)4-n ×5n +1,∴T n =516(4n ×5n -5n +1),S n =516(4n ×5n -5n +1)log 45.(2)∵b n =a n log 4a n =n ⎝⎛⎭⎫1415n log 41415,∴b n +1-b n =(n +1)⎝⎛⎭⎫1415n +1log 41415- n ⎝⎛⎭⎫1415n log 41415 =⎝⎛⎭⎫1415n ⎝⎛⎭⎫1415-n 15log 41415>0, ∵⎝⎛⎭⎫1415n >0,log 41415<0, ∴1415-n15<0,∴n >14, 即n ≥15时,b n <b n +1.故所求的n 的最小值是15. 变式迁移3 解 当a =1时,S n =1+2+3+…+n =n (n +1)2,当a ≠1时,S n =1a +2a 2+3a 3+…+nan ,①∴1a S n =1a 2+2a 3+3a 4+…+nan +1,② ①-②,得⎝⎛⎭⎫1-1a ·S n=1a +1a 2+1a 3+…+1a n -n an +1, ⎝⎛⎭⎫1-1a S n =1a ⎝⎛⎭⎫1-1a n 1-1a-n a n +1=1-1a na -1-n an 1, ∴S n =a ⎝⎛⎭⎫1-1a n (a -1)2-n(a -1)·a n.∴S n=⎩⎪⎨⎪⎧n (n +1)2, a =1,a ⎝⎛⎭⎫1-1a n (a -1)2-n (a -1)·an, a ≠1.课后练习区1.C 2.A 3.D 4.B 5.D 6.9解析 ∵a n +1=3S n ,∴a n =3S n -1 (n ≥2). 两式相减得a n +1-a n =3(S n -S n -1)=3a n ,∴a n +1=4a n ,即a n +1a n=4.∴{a n }为以a 2为首项,公比为4的等比数列. 当n =1时,a 2=3S 1=3,∴n ≥2时,a n =3·4n -2, S 10=a 1+a 2+…+a 10=1+3+3×4+3×42+...+3×48 =1+3×(1+4+ (48)=1+3×49-14-1=1+49-1=49.∴log 4S 10=log 449=9. 7.-10解析 依题意得,a 1=1,a 2=-2,a 3=-1,a 4=12,a 5=1,a 6=-2,a 7=-1,a 8=12,所以数列周期为4,S 26=6×(1-2-1+12)+1-2=-10.8.2n +1-2解析 依题意,有a 2-a 1=2,a 3-a 2=22,a 4-a 3=23,…,a n -a n -1=2n -1,所有的代数式相加得a n -a 1=2n -2,即a n =2n ,所以S n =2n +1-2.9.解 f (x )=x 2-2(n +1)x +n 2+5n -7=[x -(n +1)]2+3n -8.…………………………………………………………………(3分) (1)由题意,a n =n +1,故a n +1-a n =(n +1)+1-(n +1)=1, 故数列{a n }是以1为公差,2为首项的等差数列.……………………………………(5分) (2)由题意,b n =|3n -8|.……………………………………………………………………(7分)当1≤n ≤2时,b n =-3n +8, 数列{b n }为等差数列,b 1=5,∴S n =n (5-3n +8)2=-3n 2+13n 2;………………………………………………………(9分)当n ≥3时,b n =3n -8,数列{b n }是等差数列,b 3=1.∴S n =S 2+(n -2)(1+3n -8)2=3n 2-13n +282.…………………………………………(11分)∴S n=⎩⎨⎧-3n 2+13n2, 1≤n ≤2,3n 2-13n +282, n ≥3.……………………………………………(12分)10.(1)解 因为S n =12na n +a n -c ,所以当n =1时,S 1=12a 1+a 1-c ,解得a 1=2c ,………………………………………………………………………………(2分)当n =2时,S 2=a 2+a 2-c , 即a 1+a 2=2a 2-c ,解得a 2=3c ,………………………………………………………(3分) 所以3c =6,解得c =2;…………………………………………………………………(4分)则a 1=4,数列{a n }的公差d =a 2-a 1=2,所以a n =a 1+(n -1)d =2n +2.……………………………………………………………(6分)(2)证明 因为1a 1a 2+1a 2a 3+…+1a n a n +1=14×6+16×8+…+1(2n +2)(2n +4) =12(14-16)+12(16-18)+…+12(12n +2-12n +4) =12[(14-16)+(16-18)+…+(12n +2-12n +4)]……………………………………………(8分) =12(14-12n +4)=18-14(n +2).……………………………………………………………(10分)因为n ∈N *,所以1a 1a 2+1a 2a 3+…+1a n a n +1<18.…………………………………………(12分)11.解 (1)∵S n =3n ,∴S n -1=3n -1 (n ≥2).∴a n =S n -S n -1=3n -3n -1=2×3n -1 (n ≥2).……………………………………………(3分)当n =1时,2×31-1=2≠S 1=a 1=3,…………………………………………………(4分)∴a n =⎩⎪⎨⎪⎧3, n =1,2×3n -1, n ≥2, n ∈N *……………………………………………………(5分) (2)∵b n +1=b n +(2n -1),∴b 2-b 1=1,b 3-b 2=3,b 4-b 3=5,…, b n -b n -1=2n -3. 以上各式相加得b n -b 1=1+3+5+…+(2n -3) =(n -1)(1+2n -3)2=(n -1)2.∵b 1=-1,∴b n =n 2-2n .………………………………………………………………(7分) (3)由题意得c n =⎩⎪⎨⎪⎧-3,n =1,2(n -2)×3n -1,n ≥2,n ∈N *.……………………………………………………(9分)当n ≥2时,T n =-3+2×0×31+2×1×32+2×2×33+…+2(n -2)×3n -1, ∴3T n =-9+2×0×32+2×1×33+2×2×34+…+2(n -2)×3n ,相减得-2T n =6+2×32+2×33+…+2×3n -1-2(n -2)×3n .∴T n =(n -2)×3n -(3+32+33+…+3n -1)=(n -2)×3n-3n -32=(2n -5)3n +32.…………………………………………………(13分)T 1=-3也适合.∴T n =(2n -5)3n +32(n ∈N *).…………………………………………………………(14分)。