浙江省高考真题三角函数

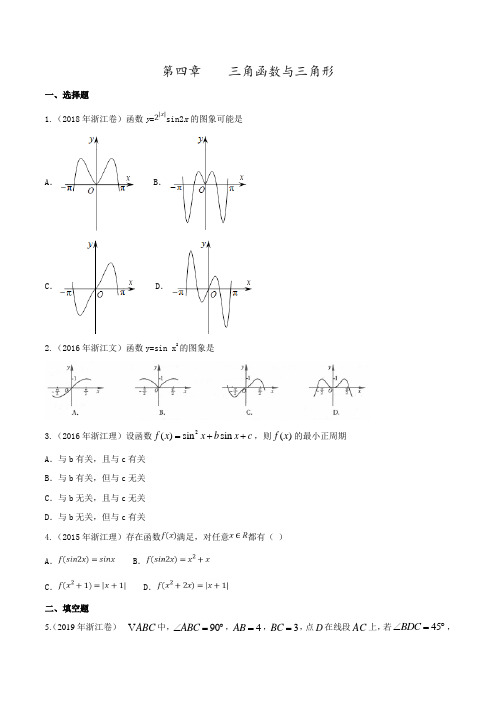
第四章 三角函数与三角形一、选择题1.（2018年浙江卷）函数y =sin2x 的图象可能是A ．B ．C ．D ．2.（2016年浙江文）函数y=sin x 2的图象是3.（2016年浙江理）设函数2()sin sin f x x b x c =++，则()f x 的最小正周期A ．与b 有关，且与c 有关B ．与b 有关，但与c 无关C ．与b 无关，且与c 无关D ．与b 无关，但与c 有关4.（2015年浙江理）存在函数满足，对任意都有（ ） A ．B ．C ．D ．二、填空题5.（2019年浙江卷）V ABC 中，90ABC ∠=︒，4AB =，3BC =，点D 在线段AC 上，若45BDC ∠=︒，则BD =____；cos ABD ∠=________.6.（2018年浙江卷）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ．若，b=2，A=60°，则sinB=___________，c=___________．7.（2017年浙江卷）我国古代数学家刘徽创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度．祖冲之继承并发展了“割圆术”，将π的值精确到小数点后七位，其结果领先世界一千多年，“割圆术”的第一步是计算单位圆内接正六边形的面积，________． 8.（2017年浙江卷）已知△ABC ，AB =AC =4，BC =2． 点D 为AB 延长线上一点，BD =2，连结CD ，则△BDC 的面积是______，cos ∠BDC =_______．9.（2016年浙江文）已知22cos sin 2sin()(0)x x A x b A ωϕ+=++>，则A =_______，b=______． 10.（2016年浙江理）已知2cos 2x+sin 2x=Asin(ωx+φ)+b(A ＞0)，则A=______，b=________．11.（2015年浙江文）函数的最小正周期是__________，单调递增区间是__________.12.（2015年浙江理）函数的最小正周期是 ，单调递减区间是 ． 三、解答题13.（2019年浙江卷）设函数()sin ,f x x x =∈R .（1）已知[0,2),θ∈π函数()f x θ+是偶函数，求θ的值；（2）求函数22[()][()]124y f x f x ππ=+++ 的值域. 14.（2018年浙江卷）已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点P （）． （Ⅰ）求sin （α+π）的值；（Ⅱ）若角β满足sin （α+β）=，求cos β的值．15.（2017年浙江卷）已知函数()()22f x sin x cos x x R =--∈（I ）求2f 3π⎛⎫ ⎪⎝⎭的值 （II ）求()f x 的最小正周期及单调递增区间.16.（2016年浙江文）在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c.已知b+c="2acos" B.（Ⅰ）证明：A=2B ；（Ⅱ）若cos B=，求cos C 的值．17.（2016年浙江理）在ABC ∆中，内角,,A B C 所对的边分别为,,a b c ，已知2cos b c a B +=．（1）证明： 2A B =；（2）若ABC ∆的面积24a S =，求角A 的大小． 18.（2015年浙江文）在中，内角A ，B ，C 所对的边分别为.已知.（1）求的值；（2）若，求的面积.19.（2015年浙江理）在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知4A π=，22b a -=122c . （1）求tan C 的值；（2）若ABC ∆的面积为7，求b 的值.。

一．基础题组1. 【2014年.浙江卷.理4】为了得到函数x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（ ）A.向右平移4π个单位B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位答案：Ｄ解析：sin 3cos3234y x x x π⎛⎫=+=+ ⎪⎝⎭，故只需将23y x =向左平移4π个单位．考点：三角函数化简,图像平移.2. 【2013年.浙江卷.理4】已知函数f (x )＝A cos(ωx ＋φ)(A ＞0，ω＞0，φ∈R )，则“f (x )是奇函数”是“π2ϕ=”的( )． A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件3. 【2013年.浙江卷.理6】已知α∈R ，sin α＋2cos α10tan 2α＝( )． A ．43 B ．34 C ．34- D ．43- 【答案】：C【解析】：由sin α＋2cos α＝102得，sin α＝102－2cos α.① 把①式代入sin 2α＋cos 2α＝1中可解出cos α＝1010或31010，当cos α＝1010时，sin α＝31010； 当cos α＝310时，sin α＝10-. ∴tan α＝3或tan α＝13-，∴tan 2α＝34-. 4. 【2012年.浙江卷.理4】把函数y ＝cos2x ＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图象是( )5. 【2011年.浙江卷.理6】若02πα＜＜，02πβ-＜＜，1cos()43πα+=，3cos()423πβ-=，则cos()2βα+=（A ）33 （B ）33- （C ）539 （D ）69-02<<-βπ，∴36)24sin(=-βπ，∴)]24()4cos[()2cos(βπαπβα--+=+＝)24sin()4sin()24cos()4cos(βπαπβπαπ-++-+＝363323331⨯+⨯＝935. 6. 【2010年.浙江卷.理9】设函数()4sin(21)f x x x =+-，则在下列区间中函数()f x 不．存在零点的是（A ）[]4,2-- （B ）[]2,0- （C ）[]0,2 （D ）[]2,4 【答案】A【解析】：根据函数零点的概念知，()x f 在某个区间上无零点，即方程转()4sin(21)f x x x =+-=0在这个区间上无解，设()g x =()4sin 21x +，()h x =x ，即这两个函数图像在这个区间上无交点，作出()g x =()4sin 21x +，()h x =x 图像，由图像知，选A.7. 【2010年.浙江卷.理11】函数2()sin(2)22sin 4f x x x π=--的最小正周期是__________________ .8. 【2009年.浙江卷.理8】已知a 是实数，则函数()1sin f x a ax =+的图象不可能．．．是 ( )答案：D【解析】对于振幅大于1时，三角函数的周期为2,1,2T a T aππ=>∴<，而D 不符合要求，它的振幅大于1，但周期反而大于了2π．9. 【2008年.浙江卷.理5】在同一平面直角坐标系中，函数])20[)(232cos(ππ，∈+=x x y 的图象和直线21=y 的交点个数是 （A ）0 （B ）1 （C ）2 （D ）410. 【2008年.浙江卷.理13】在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若()C a A c b cos cos 3=-，则=A cos3【解析】：本小题主要考查三角形中正弦定理的应用。

历年三角函数高考真题第一部分：选择题1、（2010浙江理数）（9）设函数，则在下列区间中函数不存在零点的是（A）（B）（C）（D）2、（2010浙江理数）（4）设，则“”是“”的（A）充分而不必要条件（B）必要而不充分条件（C）充分必要条件（D）既不充分也不必要条件3、（2010四川理数）（6）将函数的图像上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是（A）（B）（C）（D）4.（浙江理6）若，，，，则A．B．C．D．4.（四川理6）在ABC中．．则A的取值范围是A．（0，] B．[，） C．（0，] D．[，）5.（辽宁理4）△ABC的三个内角A，B，C所对的边分别为a，b，c，asinAsinB+bcos2A=，则（A）（B）（C）（D）6.（全国新课标理11）设函数的最小正周期为，且则（A）在单调递减（B）在单调递减（C）在单调递增（D）在单调递增7.（安徽理9）已知函数，其中为实数，若对恒成立，且，则的单调递增区间是（A）（B）（C）（D）8.【2012高考新课标理9】已知，函数在上单调递减.则的取值范围是（）9.【2012高考陕西理9】在中，角所对边长分别为，若，则的最小值为（）A.B.C.D.10.【2012高考江西理4】若tan+=4,则sin2=A．B.C.D.11.【2012高考上海理16】在中，若，则的形状是（）A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定12．（2013年普通高等学校招生统一考试浙江数学（理））已知,则A.B.C.D.13 ．（2013年高考陕西卷（理））设△ABC的内角A, B, C所对的边分别为a, b, c, 若, 则△ABC的形状为(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定14 ．（2013年普通高等学校招生统一考试山东数学（理））将函数的图象沿轴向左平移个单位后,得到一个偶函数的图象,则的一个可能取值为(A)(B)(C)0 (D)15 ．（2013年普通高等学校招生统一考试辽宁数学（理））在,内角所对的边长分别为且,则A.B.C.D.16 ．（2013年普通高等学校招生统一考试大纲版数学（理））已知函数,下列结论中错误的是(A)的图像关于中心对称 (B)的图像关于直线对称(C)的最大值为(D)既奇函数,又是周期函数17（2014湖南9）．已知函数则函数的图象的一条对称轴是A．B．C．D．18（2014江西）在中，内角A,B,C所对应的边分别为，若则的面积（）A.3B.C.D.（2014重庆）已知的内角满足，面积满足，记分别为所对的边，则下列不等式一定成立的是（A）（B）（C）（D）a第二部分：填空题1（2010福建文数）16.观察下列等式：K^S*5U.C#O① cos2a=2-1;② cos4a=8- 8+ 1;③ cos6a=32- 48+ 18- 1;④ cos8a=128- 256+ 160- 32+ 1;⑤ cos10a= m- 1280+ 1120+ n+ p- 1．可以推测，m – n + p = ．2. （2010福建理数）14．已知函数和的图象的对称轴完全相同。

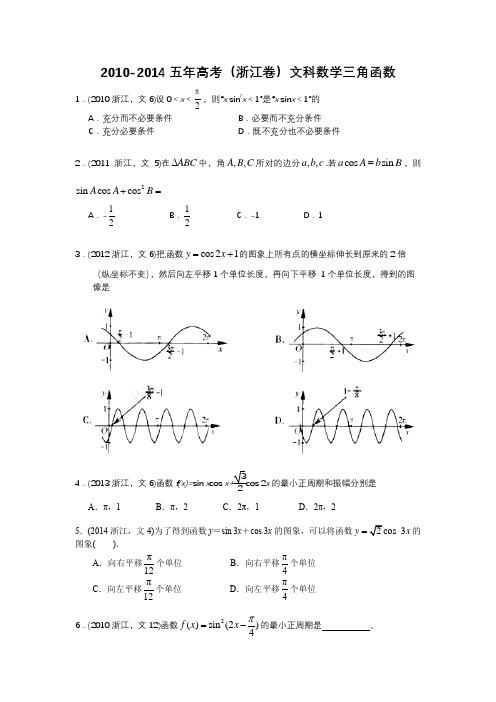
2010-2014五年高考（浙江卷）文科数学三角函数1．(2010浙江，文6)设0＜x ＜2π，则“x sin 2x ＜1”是“x sin x ＜1”的 A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件2．(2011浙江，文5)在ABC ∆中，角,,A B C 所对的边分,,a b c .若cos sin a A b B =，则2sin cos cos A A B +=A ．-12 B ．12C ．-1D ．13．(2012浙江，文6)把函数cos 21y x =+的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移 1个单位长度，得到的图像是4．(2013浙江，文6)函数f(x)=sin x cos x+32cos 2x 的最小正周期和振幅分别是 A ．π，1 B ．π，2 C ．2π，1 D ．2π，25．(2014浙江，文4)为了得到函数y ＝sin 3x ＋cos 3x 的图象，可以将函数2 3y x =的图象( )． A ．向右平移π12个单位 B ．向右平移π4个单位 C ．向左平移π12个单位 D ．向左平移π4个单位6．(2010浙江，文12)函数2()sin (2)4f x x π=-的最小正周期是 。

7．(2012浙江，文15)在ABC ∆中，M 是BC 的中点，3,10AM BC ==，则AB AC ⋅=________。

8．(2014浙江，文10)如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练．已知点A 到墙面的距离为AB ，某目标点P 沿墙面上的射线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小．(仰角θ为直线AP 与平面ABC 所成角)．若AB ＝15 m ，AC ＝25 m ，∠BCM ＝30°，则tan θ的最大值是________。

近五年浙江三角函数高考真题、(2013 理)2 C .2兀,1 D .2兀,18.在锐角^ ABC 中，内角A,B,C 的对边分别为a,b,c,且（I ）求角A 的大小;(n)若a 6,b c 8,求△ ABC 的面积.二、（2012 理）4.把函数y cos2x 1的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移1个单位长度，得到的图像是4.已知函数 f(x) Acos( x)(A 0, 0, R ）,则“ f （x ）是奇函数”是“A.充分不必要条件B. 必要不充分条件C.充分必要条件D. 既不充分也不必要条件6.已知 R,sin2 cos-T '则 tan2A.-3B. C.D. 16.在^ ABC 中,90°, M 是BC 的中点.若sinBAM1 L 一一—，则 sin BAC 3(2013 文) 3.（与理4姐妹题） cosA .充分不必要条件 .必要不充分条件 C .充分必要条件 .既不充分也不必要条件6.函数 f(x) sinxcosx近cos2x 的最小正周期和振幅分别是22asin B 3b .八2cos A - ,sin B %1 5 cosC .3 (1)求tanC 的值；(2)若a 用，求△ ABC 的面积.(2012 文)6.(同理4) 18. (14分)在^ ABC 中，内角 A,B,C 的对边分别为 a,b,c,且bsin A gacosB.(I)求角B 的大小;三、(2011 理)18. (14分)在△ ABC 中，角A,B,C 所对的边分别为 2空储.已知$丽人sinC1 2 ac b . 4， 一 5.. ....(I)当p 一,b 1时，求a,c 的值;4 (n )若角B 为锐角，求p 的取值范围(2011 文)(n)若 b 3,sinC2sin A ,求 a,c 的值.6.若00 , cos (一4B3、1^、) V c 叫 I)5 3则 cos( —)一 29psinB(p R)18. ( 14 分) 在 △ ABC 中，内角 A,B,C 的对边分别为a,b,c5 .在 ABC 中，角 A, B, C 所对的边分别是a, b,c ,若acosA bsinB ,则2 、sinAcosA cos B11, (A) —(B) —(C) 1(D) 12 218. (14 分)已知函数 f(x) Asin (-x ), x R, A 0, 0- . y f (x)的 部分图像如图所示，P 、Q 分别为该图像的最高点和最低点，点P 的坐标为(1,A).(第18避)(I)求f(x)的最小正周期及 的值;三、(2010 理)4.设 0<x< —,则“ xsin 2x<1” 是 “ xsinx< 1” 的2(A)充分而不必要条件(B)必要而不充分条件 (C)充分必要条件(D)既不充分也不必要条件9.设函数f(x) 4sin(2 x 1) x ,则在下列区间中函数 f(x)不存在零点的是(A) 4, 2(B)2,0 (C) 0,2(D) 2,411.函数f(x) sin(2x —) 2 J2sin 2 x 的最小正周期是41 18. (l4 分)在△ ABC 中，角A,B,C 所对的边分别为 a,b,c ,已知cos2c-. 4(1)求sinC 的值；(n)当 a 2,2sin A sin C 时，求 b 及 c 的长.（2010 文）(n)若点R 的坐标为(1,0),PRQ 2一,求A 的值.36.（同理4）12.(与理11姐妹题)函数f(x) sin2(2x 7)的最小正周期是18.(本题满分)在^ ABC,角AB,C所对的边分别为a,b,c,设$为乙ABC的面积，满足%；3 2 2 2S —(a b c ). 4(I )求角C的大小；(n )求sin A sin B的最大值.三、(2009 理)D【命题意图】此题是一个考查三角函数图象的问题，但考查的知识点因含有参数而丰富, 结合图形考查使得所考查的问题形象而富有深度.A 2 518. (14分)在ABC中，角A,B,C所对的边分别为a,b,c,且满足cos- 」5 2 5 AB AC 3.(I)求ABC的面积；(II )若b c 6 ,求a的值.(2009 文)10.(同理8)18.(同理18)。

2022年高考数学真题分类汇编专题08：三角函数一、单选题(共11题；共55分)1．（5分）（2022·浙江）为了得到函数y=2sin3x的图象，只要把函数y=2sin(3x+π5)图象上所有的点（）A．向左平移π5个单位长度B．向右平移π5个单位长度C．向左平移π15个单位长度D．向右平移π15个单位长度【答案】D【解析】【解答】函数图象平移满足左加右减，y=2sin(3x+π5)=2sin[3(x−π15)+π5]=2sin3x，因此需要将函数图象向右平移π15个单位长度，可以得到y=2sin3x的图象.故答案为：D【分析】由已知结合正弦函数图象的平移即可求解．2．（5分）（2022·浙江）设x∈R，则“ sinx=1”是“ cosx=0”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【答案】A【解析】【解答】sinx=1，则x=π2+2kπ，k∈Z；cosx=0，则x=π2+kπ，k∈Z，若sinx=1可推出cosx=0，充分性成立；反之不成立，必要性不成立，故充分部必要条件.故答案为：A【分析】利用同角三角函数间的基本关系，充要条件的定义判定即可．3．（5分）（2022·新高考Ⅱ卷）若sin(α+β)+cos(α+β)=2√2cos(α+π4)sinβ，则（）A．tan(α+β)=−1B．tan(α+β)=1C．tan(α−β)=−1D．tan(α−β)=1【答案】C【解析】【解答】根据两角和的正弦、余弦公式化简已知式子得：sinαcosβ+cosαsinβ+ cosαcosβ−sinαsinβ=2(cosα−sinα)sinβ，即：sinαcosβ−cosαsinβ+cosαcosβ+sinαsinβ=0，即：sin(α−β)+cos(α−β)=0，所以tan(α−β)=−1，故答案为：C【分析】由两角和差的正、余弦公式化简，结合同角三角函数的商数关系即可得解.4．（5分）（2022·全国甲卷）沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”，如图，AB⌢是以O为圆心，OA为半径的圆弧，C是AB的中点，D在AB⌢上，CD⊥AB．“会圆术”给出AB⌢的弧长的近似值s的计算公式：s=AB+CD 2OA．当OA= 2，∠AOB=60°时，s=（）A．11−3√32B．11−4√32C．9−3√32D．9−4√32【答案】B【解析】【解答】解：如图，连接OC，因为C是AB的中点，所以OC⊥AB，又CD⊥AB，所以O，C，D三点共线，即OD=OA=OB=2 ，又⊥AOB=60° ， 所以AB=OA=OB=2， 则OC =√3 ， 故CD =2−√3 ， 所以s =AB +CD 2OA =2+(2−√3)22=11−4√32. 故选：B.【分析】连接OC ，分别求出AB ，OC ，CD ，再根据题意的新定义即可得出答案.5．（5分）（2022·全国甲卷）设函数 f(x)=sin(ωx +π3) 在区间 (0，π) 恰有三个极值点、两个零点，则 ω 的取值范围是（ ） A ．[53，136)B ．[53，196)C ．(136，83]D ．(136，196]【答案】C【解析】【解答】解：依题意可得ω>0 ，因为x⊥（0，π），所以ωx +π3∈(π3，ωπ+π3) ， 要使函数在区间（0，π）恰有三个极值点、两个零点，又y=sinx ，(π3，3π) 的图象如下所示：则5π2<ωπ+π3≤3π， 解得136<ω≤83，即ω⊥ (136，83] ．故选：C【分析】由x 的取值范围得到ωx +π3的取值范围，再结合正弦函数的性质得到不等式，解得即可．6．（5分）（2022·全国甲卷）已知 a =3132，b =cos 14，c =4sin 14，则（ ） A ．c >b >aB ．b >a >cC ．a >b >cD ．a >c >b【答案】A【解析】【解答】解：因为c b =4tan 14，因为当x ∈(0，π2)，sinx<x<tanx ，所以tan 14>14 ，即c b >1， 所以c>b ；设f (x )=cosx +12x 2−1，x ∈(0，+∞)，f'(x)=-sinx+x>0 ，所以f(x)在（0，+∞）单调递增，则f (14)>f (0)=0， 所以cos 14−3132>0 ，所以b>a ， 所以c>b>a ， 故选：A【分析】由c b =4tan 14结合三角函数的性质可得c>b ；构造函数f (x )=cosx +12x 2−1，x ∈(0，+∞)，利用导数可得b>a ，即可得解.7．（5分）（2022·全国甲卷）将函数 f(x)=sin(ωx +π3)(ω>0) 的图像向左平移 π2 个单位长度后得到曲线C ，若C 关于y 轴对称，则 ω 的最小值是（ ） A ．16B ．14C ．13D ．12【答案】C【解析】【解答】解：由题意知：曲线C 为 y =sin [ω(x +π2)π3]=sin (ωx +ωπ2+π3) ， 又曲线C 关于y 轴对称，则ωπ2+π3=π2+kπ，k ∈Z ， 解得ω=13+2k ，k ∈Z ，又ω>0，故当k=0时，ω的最小值为 13 .故选：C.【分析】先由平移求出曲线C 的解析式，再结合对称性得ωπ2+π3=π2+kπ，k ∈Z ，即可求出ω的最小值.8．（5分）（2022·北京）已知函数 f(x)=cos 2x −sin 2x ，则（ ）A ．f(x) 在 (−π2，−π6) 上单调递增 B ．f(x) 在 (−π4，π12) 上单调递增C ．f(x) 在 (0，π3) 上单调递减D ．f(x) 在 (π4，7π12) 上单调递增【答案】C【解析】【解答】 f(x)=cos 2x −sin 2x =cos2x ，选项A 中： 2x ∈(−π，−π3) ，此时 f(x) 单调递增；选项B 中： 2x ∈(−π2，π6) ，此时 f(x) 先递增后递减；选项C 中： 2x ∈(0，2π3) ，此时 f(x) 单调递减；选项D 中： 2x ∈(π2，7π6) ，此时 f(x) 先递减后递增.故答案为：C【分析】先根据余弦的二倍角公式化简 f(x)=cos2x ，再逐项分析选项即可.9．（5分）（2022·新高考Ⅱ卷）记函数 f(x)=sin(ωx +π4)+b(ω>0) 的最小正周期为T ，若 2π3<T <π， 则 y =f(x) 的图像关于点 (3π2，2) 中心对称，则 f(π2)= （ ）A ．1B ．32C ．52D ．3【答案】A【解析】【解答】解：由题意得，ω=2πT∈(2，3)， 又 y =f(x) 的图像关于点 (3π2，2) 中心对称，则b=2，且f (3π2)=2，所以sin (3π2ω+π4)+2=2，则3π2ω+π4=2kπ，k ∈Z ，解得ω=8k−16，又ω∈(2，3)， 则k=2，ω=52，故f (π2)=sin (52·π2+π4)+2=1，故选：A【分析】由正弦函数的图象与性质，先求得b ，ω，再求得f (π2)即可.10．（5分）（2022·浙江学考）已知α⊥R ，则cos （π-α）=（）A ．sinαB ．-sinαC ．cosαD ．-cosα【答案】D【解析】【解答】因为 cos(π−α)=−cosα 。

近五年浙江三角函数高考真题一、（2013理）4．已知函数()cos()(0,0,R)f x A x A ωφωφ=+>>∈，则“()f x 是奇函数”是“2πφ=”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件6．已知R,sin 2cos ααα∈+=tan2α= A ．43B ．34 C ．34-D ．43-16．在△ABC 中，90C ∠=，M 是BC 的中点．若1sin 3BAM ∠=，则sin BAC ∠= ．（2013文）3．（与理4姐妹题）若R α∈，则“0α=”是“sin cos αα<”的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件6．函数()sin cos f x x x x =+的最小正周期和振幅分别是 A ．π，1 B ．π，2 C ．2π，1 D ．2π，218.在锐角△ABC 中，内角,,A B C 的对边分别为,,a b c ，且2sin a B =. （Ⅰ）求角A 的大小；（Ⅱ) 若6,8a b c =+=，求△ABC 的面积.二、（2012理）4.把函数cos21y x =+的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移 1个单位长度，得到的图像是18.（14分）在△ABC 中，内角,,A B C 的对边分别为,,a b c ．已知C B A cos 5sin ,32cos ==． （1）求tan C 的值；（2）若2a =ABC 的面积．（2012文） 6．（同理4）18．（ 14分）在△ABC 中，内角,,A B C 的对边分别为,,a b c ，且sin 3cos b A a B =． （Ⅰ）求角B 的大小；（Ⅱ）若3,sin 2sin b C A ==，求,a c 的值．三、（2011理） 6．若0,022ππαβ<<-<<，1cos()43πα+=，3cos()42πβ-=，则cos()2βα+= A 3B ．3C 53D ．618.（14分）在△ABC 中，角,,A B C 所对的边分别为,,a b c .已知sin sin sin (R)A C pB p +=∈，且214ac b =.（Ⅰ）当5,14p b ==时，求,a c 的值；(Ⅱ)若角B 为锐角，求p 的取值范围.（2011文）5．在ABC ∆中，角C B A ,,所对的边分别是c b a ,,，若B b A a sin cos =，则=+B A A 2cos cos sin（A ）21-（B ）21 （C ）1- （D ）118.（14分）已知函数()sin ()3f x A x πϕ=+，x R ∈，0A >，02πϕ<<.()y f x =的部分图像如图所示，P 、Q 分别为该图像的最高点和最低点，点P 的坐标为(1,)A .（Ⅰ）求()f x 的最小正周期及ϕ的值； （Ⅱ）若点R 的坐标为(1,0)，23PRQ π∠=，求A 的值.三、（2010理） 4．设02x π＜＜，则“2sin 1x x ＜”是“sin 1x x ＜”的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件9．设函数()4sin(21)f x x x =+-，则在下列区间中函数()f x 不．存在零点的是 （A ）[]4,2-- （B ）[]2,0- （C ）[]0,2 （D ）[]2,4 11.函数2()sin(2)224f x x x π=--的最小正周期是__________________ .18. (l4分)在△ABC 中,角,,A B C 所对的边分别为,,a b c ，已知1cos24C =-.(I)求sin C 的值；(Ⅱ)当2,2sin sin a A C ==时，求b 及c 的长． （2010文） 6．（同理4）12.（与理11姐妹题）函数2()sin (2)4f x x π=-的最小正周期是18.（本题满分）在△ABC ，角,,A B C 所对的边分别为,,a b c ,设S 为△ABC 的面积，满足2223()4S a b c =+-. （Ⅰ）求角C 的大小； （Ⅱ）求sin sin A B +的最大值.三、（2009理）8．已知a 是实数，则函数()1sin f x a ax =+的图象不可能．．．是D 【命题意图】此题是一个考查三角函数图象的问题，但考查的知识点因含有参数而丰富，结合图形考查使得所考查的问题形象而富有深度．18．（14分）在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，且满足25cos25A =，3=⋅AC AB ．（I ）求ABC ∆的面积； （II ）若6b c +=，求a 的值． （2009文） 10．（同理8） 18．（同理18）。

专题09 三角函数的图象与性质问题【高考真题】1．(2022·北京)已知函数f (x )＝cos 2x －sin 2x ，则( )A ．f (x )在(－π2，－π6)上单调递减B ．f (x )在(－π4，π12)上单调递增C ．f (x )在(0，π3)上单调递减D ．f (x )在(π4，7π12)上单调递增2．(2022·浙江) 为了得到函数y ＝2sin3x 的图象，只要把函数y ＝2sin ⎝⎛⎭⎫3x ＋π5图象上所有的点( ) A ．向左平移π5个单位长度 B ．向右平移π5个单位长度C ．向左平移π15个单位长度D ．向右平移π15个单位长度3．(2022·全国甲文) 将函数f (x )＝sin(ωx ＋π3)(ω＞0)的图像向左平移π2个单位长度后得到曲线C ，若C 关于y轴对称，则ω的最小值是( )A ．16B ．14C ．13D ．124．(2022·全国乙理) 记函数f (x )＝cos(ωx ＋φ)(ω＞0，0＜φ＜π)的最小正周期为T ，若f (T )＝32，x ＝π9为f (x ) 的零点，则ω的最小值为____________．5．(2022·新高考Ⅰ)记函数f (x )＝sin(ωx ＋π4)＋b (ω＞0)，的最小正周期为T ．若2π3＜T ＜π，且y ＝f (x )的图象关于点(3π2，2)中心对称，则f (π2)＝( )A ．1B ．32C ．52D ．36．(2022·全国甲理)设函数f (x )＝sin(ωx ＋π3)在区间(0，π)恰有三个极值点、两个零点，则ω的取值范围是( )A ．[53，136)B ．[53，196)C ．(136，83]D ．(136，196]【知识总结】1．三种三角函数的图象和性质2．函数y ＝A sin(ωx ＋φ)(ω>0，A >0)的图象 (1)“五点法”作图设z ＝ωx ＋φ，令z ＝0，π2，π，3π2，2π，求出相应的x 的值与y 的值，描点、连线可得．(2)由三角函数的图象确定解析式时，一般利用五点中的零点或最值点作为解题突破口． (3)图象变换y ＝sin x ―――――――――→向左(φ>0)或向右(φ<0)平移|φ|个单位长度y ＝sin(x ＋φ) ――――――――――――→横坐标变为原来的1ω(ω>0) 倍纵坐标不变y ＝sin(ωx ＋φ) ――――――――――――→纵坐标变为原来的A (A >0)倍横坐标不变y ＝A sin(ωx ＋φ)． 【同类问题】题型一 三角函数的性质1．(2017·山东)函数y ＝3sin 2x ＋cos 2x 的最小正周期为( )A ．π2B ．2π3 C ．π D ．2π2．函数f (x )＝(3sin x ＋cos x )(3cos x －sin x )的最小正周期是( )A ．π2B ．πC ．3π2D ．2π3．(2018·全国Ⅰ)函数f (x )＝tan x1＋tan 2x的最小正周期为( )A ．π4B ．π2C ．πD ．2π4．已知函数f (x )＝3sin ωx －cos ωx (ω>0)的最小正周期为2π，则f (x )的单调递增区间是( )A ．⎣⎡⎦⎤2k π－π6，2k π＋π6(k ∈Z ) B.⎣⎡⎦⎤2k π－π3，2k π＋2π3(k ∈Z ) C ．⎣⎡⎦⎤2k π－2π3，2k π＋π3(k ∈Z ) D.⎣⎡⎦⎤2k π－π6，2k π＋5π6(k ∈Z ) 5．(2018·全国Ⅰ)若f (x )＝cos x －sin x 在[－a ，a ]上是减函数，则a 的最大值是( )A ．π4B ．π2C ．3π4D ．π6．已知函数f (x )＝sin ωx ＋3cos ωx (ω>0)，f (π6)＋f (π2)＝0，且f (x )在区间(π6，π2)上递减，则ω＝( )A ．3B ．2C ．6D ．57．(2019·全国Ⅰ)函数f (x )＝sin ⎝⎛⎭⎫2x ＋3π2－3cos x 的最小值为________． 8．(2017·全国Ⅰ)函数f (x )＝sin 2x ＋3cos x －34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0，π2的最大值是________． 9．(2013·全国Ⅰ)设当x ＝θ时，函数f (x )＝sin x －2cos x 取得最大值，则cos θ＝________. 10．已知ω>0，函数f (x )＝sin ωx cos ωx ＋3cos 2ωx －32的最小正周期为π，则下列结论正确的是( ) A ．函数f (x )的图象关于直线x ＝π3对称B ．函数f (x )在区间⎣⎡⎦⎤π12，7π12上单调递增C ．将函数f (x )的图象向右平移π6个单位长度可得函数g (x )＝cos2x 的图象D ．当x ∈⎣⎡⎦⎤0，π2时，函数f (x )的最大值为1，最小值为－32题型二 三角函数的图象变换11．(2021·全国乙)把函数y ＝f (x )图象上所有点的横坐标缩短到原来的12倍，纵坐标不变，再把所得曲线向右平移π3个单位长度，得到函数y ＝sin ⎝⎛⎭⎫x －π4的图象，则f (x )等于( ) A ．sin ⎝⎛⎭⎫x 2－7π12 B ．sin ⎝⎛⎭⎫x 2＋π12 C ．sin ⎝⎛⎭⎫2x －7π12 D ．sin ⎝⎛⎭⎫2x ＋π12 12．(2016·四川)为了得到函数y ＝sin ⎝⎛⎭⎫2x －π3的图象，只需把函数y ＝sin2x 的图象上所有的点( ) A ．向左平行移动π3个单位长度 B ．向右平行移动π3个单位长度C ．向左平行移动π6个单位长度D ．向右平行移动π6个单位长度13．(2017·全国Ⅰ)已知曲线C 1：y ＝cos x ，C 2：y ＝sin ⎝⎛⎭⎫2x ＋2π3，则下面结论正确的是( ) A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 214．(2018·天津)将函数y ＝sin ⎝⎛⎭⎫2x ＋π5的图象向右平移π10个单位长度，所得图象对应的函数( ) A ．在区间⎣⎡⎦⎤3π4，5π4上单调递增 B ．在区间⎣⎡⎦⎤3π4，π上单调递减 C ．在区间⎣⎡⎦⎤5π4，3π2上单调递增 D ．在区间⎣⎡⎦⎤3π2，2π上单调递减 15．函数y ＝3sin 2x －cos 2x 的图象向右平移φ⎝⎛⎭⎫0<φ<π2个单位长度后，得到函数g (x )的图象，若函数g (x ) 为偶函数，则φ的值为( )A ．π12B ．π6C ．π4D ．π315．将函数f (x )＝tan ⎝⎛⎭⎫ωx ＋π3(0<ω<10)的图象向右平移π6个单位长度后与函数f (x )的图象重合，则ω＝( ) A ．9 B ．6 C ．4 D ．817．若函数f (x )＝cos ⎝⎛⎭⎫2x －π6，为了得到函数g (x )＝sin2x 的图象，则只需将f (x )的图象( ) A ．向右平移π6个单位长度 B ．向右平移π3个单位长度C ．向左平移π6个单位长度D ．向左平移π3个单位长度18．(2019·天津)已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，|φ|<π)是奇函数，且f (x )的最小正周期为π，将y ＝f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象对应的函数为g (x )．若g ⎝⎛⎭⎫π4＝2，则f ⎝⎛⎭⎫3π8＝( )A ．－2B ．－2C ．2D ．219．(2016·全国)若将函数y ＝2sin 2x 的图象向左平移π12个单位长度，则平移后图象的对称轴为( )A ．x ＝k π2－π6(k ∈Z )B ．x ＝k π2＋π6(k ∈Z )C ．x ＝k π2－π12(k ∈Z )D ．x ＝k π2＋π12(k ∈Z )20．将函数f (x )的图象向右平移π6个单位长度，再将所得函数图象上的所有点的横坐标缩短到原来的23，得到函数g (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫A >0，ω>0，|φ|<π2的图象．已知函数g (x )的部分图象如图所示，则函数A ．最小正周期为23π，最大值为2 B ．最小正周期为π，图象关于点⎝⎛⎭⎫π6，0中心对称 C ．最小正周期为23π，图象关于直线x ＝π6对称 D ．最小正周期为π，在区间⎣⎡⎦⎤π6，π3上单调递减 题型三 关于ω的取值范围21．已知函数()sin (0)f x x ωω=>在3[,]44ππ-上单调递增，则ω的取值范围是( )A ．[2，)+∞B ．(0，2]C ．2[,)3+∞D ．2(0,]322．将函数()cos()(0)4f x x πωω=+>的图象向右平移4π个单位长度后得到函数()g x 的图象，若()g x 在5(,)44ππ上单调递减，则ω的最大值为( ) A ．14 B ．34 C ．12D ．1 23．函数()sin()(0)6f x x πωω=+>图象向右平移4π个单位后所得函数图象与函数()f x 的图象关于x 轴对称，则ω最小值为( )A ．2B ．3C ．4D ．624．已知函数()3sin()f x x ωϕ=+，(0,0)2πωϕ><<，()03f π-=，2()()3f x f x π-=，且函数()f x 在区间(,)124ππ上单调，则ω的最大值为( ) A ．274 B ．214 C ．154 D ．9425．已知函数()sin()f x x ωϕ=+，0ω>，若()19f π=，(449)0f π=，()f x 在(,)93ππ上单调递减，那么ω的取值个数是( )A ．2019B ．2020C ．2021D ．202226．已知函数()sin()(0)6f x x πωω=->，若函数()f x 在区间(0,)π上有且只有两个零点，则ω的取值范围为( )A ．713(,)66B ．713(,]66C ．611(,)56D ．611(,]5627．已知函数()2sin()sin()(0)63f x x x ππωωω=-+>，若函数3()()2g x f x =+在[0，]2π上有且只有三个零点，则ω的取值范围为( ) A ．[2，11)3 B ．11(2,)3 C ．710[,)33 D ．710(,)3328．已知函数()3sin cos (0)f x x x ωωω=+>在区间[,]43ππ-上恰有一个最大值点和最小值点，则实数ω的 取值范围为( )A ．8[,7)3B ．8[,4)3C ．20[4,)3D ．20(,7)329．已知函数1()sin (sin cos )(0)2f x x x x ωωωω=+->在区间(0,)π上恰有1个最大值点和1个最小值点，则ω的取值范围是( )A ．711(,)88B ．711(,]88C ．79(,]88D ．79(,)8830．已知函数3()sin()sin()(0)21472xxf x ωππωω=+->在[0，)π上恰有6个零点，则ω的取值范围是 ( ) A ．4148(,]77B ．3441(,]77C ．4148[,)77D ．3441[,)77。