一阶系统模型经欧拉变换与双线性变换的输出误差分析

机械工程控制基础31_系统误差分析与计算系统误差是机械系统中不可避免的误差，它是由于各种因素引起的系统输出和期望输出之间的差异。

在机械工程中，系统误差是需要考虑和分析的一个重要问题，因为它会对系统的性能和精度产生影响。

系统误差可分为常数误差、线性误差和非线性误差。

常数误差是指系统输出与期望输出之间存在常数差异，如偏差或偏移。

线性误差是指系统输出与期望输出之间存在直线关系的差异，如增益失真或放大失真。

非线性误差是指系统输出与期望输出之间存在非线性关系的差异，如非线性失真或非线性曲线偏差。

理想模型是指系统输出与期望输出完全一致的模型，没有任何误差。

但在实际应用中，理想模型很难实现，因为存在各种误差源。

因此，需要通过准确的数学模型来描述系统误差。

线性模型是指系统误差与输入信号之间存在线性关系的模型。

线性模型可以通过线性回归等方法来计算和分析。

线性模型可以用来描述系统的增益特性、失真特性等。

线性模型通常可以通过标定和校准来修正和补偿。

非线性模型是指系统误差与输入信号之间存在非线性关系的模型。

非线性模型通常比线性模型更复杂，需要采用更高级的数学方法来描述和计算。

非线性模型可以用来描述系统的曲线特性、震荡特性等。

非线性模型通常可以通过拟合和优化来修正和补偿。

系统误差分析和计算需要进行实际测试和实验来获取系统的输入输出数据，并基于这些数据进行模型的建立和计算。

在实际应用中，还需要考虑系统的稳定性、可靠性和实时性等因素。

因此，系统误差分析和计算是一项复杂而重要的工作。

总之，系统误差分析和计算是机械工程控制基础中的一个重要内容。

它涉及到系统的性能和精度问题，在实际工程设计和应用中具有重要的意义。

系统误差的分析和计算需要考虑多种因素，包括常数误差、线性误差和非线性误差，并采取相应的措施来减少误差。

系统误差分析和计算需要进行实际测试和实验，并基于实验数据建立数学模型来描述系统误差。

一阶倒立摆模糊控制实验报告本次实验旨在研究一阶倒立摆系统的模糊控制方法，通过对系统进行建模、设计控制器并进行仿真，最终评估控制效果。

实验过程主要包括系统建模、控制器设计、模糊控制器参数调节和性能评价四个步骤。

首先，我们对一阶倒立摆系统进行建模。

一阶倒立摆系统是一种具有非线性特性的控制系统，主要由电机、倒立摆、支撑杆等组成。

我们需要建立数学模型描述系统的动力学特性，包括倒立角度、倒立角速度、杆角度等状态变量，并考虑控制输入电压对系统的影响。

接着，我们设计模糊控制器。

模糊控制是一种基于模糊逻辑的控制方法，适用于非线性系统和模糊系统。

我们根据系统模型，设计模糊控制器的模糊规则、隶属函数等参数，以实现系统的稳定控制。

在设计过程中，我们需要考虑系统的性能指标，如超调量、稳态误差等。

第三步是模糊控制器参数调节。

通过仿真实验，我们可以对模糊控制器的参数进行调节，以使系统的性能达到最佳状态。

调节参数的过程需要考虑系统的稳定性、鲁棒性和响应速度，以达到控制效果的要求。

最后，我们对模糊控制系统进行性能评价。

通过对系统的响应曲线、稳定性、控制精度等指标进行分析，评价模糊控制器的控制效果。

我们可以比较模糊控制系统和传统控制系统的性能，探讨模糊控制在一阶倒立摆系统中的优势和局限性。

总的来说，本次实验通过研究一阶倒立摆系统的模糊控制方法，探讨了模糊控制在非线性系统中的应用。

通过实验，我们对模糊控制的基本原理和设计方法有了更深入的理解，同时也对一阶倒立摆系统的控制特性有了更清晰的认识。

希望通过实验的研究，能够为控制系统的设计和应用提供一定的参考和借鉴。

学校编码：15014 分类号密级学号： UDC本科毕业论文(设计)xxxx(题目、居中、黑体、二号)学生姓名：xxxx（楷体、三号、居中）所属院部：xxxx（楷体、三号、居中）专业：xxxx（楷体、三号、居中）指导教师：xxxx（楷体、三号、居中）年月日（Times New Roman、三号、居中）赤峰学院本科毕业论文(设计)原创性声明兹呈交的毕业论文(设计)，是本人在导师指导下独立完成的研究成果。

本人在论文(设计)写作中参考的其他个人或集体的研究成果，均在文中以明确方式标明。

本人依法享有和承担由此论文(设计)而产生的权利和责任。

声明人（签名）：指导教师（签名）：年月日一阶电路的分析方法陈昊（赤峰学院物理与电子信息工程学院学院，内蒙古 赤峰 024000）摘要：本文主要讨论了三种分析一阶电路的的方法：1、利用基尔霍夫定律和电容、电感的关系及微积分的知识。

2、三要素法进行分析。

3、利用拉普拉斯变换进行分析。

关键词：电流、电压、节点、初始值、终了值、拉普拉斯变换、反拉普拉斯变换对于一个复杂的电路，当电路的工作条件发生改变时，电阻电路和动态电路的工作状态都将随之发生变化。

电阻电路的变化可在瞬间完成，无需经历任何过程。

但动态电路的变化一般是一个渐变的过程，而不能在瞬间完成，这一渐变的过程称为瞬态过程，处于瞬态过程中的状态称为瞬态。

关于动态电路，常以描述该电路性状的微分方程的阶数加以区别，对应于一阶微分方程的电路，称为一阶电路。

只含有一个储能元件（电感或电容）的电路就是一阶电路。

所谓瞬态过程的分析就是指对于给定的电路，当电路或电源的接通与断开，电路连接结构或元件参数改变时计算出各支路中的电流或电压随时间的变化规律。

下面介绍三种分析一阶瞬态电路的方法。

1. 基尔霍夫定律分析法利用基尔霍夫电流定律：对于任一节点，所有与之相边的支路电流的代数和恒等于零，即：∑=0i ；电压定律：对于任一回路，所有支路电压的代数和恒等于零，即：∑=0u ；以及电感感应电动势与电流的关系：dtdiL e -=；电容的电压与电容电流之间的关系dtduci =来分析研究瞬态过程的一种方法。

自动控制原理控制系统的时域分析杨金显yangjinxian@河南理工大学电气工程与自动化学院本章主要内容与重点响应性能指标控制系统的时域分析一阶系统时域分析 二阶系统时域分析 高阶系统的时域分析 线性系统的稳定性分析 线性系统的稳态误差计算2对于线性系统，常用的分析方法有三种： 时域分析方法 根轨迹法 频率特性法 分析性能指标——动态性能、稳态性能 改善系统性能 时域分析方法，是一种直接分析方法，具有 直观准确的优点，尤其适用于低阶系统。

3时域分析：是根据微分方程，利用拉氏变换直接求出系 统的时间响应，然后按照响应曲线来分析系统的性能。

输 入 信 号控制 拉普拉 传 系统 斯变换 递 函 微分 数 方程稳定性 输 出 信 号 准确性 响应过程稳定 稳态误差 动态指标4时域分析对于一单输入单输出n阶线性定常系统，可用一n阶 常系数线性微分方程来描述。

dc(t) d c(t) d c(t) + anc(t) a0 n + a1 n−1 + + an−1 dt dt dt d mr(t) d m−1r(t) dr(t) = b0 m + b1 m−1 + + bm−1 + bmr(t) dt dt dt系统在输入信号r(t )作用下，输出c(t )随时间变化的规律，即上式 微分方程的解，就是系统的时域响应。

nn−1动态过程—从初始态到接近稳态的响应。

稳态过程—t趋于无穷大时的输出状态。

5假定初始条件为0时2 s Y ( s ) + 5sY ( s ) + 6Y ( s ) = 1 2 s y (t ) = ∗1 − 1 ∗ e −2t − ∗ e −3t , (无初始值) 3 3 2 2 Y (s) = = 2 s ( s + 5s + 6) s ( s + 2)( s + 3) 1 1 1 1 2 y (t ) = ∗1 − ∗ e −2t + ∗ e −3t , 输入为1，无初始值 6 2 3 3− 1 − 3 = s s+2 s+3 1 10 −3t −2 t y (t ) = ∗1 + 4 ∗ e − ∗ e , t ≥ 0 (有初始值时) 3 32系统响应=稳态分量+暂态分量影响输出的有：系统本身结构与参数、输入信号、初始状态统一条件：静止状态和典型输入信号63.1 典型输入信号f (t )（1）单位脉冲 （2）单位阶跃 （3）单位斜坡 （4）单位加速度 （5）指数函数 （6）正弦函数 （7）余弦函数F (s )1δ (t )1( t )1s1s 1s2 3tt 22e − at sin ω t1 (s + a)ω (s2 + ω 2 )s (s + ω )2 27cos ω t典型输入信号之间关系83.2 时域性能指标1）稳态性能指标 采用稳态误差ess来衡量，其定义为：当 时间t 趋于无穷时，系统输出响应的期 望值与实际值之差。

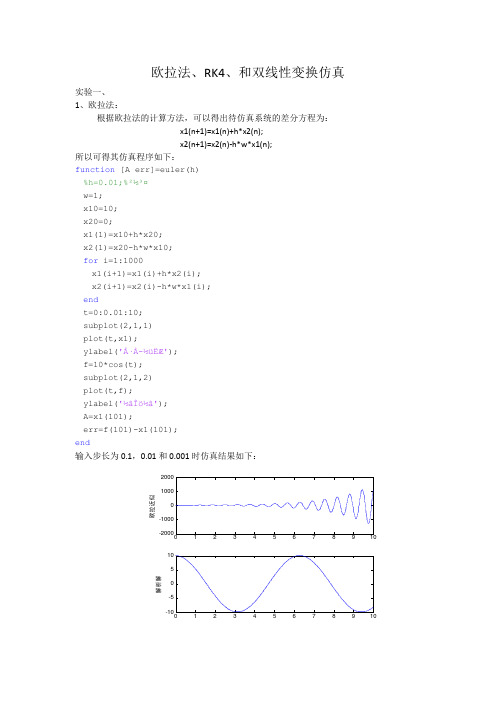
欧拉法、RK4、和双线性变换仿真实验一、 1、欧拉法：根据欧拉法的计算方法，可以得出待仿真系统的差分方程为： x1(n+1)=x1(n)+h*x2(n); x2(n+1)=x2(n)-h*w*x1(n); 所以可得其仿真程序如下：function [A err]=euler(h) %h=0.01;%²½³¤ w=1; x10=10; x20=0;x1(1)=x10+h*x20; x2(1)=x20-h*w*x10; for i=1:1000x1(i+1)=x1(i)+h*x2(i); x2(i+1)=x2(i)-h*w*x1(i); endt=0:0.01:10; subplot(2,1,1) plot(t,x1);ylabel('Å·À-½üËÆ'); f=10*cos(t); subplot(2,1,2) plot(t,f); ylabel('½âÎö½â'); A=x1(101);err=f(101)-x1(101); end输入步长为0.1，0.01和0.001时仿真结果如下：012345678910欧拉近似解析解h=0.1h=0.01h=0.0012、RK —4法：根据RK —4方法编制的仿真程序如下： function [y err]=rk4_2(h,n)%n=10; %h=0.01; x1_0=10; x2_0=0; k11_0=h*x2_0; k21_0=-h*x1_0;k12_0=h*(x2_0+0.5*k21_0); k22_0=-h*(x1_0+0.5*k11_0);欧拉近似012345678910解析解0102030405060708090100欧拉近似102030405060708090100解析解k13_0=h*(x2_0+0.5*k22_0); k23_0=-h*(x1_0+0.5*k12_0); k14_0=h*(x2_0+0.5*k23_0); k24_0=-h*(x1_0+0.5*k13_0);x1(1)=x1_0+(1/6)*(k11_0+2*k12_0+2*k13_0+k14_0); x2(1)=x2_0+(1/6)*(k21_0+2*k22_0+2*k23_0+k24_0); for i=1:100*n k11(i)=h*x2(i); k21(i)=-h*x1(i);k12(i)=h*(x2(i)+0.5*k21(i)); k22(i)=-h*(x1(i)+0.5*k11(i)); k13(i)=h*(x2(i)+0.5*k22(i)); k23(i)=-h*(x1(i)+0.5*k12(i)); k14(i)=h*(x2(i)+0.5*k23(i)); k24(i)=-h*(x1(i)+0.5*k13(i));x1(i+1)=x1(i)+(1/6)*(k11(i)+2*k12(i)+2*k13(i)+k14(i)); x2(i+1)=x2(i)+(1/6)*(k21(i)+2*k22(i)+2*k23(i)+k24(i)); endy=x1(100*n+1); t=0:0.01:n; f=10*cos(t); err=f(100*n+1)-y; subplot(2,1,1) plot(t,x1); ylabel('rk4'); subplot(2,1,2) plot(t,f); ylabel('½âÎö½â'); end取步长为0.1，0.01，0.001时结果如下：r k4解析解h=0.1h=0.01h=0.001通过对以上两种算法的结果的观察与比较我们发现：首先，对于零阶稳定的原系统，由于计算机的舍入误差和算法的阶段误差的存在，不可能得到一个稳定的数值解；其次，当h 较小时，RK —4的方法的效果更好一些。

仿真实验一直流激励下的甩一阶电路的响应实验目的：1、掌握一阶电路响应的两种分解方法及计算的三要素法。

2、理解阶跃响应的概念与电路响应信号所对应的波形。

实验原理：当电路中含有储能元件，即含有电感和电容，这类元件的电压和电流关系是微分、积分关系，而不是代数关系，因此根据基尔霍夫定律和元件特性方所列写的电路方程是以电流或电压为变量的微分方程。

如果电路中只含有一个动态元件，描述电路的方程是一阶微分方程，这种电路称为一阶电路。

在动态电路中，当电路的结构或元件参数发生改变时，可能使电路改变原来的工作状态，而转到另一个工作状态,这种转变往往需要经历一个过程, 工程上称为过渡过程。

一阶电路的全响应的问题，其实仍是求解非齐次微分方程的问题，既要考虑初始状态乂要考虑输入状态，全响应有两种分解方式一是：全响应二稳态分量+暂态分量u c=u c+u'c ;二是：全响应二零输入响应+零状态响应U . +U［2' OC C C三要素法是从直流或正弦激励下的一阶电路求解法中归纳总结出来的一种通用法则。

叫=代+“：=U S +（U Q-U x）e E =匕（8）+［代（0+）-色（s）］e 7（1）冷（8）——稳态值，又称终值。

（2）冷（0+）——初始值，乂称初值。

（3）r——电路的时间常数。

以上的三个量为全响应代的三要素，将上述分析结论推广到一般，设时间函数/（/）表示一阶电路在直流激励下的全响应（可以使电路中任意元件的电压和电流)则/(/)的一般表达式为：/(?) = /+/ = /(s) +Ae 「若已知初始值/(0+)，将/=0+代入上式得：/(0+) = /(oo) + Ae°所以：A = /(0+)-/(oo)结果：/(0=/+/ =/W+[/(o +)-/W]^如下图所示电路，计算R2两端电压：R11 kOhm -AAArR21 kOhm想要知道R2两端的电压，可以先计算出通过其的电流，则先使用三要素法讣算电流：零时刻时的电流：«0_)=1°X £ = 5〃L 4 i (o+)= i(g = 5mA时间无穷远点的电流：/? = 1+1||1 = 1.5^ 匸=罟占+ 也=8.333曲n L 1R=l + l||i5M心厂而' 则电流随时间变化为：ti ⑴=厲+(沁-洽)厂=8.333-3.333』50%诅即可算得R2两端的电圧为: [S]10V R31 kOhm(T)10mA（/的=1000x「）=8.333 —3.333『5°°V三. 电路仿真实验过程与步骤：按照上述电路图在ewb仿真软件中连接电路元件，并在运行仿真电路后一段时间后按下S键以切换开关必和端口。

指导教师评定成绩：审定成绩：重庆邮电大学移通学院自动控制原理课程设计报告系部：自动化系学生姓名：专业：自动化班级：学号：指导教师：设计时间：2013 年12月重庆邮电大学移通学院制目录摘要......................................................................................................................... - 1 - 一设计题目与要求................................................................................................. - 2 -1.1设计题目...................................................................................................... - 2 -1.2系统说明...................................................................................................... - 2 -1.3课程设计指标.............................................................................................. - 2 -1.4课程设计要求.............................................................................................. - 3 - 二各环节功能说明................................................................................................. - 3 -2.1积分环节...................................................................................................... - 3 -2.2惯性环节...................................................................................................... - 4 -2.3反相器环节.................................................................................................. - 4 - 三系统分析............................................................................................................. - 4 -3.1传递函数的确定.......................................................................................... - 4 -3.2稳定性分析.................................................................................................. - 6 - 四系统的校正......................................................................................................... - 7 -4.1计算校正参数.............................................................................................. - 7 - 五系统的模拟....................................................................................................... - 10 -5.1计算校正装置物理模型............................................................................ - 10 -5.2校正后系统物理模拟结构图.................................................................... - 11 - 六系统的仿真....................................................................................................... - 11 -6.1校正前的系统的阶跃响应........................................................................ - 11 -6.2校正后系统的阶跃响应............................................................................ - 12 -6.3校正前后系统阶跃响应比较.................................................................... - 12 - 七设计总结........................................................................................................... - 14 - 八参考文献........................................................................................................... - 15 -摘要首先通过对未校正系统进行分析，判断该系统是否稳定，画出Bode图，用频率分析法分析系统是超前还是滞后，根据分析的结果，选择正确的串联校正装置。

Science &Technology Vision科技视界0引言PID 控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。

当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依据经验和现场调试来确定,这时应用PID 控制技术最为方便。

即当我们不完全了解一个系统和被控对象﹐或不能通过有效的测量手段来获得系统参数时,最适合用PID 控制技术。

随着数字化的发展,对PID 控制器的各种离散方法的层出不穷,各种离散方法都有本身的优点和局限性,本文就其采用双线性变换法离散存在的问题进行分析,从而得出PID 控制器不能采用双线性变换法离散的原因所在。

1PID 控制器及双线性变换法具有比例、积分和微分控制规律的控制称为PID 控制器。

调节PID 的参数,可实现在系统稳定的前提下,兼顾系统的带载能力和抗扰能力,同时,在PID 控制器中引入积分项,系统增加了一个零极点,使之成为一阶或一阶以上的系统,这样系统阶跃响应的稳态误差就为零。

PID 控制器的传递函数为:G C (s )=K p 1+1T is +T d s ()(1)式中,K p 为比例系数;T i 为积分时间常数;T d 为微分时间常数。

双线性变换法也叫做梯形积分法,或称作突斯汀(Tustin)变换法。

用u (k )=u (k -1)+T 2[r (k )+r (k -1)]近似kT(k-1)∫r (t )d t ,也就是用梯形面积之和近似代替数值积分。

其离散公式为:D (z )=D (s )|s =2T z -1z +1(2)映射关系为:|z |2=1+T 2σ()2+ωT 2()21-T 2σ()2+ωT 2()2(3)其特点是:如果D (s )稳定,则相应的D (z )也稳定。

所得D (z )的频率响应在低频段与D (s )频率响应相近,而在高频段相对于D (s )的频率响应有严重畸变[1]。