x
练习 判定 ( x y)dx ( x y)dy 在整个xoy面内是否是
某一函数u( x, y)的全微分,若是,求出一个这样的函数.
解 记P x y, Q x y,
Q 1 P 在xoy面内恒成立,
x
y
在xoy面内原式是某一函数u( x, y)的全微分;
Q P 在G内恒成立. x y
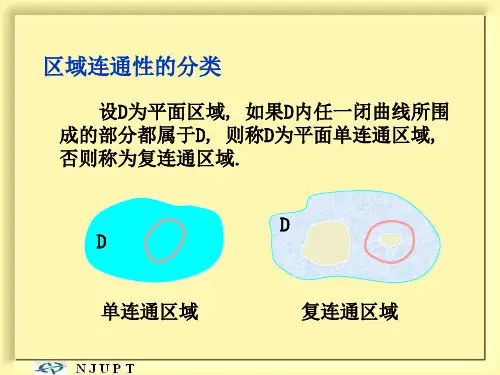
定理3 设G是一个单连通区域, 函数P( x, y),Q( x, y)在G内
具有一阶连续偏导数, 则P( x, y)dx Q( x, y)dy在G内是某 二元函数u( x, y)的全微分的充要条件是:
Q P 在G内恒成立. x y
证明 (必要性). 设du P( x, y)dx Q( x, y)dy, 则
令 u( x, y) ( x, y)( x y3 )dx 3xy2dy (0,0)
y
( x,0)( x y3 )dx ( x, y) 3xy2dy
(0,0)
( x,0)
(x, y)
x
0
xdx
y
0
3
xy2dy
1 2
x2
xy 3 .
o
( x,0)
P y
在左半平面内恒成立,
o
x
在左半平面内原式是某函数u( x, y)的全微分;
令
u( x,
y)
( x, y)
(?1,0)
y x2 y2dx
x2
x
y2
dy
令 u( x,
y)
( x, y)
(1,0)