SimuLink卫星姿态控制_运动学模块的建立
- 格式:docx
- 大小:1.44 MB
- 文档页数:5


matlab simulink模型搭建方法Matlab Simulink是一个强大的多领域仿真和模型搭建环境,广泛应用于控制系统、信号处理、通信系统等多个领域。
本文将详细介绍Matlab Simulink模型搭建的方法,帮助您快速掌握这一技能。
一、Simulink基础操作1.启动Simulink:在Matlab命令窗口输入“simulink”,然后按回车键,即可启动Simulink。
2.创建新模型:在Simulink开始页面,点击“新建模型”按钮,或在菜单栏中选择“文件”→“新建”→“模型”,创建一个空白模型。
3.添加模块:在Simulink库浏览器中,找到所需的模块,将其拖拽到模型窗口中。
4.连接模块:将鼠标光标放在一个模块的输出端口上,按住鼠标左键并拖拽到另一个模块的输入端口,松开鼠标左键,完成模块间的连接。
5.参数设置:双击模型窗口中的模块,可以设置模块的参数。
6.模型仿真:在模型窗口中,点击工具栏上的“开始仿真”按钮,或选择“仿真”→“开始仿真”进行模型仿真。
二、常见模块介绍1.源模块:用于生成信号,如Step、Ramp、Sine Wave等。
2.转换模块:用于信号转换和处理,如Gain、Sum、Product、Scope 等。
3.控制模块:用于实现控制算法,如PID Controller、State-Space等。
4.建模模块:用于构建物理系统的数学模型,如Transfer Fcn、State-Space等。
5.仿真模块:用于设置仿真参数,如Stop Time、Solver Options等。
三、模型搭建实例以下以一个简单的线性系统为例,介绍Simulink模型搭建过程。
1.打开Simulink,创建一个空白模型。
2.在库浏览器中找到以下模块,并将其添加到模型窗口中:- Sine Wave(正弦波信号源)- Transfer Fcn(传递函数模块)- Scope(示波器模块)3.连接模块:- 将Sine Wave的输出端口连接到Transfer Fcn的输入端口。


基于Simulink实时工具的小卫星姿控物理仿真
王屹;裴蓓
【期刊名称】《机械设计与制造工程》
【年(卷),期】2011(040)015
【摘要】针对小卫星姿态控制系统的设计和研制需要,应用高精度单轴气浮台模拟小卫星在轨运行时的微重力、无摩擦的环境,借助Simulink模块库建立了实时控制系统软件模型,利用反作用飞轮、光纤陀螺、数显表、控制计算机等物理设备快速构建了简化的小卫星姿态控制仿真硬件系统,并进行了姿态控制物理仿真实验,实验结果表明,仿真系统具有较高的姿态指向精度和稳定度,能够达到小卫星姿态控制仿真要求.
【总页数】4页(P53-56)
【作者】王屹;裴蓓
【作者单位】长春职业技术学院工程技术分院,吉林长春130033;长春职业技术学院工程技术分院,吉林长春130033
【正文语种】中文
【中图分类】TP23
【相关文献】
1.基于SoPC的微小卫星姿轨控计算机设计与实现 [J], 康国华;夏青;成婧
2.小卫星姿控xPC半物理仿真系统设计 [J], 徐开;陈长青;关文翠;金光
3.一种基于新型智能模拟器的小卫星姿轨控测试系统 [J], 卢彦杰;姜鼎;宋明轩
4.基于SIMULINK的卫星姿控系统的仿真实现 [J], 余涌涛;梁加红
5.基于Simulink实时工具的小卫星姿控物理仿真 [J], 王屹;裴蓓
因版权原因,仅展示原文概要,查看原文内容请购买。

卫星姿态稳定系统的建模与控制卫星姿态稳定是指通过控制卫星的姿态(即旋转角度和轴向),使其保持稳定状态,以确保卫星能够正确地完成各项任务。
由于卫星在太空中受到各种外部扰动力,如引力、太阳辐射压力和空气阻力等,因此需要设计一套卫星姿态稳定系统,来实现准确的定位和导航功能。
卫星姿态稳定系统主要由三个部分组成:传感器、控制器和执行器。
传感器用于测量和监测卫星的姿态状态,主要包括陀螺仪、加速度计和磁强计等;控制器根据传感器的信号进行计算和判断,决定执行器的输出信号;执行器根据控制信号对卫星进行控制,以实现姿态调整和稳定。
首先,卫星姿态的建模是设计卫星姿态稳定系统的基础。
建模过程主要分为动力学建模和姿态动力学建模两个方面。
动力学建模是描述卫星在太空中受到的外部扰动力和惯性力作用下的运动规律,通常采用牛顿力学定律和质点模型进行建模。
姿态动力学建模则是描述卫星在稳定状态下的姿态运动规律,通常采用旋转刚体模型和欧拉动力学方程进行建模。
通过建立准确的卫星姿态动力学模型,能够为后续的控制器设计和系统优化提供理论基础。
其次,控制器的设计是卫星姿态稳定系统的核心部分。
常用的控制器设计方法有PID控制器、模糊控制器和自适应控制器等。
PID控制器是一种经典的控制器设计方法,通过对误差、偏差和积分值进行比例、积分和微分的加权计算,生成控制信号来调整卫星的姿态。
模糊控制器则是一种基于模糊逻辑推理的控制器设计方法,能够处理复杂的非线性控制问题。
自适应控制器则是根据系统的状态变化和外部环境的变化来自适应地调整控制参数,以实现更好的控制效果。
以上三种控制器设计方法各有优缺点,需要根据实际情况选择合适的控制器设计方法。
最后,执行器的选型和控制算法的实现是卫星姿态稳定系统的重要组成部分。
常用的执行器包括反作用轮、磁力矩杆和姿态控制喷气装置等。
反作用轮通过调整转速和转向来产生控制力矩,磁力矩杆通过改变磁力矩的大小和方向来产生控制力矩,姿态控制喷气装置则通过喷气推力来改变卫星的姿态。



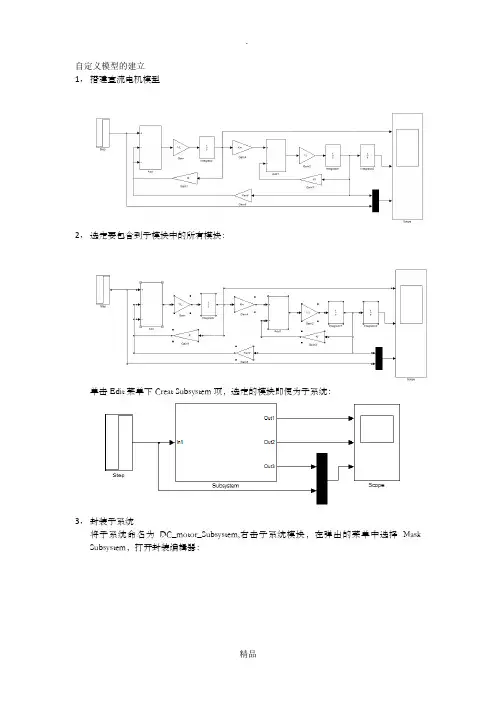
自定义模型的建立1,搭建直流电机模型2,选定要包含到子模块中的所有模块:单击Edit菜单下Creat Subsystem项,选定的模块即便为子系统:3,封装子系统将子系统命名为DC_motor_Subsystem,右击子系统模块,在弹出的菜单中选择Mask Subsystem,打开封装编辑器:Icon&Ports选项卡可对模块的外框,透明度,图表等进行设置。
在Icon Drawing Command 区域中可用命令改变端口名称,添加图片,修改颜色等。
以下命令用于修改端口名称及颜色:color('red');port_label('input',1,'Control Signal');color('red');port_label('output',1,'Torque');color('red');port_label('output',2,'Angle');color('red');port_label('output',3,'Speed');输入命令后单击OK,则则子模块变为:若要添加图片,需将图片放在模型所在目录下,命名为‘DC_motor’,在Icon Drawing Command区域内输入命令:image(imread('DC_motor.jpg'))则子模块变为:4,添加模块到库浏览器在Simulink库浏览器窗口,选择File菜单下New—Library,打开库编辑窗口,将封装后的DC_motor_subsystem拖入库编辑器并保存为DC_motor_subsystem_lib.mdl 。
编写M函数代码:并保存在DC_motor_subsystem_lib.mdl所在目录下,重新打开模块库,则自定义模块添加成功:注意事项:在建模过程中,应注意模型名称是否拼写正确等细节问题。


Simulink使用基本Simulink是一种功能强大的图形化建模和仿真环境,用于分析和设计控制系统。
它是MATLAB的一个扩展工具箱,提供了一种直观和可视化的方法来创建和模拟动态系统模型。
在本文中,我们将介绍Simulink的基本使用方法。
在Simulink中,模型由一个个模块组成,每个模块代表系统的一个部分,例如传感器、执行器、控制器等。
这些模块通过线缆相互连接,以传递信号和数据。
要添加模块到模型中,我们可以在库浏览器中选择合适的模块,然后将其拖动到模型窗口中。
我们还可以使用快捷键B打开库浏览器,并通过栏来快速找到需要的模块。
一旦添加了模块,我们可以使用鼠标点击模块并拖动来改变连接线的位置。
要连接两个模块,只需将鼠标从一个模块上的端口位置拖动到另一个模块上的端口位置。
另外,我们还可以使用连接线工具栏上的线条样式来自定义连接线的样式,例如线的颜色、宽度等。
在进行仿真之前,我们需要设置模型的参数。
这包括设置仿真时间、步长和求解器等。
可以在模型窗口的工具栏上找到仿真按钮,点击后将启动仿真过程。
Simulink将按照设定的时间和步长,以及模型中各模块的逻辑,模拟系统的动态行为,并生成仿真结果。
仿真结果可以在仿真数据视图中查看和分析,包括系统的输入、输出、状态变量等。
除了基本的建模和仿真功能,Simulink还提供了许多高级功能和工具,用于系统控制、优化、验证等。
例如,我们可以使用状态流程图(Stateflow)来建模系统的离散事件行为,使用原型环境(Simscape)来建模物理系统,使用代码生成工具箱来生成嵌入式代码等。
Simulink还支持与MATLAB的混合编程,可以通过MATLAB脚本和函数来调用Simulink 模型,并在Simulink模型中使用MATLAB函数。
总结起来,Simulink是一个强大的图形化建模和仿真环境,适用于各种控制系统的分析和设计。
它提供了直观和可视化的方法来创建和模拟系统模型,并提供了丰富的工具和功能来支持系统开发的各个方面。
三轴稳定卫星姿态确定及控制系统的研究一、本文概述随着航天技术的飞速发展,三轴稳定卫星已成为现代空间科技领域的重要组成部分。
这类卫星通过其精确的姿态确定及控制系统,实现了在太空环境中的稳定运行和高效工作。
本文旨在深入研究三轴稳定卫星的姿态确定及控制系统,探讨其工作原理、技术挑战以及优化策略,为未来的卫星设计与控制提供理论支持和实践指导。
本文首先将对三轴稳定卫星的基本概念和特点进行介绍,明确研究背景和目的。
随后,将详细分析卫星姿态确定的基本原理和方法,包括传感器技术、数据处理算法以及姿态估计理论等。
在此基础上,将探讨控制系统的设计原则和实现方式,包括姿态控制策略、执行机构选择以及控制算法优化等。
本文还将对三轴稳定卫星姿态确定及控制系统中的关键技术进行深入剖析,如姿态传感器误差补偿、控制算法鲁棒性增强以及卫星在轨自主定姿等。
将结合国内外相关研究成果,对现有的姿态确定及控制技术进行总结和评价,指出存在的问题和改进方向。
本文将提出一种优化的三轴稳定卫星姿态确定及控制系统设计方案,通过仿真实验和实地测试验证其有效性和可行性。
这一方案将为未来卫星的设计和制造提供有益的参考,推动航天技术的持续进步和发展。
二、三轴稳定卫星姿态确定原理三轴稳定卫星的姿态确定是其控制系统中的核心环节,它涉及到卫星在空间中的方向感知和姿态调整。
三轴稳定卫星的姿态确定原理主要基于惯性测量单元(IMU)和星敏感器(Star Tracker)等传感器的数据融合处理。
惯性测量单元(IMU)是卫星姿态确定的基础设备,它通过内部的陀螺仪和加速度计来测量卫星的角速度和加速度,进而推算出卫星的姿态变化。
然而,由于IMU的长期误差积累,单纯依赖IMU进行姿态确定无法满足长时间、高精度的要求。
因此,需要引入星敏感器(Star Tracker)等光学传感器进行辅助。
星敏感器通过拍摄星空图像,识别出已知的天体位置,进而解算出卫星的姿态。
这种方式的优点是精度高、误差积累小,但其缺点是受到观测条件的限制,例如在地球阴影区、太阳光照强烈等情况下,星敏感器可能无法正常工作。
simulink基本模块的使用Simulink是一种强大的仿真和建模工具,常用于开发控制系统、信号处理和通信系统等。
本文将一步一步介绍Simulink的基本模块的使用,并讨论它们在不同领域中的应用。
一、Simulink基础知识在开始介绍基本模块之前,我们需要了解Simulink的一些基础知识。
Simulink是MATLAB软件的一个附加模块,用于建立模型以及执行仿真。
Simulink模型是由各种模块组成的,这些模块通过连线连接在一起,形成一个图形化的仿真模型。
它使用图形化界面,使用户能够直观地构建和修改模型。
二、Simulink基本模块1. 恒定值(constant)模块:恒定值模块用于生成恒定的信号,其输出值不会改变。
在模型中,我们可以通过恒定值模块设置输入信号的初始值、幅值以及一些其他属性。
该模块常用于生成常数信号,如直流电压或恒定的参考信号。
2. 脉冲(gain)模块:脉冲模块将输入信号的幅值乘以一个常数增益,然后输出结果。
通过改变增益系数,可以调整输出信号的幅值。
该模块常用于放大或缩小信号的幅值。
3. 积分器(integrator)模块:积分器模块对输入信号进行积分,并输出积分值。
积分器模块用于对信号进行数值积分操作,可用于控制系统中的积分环节,如PID控制器中的积分环节。
4. 微分器(derivative)模块:微分器模块对输入信号进行微分计算,并输出结果。
微分器模块适用于需要对信号进行微分操作的场景,如滤波器设计和导数控制器。
5. 比例积分微分(PID)控制器模块:PID控制器模块是Simulink中非常重要的一个模块,它结合了前面介绍的比例、积分和微分模块,实现了闭环控制。
PID控制器模块根据输入信号和误差信号生成控制信号,以实现期望输出。
该模块在自动控制系统中应用广泛。
6. 转换器(Switch)模块:转换器模块根据输入信号的值和条件判断,选择输出信号的路径。
该模块可以用于实现逻辑判断,选择不同的信号传递路径。
simulink 的用法
Simulink是一种图形化建模和仿真环境,用于设计、建模和仿真动态系统。
它是MATLAB软件的一部分,提供了一种直观的方法来构建和模拟各种系统,包括控制系统、通信系统、图像处理系统等。
Simulink的用法包括以下几个步骤:
1.打开Simulink:使用MATLAB软件打开Simulink工具包,或者直接在MATLAB命令窗口中输入"simulink"打开。
2.创建模型:在Simulink界面上使用不同的模块和线段,构建系统模型。
模块可以代表各种组件,如传感器、控制器、执行器等,线段则表示信号和数据流。
3.连接模块:使用适当的线段连接不同的模块,建立模型中各个组件之间的数据流和控制逻辑。
4.参数设置:对模型中的各个模块进行参数设置,以确保其行为与实际系统相符。
5.仿真运行:运行模型进行仿真,观察系统的动态行为和输出结果。
可以通过修改模型参数、调整模型结构来进一步优化和改进系统设计。
除了以上基本用法,Simulink还提供了许多高级功能,如模型验证、优化设计、代码生成等。
模型验证功能可以检测和解决模型中的错误和问题。
优化设计功能可以通过自动搜索和调整模型参数,实现系统性能的最优化。
代码生成功能可以将Simulink模型转换为C代码或其他可执行文件,以便在嵌入式系统中进行实时部署。
总的来说,Simulink提供了一种直观的图形化建模方法,将系统设计过程可视化,使得系统建模和仿真更加简单和高效。
四元数姿态运动学方程:(见《基于星敏感器角速度估计的陀螺故障诊断》)
()b b b b b b o
o o ob o ib o io 11C 22
∙
=⊗=⊗-Q Q w Q w w 其中b
o Q 表示星体坐标系b 相对于轨道坐标系o 的姿态四元数在体坐标系b 中的投影(在星
体坐标系中轨道坐标系o 转到与星体坐标系b 重合(与后面的姿态坐标转换矩阵对应)所
需的姿态四元数);⊗表示四元数乘法;b ob w 表示星体坐标系b 相对于轨道坐标系o 的角速度在b 坐标系中的投影;b ib w 表示体坐标系b 相对于惯性坐标系i 的角速度在b 坐标系中的投影,由动力学模块给出;b o C 表示o 系到b 系的坐标转换矩阵,由四元数Q 计算得到;o io
w 表示轨道坐标系o 相对于惯性坐标系i 的角速度在o 坐标系中的投影,该角速度在轨道坐标系中表示简单,该值在m 文件中给出。
利用运动学方程画运动学模块图如下:
建立四元数转姿态矩阵模块: 用mask 修改模块封面。
依照下面的转换公式,使用Fcn 模块和Create3*3 Matrix 模块建立四元数转换模块如下:
2222103212031302b
T 22222
o 01203203123012222130223013012q q q q 2(q q q q )2(q q q q )C (q )2(q q q q )
q q q q 2(q q q q )2(q q q q )2(q q q q )
q q q q ⎡⎤
+--+-⎢⎥
=+-=-+--+⎢⎥
⎢⎥+-+--⎣
⎦
qq E q
建立四元数求解模块:
使用Subsystem 模块建立Quaternion Solve Model ,并create mask 如下:
四元数主部与矢部分开计算积分如下:
根据上式画模块图如下:
利用Integrator、Mux、Gain、Add模块建立初始如下:
利用Demux模块将Q的矢部与主部分开。
其中Demux模块设置如下(将四个数按[1 3]分成两部分):
利用Dot Product模块求q0的导:
利用动力学模块中的叉乘模块来完成q的导的求解如下:
这样四元数求解模块即建立,输入w输出Q。
建立运动学模块:
利用from模块引入动力学模块计算的姿态角速度wb和m文件中的轨道角速度wo,建立运动学模块如下(注意product的multiplication应为Matrix):
这样运动学模块即建立,输入w得到Q。