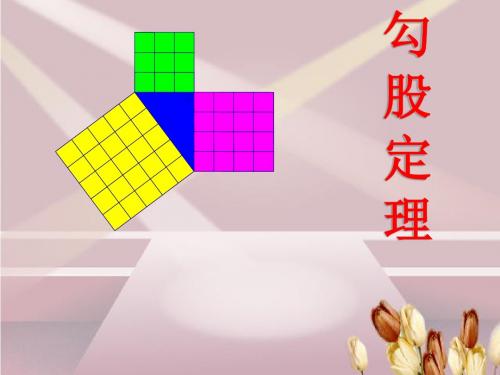
邪至日2=勾2+股2
陈子已不限于:三、四、五的特殊情形,而是推广到一般情形了。
人们对勾股定理的认识,经历过一个从特殊到一般的过程,很难区分是谁最 先发明的.
勾股定理曾引起很多人的兴趣,世界上对这个定理的证明方法很多,1940 年卢米斯收集了这个定理的370种证明,期中包括大画家达·芬奇和美国总统 詹姆士·阿·加菲尔德的证法。到目前为止,已有四百多种证法.
可要当心噢!
在直角△ABC中, a=3, b=4, 则求c的值?
已知∠ACB=90°,
A
CD⊥AB,AC=3,BC=4.
D
求CD的长.
3
C
B
4
求下列直角三角形中未知边的长:
8
17
x
12 5
x
解:在直角三角形中, 解:在直角三角形中, 依勾股定理可得: 依勾股定理可得:
82+ X2=172
52+ 122= X2
BC=2.16, CA=5.41,
根据勾股定理得
A B A 2 C B 2 C 5 .4 2 1 2 .1 26
≈4.96(米)
问题解决
问题情境
某楼房三楼失火,消防队员赶来救火, 了解到每层楼高3米,消防队员取来6.5米长 的云梯,如果梯子的底部离墙基的距离是2.5 米,请问消防队员能否进入三楼灭火?
勾股定理的证明(一)
“弦图”
a
最早是由1700
多年前三国时
期的数学家赵
b
c 爽为《周髀算
b
经》作注时给
b a
出的,他用面 积法证明了勾
股定理
c
你能用面积法
证明勾股定理
吗?
勾股定理的证明(二)