河南省南阳市方城县第一高级中学学年高二数学下学期学期第一次月考试题 文

河南省方城县第一高级中学高二第一次月考（数学文）第Ⅰ卷一、 选择题（12×5=60，在所给的四个选项中，只有一项是符合题目要求的，将其标号填涂在答题卡相应位置）1． 在等比数列{a n }中，a 2=8,a 5=64则公比q=A. 2B. 3 C 4 D. 82．Sn 是等差数列{a n }的前n 项和，a 4+a 5=18,则S 8=A ． 18 B. 36 C. 54 D. 723．等差数列{a n }的前n 项和Sn=n 2+2n,其公差为A. 1B. -1C. -2D. 24．在等差数列{a n }中，a 1+a 2+a 3=1,a 7+a 8+a 9=3,则a 16+a 17+a 18=A. 5B. 6C. 7D. 85. 在等比数列{a n }中,a 1=1,a 3=9,则a 2=A ． 3 B. -3 C. ±3. D. ±26.在⊿ABC 中，∠A=60o ，BC=3，AB=6，则∠C= A. 30o B. 45o C. 135o D. 45o 或135o7. 在⊿ABC 中,∠A ，∠B,∠C 的对边分别为a 、b 、c,且a+b+c=8，SinA+SinB=3SinC 则AB=A . 1B . 2 C. 3 D. 48．在等比数列{a n }中，ａ１×ａ２×ａ３…×ａ９＝２９，则ａ５＝Ａ．１ Ｂ． ２ Ｃ． ４ Ｄ． ８9.在⊿ABC 中,Sin2C=Sin2A, 则⊿ABC 的形状是A . 直角三角形 B. 等腰三角形C 直角三角形或等腰三角形 D. 等腰直角三角形10. 在⊿ABC 中,AB=AC=1,∠BAC=1则⊿ABC 的外接圆直径是A. 1/2B.． 1C. 2D. 411．２＋２２＋２３＋２４＋…＋２ｎ＞62，则正整数ｎ的最小值是A 4 B. 5 C. 6 D.712. Sn 是等差数列{a n }的前n 项和, Tn 是等差数列{b n }的前n 项和,若n n T S =1514+-n n ,则55b a = A 2619 Ｂ 4635 Ｃ5139 Ｄ 4131第Ⅱ卷二、填空题（５×４＝２０，把答案写在题中横线上）１３.．在⊿ABC 中,∠A ，∠B,∠C 的对边分别为a 、b 、c, 已知ａ２＋ｂ２＝ｃ２＋ａｂ，则∠Ｃ＝ １４．Sn 是数列{a n }的前n 项和，且Ｓｎ＝３ｎ＋１，则数列｛ａｎ｝的通项公式为———１５．已知数列{a n }的通项公式为ａｎ＝１００－４ｎ，Sn 是数列{a n }的前n 项和，则使Ｓｎ最大的自然数ｎ为————１６．在⊿ABC 中,∠A ，∠B,∠C 的对边分别为a 、b 、c,若a=3,b=4,c=5,则⊿ABC 的内切圆半径是————三、解答题（应写出文字说明、证明过程、演算步骤）１７.（10分）在等差数列{a n }中, a 3=7,a 10=21,求数列{a n }的通项公式ａｎ及前n 项和Sn.18. （12分）数列｛ａｎ｝满足a 1=2,a n+1=3a n +8,（n ≥1）(Ⅰ)证明数列{a n +4}是等比数列.(Ⅱ) 求数列｛ａｎ｝的通项公式19（12分）已知数列{a n }中，a 1=1,a 2=x,a 3=x 2,a 4=x 3,…,a n =x n-1,(x ∈R,n ∈N +),（Ⅰ）当x=0时，求数列{a n }的前n 项和Sn.(Ⅱ) 当x ≠0时，求数列{a n }的前n 项和Sn（12分）在⊿ABC 中，SinA=53, SinB=135, 求SinC 的值. 21. （12分）已知a n =n,b n =3n ,c n =a n ×b n 求数列{c n}的前n 项和Sn22. （12分）在⊿ABC 中，三内角A 、B 、C 成等差数列，AC=23,设内角A=x,周长为y,(1)求函数y=f(x)的解析式和定义域(2)求y 的最大值。

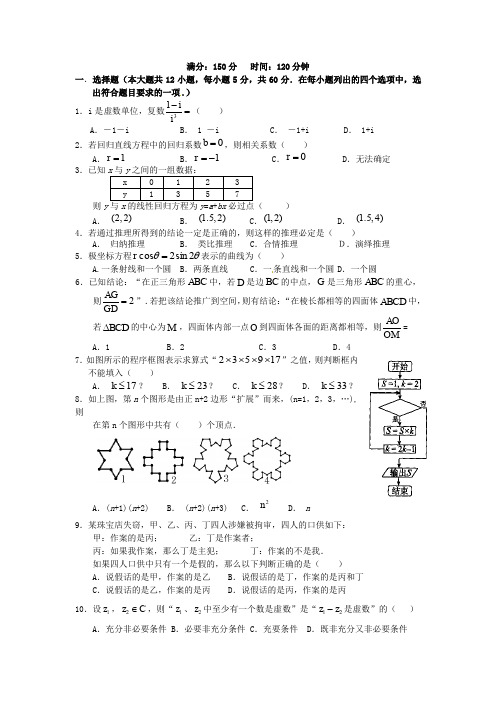
满分：150分 时间：120分钟一．选择题（本大题共12小题，每小题5分，共60分．在每小题列出的四个选项中，选出符合题目要求的一项．） 1．i 是虚数单位，复数31ii-=（ ）A ．－1－iB ． 1 －iC ． －1+iD ． 1+i2．若回归直线方程中的回归系数0b =，则相关系数（ ）A ．1r =B ．1r =-C ．0r =D ．无法确定 3．已知则y ） A ． (2,2) B ． (1.5,2) C ．(1,2) D ． (1.5,4) 4．若通过推理所得到的结论一定是正确的，则这样的推理必定是（ ）A ． 归纳推理B ． 类比推理C ．合情推理 Ｄ．演绎推理 5．极坐标方程θθ2sin 2cos =r 表示的曲线为（ ）A.一条射线和一个圆 B ．两条直线 C ．一条直线和一个圆 D ．一个圆6．已知结论：“在正三角形ABC 中，若D 是边BC 的中点，G 是三角形ABC 的重心，则2AGGD=”．若把该结论推广到空间，则有结论：“在棱长都相等的四面体ABCD 中，若BCD ∆的中心为M ，四面体内部一点O 到四面体各面的距离都相等，则AOOM=A ．1B ．2C ．3D ．4 7．如图所示的程序框图表示求算式“179532⨯⨯⨯⨯”之值，则判断框内不能填入（ ）A ． 17≤k ？B ． 23≤k ？C ． 28≤k ？D ． 33≤k ？ 8．如上图，第n 个图形是由正n+2边形“扩展”而来，(n=1，2，3，…),则在第n 个图形中共有（ ）个顶点．A ．(n +1)(n +2)B ． (n +2)(n +3)C ． 2nD ． n9．某珠宝店失窃，甲、乙、丙、丁四人涉嫌被拘审，四人的口供如下：甲：作案的是丙； 乙：丁是作案者；丙：如果我作案，那么丁是主犯； 丁：作案的不是我． 如果四人口供中只有一个是假的，那么以下判断正确的是（ ） A ．说假话的是甲，作案的是乙 B ．说假话的是丁，作案的是丙和丁 C ．说假话的是乙，作案的是丙 D ．说假话的是丙，作案的是丙10．设1z ，2C z ∈，则“1z 、2z 中至少有一个数是虚数”是“12z z -是虚数”的（ ）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分又非必要条件11．已知2421(2),2(2)2a a p a a q a a -+-=+>=>-，则( ) A ． p q > B ． p q < C ． p q ≥ D ． p q ≤12．给出下面类比推理命题（其中Q 为有理数集，R 为实数集，C 为复数集）⑴“若,,R b a ∈则b a b a =⇒=-0”类比推出“若,,C b a ∈则b a b a =⇒=-0”⑵“若,,,,R d c b a ∈则复数d b c a di c bi a ==⇒+=+,”类比推出“若,,,,Q d c b a ∈ 则复数d b c a d c b a ==⇒+=+,22”⑶“若,,R b a ∈则b a b a >⇒>-0”类比推出“若,,C b a ∈则b a b a >⇒>-0”其中类比正确的个数为( )A ． 0B ． 1C ． 2D ． 3二、填空题（每题5分，共20分）13．若纯虚数z 满足()11i z ai -=+，则实数a 等于14．已知直线的极坐标方程为23)3cos(=+πθr ，则极点到该直线的距离是 。

河南省南阳市第一中学2017-2018学年高二数学下学期第一次月考试题 理第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知i 是虚数单位，则复数512ii+=（ ） A ．2i - B ．12i - C ．2i + D ．12i -+2. 设1111()(*)1232f n n N n n n n =++++∈+++L ，那么(1)()f n f n +-等于（ ） A ．112122n n -++ B ．112122n n +++ C ．122n + D ．121n + 3.曲线()31xf x e x =-+在点(0,2)处的切线与坐标轴围成的三角形的面积为（ ） A ．2 B ．32 C ．54D ．1 4.定义*,*,*,*A B B C C D D A 的运算分别对应下面图中的（1），（2），（3），（4），则图中（5），（6）对应的运算是（ ）A ．*,*B D A D B ．*,*B D AC C. *,*B C AD D ．*,*C D A D 5.设()f x 在0x 可导，则000()(3)limx f x x f x x x→+--等于（ ）A ．04'()f xB ．0'()f x C. 02'()f x D ．03'()f x 6.已知1i +是关于x 的方程220(,)ax bx a b R ++=∈的一个根，则a b +=（ ） A ．-1 B ．1 C.-3 D ．37.以正弦曲线sin y x =上一点P 为切点得切线为直线l ，则直线l 的倾斜角的范围是（ ）A ．30,,44πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭U B ．[)0,π C. 3,44ππ⎡⎤⎢⎥⎣⎦ D ．30,,424πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭U 8.在下列命题中，正确命题的个数是（ ） ①两个复数不能比较大小；②复数1z i =-对应的点在第四象限；③若22(1)(32)x x x i -+++是纯虚数，则实数1x =±；④若221223()()0z z z z -+-=，则123z z z ==.A ．0B ．1 C.2 D ．3 9.已知函数21()sin cos 2f x x x x x =+，则其导函数'()f x 的图象大致是（ ） A ． B ． C.D ．10.“一支医疗救援队里的医生和护士，包括我在内，总共是13名.下面讲到的人员情况，无论是否把我计算在内，都不会有任何变化.在这些医务人员中：①护士不少于医生；②男医生多于女护士；③女护士多于男护士；④至少有一位女医生.”由此推测这位说话人的性别和职务是（ ）A ．男护士B ．女护士 C.男医生 D ．女医生11.给出定义：设'()f x 是函数()y f x =的导函数，''()f x 是函数'()f x 的导函数，若方程''()0f x =有实数解0x ，则称点()00,()x f x 为函数()y f x =的“拐点”.已知函数()34sin cos f x x x x =+-的拐点是()00,()M x f x ，则点M （ ）A ．在直线3y x =上B ．在直线3y x =-上 C.在直线4y x =-上 D ．在直线4y x =上12.若自然数n 使得作竖式加法(1)(2)n n n ++++均不产生进位现象，则称n 为“开心数”.例如：32是“开心数”.因32+33+34不产生进位现象；23不是“开心数”，因23+24+25产生进位现象，那么，小于100的“开心数”的个数为（ ） A ．9 B ．10 C.11 D ．12第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.复数cos75sin75z i =︒+︒（i 是虚数单位），则在复平面内2z 对应的点位于第 象限．14.已知函数()f x 的导函数为'()f x ，且满足关系式1()3'(1)f x xf x=+，则'(2)f 的值等于 ．15.我们知道，在边长为a 的正四面体内任一点到其四个面的距离之和为定值 ． 16.二维空间中圆的一维测量（周长）2l r π=，二维测量（面积）2S r π=，观察发现；三维空间中球的二维测度（表面积）24S r π=，三维测度（体积）343V r π=，观察发现'V S =.已知四维空间中“超球”的三维测度38V r π=，猜想其四维测度W = ． 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 求下列函数的导数.（1）x e y x =； （2）2(21)(31)y x x =-+； （3）sin(1)cos 2x y x =+-.18. m 为何实数时，复数2(2)3(1)2(1)z i m i m i =+-+--满足下列要求： （1）z 是纯虚数；（2）z 在复平面内对应的点在第二象限；（3）z 在复平面内对应的点在直线50x y --=上. 19. 设函数2()f x ax bx c =++且(1),3222af a c b =->>. （1）试用反证法证明：0a >； （2）证明：334b a -<<-.20. 若存在过点(1,0)的直线与曲线3y x =和21594y ax x =+-都相切，求实数a 的值. 21. 设函数()bf x ax x=-，曲线()y f x =在点(2,(2))f 处的切线方程为74120x y --=. （1）求()y f x =的解析式；（2）证明：曲线()y f x =上任一点处的切线与直线0x =和直线y x =所围成的三角形面积为定值，并求此定值.22.已知数列{}n a 的前n 项和1122n n n S a -⎛⎫=--+ ⎪⎝⎭（n 为正整数）.（1）令2nn n b a =，求证数列{}n b 是等差数列，并求数列{}n a 的通项公式；（2）令121,n n n n n c a T c c c n +==+++L ，试比较n T 与521nn +的大小，并予以证明.试卷答案一、选择题1-5:CADBA 6-10:AAACA 11、12：AD 二、填空题 13.二 14. 5415. 3a 16. 42r π 三、解答题17.（1）()222(1)x xx x x x e x e x e e x e e x y x x x x '''-⋅⎛⎫⋅--'==== ⎪⎝⎭. （2）因为232(21)(31)6231y x x x x x =-+=+--，所以32322(6231)(6)(2)(3)(1)1843y x x x x x x x x ''''''=+--=+--=+-. （3）函数sin(1)y x =+看作sin y u =和1u x =+的复合复数，(sin )(1)cos cos(1)x u xy y u u x u x '''''=⋅=⋅+==+，同样的可以求出cos 2xy =的导数1sin 22x y '=-，所以题中函数的导数为1cos(1)sin 22x y x '=++.18.（1）222(2)3(1)2(1)23322z i m i m i m m i mi m i =+-+--=+---+22(232)(32)m m m m i =--+-+.222320320m m m m ⎧--=⎪⎨-+≠⎪⎩，得12m =-，即12m =-时，z 是纯虚数. （2）由222320320m m m m ⎧--<⎪⎨-+>⎪⎩，得112m -<<，即1,12m ⎛⎫∈-⎪⎝⎭时，z 在复平面内对应的点在第二象限. （3）由22(232)(32)50m m m m ----+-=，得3m =±， 即3m =±时，z 在复平面内对应的点在直线50x y --=上. 19.（1）假设0a ≤，322,30,20,20,a c b a c b >>∴≤<<Q将上述不等式相加得3220a c b ++<，(1),32202af a c b =-∴++=Q ，这与3220a c b ++<矛盾，∴假设不成立，∴0a >. （2）3(1),22a f abc c a b =++=-∴=--Q ， 3232,3a c a b a b ∴>=--∴>-.322,34.0,34b c b a b a a >∴->>∴-<<-Q Q . 20.设直线与曲线3y x =的切点坐标为00(,)x y ，则300200031y x y x x ⎧=⎪⎨=⎪-⎩，则切线的斜率2030k x ==或274k =，若0k =，此时切线的方程为0y =， 由201594y y ax x =⎧⎪⎨=+-⎪⎩，消去y ，可得215904ax x +-=，其中0∆=，即2153604a ⎛⎫+= ⎪⎝⎭， 解可得2564a =-；若274k =，其切线方程为27(1)4y x =-， 由227(1)41594y x y ax x ⎧=-⎪⎪⎨⎪=+-⎪⎩，消去y 可得29304ax x --=，又由0∆=，即990a +=，解可得1a =-.故2564a =-或1-. 21.（1）方程74120x y --=可化为734y x =-.当2x =时，12y =. 又2()b f x a x '=+，于是1222744b a b a ⎧-=⎪⎪⎨⎪+=⎪⎩，解得13a b =⎧⎨=⎩，故3()f x x x =-.（2）设00(,)P x y 为曲线上任一点，由231y x'=+知曲线在点00(,)P x y 处的切线方程为()002031y y x x x ⎛⎫-=+- ⎪⎝⎭，即()00200331y x x x x x ⎛⎫⎛⎫--=+- ⎪ ⎪⎝⎭⎝⎭.令0x =得06y x =-，从而得切线与直线0x =的交点坐标为060,x ⎛⎫- ⎪⎝⎭.令y x =得02y x x ==，从而得切线与直线y x =的交点坐标为()002,2x x . 所以点00(,)P x y 处的切线与直线0x =，y x =所围成的三角形面积为016262x x-=. 故曲线()y f x =上任一点处的切线与直线0x =，y x =所围成的三角形面积为定值，此定值为6.22.（1）在1122n n n S a -⎛⎫=--+ ⎪⎝⎭中，令1n =，可得1112n S a a =--+=，即112a =. 当2n ≥时，211122n n n S a ---⎛⎫=--+ ⎪⎝⎭，11112n n n n n n a S S a a ---⎛⎫∴=-=-++ ⎪⎝⎭，11122n n n a a --⎛⎫∴=+ ⎪⎝⎭，即11221n n n n a a --=+，12,1n n n n n b a b b -=∴=+Q ，即当2n ≥时，11n n b b --=.又1121b a ==，∴数列{}n b 是首项和公差均为1的等差数列， 于是1(1)12,2nn n n n n b n n a a =+-⋅==∴=. （2）由（1）得11(1)2nn n n c a n n +⎛⎫==+ ⎪⎝⎭，所以231111234(1)2222nn T n ⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L234111111234(1)22222n n T n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭L ，得231111111(1)22222n n n T n +⎛⎫⎛⎫⎛⎫⎛⎫=++++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭L111111421331(1)122212n n n n n -++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭+⎢⎥⎛⎫⎣⎦=+-+=- ⎪⎝⎭-，332n n n T +∴=-. 535(3)(221)3212212(21)n n n n n n n n n T n n n ++---=--=+++，于是确定n T 与521nn +的大小关系等价于比较2n 与21n +的大小. 23452211;2221;2231;2241;2251;<⨯+<⨯+<⨯+<⨯+<⨯+猜想：当3n ≥时，221nn >+.证明如下： 证法1：（1）当3n =时，由猜想显然成立. （2）假设n k =时猜想成立，即221kk >+.则1n k =+时，()1222221422(1)1(21)2(1)1k k k k k k k +=⋅>+=+=+++->++， 所以当1n k =+时猜想也成立.综合（1）（2）可知，对一切3n ≥的正整数，都有221nn >+. 证法2: 当3n ≥时,01210112(11)2221n n n n n n n n n n n n n n n C C C C C C C C C n n --=+=+++++≥+++=+>+L ，综上所述，当1,2n =时，521n n T n <+；当3n ≥时，521n nT n >+.。

南阳一中2016春期高二第一次月考理数试题第Ⅰ卷一、选择题（12小题，每题5分）1．设曲线11x y x +=-在点(32)，处的切线与直线10ax y ++=垂直，则a =（ ） A ．2 B ．12 C ．12- D ．2-2．设()f x 是可导函数，且000()(2)lim 3x f x x f x x x∆→-∆-+∆=∆，则0()f x '=（ ） A ．12B ．1-C ．0D ．2-3．用数学归纳法证明412135()n n n +++∈N 能被8整除时，当1n k =+时，对于4(1)12(1)135k k +++++可变形为（ ）Ａ．41412156325(35)k k k +++++·Ｂ．441223355k k ++·· Ｃ．412135k k +++Ｄ．412125(35)k k +++4．已知直线y x m =-+是曲线23ln y x x =-的一条切线，则m 的值为（ ）A ．0B ．2C ．1D ．3 5．定积分π220sin 2x dx ⎰⎰+xdx e xsin 11-的值等于（ ） A ．π142- B ．π142+ C ．1π24- D ．π12- 6．函数f(x)的定义域为R ，f(-1)=2,对任意x R ∈，f′(x)＞2,则()24f x x >+的解集为A ．(-1，1)B ．(-1，+∞) C．(-∞，-l) D ．(-∞,+∞) 7．设点P 是曲323+-=x e y x 线上的任意一点，P 点处的切线的倾斜角为α，则角α的取值范围是（ ） A ．),32[ππB ． ),32()2,0[πππ⋃C ． ),65[)2,0[πππ⋃D ．)65,2[ππ8．设f (x )，g (x )分别是定义在R 上的奇函数和偶函数,当x <0时，f ′(x )g (x )＋f (x )g ′(x )>0，且(3)0g -=，则不等式f (x )g (x )<0的解集是（ ）A ． (－3，0)∪(3，+∞)B ．(－3，0)∪(0，3)C ．(－∞，－3)∪(3，+∞)D ．(－∞，－3)∪(0，3)9．设△ABC 的三边长分别为a 、b 、c ，△ABC 的面积为S ，内切圆半径为r ，则，类比这个结论可知：四面体S ﹣ABC 的四个面的面积分别为S 1、S 2、S 3、S 4，内切球半径为r ，四面体S ﹣ABC 的体积为V ，则r=（ ） A ．B ．C ．D ．10．函数()f x 是定义在(0,)+∞上的单调函数，且对定义域内的任意x ，均有3(()ln )2f f x x x --=，则()f e =（ ）（A ）31e + （B ）32e + （C ）31e e ++ （D ）32e e ++ 11．已知函数()()2ln x x b f x x+-=（R b ∈）．若存在1,22x ⎡⎤∈⎢⎥⎣⎦，使得)(x f ＞－)(x f x '⋅，则实数b 的取值范围是（ ）A ．(),2-∞ B ．3,2⎛⎫-∞⎪⎝⎭C ．9,4⎛⎫-∞ ⎪⎝⎭D ．(),3-∞12．函数32()393,f x x x x =--+若函数()()[2,5]g x f x m x =-∈-在上有3个零点，则m 的取值范围为（ ） A ．（-24,8）B ．（-24,1]C ．[1,8]D ．[1,8）第Ⅱ卷二、填空题（4小题，每小题5分） 13．由直线，曲线及x 轴所围图形的面积为14．函数()x x x f ln -=的单调增区间是_________________ 15．若函数24()1xf x x =+在区间(21)m m +，上是单调递增函数，则实数m 的取值范围是 ． 16．将全体正整数排成一个三角形数阵：按照以上排列的规律，第n 行（3≥n ）从左向右的第3个数为三、解答题： 17．（10分）（1）求证：(1)2233()a b ab a b ++≥+; （2）已知c b a ,,均为实数，且62,32,22222πππ++=++=++=x z c z y b y xa ，求证：c b a ,,1 3 2 4 5 6 10 9 8 7 11 12 13 14 15………………中至少有一个大于0. 18．（12分）已知()111123f n n =+++⋅⋅⋅+．经计算得()()()()5742,8,163,3222f f f f >>>>． （Ⅰ）由上面数据，试猜想出一个一般性结论； （Ⅱ）用数学归纳法证明你的猜想．19．（12分）某地区的电价为0.8元/(kW ·h)，年用电量为1亿kW ·h ，今年电力部门计划下调电价以提高用电量、增加收益。

一、选择题（本大题共12小题，每小题5分，共60分，每小题有且只有一个选项是符合要求的） 1.下列语句是命题的为( )A. x-1>0B. 他还年青C. 20-5×3=10D. 在20020年前,将有人登上为火星 2.化简AB CD CB AD +--的结果是( )A ．0B ．ABC ．ACD ．AD 3．甲乙两人至少有一个是三好学生是指： （ ） A ． 甲是三好学生，或乙是三好学生 B ．甲乙两人都是三好学生 C ．甲乙两人至多有一个是三好学生 D ．甲乙两人都不是三好学生 4.下列命题中为真命题的是( )A ．命题“若x >y ，则x >|y |”的逆命题B ．命题“若x >1，则x 2>1”的否命题 C ．命题“若x ＝1，则x 2＋x －2＝0”的否命题D ．命题“若x 2>0，则x >1”的逆否命题5.若点A （42+λ，4－μ，1+2γ）关于y 轴的对称点是B （－4λ，9， 7－γ），则λ，μ，γ的值依次为：( )A ．1，－4，9B ．2，－5，－8C ．－3，－5，8D ．2，5，86.已知,a b 是平面α内的两个非零向量，c 是直线l 的方向向量，那么“0,0c a c b ⋅=⋅=且”是“l α⊥”的什么条件（ ）A.充分不必要B.必要不充分C.充要D.既不充分又不必要 7．在以下四个命题中，不正确．．．的个数为（ ） (1) ,()a b c a b a c a b c -=⊥-若与都是非零向量则是的充要条件(2)已知不共线的三点A 、B 、C 和平面ABC 外任意一点O ，点P 在平面ABC 内的充要条件是存在,,,x y z R OP xOA yOB zOC ∈=++且1x y z ++=（3）空间三个向量,,a b c ，若//,//,//a b b c a c 则（4）对于任意空间任意两个向量,a b ，//a b 的充要条件是存在唯一的实数λ，使a b λ= A ．1 B ．2 C ．3 D ．48.已知A(4,1,3),B(2,3,1),C(3,7,-5),点P(x,-1,3)在平面ABC 内，则x 的值为（ ） A. –4 B. 1 C. 10 D. 11 9．已知正方体1111ABCD A B C D -中，11114A E AC =，若1()AE xAA y AB AD =++，则（ ） A ．1122x y ==， B ．112x y ==， C ．113x y ==， D ．114x y ==，10.已知1F =i+2j+3k ，2F =-2i+3j-k,3F =3i-4j+5k ，其中i,j,k 为单位正交基底，若1F ，2F ，3F 共同作用在一个物体上，使物体从点1M (1, －2, 1)移到2M (3, 1, 2)，则这三个合力所作的功为( )A.14B. 621C. -14D. 621- 11．已知正方体外接球的体积是323π，那么正方体的棱长等于 （ ） （A ）22 （B ）233 （C ）423 （D ）43312、下列说法中错误．．的个数为 ( ) ①一个命题的逆命题为真，它的否命题也一定为真； ②若一个命题的否命题为假，则它本身一定为真； ③12x y >⎧⎨>⎩是32x y xy +>⎧⎨>⎩的充要条件；④a b =与a b =是等价的； ⑤“3x ≠”是“3x ≠”成立的充分条件.A 、2B 、3C 、4D 、5 二、填空题：（本大题共7个小题，每小题4分，共28分）13．已知命题:p x ∀∈R ，sin 1x ≤，则p ⌝是 ．14．设e 1,e 2为单位向量，非零向量b=xe 1+ye 2,x,y ∈R.若e 1,e 2的夹角为600,则x b ︱︱︱︱的最大值等于15.如右图，在正三棱柱111C B A ABC -中，1=AB ．若二面角1C AB C --的大小为 60，则点C 到平面1ABC 的距离为__________．16.设不同的直线,a b 的方向向量分别是12,e e ，平面α的法向量是n ，则下列推理中①121b α⎫⇒⎬⎭∥∥∥e e e n ；②12a b ⎫⇒⎬⎭∥∥∥e n e n ；③112b b αα⎫⎪⊄⇒⎬⎪⎭∥∥⊥e ne e；④121b α⎫⇒⎬⎭∥⊥∥e e e n 正确的命题序号是 ． 三、解答题：（本大题共6小题，共70分。

河南省南阳一中2011-2012学年高二下学期第一次月考数学（文）试题一、选择题(每小题5分,共60分)1. 统计中用相关系数r 来衡量两个变量之间线性相关关系的强弱，对于变量x,y 计算得 r =-0.01,则x,y 的相关强弱为（ ）A. 相关性很强B. 相关性较弱C. 相关性一般D. 不相关2.某程序框图如图所示，若输出的S=57，则判断框内为（ ） A. k ＞4? B.k ＞5? C. k ＞6? D.k ＞7?3.流程图的基本单元之间由什么线连接（ ） A.流向线 B.虚线 C.流程线 D.波浪线4. 在吸烟与患肺病这两个分类变量的计算中，若从统计量计算中得出有99%的把握说吸烟患肺病有关的结论，下列说法中正确的是（ ）A. 若某人吸烟，那么他有99%的可能患有肺病B. 在100个吸烟者中必有99人患肺病C. 在100个吸烟者中必有1个患肺病D. 所得结论错误的可能性至多为1% 5. “因为四边形 ABCD 是平行四边形，所以AC 与BD 互相平分”这个“三段论”证明中省略了（ ）A. 大前提B. 小前提C. 结论D. 以上都不对 6. 观察两个相关变量的如下数据：A. 0.7 6.65y x =-+B. 0.350.7y x =+C. 0.70.35y x =+D. y x =7.如果执行右面的程序框图，输入6,4n m ==， 那么输出的p 等于( )A.720B. 360C. 240D. 1208. 若A 、B 是相互独立事件，13=(),34PP B =（A ），则()P A B ⋅=( )A.14B.112C.12D.169.设1,0,0≤+>>y x y x ，则有（ ）A.11≤+y x B.411≥+y x C.21≥xy D.81≥xy10.设R c b a ∈,,，则三个数22,22,22222++++++a c c b b a （ ）A.都大于1B.都大于2C.至少有一个不小于1D.至少有一个不小于211. 已知“整数对”按如下规律排成一列：（1，1），（1，2），（2，1），（1，3），（2，2）（3，1），（1，4），……，则第60个数对是（ ）A. (7,5)B. (5,7)C. (2,10)D. (10,1) 12. 如图所示的三角形数阵叫“莱布尼兹调和三角形”，它们是由整数的倒数组成的，第n行有n 个数且两端的数均为1(2)n n≥，其余每个数是它下一行左右相邻两数的和，如111111111===1222363412+++⋅⋅⋅，，，，则第7行第4个数（从左往右数）为（ ） A. 1140 B. 1105 C. 160D. 142二、填空题(每小题5分,共20分) 13.甲射中目标的概率是21，乙射中目标的概率是31，丙射中目标的概率是41，现在三人同时射击目标，则目标被射中的概率为 .14. 某公司的组织结构图如图所示，则后勤部的直接领导是 .15.五位同学围成一圈依次循环报数，规定：第一位同学首次报出的数为2，第二位同学首次报出的数为3，之后每位同学所报出的数都是前两位同学所报出数的乘积的个位数字，则第2012个被报出的数为 .16.在平面几何中有如下结论：若正三角形ABC 的内切圆面积为1S ，外接圆面积为2S ，则1214S S =.推广到空间几何可以得到类似结论：若正面体A-BCD 的内切球体积为1V ，外接球体积为2V ，则12V V = . 三、解答题(共70分)17.(10分)已知某种动物能活到20岁的概率为54，能活到30岁的概率为21，现有一只这种动物已经活到了20岁，求它能活到30岁的概率.18. (12分)为考察某种药物预防禽流感的效果而进行家禽试验，调查了100只家禽，统计结果为：服用药的共有60只家禽，服用药但患病的仍有20只家禽，没有服用药且未患病的有20只家禽。

姓名：___________班级：___________考号：___________ 注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上的指定区域第I 卷（选择题） 评卷人 得分一、选择题（每小题5分共60分）1.下列给出的四个命题中，说法正确的是（ ）A ．命题“若21x =，则1x =”的否命题是“若21x =，则1x ≠”；B ．“1x =-”是“2560x x --=”的必要不充分条件；C ．命题“存在x R ∈，使得210x x ++<”的否定是“对任意x R ∈，均有210x x ++<”；D ．命题“若x y =，则sin sin x y =”的逆否命题为真.2.设{1,2}M =，2{}N a =，则“1a =”是“N M ⊆”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分又不必要条件3.已知,02:,04:2>--<+x x q m x p 若p 是q 的一个充分不必要条件，则实数m 的取值范围是（ ） A.[)+∞,8B. [)+∞,4C. (]4,∞-D. (]4,-∞-4.已知命题:,23xxp x R ∀∈<；命题32:,1q x R x x ∃∈=-，则下列命题中为真命题的是 A.p q ∧ B.p q ∧⌝ C.p q ⌝∧ D.p q ⌝∧⌝5.椭圆()012222>>=+b a by a x ，B 为上顶点，F 为左焦点，A 为右顶点，且右顶点A 到直线FB的距离为b 2，则该椭圆的离心率为（ ）A.22 B.22- C.12- D. 23-6.设定点()3,01-F ,()3,02F ,动点P 满足()0921>+=+a aa PF PF ，则点P 的轨迹是（ ）A. 椭圆B. 椭圆或线段C. 线段D. 无法判断7.双曲线14322=-x y 的渐近线方程是( ) A. x y 23±= B. x y 332±= C. x y 43±= D. x y 34±=8.过抛物线x y 42=的焦点所作直线中，被抛物线截得弦长为8的直线有（ ） A. 1条B. 2条C. 3条D. 不确定9.抛物线22y x =的焦点坐标是 （ ） A ．)0,1(B ．)41,0(C ．)0,41(D ．)81,0(10.过抛物线24y x =的焦点F 的直线交抛物线于A B 、两点，点O 是坐标原点，若||5AF =，则△AOB 的面积为（ ）A ．5B ．52C ．32D ．17811.已知抛物线243x y =的准线过双曲线2221x y m-=-的一个焦点，则双曲线的离心率为( )A.324 B.62C.3D.3312.已知方程ab by ax =+22和01=++by ax (其中0≠ab ,b a ≠)，它们所表示的曲线可能是（ ）第II 卷（非选择题）评卷人 得分二、填空题（每小题5分共20分）13.设2:430,:3p q p x x q x -+<<,则是的 _____________________条件（填“充分不必要”或“必要不充分”或“充要”或“既不充分也不必要”） .14.已知1F 、2F 是椭圆1:2222=+by a x C （a ＞b ＞0）的两个焦点，P 为椭圆C 上一点，且21PF PF ⊥.若21F PF ∆的面积为9，则b =____________ ．15.方程11422=-+-t y t x 表示曲线C ，给出以下命题： ①曲线C 不可能为圆； ②若1<t<4，则曲线C 为椭圆； ③若曲线C 为双曲线，则t<1或t>4； ④若曲线C 为焦点在x 轴上的椭圆，则1<t<52. 其中真命题的序号是____________(写出所有正确命题的序号)．16.已知点P 是抛物线x y 42=上的动点，点P 在y 轴上射影是M ,点()6,4A ,则PM PA +的最小值是___________________. 评卷人 得分三、解答题（共70分）17. (本题满分10分)(1)双曲线与椭圆1362722=+y x 有相同焦点，且经过点(15,4)，求其方程。

方城县高中2018-2019学年高二下学期第一次月考试卷数学一、选择题1． 已知双曲线2222:1(0,0)x y C a b a b-=>>，12,F F 分别在其左、右焦点，点P 为双曲线的右支上的一点，圆M 为三角形12PF F 的内切圆，PM 所在直线与轴的交点坐标为(1,0)，与双曲线的一条渐近线平行且距离为2，则双曲线C 的离心率是（ ） AB ．2 CD．22． 给出下列各函数值：①sin100°；②cos （﹣100°）；③tan （﹣100°）；④．其中符号为负的是（ ） A ．①B ．②C ．③D ．④3． 在极坐标系中，圆的圆心的极坐标系是( )。

ABC D4． 设f （x ）=asin （πx+α）+bcos （πx+β）+4，其中a ，b ，α，β均为非零的常数，f （1988）=3，则f （2008）的值为（ ）A ．1B ．3C ．5D ．不确定5． 下列各组函数为同一函数的是（ ） A ．f （x ）=1；g （x ）= B ．f （x ）=x ﹣2；g （x ）= C ．f （x ）=|x|；g （x ）=D ．f （x ）=•；g （x ）=6． 已知函数 f （x ）的定义域为R ，其导函数f ′（x ）的图象如图所示，则对于任意x 1，x 2∈R （ x 1≠x 2），下列结论正确的是（ ） ①f （x ）＜0恒成立；②（x 1﹣x 2）[f （x 1）﹣f （x 2）]＜0； ③（x 1﹣x 2）[f （x 1）﹣f （x 2）]＞0；④；⑤．班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A ．①③B ．①③④C ．②④D ．②⑤7． A={x|x ＜1}，B={x|x ＜﹣2或x ＞0}，则A ∩B=（ ）A ．（0，1）B ．（﹣∞，﹣2）C ．（﹣2，0）D ．（﹣∞，﹣2）∪（0，1）8． 复数z=（其中i 是虚数单位），则z 的共轭复数=（ ）A ．﹣iB ．﹣﹣iC ． +iD ．﹣ +i9． 将甲，乙等5位同学分别保送到北京大学，清华大学，浙江大学等三所大学就读，则每所大学至少保送一人的不同保送的方法数为（ ）（A ）150种 （ B ） 180 种 （C ） 240 种 （D ） 540 种10．函数f （x ）=﹣lnx 的零点个数为（ ） A ．0B ．1C ．2D ．311．已知集合{2,1,1,2,4}A =--，2{|log ||1,}B y y x x A ==-∈，则A B =（ ）A ．{2,1,1}--B ．{1,1,2}-C ．{1,1}-D ．{2,1}--【命题意图】本题考查集合的交集运算，意在考查计算能力． 12．下列各组表示同一函数的是（ ）A ．y=与y=（）2B ．y=lgx 2与y=2lgxC ．y=1+与y=1+D ．y=x 2﹣1（x ∈R ）与y=x 2﹣1（x ∈N ）二、填空题13．已知集合M={x||x|≤2，x ∈R}，N={x ∈R|（x ﹣3）lnx 2=0}，那么M ∩N= ．14．【常熟中学2018届高三10月阶段性抽测（一）】已知函数()()ln R xf x x a a x=+-∈，若曲线122e e 1x x y +=+（e 为自然对数的底数）上存在点()00,x y 使得()()00f f y y =，则实数a 的取值范围为__________.15．【2017-2018学年度第一学期如皋市高三年级第一次联考】已知函数()ln 4f x x x =+-的零点在区间()1k k +，内，则正整数k 的值为________． 16．若曲线f （x ）=ae x +bsinx （a ，b ∈R ）在x=0处与直线y=﹣1相切，则b ﹣a= ．17．在复平面内，记复数+i 对应的向量为，若向量饶坐标原点逆时针旋转60°得到向量所对应的复数为 ．18．设MP和OM分别是角的正弦线和余弦线，则给出的以下不等式：①MP＜OM＜0；②OM＜0＜MP；③OM＜MP＜0；④MP＜0＜OM，其中正确的是（把所有正确的序号都填上）．三、解答题19．定义在R上的增函数y=f（x）对任意x，y∈R都有f（x+y）=f（x）+f（y），则（1）求f（0）；（2）证明：f（x）为奇函数；（3）若f（k•3x）+f（3x﹣9x﹣2）＜0对任意x∈R恒成立，求实数k的取值范围．20．已知函数f（x）=（log2x﹣2）（log4x﹣）（1）当x∈[2，4]时，求该函数的值域；（2）若f（x）＞mlog2x对于x∈[4，16]恒成立，求m的取值范围．21．已知函数f（x）=（sinx+cosx）2+cos2x（1）求f（x）最小正周期；（2）求f（x）在区间[]上的最大值和最小值．22．已知函数f（x）=．（1）求f（f（﹣2））；（2）画出函数f（x）的图象，根据图象写出函数的单调增区间并求出函数f（x）在区间（﹣4，0）上的值域．23．已知二次函数f（x）=x2+2bx+c（b，c∈R）．（1）若函数y=f（x）的零点为﹣1和1，求实数b，c的值；（2）若f（x）满足f（1）=0，且关于x的方程f（x）+x+b=0的两个实数根分别在区间（﹣3，﹣2），（0，1）内，求实数b的取值范围．24．如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D、E分别是AC、AB上的点，且DE∥BC，将△ADE 沿DE折起到△A1DE的位置，使A1D⊥CD，如图2．（Ⅰ）求证：平面A1BC⊥平面A1DC；（Ⅱ）若CD=2，求BD与平面A1BC所成角的正弦值；（Ⅲ）当D点在何处时，A1B的长度最小，并求出最小值．25．已知数列{a n}的首项a1=2，且满足a n+1=2a n+3•2n+1，（n∈N*）．（1）设b n=，证明数列{b n}是等差数列；（2）求数列{a n}的前n项和S n．26．在极坐标系下，已知圆O：ρ=cosθ+sinθ和直线l：．（1）求圆O和直线l的直角坐标方程；（2）当θ∈（0，π）时，求直线l与圆O公共点的极坐标．方城县高中2018-2019学年高二下学期第一次月考试卷数学（参考答案）一、选择题1． 【答案】C 【解析】试题分析：由题意知()1,0到直线0bx ay -=的距离为22=，得a b =，则为等轴双曲.故本题答案选C. 1 考点：双曲线的标准方程与几何性质．【方法点睛】本题主要考查双曲线的标准方程与几何性质.求解双曲线的离心率问题的关键是利用图形中的几何条件构造,,a b c 的关系,处理方法与椭圆相同,但需要注意双曲线中,,a b c 与椭圆中,,a b c 的关系不同.求双曲线离心率的值或离心率取值范围的两种方法：（1）直接求出,a c 的值,可得；（2）建立,,a b c 的齐次关系式,将用,a c 表示,令两边同除以或2a 化为的关系式,解方程或者不等式求值或取值范围.2． 【答案】B【解析】解：：①sin100°＞0，②cos （﹣100°）=cos100°＜0，③tan （﹣100°）=﹣tan100＞0，④∵sin＞0，cos π=﹣1，tan＜0，∴＞0，其中符号为负的是②， 故选：B ．【点评】本题主要考查三角函数值的符号的判断，判断角所在的象限是解决本题的关键，比较基础．3． 【答案】B 【解析】，圆心直角坐标为（0,-1），极坐标为，选B 。

河南省方城县第一高级中学2013—2014学年高二5月月考数学(文）试题 第I 卷（选择题)一、选择题（本大题共12小题，每小题5分，共60分。

在每个小题给出的四个选项中，只有一项符合题目要求） 1．若关于x 的不等式2124x x a a +--<-有实数解，则实数a 的取值范围为（ ）A ．(1,3)B ．(,1)(3,)-∞+∞C ．(,3)(1,)-∞--+∞D ．(3,1)--2．函数46y x x =-+-的最小值为（ ） A ．2 BC ．4D ．63．下列关于实数x 的不等式关系中,恒成立的是（ ) A．212x x +>CD ．|1||2|3x x --+≤4．不等式0)12(|1|≥-+x x 的解集是A ．),21[+∞ B ．),21[]1,(+∞⋃--∞ C ．),21[}1{+∞- D ．]21,1[--5．点()3,1-P ，则它的极坐标是．（ )A ．⎪⎭⎫ ⎝⎛3,2π B ．⎪⎭⎫⎝⎛34,2π C ．⎪⎭⎫ ⎝⎛-3,2π D ．⎪⎭⎫ ⎝⎛-34,2π 6．在极坐标系中，点π(2,)3和圆θρcos 2=的圆心的距离为( )A 3B 2CD7．直线的参数方程为⎪⎩⎪⎨⎧-=-=050cos 150sin t y t x （t 为参数),则直线的倾斜角为( ）A ．40°B ．50°C ．140°D ．130°8．曲线的参数方程为⎩⎨⎧-=+=12322t y t x （t 是参数）,则曲线是（ )A 、线段B 、直线C 、圆D 、射线9．在极坐标系中，点π4⎫⎪⎭，到直线cos sin 10ρθρθ--=的距离等于（ ）．AB C D ．210． 在极坐标系中，直线sin )2ρθθ-=与圆θρsin 4=的交点的极坐标为（ ）A.⎪⎭⎫ ⎝⎛62π， B 。

⎪⎭⎫ ⎝⎛32π， C 。

⎪⎭⎫ ⎝⎛64π， D 。