苏教版高中数学必修五高一第二学期周末素质训练.doc

睢宁县菁华学校高一实验班2008-2009学年第二学期高一双周考试题（数列部分）一、填空题1．已知数列2、6、10、14、32……那么72是这个数列的第________项。

2．某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个），经过3小时，这种细菌由1个可繁殖成______________。

3．等比数列{a n }，a n >0，q ≠1，且a 2、21a 3、a 1成等差数列，则5443a a a a ++等于__________. 4．已知一等比数列的前三项依次为33,22,++x x x ，那么2113-是此数列的第_______ 项. 5．已知数列{}n a 是等差数列，若471017a a a ++=,45612131477a a a a a a ++++++= 且13k a =,则k =_________。

6．在等比数列{}n a 中, 若,75,393==a a 则10a =___________.7． 某公司今年初向银行贷款a 万元，年利率为q （复利计息），从今年末开始每年末偿还相同的金额，预计五年内还清，则每年末应偿还的金额是_________。

8．设n S 是等差数列{}n a 的前n 项和，若==5935,95S S a a 则__________. 9．若)32lg(),12lg(,2lg +-x x 成等差数列，则x 的值等于__________.10．已知三角形的三边构成等比数列,它们的公比为q ,则q 的取值范围是__________.11．数列{}n a 的通项公式11++=n n a n ，则该数列的前n 项之和等于9,则n ＝__________.12．两个等差数列{}{},,n n b a ,327......2121++=++++++n n b b b a a a n n 则55b a =___________. 13。

已知数列{}n a 的前n 项和n n S 23+=，求n a __________.14．已知等差数列{}n a 的公差为2,若431,,a a a 成等比数列, 则2a =__________.二、解答题15.已知y =f （x ）为一次函数，且f （2）、f （5）、f （4）成等比数列，f （8）=15，求S n =f（1）+f （2）+…+f （n ）的表达式．16. 设a n 是正数组成的数列，其前n 项和为S n ，且对所有自然数n ，a n 与2的等差中项等于S n 与2的等比中项，求数列{a n }的通项公式．17. 设等比数列{}n a 前n 项和为n S ，若9632S S S =+，求数列的公比q18. 是否存在互不相等的三个数，使它们同时满足三个条件①a +b +c =6，②a 、b 、c 成等差数列，③将a 、b 、c 适当排列后，能构成一个等比数列．19．某鱼塘养鱼，由于改进饲养技术，预计第一年的增长率为200%，以后每年的增长率是前一年的一半，设原有产量为a ，（1）写出改进饲养技术后的第一年、第二年、第三年的产量，并写出第n 年与第n －1年（n ≥2，+∈N n ）的产量之间的关系式；（2）由于存在环境污染等问题，估计每年将损失年产量的10%，照这样下去，以后每年的产量是否始终是逐步提高的？若是，请给予证明；若不是，请说明从第几年起，产量将不如上一年。

泰兴第四高级中学高一第三次双周练数学试卷 5.19一、填空题（本大题共14小题，每小题5分，共70分）1．在△ABC 中，sin A ∶sin B ∶sin C ＝3∶2∶4，则A 、B 、C 分别所对边::a b c =__________． 2. 在等比数列{}n a 中，12435460,236a a a a a a a <++=，则35a a += ． 3．在△ABC 中，∠A、∠B、∠C 的对边分别是a 、b 、c ，若1a =，3b =，∠C＝30º；则△ABC 的面积是 ．4．已知数列4,,,121--a a 成等差数列，4,,,,1321--b b b 成等比数列，则212b a a -的值为 ． 5.若整数,x y 满足1,1,3,2x y x y y ìïïï-?ïïï+?íïïïï£ïïî则2x y +的最大值是 6．若框图所给的程序运行的结果为S=132，那么判断框中应填入的关于k 的判断条件是 ．7．ABC ∆的内角A 、B 、C 的对边分别为，若c b a ,,成等比数列，且2c a =，则cos B = ． 8．某学校共有师生2400人，现用分层抽样的方法，从所有师生中抽取一个容量为160的样本，已知从学生中抽取的人数为150，那么该学校的学生人数是 ．9．某同学五次考试的数学成绩分别是120， 129， 121，125，130，则这五次考试成绩 的方差是否结束开始 k ←12 , s ←1输出ss ←s ×k k ←k -1 是10．某种产品的广告费支出x 与销售额y 之间有如下对应数据：x ∕610元2 4 5 6 8 y ∕610元3040605070根据散点图分析，x 与y 具有线性相关关系，且线性回归方程为 6.5y x a =+， 则a 的值为 ．11． 若正实数x 、y 满足xy y x =++54，则xy 的最小值是 .12.已知数列{}n a 的前n 项和为n S ，对任意的*n N ∈都有21n n S a =-，则数列{}n a 的通项公式n a =_____________.13．等腰△ABC 的周长为23，则△ABC 腰AB 上的中线CD 的长的最小值 ． 14.在如图所示的数表中，第i 行第j 列的数记为,i j a ，且满足11,,12,j j i a a i -==，1,1,1,(,)N i j i j i j a a a i j *+++=+∈，记第3行的 数3，5，8，13，22， ⋅⋅⋅ 为数列{}n b ，则数列 {}n b 的通项公式为 .二、解答题（本大题共有6个小题，共90分）15（14分）在锐角△ABC 中，a 、b 、c 分别为角A 、B 、C 所对的边，且32sin a c A =.(Ⅰ)确定角C 的大小： （Ⅱ）若c ＝7,且△ABC 的面积为233,求a ＋b 的值。

桑水桑水绝密★启用前第五高级中学高一数学周周练（7）满分160分；考试时间：120分钟；命题人：朱红美注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上得分一、填空题（共70分）1．在△ABC 中，4:2:3sin :sin :sin =C B A ，则cos C 的值为 。

2．在ABC ∆中，60,3A b =︒=，面积33=S ，则a 等于 。

3．已知ABC ∆中，32sin ,2,5.1===B AC AB .则=C 。

4．在各项均不为零的等差数列{}n a 中，若a 1n +- an 2+ a 1-n =0（n ≥2），则S 1-n 2-4n = 。

5．在等比数列{}n a 中，若23691032a a a a a =,则21014a a 的值为 。

6．已知{}n a 是等比数列，2512,4a a ==，则12231n n a a a a a a ++++= 。

7．数列{}n a 满足11a =，223a =，且11112(2)n n n n a a a -++=≥，则n a = 。

8．用火柴棒摆“金鱼”，如图所示：按照上面的规律，第n 个“金鱼”图需要火柴棒的根数为 。

9．已知等差数列{}n a 满足，18130,58a a a >=，则前n 项和n S 取最大值时，n 的值为 。

10．已知数列－1，a 1，a 2，－4成等差数列，－1，b 1，b 2，b 3，－4成等比数列，则212b a a -的值是 。

11．设S n 是等差数列{}n a 的前n 项和，若35a a ＝95，则59S S ＝ 。

12．已知△ABC 的外接圆半径为R ，角 A 、B 、C 的对边分别为a 、b 、c 且()(),sin 2sin sin 222B b a C A R -=-那么角C 的大小为 。

13．已知等比数列{}n a 的前n 项和为1136n n S x -=⋅-，则x 的值为 。

高中数学学习材料唐玲出品扬州中学西区校高一数学周练一命题人：陶福忠 2008-2-27班级__________姓名______________学号_________ 成绩___________一. 填空题1．在△ABC 中，若sin A ∶sin B ∶sin C =7∶8∶13，则C =_________2．在△ABC 中，若8,3,7===c b a ，则其面积等于___________3．锐角三角形中,边a,b 是方程22320x x -+=的两根,且6c =则角C = 4．在△ABC 中，060,1,3,ABC A b S ∆∠===则CB A c b a sin sin sin ++++=___________ 5．在△ABC 中，若2lg sin lg cos lg sin lg =--C B A ，则△ABC 的形状是__________6．在ABC ∆中，3=a ，1=b ， 30=B ，则ABC ∆的面积为____________7．在△ABC 中，a 、b 、c 分别为A 、B 、C 的对边，c c b A 22cos 2+=，则△ABC 的形状为______ 8．在∆ABC 中，根据条件：①b=10，A=45，C=70 ②a=60，c=48，B=60 ③a=7，b=5，A=80④a=14，b=16，A=45解三角形，其中有2个解的有 二．解答题9．在△AB C 中，A 、B 、C 的对边分别是a 、b 、c ，已知C ab B ca A bc c cos cos cos 2++=（1）判断△AB C 的形状； （2）若3,9AB BC AB AC ⋅=-⋅=，求角B 的大小。

10．2003年伊拉克战争初期,美英联军为了准确分析战场形势,有分别位于科威特和沙特的两个距离为32a 的军事基地C 和D ，测得伊拉克两支精锐部队分别在A 处、B 处, 如图所示,30ADB ∠=，30BDC ∠=，60DCA ∠=，45ACB ∠=，求伊军这两支精锐部队的距离。

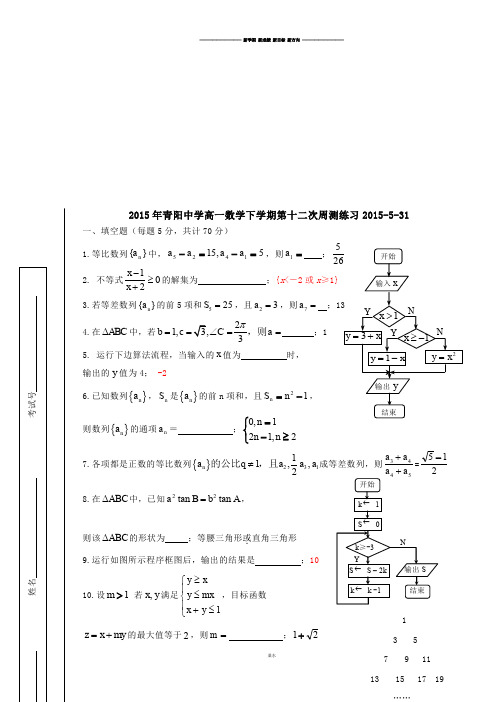
2015年青阳中学高一数学下学期第十二次周测练习2015-5-31一、填空题（每题5分，共计70分）1.等比数列}{n a 中，5,151425=-=-a a a a ，则=1a ；265 2. 不等式102x x -≥+的解集为 ；{x <－2或x ≥1} 3.若等差数列{}n a 的前5项和525S =，且23a =，则7a = ；13 4.在ABC ∆中，若21,3,3b c C a π==∠==，则 ；1 5. 运行下边算法流程，当输入的x 值为 时， 输出的y 值为4； -26.已知数列{}n a ，n S 是{}n a 的前n 项和，且12-=n S n ，则数列{}n a 的通项n a ＝ ；⎩⎨⎧≥-=2,121,0n n n7.各项都是正数的等比数列{}23111,,2n a q a a a ≠的公比，且成等差数列，则3445a a a a ++=215- 8.在ABC ∆中，已知22tan tan a B b A =，则该ABC ∆的形状为 ；等腰三角形或．直角三角形 9.运行如图所示程序框图后，输出的结果是 ；1010.设1>m 若y x ,满足1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩，目标函数z x my =+的最大值等于2，则m = ；21+开始输入x1>x x y +=31-≥x 2x y =x y -=1输出y结束NY Y Nk ≥-3 开始 k ← 1 S ← 0 S ← S – 2k k ← k -1结束 输出S Y N1 35姓名 考试号11.将正奇数按如图所示的规律排列：若2015是第n （n ≥4）行 从左向右的第m )(n m ≤个数，则=+n m ；6312.已知等差数列}{n a 前n 项和为n S ，6622,105115≤≤≤≤S S ，则9a 的取值范围 ；]11,2[13.若实数,,a b c 成等比数列，且1a b c ++=，则a c +的取值范围是 ；[23, 1)∪(1, 2]14.ABC ∆中，角A ，B ，C 所对的边为,,a b c ．若2b ac =，则sin cos tan sin cos tan A A CB B C++的取值范围是；5151(,)22-+ 二、解答题（共6小题，15-17每题14分，18-20题每题16分，共计90分）15.在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos 2cos b A a B c C ⋅+⋅=-⋅①求角C 的大小；②若a b 2=，且△ABC 的面积为32，求边c 的长． 15.（1）由cos cos 2cos b A a B c C ⋅+⋅=-⋅，及正弦定理可得sin cos sin cos 2sin cos B A A B C C +=-， 即sin()2sin cos A B C C +=-由A ，B ，C 是三角形内角可知sin()sin 0A B C +=≠∴1cos 2C =-，π<<C 023C π=；…………………………………………………………7分(没有C 范围扣2分) （2）由△ABC 的面积可得1sin 232ab C =，即1322322a a ⋅⋅=， ∴a =2，∴b=4，……………………10分由正弦定理可得：22212cos 416224282c a b ab C ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭， ∴27c =．……………………14分16.数列{}n a 的前n 项和为n S ，满足22n S n n =+．等比数列{}n b 满足：143,81b b ==．①求证：数列{}n a 为等差数列； ②若312123nn na a a a Tb b b b =++++，求n T ． 解：①由已知得：13a =，2n ≥且*n N ∈时，221(2)[(1)2(1)]21n n n a S S n n n n n -=-=+--+-=+经检验1a 亦满足21n a n =+ ∴21(*)n a n n N =+∈ ∴1[2(1)1](21)2n n a a n n +-=++-+=为常数∴{}n a 为等差数列，且通项公式为21(*)n a n n N =+∈ ②设等比数列{}n b 的公比为q ，则34127b q b ==， ∴3q =，则1333n n n b -=⨯=，*n N ∈ ∴213n n n a n b += 23357213333n n n T +∴=++++234113572121333333n n n n n T +-+=+++++ 2123411111(1)2111121214243312()12133333333313n n n n n n n n n T -+++-+++=++++-=+⨯-=--22,*3n nn T n N +∴=-∈ 17.某市某棚户区改造建筑用地平面示意图如图所示．经规划调研确定，棚改规划建筑用 地区域是半径为R 的圆面．该圆面的内接四边形ABCD 是原棚户建筑用地，测量可知边 界4==AD AB 千米，6=BC 千米，2=CD 千米， ①求原棚户区建筑用地ABCD 中对角线AC 的长度；②请计算原棚户区建筑用地ABCD 的面积及圆面的半径R 的值．18.如图，ABCD 是长方形海域，其中10AB =海里，102AD =海里．现有一架飞机在该海域失事，两艘海事搜救船在A 处同时出发，沿直线AP 、AQ 向前联合搜索，且4PAQ π∠=（其ABC DO中P 、Q 分别在边BC 、CD 上），搜索区域为平面四边形APCQ 围成的海平面．设PAB θ∠=，搜索区域的面积为S ．①试建立S 与tan θ的关系式，并指出tan θ的取值范围； ②求S 的最大值，并指出此时θ的值．解：①在Rt APB ∆中，10tan BP θ=， 11010tan 50tan 2ABP S θθ∆=⨯⨯= 在Rt ADQ ∆中，102tan()4DQ πθ=-，1102102tan()100tan()244ADQ S ππθθ∆=⨯⨯-=- ∴100250tan 100tan()4S πθθ=---1tan 100250tan 1001tan θθθ-=--⨯+其中0tan 120tan()42θπθ≤≤⎧⎪⎨≤-≤⎪⎩，解得：322tan 1θ-≤≤（注：观察图形的极端位置，计算出tan θ的范围也可得分．） ∴1tan 100250tan 1001tan S θθθ-=--⨯+，322tan 1θ-≤≤②∵tan 0θ>，1tan 4100250(tan 2)100250(tan 13)1tan tan 1S θθθθθ-=-+⨯=-++-++4100250(2(tan 1)3)100250tan 1θθ≤-+⋅-=-+当且仅当4tan 1tan 1θθ+=+时取等号，亦即tan 1θ=时，max 100250S =-∵(0,)2πθ∈ 4πθ∴=答：当4πθ=时，S 有最大值100250-．19. 已知数列{}n a 满足121,0a a a ==>，数列{}n b 满足1+=n n n a a b ①若{}n a 为等比数列，求{}n b 的前n 项的和n S ；②若3nn b =，求数列{}n a 的通项公式；③若2n b n =+，求证：12111223nn a a a +++>+-19. （1）1121,n n n n n n a a b a a a ---=∴==……………………….……….…………2分当a=1时1n b =，则n s n =……………………………………………………………3分当1a ≠时，22(1)1n n a a s a-=-………………………………………………………….…4分 （2）13n n n a a +=113(2,)n n n a a n n N --∴=≥∈ 113(2,)n n an n N a +-∴=≥∈………………………………………………………………6分 当*21,()n k k N =+∈时，*11222223()3=a3k k k k k a k N a a a --+∴=∈∴=当*2,()n k k N =∈时，*121212-13()3k k k k a k N a a -+-∴=∈∴=12223(=21)3(2)n n n n k a a n k --⎧-⎪∴=⎨⎪=⎩………………………………………………………………10分（3）12,n n a a n +=+①，121,3a a =∴=11n n a a n -∴=+(2)n ≥②①－②得11111)1(2)n n n n n na a a a a n a +-+--=∴-=≥（ 23111n a a a ∴+++ 314211()()()n n a a a a a a +-=-+-++-=112n n a a a a ++-- 1231111n a a a a ∴++++ =112111+3n n n n a a a a a a a +++--=+- 0)(22111>-=-++++n n n n n n a a a a a a （两者不相等）即22211+=>+++n a a a a n n n n 1231111na a a a ∴++++＞22n +－3．……16分20.已知数列{}n a 是公差不为0的等差数列，13,2a =数列{}n b 是等比数列，且11b a =，2334,b a b a =-=，数列{}n b 的前n 项和为n S ，记点*(,),n n n Q b S n N ∈．③求数列{}n b 的通项公式；②证明：点123n Q Q Q Q 、、、、、在同一直线l 上，并求出直线l 方程； ③若1n nA SB S ≤-≤对*n N ∈恒成立，求B A -的最小值． 20. （1）设等差数列{}n a 的公差为d ，等比数列{}n b 的公比为q ，由题设可得q d 23223-=+....(1),223323q d =+...........(2),联立（1）（2）得方程组，解方程组得：83,21-=-=d q 或0,1=-=d q ，因为数列{}n a 是公差不为0的等差数列，所以12q =-，即131()22n n b -=-…………4分（2）),(n n n S b Q ,131()22n n b -=-,n n S )21(1--=,令n n y x )21(1,)21()3(--=-⨯-=，两式消去n )21(-得330x y -+=，即点123nQ Q Q Q 、、、、、，在同一条直线330x y -+=上。

高中数学学习材料唐玲出品宇文星航高一第二学期期末复习综合练习（2）1．已知数列是等差数列，且18,12654321=++=++a a a a a a ，则987a a a ++等于___ __ __．2．在ABC ∆中，5, 3, 7AB AC BC ===，则BAC ∠的大小为 ．3．已知0x >，函数4y x x=+的最小值是---------- 4．各项均为正数的等比数列{a n }的前n 项和为Sn ，若10s =2,30s =14,则40s 等于5．在数列{}n a 中，11a =，且对于任意正整数n ，都有12n n a n a n++=，则n a =_____ 6．首项为－24的等差数列，从第10项开始为正，则公差d 的取值范围是__ __．7．若A 为不等式组002x y y x ≤⎧⎪≥⎨⎪-≤⎩表示的平面区域，则当a 从2-连续变化到1时，动直线x y a +=扫过A 中的那部分区域的面积为 ．8．在等比数列{}n a 中,14133a a +=,2370a a +=,则这个数列的通项公式是___ _ __．9. 等差数列{}n a 的前m 项和为20，前2m 项和为70，则它的前3m 的和为10．在等比数列}{n a 中，公比q=2，且30303212=⋅⋅⋅⋅a a a a ，则30963a a a a ⋅⋅⋅⋅ 等于11．函数y ＝2x （1－3x ）（0＜x ＜13)的最大值是___ __ __． 12. 已知n n a )(231⋅=，把数列{}n a 的各项排成三角形状；1a2a 3a 4a5a 6a 7a 8a……记A （m,n ）表示第m 行，第n 列的项，则A （10，8）= .13．数列,43211,3211,211++++++的前n 项之和为 ． 14．在1,2之间依次插入个正数a 1，a 2，a 3，…，a n ，使这n +2个数成等比数列，则a 1a 2a 3…a n = ． 15．已知ABC ∆的面积为34，角A 、B 、C 成等差数列，求11a c c a+++的最小值及相应的a 和的c 值．16.解不等式 1 + )1(log )2(log 21221->--x x x17．设{a n }为等差数列,{b n }为等比数列,且a 1=b 1=1,a 2+a 4=b 3,b 2b 4=a 3分别求出{a n }及{b n }的前10项的和S 10及T 10．18．如图，一个铝合金窗分为上、下两栏，四周框架和中间隔档的材料为铝合金，宽均为6cm ，上栏与下栏的框内高度（不含铝合金部分）的比为1:2，此铝合金占用的墙面面积为28800cm 2；设该铝合金的宽和高分别为a （cm ）、b （cm ）；铝合金窗的透光部分的面积为S （cm 2）；（1）试用a 、b 表示S ；（2）若要使S 最大，则铝合金的宽和高分别为多少？19．已知正项数列}{n a 的前n 项和为n S ，且*,12N n a S n n ∈+=(1)试求数列}{n a 的通项公式；（2）设11+=n n n a a b ，数列}{n b 的前n 项和为n B ，求证：21<n B . 20．已知函数2()()f x x ax a a R =-+∈同时满足：○1不等式()0f x ≤ 的解集有且只有一个元素；○2在定义域内存在120x x <<，使得不等式12()()f x f x >成立．设数列{}n a 的前n 项和为()n S f n =（1）求数列{}n a 的通项公式；（2）设各项均不为零的数列{}n c 中，所有满足10i i c c +⋅<的正整数i 的个数．．称为这个数列{}n c 的变号数，令1n na c a =-（n 为正整数），求数列{}n c 的变号数 1． 242．120︒3.44．305.2)1(+n n6．833d <≤ 7、74； 8．158()2n n a -=⋅或12125()5n n a -=⋅ 9. 15010. 20211． 61 12.8931)(2⋅ 13．2+n n 14．22n15.最小值是4；1a c ==．16．解：原不等式可化为⎪⎩⎪⎨⎧-<-->->--⇔->--22201022222221221x x x x x x x x x )(log )(log3230203010122<<⇔⎩⎨⎧<<>⇔⎪⎩⎪⎨⎧<->->+-⇔x x x x x x x x ))((17．解：设{a n }的公差为d ，{b n }的公比为q ，则：⎩⎨⎧=+=+4221)21(2qd q d 解得：22,83±=-=q d ∴32)22(3111,855451010110110±=--=-=+=q q b T d a S18.（1）290881816S a b =--；（2）23328S ≤，当160a =、180b =时取最大值． 19．(1)12-=n a n (2)略解：（1）由○1()0f x ≤的解集有且只有一个元素知2400a a a ∆=-=⇒=或4a =当0a =时，函数2()f x x =在(0,)+∞上递增，此时不满足条件○2综上可知24,()44a f x x x ==-+ 21,144,25,2n n n S n n a n n =⎧∴=-+∴=⎨-≥⎩（2）由条件可知3,141,225n n c n n ⎧-=⎪=⎨-≥⎪-⎩ 当2n ≥时，令129273500252322n n n n c c n n n +--⋅<⇒⋅<⇒<<--或7922n << 所以2n =或4n = 又123,5,1c c n =-=∴=时，也有120c c ⋅< 综上可得数列{}n c 的变号数为3。

周庄高中2011-2012学年度高一第二学期周末素质训练（解三角形与等差数列）一、填空题（本大题共14小题，每小题5分，满分70分，把正确的答案写在题中横线上）．1．已知△ABC 中，4a =，43b =，∠A ＝30°，则∠B 等于2．数列 11,22,5,2则52是该数列的3．已知△ABC 中，AB ＝6，∠A ＝30°，∠B ＝120°，则△ABC 的面积为4．在△ABC 中，sinA:sinB:sinC=3:2:4，则cosC 的值为5.已知数列{}6,321==a a a n 中且n n n a a a -=++12，那么4a = 6．在△ABC 中，若B A sin sin >，则A 与B 的大小关系为7. 在等差数列{}n a 中，若,26,3732=+=a a a 则8a =8.在△ABC 中，,45,2,0===B cm b cm x a 若△ABC 有两解则x 的取值范围是 9．在△ABC 中，若AB ＝5，AC ＝5，且cos C ＝109，则BC ＝___． 10.在等差数列{}n a 中263143,234212===n a a a ，，则n =11. 在等差数列{}n a 中，若)(225*∈-=N n n a n ,那么使其前n 项之和n S 取得最大值 的n=12.若(a+b+c)(b+c －a)=3abc,且sinA=2sinBcosC, 那么ΔABC 是 三角形13．两等差数列{a n }、{b n }的前n 项和的比'5327n n S n S n +=+，33a b 的值是 14．一个有限项的等差数列，前4项之和为40，最后4项之和是80，所有项之和是210，则此数列的项数为二、解答题, 本大题共6小题，共90分，解答应写出必要的文字说明、证明过程和演算步骤．15．（14分） 若三个数成等差数列，其和为15，其平方和为83，求此三个数16．(本题满分16分)已知a 、b 、c 分别是ABC ∆的三个内角A 、B 、C 所对的边.(1) 若ABC ∆面积,60,2,23︒===∆A c S ABC 求a 、b 的值； (2)若B c a cos =，且A c b sin =，试判断ABC ∆的形状．17. (本题满分16分)在等差数列{}n a 中，已知38a =，924a =，求612,a a 以及11S18.（14分）在∆ABC 中，设bb c B A -=2tan tan ，求A 的值。

扬州中学西区校高一数学周练三命题、校对：陶福忠 2008-4-11班级__________姓名______________学号_________ 成绩___________一、填空题1、设x 、y ∈R ＋ 且19x y+＝1,则x ＋y 的最小值为_____________ 2、设,x y R ∈，且4x y +=，则55x y +的最小值是____________ 3、已知320,3271x y x y +-=++则的最小值是_________4、已知103x <<，则(13)x x -取最大值时x 的值是_____________ 5、下列结论正确的有_____________①1y x x =+的最小值为2 ②当101,lg 2lg x x x x >≠+≥且时 ③2232x y x +=+的最小值为2 ④10,2x x x>+≥当时 ⑤221sin sin y x x =+，(0,)2x π∈的最小值为2 ⑥12,x x x ≥+当时的最小值为2 ⑦221y x x=+的最小值为2 6、设y x ,满足,404=+y x 且,,+∈R y x 则y x lg lg +的最大值是7、若,a b R +∈、且满足3,ab a b =++则a b +的取值范围是 _____________8、设1,x -函数(5)(2)1x x y x ++=+的最小值是_____________9、我市某公司，第一年产值增长率为p ，第二年产值增长率q ，这二年的平均增长率为x ，那x 与2q p +大小关系（)q p ≠是________________（填＞、=、＜） 10、若x,y +∈R 且2x+8y - xy=0,则x + y 的最小值为_______11、函数2254x y x +=+的最小值是_____________二、解答题：12、某村计划建造一个室内面积为 800m 2的矩形蔬菜温室．在温室内，沿左、右两侧与后侧内墙各保留 l m 宽的通道，沿前侧内墙保留3m 宽的空地．当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？13、某公司按现有能力，每月收入为70万元，公司分析部门测算，若不进行改革，入世后因竞争加剧收入将逐月减少．分析测算得入世第一个月收入将减少3万元，以后逐月多减少2万元，如果进行改革，即投入技术改造300万元，且入世后每月再投入1万元进行员工培训，则测算得自入世后第一个月起累计收入n T 与时间n （以月为单位）的关系为n T =b an +，且入世第一个月时收入将为90万元，第二个月时累计收入为170万元，问入世后经过几个月，该公司改革后的累计纯收入高于不改革时的累计纯收入．参 考 答 案1、 162、 503、74、 165、⑷⑺6、 27、 [6,)+∞8、255+9、 ＜ 10、 1811、 5212、解：设矩形温室的一边长为x 米，则另一边长为800x 米，设蔬菜的种植面积为y 平方米，根据题意，得：800(4)(2)y x x=-- =808-2（1600()x x + ≤808-2*21600xx =648当且仅当1600x x =即40x =时，取“=”号。

章末综合测评(二)(时间120分钟，满分160分)一、填空题(本大题共14小题，每小题5分，共70分．请把答案填在题中的横线上)1．(2016·江苏高考)已知{a n }是等差数列，S n 是其前n 项和．若a 1＋a 22＝－3，S 5＝10，则a 9的值是________．【解析】 法一：设等差数列{a n }的公差为d ，由S 5＝10，知S 5＝5a 1＋5×42d ＝10，得a 1＋2d ＝2，即a 1＝2－2d .所以a 2＝a 1＋d ＝2－d ，代入a 1＋a 22＝－3，化简得d 2－6d ＋9＝0，所以d ＝3，a 1＝－4.故a 9＝a 1＋8d ＝－4＋24＝20.法二：设等差数列{a n }的公差为d ，由S 5＝10，知5(a 1＋a 5)2＝5a 3＝10，所以a 3＝2.所以由a 1＋a 3＝2a 2，得a 1＝2a 2－2，代入a 1＋a 22＝－3，化简得a 22＋2a 2＋1＝0，所以a 2＝－1.公差d ＝a 3－a 2＝2＋1＝3，故a 9＝a 3＋6d ＝2＋18＝20. 【答案】 202．(2016·全国卷Ⅰ改编)已知等差数列{a n }前9项的和为27，a 10＝8，则a 100＝________.【解析】 法一：∵{a n }是等差数列，设其公差为d ， ∴S 9＝92(a 1＋a 9)＝9a 5＝27，∴a 5＝3.又∵a 10＝8，∴⎩⎪⎨⎪⎧ a 1＋4d ＝3，a 1＋9d ＝8，∴⎩⎪⎨⎪⎧a 1＝－1，d ＝1.∴a 100＝a 1＋99d ＝－1＋99×1＝98.法二：∵{a n }是等差数列， ∴S 9＝92(a 1＋a 9)＝9a 5＝27，∴a 5＝3.在等差数列{a n }中，a 5，a 10，a 15，…，a 100成等差数列，且公差d ′＝a 10－a 5＝8－3＝5.故a 100＝a 5＋(20－1)×5＝98. 【答案】 983．已知数列{a n }的前n 项和为S n ＝kn 2，若对所有的n ∈N *，都有a n ＋1>a n ，则实数k 的取值范围是________．【解析】 由S n ＝kn 2，得a n ＝k (2n －1)． ∵a n ＋1>a n ，∴{a n }是递增数列， ∴k >0.【答案】 (0，＋∞)4．已知数列{a n }，a n ≠0，若a 1＝3,2a n ＋1－a n ＝0，则a 6等于________． 【解析】 因为2a n ＋1－a n ＝0，a n ≠0，所以a n ＋1a n＝12，所以数列{a n }是首项为a 1＝3，公比为q ＝12的等比数列，所以a n ＝a 1q n －1＝3×⎝ ⎛⎭⎪⎫12n －1，所以a 6＝3×⎝ ⎛⎭⎪⎫126－1＝332.【答案】 3325．数列{a n }是等差数列，若a 1＋1，a 3＋3，a 5＋5构成公比为q 的等比数列，则q ＝________.【解析】 设等差数列的公差为d ，则a 3＝a 1＋2d ，a 5＝a 1＋4d ， ∴(a 1＋2d ＋3)2＝(a 1＋1)(a 1＋4d ＋5)， 解得d ＝－1，∴q ＝a 3＋3a 1＋1＝a 1－2＋3a 1＋1＝1.【答案】 16．如果数列{a n }的前n 项和S n ＝2a n －1，则此数列的通项公式a n ＝________. 【解析】 当n ＝1时，S 1＝2a 1－1， ∴a 1＝2a 1－1，∴a 1＝1.当n ≥2时，a n ＝S n －S n －1＝(2a n －1)－(2a n －1－1)， ∴a n ＝2a n －1，∴{a n }是等比数列， ∴a n ＝2n －1，n ∈N *. 【答案】 2n －1，n ∈N *7．一个直角三角形的三边成等比数列，则较小锐角的正弦值是________． 【解析】 设三边为a ，aq ，aq 2(q >1)， 则(aq 2)2＝(aq )2＋a 2，∴q 2＝5＋12，较小锐角记为θ，则sin θ＝1q 2＝5－12. 【答案】5－128．(2016·徐州高二检测)若两个等差数列{a n }和{b n }的前n 项和分别是S n 和T n ，已知S n T n ＝7n n ＋3，则a 5b 5＝________.【解析】 a 5b 5＝2a 52b 5＝a 1＋a 9b 1＋b 9＝9(a 1＋a 9)29(b 1＋b 9)2＝S 9T 9＝214.【答案】 2149．下列关于星星的图案构成一个数列，则该数列的一个通项公式是________．图1【解析】 从题图中可观察图案的构成规律： n ＝1时，有1个；n ＝2时，有3个； n ＝3时，有6个；n ＝4时，有10个；…… 第n 个图案比第n －1(n ≥2)个图案增加了n 个星星． ∴a n ＝1＋2＋3＋4＋…＋n ＝n (n ＋1)2. 【答案】 a n ＝n (n ＋1)210．等比数列{a n }的公比q <0，已知a 2＝1，a n ＋2＝a n ＋1＋2a n ，则{a n }的前2 016项和等于________．【解析】 由a n ＋2＝a n ＋1＋2a n ，得q n ＋1＝q n ＋2q n －1， 即q 2－q －2＝0，又q <0，解得q ＝－1， 又a 2＝1，∴a 1＝－1， S 2 016＝－1×[1－(－1)2 016]1－(－1)＝0.【答案】 011．设数列{a n }的通项公式为a n ＝2n －7(n ∈N *)，则|a 1|＋|a 2|＋…＋|a 15|＝________.【解析】 ∵a n ＝2n －7，∴a 1＝－5，a 2＝－3，a 3＝－1，a 4＝1， a 5＝3，…，a 15＝23，∴|a 1|＋|a 2|＋…＋|a 15|＝(5＋3＋1)＋(1＋3＋5＋…＋23)＝9＋12×(1＋23)2＝153.【答案】 15312．把正偶数按下列方法分组：(2)，(4,6)，(8,10,12)，…，其中每一组都比它的前一组多一个数，那么第11组的第2个数是________．【解析】 按照题中的分组方法，前10组共有1＋2＋ (10)10×(1＋10)2＝55个偶数，故第10组的最后一个偶数为110，所以第11组的第2个数是114.【答案】 11413．某房地产开发商在销售一幢23层的商品楼之前按下列方法确定房价：由于首层与顶层均为复式结构，因此首层价格为a 1 元/m 2，顶层由于景观好价格为a 2 元/m 2，第二层价格为a 元/m 2，从第三层开始每层在前一层价格上加价a100 元/m 2，则该商品房各层的平均价格为________元/m 2.【解析】 设第二层到第22层的价格构成数列{b n }，则{b n }是等差数列，b 1＝a ，公差d ＝a100，共21项，所以其和为S 21＝21a ＋21×202·a 100＝23.1a ，故平均价格为123(a 1＋a 2＋23.1a )元/m 2.【答案】 123(a 1＋a 2＋23.1a ) 14．给出数阵： 0 1 … 9 1 2 … 10 ⋮ ⋮ ⋮ ⋮ 9 … … …其中每行、每列均为等差数列，则此数阵所有数的和为________.【导学号：91730049】【解析】 设b 1＝0＋1＋2＋…＋9，b 2＝1＋2＋3＋…＋10，…，b 10＝9＋10＋…＋18，则{b n }是首项b 1＝45，公差d ＝10的等差数列，∴S 10＝45×10＋10×92×10＝900.【答案】 900二、解答题(本大题共6小题，共90分．解答时应写出文字说明、证明过程或演算步骤)15．(本小题满分14分)(2015·北京高考)已知等差数列{a n }满足a 1＋a 2＝10，a 4－a 3＝2.(1)求{a n }的通项公式；(2)设等比数列{b n }满足b 2＝a 3，b 3＝a 7，问：b 6与数列{a n }的第几项相等？ 【解】 (1)设等差数列{a n }的公差为d . 因为a 4－a 3＝2，所以d ＝2.又因为a 1＋a 2＝10，所以2a 1＋d ＝10，故a 1＝4. 所以a n ＝4＋2(n －1)＝2n ＋2(n ＝1,2，…)． (2)设等比数列{b n }的公比为q . 因为b 2＝a 3＝8，b 3＝a 7＝16， 所以q ＝2，b 1＝4. 所以b 6＝4×26－1＝128. 由128＝2n ＋2得n ＝63，所以b 6与数列{a n }的第63项相等．16．(本小题满分14分)在数列{a n }中，a 1＝1，a n ＋1＝2a n ＋2n . (1)设b n ＝a n2n －1.证明：数列{b n }是等差数列． (2)求数列{a n }的前n 项和S n .【解】 (1)证明：由已知a n ＋1＝2a n ＋2n ，得b n ＋1＝a n ＋12n ＝2a n ＋2n 2n ＝a n2n －1＋1＝b n ＋1.∴b n ＋1－b n ＝1，又b 1＝a 1＝1.∴{b n}是首项为1，公差为1的等差数列．(2)由(1)知，b n＝n，a n2n－1＝b n＝n.∴a n＝n·2n－1.∴S n＝1＋2·21＋3·22＋…＋n·2n－1，两边乘以2得，2S n＝1·21＋2·22＋…＋(n －1)·2n－1＋n·2n，两式相减得，－S n＝1＋21＋22＋…＋2n－1－n·2n＝2n－1－n·2n＝(1－n)2n－1，∴S n＝(n－1)·2n＋1.17．(本小题满分14分)数列{a n}的前n项和记为S n，a1＝t，点(S n，a n＋1)在直线y＝3x＋1上，n∈N*.(1)当实数t为何值时，数列{a n}是等比数列．(2)在(1)的结论下，设b n＝log4a n＋1，c n＝a n＋b n，T n是数列{c n}的前n项和，求T n.【解】(1)∵点(S n，a n＋1)在直线y＝3x＋1上，∴a n＋1＝3S n＋1，a n＝3S n－1＋1(n≥2，且n∈N*)．∴a n＋1－a n＝3(S n－S n－1)＝3a n，即a n＋1＝4a n，n≥2.又a2＝3S1＋1＝3a1＋1＝3t＋1，∴当t＝1时，a2＝4a1，数列{a n}是等比数列．(2)在(1)的结论下，a n＋1＝4a n，a n＋1＝4n，a n＝4n－1，所以b n＝log4a n＋1＝n.c n＝a n＋b n＝4n－1＋n,那么T n＝c1＋c2＋…＋c n＝(40＋1)＋(41＋2)＋…＋(4n－1＋n)＝(1＋4＋42＋…＋4n－1)＋(1＋2＋3＋…＋n)＝4n－13＋(1＋n)n2.18．(本小题满分16分)已知{a n}是以a为首项，q为公比的等比数列，S n为它的前n 项和．(1)当S 1，S 3，S 4成等差数列时，求q 的值；(2)当S m ，S n ，S l 成等差数列时，求证：对任意自然数k ，a m ＋k ，a n ＋k ，a l ＋k 也成等差数列．【解】 (1)由已知，a n ＝aq n －1，因此S 1＝a ，S 3＝a (1＋q ＋q 2)，S 4＝a (1＋q ＋q 2＋q 3)．当S 1，S 3，S 4成等差数列时，S 4－S 3＝S 3－S 1，可得aq 3＝aq ＋aq 2， 化简得q 2－q －1＝0， 解得q ＝1±52.(2)证明：若q ＝1，则{a n }的每项a n ＝a ，此时a m ＋k ，a n ＋k ，a l ＋k 显然构成等差数列．若q ≠1，由S m ，S n ，S l 构成等差数列可得S m ＋S l ＝2S n ，即a (q m －1)q －1＋a (q l －1)q －1＝2a (q n －1)q －1，整理得q m ＋q l ＝2q n ，因此，a m ＋k ＋a l ＋k ＝aq k －1(q m ＋q l )＝2aq n ＋k －1＝2a n ＋k ， 所以a m ＋k ，a n ＋k ，a l ＋k 也成等差数列．19．(本小题满分16分)设{a n }是正数组成的数列，其前n 项和S n ，并且对于所有的n ∈N *，都有8S n ＝(a n ＋2)2.(1)写出数列{a n }的前3项；(2)求数列{a n }的通项公式(写出推证过程)； (3)设b n ＝4a n ·a n ＋1，T n 是数列{b n }的前n 项和，求使得T n <m20对所有n ∈N *都成立的最小正整数m 的值．【解】 (1)当n ＝1时，8a 1＝(a 1＋2)2，∴a 1＝2；当n ＝2时，8(a 1＋a 2)＝(a 2＋2)2， ∴a 2＝6；当n ＝3时，8(a 1＋a 2＋a 3)＝(a 3＋2)2， ∴a 3＝10.(2)∵8S n ＝(a n ＋2)2， ∴8S n －1＝(a n －1＋2)2(n >1)，两式相减得：8a n ＝(a n ＋2)2－(a n －1＋2)2，即a 2n －a 2n －1－4a n －4a n －1＝0，也即(a n ＋a n －1)(a n －a n －1－4)＝0. ∵a n >0，∴a n －a n －1＝4，即{a n }是首项为2，公差为4的等差数列， ∴a n ＝2＋(n －1)·4＝4n －2.(3)b n ＝4a n ·a n ＋1＝4(4n －2)(4n ＋2)＝1(2n －1)(2n ＋1)＝12⎝⎛⎭⎪⎫1(2n －1)－1(2n ＋1). ∴T n ＝b 1＋b 2＋…＋b n ＝12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫13－15＋…＋⎝ ⎛⎭⎪⎫1(2n －1)－1(2n ＋1)＝12⎝ ⎛⎭⎪⎫1－12n ＋1＝12－14n ＋2<12.∵T n <m20 对所有n ∈N *都成立， ∴m 20≥12，即m ≥10， 故m 的最小值是10.20．(本小题满分16分)某公司一下属企业从事某种高科技产品的生产．该企业第一年年初有资金2 000万元，将其投入生产，到当年年底资金增长了50%.预计以后每年资金年增长率与第一年的相同．公司要求企业从第一年开始，每年年底上缴资金d 万元，并将剩余资金全部投入下一年生产．设第n 年年底企业上缴资金后的剩余资金为a n 万元．(1)用d 表示a 1，a 2，并写出a n ＋1与a n 的关系式；(2)若公司希望经过m (m ≥3)年使企业的剩余资金为4 000万元，试确定企业每年上缴资金d 的值(用m 表示)．【解】 (1)由题意得a 1＝2 000(1＋50%)－d ＝3 000－d ，a 2＝a 1(1＋50%)－d ＝32a 1－d ＝4 500－52d ， a n ＋1＝a n (1＋50%)－d ＝32a n －d . (2)由(1)得a n ＝32a n －1－d ＝32⎝ ⎛⎭⎪⎫32a n －2－d －d＝⎝ ⎛⎭⎪⎫322a n －2－32d －d ＝…＝⎝ ⎛⎭⎪⎫32n －1a 1－d ⎣⎢⎡⎦⎥⎤1＋32＋⎝ ⎛⎭⎪⎫322＋…＋⎝ ⎛⎭⎪⎫32n －2. 整理得a n ＝⎝ ⎛⎭⎪⎫32n －1(3 000－d )－2d ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫32n －1－1＝⎝ ⎛⎭⎪⎫32n －1(3 000－3d )＋2d . 由题意，a m ＝4 000，即⎝ ⎛⎭⎪⎫32m －1(3 000－3d )＋2d ＝4 000，解得d ＝⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫32m －2×1 000⎝ ⎛⎭⎪⎫32m－1＝1 000(3m－2m＋1)3m－2m.故该企业每年上缴资金d的值为1 000(3m－2m＋1)3m－2m时，经过m(m≥3)年使企业的剩余资金为4 000万元．。

高中数学学习材料马鸣风萧萧*整理制作泰兴市第二高级中学高一数学双周练考试必修5命题人：袁效德 2006-5-13第一卷（选择题 共50分）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中,只有一项是符合题目的要求的.(1)⊿ABC 中,若(a+b+c )(b+c-a )=3bc ,并且C B A cos sin 2sin =,那么三角形ABC 是 A 直角三角形 B 等边三角形 C 等腰三角形 D 等腰直角三角形 (2)若⊿ABC 的三个内角成等差数列,同时ac b =2,那么⊿ABC 为A 等腰三角形B 等边三角形C 等腰直角三角形D 钝角三角形 (3) 在等差数列}{n a 中，已知1551,20S S a ==，n S 最大时n 为 A9 B10 C11 D12(4) ⊿ABC 中，分别根据下列条件解三角形，其中有惟一解的条件个数为 ①2,1,60===︒b a A ②4,2,30===︒b a A ③4,3,2===c b a ④4,2,30===︒c b AA0 B1 C2 D3 (5)设y a a a x ,,,,321成等差数列,y b b b b x ,,,,,4321成等差数列,则1413b b a a --的值是A65 B 54 C 43 D 32 (6)已知}{},{n n b a 都是等差数列,其前n 项和分别是,n S 和n T ,若326--=n n T S n n ,则88b a 的值 A32 B 31 C 41 D 43(7)在等差数列}{n a 中,已知,1254=+a a 则8S 等于A12 B24 C36 D48(8)在等差数列}{n a 中，===402010.30,20S S S 则A20 B30 C30 D40(9)⊿ABC 中,a,b,c 分别为∠A,∠B,∠C 的对边,如果a,b,c 成等差数列, ∠B=300,⊿ABC 的面积为0.5,那么b 为 A 31+ B 33+ C333+ D 32+ (10)三角形三边之比为(b+c ):(c +a ):(a+b )=4:5:6,则最大内角是 A2πB 32πC 43πD 65π第二卷（非选择题 共100分）二、填空题：本大题共6小题，每小题5分，共30分.把答案写在相应空格上 11.在⊿ABC 中，已知C=2B ，求bc的取值范围___________________ 12.设等差数列}{n a 中，===+4893,4,10a a a a 则_____________ 13.设等差数列}{n a 中,已知====n S a d n n 则,32,11,2_________14.已知两个等差数列}{n a ：5，8，11，…；}{n b ：3，7，11，…,各100 项，则由他们共同项所构成的数列的和为______________15.若以2,3,x 为三边组成一个锐角三角形,则x 的取值 范围__________________16.函数的图象,如图所示,其定义域为[-4,4],那么不等式0sin )(≤x x f 的解集为_______________________三、解答题:本大题共5小题,共70分.解答应写在文字说明、证明过程或演算步骤 17.(本小题满分12分)如图是第七界国际数学教育大会(ICME-7)的会徽图案，它是由一串直角三角形演化而成的，其中18732211=====A A A A A A OA 它可以形成近似的等角螺线，记821,,OA OA OA 的长度所组成的数列为)81,}({≤≤∈*n N n a n(1)写出数列}{n a 的通项公式(2)如果把图中的直角三角形继续下去，那么2008OA 长为多少？4A1AO4-4π-π 2π- 2π8A18. (本小题满分14分)在等差数列}{n a 中，已知前n 项和为n S ，且)2,2(2222≠≠--=n m nn mm S S n m ，求n m a a 的表达式19. (本小题满分14分)在等差数列}{n a 中,若233-=a 且从第15项起开始大于0,(1)求公差d 的取值范围 (2)若,*∈N d 则求数列n a 的前n 项和的最小值20.(本小题满分15分) 设函数a x x x f 22sin 3)32cos()(+++=π(1)求函数的周期(2)求函数的单调增区间 (3)当40π≤≤x 时，)(x f 的最小值为0，求a 的值21. (本小题满分15分)已知数列}{n a 的前n 项和为872--=n n S n(1)求数列}{n a 的通项公式,并判断}{n a 是不是等差数列，如果是求出公差，如果不是说明理由(2)求数列}{n a 的前n 项和n T答案一、选择题1、B2、B3、B4、D5、A6、B7、D8、A9、C 10、B 二、填空题11、)2,1( 12、6 13、4或8 14、3875 15、)13,5( 16、]4,[]2,0[ππ⋃或π-三、解答题 17、),81(,*∈≤≤=N n n n a n 50222008=OA18、323212121221222212121212121121--=--⋅=--=++==------n m m n S S n S m S a a a a a a a a n m n m n m n m n m 19、19614282)1(2722)2(122312230231102312011012)1(min 21113314315-==∴-=-+=-=∴+==∴∈≤<∴⎩⎨⎧≤->-∴⎩⎨⎧≤+=>+=n n S n n n dn n na S a d a a d Z d d d d d a a d a a 时，当20、41026sin ]32,6[62].4,0[)3(),6,3()22,22(62)2(2)62sin()()1(min -=∴=+=∴∈+∈∈+-∈⇒+--∈+=∴++=a a y x x Zk k k x k k x T ax x f πππππππππππππππππ函数的小值为函数的单调增区间为21、*-∈⎪⎩⎪⎨⎧≥+-≤≤++-=∴⎪⎩⎪⎨⎧≥-≤≤+-==∴⎩⎨⎧≥-=-=∴⎩⎨⎧≥-=-=∴-=-------=-=≥-===N n n n n n n n T n n n n n a n n n a a n n n a n n n n n S S a n S a n n n n n n n n n ,5327418758242821142821142}{28211482)8)1(7)1((8721412222111）（一个常数与它前一项的差不是同数列从第二项起每一项不是等差数列，因为此时，当时，当。