高中数学《向量的应用》教案 苏教版必修4

专题十平面向量的线性运算
邵伯高级中学赵仁军
教学目标：
1．平面向量的线性运算
1加法、减法、数乘运算．
2三角形法那么、平行四边形法那么．
2．两个定理
1向量共线定理
如果存在一个实数λ，使b＝λaa≠0，那么b与a是共线向量；反之，如果b与aa≠0是共线向量，那么有且只有一个实数λ，使b＝λa
2平面向量根本定理
如果e1和e2是同一平面内的两个不共线的向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1，λ2，使a＝λ1e1＋λ2e2
教学重点：
向量的基底运算
教学难点：
三角形和四边形中向量的运算．
教学方法：
复习课、启发式——引导发现、合作探究．
教学过程：
一、问题情境
我们已经学过平面向量的运算及其性质，知道：
建立坐标系是解决平面向量问题的一个好方法。

那么，在不可以建立坐标系的问题中，一般都牵涉向量的基底的运算．基底是指平面内两个不共线向量，在几何图形中常见基底向量多为多边形的边上的向量．
二、建构数学
1．平面向量的根本概念填写下表：
2．共线向量．
如果平面向量表示的有向线段所在的直线互相平行或重合，那么这些向量叫做
共线向量或平行向量．平行于记作
例2 如图10－2，在△ABC 和△AEF 中，B 是EF 的中点，AB ＝EF ＝1，CA ＝CB ＝2，假设错误!错误!，n ∈R ，那么m 2
＋n －22
的取值范围为________．
O
五、要点归纳与方法小结
本节课学习了以下内容：
1．平面向量的定义与运算法那么；
2．平面向量的一维共线问题；
3．平面向量要注重数形结合，注重培养我们的想象能力．。

第 12 课时：§ 向量的应用【三维目标】：一、知识与技术1.经历用向量方式解决某些简单的平面几何问题、力学问题与其他一些实际问题的进程，体会向量是一种处置几何问题、物理问题等的工具，进展运算能力2.运用向量的有关知识对物理中的问题进行相关分析和计算，并在那个进程中培育学生探讨问题和解决问题的能力二、进程与方式1.通过例题，研究利用向量知识解决物理中有关“速度的合成与分解”等问题2.通过本节课的学习，让学生体会应用向量知识处置平面几何问题、力学问题与其它一些实际问题是一种行之有效的工具；和同窗一路总结方式，巩固强化.三、情感、态度与价值观1.以学生为主体，通过问题和情境的设置，充分调动和激发学生的学习兴趣，培育学生解决实际问题的能力.2.通过本节的学习，使同窗们对用向量研究几何和其它学科有了一个初步的熟悉；提高学生迁移知识的能力、运算能力和解决实际问题的能力.【教学重点与难点】：重点：运用向量的有关知识对物理中的问题进行相关分析和计算，用向量方式解决实际问题的大体方式；向量法解决几何问题的“三步曲”。

难点：实际问题转化为向量问题，表现向量的工具作用。

用向量的方式解决某些简单的平面几何问题、力学问题与其它一些实际问题，体会向量在几何、物理中的应用.【学法与教学用具】：1. 学法：(1)自主性学习法+探讨式学习法(2)反馈练习法：以练习来查验知识的应用情形，找出未掌握的内容及其存在的差距.2. 教学用具：多媒体、实物投影仪.【讲课类型】：新讲课【课时安排】：1课时【教学思路】：一、创设情景，揭露课题1.向量既有大小又有方向的量，在实际问题中有很多如此的量，它既有代数特征，又有几何特征；今天，咱们就来用向量知识研究解决一些实际问题。

2.研究的方式：用数学知识解决实际问题，第一要将实际问题转化成数学问题，即将问题中各量之间的关系抽象成数学模型，然后再通过对那个数学模型的研究来解决实际问题中的有关量。

苏教版必修4《向量的应用》说课稿一、教材分析《向量的应用》是苏教版必修4的一章内容，主要涵盖了向量在几何、力学和运动学中的应用。

本章内容紧密联系，具有一定难度，但通过生活中的实际例子，能帮助学生更好地理解和应用向量的概念。

该章节在必修4中的位置为第3章，共有4个小节，包括：1.向量的基本概念：讲解了向量的定义、向量的加法和减法，以及与数的乘法的区别。

2.平面向量及其坐标表示：介绍了平面向量的坐标表示和向量的数量等概念。

3.平面向量的共线、共面与线性运算：讲解了共线向量、共面向量的判定方法和向量与常数的乘法。

4.平面向量与几何应用：主要包括三角形的向量解法、平行四边形面积与叉积以及垂直平分线问题。

通过学习这些内容，学生将能够把向量概念应用到几何、力学和运动学的问题中，提高问题解决的能力。

二、教学目标本章的教学目标主要包括：1.理解向量的定义和基本运算规则，掌握向量的加法、减法和数乘运算。

2.掌握平面向量的坐标表示方法，能够在几何图形中使用坐标表示向量。

3.判断平面向量的共线、共面性质，掌握线性运算的性质。

4.运用向量解决几何问题，如利用向量求三角形的面积、判断平行四边形是否共面等。

5.培养学生的综合思考和解决问题的能力，培养学生合作学习和信息获取的能力。

三、教学内容及教学步骤1. 向量的基本概念1.向量的定义：向量是有大小和方向的量，用加粗字母表示，如a。

2.向量的加法和减法：向量的加法是按照平行四边形法则进行，向量的减法是加上被减向量的相反数。

3.向量与数的乘法：向量与数的乘法是将向量的大小乘以一个数，方向不变。

2. 平面向量及其坐标表示1.平面向量的概念：平面向量是一个有大小和方向的有序对，在数学上可用有向线段表示。

2.平面向量的坐标表示：平面向量的坐标表示是用有序实数对表示，如向量a=(a₁, a₂)。

3.平面向量的数量：向量的数量等于其终点的坐标与起点的坐标之差。

3. 平面向量的共线、共面与线性运算1.共线向量的判定：若两个向量a和b的方向相同或相反，则它们共线；若向量a与b共线，且有一实数k使得a=k b，则a与b共向或反向。

苏教版高中高二数学必修4《向量的应用》教案及教学反思一、教学目标1.了解向量的概念，能够准确描述向量的特征和性质。

2.掌握向量的基本运算法则，能够正确地进行加、减、数乘运算。

3.掌握向量的点积和叉积运算，能够熟练地进行计算，并理解其几何意义。

4.熟悉向量的应用，能够解决空间中向量问题。

5.培养学生的空间直观思维和数学思想，提高学生的数学素养和学习能力。

二、教学内容1. 向量的概念（1）向量的定义向量是大小有方向的量，通常用有向线段表示。

（2）向量的特征和性质向量具有大小和方向两个特征，可以进行加、减、数乘等运算。

（3）向量的表示方式向量可以通过起点和终点、坐标表示、列向量等方式表示。

2. 向量的基本运算（1）向量的加减法向量的加减法遵循平行四边形法则。

（2）向量的数乘向量的数乘是将向量的大小乘以一个实数。

3. 向量的点积和叉积运算（1）向量的点积运算向量的点积是将两个向量按位相乘后加起来得到的标量。

（2）向量的叉积运算向量的叉积是将两个向量按照一定的顺序进行叉积运算而得到的向量。

4. 向量的应用（1）向量的共线和平面判定通过向量的数乘和叉积可以判断两个向量是否共线以及三个向量是否在同一平面内。

（2）向量的投影和正交分解向量的投影是指一个向量在另一个向量上的投影，在实际问题中经常用到。

（3）空间中向量的运用空间中向量的应用丰富多彩，例如在力学、几何、物理等领域都有广泛的应用。

三、教学方法1. 案例教学法通过具体生活案例介绍向量的概念和特点，从而引导学生理解和掌握向量的基本概念和性质。

2. 案例分析法通过实际问题的分析引导学生掌握向量的应用技巧和解题方法，提高学生的数学解决实际问题能力。

3. 讨论式教学法通过小组讨论的形式，引导学生探讨向量相关问题，激发学生的学习兴趣，提高学生的自主学习能力。

4. 演示法通过演示和实例解析等方式，让学生更直观地理解和掌握向量的基本运算法则和应用技巧。

四、教学反思在这次教学中，我采用了多种教学方法，例如案例教学法、案例分析法、讨论式教学法等。

江苏省南京市溧水县高中数学 第28课时《向量的应用》教学案 苏教版必修4 总 课 题 平面向量 总课时 第28课时 分 课 题 向量的应用 分课时 第 1 课时教学目标 用向量的知识解决有关实际问题；进一步巩固所学知识，提高分析和解决实际问题的能力，增强应用数学的意识；能用向量知识解决相关的物理问题。

重点难点 建立数学模型，并用所学知识解决有关测量和相关的物理问题。

运用向量知识解决有关物理问题。

引入新课1、已知A (1，2)，B (4，3)，C (2，4)，则|AB |= ，AB ·AC = 。

CAB = ；若四边形ABCD 为平行四边形，则点D 坐标为 。

2、a 与b =(1,2)同向，且a ·b =10，则a = ；若c r =（2，－1），则c r ·b ·a = 。

3、若|a |=1，|b |=2，则：（1）若a ∥b ，则a ·b = ；（2）若a 与b 的夹角为60°，则|a +b |= ，|a －b |= 。

（3）若a －b 与a 垂直，则a 与b 的夹角为 。

4、一条向正东方流淌的河，河水流速为3m/s ，若一条小船为33m/s 的速度向正北方向航行，求该船的实际航速和航向。

例题剖析例1、如图所示，无弹性的细绳OA ，OB 的一端分别固定在A ，B 处，同质量的细绳OC 下端系着一个称盘，且使得OB ⊥OC ，试分析OA ，OB ，OC 三根绳子受力的大小，并判断哪根绳受力最大。

例2、已知OA ⊥BC ，OB ⊥AC ，求证：OC ⊥AB 。

思考：你能画一个几何图形来解释例2吗？例3、已知A (7，8)，B (3，5)，C (4，3)，若2AM MB =u u u u r u u u r ，2CN NA =u u u r u u u r ，CM 与BN 交于点G ，求向量AG u u u r 。

巩固练习1、在ABC ∆中，,,BC CA AB 的长分别为,,a b c ，试用向量的方法证明： 2222cos a b c bc A =+-。

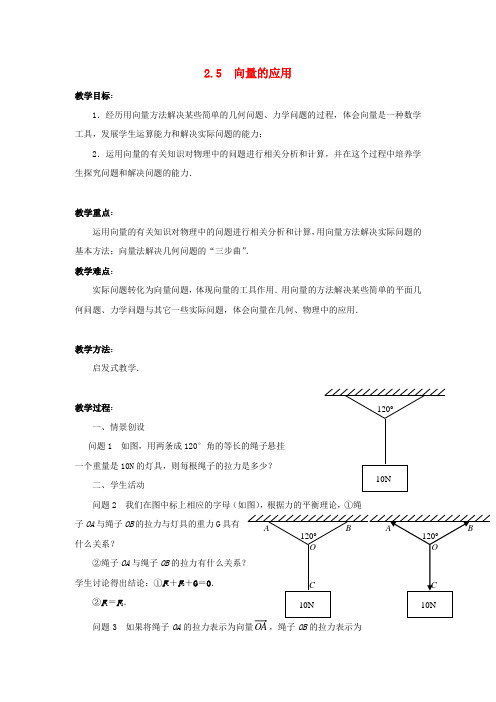
2.5 向量的应用教学目标：1．经历用向量方法解决某些简单的几何问题、力学问题的过程，体会向量是一种数学工具，发展学生运算能力和解决实际问题的能力；2．运用向量的有关知识对物理中的问题进行相关分析和计算，并在这个过程中培养学生探究问题和解决问题的能力．教学重点：运用向量的有关知识对物理中的问题进行相关分析和计算，用向量方法解决实际问题的基本方法；向量法解决几何问题的“三步曲”．教学难点：实际问题转化为向量问题，体现向量的工具作用．用向量的方法解决某些简单的平面几何问题、力学问题与其它一些实际问题，体会向量在几何、物理中的应用．教学方法：启发式教学．教学过程：一、情景创设问题1 如图，用两条成120°角的等长的绳子悬挂一个重量是10N的灯具，则每根绳子的拉力是多少？二、学生活动问题2 我们在图中标上相应的字母（如图），根据力的平衡理论，①绳子OA与绳子OB的拉力与灯具的重力G具有什么关系？②绳子OA与绳子OB学生讨论得出结论：①F1＋F2＋G＝0．②F1＝F2．问题3 如果将绳子OA的拉力表示为向量，绳子OB的拉力表示为120o 10N向量OB ，重力表示为向量OC ，则向量OA ，OB ，OC 之间有什么关系？学生讨论得出结论：++＝．这样物理问题就与数学中的向量产生了联系．三、建构数学问题4 你能否根据以上信息，将这个物理问题编写成一个数学问题？你能解决这个问题吗？学生讨论，教师整理，形成数学问题：已知向量OA ，OB 之间的夹角为120o，且向量的模等于向量的模，向量的模为10，求向量，的模．学生讨论解决问题：过A ，B 两点分别作OB ，OA 的平行线，相交于D 点，则四边形OADB 是菱形，连接OD ，则OD ＝||＝10，因为OA ＝OB ＝AD ＝BD ，且∠AOB ＝120o，所以ΔOAD 是等边三角形，所以OA ＝AD ＝OD ＝10，即||＝10，||＝10．亦即每根绳子的拉力都是10N ． 变题：在汽车站或火车站我们常见：两个人共提一个旅行包，若包重20N ，还需什么条件，你能求每一个人手臂的拉力？小结：（由学生讨论，教师整理）1．利用向量解决物理问题的基本步骤：①问题转化，即把物理问题转化为数学问题；②建立模型，即建立以向量为载体的数学模型；③求解参数，即求向量的模、夹角、数量积等；④回答问题，即把所得的数学结论回归到物理问题．2．用向量知识解决物理问题时，要注意数形结合.一般先要作出向量示意图，必要时可建立直角坐标系，再通过解三角形或坐标运算，求有关量的值．四、数学应用 1．例题．例 1 如图（1）所示，无弹性的细绳,OA OB 的一端分别固定在,A B 处，同质量的细绳OC 下端系着一个称盘，且使得OB OC ⊥，试分析,,OA OB OC 三根绳子受力的大小，判断哪根绳受力最大？A 11(2)题后反思：（1）本题你还最想知道什么？（2）绳子OB 与绳子OC 所受力的大小比较的本质是什么？ （3）你还能提出一些什么问题？例2 已知： AC OB BC OA ⊥⊥,，求证：AB OC ⊥． 题后反思：（1）你能否画出一个几何图形来解释例2？ （2）从例2中你能得出什么结论？学生讨论得出结论：三角形ABC 的三条高交于一点．例3 已知直线l 经过点111(,)P x y 222(,)P x y ，用向量方法求l 的方程．分析：设P 是直线l 上任意一点，由−→−P P 1与−→−21P P 共线的条件可推导得直线方程． 2．练习．（1）已知作用于点O 的力21,F F 的大小分别为6，8，且两力间的夹角为060，则两力合力的大小为__ ．（2）在四边形ABCD 中，·＝0，＝，则四边形ABCD 是____ ___（直角梯形、菱形、矩形、正方形）．（3）如图，一个三角形角铁支架ABC 安装在墙壁上，AB ∶AC ∶BC ＝3∶4∶5，在B 处挂一个6kg 的物体，求角铁AB 与BC 所受的力（取g ＝10m/s 2）．（4）已知两点),(11y x A ，),(22y x B ，试用向量的方法证明以线段AB程为0))(())((2121=--+--y y y y x x x x ．（5）一条河两岸平行，河宽500m d =，一艘船从A 处出发航行到河的正对岸的B 处，船航行速度1||10/km h v =，水速2||4/km h v =，要使船垂直到达对岸所用的时间最少，1v 与2v 的夹角是多少？五、要点归纳与方法小结 本节课学习了以下内容：1．如何把物理学问题转化为数学问题？2．如何把几何学问题转化为向量问题？3．如何运用向量的平行四边形法则和力的平衡知识，作好力的分解和合成．4．通过本节课的学习，让学生体会应用向量知识处理平面几何问题、力学问题与其它一些实际问题是一种行之有效的工具5．数形结合法．。

§2.5向量的应用教学目标：经历用向量方法解决某些简单的几何问题、力学问题的过程，体会向量是一种数学工具，发展学生运算能力和解决实际问题的能力．教学重点：运用平面向量解决简单的几何问题、力学问题．教学难点：将实际问题建立成向量的基本问题．教学过程： Ⅰ.问题情境向量是既有大小，又有方向的量，既有代数特征，又有几何特征； 通过向量可以实现代数问题与几何问题的互相转化，所以说向量是数形结合的桥梁．课前练习:1.已知A （2，1），B （3，2），D （－1，4），（1）求证：AB ⊥AD ；（2）若四边形ABCD 为矩形，求点C 的坐标.（1）证明：∵AB＝（1，1），AD ＝（－3，3）∴AB ·AD ＝1×3＋1×(－3)＝0， ∴AB ⊥AD.（2）解：∵ABCD 为矩形，设C （x ，y ），∴AB ＝DC ，（1，1）＝（x+1，y －4)∴x ＝0，y ＝5， ∴C （0，5）.2．已知a ＝（3，－2），b ＝(k，k ）（k ∈R)，t＝||a b，当k 取何值时，t有最小值？最小值为多少？解：∵a b -＝(3－k，－2－k )∴t ＝||a b -＝（3－k ）2＋（－2－k ）2＝2k 2－2k ＋13 ＝2（k －12 ）2＋252∴当k＝12 时，t 取最小值，最小值为522.(课时训练P63例3)解析:Ⅱ．例题选讲例1(课本P84)．分析：根据力学知识，首先应该认识到有：三根绳子上受到的力达到了平衡的效果，也就是合力为零，即0OA OB OC ++=．有了这样的思考，余下的就是数学模型的建立了．点评：此问题并没有什么难度，就是要能够从问题的实际意义中抽象出向量问题，用数学的知识解决这个物理问题．练习1(教材Ｐ85第1题)：分析：问题中有：0BA CB BT ++=．解：作受力分析图如右，依题意得：0BA CB BT ++= ，||60()BT N =，又||:||:||3:4:5AB AC BC = ，3||6045()4AB N ∴=⨯=5||6075()4BC N =⨯= ．CAI评：向量源自力学（教材P86阅读的标题），自然，向量会对力学问题发挥它的作用，我们这里所见到的只是非常非常简单的问题，是我们对向量应用的初步的感受． 类似题还有教材Ｐ86第5题：请同学们课外认真思考．例２(课本P84例2)．分析：证明应该是很容易的，所用的就是向量垂直的判定条件：0a b a b ⊥⇔⋅=．思考（课本P85提出来的问题）：回答：这是一个非常容易答的一个问题，简单的说，就是平面几何中的一个常见命题：三角形三条高线交于一点．练习：用向量方法证明梯形的中位线定理．ABCAB证：设梯形ＡＢＣＤ中，//AB DC，Ｅ、Ｆ分别为ＡＤ、ＢＣ的中点，EF EA AB BF =++ ，又EF ED DC CF =++ ，0,0EA ED BF CF +=+= ，2EF AB DC ∴=+ ，又AB 与DC平行且同向，//EF AB ∴且1||(||||)2EF AB DC ∴=+ ．此即梯形中位线定理．点评：平面几何中的许多命题都可以用向量方法证明，对此我们应该略有感受了，但是不需要在这个问题上作过多的挖掘，适可而止就可以了．(课时训练)解析:解析:例３（教材Ｐ86〖思考与运用〗第6题）说明：本题的结论是三角形中的两个基本定理：一个叫做射影定理；另一个叫做余弦定理．说的详细一些，就是：三角形中的射影定理：已知在ABC 中，BC 、CA 、AB 的长分别为a 、b 、c ，则有： cos cos a b C c B =+；cos cos b a C c A =+； cos cos c a B b A =+．三角形中的余弦定理：已知在ABC 中，BC 、CA 、AB 的长分别为a 、b 、c ，则有： 2222cos a b c bc A =+-；2222cos b a c ac B =+-；2222cos c a b ab C =+-．下面来思考本题的证明．BC(1)证： BC BA AC =+ ， BC BC BC BA BC AC ∴⋅=⋅+⋅ ，即2cos cos a ca B ab C =+． ∴cos cos a b C c B =+.(2) 证：22()BC BA AC =+， 2222a c b BA AC ∴=++⋅ 222cos(180)c b cb A =++-222cos c b cb A =+-，即2222cos a b c bc A =+-． 两个定理中其余几个式子可仿上证出．点评：向量作为工具，它的用途是非常广阔的，课本中的Ｐ85例３是必修Ⅱ中的一个解析几何的基本结论，但由于我们的教学安排是先学必修Ⅳ，把必修Ⅱ调到后面学了，所以对这个例题的价值暂时我们还难以体会真切，我们暂时只要知道有用向量能推导出这个结论就可以了，深刻的体会可以随着学习的深入和知识面的拓宽慢慢地去感受．P86第3题属于一样的情况，现在不要去做这个题了．这是教材中的旁白，或者叫做边注，给我们指出的是证明三点共线的一种方法，在今后的解析几何学习中有较为重要的用处．Ⅲ．课堂小结本节学习了用向量解决问题的基本类型和方法，只是一个开头和示范，更多、更灵活的应用，应该由同学们自己去体会和总结．Ⅳ．课外作业课时训练Ｐ63第12课时向量的应用.。

江苏省泰兴中学高一数学教学案(61)必修4_02 向量的应用班级 姓名目标要求经历用向量方法解决某些简单的几何问题、力学问题的过程，体会向量是一种数学工具，发展和提高运算能力和解决实际问题的能力。

重点难点重点：用向量方法解决某些简单的几何问题、力学问题； 难点：用向量方法解决几何问题。

典例剖析例1、平面内有向量(1,7),(5,1),(2,1)OA OB OP ===u u u ru u u ru u u r，点X 为直线OP 上的一动点. （1） 当XA XB u u u r u u u rg 取最小值时，求OX u u u r 的坐标；（2） 当点X 满足（1）的条件和结论时，求cos AXB ∠的值.例2、已知P 为AOB ∆的边AB 上一定点,且,OA a OB b ==u u u r r u u u r r,求证:存在实数t ,且01t <<,使(1)OP ta t b =+-u u u r r r;例3、已知||1,||2,,a b a b ==r r r r 的夹角为3π,试求:(1)a b +r r 与a b -r r夹角的余弦值;(2)使向量a b λ+r r 与a b λ-r r的夹角为钝角时,λ的取值范围.例4、已知点G 是ABC ∆的重心,过G 的直线与CA 、CB 分别交于P 和Q ，且,(0,0)CP mCA CQ nCB m n ==>>u u u r u u u r u u u r u u u r，试问,m n 的倒数和是否为定值？若是，求出这个定值；若不是，请说明理由。

学习反思1、用向量解决力学问题，要用到平行四边形法则和三角形法则，以及相关的力的夹角、大小的求法等。

2、解析几何就是用坐标的方法研究图形，而向量也引入了坐标运算，因此可以用向量的坐标运算解决解析几何中的证明与计算。

3、平面几何问题也可以引入坐标系用向量的坐标运算求解。

向量的应用●三维目标1．知识与技能会用向量方法处理简单的物理和几何问题．2．过程与方法通过本节的学习，研究向量法和坐标法处理物理和几何问题的思想．3．情感、态度与价值观(1)培养分析事物间相互联系的能力，提高学科间相互渗透的学习方法．(2)通过对实际问题的抽象思考，培养分析问题和应用知识解决问题的意识与能力．(3)培养热爱生活、热爱自然的高尚情怀．●重点难点重点：用向量方法解决简单的几何问题、力学问题等一些实际问题．难点：用向量方法解决实际问题的基本方法．●教学建议关于向量方法在平面几何及物理中的教学教学时，建议教师在引导学生回顾向量的线性运算、数量积运算及向量加减法的几何意义、向量共线定理、平面向量基本定理等知识的前提下，通过实例充分展示向量的工具性，突出其在生产实际中的应用，在巩固知识的同时，激发学生的学习兴趣，培养学生的创新和开拓能力．●教学流程通过例1及其变式训练，使学生掌握用平面向量知识解决物理问题的思路及方法.⇒通过例2及其变式训练，使学生掌握用向量知识解决平面几何问题的求解策略及方法.⇒通过例3及其变式训练，使学生掌握用向量法求解解析几何问题的方法.⇒归纳整理，进行课堂小结，整体认识本节课所学知识.⇒完成当堂双基达标，巩固所学知识并进行反馈矫正.1.会用向量方法解决简单的物理问题及其他的一些实际问题．课标解读2.会用向量方法解决某些简单的几何问题．(重点、难点)用向量方法解决平面几何问题的“三步曲”向量在物理中的应用图2－5－1如图2－5－1，在细绳O处用水平力F2缓慢拉起所受重力G的物体，绳子与铅垂方向的夹角为θ，绳子所受到的拉力为F1，求：(1)|F1|，|F2|随角θ的变化而变化的情况；(2)当|F1|≤2|G|时，θ角的取值范围．【思路探究】由力的平衡原理知，重力G是绳子的拉力和水平拉力的合力，且G⊥F2，F1与G的夹角为π－θ，解三角形求得力的大小与θ的关系，再回答相关问题．【自主解答】 (1)由力的平衡原理知，G ＋F 1＋F 2＝0，作向量OA →＝F 1，OB →＝F 2，OC →＝－G ，则OA →＋OB →＝OC →，∴四边形OACB 为平行四边形，如图．由已知∠AOC ＝θ，∠BOC ＝π2， ∴|OA →|＝|OC →|cos θ，|OB →|＝|AC →|＝|OC →|tan θ.即|F 1|＝|G |cos θ，|F 2|＝|G |tan θ，θ∈[0，π2)． 由此可知，当θ从0逐渐增大趋向于π2时，|F 1|，|F 2|都逐渐增大．(2)当|F 1|≤2|G |时，有|G |cos θ≤2|G |，∴cos θ≥12，又θ∈[0，π2)．∴θ∈[0，π3]．1．解力向量题时，依据题意对物体进行受力分析，通过向量加法的平行四边形法则对力进行分解和合成．2．解题时要明确各个向量之间的关系及它们各自在题目中的地位，借助于图形，将物理量之间的关系抽象为数学模型．图2－5－2如图2－5－2，作用于同一点O 的三个力F 1，F 2，F 3处于平衡状态，已知|F 1|＝1，|F 2|＝2，F 1与F 2的夹角为2π3，求F 3的大小．【解】 ∵F 1，F 2，F 3三个力处于平衡状态， ∴F 1＋F 2＋F 3＝0，即F 3＝－(F 1＋F 2)， ∴|F 3|＝|F 1＋F 2|＝F 1＋F 22＝F 21＋2F 1·F 2＋F 22＝1＋2×1×2×cos2π3＋4＝ 3.向量在平面几何中的应用图2－5－3如图2－5－3所示，四边形ABCD 是正方形，P 是对角线DB 上的一点(不包括端点)，E ，F 分别在边BC ，DC 上，且四边形PFCE 是矩形，试用向量法证明：PA ＝EF .【思路探究】 以点D 为原点建立直角坐标系，设正方形的边长为1，DP ＝λ，求出向量PA →与EF →的坐标，分别求出它们的长度判断即可．【自主解答】 建立如图所示的平面直角坐标系，设正方形的边长为1，DP ＝λ(0＜λ＜2)，则A (0,1)，P (22λ，22λ)，E (1，22λ)，F (22λ，0)． ∴PA →＝(－22λ，1－22λ)，EF →＝(22λ－1，－22λ)，∴|PA →|＝－22λ2＋1－22λ2＝λ2－2λ＋1，|EF →|＝22λ－12＋－22λ2＝λ2－2λ＋1，∴|PA →|＝|EF →|，∴PA ＝EF .用向量证明平面几何问题的方法，常见有两种思路： (1)向量的线性运算法选取基底→把待证问题用基底线性表示→利用向量的线性运算或数量积找相应关系→把向量问题几何化 (2)向量的坐标运算法建立适当的坐标系→把相关量坐标向量化→ 利用向量的坐标运算找相应关系→把向量问题几何化已知直角三角形的两直角边长分别为2和4，求两直角边上的中线所夹的锐角的余弦值．【解】 如图，在Rt △ABC 中，∠C ＝90°，D ，E 分别是BC ，AC 边的中点．BC ＝2，AC ＝4.则CD ＝1，CE ＝2.∴|AD →|＝AC →2＋CD →2＝17， |BE →|＝BC →2＋CE →2＝2 2. AD →·EB →＝(AC →＋CD →)·(EC →＋CB →)＝AC →·EC →＋AC →·CB →＋CD →·EC →＋CD →·CB → ＝4×2＋0＋0＋1×2＝10. 设AD →与EB →的夹角为θ，则cos θ＝AD →·EB→|AD →||EB →|＝1017×22＝53434. 故直线AD 和BE 所夹的锐角的余弦值为53434.法二 如图所示建立直角坐标系，点C 为原点，两直角边为坐标轴．其中点A (0,4)，B (2,0)，D (1,0)，E (0,2)．则AD →＝(1，－4)，EB →＝(2，－2)．∴AD →·EB →＝1×2＋(－4)×(－2)＝10. |AD →|＝12＋－42＝17， |EB →|＝22＋－22＝2 2.设AD →与EB →的夹角为θ，则cos θ＝AD →·EB→|AD →||EB →|＝1017×22＝53434. 故直线AD 和BE 所夹的锐角的余弦值为53434.向量在解析几何中的应用AQ 上，满足PA →·AM →＝0，AM →＝－32MQ →，当点A 在y 轴上移动时，求动点M 的轨迹方程．【思路探究】 一般要先设出动点坐标即M (x ，y )，再结合已知条件用动点坐标与已知点坐标表示AM →，MQ →，找出坐标间的关系，从而求出动点的轨迹方程．【自主解答】 设点M (x ，y )为轨迹上的任意一点，设A (0，b )，Q (a,0)(a ＞0)，则AM →＝(x ，y －b )，MQ →＝(a －x ，－y )．∵AM →＝－32MQ →，∴(x ，y－b )＝－32(a－x ，－y )．∴a ＝x 3，b ＝－y2， 则A (0，－y 2)，Q (x 3，0)，PA →＝(3，－y 2)，AM →＝(x ，32y )．∵PA →·AM →＝0，∴(3，－y 2)·(x ，32y )＝0.∴3x －34y 2＝0，∴所求轨迹方程为y 2＝4x (x ＞0)．利用向量法解决解析几何问题，如有关平行、共线、垂直、夹角、距离等问题均可用向量表示或用向量解决，要先将线段看成向量，再利用向量法则进行坐标运算使问题得以解决．已知点A (1,0)，直线l ：y ＝2x －6，点R 是直线l 上的一点，若RA →＝2AP →，求点P 的轨迹方程．【解】 设P (x ，y )，R (x 0，y 0)， 则RA →＝(1,0)－(x 0，y 0)＝(1－x 0，－y 0)， AP →＝(x ，y )－(1,0)＝(x －1，y )．由RA →＝2AP →，得⎩⎪⎨⎪⎧1－x 0＝2x －1，－y 0＝2y ，又∵点R 在直线l ：y ＝2x －6上，∴y 0＝2x 0－6，∴⎩⎪⎨⎪⎧ 1－x 0＝2x －26－2x 0＝2y①②由①得x 0＝3－2x ，代入②得6－2(3－2x )＝2y ，整理得y ＝2x ， 即为点P 的轨迹方程.应用问题的题意理解不清致误在水流速度为4 3 km ∠DAB ＝1243＝3，∴∠DAB ＝60°， ∴船的航行速度的大小为8 3 km ∠ACB ＝4312＝33. ∴∠CAD ＝∠ACB ＝30°，∴∠BAD ＝120°， ∴船的航行速度的大小为8 3 km 60°＝10. ∴|OP →|＝10sin 60°＝2033.∴|ON →|＝|OP →|cos 60°＝2033×12＝1033.∴水流速度为1033km BP →，故OR →＝OB →＋BR →＝b ＋n (OP →－OB →)＝n 3a ＋(1－n )b ，由于a 与b 不共线，则⎩⎪⎨⎪⎧1－m ＝n 3，35m ＝1－n .解得⎩⎪⎨⎪⎧m ＝56，n ＝12.∴OR →＝16a ＋12b .(2)由A 、H 、B 共线，可设BH →＝λBA →，则 OH →＝λa ＋(1－λ)b ，RH →＝OH →－OR →＝(λ－16)a ＋(12－λ)b .又RH →⊥AB →，∴RH →·AB →＝0，即[(λ－16)a ＋(12－λ)b ]·(b －a )＝0.又a ·b ＝|a |·|b |cos θ＝1，θ＝60°， ∴λ＝12，∴OH →＝12a ＋12b .利用向量的方法很容易解决几何中的长度计算与角度计算问题，特别在证明一些垂直关系等问题中充分体现了向量的广泛应用．(2013·太原高一检测)如图，平行四边形ABCD 中，AB →＝a ，AD →＝b ，H ，M 是AD ，DC 的中点，BF ＝13BC ，(1)以a ，b 为基底表示向量AM →与HF →；(2)若|a |＝3，|b |＝4，a 与b 的夹角为120°，求AM →·HF →. 【解】 (1)∵M 为DC 的中点， ∴DM →＝12DC →，又DC →＝AB →，∴AM →＝AD →＋DM →＝AD →＋12AB →＝12a ＋b ，∵H 为AD 的中点，BF ＝13BC ，∴AH →＝12AD →，BF →＝13BC →，又BC →＝AD →， ∴HF →＝HA →＋AB →＋BF → ＝－12AD →＋AB →＋13AD →＝AB →－16AD →＝a －16b .(2)由已知得a ·b ＝3×4×cos 120°＝－6， AM →·HF →＝(12a ＋b )·(a －16b )＝12a2＋(1－112)a·b－16b2＝12×32＋1112×(－6)－16×42＝－113.。

第11课时 §2.5 向量的应用
【教学目标】
一、知识与技能
体会向量是一种数学工具,发展学生运算能力和解决实际问题的能力.
二、过程与方法
.经历用向量法解决某些简单的几何问题,力学问题的过程.
三、情感、态度与价值观
使学生通过对问题的分析，转化，从深层次上认识学科之间的内在联系，并深刻认识数学的工具性作用，学会转化矛盾的方法，增强解决矛盾的能力，培养学生的创新精神
【教学重点难点】向量知识的应用
【教学过程】
一、复习：
①向量是既有大小又有方向的量,它既有代数特征,又有几何特征;
②通过向量可以实现代数问题与几何问题的相互转化,所以向量是数型结合的桥梁; ③向量也是解决许多物理问题的有力工具
二、新课讲解：
三、例题分析：
例1、如图所示,无弹性的细绳OB OA ,的一端分别固定在B A ,处,同质量的细绳OC 下端系着一个称盘,且使得OC OB ⊥试分析OC OB OA ,,三根绳子受力的大小,判断哪根绳子受力最大.(物理学中的应用)
例2、.已知:BC OA ⊥,AC OB ⊥，求证:AB OC ⊥
思考:你能否画一个几何图形来解释例2
例3、已知直线l 经过点),(111y x P 和),(222y x P ,用向量方法求l 的方程.
四、课时小结：本节课主要内容是应用向量解决某些简单问题.
五、反馈练习：。