当前位置：文档之家 › 三重积分习题课 优质课件

三重积分习题课 优质课件

  • 格式：ppt
  • 大小：1.24 MB
  • 文档页数：37

下载文档原格式

  / 37

合集下载

重积分三重积分的应用课件.ppt

重积分三重积分的应用课件.ppt


解 立体的图形为 设1为 在第一卦限内
的部分, 利用对称性得
z 1
M 4M1 4 ( x, y, z)dv
1
o
y
4( x y )dv 柱坐标变换 x
1
1
1
4 2 d rdr r(cos sin )dz
0
0
r2
4
2 (cos sin )d
1
r
2
(1
r
2
)dr
0
0
16。 15
13
设有一平面薄片占有 y
平面闭区域D, 在点(x,y)
处具有连续面密度
=(x,y)，下面利用元素
y
•d
D
法求该平面薄片对两坐
标轴的转动惯量。
O
x
x
先将物体分割为许多小部分，考虑其中的一
个部分d，它的质量元素为
dm ( x, y)d
这个部分d对于x轴以及对于y轴的转动惯
量元素为
dIx y2( x, y)d dI y x2( x, y)d
F
x, y, a 一致。
F0
x r
,
y,a rr
o x
x
y
• P(x,y,0) y
cos,cos ,cos , (r x2 y2 a2 )
dF {dFx , dFy , dFz }
{| d F | cos,| d F | cos ,| d F | cos },
( x, y)xd ( x, y) yd a( x, y)d
14
y
以这些元素为被积表达 式，在闭区域D上积分， 可得
y
•d
D
Ix y2( x, y)d ,OD源自I y x2( x, y)d
《D933三重积分》课件

《D933三重积分》课件


弹性力学问题中的三重积分应用
弹性力学问题中的 三重积分应用：在 弹性力学问题中， 三重积分被广泛应 用于求解应力、应 变和位移等问题。
应力分布：三重 积分可以用来求 解弹性体中的应 力分布，从而了 解弹性体的受力
情况。
应变分析：三重 积分可以用来求 解弹性体中的应 变分布，从而了 解弹性体的变形
情况。
D933三重积分PPT课件 大纲
汇报人：
目录
添加目录标题
01
三重积分的性质和定 理
04
三重积分的概念
02
三重积分的几何应用
05
三重积分的计算方法
03
三重积分的物理应用
06
添加章节标题
三重积分的概念
三重积分的定义
三重积分是计算空 间区域体积的一种 方法
积分区域为三维空 间中的有限区域
积分变量为x, y, z
柱坐标系下的三重积分计算 实例
柱坐标系下的三重积分定义
柱坐标系下的三重积分计算 注意事项
球坐标系下的三重积分计算
球坐标系的定义和性质 球坐标系下的三重积分公式 球坐标系下的三重积分计算步骤 球坐标系下的三重积分应用实例
坐标变换法
坐标变换法的基本思想：将原积分区域变换到新的坐标系下，使得新的积分区域更容易计算
三重积分在气象学中的应用
气象学中的三 重积分：用于 计算大气中的 温度、湿度、 气压等物理量
应用实例：计 算大气中的温 度分布、湿度 分布、气压分
布等
应用方法：通过 三重积分计算大 气中的物理量， 然后进行数据分
析和预测
应用效果：提高 气象预报的准确 性和可靠性，为 气象研究和应用
提供有力支持
三重积分在生物学中的应用
93三重积分2省优质课赛课获奖课件市赛课一等奖课件

93三重积分2省优质课赛课获奖课件市赛课一等奖课件


原式 = d x d y
x2 y2 z2 1 d z
x2 y2 1
1 x2 y2
0 奇函数
24
四川大学数学学院 邓瑾
V d v
z
r a 3 cos a
4 2 d 2 sin d
a 3 cos r 2 d r
0
0
0
r
2 a3
2 sin cos d
1 a3
y
x
3
0
3 dv r 2 sindrd d
20
四川大学数学学院 邓瑾
例3. 设由锥面 z x2 y2 和球面 x2 y2 z2 4
例1. 计算三重积分 z x2 y2 dxd ydz其中为由
柱面 x2 y2 2x 及平面 z 0, z a (a 0), y 0 所围
成半圆柱体.
0 2cos z
解: 在柱面坐标系下 :
0
2
a
0 z a
原式 z 2 d ddz
a
zdz 2 d
2cos 2 d
d
其中 F (r, , ) f (r sin cos , r sin sin , r cos )
合用范围: 1) 积分域表面用球面坐标表达时方程简朴;
2) 被积函数用球面坐标表达时变量相互分离.
18
四川大学数学学院 邓瑾
例1. 计算三重积分 ( x2 y2 z2 )d xd yd z , 其中
y0
1 x2 y2
f dz
1 x1 dx d y
0 y1
1 x2
f dz
1
dz 1
1 x2 z2 y1 f dx d y
1 z2 x 1 z2
11
[理学]三重积分习题课ppt课件

[理学]三重积分习题课ppt课件


2Rcos r 2 cos2 r 2 sindr
0
3
2
d
3 d
R
r
2
cos
2
r
2
s
in
dr
0
0
0
59 R5 480
解法2：利用柱面坐标计算。
由于 在 x平oy面的投影区域
故在柱面坐标下，
D xy
:
x2
；y 2
3R2 4
: R R2 r2 z R2 r2 , 0 r 3R , 0 2 2
主要内容
三重积分
一、三重积分的概念
n
1．定义:
f (x,
y,
z)dv lim 0 i1
f (i ,
i ,
i )vi
2．物理意义: M (x, y, z)dv
表示体密度为 ( x, y, z) 的空间物体 的质量。
二、三重积分的性质
三、三重积分的计算方法
1．利用直角坐标计算
f (x, y, z)dv f ( x, y, z)dxdydz
e z tan(x 2 y3 )dv 3dv
0 3dv 3
[e z tan(x 2，y 3 ) 3]dv z 1
o
y
1
x
于是有
z2dxdydz
2
d
3R
2 dr
R2 r2 z2 rdz
0
0
R R2 r2
2
3R
2 r[( R2 r 2 )3 2 ( R R2 r 2 )3 ]dr
30
59 R5 480
解法3：用“先二后一”法计算。
用平面 z R将积分区域
2
划分为两部分：
三重积分公开课一等奖优质课大赛微课获奖课件

三重积分公开课一等奖优质课大赛微课获奖课件

第五节 三重积分(二)
• 一、利用柱面坐标计算三重积分 • 二、利用球面坐标计算三重积分 • 三、小结 练习题
第1页
一、利用柱面坐标计算三重积分
柱面坐标：设 M ( x, y, z) 为空间内一点，
点 M 在xoy 面上的投影 为P ( x, y)
设点 P 的极坐标为 ( , )，
则三元有序数组( , , z) 唯一确定了点 M 的位置．
此为 柱坐标表示
第5页
f ( x, y, z)dv f ( cos , sin , z)dd dz.
问题：如何将柱坐标下三重积分化为三次积分？
{( x, y, z) | z1( x, y) z z2( x, y), ( x, y) Dxy }
Dx y {( x, y,) | , 1( ) 2( )}
由 x 2 y2 z 2 2a 2
z r 2a
r 2a,
z x2 y2 , 4
: 0 2 , 0 , 0 r 2a.
4 由三重积分的性质知
x
V dxdydz
4
o
y
第23页
例 6 求曲面 x2 y2 z2 2a2与z x2 y2 所围 成的立体体积.
4 z2
z1
z1 x2 y2 2, z2 4,
o
(x, y) y
x
: 0 2 , 0 2, 2 z 4，
I 02 d 02 d 42 zdz 2
02(16 4 )d
64 .
3
02
z2 2
4
d
2
第9页
例 6 计算I zdxdydz，其中 是球面
x2 y2 z2 4与抛物面 x2 y2 3z
x2 y2 z2， 与平面z a (a 0)所围的立体.
三重积分习题ppt课件

三重积分习题ppt课件


z
2
解法1：利用“先二后一”方法计算。
1
因 {(x, y, z) | (x, y) Dz, 0 z 2}
oD
y
由于当 0 z 1 时， Dz : x 2 y 2 z 2；
x
而当 1 z 2 时， Dz : x2 y2 2 z2 。
机动 目录 上页 下页 返回 结束
故需用平面 z 1 将积分区域 划分为两部分： 1 2
h
所以本题也可采用柱面坐标计算
解法1：利用“先二后一”方法计算。
由于 {( x, y, z) | ( x, y) Dz , 0 z ，h}
o R x
Dz
R
y
其中 Dz : x 2 y 2 Rh22z，2 故
zdxdydz
h
zdz
dxdy
h
R2z2
z
dz
0 Dz
0
h2
R 2
注意：从上面两种解法的过程来看, 虽然本题可用两种方法
来计算，但“先二后一”法相对简便。
26/37
9(2). 计算三重积分 zdxdydz , 其中 是由圆锥面 z x2 y2 与上半球面 z 2 x2 y2 所围成的闭区域。
分析：本题可考虑用直角坐标系中的“先二后一”法和柱面
坐标方法进行计算。
D
a
b ax
xy
Dxy
dx a
dy c f ( x, y, z)dz 0
a
20/37
y x
x
机动 目录 上页 下页 返回 结束
4. 计算三重积分 xy2z 3dxdydz。其中 是由曲面 z xy
与平面
y
x，x
1
及
重积分直角坐标系下三重积分的计算PPT课件

重积分直角坐标系下三重积分的计算PPT课件


z
(2) x2 yzdv
H
: x2 y2 z H (H 0) •
•
解 区域 是关于zox面是对称的
o
y
f ( x, y, z)关于y是奇函数 x
x2 yzdv
x 2 zdxdz
z x2
ydy
zx2
Dzx
x2z 0dxdz 0 。
Dzx
16
第16页/共45页
z ln(x2 y2 z2 1)
f ( x, y, z)dv
0
2
1
f (x,
y, z)dv
f 关于y是奇函数 f 关于y是偶函数
其中1是的右半部分
11
第11页/共45页
2、若 空间区域 是关于yoz面是对称的, 则
f ( x, y, z)dv
其中1是的前半部分
0
f 关于x是奇函数
2
1
f
( x,
y, z)dv
f 关于x是偶函数
• z Dz
o
y
1
x
zdv 0 dz zd
: x2 y2 z 1
Dz
1
0 zdzd
1
z(z
2
)dz
0
Dz
1 z3dz
0
z4
4
1 0
。
4
Dz oz
Dz:x2 y2 z2
24
第24页/共45页
练习二计算 I ( y4 sin x z)dv z
: x2 y2 z2 2Rz。
(1) : y1(z, x) y y2(z, x),(z, x) Dzx
f ( x, y, z)dv dzdx y2 (z,x) f ( x, y, z)dy
同济大学 高数 三重积分ppt课件

同济大学 高数 三重积分ppt课件


对应雅可比行列式为 J (x, y, z) (u, v, w)
直角坐标与柱面坐标的关系:
x cos y sin zz
J (x, y, z)
(,, z)
x y
x y
xz cos sin 0
yz sin cos 0
z z zz
0
01
dv J dddz dddz
x2 y2 2
z
h
解: 在柱面坐标系下
原式 =
2π 2
d
0
0
h
1
2
d
h
2 d z
xO y
4 dv d ddz
2
2π
0
h
1
2
(h
2
4
)
d
22
目录 上页 下页 返回 结束
3. 利用球坐标计算三重积分
设 M (x, y, z) R3, 其柱坐标为(, , z), 令 OM r,
zOM ,则(r,, ) 就称为点M 的球坐标.
16
目录 上页 下页 返回 结束
f (x, y, z)dxdydz
d d dz
d
d 2 ( )
z2 (, ) F(, , z)dz
1 ( )
z1 ( , )
其中 F(, , z) f ( cos , sin , z )
(,, z) , 1( ) 2( ), z1(, ) z z2(, )
就称为点M 的柱坐标. 直角坐标与柱面坐标的关系:
x cos y sin
zz
坐标面分别为
00z2π
z z
M (x, y, z)
常数 常数
z 常数
圆柱面 半平面 平面
高数A(2)习题课(9)三重积分(1)-PPT文档资料

高数A(2)习题课(9)三重积分(1)-PPT文档资料

, )，使得 的体积，则在 上至少存在一点 (,
f ( x ,y ,z ) dv f ( , , ) V

3、三重积分的计算方法
(1)利用直角坐标计算
f ( x ,y ,z ) dv f ( x ,y ,z ) dxdydz

a) “先一后二”法 若D为 在 xoy 面上的投影区域
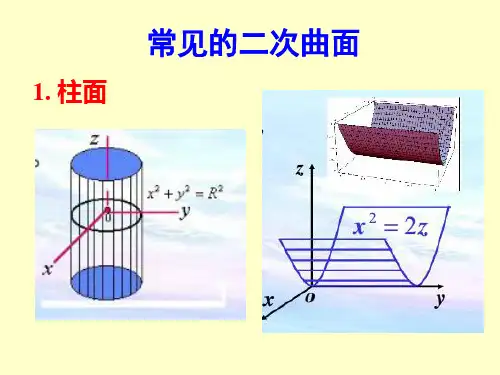
(2)利用柱面坐标计算
f ( x , y , z ) dxdydz f ( cos , sin , z ) drd dz 则

{( , , z ) | z ( , ) z z ( , ), ( ) ( ), } 若 1 2 1 2
f (x , y, z)dv f ( x ,y ,z ) dv f ( x ,y ,z ) dv (2)可加性：
1 2
1 2
(3) 的体积：V
dv

( x ,y , z ) g ( x ,y , z ) (4)单调性：若 在上，f ，则
d d
( ) 1

( ) 2
z ( , ) 2
z ( , ) 1
f ( cos , sin , z ) dz
(3)利用球面坐标计算
{( r , , ) | r ( , ) r r ( , ), ( ) ( ), } 若 1 2 1 2
则
f(x, y, z)dxdydz

2 f ( r sin cos , r sin sin , r cos ) r sin drd d ( ) 2
7-3三重积分及其计算市公开课获奖课件省名师示范课获奖课件

7-3三重积分及其计算市公开课获奖课件省名师示范课获奖课件


注：
（1）柱面坐标本质是对z采用直角坐标积分，另外两个变量采用平面极坐标变换积分；
（2）柱面坐标变换时，先找立体旳投影区域，拟定上下曲面。然后利用柱面坐标变换，把上下曲面表成两个极坐标分量旳函数，投影区域用极坐标旳不等式表达。
二、利用球面坐标计算三重积分
球面坐标与直角坐标旳关系为
如图，
要求：
如图，三坐标面分别为
圆锥面；
球面；
半平面．
r
dr
d
rsin
圆锥面
rd
球面r
圆锥面 +d
球面r+d r
元素区域由六个坐标面围成：
d
rsin d
半平面及 + d ； 半径为r及r + dr旳球面；圆锥面 及 + d
球面坐标下旳体积元素：
rsin d
r
dr
d
x
z
y
0
d
rd
球面坐标系中旳体积元素为
第三节 三重积分及其计算(2)
一、利用柱面坐标计算三重积分
要求：
柱面坐标与直角坐标旳关系为
三坐标面分别为
圆Hale Waihona Puke 面；半平面；平面．
（如图所示）
元素区域由六个坐标面围成
半平面及 + d ；半径为及 + d 旳圆柱面；平面 z及 z + dz；
柱面坐标下旳体积元素：
d
d
d
z
d
r
d
d
z
dz
如图，柱面坐标系中旳体积元素为
如图，
练习
设由锥面
和球面
所围成 , 计算
提醒:
利用对称性
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2
d

sin d
R r4 cos2 dr （球面坐标）
0
0
0
Ω
6 sin cos2 d R r4 dr 4 R5
0
0
5
机动 目录 上页 下页 返回 结束
7/37
一、关于三重积分性质和应用的题类
【例2】设 : x2 y2 z2 h2
M ( x3 cos y x2 y2 x4 )dV
4/37
2.改变累次积分的积分次序
题目要求改变积分次序或按原积分次序 积不出来，必须改变积分次序.
3.求由曲面所围立体的体积
用三重积分：V dxdydz

4.用二重积分求曲面的面积
A
Dxy
1 ( z )2 (z )2dxdy x y
A 1 (y )2 (y)2dxdz

【解Ⅰ】 被积函数仅为z 的函数，截面D(z) 为圆域
x2 y2 1 z2，故采用“先二后一”法．
e z dv 2 ezdv

上
1
2 ez dz[
edzdxxddyy]
0
DDzz
面
积 2 1 (1 z2 )e zdz 2. 0
分块积分法
(3) 消去被积函数绝对值符号
利用对称性
(4)被积函数为1时巧用其几何意义
dxdydz 的体积

机动 目录 上页 下页 返回 结束
6/37
【例1 】计算 (x y z)2dV，x2 y2 z2 R2 作业题

【解】由对称性知 xydV yzdV xzdV 0
于是
1z
z2 y2
I dz dy
f ( x, y, z)dx
0
z
z2 y2
13/37
z
o
x
z x2 y2
d
2
2 d
1 2
zdz
.
0
0

8
【解Ⅲ】 利用直角坐标
( x z)dv zdv


2
1 x2
1 x2 y2
2 dx 2 dy
zdz
2
1x2
x2 y2
2
2
. 8/37
【例4】 计算 e z dv， : x2 y2 z2 1.
a. 选择坐标系 使积分域多为坐标面围成; 被积函数用此坐标表示简洁或变量分离.
b. 确定积分序 积分域分块要少, 累次积分易算为妙 .
c. 写出积分限 图示法 ( 先积一条线, 后扫积分域 )
列不等式法 (从内到外: 面、线、点) 充分利用对称性
d. 计算要简便 应用换元公式
机动 目录 上页 下页 返回 结束
Dxz
x z
A 1 (x)2 (x)2dydz
D yz
y z
机动 目录 上页 下页 返回 结束
5/37
6.三重积分性质的应用题
估计重积分的值 比较重积分的大小
重积分中值定理的应用
（二）、三重积分计算的基本技巧
(1) 交换积分顺序的方法
(2) 利用对称性简化计算
【解Ⅰ】 利用球面坐标
( x z)dv zdv



2
d

4 d
1 r cos r2 sin dr
0
0
0
. 8
机动 目录 上页 下页 返回 结束
9/37
【解Ⅱ】 利用柱面坐标
( x z)dv zdv


2
x2 y2 z 1
z
再画出的图形
z x2 y2
y
x
x2 y2 1
机动 目录 上页 下页 返回 结束
（1）将投影到 yoz面
由 z x2 y2
x z2 y2
得

0z1

:

D
yz
: z y z
z2 y2 x z2 y2

N ( x2 sin y x2 y3 z3 )dV

P (z3 x4 cos2 y x2z2 )dV
比较M,N,P的大小. 【分析】通过计算比较大小很烦琐,注意到积分区域为一以 原点为球心的球体,具有对称性,于是想到是否可利用对称 性直接作出比较呢?
M0 N 0 P0
0
0
0
上
计算较繁
机动 目录 上页 下页 返回 结束
12/37
【补例】
略
试将三次积分 I
1
dx
1 x2
1
dy
f ( x, y, z)dz
1 1 x2
x2 y2
按x、y、z的次序积分；然后再按y、z、x
的次序积分
1 x 1 【解】先写出 : 1 x2 y 1 x2
1/37
第十章
习题课
三重积分
一、关于三重积分性质和应用的题类 二、关于三重积分的题类 三、杂题
机动 目录 上页 下页 返回 结束
主要内容
定义 几何意义(无)
性质 计算法 应用 物理意义
2/37
三 重 积 分
机动 目录 上页 下页 返回 结束
（一）、三重积分常见题目类型
3/37
1.一般三重积分的计算： —— 累次积分法
机动 目录 上页 下页 返回 结束
11/37
【解Ⅱ】 柱面坐标
原式 2 ezdv
上
2
1
2 d d
1 2 ez dz
0
0
0
计算较繁
【解Ⅲ】 球面坐标
原式 2
ezdv 2
2
d

2 d
1er cos r 2 sindr
故 PNM
机动 目录 上页 下页 返回 结束
8/37
二、关于三重积分的题类
【例3】 计算 ( x z)dv，其中 由 z x2 y2 与

z 1 x2 y2 所围成的．
【分析】 关于 yoz 面为对称，f ( x, y, z) x 为 x 的
奇函数， 有 xdv 0.



x2dV y2dV z2dV
(x y z)2dV Ω
Ω
Ω

x2dV y2dV z2dV



2 xydV 2 yzdV 2 xzdV



3
z2dV 3