正弦交变电流有效值和最大值关系的简单推证
- 格式:doc
- 大小:58.50 KB
- 文档页数:3

探究正弦交流电有效值与最大值的关系许文【摘要】@@ 交变电流的最大值I<,m>和U<,m>是交变电流在一个周期内所能达到的最大数值.交变电流的有效值I和U是根据电流的热效应定义的,即让交流与直流通过相同阻值的电阻,如果它们在相同的时间内产生的热量相等,这一直流的数值叫做这一交流的有效值.【期刊名称】《物理通报》【年(卷),期】2011(000)005【总页数】3页(P29-31)【作者】许文【作者单位】华中科技大学附属中学,湖北武汉,430074【正文语种】中文交变电流的最大值Im和Um是交变电流在一个周期内所能达到的最大数值.交变电流的有效值I和U是根据电流的热效应定义的,即让交流与直流通过相同阻值的电阻,如果它们在相同的时间内产生的热量相等,这一直流的数值叫做这一交流的有效值.对于某一确定的交流电,其有效值与最大值间存在一定的关系.正弦交流电的有效值与最大值之间的关系,目前中学物理各种版本的教材中一般都是直接给出.在当今新课标的理念下,我们可以从理论与实验两方面对这一问题展开探究,有利于培养学生的探究能力、实验能力、分析问题与解决问题的能力.1 理论探究方法1:设想将正弦交流电i=Imsinωt通过阻值为R的电阻,则电阻发热的功率为作出P-t图像(图1),在一个周期T内电阻发热量Q1即为图中曲线下的面积(也等于图1中长为T高为即若将某一直流电流I通入该电阻,则在时间T内的发热量Q2 = I2RT.当Q1=Q2时,可得图1方法2:我们据交变电流有效值的定义知交流电ia=Imsinωt(图2)与ib=Imcosωt (图3)的有效值应相同.设想让它们分别通过同一电阻R,则在时间T内产生的热量均为Q .现把时间T分成很多时间微元ΔT,则Q=∑ia2RΔT=∑(Imsinωt)2RΔTQ=∑ib2RΔT=∑(Imcosωt)2RΔT则有2Q=∑Im2(sin2ωt+cos2ωt)RΔT=Im2R∑ΔT=Im2RT若将某一直流电流I通入该电阻,则在时间T内发热量Q=I2RT,可得图2图3方法3:设流过定值电阻R的电流按正弦规律变化,即i=Imsinωt,交流电的瞬时功率为P=i2R=Im2Rsin2ωt因为代入得此式中后一项在一个周期内平均值为零,因此在一个周期内交流电平均功率为(为最大瞬时功率的一半).如果考虑一个恒定电流I与其等效,即P=I2R,就有即所以方法4:设通过定值电阻R的电流按正弦规律变化,即i=Imsinωt ,交流电的瞬时功率为P=i2R=Im2Rsin2ωt则一个周期内电阻R上产生的热量为因为代入得有此式第二项积分为零,所以如果有一个恒定电流I与其等效,即Q′=I2RT,则所以有2 实验探究2.1 设计方案如图4所示,a、b两端接6 V的正弦交流电源,R为总阻值为200 Ω的滑动变阻器,用演示交流电压表的10 V挡测滑动变阻器输出端电压的有效值U,用J2459演示示波器测滑动变阻器输出端电压的最大值Um.(这里也可用双踪示波器同时测量U与Um)图42.2 数据记录与处理按图4将各实物器材连成实验电路.调节示波器Y衰减和Y增益,使纵坐标定格为每格2 V,调节扫描范围与扫描微调,使荧光屏上显示2~3个正弦波形.实验中调节滑动头的位置,测出20组U与Um的值,并将测量值填入Excel的表中,用Excel对数据进行分析与处理.(1)启开软件Excel,在A1中输入符号U/V,在B1中输入符号Um/V;(2)在A2~A21 中记录U的测量值,在B2~B21中记录相应的Um测量值;(3)选中A2:B21区域,单击图表按钮出现“图表向导对话框”,在“图表类型”中选取“X、Y散点图”,在子图表类型中选“平滑线散点图”,再依次按下一步按钮,直到完成(图5);(4)右击图5中任一数据点,选“添加趋势线”,在“类型”中选“线性”,在“选项”中选“显示公式”,确定后就会出现Um 与U的函数关系式.图52.3 结论在一定的实验误差范围内,正弦交流电的最大值与有效值的关系为3 发散思考问题:正弦交流电的有效值I与最大值Im的关系是那么当有效值与最大值关系为时,该电流一定是正弦交流电吗?答案:电流有效值与最大值关系是的不一定都是正弦交流电.如图6所示的交变电流显然不是正弦交流电,但这个交变电流的最大值是Im ,设其有效值为I.据有效值的定义有故图64 教学反思新课标的教学理念强调学生获取知识的过程.微积分知识已经引入到目前高中数学课程中.探究正弦交流电的有效值与最大值的关系,可以很好的引导学生从数学方法与物理实验的多角度进行探索,充分培养学生的探究能力.以实验为基础是物理教学的基本特征;物理实验对激发学生学习兴趣、启迪学生思维、培养科学方法和创新精神均能产生积极有效的作用.课堂上教师应千方百计地提供机会,让学生亲身体验物理实验操作过程,使物理创新式的学习过程成为一种“活、乐、动”的过程;在物理实验操作过程中去发现新问题、萌发新思想、形成新思路、寻找新方法、开拓新领域、获得新知识和技能.这种让他们亲自参与亲身体验的学习方法,能极大地调动其学习积极性,提高学习效率.。

交流电的瞬时值、最大值、有效值和平均值1. 瞬时值:交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。
瞬时值随时间的变化而变化。
不同时刻,瞬时值的大小和方向均不同。
交流电的瞬时值取决于它的周期、幅值和初相位。
以正弦交流电为例(从中性面开始计时)。
则有:其瞬时值为:e=E m sin ωti=I m sin ωt u=U m sin ωt2.最大值:交变电流的最大值是指交变电流在一个周期内所能达到的最大值,它可以用来表示交变电流的强弱或电压的高低。
以正弦交流电为例。
则有:E m =nB ωS ,此时电路中的电流强度及用电器两端的电压都具有最大值,即I m =rR E m , U m =I m R 。
3.有效值:交变电流的有效值是根据电流的热效应来定义的,让交变电流和恒定电流通过相同阻值的电阻,如果在相同的时间内产生的热量相等,我们就把这一恒定电流的数值叫做这一交变电流的有效值。
交流电的有效值是根据它的热效应确定的。
交流电流i 通过电阻R 在一个周期内所产生的热量和直流电流I 通过同一电阻R 在相同时间内所产生的热量相等, 则这个直流电流I 的数值叫做交流电流i 的有效值, 用大写字母表示, 如I 、 U 等。
一个周期内直流电通过电阻R 所产生的热量为:交流电通过同样的电阻R ,在一个周期内所产生热量:根据定义,这两个电流所产生的热量应相等,即将代入上式i=I m sin ωt4.平均值:交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。
对于某一段时间或某一过程,其平均感应电动势:I tN E 平均电流→∆∆∙=φ=U r R E 平均电压→+=I R ∙二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系: U=m m U U 707.02=,I=m mI I 707.02= 注:I U 是电流、电压的有效值,I m 、U m 是电流、电压的最大值2、正弦交流电的平均值与最大值和有效值的关系:m m P I I I 637.02==π,m m P U U U 637.02==π,I I P 90.0=,U U P 90.0=注:I p 、U p 是电流、电压的平均值交变电流有四值,即有效值、平均值、最大值和瞬时值.各值何时应用,对照如下情况确定:(1)在研究电容器是否被击穿时,要用峰值(最大值).因电容器上标明的电压是它在直流电源下工作时所承受的最大值.(2)在研究交变电流的功率和产生的热量时,只能用有效值.(3)在求解某一时刻线圈受到的磁力矩时,只能用瞬时值.(4)在求交变电流流过导体的过程中通过导体截面积的电量时,要用平均值.。


有效值和最大值的关系公式
1. 正弦交流电中有效值和最大值的关系。
- 对于正弦交流电,设其瞬时值表达式为e = E_msinω t(e为电动势,E_m为电动势最大值),u = U_msinω t(u为电压,U_m为电压最大值),i = I_msinω t(i为电流,I_m为电流最大值)。
- 有效值的定义是让交流电和直流电通过相同的电阻,如果在相同时间内产生的热量相等,那么这个直流电的值就是交流电的有效值。
- 根据焦耳定律Q = I^2Rt(对于直流电),对于交流电Q=∫_0^Ti^2Rdt(T为周期)。
- 对于正弦交流电i = I_msinω t,计算可得Q=∫_0^TI_m^2sin^2ω tRdt。
- 因为sin^2ω t=(1 - cos2ω t)/(2),所以Q=∫_0^TI_m^2(1-cos2ω
t)/(2)Rdt=frac{I_m^2R}{2}∫_0^T(1 - cos2ω t)dt。
- 计算∫_0^T(1-cos2ω t)dt=T,所以Q=frac{I_m^2RT}{2}。
- 设电流有效值为I,根据有效值定义Q = I^2RT,所以
I^2RT=frac{I_m^2RT}{2},解得I=frac{I_m}{√(2)}。
- 同理,对于电压U=frac{U_m}{√(2)},对于电动势E=frac{E_m}{√(2)}。
- 所以在正弦交流电中,有效值E、U、I与最大值E_m、U_m、I_m的关系公式为:E=frac{E_m}{√(2)},U=frac{U_m}{√(2)},I=frac{I_m}{√(2)}。

交流电的瞬时值、最大值、有效值和平均值 交变电流的大小和方向都随时间作周期性变化,所以要准确描述交变电流的产生的效果,需要用到“最大值、有效值、瞬时值、平均值”四个物理量。
交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。
这四个类似但又有区别的物理量,容易造成混乱,理解好“四值”对于学习交流电有极大的帮助。
一、 准确把握概念1. 瞬时值:交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。
瞬时值随时间的变化而变化。
不同时刻,瞬时值的大小和方向均不同。
交流电的瞬时值取决于它的周期、幅值和初相位。
以正弦交流电为例(从中性面开始计时)。
则有:其瞬时值为:e=E m sinωti=I m sinωt u=U m sinωt2.最大值:交变电流的最大值是指交变电流在一个周期内所能达到的最大值,它可以用来表示交变电流的强弱或电压的高低。
以正弦交流电为例。
则有:E m =nB ωS ,此时电路中的电流强度及用电器两端的电压都具有最大值,即I m =r R E m , U m =I m R 。
3.有效值:交变电流的有效值是根据电流的热效应来定义的,让交变电流和恒定电流通过相同阻值的电阻,如果在相同的时间内产生的热量相等,我们就把这一恒定电流的数值叫做这一交变电流的有效值。
交流电的有效值是根据它的热效应确定的。
交流电流i 通过电阻R在一个周期内所产生的热量和直流电流I通过同一电阻R在相同时间内所产生的热量相等, 则这个直流电流I的数值叫做交流电流i的有效值, 用大写字母表示, 如I、U 等。
一个周期内直流电通过电阻R所产生的热量为:交流电通过同样的电阻R,在一个周期内所产生热量:根据定义,这两个电流所产生的热量应相等,即将代入上式i=I m sinωt4.平均值:交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。
对于某一段时间或某一过程,其平均感应电动势:I tN E 平均电流→∆∆•=φ=U r R E 平均电压→+=I R •二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系: U=m m U U 707.02=,I=m mI I 707.02= 注:I U 是电流、电压的有效值,I m 、U m 是电流、电压的最大值2、正弦交流电的平均值与最大值和有效值的关系:m m P I I I 637.02==π,m m P U U U 637.02==π,I I P 90.0=,U U P 90.0=注:I p 、U p 是电流、电压的平均值三、“四值”解题方法小结:交变电流有四值,即有效值、平均值、最大值和瞬时值.各值何时应用,对照如下情况确定:(1)在研究电容器是否被击穿时,要用峰值(最大值).因电容器上标明的电压是它在直流电源下工作时所承受的最大值.(2)在研究交变电流的功率和产生的热量时,只能用有效值.(3)在求解某一时刻线圈受到的磁力矩时,只能用瞬时值.(4)在求交变电流流过导体的过程中通过导体截面积的电量时,要用平均值.。

有效值的计算有效值:交变电流的有效值是根据电流的热效应规定的,即在同一时间内,跟某一交变电流使同一电阻产生相等的直流电的数值,叫该交变电流的有效值。
正弦式电流的有效值和最大值之间的关系是2E E m =,2U U m =,2I I m =。
复习时注意以下几个方面:①某段时间内的交变电流的平均值不等于这段时间始、终时刻瞬时值的算术平均值,对正弦交流电流电来说,在T/4时间内,π=m E 2E 。
②交流电表测量的数值均为有效值,对交流电的数值凡是没有特别说明的均指有效值。
③对非正弦交流电的有效值必须按有效值定义求出。
④在计算交变电流通过导体产生的热量和电功率及确定保险丝的熔断电流时,只能用交变电流的有效值;在考虑电容器的耐压值时,则应根据交变电流的最大值;在计算通过导体的电量时,只能用交变电流的平均值。
1、如图所示电路,电阻R 1与电阻R 2阻值相同,都为R ,和R 1并联的D 为理想二极管(正向电阻可看作零,反向电阻可看作无穷大),在A 、B 间加一正弦交流电u =20sin100πt (V),则加在R 2上的电压有效值为A .10VB .20VC .15VD .5V2、已知交变电流i=I m sin ωt A,线圈从中性面起开始转动,转动了多长时间,其瞬时值等于有效值( ) A.wC.4wπD.2wπ3、如图甲为电热毯的电路图,电热丝接在u =311sin 100πt V 的电源上,电热毯被加热到一定温度后,通过装置P 使输入电压变为如图乙所示的波形,从而进入保温状态,若电热丝电阻保持不变,此时交流电压表的读数是( )A.110 VB.156 VC.220 VD.311 V4、4.如图所示的电路,已知交变电流的电压U=2202sin 100πt V,电阻R=200 Ω,不考虑电表内阻对电路的影响,则电流表和电压表的读数分别为( )210A.1.12 A , 2202 VB.1.1 A , 220 VC.1.12 A , 220 VD.1.1 A , 220 2V 5、(2010·盐城模拟)一根电阻丝接入100 V 的恒定电压电路中,在1 min 内产生的热量为Q ,同样的电阻丝接入正弦式交变电流的电路中,在2 min 内产生的热量也为Q ,则该交流电压的峰值是()A.141.4 VB.100 VC.70.7 VD.50 V6、如图所示,理想变压器的原、副线圈匝数比为1:5,原线圈两端的交变电压为100V u t π=氖泡在两端电压达到100V 时开始发光,下列说法中正确的有A .开关接通后,氖泡的发光频率为100HzB .开关接通后,电压表的示数为100 VC .开关断开后,电压表的示数变大D .开关断开后,变压器的输出功率不变 答案:AB【解析】由交变电压的瞬时值表达式知,原线圈两端电压的有效值为1U =V=20V ,由1122n U n U =得副线圈两端的电压为2100U =V ,电压表的示数为交流电的有效值,B 项正确;交变电压的频率为100502f ππ==Hz ,一个周期内电压两次大于100V ,即一个周期内氖泡能两次发光,所以其发光频率为100Hz ,A 项正确;开关断开前后,输入电压不变,变压器的变压比不变,故输出电压不变,C 项错误;断开后,电路消耗的功率减小,输出功率决定输入功率,D 项错误。
【高中物理:怎么求正弦式交变电流的有效值...
【高中物理:怎么求正弦式交变电流的有效值?】
有效值的定义:让交变电流与恒定电流分别通过阻值相同的电阻,在交变电流的一个周期T内它们产生的热量相等,我们把这个恒定电流I、电压U称作这个交变电流的有效值。
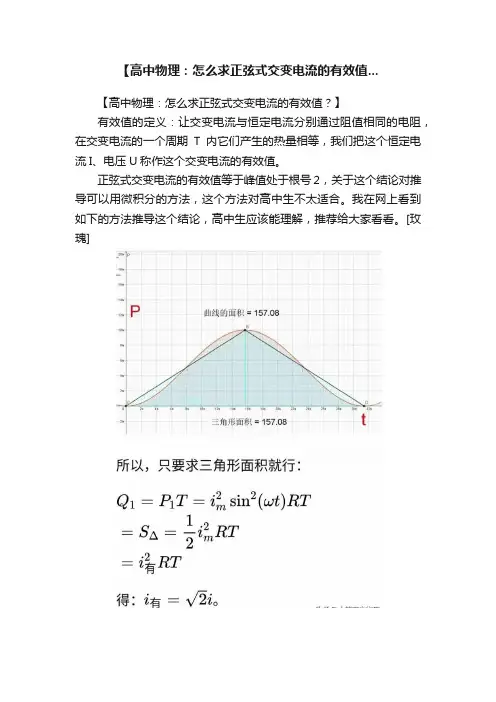
正弦式交变电流的有效值等于峰值处于根号2,关于这个结论对推导可以用微积分的方法,这个方法对高中生不太适合。
我在网上看到如下的方法推导这个结论,高中生应该能理解,推荐给大家看看。
[玫瑰]。

正弦式交变电流有效值与最大值的关系
当我们谈论正弦式交变电流时,我们经常会涉及有效值和最大值之间的关系。
有效值是指交流电流的平均值,它表示了交流电流在电路中产生的功率大小。
最大值是交流电流的峰值,它表示了电流在正负方向上的最大幅值。
有效值与最大值之间的关系可以通过一个简单的比例来描述。
有效值是最大值乘以一个系数,这个系数由正弦函数的周期性决定。
具体地说,有效值等于最大值乘以1/√2。
这个比例反映了正弦函数的性质。
正弦函数在一个完整的周期内,从最大值到最小值再到最大值,经历了一次完整的波动。
而有效值则是在这个周期内的平均值。
为了更好地理解有效值与最大值之间的关系,我们可以举一个简单的例子。
假设我们有一个正弦波形的交流电流,其最大值为10安培。
根据上述比例,我们可以计算出其有效值为10/√2 ≈ 7.07安培。
这个例子表明,有效值是最大值的一种衡量方式,它表示了交流电流在电路中所产生的平均功率。
而最大值则表示了电流在正负方向上的最大幅值,它可以帮助我们确定电路的额定容量,以确保电路能够正常运行。
因此,了解有效值与最大值之间的关系对于电路设计和电力系统的
运行非常重要。
它可以帮助我们合理安排电力资源,提高电路的效率和安全性。
正弦式交变电流的有效值与最大值之间存在着明确的关系。
通过了解和应用这个关系,我们可以更好地理解和控制交流电流,确保电路的正常运行。

交流电(一)的瞬时值、最大值、有效值和平均值 交变电流的大小和方向都随时间作周期性变化,所以要准确描述交变电流的产生的效果,需要用到“最大值、有效值、瞬时值、平均值”四个物理量。
交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。
这四个类似但又有区别的物理量,容易造成混乱,理解好“四值”对于学习交流电有极大的帮助。
一、 准确把握概念1. 瞬时值:交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。
瞬时值随时间的变化而变化。
不同时刻,瞬时值的大小和方向均不同。
交流电的瞬时值取决于它的周期、幅值和初相位。
以正弦交流电为例(从中性面开始计时)。
则有:其瞬时值为:e=E m sinωti=I m sinωt u=U m sinωt2.最大值:交变电流的最大值是指交变电流在一个周期内所能达到的最大值,它可以用来表示交变电流的强弱或电压的高低。
以正弦交流电为例。
则有:E m =nB ωS ,此时电路中的电流强度及用电器两端的电压都具有最大值,即I m =r R E m , U m =I m R 。
3.有效值:交变电流的有效值是根据电流的热效应来定义的,让交变电流和恒定电流通过相同阻值的电阻,如果在相同的时间内产生的热量相等,我们就把这一恒定电流的数值叫做这一交变电流的有效值。
交流电的有效值是根据它的热效应确定的。
交流电流i 通过电阻R在一个周期内所产生的热量和直流电流I通过同一电阻R在相同时间内所产生的热量相等, 则这个直流电流I的数值叫做交流电流i的有效值, 用大写字母表示, 如I、 U等。
一个周期内直流电通过电阻R所产生的热量为:交流电通过同样的电阻R,在一个周期内所产生热量:根据定义,这两个电流所产生的热量应相等,即将代入上式i=I m sinωt4.平均值:交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。
对于某一段时间或某一过程,其平均感应电动势:I tN E 平均电流→∆∆•=φ=U r R E 平均电压→+=I R •二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系: U=m mU U 707.02=,I=m m I I 707.02=注:I U 是电流、电压的有效值,I m 、U m 是电流、电压的最大值2、正弦交流电的平均值与最大值和有效值的关系:m m P I I I 637.02==π,m m P U U U 637.02==π,I I P 90.0=,U U P 90.0=注:I p 、U p 是电流、电压的平均值三、“四值”解题方法小结:交变电流有四值,即有效值、平均值、最大值和瞬时值.各值何时应用,对照如下情况确定:(1)在研究电容器是否被击穿时,要用峰值(最大值).因电容器上标明的电压是它在直流电源下工作时所承受的最大值.(2)在研究交变电流的功率和产生的热量时,只能用有效值.(3)在求解某一时刻线圈受到的磁力矩时,只能用瞬时值.(4)在求交变电流流过导体的过程中通过导体截面积的电量时,要用平均值.。


交流电得瞬时值、最大值、有效值与平均值交变电流得大小与方向都随时间作周期性变化,所以要准确描述交变电流得产生得效果,需要用到“最大值、有效值、瞬时值、平均值”四个物理量。
交流电得“最大值、有效值、瞬时值、平均值”常称为交流电得“四值”。
这四个类似但又有区别得物理量,容易造成混乱,理解好“四值”对于学习交流电有极大得帮助。
一、准确把握概念1、瞬时值:交流电流、电压、电动势在某一时刻所对应得值称为它们得瞬时值。
瞬时值随时间得变化而变化。
不同时刻,瞬时值得大小与方向均不同。
交流电得瞬时值取决于它得周期、幅值与初相位。
以正弦交流电为例(从中性面开始计时)。
则有:其瞬时值为:e=E m sinωti=Im sinωt u=Umsinωt2.最大值:交变电流得最大值就是指交变电流在一个周期内所能达到得最大值,它可以用来表示交变电流得强弱或电压得高低。
以正弦交流电为例。
则有:Em=nBωS,此时电路中得电流强度及用电器两端得电压都具有最大值,即Im=,U m=I m R。
3.有效值:交变电流得有效值就是根据电流得热效应来定义得,让交变电流与恒定电流通过相同阻值得电阻,如果在相同得时间内产生得热量相等,我们就把这一恒定电流得数值叫做这一交变电流得有效值。
交流电得有效值就是根据它得热效应确定得。
交流电流i 通过电阻R在一个周期内所产生得热量与直流电流I通过同一电阻R在相同时间内所产生得热量相等,则这个直流电流I得数值叫做交流电流i得有效值, 用大写字母表示, 如I、U等。
一个周期内直流电通过电阻R所产生得热量为:交流电通过同样得电阻R,在一个周期内所产生热量:根据定义,这两个电流所产生得热量应相等,即将代入上式i=I m sinωt4.平均值:交变电流得平均值就是指在某一段时间内产生得交变电流对时间得平均值。
对于某一段时间或某一过程,其平均感应电动势:==二、正弦交流电得“四值”之间得关系1、正弦交流电得有效值与最大值得关系:U=,I= 注:I U就是电流、电压得有效值,I m、Um就是电流、电压得最大值2、正弦交流电得平均值与最大值与有效值得关系:,,,注:Ip、Up就是电流、电压得平均值三、“四值”解题方法小结:交变电流有四值,即有效值、平均值、最大值与瞬时值.各值何时应用,对照如下情况确定:(1)在研究电容器就是否被击穿时,要用峰值(最大值).因电容器上标明得电压就是它在直流电源下工作时所承受得最大值.(2)在研究交变电流得功率与产生得热量时,只能用有效值.(3)在求解某一时刻线圈受到得磁力矩时,只能用瞬时值.(4)在求交变电流流过导体得过程中通过导体截面积得电量时,要用平均值.。
1解:直流电在交流电变化的一个周期内,在电阻R 上做的功为:2I RT W 直= …… ①设正弦交流电流为:sin t w m i=I ,由于电流在一个周期内数值随时间变化,为了求出一个周期内交流电流在电阻R 上做的功,我们将一个周期时间T 分成n 等分,每一等分的时间为t D ,即T n t =D 。
时间从0变化到T 时,电流从1~n i i ,则交流电在一个周期内在电阻R 上做的功,就为各小段时间电流所做功的总和。
即:()()222212322221232222123n n n W i R t i R t i R t i R tR i i i i ti i i i R n t n D +D +D ++D =++++D 骣++++÷ç=D ÷ç÷ç桫L L L 交=上式中()2222123n i i i i ++++L 是sin m i I t w =的各即时 平方和,而:()2222123n i i i i n 骣++++÷ç÷ç÷ç桫L 为各即时电流平方的平均值,与222sin m i I t w =在一个周期内的平均值是相等的。
即:()()22221232n i i i i i n 骣++++÷ç=÷ç÷ç桫L 平均值 又:()()()2222m 1cos 2I sin I 22m t i t w w -平均值平均值平均值==式中cos 2t w 在一个周期内的平均值为零,因此上式值为:()2212m i I 平均值= 所以交流电在一个周期内在电阻R 上所作的电功为:21I 2m W RT 交流=所以:m I =。
交流电的瞬时值、最大值、有效值和平均值之蔡仲巾千创作交变电流的大小和方向都随时间作周期性变更,所以要准确描述交变电流的发生的效果,需要用到“最大值、有效值、瞬时值、平均值”四个物理量。
交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。
这四个类似但又有区此外物理量,容易造成混乱,理解好“四值”对于学习交流电有极大的帮忙。
一、 准确掌控概念1. 瞬时值:交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。
瞬时值随时间的变更而变更。
分歧时刻,瞬时值的大小和方向均分歧。
交流电的瞬时值取决于它的周期、幅值和初相位。
以正弦交流电为例(从中性面开始计时)。
则有:其瞬时值为:e=E m sinωti=I m sinωt u=U m sinωt2.最大值:交变电流的最大值是指交变电流在一个周期内所能达到的最大值,它可以用来暗示交变电流的强弱或电压的高低。
以正弦交流电为例。
则有:E m =nBωS,此时电路中的电流强度及用电器两端的电压都具有最大值,即I m =rR E m , U m =I m R 。
3.有效值:交变电流的有效值是根据电流的热效应来定义的,让交变电流和恒定电流通过相同阻值的电阻,如果在相同的时间内发生的热量相等,我们就把这一恒定电流的数值叫做这一交变电流的有效值。
交流电的有效值是根据它的热效应确定的。
交流电流i 通过电阻R 在一个周期内所发生的热量和直流电流I 通过同一电阻R 在相同时间内所发生的热量相等, 则这个直流电流I 的数值叫做交流电流i 的有效值, 用大写字母暗示, 如I 、 U 等。
一个周期内直流电通过电阻R 所发生的热量为:交流电通过同样的电阻R ,在一个周期内所发生热量: 根据定义,这两个电流所发生的热量应相等,即将代入上式i=I m sinωt4.平均值:交变电流的平均值是指在某一段时间内发生的交变电流对时间的平均值。
对于某一段时间或某一过程,其平均感应电动势:I t N E 平均电流→∆∆•=φ=U rR E 平均电压→+=I R • 二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系: U=m m U U 707.02=,I=m mI I 707.02= 注:I U 是电流、电压的有效值,I m 、U m 是电流、电压的最大值2、正弦交流电的平均值与最大值和有效值的关系:m m P I I I 637.02==π,m m P U U U 637.02==π,I I P 90.0=,U U P 90.0=注:I p 、U p 是电流、电压的平均值三、“四值”解题方法小结:交变电流有四值,即有效值、平均值、最大值和瞬时值.各值何时应用,对照如下情况确定:(1)在研究电容器是否被击穿时,要用峰值(最大值).因电容器上标明的电压是它在直流电源下工作时所承受的最大值.(2)在研究交变电流的功率和发生的热量时,只能用有效值.(3)在求解某一时刻线圈受到的磁力矩时,只能用瞬时值.(4)在求交变电流流过导体的过程中通过导体截面积的电量时,要用平均值.。
一文弄清电压和电流的有效值、瞬时值、平均值、最大值及其关系电压电压(voltage),也称作电势差或电位差,是衡量单位电荷在静电场中由于电势不同所产生的能量差的物理量。
其大小等于单位正电荷因受电场力作用从A点移动到B点所做的功,电压的方向规定为从高电位指向低电位的方向。
电压的国际单位制为伏特(V,简称伏),常用的单位还有毫伏(mV)、微伏(μV)、千伏(kV)等。
“电压”一词一般只用于电路当中,“电势差”和“电位差”则普遍应用于一切电现象当中,也就是说专词专用,以免混淆。
直流电压与交流电压如果电压的大小及方向都不随时间变化,则称之为稳恒电压或恒定电压,简称为直流电压,用大写字母U表示。
如果电压的大小及方向随时间变化,则称为变动电压。
对电路分析来说,一种最为重要的变动电压是正弦交流电压(简称交流电压),其大小及方向均随时间按正弦规律作周期性变化。
交流电压的瞬时值要用小写字母u或u(t)表示。
在电路中提供电压的装置是电源(电压源)。
因为有这两种电压的存在,所以才有了几种不同的名称,同时不同的名称也代表不同的含义。
所以我们分为两个方面讨论:直流电压:根据定义直流电压的的大小及方向都不随时间变化,因此就没有瞬时值的概念,在作用时间内电压值处处相等。
或者也可以说存在瞬时值,只是处处都相等,就没有必要在去讨论这个瞬时值的概念了。
同时也没有最大值以及平均值,有效值都没有讨论的意义,所以我们只讨论交流电。
交流电的瞬时值、最大值、有效值和平均值交变电流的大小和方向都随时间作周期性变化,所以要准确描述交变电流的产生的效果,需要用到“最大值、有效值、瞬时值、平均值”四个物理量。
交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。
这四个类似但又有区别的物理量,容易造成混乱,理解好“四值”对于学习交流电有极大的帮助。
1.瞬时值:交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。
瞬时值随时间的变化而变化。
正弦电流最大值和有效值的关系推导首先啊,正弦电流,顾名思义,就是像正弦波一样,周期性地变化的电流。
你想象一下,电流一会儿强,一会儿弱,就像你跟朋友聊个天,有时声音很大,有时又突然小得听不见。
这种电流在生活中随处可见,比方说咱们的家庭电器,空调、电风扇、冰箱这些家伙,都是在用正弦电流工作。
你用电器时,它们接收到的电流就像一个过山车一样,一会儿高,一会儿低。
那么问题来了,这个电流高低不等,最大的电流值和“有效值”之间有什么关系呢?别急,慢慢来。
我们知道,电流有时候很强,像是开足了马力的赛车;有时候又很弱,像是偶尔打个哈欠的懒猫。
而有效值,就是咱们常说的“平时用来量电流强度”的那个数值。
你可以把它理解为一种“平均水平”,它不像最大值那样会因为瞬间的波动而给你吓一跳,但却能真实反映你所用电流的平均“威力”。
再来说说“最大值”这个概念,它就是正弦波电流达到的最高点。
这个最大值,你可以把它当作是那辆赛车的最快速度,飞快,瞬间就能达到那个顶点。
不过,你也知道,赛车虽然一度可以飞快,但它并不会一直保持那种速度,它总有个相对平稳的速度,对吧?有效值就是电流“表现出来”的稳定水平,就像这辆赛车的平均速度,虽然不如最高速度那么快,但却能一直维持下去。
所以最大值和有效值的关系就像是“冲刺”和“平稳”的关系。
有趣的是,咱们可以通过一个公式来表达这个关系。
根据数学上的推导,正弦电流的有效值是它最大值的一个固定比例。
具体来说,就是最大值除以√2,得出的结果就是有效值。
说得简单点,假设最大电流是10安培,那有效值大约就是10除以√2,得出的是7.07安培。
看,这个数值虽然小了点,但却更能真实反映电流的“日常表现”。
用个通俗点的比喻,这就像你开车时,车速表上指示的平稳速度,不是瞬间的极速,而是长时间行驶下来的平均速度。
你可能会想,哎,那我到底是该关注最大值呢,还是有效值呢?好问题!其实两者各有各的用途。
如果你想知道电器的最大负荷能力,最大值就很重要。
正弦交流电有效值与最大值的关系正弦交流电的有效值和最大值的关系,听起来似乎有点儿高大上,其实说白了就是电流的“脸面”和“实力”问题。
你知道吗?在交流电中,我们常常会提到有效值,简直就像是电流的“名片”,它告诉我们这股电流能干多少实事儿。
最大值呢,就像是电流的“猛料”,代表着它的最高峰。
想象一下,假如电流是一位选手,有效值就是他平时的成绩,而最大值就是他参加比赛时的最好成绩。
听上去有点儿像明星的巅峰时刻对吧?有效值的计算就像是给电流量身定做的,实际上,它是通过把波形的平方取平均,再开方算出来的。
这就意味着有效值不会因为电流在波动而轻易变化,真是个稳重的角色。
交流电的波形大部分都是正弦波,这种波形就像是海浪,起伏不定,但总归有那么一股韵味儿。
要是你仔细观察,就会发现,正弦波的波峰和波谷,像极了我们生活中的酸甜苦辣。
要是说这波形是一幅画,那么有效值就是画的主题,最大值则是画中的光彩夺目的细节。
有个有趣的点是,有效值其实和最大值之间有个固定的关系。
对于正弦波来说,最大值和有效值的比例就像是老朋友,亲密无间,公式很简单:有效值等于最大值除以根号2。
听起来有点儿复杂?别担心,记住这个比例就好。
比如说,假如你的最大值是10伏特,那么有效值大概就是7.07伏特。
是不是很神奇?这个关系就像是生活中的道理,越是高峰,越要有稳定的基础。
谈到这里,不得不提的是,在实际应用中,有效值更能体现电流的实际功率,就像是你工作的时候拿到的薪水,才是最实际的回报。
你要知道,电流不只是停留在数学公式上,更是为我们的生活带来光明与温暖。
想想看,家里的电器离不开电流,它们需要的就是这个“有效值”,这才是它们运转的动力源泉。
而最大值则更多是一个理论上的概念,虽然重要,但在实际中并不常用。
很多时候,我们只需要关注有效值,因为它能直接反映出电流为我们提供的真实能量。
在交流电路中,设备的选择和使用,往往以有效值为准,最大值可能在某个时刻出现,但我们可不想让设备一直处于“顶峰”状态,毕竟,这样不仅耗能还容易损坏。
正弦交变电流有效值和最大值关系的简单推证
我们知道,交变电流的有效值是根据电流的热效应加以规定的.让交变电流和直流电分别通过相同的电阻R,如果它们在相同时间(比方一个周期)内产生的热量相等,就将这一直流电的数值称为这一交变电流的有效值.
正弦交变电流i(t)、正弦交变电压u(t)的有效值I、U与最大值I m、U m之间存在以下关系
设有一个电阻R,通以交变电流i,在很短的一段时间△tj内,流过电阻R的交变电流值ij可以认为是恒定的,因而很短时间△tj内在电阻R
如果一个周期T由N段极短时间间隔△t1、△t2、……△t j、……△t N(N是一个大数)组成,那么在一个周期内.交变电流在电阻R上产生的总热量Q为
而直流电流在同一时间内在电阻R上产生的热量
Q=I2RT
根据有效值的定义,当以上两种热量相等时,这个直流电流I的数值就等于交变电流i 的有效值,于是
上式右边常量R提到总和符号之外,就得到交变电流有效值为
(2)式右边是交变电流的平方,在一个周期内取平均后再取平方根.即交变电流的有效值实际等于它的方均根值,即
对于正弦交变电流,有
i=I m sinωt,i j=I m sinωtj
式中ω=2πf是角频率(f是频率).因而
现在就将求有效值归结为求sin2ωt的平均值,然后开方,即求sinωt的方均根值.
利用三角函数关系
将它们分别在一周期内取平均.由于在一个周期内交流电的波形是对称的,sinωt、sin2ωt、…cosωt、cos2ωt…在一周期内的平均值为零,于是
由(5)、(6)
由(4)、(8)二式,最后得交变电流i的有效值
同理有交变电压u的有效值所以(1)式得证.。