交变电流的有效值和平均值

交流电的瞬时值、最大值、有效值和平均值交变电流的大小和方向都随时间作周期性变化，所以要准确描述交变电流的产生的效果，需要用到“最大值、有效值、瞬时值、平均值”四个物理量。

交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。

这四个类似但又有区别的物理量，容易造成混乱，理解好“四值”对于学习交流电有极大的帮助。

一、 准确把握概念1. 瞬时值：交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。

瞬时值随时间的变化而变化。

不同时刻，瞬时值的大小和方向均不同。

交流电的瞬时值取决于它的周期、幅值和初相位。

以正弦交流电为例（从中性面开始计时）。

则有：其瞬时值为：e=E m sinωti=I m sinωt u=U m sinωt2．最大值：交变电流的最大值是指交变电流在一个周期内所能达到的最大值，它可以用来表示交变电流的强弱或电压的高低。

以正弦交流电为例。

则有：E m =nB ωS ，此时电路中的电流强度及用电器两端的电压都具有最大值，即I m =r R E m ， U m =I m R 。

3．有效值：交变电流的有效值是根据电流的热效应来定义的，让交变电流和恒定电流通过相同阻值的电阻，如果在相同的时间内产生的热量相等，我们就把这一恒定电流的数值叫做这一交变电流的有效值。

交流电的有效值是根据它的热效应确定的。

交流电流i 通过电阻R在一个周期内所产生的热量和直流电流I通过同一电阻R在相同时间内所产生的热量相等, 则这个直流电流I的数值叫做交流电流i的有效值, 用大写字母表示, 如I、U 等。

一个周期内直流电通过电阻R所产生的热量为：交流电通过同样的电阻R，在一个周期内所产生热量：根据定义，这两个电流所产生的热量应相等，即将代入上式i=I m sinωt4．平均值：交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。

对于某一段时间或某一过程，其平均感应电动势：I t N E 平均电流→∆∆∙=φ=U r R E 平均电压→+=I R ∙二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系： U=m mU U 707.02=，I=m m I I 707.02= 注：I U 是电流、电压的有效值，I m 、U m 是电流、电压的最大值2、正弦交流电的平均值与最大值和有效值的关系：m m P I I I 637.02==π，m m P U U U 637.02==π，I I P 90.0=，U U P 90.0=注：I p 、U p 是电流、电压的平均值三、“四值”解题方法小结：交变电流有四值，即有效值、平均值、最大值和瞬时值．各值何时应用，对照如下情况确定：（1）在研究电容器是否被击穿时，要用峰值（最大值）．因电容器上标明的电压是它在直流电源下工作时所承受的最大值．（2）在研究交变电流的功率和产生的热量时，只能用有效值．（3）在求解某一时刻线圈受到的磁力矩时，只能用瞬时值．（4）在求交变电流流过导体的过程中通过导体截面积的电量时，要用平均值．。

交流电的瞬时值、最大值、有效值和平均值交变电流的大小和方向都随时间作周期性变化，所以要准确描述交变电流的产生的效果，需要用到“最大值、有效值、瞬时值、平均值”四个物理量。

交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。

这四个类似但又有区别的物理量，容易造成混乱，理解好“四值”对于学习交流电有极大的帮助。

一、准确把握概念1. 瞬时值：交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。

瞬时值随时间的变化而变化。

不同时刻，瞬时值的大小和方向均不同。

交流电的瞬时值取决于它的周期、幅值和初相位。

以正弦交流电为例（从中性面开始计时）。

则有：其瞬时值为：e=Emsinωti=Imsinωt u=Umsinωt2．最大值：交变电流的最大值是指交变电流在一个周期内所能达到的最大值，它可以用来表示交变电流的强弱或电压的高低。

以正弦交流电为例。

则有：Em=nBωS，此时电路中的电流强度及用电器两端的电压都具有最大值，即Im=， Um=ImR。

3．有效值：交变电流的有效值是根据电流的热效应来定义的，让交变电流和恒定电流通过相同阻值的电阻，如果在相同的时间内产生的热量相等，我们就把这一恒定电流的数值叫做这一交变电流的有效值。

交流电的有效值是根据它的热效应确定的。

交流电流i通过电阻R在一个周期内所产生的热量和直流电流I通过同一电阻R在相同时间内所产生的热量相等, 则这个直流电流I的数值叫做交流电流i的有效值, 用大写字母表示, 如I、 U等。

一个周期内直流电通过电阻R所产生的热量为：交流电通过同样的电阻R，在一个周期内所产生热量：根据定义，这两个电流所产生的热量应相等，即将代入上式i=Imsinωt4．平均值：交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。

对于某一段时间或某一过程，其平均感应电动势：==二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系： U=，I=注：I U 是、的，Im、Um是电流、电压的最大值2、正弦交流电的与最大值和有效值的关系：，，，注：Ip、Up是电流、电压的平均值三、“四值”解题方法小结：交变电流有四值，即有效值、平均值、最大值和瞬时值．各值何时应用，对照如下情况确定：（1）在研究电容器是否被击穿时，要用峰值（最大值）．因电容器上标明的电压是它在直流电源下工作时所承受的最大值．（2）在研究交变电流的功率和产生的热量时，只能用有效值．（3）在求解某一时刻线圈受到的磁力矩时，只能用瞬时值．（4）在求交变电流流过导体的过程中通过导体截面积的电量时，要用平均值．。

交变电流有效值推导交变电流有效值是衡量交流电流强度大小的一个重要指标。

在电力领域，电流通常是交流电，因此了解交变电流的有效值不仅对工程师和技术人员有意义，对一般公众也有一定的实用价值。

1. 交变电流定义在介绍交变电流有效值之前，需要先了解交变电流的定义。

交变电流是指周期性变化的电流信号，其方向和大小在一个周期内不断地变化。

在实际应用中，交变电流会在电路中引发一系列的电磁现象，如电感、电容、电阻等。

2. 交变电流的平均值和有效值交变电流的平均值可以通过求出一个周期内电流信号的面积来计算。

然而，由于交变电流的正负值在一个周期内相互抵消，因此其平均值为零。

因此，在衡量交变电流强度大小时，我们需要使用另一个指标——有效值。

有效值是指与交变电流平均值相等的直流电流，其产生的效应与交变电流相等。

如何推导交变电流的有效值呢？我们可以从物理角度出发，通过对交变电流信号的时间和方向进行分析得到有效值的公式。

首先，我们需要知道一个重要的物理定理——欧姆定律。

欧姆定律指出，电流和电压的关系可以通过一个常数R（电阻）来描述，即I=V/R。

在交变电路中，我们可以对每个时间点上的电流进行求和，以得到整个周期内的总电流强度，如下所示：I = (i1+i2+...+in) / n其中i1、i2、...、in分别表示一个周期内每个时间点上的电流强度，n代表周期内测量电流的次数。

接下来，我们将每个时间点上的电流强度i表示成其有效值Irms和相位角θ的函数形式。

i = Irms * sin(ωt+θ)其中，ω为角频率，t为时间。

在一周期内，ωt的取值范围为0~2π。

将上式带入前面的式子，得到：通过三角函数的知识，我们知道，sinθ的平方值的平均值为1/2，即：因此，上式可以进一步化简为：这就是交变电流的有效值公式，也是交变电流强度大小的标准指标。

需要注意的是，上述推导过程默认电路中只有电阻元件，若电路中还存在电感或电容等元件，则需要考虑其对交变电流的影响，具体推导过程可以参考电路理论相关书籍。

交变电流四值交变电流四值的意义交变电流的“四值”即最大值、瞬时值、有效值、平均值，近几年来的高考在考查“交变电流”一章的有关内容时，主要是考查了交变电流的“四值”。

很多学生在学习和复习中对这四个类似但又需要严格区别的物理量分辨不清。

理解好这四个值对于解交变电流相关的习题帮助很大。

交变电流四值的学习一、瞬时值反映不同时刻交变电流的大小和方向，正弦交变电流瞬时值表达式为：t E e m ωsin =，t I i m ωsin =。

应当注意必须从中性面开始转动。

计算电路中与某一时刻有关的问题时要用交变电流的瞬时值。

生活中用的市电电压为所以其电压瞬时值的表达式为例题1. 10Ω，线圈绕'OO 轴在图示位置转过30解析：由题意，先求出角速度感应电动势的最大值为： ωNBS E m =＝sin m e E t ω=。

所以转过30m E ＝78.5×12V=39.3V 【总结】求解感应电动势的瞬时值应有一个正确的解题思路，其解题步骤为： ⑴确定线圈转动是从哪个位置开始计时。

⑵确定表达式是正弦还是余弦。

⑶确定转动的角速度ω及N 、B 、S 等。

⑷求出峰值m E ，写出表达式，代入角速度求瞬时值。

二、最大值交变电流的最大值也叫峰值，它是瞬时值的最大值，它反映的是交变电流大小的变化范围，当线圈平面跟磁感线平行时，交流电动势最大，m E NBS ω=（转轴垂直于磁感线）。

电容器接在交流电路中，则交变电压的最大值不能超过电容器的耐压值。

例2：一电容器两端允许的直流电压最大值是260V ，能否将它接在按正弦规律变化的交流电压为220V 的电路中？解析：题中所述的220V 交流电压是指有效值，其最大值为U m =2202V≈311V＞260V ，故不能接于220V 的交流电路中，否则电容器将会被击穿。

【总结】不少同学往往把电容器与灯泡类比，额定电压220 V 的灯泡接在220 V 的交流电源上正常发光，从而错误的认为电容器的耐压值也是指有效值，事实上，电容器接在交流电路中一直不断地进行充、放电过程。

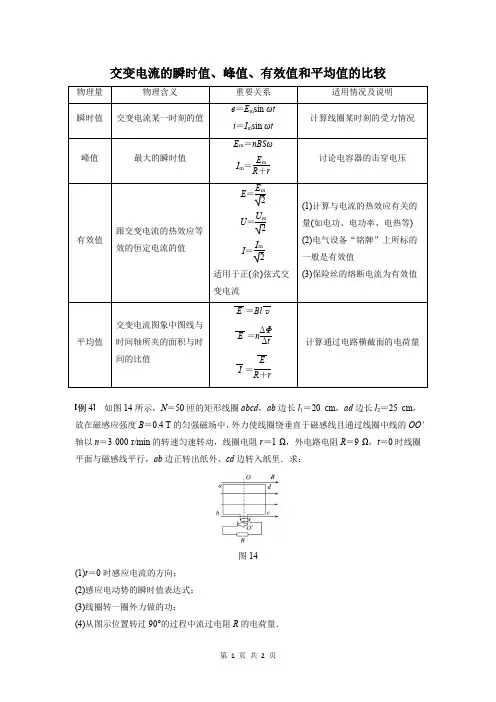
交变电流的瞬时值、峰值、有效值和平均值的比较例4如图14所示，N＝50匝的矩形线圈abcd，ab边长l1＝20 cm，ad边长l2＝25 cm，放在磁感应强度B＝0.4 T的匀强磁场中，外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n＝3 000 r/min的转速匀速转动，线圈电阻r＝1 Ω，外电路电阻R＝9 Ω，t＝0时线圈平面与磁感线平行，ab边正转出纸外、cd边转入纸里．求：图14(1)t＝0时感应电流的方向；(2)感应电动势的瞬时值表达式；(3)线圈转一圈外力做的功；(4)从图示位置转过90°的过程中流过电阻R的电荷量．t ＝0时线圈平面与磁感线平行，ab 边正转出纸外，cd 边转入纸里．答案 (1)感应电流方向沿adcba(2)e ＝314cos (100πt ) V (3)98.6 J (4)0.1 C解析 (1)根据右手定则，线圈感应电流方向为adcba . (2)线圈的角速度 ω＝2πn ＝100π rad/s图示位置的感应电动势最大，其大小为 E m ＝NBl 1l 2ω代入数据得E m ＝314 V 感应电动势的瞬时值表达式 e ＝E m cos ωt ＝314cos (100πt ) V . (3)电动势的有效值 E ＝E m2线圈匀速转动的周期 T ＝2πω＝0.02 s线圈匀速转动一圈，外力做功大小等于电功的大小，即 W ＝I 2(R ＋r )T ＝E 2R ＋r·T 代入数据得W ≈98.6 J.(4)从t ＝0起线圈转过90°的过程中，Δt 内流过R 的电荷量： q ＝N ΔΦ(R ＋r )Δt Δt ＝NB ΔS R ＋r ＝NBl 1l 2R ＋r 代入数据得q ＝0.1 C.。

交变电流有效值和平均值的计算关系嘿，朋友！咱今天来聊聊交变电流有效值和平均值的计算关系，这
可有意思啦！
你想想，电流就像个调皮的孩子，一会儿跑得快，一会儿跑得慢，
这就是交变电流。

那怎么去衡量它的大小呢？这就引出了有效值和平
均值。

有效值啊，就好比是这个调皮孩子在一段时间内表现的“综合实力”。

它能反映出电流产生的热效应。

比如说，一个交流电通过电阻产生的
热量，和一个直流电通过同样的电阻产生相同的热量，那这个直流电
的数值就是交流电的有效值。

这是不是很神奇？
再来说说平均值，它就像是一段时间内这个调皮孩子的“平均表现”。

它是电流在这段时间内的平均大小。

那怎么计算它们呢？这可得好好琢磨琢磨。

对于正弦式交变电流，有效值等于最大值除以根号 2 。

这就好像是
把一个山峰的高度削掉一部分，得到一个比较“平和”的数值。

你说，
这像不像我们把过于突出的部分给“平均”了一下？
而平均值呢，是用磁通量的变化量除以时间。

这就好比是把一段时
间内的“成果”平均分配到每一刻。

如果不好好理解这两者的计算关系，那在解决问题的时候可就抓瞎啦！比如说，计算电器的功率，就得用有效值；计算通过导体的电荷量，就得用平均值。

这要是搞混了，那不就乱套了？
所以啊，一定要把这两个概念和计算方法牢牢记住，就像记住自己
的名字一样清楚！这样在面对各种电学问题时，才能游刃有余，轻松
应对。

总之，交变电流有效值和平均值的计算关系可重要了，搞清楚它们，电学的世界就能被我们更好地掌控！。

交变电流的有效值和平均值在高中物理教学中,许多同学很难理解交流电的有效值这一概念。

针对这种情况谈一下笔者在教学中的一点体会。

有效值说明交流电产生的平均效果,为了引入有效值的概念可以提出:交流电随时间变化,产生的效果也随时间变化。

但实际上只要知道交流电的平均效果就可以了。

怎样衡量交流电的平均效果呢?可以做一实验。

如图1用两个相同的小电珠A、B。

一个接在直流电源上,一个接在交流电源上,让两个小电珠发光情况相同。

B灯通过的是交流电流,大小、方向随时间变化,但在相同时间内交流电流与直流电流产生的热量相同,所以B灯发光与A灯相同。

既然通过A灯的直流电流I与通过B灯的交流电流i产生的效果相同,可以把直流电流的大小I作为衡量交流电流i产生的平均效果。

在此基础上给出有效值比较准确的定义。

对于正弦交流电来说,有效值与最大值的关系可用数学方法推导出来。

设通过电阻R的交流为i =Imsinωt,则在dt时间内产生的热量是dQ=i2Rdt。

在一周期T内所产生的热量是：即正弦交流电的有效值等于最大值被2除。

对图2所示的方波而说,由定义显然可得有效值与最大值相等。

对图3所示的三角波和图4所示的锯齿波。

由定义可得有效值等于最大值被3除I≈0.577Im。

一般不同时间内的交流电有效值是不同的。

当时间段远大于其周期时,则可以认为这一时间内有效值等于一个周期内的有效值。

既然交流电的有效值是根据热效应规定的,则在计算电功、电功率、热量及确定保险丝的熔断电流时应运用有效值。

交流电流的平均值是交流图象中波形对横轴(t轴)所围"面积"对时间的比值。

由于其值大小表示单位时间内通过的电量平均值,因此,计算通过导体的电量时应用交流电的的平均值。

因平均值大小与所取时间间隔有关,对正弦交流电正半周或负半周的平均值由定义可得：。

几种常见的交变电流的有效值和平均值的计算湖北省襄樊市第一中学（441000）赵兴华高中物理第二册（实验修订本）《交变电流》一章中列举了几种常见交变电流，即：正弦交变电流、锯齿波电流、矩形脉冲电流和尖脉冲电流。

交变电流的有效值和平均值是两个不同的概念，不少学生在解题中不能很好地区分，造成解题失误。

交变电流的有效值是根据电流的热效应来规定的，让交流电和直流电通过相同阻值的电阻，如果它们在相同的时间里产生的热量相等，就把这一直流电的数值叫这一交流电的有效值；交变电流的平均值是指交变电流在一个周期内交流电的绝对值的平均值。

教材中只给出了正弦交变电流的有效值，没有给出其他几种交变电流的有效值，也没有给出平均值的大小。

笔者在这里给出它们供大家参考。

一、交变电流的有效值1、正弦交变电流的有效值方法一：设有一直流电和一正弦交流电，分别通过同样的电阻R ，经过时间T （T 为该交流电的周期）内产生的热量分别为：Q 直＝I 2RT ，Q 交＝P T ，则有： I ＝RP正弦交流电的瞬时功率： P ＝i 2R ＝t R I m ω22sin ＝)2cos 1(212t R I m ω-•＝t R I R I m m ω2cos 212122- 上式中第一项是不随时间变化的常量，第二项是按余弦变化的量，在一个周期内，第二项的平均值是零，故有：R I P m 221=可得： I ＝m m I IR P 707.02==方法二：用积分的方法对于I ＝I m sin t ω，通过阻值为R 的电阻在dt 时间里产生的热量dQ ，则有：dQ ＝i 2Rdt ＝（I m sin t ω）2Rdt在1个周期内，t=T ，R 产生的热量： Q ＝⎰Tm Rdt t I 02)sin (ω＝⎰-T m dt t R I 02)2sin 2121(ω＝RT I m 221而等效电流I 在相等的时间产生的热量也为Q ，则有：Q ＝I 2RT 所以正弦交变电流的有效值与最大值之间的关系为：I ＝m mI I 707.02=2、锯齿波电流的有效值：设有一锯齿波电流的最大值为I m ，周期是T ，且I m ＝2T k， 在半个周期内瞬时电流：i ＝kt在dt 时间里通过电阻R 上产生热量为： dQ ＝（kt ）2Rdt在t ＝T 时间通过电阻R 上产生热量为：Q ＝32022121RT k Rdt t k T=⎰故有：I 2＝3)2(12112122222mm I T T I T k == 即锯齿波电流的有效值与最大值之间的关系为：I ＝3mI3、矩形脉冲电流的有效值：（1）若有一矩形脉冲电流，正反向的电流值相等为I m ，且正反向通电时间相等，周期为T ，（如图所示）。

几种常见的交变电流的有效值和平均值的计算湖北省襄樊市第一中学（441000）赵兴华高中物理第二册（实验修订本）《交变电流》一章中列举了几种常见交变电流，即：正弦交变电流、锯齿波电流、矩形脉冲电流和尖脉冲电流。

交变电流的有效值和平均值是两个不同的概念，不少学生在解题中不能很好地区分，造成解题失误。

交变电流的有效值是根据电流的热效应来规定的，让交流电和直流电通过相同阻值的电阻，如果它们在相同的时间里产生的热量相等，就把这一直流电的数值叫这一交流电的有效值；交变电流的平均值是指交变电流在一个周期内交流电的绝对值的平均值。

教材中只给出了正弦交变电流的有效值，没有给出其他几种交变电流的有效值，也没有给出平均值的大小。

笔者在这里给出它们供大家参考。

一、交变电流的有效值1、正弦交变电流的有效值方法一：设有一直流电和一正弦交流电，分别通过同样的电阻R ，经过时间T （T 为该交流电的周期）内产生的热量分别为：Q 直＝I 2RT ，Q 交＝T ，P 则有：I ＝RP正弦交流电的瞬时功率： P ＝i 2R ＝＝t R I m ω22sin)2cos 1(212t R I mω-∙ ＝t R I R I m m ω2cos 212122-上式中第一项是不随时间变化的常量，第二项是按余弦变化的量，在一个周期内，第二项的平均值是零，故有：R I P m 221=可得： I ＝m mI IR P 707.02==方法二：用积分的方法对于I ＝I m sin ，通过阻值为R 的电阻在dt 时间里产生的热量t ωdQ ，则有：dQ ＝i 2Rdt ＝（I m sin ）2Rdtt ω在1个周期内，t=T ，R 产生的热量：Q ＝＝＝⎰Tm Rdt t I 02)sin (ω⎰-Tmdt t R I 02)2sin 2121(ωRT I m221而等效电流I 在相等的时间产生的热量也为Q ，则有：Q ＝I 2RT所以正弦交变电流的有效值与最大值之间的关系为：I ＝mmI I 707.02=2、锯齿波电流的有效值：设有一锯齿波电流的最大值为I m ，周期是T ，且I m ＝，2T k在半个周期内瞬时电流：i ＝kt在dt 时间里通过电阻R 上产生热量为：dQ ＝（kt ）2Rdt在t ＝T 时间通过电阻R 上产生热量为：Q ＝32022121RT k Rdt t k T=⎰故有：I 2＝3)2(12112122222mm I T T I T k ==即锯齿波电流的有效值与最大值之间的关系为：I ＝3mI 3、矩形脉冲电流的有效值：（1）若有一矩形脉冲电流，正反向的电流值相等为I m ，且正反向通电时间相等，周期为T ，（如图所示）。